Bayesian inference of ancient human demography from individual genome sequences

Abstract

Besides their value for biomedicine, individual genome sequences are a rich source of information about human evolution. Here we describe an effort to estimate key evolutionary parameters from sequences for six individuals from diverse human populations. We use a Bayesian, coalescent-based approach to extract information about ancestral population sizes, divergence times, and migration rates from inferred genealogies at many neutrally evolving loci from across the genome. We introduce new methods for accommodating gene flow between populations and integrating over possible phasings of diploid genotypes. We also describe a custom pipeline for genotype inference to mitigate biases from heterogeneous sequencing technologies and coverage levels. Our analysis indicates that the San of Southern Africa diverged from other human populations 108–157 thousand years ago (kya), that Eurasians diverged from an ancestral African population 38–64 kya, and that the effective population size of the ancestors of all modern humans was ~9,000.

During the past several decades, investigators from various disciplines have produced a broad outline of the events that gave rise to major human population groups, drawing from genetic, anthropological, and archaeological evidence¹. The general picture that has emerged is that anatomically modern humans (AMHs) arose roughly 200 thousand years ago (kya) in Eastern or Southern Africa; that a small tribe began to expand throughout Africa ~100 kya; that a major migration out of Africa occurred ~40–60 kya; and that the descendants of these migrants subsequently populated Europe, Asia, and the remaining inhabitable regions of the world, possibly with some introgression from archaic hominids^2,3. This outline is supported by analyses of mitochondrial and Y-chromosomal data^4,5, autosomal microsatellite markers^6,7, sequences for selected autosomal loci^8–11, and genome-wide genotyping data¹². Nevertheless, much remains unknown about early human demography. Indeed, current estimates of key parameters such as the date of the migration out of Africa often vary by factors of two or three.

We attempted to investigate these issues using recently released complete genome sequences for individual humans^13–17. While individual genome-sequencing studies so far have emphasized the technical feasibility of sequencing, discovery of novel genetic variants, and identification of disease causing mutations, these data are also potentially informative about human evolution. We examined the published sequences of six individuals from six different population groups (Table 1). One of these individuals is a member of the Khoisan-speaking hunter-gatherer populations of Southern Africa, known collectively as the San¹⁷. Along with other indigenous groups from Central and Southern Africa^18,19, the San exhibit the highest known levels of genetic divergence from other human populations, and therefore should be highly informative about ancient human demography. For reasons of statistical power, our demographic analysis focused on the timing of early divergence events between major population groups—in particular, between the San and the other groups (the “San divergence”; Fig. 1), and between the Eurasians and other African groups (the “African-Eurasian divergence”).

Table 1.

Individual Genomes Analyzed in this Paper

Genomea	Population	Technol.b	Readsc	Red.d	Cov.e	Depthf	HQCg	Ref.
Venter	European	Sanger	800bp PE	7.5	0.912	8.4	0.577	13
NA18507	Yoruban	Illumina	35bp PE	40.6	0.900	41.1	0.672	14
YH	Han Chinese	Illumina	35bp PE	36	0.896	25.4	0.671	15
SJK	Korean	Illumina	36, 75bp	28.95	0.903	19.7	0.672	16
ABT	Bantu	SOLiD	49bp	>30	0.874	21.4	0.641	17
KB1	San	Illuminah	76bp	23.1	0.901	23.6	0.621	17

^aGenome identifiers are surnames of sequenced individuals (Venter), identifiers for Coriell DNA samples (NA18507), or abbreviations introduced in published papers (YH, SJK, ABT, and KB1).

^bSequencing technology: Sanger = Sanger (capillary) sequencing, Illumina = Illumina GenomeAnalyzer, SOLiD = SOLiD system by Applied Biosystems.

^cAverage read length in bp, and whether or not paired-end (PE) reads were used.

^dSequencing redundancy, or fold coverage, as reported in published paper.

^eFraction of genome covered by uniquely aligned reads, according to the pipeline used here.

^fActual depth: average number of uniquely aligned reads at positions having at least one uniquely aligned read. Excludes duplicate reads.

^gHigh quality coverage: fraction of genome covered by aligned reads that pass data quality filters.

^hKB1 was sequenced using both the 454 and Illumina methods, but this analysis used the more abundant Illumina data.

Fig 1. Population phylogeny and genealogies.

The population phylogeny assumed in this study, with one diploid genome per population (see Table 1) and a haploid chimpanzee outgroup. The Yoruban and Bantu individuals were included in the analysis as alternative African ingroups (denoted X), because their relationship to one another was uncertain (Supplementary Note). The free parameters in our model include the five population divergence times (τ) and ten effective population sizes (θ), all expressed in units of expected mutations per site. Various “migration bands” (gray arrow), allowing for gene flow between populations, were also considered, with the (constant) migration rates along these bands also treated as free parameters. The two parameters of primary interest were the San (τ_KHEXS) and African-Eurasian (τ_KHEX) divergence times. Absolute divergence times (in years) and effective population sizes (in numbers of individuals) were obtained by assuming a human-chimpanzee average genomic divergence time of 5.6–7.6 Mya, with a point estimate of 6.5 Mya.

In analyzing these data, we used a Bayesian statistical approach, based on coalescent theory, that was originally developed for individuals belonging to closely related but distinct species, such as human, chimpanzee, and gorilla^20,21. This approach (as implemented in the computer program MCMCcoal) derives information about ancestral population sizes and population divergence times from the patterns of variation in the genealogies at many neutrally evolving loci, given a population phylogeny and a set of sequence alignments. Essentially, it exploits the fact that even small numbers of present-day genomes represent many ancestral genomes, which have been shuffled and assorted by the process of recombination. Because the sequences provide only very weak information about the genealogy at each locus, the method integrates over candidate genealogies using Markov chain Monte Carlo (MCMC) methods, and pools information across loci in obtaining an approximate posterior distribution for the parameters of interest.

A major challenge in carrying out a population genetic analysis of the available individual genome sequences is that biases may result from differences in power and accuracy in single nucleotide variant detection, stemming from differences in sequencing technologies, depth of coverage, and bioinformatic methods (Table 1). To address this problem, we developed our own pipeline for genotype inference, which re-aligns all raw sequence reads in a uniform manner, empirically recalibrates basecall quality scores, calls genotypes using our own reference-genome-free Bayesian genotype inference algorithm (BSNP), and applies a series of rigorous data-quality filters (Supplementary Fig. 1). We validated this pipeline using alternative array- and sequence-based calls for two genomes, and found that our calls were similar to these others in overall accuracy, while avoiding biases from the use of the reference genome in genotype inference. We also found that our pipeline eliminated inconsistencies in heterozygosity and SNP density exhibited by the published genotype calls for these genomes (Supplementary Note).

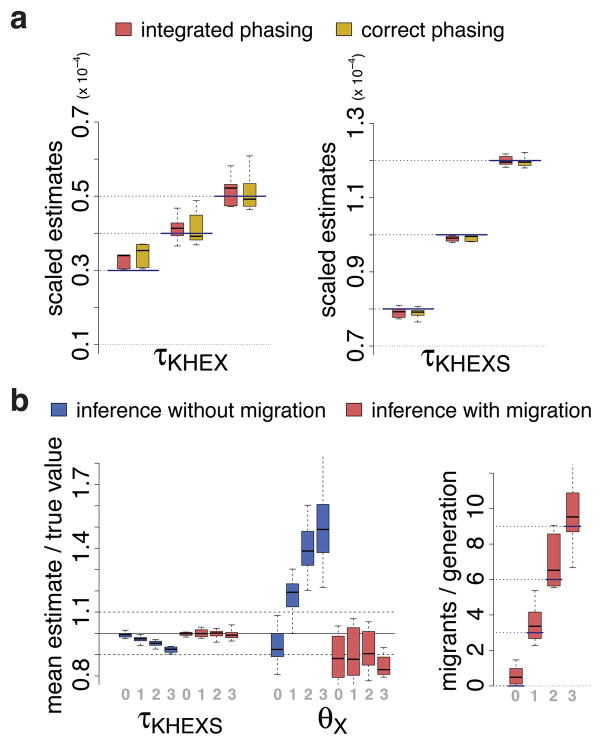
A second problem is that MCMCcoal relies on two assumptions that do not apply here: (1) an absence of gene flow between populations, and (2) the existence of haploid samples from each individual. Using the MCMCcoal source code as a starting point, we developed our own program, called G-PhoCS (Generalized Phylogenetic Coalescent Sampler; “G-fox”), that relaxes these assumptions. To allow for gene flow, we introduced “migration bands” that allow for continuous migration at constant rates between designated populations. Following previous isolation-with-migration (IM) methods^22,23, we altered the sampling procedure so that it would explore genealogies that crossed population boundaries within these bands (Fig. 1). To allow the use of unphased diploid genotype data, we devised a method that integrates over all possible phasings of heterozygous genotypes when computing genealogy likelihoods. Importantly, this method makes use of both chromosomes per individual, effectively doubling the size of the data set. We carried out a series of simulations to test whether G-PhoCS is capable of recovering known parameters from a data set like ours, and found that the parameters of primary interest—the San and African-Eurasian divergence times—can be estimated without bias and with reasonably narrow credible intervals, even when genotypes are unphased and gene flow is present (Fig. 2, Supplementary Figs. 2 & 3, Supplementary Note). We observed reduced power for recent divergence times, current effective population sizes, and migration direction.

Fig. 2. Results of simulation study.

Simulations assumed a population tree like the one shown in Fig. 1 and plausible divergence times, population sizes, and migration scenarios (Supplementary Note). (a) Accuracy of estimated African-Eurasian (τ_KHEX) and San (τ_KHEXS) divergence times without migration. Dotted lines indicate the values assumed for the simulations and each boxplot summarizes posterior mean estimates in six separate runs of G-PhoCS. Results are shown for correctly phased data (gold) and integration over unknown phasings (red). A random phasing procedure produced substantially poorer results (Supplementary Fig. 2). Most estimates fall within 10% of the true value, except for the smallest assumed divergence times, where weak information in the data leads to an upward bias. (b) Accuracy of the estimated San divergence time (τ_KHEXS) and the Yoruban/Bantu population size (θ_X) in simulations with four levels of constant-rate migration (denoted 0, 1, 2, and 3, in order of increasing strength) from population S to population X. Ratios of estimated to true values are shown when migration is not (blue) and is (red) allowed in the model. Each boxplot summarizes twelve runs. Notice that there is a pronounced bias when migration is present but is not modeled, but this bias is eliminated when migration is added to the model. Simulated and estimated migration rates (measured in expected number of migrants per generation) are shown at right. See Supplementary Figs. 2 & 3 for complete results.

Next, we analyzed alignments of the six individual genomes and chimpanzee reference genome at 37,574 1-kilobase “neutral loci” excluding protein-coding and conserved noncoding regions. These loci were defined to minimize intralocus recombination but ensure frequent recombination between loci. We assumed the five-population phylogeny shown in Fig. 1, using as an “African ingroup” either the Yoruban or the Bantu. We evaluated 16 alternative scenarios with various migration bands and performed two replicate runs per scenario (Supplementary Table 1), cross-checking all results to ensure convergence. To convert estimates of divergence time (τ) and population size (θ) from mutations per site to years (T) and effective numbers of individuals (N), respectively, we assumed a human/chimpanzee average genomic divergence time of T_div = 5.6–7.6 Mya, with a point estimate of T_div = 6.5 Mya^2,24 (Methods). Consistently across runs, a calibration of T_div = 6.5 Mya implied a mutation rate of ~2.0×10⁻⁸/generation/site, in good agreement with independent estimates²⁵. Unless otherwise stated, all parameter estimates are reported as posterior means (with 95% credible intervals) in calibrated form, based on T_div = 6.5 Mya. For estimates of N, we also assume an average generation time of 25 years.

Assuming no gene flow, we estimate a San divergence time of 125 (121–128) kya with the Yoruban ingroup and 121 (117–124) kya with the Bantu ingroup (Fig. 3a). If gene flow is allowed between the San and the African ingroup, these estimates increase slightly to 131 (127–135) kya and 129 (126–133) kya, respectively. Thus, our best estimate of the San divergence time is ~130 kya, or 108–157 kya across calibration times (Table 2). Of the several migration scenarios considered, those involving the San and the Yoruban or Bantu ingroups were the only ones showing pronounced evidence of gene flow, within the limitations of our model (Fig. 3b). Notably, the strongest migration signal was detected for the Bantu and San populations, for which gene flow has been reported previously¹⁷.

Fig. 3. Parameter estimates from real data.

Estimates of (a) population divergence times, (b) migration rates, and (c) effective population sizes obtained for various scenarios. In (a) and (c), both mutation-scaled (left) and calibrated (right) y-axes are shown (with a calibration of T_div = 6.5 Mya). Results are shown for scenarios with either the Yoruban or Bantu ingroup X, and with or without a migration band between X and the San. Panel (b) shows estimated migration rates for fourteen different migration bands. Only the Yoruban-San (Y-S) and Bantu-San (B-S) migration scenarios are strongly supported. In all panels, each bar represents the mean estimate and 95% credible interval of a single representative run of the program. See Supplementary Tables 2 & 3 and Supplementary Fig. 4 for complete results.

Table 2.

Estimated Divergence Times, with Migration

Divergence Event	Ingroup (X)	Raw Estimates	Calibrated Estimates
			Tdiv = 5.6 Mya	Tdiv = 6.5 Mya	Tdiv = 7.6 Mya
San (τKHEXS)	Yoruban	0.91 (0.89–0.94)	113 (110–116)	131 (127–135)	153 (149–157)
San (τKHEXS)	Bantu	0.90 (0.88–0.93)	111 (108–114)	129 (126–133)	151 (147–155)
AE (τKHEX)	Yoruban	0.33 (0.31–0.34)	40 (38–42)	47 (44–49)	55 (51–57)
AE (τKHEX)	Bantu	0.37 (0.35–0.38)	46 (43–47)	53 (50–55)	62 (59–64)

Raw and calibrated estimates for the San (τ_KHEXS) and African-Eurasian (AE) (τ_KHEX) divergence times. Separate results are shown for the Yoruban and Bantu representatives of the African ingroup population X. In all cases, a migration band between the San and the African ingroup X was included in the model. Raw estimates (mean and 95% Bayesian credible intervals) are given in units of expected mutations per site × 10⁻⁴. Calibrated estimates are given in thousands of years (kya), for three different human-chimpanzee calibrations (T_div = {5.6, 6.5, 7.6} Mya).

Our estimates of the African-Eurasian divergence time were also highly consistent across runs, with mean values of ~50 kya and a full range of 38–64 kya (Table 2). These estimates showed almost no influence from migration (Fig. 3a). Only slight differences were observed between those for the Yoruban (~47 kya) and Bantu (~53 kya) ingroups. Our power for more recent events is reduced, but, interestingly, we estimated 31–40 kya (26–47 kya across calibrations) for the European/East Asian divergence (Supplementary Table 2), dates that are more easily reconciled with the fossil record in Europe than estimates of ~20 kya based on allele frequency data^11,12. Our estimates of effective population size (θ) are consistent with a population expansion in Africa—we observe a steady increase from θ_KHEXS to θ_KHEX, and then to θ_X and θ_S (Fig. 3c)—while those for the Eurasian populations indicate a pronounced bottleneck. Most estimates of θ were unaffected by gene flow, except those for the ingroup populations and their immediate ancestors, which behaved in the expected manner. The effective size of the MRCA population, N_KHEXS, was estimated with high confidence at ~9,000 (~7,500–10,500 for T_div = 5.6–7.6 Mya), and was highly robust to the choice of ingroup and migration scenario.

While our estimates of several demographic parameters—including the African-Eurasian divergence time^7,9 and the ancestral effective population sizes^8,9,18—show reasonable agreement with numerous recent studies (Supplementary Note), only a few previous multilocus studies have included San representatives. Furthermore, these studies have generally produced estimates of the San divergence time that are considerably less precise than our genome-wide estimate of 126–133 kya (or 108–157 kya across calibrations); estimates have ranged from 71–142 kya⁶, 78–129 kya (assuming T_div = 6.5 Mya)², and 145–215 kya (not including large credible intervals)¹⁸. Notably, our point estimate of ~130 kya suggests that the San divergence occurred ~2.5 times as long ago as the African-Eurasian divergence, that major human population groups diverged at least ~80,000 years before the out-of-Africa migration, and that the San divergence is more than one third as ancient as the human/Neanderthal divergence (estimated at 316–341 kya, for T_div = 6.5 Mya, using somewhat different methods²). Still, human effective population sizes are sufficiently large that these divergence times are small relative to the time required for lineages to find common ancestors in ancestral populations. Indeed, of the mutations differentiating a San individual from a Eurasian individual, only about 25% are expected to have arisen since the San divergence. Thus, the ancient divergence of the San does not alter the essential fact that far more human variation occurs within population groups than between them²⁶.

In principle, our estimates could be influenced by various complex features of human evolution not adequately considered in our model. However, in a series of follow-up analyses, we could find no evidence that our estimates were strongly influenced by intralocus recombination, mutation rate variation, changes in population size along lineages, or our choice of prior distributions (Supplementary Note). Moreover, it is doubtful that the scenario hypothesized in the recent analysis of the Neanderthal genome—with low levels of gene flow from Neanderthals to ancestral non-Africans²—would substantially change the San divergence time while leaving the African-Eurasian divergence time well within the feasible range. Nevertheless, it should be possible to characterize the demographic history of early humans in greater detail as additional genome sequences become available.

Our methods represent a significant step toward coalescent-based inference of demographic parameters from complete genome sequences. This approach has a number of potential advantages compared with methods based on approximate Bayesian computation²⁷, summary likelihood approaches^8,10, and the site frequency spectrum¹¹. By explicitly representing genealogical relationships at neutrally evolving loci, the coalescent-based approach can more accurately capture the correlation structure of the data, which may lead to improvements in parameter estimation²⁷. Moreover, it allows for simple and direct estimation of the posterior distributions of any genealogy-derived quantities of interest, such as times to most recent common ancestors or rates of migration over time. Unlike a recently published method that analyzes individual genomes in isolation²⁸, our approach simultaneously considers multiple populations, and allows direct estimation of divergence times and migration rates. However, by circumventing the critical issue of recombination, through the analysis of short loci assumed to be in linkage equilibrium, our methods fail to exploit the information about demography that is provided by patterns of linkage disequilibrium (e.g., in the length distribution of shared haplotypes)¹⁰, instead relying on a relatively weak signal from mutation to drive the inference procedure (our data set contains only 1.9 polymorphic sites per locus). Therefore we see an opportunity for improved methods for multi-population coalescent-based demographic inference that consider both mutation and recombination, and allow entire chromosomes to be analyzed. Recent progress in this area^29,30 suggests that, with clever approximations and careful algorithm design, it may be possible to develop methods that scale to dozens of complete genomes.

ONLINE METHODS

Genotyping pipeline

Our pipeline for genotype inference consists of five major stages: (1) alignment of reads to the reference genome; (2) empirical recalibration of quality scores; (3) position-specific indexing of aligned reads; (4) Bayesian genotype inference; and (5) application of filters (Supplementary Fig. 1). Sequence reads were mapped to the human reference genome (UCSC assembly hg18) using version 5.0.5 of BWA³¹ and version 0.1.7 of SAMtools³². Exact duplicate reads were removed using “samtools rmdup” to avoid amplification biases. The raw quality scores were empirically recalibrated using the Genome Analysis Toolkit³³. For each base in each individual genome, a maximum a posteriori genotype call was computed using a Bayesian algorithm for genotype inference (BSNP) that made use of aligned reads, basecall quality scores, and mapping quality scores, but avoided the use of the reference allele or previously identified variants. Orthologous sequences from the chimpanzee reference genome (panTro2) were extracted from genome-wide hg18-panTro2 alignments from UC Santa Cruz.

Filtering

Our filters included both data-quality filters, designed to mitigate the effects of sequencing and alignment error, and comparative filters, designed to avoid the effects of natural selection, hypermutability, or misalignment with chimpanzee. The data quality filters excluded sites with low coverage, adjacent to indels, in clusters of apparent SNPs, or in recent transposable elements or simple repeats. The comparative filters excluded sites in regions of poor human/chimpanzee synteny, recent segmental duplications, hypermutable CpG dinucleotides, and sites either within or flanking protein-coding exons, noncoding RNAs and conserved noncoding elements. We ensured that our results were robust to parameters used to implement these filters (Supplementary Note).

Genotype validation

We compared our genotype calls with published calls for two individuals (Venter and NA12891³⁴) for whom both array-based and alterative sequence-based calls are available. In both cases, we also considered genotype calls obtained by running the program MAQ³⁵ on our alignments. This approach allowed us to evaluate the performance of both the entire alignment pipeline and the genotype inference step alone. In addition, we computed key summary statistics (such as numbers of variant sites, heterozygosity, and pairwise genomic distances) for the individual genomes in our set, and checked that they were concordant with published estimates and with the assumption of a molecular clock (Supplementary Note).

G-PhoCS

The G-PhoCS program is derived from the MCMCcoal source code^20,21, but extensive changes to the code and sampling procedure were needed to accommodate migration and the use of unphased diploid genotypes (Supplementary Note). Some additional modifications allowed for reductions in running time. We generally ran the program with a burn-in of 100,000 iterations, followed by 200,000 sampling iterations. Various analyses indicated that this was sufficient to allow for convergence of the Markov chain. Each run took about 30 days to complete on an Intel(R) Xeon(R) E5420, 2.50 GHz CPU.

Determining alignment blocks for analysis

We defined the 37,574 “neutral loci” by identifying contiguous intervals of 1000 bp that passed our filters and then selecting a subset with a minimum inter-locus distance of 50,000 bp, ensuring that recombination hot spots (regions with recombination rates >10 cM/Mb³⁶) fell between rather than within loci. The locus size and minimum inter-locus distance were determined by an approximate calculation similar to one used by Burgess and Yang²¹. We assume a mean recombination rate of 10⁻⁸ per bp per generation, an average generation time of 25 years, and minimum and maximum average genomic divergence times (among the humans) of 200,000 and 500,000 years, respectively. Thus, the expected number of recombinations on the lineages leading to two human chromosomes in a 1 kbp interval is at most 2 × 500,000 × 10⁻⁸ × 1000/25 = 0.4 and the expected number in a 50 kbp interval is at least 2 × 200,000 × 10⁻⁸ × 50,000/25 = 8. We conducted a series of validation experiments to ensure that our estimates are robust to modest amounts of intralocus recombination (Supplementary Note).

Model calibration

An estimate of a mutation-scaled version of the human/chimpanzee average genomic divergence time was obtained from the model parameters using the relationship, τ_div = τ_root + ½θ_root, where τ_root and θ_root represent the mutation-scaled human/chimpanzee speciation time and ancestral effective population size, respectively. This leads to an estimated mutation rate per year of μ = τ_div/T_div, which can be used to convert all other mutation-scaled divergence times to years (T = τ/μ). We assume a generous range of T_div = 5.6 – 7.6 Mya, as suggested by Patterson et al.²⁴, based on the relative divergence levels of the chimpanzee and orangutan genomes from the human genome, an upper bound of 20 Mya for the orangutan divergence time, and other constraints from the fossil record. We follow Green et al.² in choosing a “best guess” of T_div = 6.5 Mya. To obtain effective population sizes in numbers of diploid individuals (N) we use the relationship θ = 4Nμg, where g is the average generation time in years, and estimate N by θ/(4μg) (we assume g = 25 for human populations). We use τ_div for calibration because it is robustly estimated by G-PhoCS across a wide variety of different modeling assumptions, unlike τ_root and θ_root, which depend on the assumed model of mutation rate variation across loci. We obtained estimates of τ_div = 4.54×10⁻³ across many different runs, with 95% CIs of 4.45–4.63×10⁻³.

Validation of parameter estimates

We performed a series of validation analyses, using both simulated and real data, to examine the influence on our estimates of several factors, including: (1) the choice of prior distributions; (2) mutation rate variation across loci; (3) intralocus recombination; (4) recent population expansions and bottlenecks; and (5) parameters/thresholds defining our data-quality and comparative filters (Supplementary Note).