Ultrasensitive detection of rare mutations using next-generation targeted resequencing

Abstract

With next-generation DNA sequencing technologies, one can interrogate a specific genomic region of interest at very high depth of coverage and identify less prevalent, rare mutations in heterogeneous clinical samples. However, the mutation detection levels are limited by the error rate of the sequencing technology as well as by the availability of variant-calling algorithms with high statistical power and low false positive rates. We demonstrate that we can robustly detect mutations at 0.1% fractional representation. This represents accurate detection of one mutant per every 1000 wild-type alleles. To achieve this sensitive level of mutation detection, we integrate a high accuracy indexing strategy and reference replication for estimating sequencing error variance. We employ a statistical model to estimate the error rate at each position of the reference and to quantify the fraction of variant base in the sample. Our method is highly specific (99%) and sensitive (100%) when applied to a known 0.1% sample fraction admixture of two synthetic DNA samples to validate our method. As a clinical application of this method, we analyzed nine clinical samples of H1N1 influenza A and detected an oseltamivir (antiviral therapy) resistance mutation in the H1N1 neuraminidase gene at a sample fraction of 0.18%.

INTRODUCTION

With broad applications in research and clinical diagnostics, next-generation DNA sequencing (NGS) has become an important platform for identifying mutations and variants from clinical samples. NGS has been frequently applied to detection of polymorphisms from normal diploid genomic DNA samples where the allele frequency is based on Mendelian inheritance. In this case, a heterozygote variant comprises half the depth at its position. However, many samples represent more complex mixtures in their genetic composition where a mutation or variant may be present in only a small proportion of the relevant sequences. Deep sequencing analysis with very high levels of coverage on smaller targeted regions can sensitively detect less prevalent, minor alleles and mutations from these admixed samples. For example, ultrasensitive detection could identify mutations in individual genes that cause resistance to the drugs that target specific gene products.

Generally, applications of sensitive rare mutation and minor allele detection from admixed samples include: microbial or viral population sequencing, rare cancer-specific mutations in primary tumors, environmental diversity sampling of specific microbes and pooled sample sequencing. As noted, many studies are particularly interested in small sets of genes that are therapeutic targets. Deep sequencing has been used for the analysis of clinical samples from individuals with HIV infection or other viruses to identify the multiple related viral clones, often referred to as ‘quasi-species’, that coexist in an infected individual (1–4). This offers the opportunity to identify rare drug resistance mutations to antiviral therapies whose representation in a virus population can expand after therapeutic selection in chronically infected individuals. NGS can also provide sensitive detection of cancer-specific mutations from primary clinical cancer samples contaminated with normal stroma (5) and in a similar context, these mutations can lead to cancer therapy resistance. By pooling genomic DNA from many individuals in a cohort and sequencing the pool, one can identify rare variants from smaller size genomic regions at a much lower per-sample cost than from large population studies (6).

There are many experimental methods available for highly sensitive detection of rare mutations and variants from admixture samples containing multiple genotypes. These include denaturing high-performance liquid chromatography (DHPLC) (7), high-resolution melting analysis (HRMA) and mutation-specific PCR-based genotyping assays (8). However, DHPLC and HRMA require DNA sequencing as final confirmation of the identity of a mutation and mutation-specific genotyping assays (9), while highly sensitive and specific, require a priori knowledge of the mutation. Compared to these other methods, direct DNA sequencing offers significant advantages for both discovery and confirmation of rare mutations in samples that are complex genetic mixtures.

Presently, there are only a limited number of ways to detect rare single nucleotide mutations using a NGS platform (1,10–12). SNPseeker (11) uses quality filtering and large-deviation theory to call SNPs with a minor allele frequency (MAF) as low as 0.5–1.2%. VarScan (10) uses thresholds on coverage, quality and variant frequency to call variants with a MAF as low at 1%. CRISP (13) uses a probabilistic model to call rare variants present in pools as large as 25 individuals representing a level of 2% allele frequency. Hedskog et al. (1) report detection of 0.07–0.09% variants in a viral population using pyrosequencing technology. Some methods are designed detect both SNPs and indels. The major challenge for NGS rare variant and mutation detection is finding a true signal with the relatively high error rates of NGS. With the initial commercial release of these technologies, these errors were generally quoted as ranging from 1% to 3% (14). We demonstrate that the error rates are significantly lower based on our results of sequencing a synthetic DNA samples. Our overall objective was to develop a robust and general method to detect rare (0.1%) single nucleotide variants with current sequencing-by-synthesis NGS technology by overcoming the general sequencing error rate limitations. At this level, this represents accurately detecting one mutation among 1000 wild-type alleles.

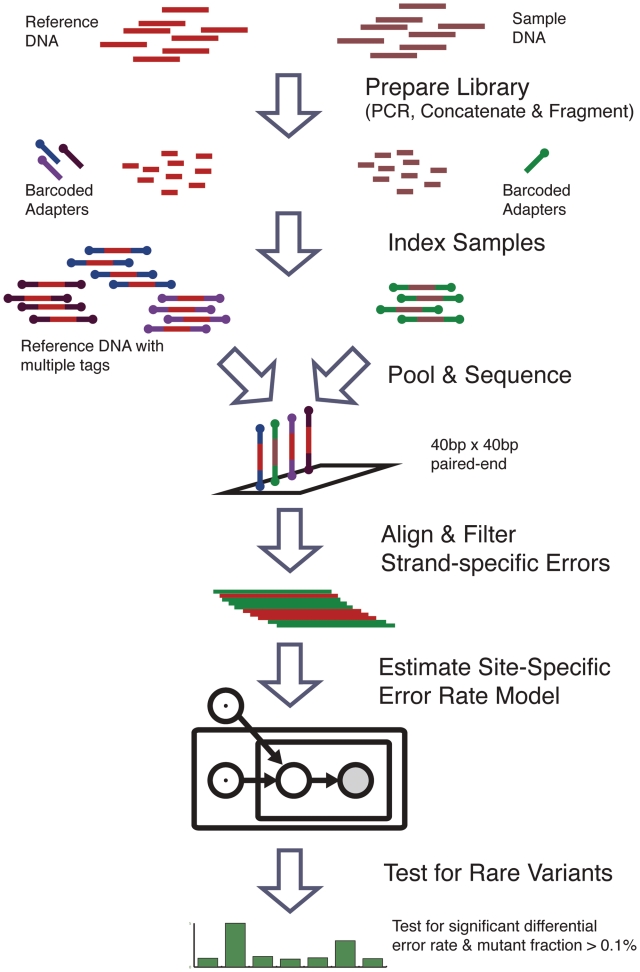
Our method for the detection of rare single nucleotide mutations at the 0.1% level relies on innovation in both experimental design and statistical algorithm (Figure 1). We use a multi-reference, indexed experimental design to minimize experimental variance and characterize a position-specific error distribution. We employ a rigorous statistical model to estimate the position-specific error rate distribution for reference sequences and thus the probability of a true mutation at each position in the sample. The statistical model provides a rigorous framework for hypothesis testing and estimation that minimizes false positives in variant calling. We demonstrate our method by accurately calling known mutant positions in a 0.1% mixture of two pure synthetic DNA constructs sequenced via Illumina NGS. The reference and mutant positions are known a priori and provide a gold standard for testing our approach. We then apply our method to identify mutations of the H1N1 influenza A (H1N1) neuraminidase gene (NA) obtained from nine infected individuals during the 2009 pandemic. We identified a known drug resistance mutation among these variants. Finally, we show a statistical power analysis of our method in order to characterize the sequencing parameters under which our method can be generalized to other novel applications.

Figure 1.

Method flowchart. The method for detecting rare variants compares the baseline error rate from multiple reference replicates to the sample error rate at each position. Sample and reference DNA are independently prepared and tagged with indexed adapters. The reference and sample libraries are pooled and sequenced on the same lane. The reads are aligned and preprocessed to filter out strand-specific errors. The parameters of a Beta-Binomial model are fit to the reference sequence data to obtain a null hypothesis error rate distribution for each position. Finally, the error rate of the sample sequencing data is compared to the null distribution to call rare variants.

MATERIALS AND METHODS

Synthetic sequence construct

Two versions of a 300-bp completely synthetic sequence were synthesized, which differ by a single base substitutions in 14 positions spaced 20 bases apart (https://www.dna20.com). The overall sequence length was 400 bp including the linkers (Supplementary Figure S1). The synthetic inserts were cloned into a pUC based Kan^R containing vector and the resulting 2971-base plasmid was used as template for subsequent experiments.

Sample and sequencing preparation

In preparation for sequencing, PCR amplified DNA from each template plasmid was prepared as follows: 50 ul reactions were prepared consisting of 25 ng template, 200 uM dNTP, 1 uM each of amplification primers, 0.5 ul (1 U) of Phusion Hot Start enzyme (New England Biolabs). We used the following amplification conditions: 98°C 30 s followed by 20 cycles of 98°C 10 s, 60°C 30 s, 72°C 30 s, followed by 72°C 7 min, then hold at 4°C. Twenty such reactions were combined for the wild-type product and six for the mutant product. Wild-type and mutant products were pooled separately and purified (Qiagen QIAquick). Products were quantitated on a spectrophotometer (Nanodrop Instruments) and the concentration was adjusted to 25 ng/ul. The mutant DNA was spiked into the wild-type to a final concentration of 0.1% of the total DNA. The sample was then split into three technical replicates. The sequence of the two synthetic templates and of the PCR primers used is provided in the Supplementary Figure S1.

To prepare the sequencing library for each of the six samples (0 and 0.1% dilutions in triplicate), each PCR sample was concatenated using T4 DNA ligase (reaction conditions: 500 ng DNA, 1× Quick Ligation Buffer, 1ul T4 DNA ligase in 50 ul total volume for 10 min at 25°C) and fragmented using a Bioruptor sonicator (Diagenode) with the following settings: 6 consecutive cycles with each cycle consisting of 30 s ‘on’, 30 s ‘off’ for 15 min on power setting ‘high’). DNA was end-repaired: 30 ul of fragmented DNA was combined in a 50 ul final reaction volume containing 0.15 U/ul T4 DNA polymerase, 0.5 U/ul polynucleotide kinase, 0.05 U/ul Klenow in 1× T4 DNA ligase buffer w/ATP and incubated for 45 min at 25°C. End-repaired DNA was A-tailed using native Taq polymerase (1× Taq buffer, 0.1 mM dATP, 0.04 U/ul Taq) at 72°C for 15 min. Reactions were purified using Fermentas GeneJet™ PCR purification kit and eluted in 20 ul TB buffer. Multiplex adapters were ligated for 1 h at 25°C in 25 ul reactions containing 1× T4DNA ligase buffer, 0.15 uM adapters, 1 ul T4DNA ligase HC. Adapter ligated material was purified using a 2% E-gel SizeSelect, excising the 300–350 bp fraction. The gel-purified fraction was PCR enriched (reaction mix: 1× Phusion HF buffer, 250 uM dNTP, 1.2 uM enrichment primers, × units Phusion Hot Start polymerase). We used the following cycling conditions: 98°C for 30 s, followed by 15 cycles of 98°C for 10 s, 72°C for 1 min, then 72°C for 7 min, then hold at 4°C. Enriched libraries were gel purified on 2% E-gel SizeSelect. The 300-350 bp fraction was collected and quantitated using SybrGold fluorescence assay (Invitrogen).

Sequencing library indexing

We developed a highly accurate 16-plex indexing strategy. We synthesized a total of 32 versions of barcode adapters that were used in a 16-plex indexing schema and the index sequences are listed in Supplementary Table S1. The modification of the standard Illumina sequencing adapter pair consists of all 16 dinucleotides combinations added at the 5′-end of one adapter molecule and all 16 combinations of the same dinucleotide ‘NN’ sequence plus a ‘T’ inserted at the 3′-end of the other standard Illumina adapter sequence. For a given sample, we ligate a specific matched pair of indexing adapters to double stranded DNA such as an amplicon. Except for the modified adapters, our design uses all the reagents and protocols of the standard Illumina single-plex protocol while obviating the need for the third read as commonly employed for other multiplexing methods. To assign a paired end read to an indexed bin we require that the same tri-nucleotide (‘NNT’) be read as the first three bases of both mate pair sequence reads. As a test of the indexing accuracy of this methods we generated 16 different amplicons from different regions of the genome using the methods as previously described (15). Using an anonymous normal diploid genomic DNA sample, these amplicons were generated in simplex reactions. Subsequently we used the standard Illumina protocol as already noted to incorporate the indexing adapters to each amplicon. The analysis regarding the indexing accuracy is also located in Supplementary Table S1.

Sequencing, alignment and filtering

Paired-end sequencing was performed on an Illumina GAIIx sequencer (Illumina SCS 2.8) with real-time image analysis and base calling (Illumina RTA 2.8). Eland II (from Illumina pipeline version 1.6) was used with the default parameters to perform sequence alignment to the 300-bp synthetic DNA construct. Aligned data were filtered to remove sequences with high error rates (greater than two mismatches) and processed into depth matrices. We find the results quoted are not altered by allowing three mismatches. The number of mismatches allowed depends on the read length and the expected mutation frequency. In addition, by comparing a single sample that was run with replicates on two separate lanes, we also determined intra-lane and inter-lane variability that was run on two different lanes (Supplementary Figure S3).

After initial pre-processing and alignment of the primary sequence reads, the error rates between read-matched pairs on the same strand are highly correlated (forward reads: r = 0.94, 95% asymptotic confidence intervals (95% CI 0.94–0.95), reverse reads r = 0.94, 95% asymptotic confidence intervals (95% CI 0.94–0.95)]. In contrast, the error rates between forward and reverse strand reads are uncorrelated in general [first in pair: r = −0.08, 95% asymptotic confidence intervals (95% CI −0.15 to −0.02), reverse reads r = −0.16 (95% CI −0.23 to −0.09)] (Supplementary Figures S4–S6). For a minority of positions, the error rate on one strand is remarkably different than the same position as read on the reverse strand. A significant fraction of the strand-specific errors are in 5′-GT-3′ sequences with an error at the T position. Our observation is consistent with Dohm et al. (16) who found that bases preceded by G have a high error rate. We remove the higher error rate direction reads that have a significantly different error rate between the forward and reverse directions (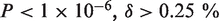) (Supplementary Figures S7–S9).

H1N1 sample sequencing

The study was conducted under a clinical protocol approved through the Stanford University School of Medicine. We collected nasopharyngeal swab samples in viral transport media. We confirmed that these nasopharyngeal samples contained the 2009 H1N1 influenza A virus through a previously published method (17). We isolated viral RNA using the Qiagen Viral RNA Mini kits, and amplified using Superscript OneStep RT–PCR reagents and two primers at positions 428 (AGG GCC CTT GCT AAA TGA CA) and 1236 (AAC TCC CGC TAT ATC CTG ACC ACT). Amplification conditions were 45°C for 30°C min, 94°C for 2 min, 35 cycles of (94°C for 15 s, 54°C for 20°C s, 72°C for 2 min), followed by 72°C for 7 min. The reaction combines 10 ul RNA and 40 ul Master Mix containing per reaction: 25 ul 2× Reaction Buffer, 0.5 ul each primer at 50 pmol/ul, 1 ul RT-Taq mix and 13 ul water. The reference for this experiment is PCR amplified DNA for plasmid GS2.3 using the same primers. Amplification conditions for the plasmid reference are 94°C for 2 min, 35 cycles of (94°C for 15 s, 54°C for 20 s, 72°C for 2 min], followed by 72°C for 7 min. The reaction combines 10 ul of DNA at 1 ng/ul and 40 ul Master Mix containing: 5 ul 10× Reaction Buffer, 0.5 ul each primer (50 pmol/ul), 1 ul dNTP mix (10 mM each), 1.5 ul MgCl (50 mM) 0.2 ul Platinum Taq (Invitrogen) and 31.3 ul water. All subsequent sequencing analyses were performed as previously described.

Statistical model

Statistical analysis was conducted using Matlab (Mathworks) and our analysis scripts are provided in the Supplementary Data. We start with the sequencing error rate that is simply defined as the fraction non-reference reads divided by the total reads. Subsequently we apply the Beta-Binomial model (Supplementary Figure S10) that is used to identify rare variants in reference sequence data. Beginning with the observed data, 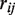is the non-reference read count for experimental replicate , at position ; n_ij is the total read count. The sequencing error rate for a given position is 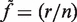. The random variable 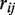is distributed as a Binomial with parameter 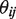, which represents the true error rate for position 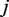in replicate . The unobserved random variable 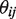is sampled once for each experimental replicate and has a Beta distribution with parameters 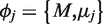. The parameter 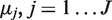corresponds to the prior error rate at position 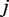. The parameter 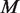is the experimental precision of the error rate; equivalently a pseudo-count for read depth at position 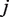. We observe that the error-rate variance is constant across positions (data not shown) and is therefore represented unconditional on position in the model.

The random variables and parameters are estimated by the maximum-likelihood method using the expectation maximization (EM) algorithm. The algorithm is initialized with the plug-in moment estimates of 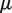, and 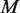. The EM algorithm alternates optimizing the log-likelihood with respect to 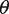and with respect to 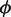by the interior point method until the change in the log-likelihood is <0.01%. The expected value of θ is estimated in closed-form, while the parameters, 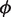are estimated by a constrained interior-point algorithm.

Experimental variation, caused by differences in sample handling, sequencing library preparation, indexing and the overall experimental protocol is captured in the experimental precision parameter 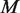, which is estimated through the total variation in θ across experimental replicates (see ‘Materials and Methods’ section for variable definitions). The moment estimate for 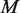in the Beta-Binomial model is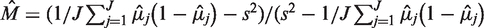 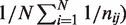, where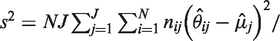 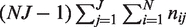and 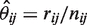. The term 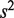captures the variation in the error rates between replicates in the summation 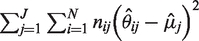and as 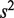increases, 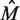decreases. Since the number of positions is generally fixed for a sample of interest, more replicates leads to an improvement in the accuracy with which 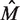is estimated. Finally, for a given mutation the sample fraction is 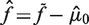. When referring to the detection level of mutations, we cite the sample fraction except when otherwise stated.

Model parameter estimation

The EM algorithm is used to compute the maximum likelihood parameter estimates for ϕ. It has been shown that the expected complete log likelihood is a lower bound on the log-likelihood of the data and the lower bound can be maximized by coordinate ascent. We optimize 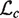by alternating constrained maximization. First we maximize 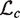numerically using an interior point algorithm with respect to the parameters 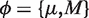in the space 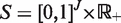. Then we maximize 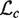with respect to 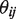fixing the parameters at 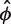. The maximum likelihood estimate has the closed form solution, .

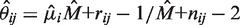Hypothesis testing

To test for rare variants in the model, the prior parameters, ϕ, are estimated from reference data using the EM algorithm. The prior parameters then contain the expected error rates for the null hypothesis of no variant. Since the Binomial distribution is well-approximated by a Gaussian distribution when the read count is large, a z-test is used to compare the observed Binomial error rate (r/n) for a new sample to the reference null distribution 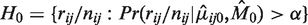, with mean 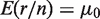and variance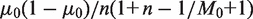 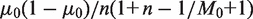. To improve the power to resolve rare variants, it is optimal to make the null-hypothesis variance, 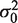, as small as possible. If y, then 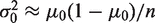and the sequence depth becomes the limiting factor in the detection power. Conversely, if 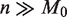, then 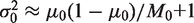and the inter-replicate variation becomes the limiting factor.

Complete details of the model specification and parameter estimation procedure are available in Supplementary Data. Executable code for the parameter estimation and hypothesis testing procedures are also available upon request.

RESULTS

We show three results of our rare mutation identification method. First, we demonstrate our approach on a controlled admixture of two synthetic DNA constructs and compare our method to other available procedures using this data. Second, we show a statistical power analysis of our algorithm and characterize its limitations. Third, we apply our method to nine clinical isolates of H1N1 influenza A from the 2009 pandemic.

Synthetic DNA admixture sequencing analysis

Two versions of a 400-bp DNA sequence were synthesized; the synthetic sequence makes up the internal 300 bp with the remainder coming from polylinker sequences. The two versions of the sequences differ only in 14 known single nucleotide positions (mutations) and do not map to any known genomes (Supplementary Figure S1). We prepared sequencing libraries from these synthetic sequences as described in the ‘Materials and Methods’ section (Supplementary Figure S2). A sample containing pure reference sequence was independently indexed with three unique barcodes. Similarly, a sample containing a 0.1% molar mixture of both sequences was indexed with three different barcodes. The dominant sequence in the mixture is the ‘reference’ sequence and the minor mixture component is the ‘mutant’ sequence.

We sequenced the six indexed libraries (three pure references and three 0.1% mutant admixture samples) on a single lane of an Illumina GAIIx, and the resultant paired-end data was aligned to the known synthetic reference to give a read depth at each position. For sequencing error filtering, all reads with more than two mismatches to the reference were eliminated. Next, at positions where reads from one strand (forward or reverse) had a high error rate relative to reads from the other strand, the strand-specific reads with high error were excluded. The depth coverage for the synthetic DNA data prior to error filtration is and post-filtration. The analysis was restricted to the central 281 bases of the synthetic DNA sequence; all 14 mutant positions were located within this interval. We identified 6.4% (18/281) of the positions as having a significantly higher forward strand error rate and 7.0% (20/281) of the positions as having a significantly higher reverse strand error rate. To assure that alignment error did not affect the analysis, we verified that the synthetic sequence was devoid of internal repeats based on looking at 14 base strings incremented through the entire synthetic reference.

Accurate assignment of indexed reads to the appropriate sample

A potential source of error is the false assignment of indexed reads from one sample to another. Other highly efficient methods for sample indexing are available, with the majority using single reads for indexing. We developed an accurate method for indexing using paired-end sequencing and mate-pair reads. We incorporate a two nucleotide indexing barcode followed by a third common T at the 5′-end. This barcode is the same for the two adapters of a given sequencing library. To correctly assign a mate pair sequence to a given sample, we require that the same barcode is present on both reads of a given mate pair set. In other words, we assign a sequence to a specific sample by imposing the presence of the correct ‘NNT’ sequence at the 5′-end of both Read 1 and of Read 2. To assign a read incorrectly to the wrong sample would require identical sequencing errors on the indexing tag on both pairs of the read.

Prior to our synthetic DNA resequencing studies for rare variant detection, we determined the frequency of false assignment errors for a given mate-pair indexing barcode. To accomplish this assessment, we tagged 16 different amplicons independently, pooling them and sequencing all of the 16 indexed libraries in a single lane of an Illumina GAIIx. We generated 19,477,723 mate-pair reads for a single lane. For all 16 barcodes, we observe that 16,311,074 of the mate pair reads are associated with the correct amplicon while just 11,255 are associated with one of the other 15 amplicons. The remainder of the reads represented adapter primer products that are commonly seen. We define the indexing error rate as the number of reads associated with an incorrect amplicon divided by the total number of reads from the 16 amplicons. Overall, we observe a 0.06% indexing error rate which was well below our reported detection threshold (Supplementary Table S1). Overall, using indexing barcodes that match on both reads provided high accuracy assignments.

Sequencing error rate variation at a particular position is less than variation across all reference positions

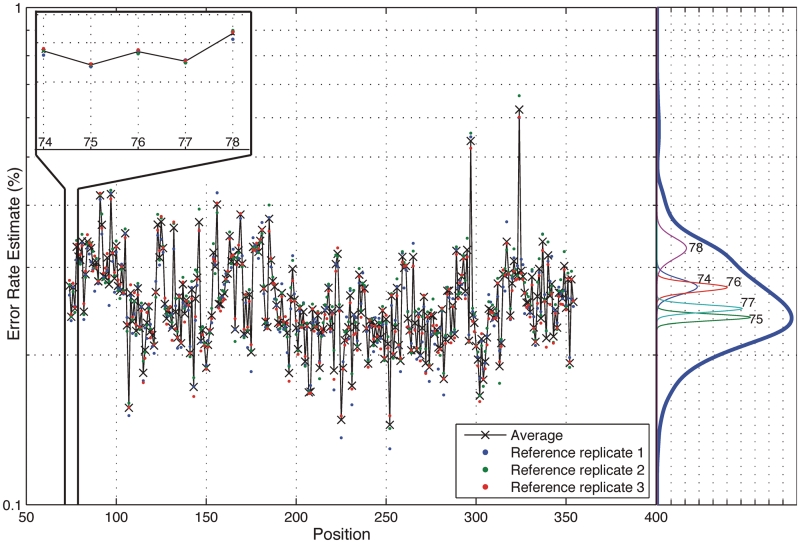
We define the position-specific sequencing error rate as the fraction of the sum of the non-reference base read depths over the total read depth at a particular position in a sample (see ‘Materials and Methods’ section). In other words, for each individual base position, we determine the sequencing error rate. Figure 2 shows the position-specific sequencing error rates for the three indexed synthetic reference samples as a profile across positions and as histogram density estimates. The variance of the error rates is much greater for all combined positions than for each position independently. Though the error rate of NGS technologies have been quoted to be 1–3%, we observe that the average error rate across all positions is 0.26% with an average standard deviation of 0.056%. The error rate distribution is skewed towards higher error rates with upper 95th percentile at 0.35% and the lower 5th percentile at 0.19%. The maximum error rate across positions and experimental replicates is 0.66% and the minimum is 0.13%. Since the rates are based on the triplicate reference which is a pure population, any errors are a result of the library preparation or sequencing processes effects. We minimized the PCR-induced errors in the preparation of the reference by using Phusion, a high fidelity polymerase, a large amount of template (25 ng) and a small number of amplification cycles in the preparation of the reference DNA.

Figure 2.

Position-specific error rate distribution. The average sequence error rate variance across positions is significantly greater than the average variability at each position. The across-position distribution is shown on the right side in dark blue and a sample of five within-position density estimates is shown below it. The empirical within-position and across-position distribution estimates show that a small number of outlying positions contribute to the excessive variance in the across-position distribution.

While the sequencing error rate across the entire reference sequence is highly variable, sequencing error rate at each specific position is significantly less variable. The sequencing error rate density estimates in Figure 2 show that the variance in sequencing error rates across positions is much greater than the variance within a specific position (five sample positions displayed). For the reference sequence, the total variance across positions and replicates is . The variance across positions is and the average variance within a base position is . Thus, the average standard deviation of the error within a base position is 0.0086% compared to 0.056% across positions—more than 6-fold smaller.

Statistical model detects mutated positions at a sample fraction of 0.1% level

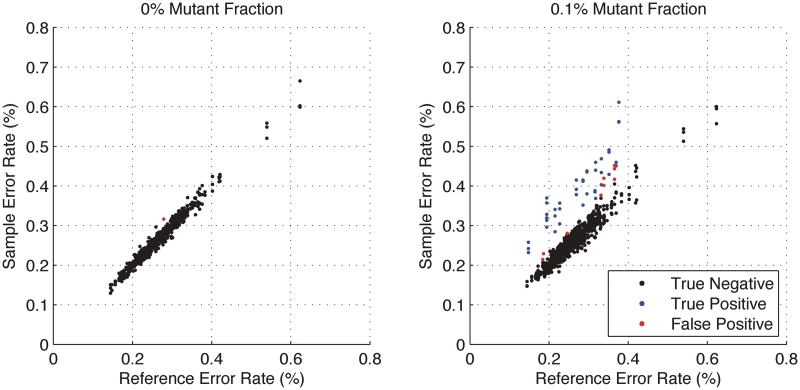
We developed a binomial error model that categorizes a sequence read as ‘reference’ or ‘non-reference’—an excess of ‘non-reference’ reads indicates the presence of a variant at the position. By using a Beta distribution prior on the binomial parameter representing the sequencing error rate, we more accurately capture the variance in the position-specific distribution across replicates that in turn decreases the false positive rate of our algorithm. Derived from our Beta-Binomial model analysis, the sample fraction value indicates the fractional representation of rare mutations from the sample of interest.

The Beta-Binomial model parameters (ϕ) were fit to reference-only sequencing data. The reference error rate as estimated in the model was compared to the actual sample error rate (error read depth/total read depth) derived from sequencing (Figure 3). As expected, the reference-based estimates of the position-specific error rates (θ) were reproducible across replicates and no significant differences between the reference error rates, µ, and the sample (Binomial) error rates were detected (Figure 3). In contrast, the sample error rate estimates for the 0.1% admixture population shows some positions with significant differences (P < 1 × 10⁻⁶) between the reference error rate and the sample error rate indicating the presence of a variant (Figure 3). Setting the threshold P-value at 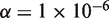is equivalent to a Bonferroni corrected level of 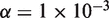for a 1-kb target region and thus has a low false positive rate after controlling for multiple hypothesis testing.

Figure 3.

Variant positions in the 0.1% mixture sample of synthetic DNA are identified by the statistical model. The x-axis is the reference error rate as estimated by 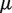in the model and the y-axis is the sample error rate (error read depth/total read depth). True negatives (black), true positives (blue) and false positives (red) for three replicates are identified in both samples. For each of the three replicates, the model finds 14 of 14 true positives; 5, 4 and 1 additional calls (false positives), respectively, are made. Requiring a consensus call of all three replicates eliminates these false positives.

The algorithm correctly identifies all 14 mutation positions out of 281 total sequenced bases in each of three replicates. The average specificity across three replicates to detect a variant admixture at a 0.1% level with 100% sensitivity is 99% (Table 1). The Beta-Binomial model misidentified 5, 4 and 1 positions out of 267 as variant for the three replicates. There were no type II errors in this data set. The precision and accuracy of the approach is high.

Table 1.

Ultrasensitive detection of 0.1% minor mutant alleles

Sample	0.1% admixture replicate
	1	2	3	Average
Sensitivity	1.000	1.000	1.000	1.000
Specificity	0.981	0.985	0.996	0.987
False positive rate	0.019	0.015	0.004	0.013
False negative rate	0.000	0.000	0.000	0.000
Positive predictive value	0.737	0.778	0.933	0.816
Negative predictive value	1.000	1.000	1.000	1.000
Accuracy	0.982	0.986	0.996	0.988
False discovery rate	0.263	0.222	0.067	0.184
Matthews correlation coefficient	0.850	0.875	0.964	0.896

Due to the small number of variant positions (5% of the total sequence) the false discovery rates for the three replicates are 0.26, 0.22 and 0.067. The false discovery rate is high due to the low number of true positives compared to true negatives in the sequence. Taking a consensus approach across replicates significant improves the specificity to 100% and reduces the false discovery rate. Given the issue of the true positives relative to the true negatives being highly skewed (18), we report a balanced measure for the classification accuracy using the Matthews Correlation coefficient (MCC) as was done for the MAQCII analysis (19). Our method has an average MCC score of 0.896 where a value 1 indicates perfect classification accuracy. These results are based on testing for statistical significance alone. Combining our statistical test with a effect size test such that only those called mutations with an estimated mutant sample fraction is ≥0.1% reduces the number of false positives to zero. While the sensitivity is reduced, in some applications, such as the analysis of long sequences with infrequent mutations, a much more specific test is more appropriate.

Comparison of our approach to other methods

We compared our Beta-Binomial model to an approach that uses only the overall error rate distribution across all positions and to the method of Hedskog et al. (1), which uses pyrosequencing data to develop a position-specific error rate comparison in order to identify mutations at a 0.05% sample fraction level. We applied all methods to the identical synthetic DNA data set. Hedskog et al. (1) do not employ a statistical model to estimate the error rate. Our approach has a lower error rate than either of these alternative approaches (Table 2). Using the same data set, commonly used variant callers including the Genome Analysis Toolkit (GATK) (20) and SAMtools (21) do not detect any true variants on this data set.

Table 2.

Comparison of high sensitivity methods of minor allele detection

	Sensitivity (%)	Specificity (%)
Sample 1
Hedskog et al. (1)	0/14 (0)	267/267 (100)
Across-position method	0/14 (0)	267/267 (100)
Position-specific method	14/14 (100)	263/267 (98.13)
Sample 2
Hedskog et al. (1)	0/14 (0)	267/267 (100)
Across-position method	0/14 (0)	267/267 (100)
Position-specific method	14/14 (100)	263/267 (98.50)
Sample 3
Hedskog et al. (1)	0/14 (0)	267/267 (100)
Across-position method	0/14 (0)	267/267 (100)
Position-specific method	14/14 (100)	266/267 (99.63)

For pyrosequencing data (e.g. 454 sequencing), the Hedskog method has power to detect mutations at 0.05%, but we find it to be less sensitive for our data. The Hedskog method produces more conservative estimates of the error rate at each position that lowers the statistical power. Also, it employs a data-cleaning method for pyrosequencing to reduce the average error rate to 0.05% and report a detection limit of 0.07%. When the Hedskog method is applied to sequence data from an Illumina Genome Analyzer, the detection limit is less sensitive. In the case of the across-positions error model approach, the average sequencing error rate is ~0.25% and the detection limit is necessarily greater for error-prone positions. We are not fundamentally limited by the average error rate across positions; our sensitivity depends instead on the variance of the error rate across replicate sequencing of the references at each position. We improve the reproducibility by controlling influential experimental parameters and sequencing the reference and samples in the same lane. Further improvements in experimental reproducibility are expected to improve the detection limit.

Statistical algorithm analysis

In order to identify mutations, we look for positions with a higher error rate than would be expected if the sequence originated from a sample that is purely reference DNA. We use the reference sequence data to estimate the parameters in our model. We then compare the observed error rate in a sample sequence to the estimated reference distribution in a classical hypothesis-testing framework. A characterization of the model provides insights into appropriate experimental design conditions.

Experimental variation is caused by differences in sample handling, sequencing library preparation, indexing, which we capture in the beta distribution experimental precision parameter. Our model indicates clear roles for experimental precision and overall read depth in improving rare variant detection levels. The iterated moment estimate for 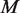in our Beta-Binomial model captures the variation between positions and within each position across replicates. Increasing the number of replicates improves the accuracy by which 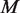is estimated (see ‘Materials and Methods’ section).

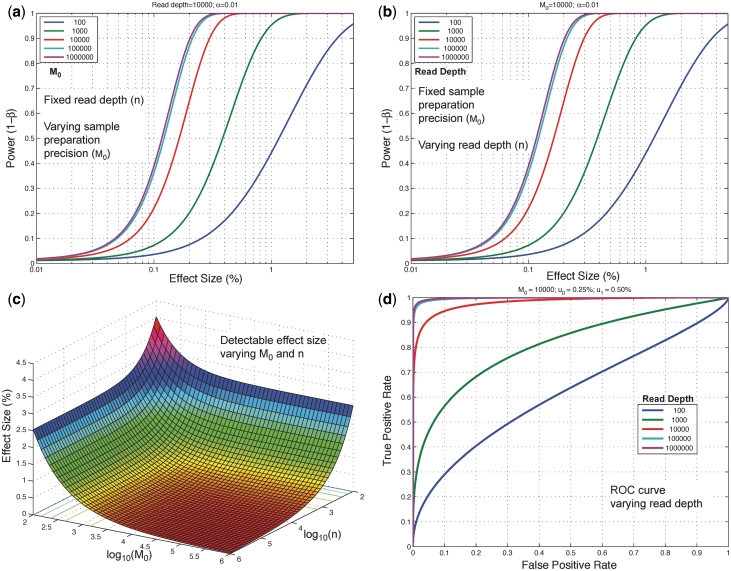
The relationship between experimental precision, read depth and variant detection limit is shown in power curve analysis in Figure 4. The experimental precision parameter we define as 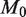. The read depth controls the sampling variation and the accuracy with which we observe the true error rate. If the read depth is too low, the uncertainty in the true sequencing error rate will be too high to call a less prevalent, rare variant as a statistically significant difference from the reference position. For example, if the read depth at a position is only 60, we will not detect a variant present in 1 out of 1000 reads. However, if the read depth is 10 000, the sampling error of the binomial distribution may be sufficiently small to detect a variant at 0.1% sample fraction.

Figure 4.

Detection power depends on both read depth and experimental precision. We show here that the statistical power of the model, the likelihood of detecting a true positive at a given effect size (level of prevalence), increases with read depth and sample preparation precision, up to asymptotic limits. (a) Read depth (n) is held constant at an example level of 10 000 and it can be seen that power increases with experimental precision (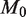) up to a limit of approximately 0.4 for an effect size of 0.1%. (b) When the experimental precision (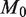) is held constant at 10 000, power increases with read depth (n) up to a limit of approximately 0.4 for an effect size of 0.1%. (c) For a fixed false positive and false negative rate, the detectable effect size decreases with both increasing sample preparation precision (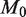) and read depth (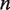). A greater gain is achieved by improving sample preparation precision than by increasing read depth if the experimental variation is large. (d) The ROC curve for a fixed effect size and sample preparation precision improves rapidly as the read depth increases. Read depth limits the sensitivity at all false positive rates when low, but when read depth is high the ROC curve approaches an asymptotic curve controlled by the experimental variation.

Holding the read depth fixed at 10 000 and the level of the test at 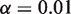, the power improves significantly as 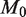increases from 100 to 10 000 (Figure 4a). This is directly related to improvements in experimental design such as the reproducibility of replicates. As 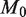increases to 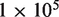and 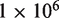we see only a marginal benefit in statistical power indicating that the read depth has become limiting. Likewise with 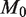fixed at 10 000 and 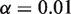, we see that further increases of sequencing depth beyond 10 000 provide no major benefit for detection (Figure 4b). The detection sensitivity increases as both the experimental precision and read depth increase (Figure 4c). Holding the reference error rate fixed at 0.25%, the detectable variant frequency is below 0.5% at 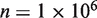, 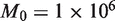and asymptotically approaches 0.25%. The expected ROC curve shows that for 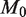of 10 000 a read depth of 10 000 yields good power (>90%) at a low false positive rate to discriminate a reference error rate of 0.25% from a variant fraction of 0.5%. Higher read depths 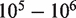yield nearly perfect classification under theoretical conditions (Figure 4d). For the ROC analysis, the area under the curve (AUC) for the read depth from 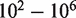is 0.61, 0.80, 0.97, 0.996 and 0.997.

Rare mutations in the NA gene in clinical samples of H1N1 influenza A

We sequenced nine independent clinical samples of H1N1 influenza NA gene using the indexing method described in two replicate sequencing lanes. Given that these were clinical samples, we use a replicate lane to improve our assessment of variance. One sample (BN1) was replicated within each lane and one sample (B23) was diluted 5-fold and 25-fold with the reference NA gene within each lane to assess reproducibility and sensitivity. The replicated reference was sequenced from a single plasmid clone containing the NA gene isolated from an individual infected with H1N1. All sequence data are reported as relative positions to the H1N1 strain A/California/07/2009 (Genbank reference GQ377078). We used the high coverage sequence data from position 468–1183 in the H1N1 reference. The reference NA sequence contains three nucleotide mutations G1044A, A1052T and T1059C compared to the GQ377078 sequence, which introduces one amino acid mutation, Y351F.

The average coverage depth is 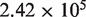for the samples in lane 1 and 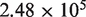in lane 2 before preprocessing and 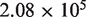for lane 1 and 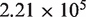for lane 2 after pre-processing. Our pre-processing filter identified 100 positions with high relative forward strand error rates and 106 positions with high reverse strand error rates in lane 1. The corresponding counts for lane 2 are 80 and 84. Overall, the reference sequence data in lane 1 showed an overall higher average sequencing error rate of 0.45%, compared with 0.22% for lane 2. However, the critical parameter for our approach, the average within-position standard deviation, was very similar at 0.017% in lane 1 and 0.013% in lane 2.

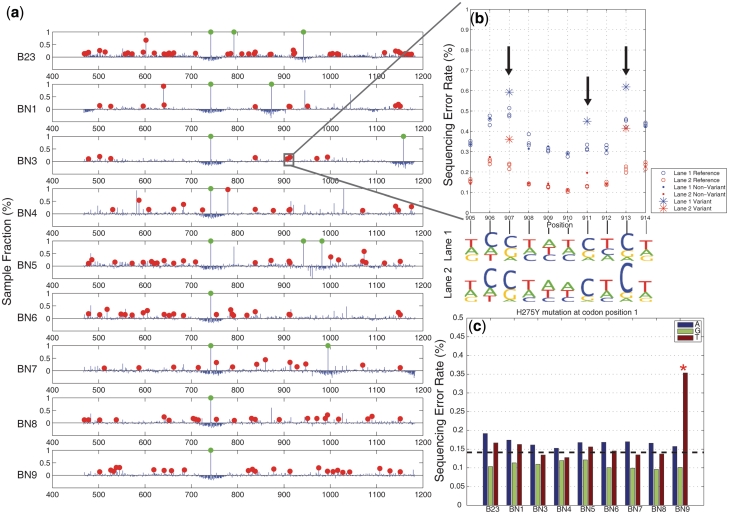
Figure 5a shows the full spectrum of detected NA mutations for the nine H1N1 clinical samples derived from the consensus. On average for the variants at 0.1% sample fraction or higher, we identified an average of 40 mutations per sample in lane 1 and 45 mutations per sample in lane 2. Taking a consensus of both sequencing lanes gives an average of 32 mutations per sample at or greater than the 0.1% level (Supplementary Table S2). For the non-synonymous mutations we identified an average of 20 per sample (Supplementary Table S3). For three replicate reference controls, there was only a single case where an erroneous call was made when examining sequence data from both lanes. The lack of called mutations from the reference is a general indicator of overall quality of our mutation detection.

Figure 5.

Sequencing results of clinical samples of H1N1 influenza A. (a) A red dot indicates a position called as a mutant (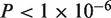) and has a sample fraction >0.1% and green dots indicate an estimated sample fraction >1%. (b) A detail display of 10 positions in sample BN3 shows the difference between the reference and sample sequencing error rates for called mutations in two replicate lanes. The non-reference base composition for both lanes (in sequence logo format) shows that the three mutations are T to C pyrimidine transitions. (c) We identified the H275Y mutation responsible for oseltamivir resistance in one clinical sample (BN9). Across all of the H1N1 clinical samples, we display a breakdown of the individual sequencing error rate for the non-reference bases at codon position 1. The mutation in sample BN9 is readily apparent. The dotted line indicates the expected base error rate from a uniform distribution across bases using the total sequencing error rate.

Figure 5b shows that even though the sequencing error rates varied from lane to lane, our detection method is unaffected by such systematic differences. Please note that the ‘raw’ sequencing error rates are derived directly from the raw sequence data prior to our statistical model analysis. For example, a detailed view of a 10-bp segment of sample BN3 shows the sequencing error rates for lanes 1 and 2. The average of the sequencing error rate for lane 1 is higher than lane 2, but the critical error differential between the reference and sample error rate, is reproducible between the two lanes. Sequence logos for the non-reference bases at each position show that the positions called mutant due to excessive error rate are indeed enriched for a particular base sequence.

To assess experimental reproducibility of our method, we compared the identified mutations for BN1 across replicates within a sequencing lane and between lanes (Supplementary Figure S3). BN1 was indexed on two different lanes and we compared the results. The concordance between replicates is high for sample fractions >0.1% and diverges for fractions less than that level.

At position 826 in the NA gene, we identified the H275Y mutation responsible for oseltamivir resistance in one clinical sample (BN9). Oseltamivir specifically inhibits NA activity and appearance of this resistance mutation was a source of significant concern given its public health ramifications. The mutation is apparent even when using that position's ‘raw’ sequencing error rate. This is shown in Figure 5c where we display a breakdown of the individual sequencing error rate for the non-reference bases at codon position 1 for all of the H1N1 clinical samples. The dotted line indicates the expected error using the total sequencing error rate. After our Beta-Binomial model analysis, we determined that the H275Y mutation in BN9 had a sample fraction of 0.18% that matches well with the difference between expected per-base error rate and the observed fraction of reads with a T base at the position in sample BN9.

To assess the sensitivity of our method we diluted the B23 sample 5-fold and 25-fold with reference NA DNA. Afterwards, we sequenced the admixtures. We determined the dilution level at which point we could determine mutations from the undiluted B23 sample. At two non-synonymous positions 604 and 742 in the undiluted sample B23, our algorithm calls mutations at sample fractions of 0.66 and 99.45%, respectively (Supplementary Table S3). Both positions were called in both replicate experiments in the 5-fold diluted sample and only the 742 position was called in the 25-fold diluted sample. In this dilution series, we did not detect the other B23 mutations that were diluted to <0.1% sample fraction. This is consistent with our rare mutation sensitivity threshold as we demonstrated with the synthetic sequence. One B23 non-synonymous mutation was called at the 25-fold dilution that was not identified in the undiluted sample. This clearly is a false positive, but with this sole exception, the dilution experiment verified the robustness of our ultrasensitive mutation detection.

DISCUSSION

We have shown that by sequencing a known reference sequence in multiplexed replicates with samples of interest and integrating a Beta-Binomial statistical model we are able to sensitively detect rare variants and mutations at low (0.1%) sample fraction levels. This represents one mutant allele being detected from among 1000 wild-type alleles in a single sample. We experimentally demonstrated our approach on a controlled system using a synthetic DNA sequence. We used our model to provide a detailed analysis of the tradeoff between experimental precision/reproducibility and sequencing depth to achieve ultrasensitive variant detection. Our approach is best suited toward studies that require analysis of small regions such as viral and human genes that are drug targets.

There is an observable lane–lane error rate bias on the NGS platform (data not shown). We controlled this variation by sequencing the reference and samples in multiplex on the same lane, but this control limits the number of samples multiplexed, sequence length and detection limit. Further improvements to the Beta-Binomial model are required to adjust for the bias by normalization rather than by control.

Our results have implications for experimental design for multiple applications. While our initial application was to identify mutations in the H1N1 influenza NA gene, including those that lead to drug resistance, our approach is also broadly applicable to identifying rare mutations for specific genes in cancer samples, characterizing viral quasispecies samples such as HIV and analyzing other clinical samples that are genetically heterogeneous. A fixed total amount of sequence () can be decomposed into a product of read depth (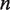), number of multiplexed samples (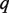) and sequence length (). This can be stated as . 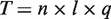The tradeoff between sample throughput and detection limit can be optimized for a particular experiment. For example, at the current sequencing capacity of a single lane of an Illumina HiSeq instrument, one could detect 0.1% variants in a 1 kb target sequenced at an average depth of 100 000 for 10 samples.

Our model is optimized for detection of mutations in viral genomes, and can be extended to other applications. For tumor mutation detection, the reference genome is haploid and point mutation may represent a loss-of-heterozygosity event. Such an application would be addressed by extending our model to diploid genomes using a Dirichlet-Multinomial model form. Furthermore, incorporation of sequence quality metrics would improve detection, though it is unclear at this stage how much gain is available with such side-information.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online: Supplementary Tables 1–3, Supplementary Figures 1–10, Supplementary Methods and Supplementary Data.

FUNDING

National Science Foundation, Division of Mathematical Sciences (NSF DMS) DMS (Grant #1043204 to N.Z. and H.P.J.); Department of Veterans Affairs (in part, to M.H.); National Institutes of Health (NIH) (grants 5K08CA96879–6 to H.P.J., DK56339 to H.P.J, 2P01HG000205 to J.B., J.M.B., H.P.J. and P.F. and R21CA140089 to G.N. and H.P.J.); Doris Duke Clinical Foundation (to H.P.J.); Reddere Foundation (to H.P.J.); Liu Bie Ju Cha and Family Fellowship in Cancer (to H.P.J.); Wang Family Foundation (to H.P.J.); Howard Hughes Medical Foundation (to H.P.J.). Funding for open access charge: NIH (grant 2P01HG000205) and NSF DMS (grant 1043204).

Conflict of interest statement. None declared.