When to Wait for More Evidence? Real Options Analysis in Proton Therapy

Trends suggest that cancer spending growth will accelerate. One method for controlling costs is to examine whether the benefits of new technologies are worth the extra costs. We have shown that real options analysis provides a transparent method of weighing the costs and benefits of adopting and/or further researching new and expensive technologies.

Abstract

Purpose.

Trends suggest that cancer spending growth will accelerate. One method for controlling costs is to examine whether the benefits of new technologies are worth the extra costs. However, especially new and emerging technologies are often more costly, while limited clinical evidence of superiority is available. In that situation it is often unclear whether to adopt the new technology now, with the risk of investing in a suboptimal therapy, or to wait for more evidence, with the risk of withholding patients their optimal treatment. This trade-off is especially difficult when it is costly to reverse the decision to adopt a technology, as is the case for proton therapy. Real options analysis, a technique originating from financial economics, assists in making this trade-off.

Methods.

We examined whether to adopt proton therapy, as compared to stereotactic body radiotherapy, in the treatment of inoperable stage I non-small cell lung cancer. Three options are available: adopt without further research; adopt and undertake a trial; or delay adoption and undertake a trial. The decision depends on the expected net gain of each option, calculated by subtracting its total costs from its expected benefits.

Results.

In The Netherlands, adopt and trial was found to be the preferred option, with an optimal sample size of 200 patients. Increase of treatment costs abroad and costs of reversal altered the preferred option.

Conclusion.

We have shown that real options analysis provides a transparent method of weighing the costs and benefits of adopting and/or further researching new and expensive technologies.

Introduction

The costs of cancer care have increased substantially in the last few decades [1, 2]. Recent trends suggest that cancer spending growth will accelerate, in part because of costly new treatments [3]. As this ongoing increase in costs is causing a serious financial burden to patients, families, and society at large, substantial changes in the health care delivery system are needed to reduce the growth rate of health care spending [2–4]. One method for controlling health care costs is to examine whether the benefits of new technologies are worth the extra costs [5]. Although cost-effectiveness analyses are increasingly used to assist decision making in cancer care, their results do not always provide sufficient evidence to make a decision [6, 7]. This is especially the case when a technology is on average cost-effective but uncertainty exists.

Protons are charged particles that can be used for radiotherapy. Because of their superior dose distribution, a clinical benefit is expected [8]. Currently, decisions are being made worldwide whether or not to adopt proton therapy as a standard treatment, as well as for which indications [9]. However, because only relatively few studies have investigated the effectiveness of proton therapy, the effects are surrounded with considerable uncertainty [10–12]. Also, proton therapy is associated with large investment costs [9, 13]. Recently, Grutters et al. concluded that proton therapy may be cost-effective in the treatment of stage I non-small cell lung cancer (NSCLC) [14]. However, the probability that proton therapy is indeed more cost-effective than stereotactic body radiotherapy (SBRT) in this population is only 63%. Hence, the probability that adopting proton therapy is a wrong decision, which implies that the high investment costs of approximately €95 million [13] are not justified, is 37%.

The real decision is whether to adopt proton therapy now, with the risk of making the wrong decision, or to postpone the adoption and collect more information in a new trial to reduce the existing uncertainty, with the risk of giving patients the suboptimal treatment in the meantime [4, 15]. A potential technique to assist in making such trade-offs is real options analysis (ROA) [16]. ROA not only provides guidance as to whether to postpone adoption but also provides guidance as to whether further research is worthwhile and, if so, what design and sample size of the trial give the best value for money. In the present paper we will illustrate how ROA can assist evidence-based decision making upon emerging promising but uncertain technologies in cancer care that require implementation costs. We will apply this state-of-the-art technique, which originates from financial economics [17, 18], to the case of proton therapy in stage I NSCLC.

Methods

Background of ROA

The real options approach stems from financial literature [17, 18]. Its advantage is that it does not only consider whether the benefits of a technology outweigh its costs (as in cost-effectiveness analyses) but also recognizes the option to postpone adoption of the technology. In health care, when we decide to delay adoption of a cost-effective but uncertain new technology, there is a risk of giving patients suboptimal treatment. This results in health benefits forgone. On the other hand, adopting a cost-effective but uncertain new technology involves the risk of wasting a considerable amount of money. In both cases, uncertainty can be reduced by obtaining additional knowledge, through performing a trial. ROA can help in assisting the decision of whether to postpone adoption. Additionally, ROA can assist the decision of whether to perform a trial and, in the case of a trial, in designing the optimal trial, with regard to sample size, endpoints, and follow-up time.

In health care, ROA is indicated when two key characteristics are present [19]. First, there should be uncertainty surrounding the decision. When a treatment is cost-effective for sure, the treatment can be adopted without any doubt because the probability that the wrong decision is made is zero. Second, it should be costly or even impossible to reverse the decision to adopt the technology. This is, for example, the case when implementation costs are very high. In that case, the consequences of making the wrong decision are much higher than when the decision to adopt can easily be reversed [20, 21]. Because both characteristics are present in many health care decisions, ROA can potentially be a useful tool in health care decision making [16, 19, 22].

Calculation of Real Options

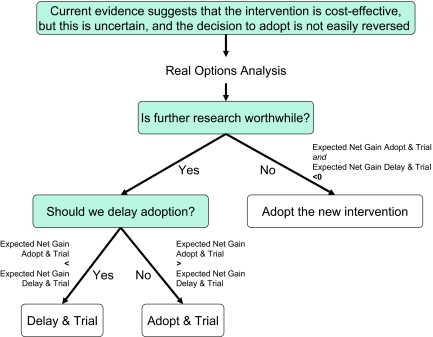
ROA can be calculated to support the adoption decision of a new technology. ROA is performed from a decision-analytic perspective, which implies that if there would be no costs of reversal the most cost-effective option should be adopted, irrespective of whether it is statistically significantly more cost-effective than its comparator [20]. However, when a health care technology is cost-effective but it is costly or impossible to reverse the decision, there are three options: (a) adopt without further research; (b) adopt and undertake a trial (“adopt and trial”); and (c) delay adoption and undertake a trial (“delay and trial”). The option to delay without further research is not considered because there would be no reason to delay the adoption of a cost-effective treatment if no further research is acquired. Which option we choose depends on the expected net gain of both “adopt and trial” and “delay and trial” (Fig. 1). If the expected net gains of both adopt and trial and delay and trial are below zero, this means that the benefits of trialing do not outweigh its costs, and the preferred option is to adopt without undertaking a trial. If the expected net gain of adopt and trial or delay and trial is higher than zero, trialing is worthwhile, and the option with the highest expected net gain is preferred (Fig. 1). In case the preferred option includes a trial (either with adopt or delay), the optimal trial design is the one that generates the highest expected net gain.

Figure 1.

Schematic diagram of the decision to adopt now or wait for more evidence.

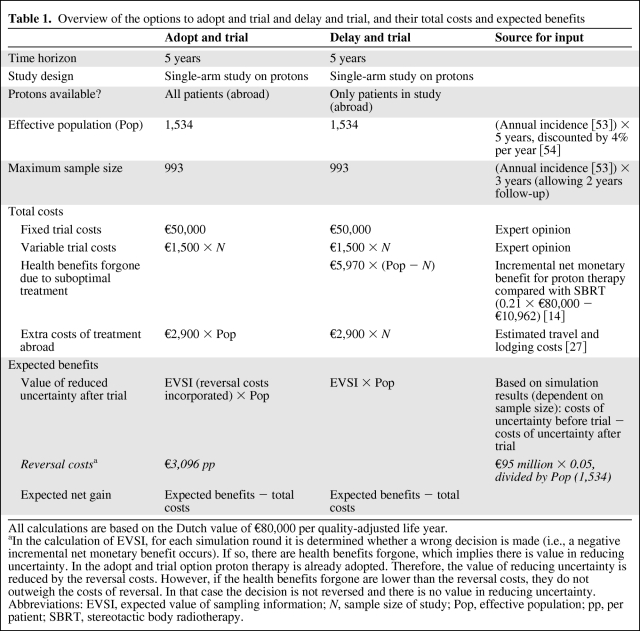
The expected net gain is calculated by subtracting the total costs from its expected benefits [16]. The total costs of the adopt and trial and delay and trial options consist of four cost categories: fixed trial costs, variable trial costs, health benefits forgone, and extra costs (Table 1). Fixed and variable trial costs are the costs associated with performing the trial. Health benefits forgone reflect the consequences of withholding patients the optimal treatment. They are represented by the expected net health gain of the technology compared to its alternative. In monetary terms, this is referred to as the expected incremental net monetary benefit of the technology. It is calculated by multiplying the additional effects of the new intervention by the value of one unit of effect, and subtracting the additional costs. Because new evidence is not yet available, health benefits forgone are based on the expected incremental net monetary benefit based on current evidence. Optionally, extra costs may be relevant such as costs associated with travelling.

Table 1.

Overview of the options to adopt and trial and delay and trial, and their total costs and expected benefits

All calculations are based on the Dutch value of €80,000 per quality-adjusted life year.

^aIn the calculation of EVSI, for each simulation round it is determined whether a wrong decision is made (i.e., a negative incremental net monetary benefit occurs). If so, there are health benefits forgone, which implies there is value in reducing uncertainty. In the adopt and trial option proton therapy is already adopted. Therefore, the value of reducing uncertainty is reduced by the reversal costs. However, if the health benefits forgone are lower than the reversal costs, they do not outweigh the costs of reversal. In that case the decision is not reversed and there is no value in reducing uncertainty.

Abbreviations: EVSI, expected value of sampling information; N, sample size of study; Pop, effective population; pp, per patient; SBRT, stereotactic body radiotherapy.

The expected benefits of the adopt and trial and delay and trial options consist of the value of reduced uncertainty as a result of performing a trial. This is referred to as the expected value of sampling information (EVSI) and is calculated using Bayesian analyses. Specific details on how to calculate EVSI are described elsewhere [21, 23, 24]. In short, the expected costs of uncertainty are determined jointly by the probability that the decision will be wrong and the health benefits forgone as a result of a wrong decision [20]. A trial will provide additional evidence and hence will reduce the probability of a wrong decision. This expected reduction in costs of uncertainty is the value of reduced uncertainty, or EVSI. For each trial design, for example, for trials with different sample sizes, the remaining costs of uncertainty are calculated. This requires an estimate of the outcome of the future trial. However, we do not know the actual results of a trial in advance. Therefore, we calculate EVSI for all possible outcomes of a trial design, and average these to elicit an expected EVSI for this trial design [24]. Because in the adopt and trial option the technology is adopted, a reversal of this decision is associated with reversal costs. Therefore, to calculate the expected benefits of adopt and trial, the EVSI is reduced by the costs of reversing the decision. However, if the costs of reversal are higher than the health benefits forgone that are associated with not reversing the decision, we choose not to reverse the decision. Therefore, there is only a positive EVSI (because the decision is indeed reversed) of adopt and trial if the reversal costs are lower than the health benefits forgone due to suboptimal treatment [16].

Application to Proton Therapy

Because of the theoretical advantage, radiotherapy with protons has gained increasing attention in the last decade. Approximately 33 institutes around the world are currently operating facilities, and at least 22 facilities are in the planning stage or under reconstruction [9]. Many countries, such as Belgium, The Netherlands, and the United Kingdom, are currently deciding or have recently decided whether or not to invest in proton facilities [25–27]. Although proton therapy is proven effective for some indications with a low incidence, for most indications evidence is lacking [10–12, 28]. This has resulted in an ongoing lively debate on whether there is sufficient evidence to expand the number of facilities, whether randomized trials are needed, and if so, how to perform these in the absence of sufficient proton facilities [9, 29–39].

To decide whether to adopt proton therapy in inoperable stage I NSCLC, we performed an ROA. This ROA builds upon a published cost-effectiveness analysis [14]. In this cost-effectiveness analysis, all evidence on costs and effects was synthesized in a decision model, estimating the total costs and effects (in terms of quality-adjusted life years) per patient over 5 years. Effectiveness of the different treatment options was synthesized using a meta-analysis of observational studies [40]. All evidence that was used as input for the model is listed in the Appendix. Because the current decisions worldwide are focused on adopting proton therapy or SBRT as a standard treatment for inoperable stage I NSCLC, for the current analysis we have restricted the decision problem to these two comparators. Because both are quickly evolving technologies, we used only the studies on effectiveness that were from 2004 or later [14]. As a setting we chose The Netherlands, a small country with 16.5 million inhabitants where no proton facility is yet available.

Because generally all studies on protons and SBRT to date are observational, and there is a debate about whether it is ethical to perform randomized studies, we assume that a future study will be a single-arm study on protons (Table 1). The study will be performed over a period of 5 years, and 5 years are needed to build the proton facility. It is assumed that after 5 years the decision can be reconsidered based on the new evidence. From the cost-effectiveness analysis we found that further research into the effectiveness of proton therapy in terms of overall survival was most valuable [14]. Therefore, the endpoint of the proposed study is two-year overall survival. It is assumed that all consecutive patients are included in the study, and there is no selection in patients.

Fixed and variable trial costs were assumed to be €50,000 and €1,500 per patient, respectively (Table 1). Health benefits forgone were based on the initial cost-effectiveness analysis. This analysis indicated that proton therapy yielded 0.21 extra quality-adjusted life years, at an additional cost of €10,962 [14]. On the basis of the Dutch value of €80,000 per quality-adjusted life year [41], this resulted in a net monetary benefit of €5,970. Extra costs of treatment abroad (€2,900) consist of travel and lodging costs and were based on a Belgian study [27].

Uncertainty was handled probabilistically, meaning that we assigned distributions to all uncertain inputs in the cost-effectiveness model (online supplemental data) [24]. Parameter values were drawn at random from the assigned distributions, using Monte Carlo simulation with 10,000 iterations. To calculate the EVSI, the possible outcomes of the future study were drawn from a predictive distribution based on the results of the meta-analysis [40, 42]. For each sample size, for 200 possible study results the Monte Carlo simulation was run to calculate the corresponding EVSI. Subsequently, these 200 EVSI estimates were averaged to obtain an expected EVSI for that sample size. In the adopt and trial option, a facility will be built. The part of the costs of building the facility that is attributable to the treatment of inoperable stage I NSCLC patients can be considered reversal costs, as these are wasted when the decision to adopt proton therapy is reversed. We estimated that about 5% of the total costs of €95 million would be attributable to inoperable stage I NSCLC patients, which results in €4.75 million, or €3,096 per patient.

All costs and expected gains for the base case analysis are listed in Table 1. Because the extra costs of treatment abroad and the reversal costs are uncertain and may differ across jurisdictions, we additionally performed sensitivity analyses excluding and duplicating these costs.

Results

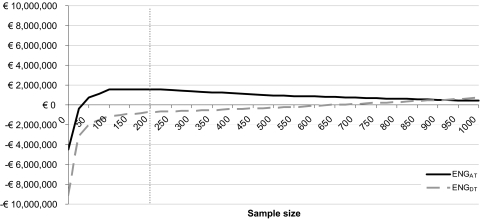
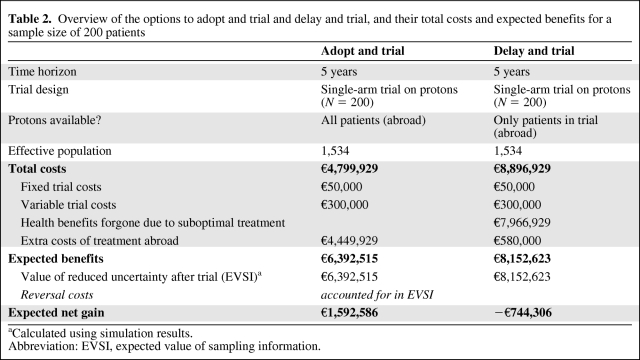
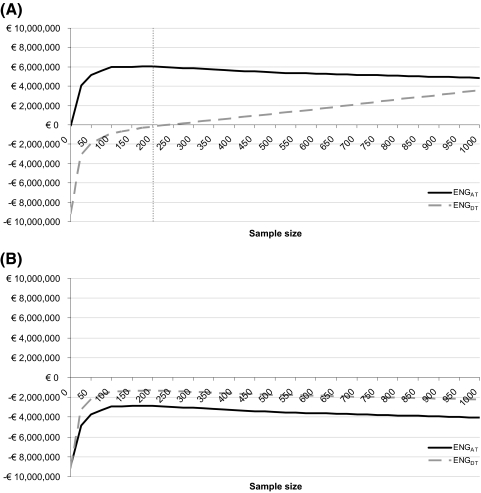
In the base case analysis the expected net gain of adopt and trial is higher than that of delay and trial for any possible sample size below 950 patients (Fig. 2). This means that, for the Dutch setting, adopting proton therapy and undertaking a trial is preferred over delaying adoption. The expected net gain of adopt and trial is positive for sample sizes of approximately 70 patients and more. The highest expected net gain is found at a sample size of 200 patients, which is thus considered the optimal sample size. This indicates that it is preferred to adopt proton therapy and undertake a trial with a sample size of 200 patients. A larger sample size may further reduce the uncertainty, but this extra benefit then does not outweigh the extra costs. In Table 2 the total costs and expected benefits of both options are listed for this study of N = 200.

Figure 2.

Expected net gain (ENG) for the options to delay and trial (ENG_DT) and adopt and trial (ENG_AT) for different sample sizes. The gray dotted line marks the optimal sample size (highest expected net gain). Abbreviations: ENG, expected net gain; ENG_DT, ENG for the options to delay and trial; ENG_AT, ENG for the options to adopt and trial.

Table 2.

Overview of the options to adopt and trial and delay and trial, and their total costs and expected benefits for a sample size of 200 patients

^aCalculated using simulation results.

Abbreviation: EVSI, expected value of sampling information.

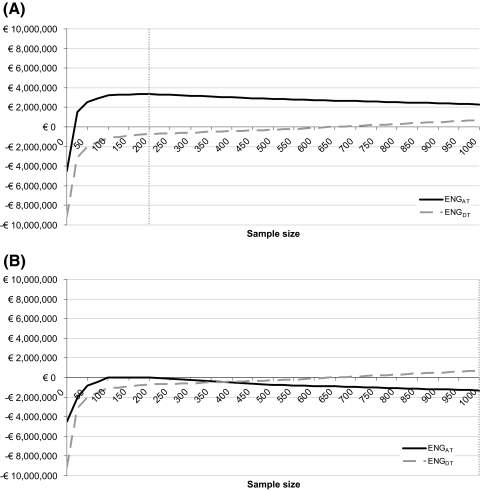
In a sensitivity analysis, excluding the extra costs of treatment abroad reduced the total costs of both adopt and trial and delay and trial and therefore increased the expected net gain of both options. Adopt and undertake a trial was still the preferred option, with an optimal sample size of 200 patients (Fig. 3A). Duplicating the costs of treatment abroad to €5,800 resulted in negative expected net gains, indicating that the optimal option would be to adopt proton therapy without undertaking a trial (Fig. 3B). The expected net gain of adopt and trial became positive when the extra treatment costs abroad were lower than €3,500.

Figure 3.

Results of the sensitivity analysis without (A) and duplicating (B) costs of treatment abroad: expected net gain (ENG) for both the option to adopt and trial (ENG_AT) and the option to delay and trial (ENG_DT) for different sample sizes. The gray dotted line marks the optimal sample size (highest expected net gain). Abbreviations: ENG, expected net gain; ENG_DT, ENG for the options to delay and trial; ENG_AT, ENG for the options to adopt and trial.

Reducing the costs of reversal to zero had no influence on the expected net gain of delay and trial. For the adopt and trial option, it increased the expected benefits, because these were not reduced by reversal costs. This resulted in an even more favorable expected net gain, with still an optimal sample size of 200 patients (Fig. 4A). A duplication of the reversal costs to €6,191 per patient decreased the expected net gain. In this sensitivity analysis, delay and trial with all patients included in the study generated the highest expected net gain (Fig. 4B). This implies that if the reversal costs are €6,191, all patients should be included in the study.

Figure 4.

Results of the sensitivity analysis without (A) and duplicating (B) reversal costs: expected net gain (ENG) for both the option to adopt and trial (ENG_AT) and the option to delay and trial (ENG_DT) for different sample sizes. The gray dotted line marks the optimal sample size (highest expected net gain). Abbreviations: ENG, expected net gain; ENG_DT, ENG for the options to delay and trial; ENG_AT, ENG for the options to adopt and trial.

Discussion

Decisions need to be made on whether to adopt proton therapy now, with the risk of wasting a considerable amount of money, or to wait, with the risk of giving patients a suboptimal treatment [15]. In the current paper, we have shown that real options analysis can assist in making such trade-offs. We found that for the current Dutch setting it is preferred to adopt proton therapy in inoperable stage I NSCLC and to undertake a single arm study with 200 patients. Sensitivity analyses on the costs of treatment abroad and reversal indicated an even stronger preference for the option to adopt and undertake a trial, except if the costs of reversal or costs of treatment abroad increased substantially.

With the present study we aimed to illustrate the usefulness of ROA in health care decision making. ROA seems to be especially useful in the field of oncology, because of the rapid increase of costly technologies in cancer care. Because the current decision problem focuses on proton therapy [9, 25, 26], and conventional radiotherapy with photons is not likely to be cost-effective in this population, we limited the analysis to proton therapy and SBRT [14]. The case of proton therapy compared to stereotactic body radiotherapy for stage I NSCLC is a timely and relevant case to apply ROA. However, the application of ROA also involves a number of challenges. First, the validity of the ROA approach is dependent on the validity of the decision model that is used to determine the cost-effectiveness. Our cost-effectiveness analysis included a synthesis of all available evidence, which is also presented in the online supplemental data. We therefore have no reason to believe that the results of the cost-effectiveness analysis, and consequently the ROA, are not valid. Second, assumptions need to be made to calculate the expected net gain of adopt and trial and delay and trial, such as the extra costs of treatment abroad and the reversal costs. In the current study we tried to make the options as realistic as possible for the Dutch decision problem. Two important assumptions regarding costs of treatment abroad and reversal were varied in a sensitivity analysis. This illustrates how ROA can assist in making decisions, even when uncertainty exists concerning the underlying assumptions. Changing parameters in a sensitivity analysis informs us on the robustness of the results. We found that changing the parameters only altered the recommendation to adopt proton therapy and undertake a single arm study if the reversal costs or costs of treatment abroad were very high. Third, because inputs such as the effective population and costs of treatment abroad are likely to differ between jurisdictions, the results of the current analysis cannot be directly extrapolated to other jurisdictions. However, the analysis can be easily adapted to allow for this extrapolation. Fourth, for the calculation of ROA we need to predict the outcome of any future trial. Because we cannot know beforehand what the results of a trial will be, we need to simulate every possible outcome [24]. Depending on the size of the model and the number of simulations, this can involve a large computational burden and therefore jeopardize feasibility of ROA. Fifth, for illustration purposes we needed so simplify some elements in the analysis. For example, we only calculated the benefits of a trial in terms of additional information on 2-year overall survival. As this trial will also yield information on disease-free survival and toxicity, the actual benefits of further research may be even larger than we found in our analysis. Also, we did not compare the value of different study designs or endpoints. ROA can be easily extended to examine other trial designs and endpoints and compare their expected net gains to see which trial design is optimal. Although this makes the analysis more comprehensive and thereby more complex, it is possible to use ROA for designing a future trial. Apart from the ethical issues raised in the current debate [33, 35, 37, 38], the present study shows that observational studies on proton therapy are also highly worthwhile, even when proton therapy is already adopted as a standard treatment.

When uncertainty exists about treatments, it is increasingly common to use access with evidence development schemes, where a treatment is temporarily adopted and all patients are monitored for a period of time before a final decision is made [43]. These schemes are used, for example, for pharmaceuticals, and they hypothesize the possibility of reversal of the temporary decision without any extra costs. However, when substantial implementation costs are associated with the adoption of a technology, reversal of a temporary adoption decision is costly. In oncology, several examples exist of technologies with high implementation costs, such as magnetic resonance imaging and positron emission tomography, and very recently the case of proton therapy [9]. In these cases, “access with evidence development” schemes are not an option, and ROA provides evidence-based arguments that can be used for decision making. A real options approach has also been used in a recent study to examine whether hospitals should invest in positron emission tomography [44, 45]. From the present study we found that adopting proton therapy and including all patients in the trial, which resembles the scheme, was never preferred, even when there were no reversal costs. This is because beyond a sample size of 200 patients, monitoring patients is no longer worthwhile. ROA can therefore be used to guide the design of these “access with evidence development” schemes.

Additional examples of ROA in health care can be found [16, 19, 22, 44–46]. However, unlike most of these applications, our application of ROA is based on Bayesian value of information analysis, which is quickly expanding in the field of health services research, particularly in oncology [14, 47–50]. ROA then not only informs about whether we should wait to implement a technology but also informs on whether to perform additional research [16]. Use of ROA therefore requires knowledge of decision analytic modeling and value of information analysis. When adopting a value of information analysis, ROA is a relatively small extra step.

Obviously, ROA will not provide a definite answer whether to invest in expensive new treatments such as proton therapy. The current analysis focused on inoperable stage I NSCLC, which is only a small part of the total patient population that could be treated with proton therapy. ROA could also be used to calculate, for example, whether the adoption of proton therapy in the treatment of children should be postponed because of the uncertainty surrounding the probability of secondary tumors. In this case it is expected that the benefits of delay would never outweigh the high costs of withholding these children the optimal treatment for 10–20 years until the study results become available. Although beyond the scope of this paper, a ROA based on the total population of cancer patients potentially eligible for proton therapy would be an interesting topic for further research. This would also assist the decision of which patients should be prioritized in the case of limited treatment capacity. Such a comprehensive analysis could help to decide whether a patient with prostate cancer or with lung cancer should be prioritized, based on their expected health benefits. Besides the results of an ROA, other factors, such as competition or research incentives, may also play an important role in the decision of whether to invest in proton therapy. However, ROA does provide evidence-based information on whether it would be worthwhile to delay such a decision. Hence, it can be used to make difficult trade-offs such as the decision of whether to adopt an expensive and uncertain therapy. This is especially relevant in the case of emerging therapies where often only limited evidence is available [51]. In addition, it can inform us with regard to the optimal study design and optimal sample size of a study [23].

There is an ongoing lively debate on whether proton therapy should be adopted in clinical practice and whether further evidence is needed [9, 29–39]. With such a promising but expensive technique, it is only natural that these debates exist. Difficult trade-offs need to be made, with lives of patients possibly at stake, while evidence is lacking. In this light, Hofmann recently pointed out that the current debate on proton therapy contains flawed elements and that these are general flaws particularly recognized in debates on technology [34]. Indeed, the current debate tends to overlook the existing evidence on clinical and cost-effectiveness. It is possible that flawed arguments result in suboptimal cancer treatment, for example, if the technology is adopted on false premises or if it is rejected on the basis of an assessment of the quality of the arguments instead of the technology [34]. Patients deserve the best technology available, on the basis of the best available evidence and also on the basis of the best arguments. When analyzing new and emerging technologies, all risks of harm as well as all possible benefits need to be taken into account [52]. This needs to be done in a way that properly acknowledges the uncertainties in predicting the consequences of adopting the technology. Although it surely is not the only argument in the adoption decision, we have illustrated that ROA is a useful state-of-the-art technique that assists in this matter. The use of real options analysis provides an evidence-based answer to the question of whether to adopt now or wait for more evidence.

Supplemental Data

A list of input parameters for the cost-effectiveness model can be found in supplemental online Table 1A.

See the accompanying commentary on pages 1672–1674 of this issue.

Author Contributions

Conception/Design: Janneke P.C. Grutters, Keith R. Abrams, Dirk de Ruysscher, Madelon Pijls-Johannesma, Philippe Lambin, Manuela A. Joore

Provision of study material or patients: Janneke P.C. Grutters, Philippe Lambin, Manuela A. Joore

Collection and/or assembly of data: Janneke P.C. Grutters, Keith R. Abrams, Madelon Pijls-Johannesma, Manuela A. Joore

Data analysis and interpretation: Janneke P.C. Grutters, Keith R. Abrams, Dirk de Ruysscher, Hans J.M. Peters, Eric Beutner, Manuela A. Joore

Manuscript writing: Janneke P.C. Grutters, Keith R. Abrams, Dirk de Ruysscher, Madelon Pijls-Johannesma, Hans J.M. Peters, Eric Beutner, Manuela A. Joore

Final approval of manuscript: Janneke P.C. Grutters, Keith R. Abrams, Dirk de Ruysscher, Madelon Pijls-Johannesma, Hans J.M. Peters, Eric Beutner, Philippe Lambin, Manuela A. Joore