Exchange-Mediated Contrast Agents for Spin-Lock Imaging

Abstract

Measurements of relaxation rates in the rotating frame with spin-locking (SL) techniques are sensitive to substances with exchanging protons with appropriate chemical shifts. We develop a novel approach to exchange rate selective imaging based on measured T_1ρ dispersion with applied locking field strength, and demonstrate the method on samples containing the X-ray contrast agent Iohexol (IO) with and without cross-linked bovine serum albumin (BSA). T_1ρ dispersion of water in the phantoms was measured with a Varian 9.4T magnet by an on-resonance SL pulse with fast spin-echo readout, and the results used to estimate exchange rates. The IO phantom alone gave a fitted exchange rate of ~1 kHz, BSA alone was ~11 kHz, and in combination gave rates in between. By using these estimated rates, we demonstrate how a novel SL imaging method may be used to enhance contrast due to the presence of a contrast agent whose protons have specific exchange rates.

INTRODUCTION

There has been much recent interest in developing new chemical exchange saturation transfer contrast (CEST) agents that take advantage of the specific MR properties of tissues or substances with large concentrations of exchanging protons with appropriate chemical shifts. The dynamics of protons in exchange with amide (RC(O)NR'R), which will be abbreviated here by its functional site (NH⁺) for brevity, or hydroxyl (⁻OH) sites on polymers, peptides, or sugars, have been explored for generating novel endogenous sources of contrast (1–4). Alternately, for exogenous contrast agents, paramagnetic metals such as europium may be used to shift proton precession frequencies to selectively increase exchange effects in conjunction with saturation contrast experiments (paraCEST) (5,6). Radiographic contrast agents such as Iohexol (Omnipaque®, GE Healthcare) or Iopamidol (Isovue®, Bracco) contain numerous NH⁺ and ⁻OH functional groups and so have also been explored recently as promising CEST contrast agents (7,8).

An alternate method of exploring chemical exchange-based contrast uses spin-locking techniques. Measurements of relaxation rates in the rotating frame (R_1ρ and R_2ρ) with spin-locking (SL) techniques have been shown to be sensitive to molecular motions and exchange processes on the time scale of the locking field (ω₁ = γB₁) (9,10). Observed variations in T_1ρ with locking-field strength (T_1ρ dispersion) provide information on molecular motions and chemical exchange on intermediate to fast time-scales (11). At high fields the increased separation of resonance frequencies between water and other chemical species such as amides can give rise to relatively greater contributions from chemical exchange. These variations can be exploited to distinguish differences in tissue composition, pH, or other chemical properties. These exchange processes are of interest not only for their effects on R_1ρ but also on R₂ and as modulators of saturation transfer contrast (12,13).

Here we demonstrate that T_1ρ dispersion may be used in conjunction with a novel image subtraction method to emphasize the presence of nuclei characterized by specific exchange rates (rather than chemical shifts) and thereby can be used to generate novel image contrast. T_1ρ dispersion techniques may complement or provide a number of advantages over traditional saturation transfer techniques. These advantages include the elimination of saturation effects near the water resonance for protons with small chemical shifts and also for the exploration of tissues or agents with non-symmetric CEST spectra such as those with significant lipid content. These two effects may complicate the off-resonance spectral subtraction technique used in CEST imaging (2,14,15). Spin locking techniques may carry an advantage in sensitivity to exchanging sites with either rapid exchange or small chemical shift such as from ⁻OH groups (typically 0.8–1.8 ppm, and k_ex > 1 kHz) where rapid exchange broadening limits CEST enhancement (16,17).

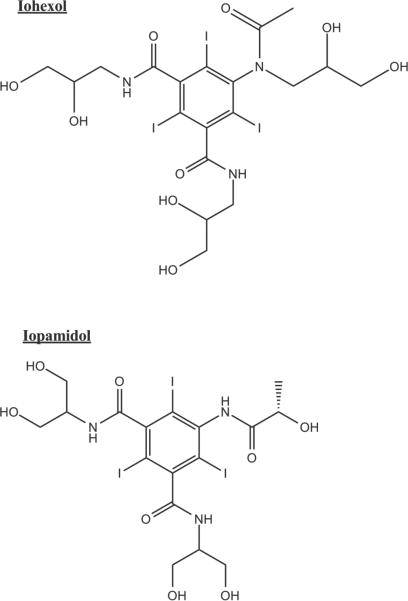
Here we show how a commonly used X-ray contrast agent can be used as an exchange-based exogenous agent to generate novel image contrast. Iohexol (CAS Num: 66108-95-0) is a member of a family of iodine-based CT contrast agents used clinically in a variety of angiographic and neurologic screening protocols. Iohexol carries two available NH⁺ and six ⁻OH functional groups that impart it with suitable MR properties for use as an exchange-based contrast agent. Note that the structure of Iohexol is different from Iopamidol. Iopamidol has three available NH⁺ and five ⁻OH sites (See Figure 1). We demonstrate how appropriate spin-locking techniques can be used to produce novel contrast in the presence of Iohexol.

Figure 1.

1.a. Structure of Iohexol.

1.b. Structure of Iopamidol. Note the differences in available NH⁺ and ⁻OH sites.

METHODS

Samples of cross-linked 10% bovine serum albumin (BSA) were created in 0.6 mL plastic tubes by the addition of 1% glutaraldehyde with and without Iohexol (IO) in 32 mM concentrations. Additional tubes of 16 mM IO were created with D₂O replacing the stock solution's tris(hydroxymethyl)aminomethane (TRIS) buffer in three increments. Finally, tubes of 16 mM IO were modified by the addition of hydrochloric acid to create phantoms with pH ranging from 5.5 to 7.4.

NMR Experiments

All NMR experiments were performed on a Varian 9.4T magnet (Varian Medical Systems, Palo Alto, CA) with a 10-mm loop-gap coil. Temperature was monitored by thermocouple connected to an animal physiologic monitoring system (SA Instruments, Stony Brook, NY) and was maintained at 37° C.

To identify the chemical shifts of exchanging protons, ¹H spectra of partially deuterated samples were acquired with the following parameters: a 50 μs 90-degree pulse, 12k complex points, TR = 12 sec, NEX = 16.

T_1ρ dispersion was measured with a spin-locking sequence consisting of an adiabatic 90-degree pulse, followed by an on-resonance spin-locking (SL) pulse for half of the spin lock time (SLT). Then a 180-degree refocusing pulse is inserted, followed by the other half of the SL pulse with phase reversal (18). The SL pulse was varied in 10 time increments (SLT) between 20 ms and one sec and also in amplitude (SLA) in 12 increments between 2π*[250 Hz and 10 kHz]. TR was set at 5 times the T₁ of the Iohexol solution.

Imaging Experiments

Imaging experiments were performed with a 38 mm birdcage coil at 9.4T. T_1ρ weighted images were recorded with a modified ΔB₀ and ΔB₁ insensitive SL pulse as described by Witschey et al. followed by a fast spin-echo acquisition (18). The spin-lock pre-pulse also utilizes an adiabatic 90-degree excitation, followed by on-resonance spin lock at a power of SLA for one half of the SLT. This is followed by a 180-degree refocusing pulse and the second half of the SL pulse with phase reversed. A reverse adiabatic 90-degree pulse returns the T_1ρ-prepped signal to the Z-axis and then residual transverse magnetization is spoiled. Ten SLTs were acquired as before at twelve SLAs between 2π*[250 and 10 kHz]. Other parameters included: FOV = 25 × 25 × 1 mm, matrix = 64 × 128 × 1, TR = 4 sec, TE = 10 ms, Echo Train Length = 8.

Theory and Data Analysis

T_1ρ values were calculated by fitting the signal variation with SLT to a three-parameter mono-exponential decay function in MATLAB (The MathWorks, Inc., Natick, MA). Then the T_1ρ dispersion data with locking field (ω₁) were fit to a three-parameter model described by Hills and Chopra et al. (shown in Eq. 1) to provide an estimate of exchange rate (k_ex), R₂, and $R_{1\rho }^{\infty }\approx {\mathrm{R}}_1$ in MATLAB (9,10,19).

$$R_{1\rho }=\left\{\frac{R_2+\frac{R_{1\rho }^{\infty }{\omega }_1^2}{k_{ex}^2}}{1+\frac{{\omega }_1^2}{k_{ex}^2}}\right\}$$ [1]

Chopra et al. considered the general case of rotating-frame relaxation in which exchanging nuclei experience different relaxation rates as well as chemical shifts when moving between phases. Chopra et al. modified the Bloch equations and showed how, under specific conditions, an experiment measuring R_1ρ at different locking field strengths (ω₁) may be used to determine solvent exchange rate. A non-linear least-squares fit of the variation of R_1ρ with ω₁ to Eq. 1 may be used to obtain best fits of R₂, $R_{1\rho }^{\infty }$, and $S_{\rho }^2$, where ${\mathrm{S}}_{\rho }^2=\sim {\mathrm{k}}_{\mathrm{ex}}^2$ given the following simplifications. It was assumed that the exchange is dominated by one exchanging site, operates in the fast-exchange limit (k_ex/Δω_b > 1), and that the exchange rate exceeds the exchanging site relaxation parameters R₁ and R₂. Metabolite R₁ and R₂ values are typically on the order of 1 s⁻¹ and 10 s⁻¹ respectively for aqueous solutions (20,21). These assumptions were deemed reasonable in light of previous reports giving amide exchange rates of 2560 Hz at 7T in a similar molecule (7), and that hydroxyl exchange rates often meet the requirements for fast-exchange (16). These assumptions are consistent with simulations and model fittings by both Hills and Woessner (6,22). Thus, a study of R_1ρ vs. ω₁ may be used to estimate exchange rates. This approach has been previously used to estimate exchange rates in cartilage systems and also in acrylamide gels(23,24).

Two image subtraction methods were used to derive contrast based upon the features of R_1ρ dispersion profiles that are a function of a species' mean exchange rate. A plot of R_1ρ dispersion (R_1ρ vs. applied locking field (ω₁)) will feature an inflection point near the mean exchange rate (10). The first approach, taken by Kogen et al. (25) and shown in Eq. 2, acts as a low-pass exchange rate filter, and emphasizes contrast from species whose mean exchange rate falls between ω₁(low) and the maximum selected locking field in Eq. 2, ω₁(high). This is because a species with exchange in this regime will also have maximum dispersion in this region, thus producing a larger difference between signal acquired at ω₁(high) and ω₁(low), to enter into Eq. 2. This method is also dependent on the magnitude of R_1ρ dispersion observed in a species, and hence is also strongly affected by variations in R₂ and $R_{1\rho }^{\infty }$.

$$\%CE({\omega }_1,SLT)=\frac{S({\omega }_1\left(high\right),SLT)-S({\omega }_1\left(low\right),SLT)}{S({\omega }_1\left(high\right),SLT)}\ast 100\%$$ [2]

where S is the signal in each pixel, ω₁(high) is the high frequency locking field, ω₁(low) is the low frequency locking field, and SLT is the spin lock time.

We propose an extension of this concept to reduce the effects of the magnitude of T_1ρ dispersion on image contrast, which is a function of ${\mathrm{R}}_2-R_{1\rho }^{\infty }$. Instead we wish to emphasize contrast based primarily upon an exchange rate of interest. Equation 3 modifies Eq. 2 with the addition of another locking-field measurement at a specific exchange rate, ω₁(ex), and now uses ω₁(high) and ω₁(low) to refer to ω₁ values much greater and much less than the expected exchange rate respectively.

$$CE({\omega }_1\left(ex\right),SLT)=4\ast \frac{(S({\omega }_1\left(high\right),SLT)-S({\omega }_1\left(ex\right),SLT))\ast (S({\omega }_1\left(ex\right),SLT)-S({\omega }_1\left(low\right),SLT))}{{(S({\omega }_1\left(high\right),SLT)-S({\omega }_1\left(low\right),SLT))}^2}$$ [3]

For the imaging experiments performed here, ω₁(high) is set to the maximum SLA acquired and ω₁(low) is set to the minimum SLA. The term in the numerator gives a maximum value when the locking field ω₁(ex) is set equal to the mean exchange rate (k_ex). The terms in the denominator scale the numerator by the magnitude of the T_1ρ dispersion (${\mathrm{R}}_2-R_{1\rho }^{\infty }$), thus minimizing the effect of a large dispersion on the resulting image. As the maximum value obtained from the ratio is ¼ when the exchange rate equals ω₁(ex) and zero when the exchange rate is far from ω₁(ex), thus a normalization factor of 4 was also used. A 5% threshold mask was applied before subtraction to reduce the effects of background noise.

RESULTS

The proton spectra acquired to estimate the frequency of exchanging species revealed a peak near 0.6 ppm that is attributed to ⁻OH protons on the Iohexol molecule. A small NH⁺ peak near 4.2 ppm is initially visible on the ¹H spectrum of the 16 mM solution but not after deuteration.

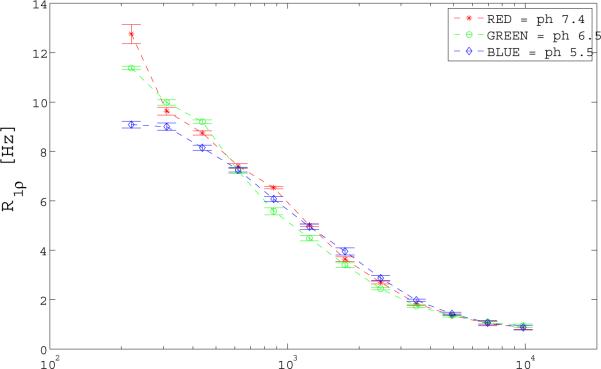
R_1ρ dispersion data with locking field and with varied pH were acquired to verify the presence of chemical exchange. Figure 2 shows R_1ρ dispersion as a function of applied locking field (γB₁) for the 16 mM IO phantoms. After pH modification the T_1ρ value at the lowest locking field, where R_1ρ ≈ R₂, showed a small increase with pH. Proton exchange rates were fitted as 750, 810, 1260 Hz for the 5.5, 6.5, and 7.4 pH phantoms respectively.

Figure 2.

R_1ρ (1/ T_1ρ) dispersion variation with pH for the 16 mM IO phantom to verify the presence of an exchanging species. Note only a slight difference in profile with the largest difference in R_1ρ occurring at the lowest acquired power of B₁ = 250 Hz.

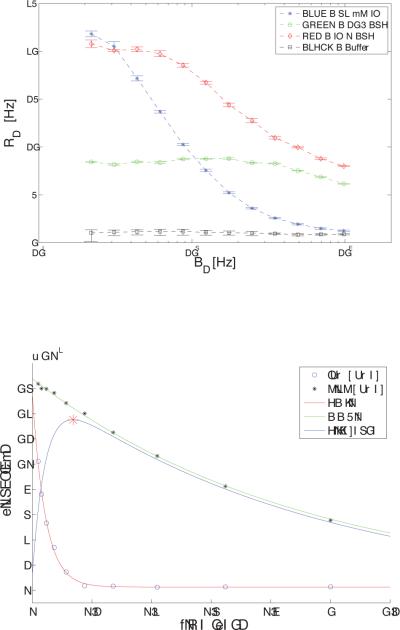
Figure 3.a shows T_1ρ dispersion profiles for the 32 mM IO with and without BSA and buffer solutions. Calculated values of R₂, $R_{1\rho }^{\infty }\approx {\mathrm{R}}_1$ and exchange rate from the Chopra fitting of these dispersion curves are given in Table 1. The 10% cross-linked BSA alone is characterized by a very flat profile with R_1ρ (1/T_1ρ) vales ranging from 8.6 s⁻¹ at a locking field of 225 Hz to near 6 s⁻¹ at 10 kHz with little contributions from apparent exchange over this range. The IO alone showed a large dispersion from a value of 23.6 s⁻¹ at a locking field of 250 Hz to 1.6 s⁻¹ at 10 kHz. The calculated exchange rate for the 32 mM IO phantom is 1128 Hz. For the combined BSA and IO substance, T_1ρ dispersion was much more marked than for BSA alone. However, the dispersion curve is not a simple sum of these components, and the inflection point moves to higher frequencies than for IO alone (Fig. 3.a). The mean exchange rate for the 32 mM IO plus 10% BSA phantom occurs near 2860 Hz. Note that the contrast is also dependent on the large dispersion between $R_{1\rho }^0$ and $R_{1\rho }^{\infty }$ as shown in Figure 3.a. and Table 1, giving a large potential enhancement to the IO and the IO plus BSA phantoms at locking field frequencies less than ~5 kHz.

Figure 3.

Shows R_1ρ (1/ T_1ρ) dispersion differences with ω₁ for the X-ray contrast agent Iohexol, BSA, and the combined IO + BSA substance, with the buffer solution for reference.

3.a. 32 mM IO (blue stars), BSA (green circles), IO+BSA (red diamonds), and buffer (black squares) phantoms. Note that the R_1ρ dispersion for the IO + BSA phantom was much more marked and occurs at a lower frequency than for BSA alone.

3.b. Time course of signal decay for 32 mM IO phantom at low (250 Hz) and high power (1 kHz). The point of maximum contrast occurs at 137 msec.

Table 1.

	R2 [s-1]	R1∞ [s-1]	Exchange Rate [Hz]
10 % BSA	8.6	2.8	11350
Buffer	1.1	0.8	2920
BSA + IO	20.8	7.9	2860
32 mM IO	23.6	1.6	1128

T_1ρ signal decay of the IO phantom at low locking field (SLA = 250 Hz) and at the mean exchange rate of 1128 Hz (SLA = ~1 kHz) was plotted in Figure 3.b to evaluate the magnitude of the signal difference between the two decay rates. The exchange dependent signal difference between low locking field and the locking field nearest the calculated exchange rate is also shown in Figure 3.b. The maximum signal difference between the signal at low and high locking fields occurs at SLT ≈ 137 msec.

Figure 4 uses Eq. 2 to enhance contrast based on exchange rate and the magnitude of R_1ρ dispersion in the IO and BSA phantoms. Figure 4.a. shows a “T₂-weighted” image to demonstrate the initial similarity of the 32 mM Iohexol, 10% BSA, and combined IO and BSA phantoms at SLT = 20 msec and SLA = 250 Hz. Figure 4.b. shows a difference image representing the numerator of Eq. 2 at the closest measured locking field to the calculated exchange rate of the combined IO and BSA phantom (SLA (2800 Hz) − SLA (250 Hz)). This high power value was chosen to enhance sensitivity to the exchange rate of the IO + BSA phantom where k_ex = ~2860 Hz. The maximum signal difference between the low and high locking fields occurs at 173 msec, and so the closest measured SLT of 176 msec was used for the subtraction image. A large contrast difference between the BSA phantoms with and without the presence of IO was observed. Additionally, the IO phantom was significantly enhanced. Figure 4.c. uses the subtraction technique from Eq. 2 to generate a percent contrast image. Phantoms with IO show a large contrast enhancement. Using this exchange selective approach, contrast in the BSA was increased by 70–80% due to the presence of Iohexol in the phantom, while BSA alone has almost no enhancement.

Figure 4.

Demonstrates the use of Eq. 2 to generate contrast based on the magnitude of dispersion and chemical exchange rate for phantoms of the X-ray contrast agent Iohexol (32 mM), BSA (10 % wt/wt), and a combined IO + BSA mixture.

4.a. Low power (SLA = 250 Hz), short duration (SLT = 20 msec) image of all three phantoms: Top Left = IO alone, Top Right = BSA alone, Bottom = Both.

4.b. An image representing the numerator of Eq. 2, with the subtraction of a low power (250 Hz) image from a higher power image (2800 kHz) at 176 msec. The high power value was chosen to enhance sensitivity to the exchange rate of the IO + BSA phantom. Note the large contrast difference between the BSA phantoms with and without the presence of IO. The spin-locking pulse acts as an exchange-rate filter, enhancing contrast from the phantoms with exchange rates slower than the high-power locking field and with large dispersions.

4.c. A normalized percent contrast enhancement image from Eq. 2. Phantoms with IO show a large contrast enhancement. Note that the BSA+IO phantom shows an enhancement of 70–80% due to the presence of IO, while BSA alone has almost no enhancement.

In order to reduce the effect of the magnitude of R_1ρ dispersion on the subtraction technique from Eq. 2, the same data from Figure 4 were used with Eq. 3 to generate Figure 5. For consistency, the same locking field time (SLT) of 156 msec was used for all image subtractions with only the ω₁ value being varied. This time point is an empirically derived choice for all phantoms, and is nearly twice the average $T_{1\rho }^0$ of all the species, and allows sufficient time for spin-lock contrast to develop, but is not so long as to allow all species' signal to deteriorate into noise. The SLT may also be varied to provide an optimal value when comparing any two substances of interest. Figure 5.a. shows the results of choosing ω₁(ex) at the nearest acquired SLA (~2π*1 kHz) to the mean exchange rate of the IO phantom (1186 Hz). Note that the signal from the IO only phantom dominates the image contrast. Figure 5.b. used a ω₁(ex) of ~2π*2800 Hz. Here the contrast from the IO+BSA contrast is maximized. Figure 5.c. shows the results of choosing ω₁(ex) to be (~2π*7800 Hz), which was the highest available SLA to use for the technique. Even though the estimated mean BSA exchange rate is near 11 kHz, sufficient separation of frequencies allows for the BSA phantom to show good selective contrast.

Figure 5.

Demonstrates a novel exchange rate based contrast enhancement method using Eq. 3. The same image data from Figure 4, which used Eq. 2, were used to generate Figure 5. Image values near one represent a good match between the selected ω₁(ex) and the average exchange rate. Values for ω₁(high) and ω₁(low) were fixed at the maximum and minimum acquired SLA. Top Left = IO alone, Top Right = BSA alone, Bottom = Both.

5.a. ω₁(ex) = ~1 kHz, SLT = 156 msec.

5.b. ω₁(ex) = ~2800 Hz, SLT =156 msec.

5.c. ω₁(ex) = ~7800 Hz, SLT = 156 msec.

Note that by choosing an exchange rate near the mean exchange rate of the phantom of interest, the contrast can be modified to emphasize the presence of a substance with an exchange rate near the selected ω₁(ex) value.

DISCUSSION AND CONCLUSION

The novel technique based on Eq. 3 and demonstrated in Fig. 5 illustrates that images can be made with spin-locking methods whose contrast reflects the presence of exchanging protons with specific exchange rates. Prior methods used spin-locking pulses as an exchange rate filter, enhancing signal from exchange rates below the selected locking field and with large R_1ρ (1/ T_1ρ) dispersions. However, these methods produce contrast that depends on the magnitude of the dispersion ($R_{1\rho }^0-R_{1\rho }^{\infty }$) with locking field, and therefore they are not specific to exchange rate. For Iohexol, a large R_1ρ dispersion is observed around 1 kHz that is due to chemical exchange at one or more of the ⁻OH or NH⁺ sites on the Iohexol molecule with the surrounding water. The exchange seen in BSA alone occurs at much higher rates and results in a much flatter dispersion profile, while the combined materials show intermediate exchange rates. By appropriate selection of the spin lock field amplitudes, maximal contrast can be derived from nuclei whose dispersion (exchange rate) occurs at the locking frequency.

Multiple exchanging peaks were identified from the proton spectrum and were reduced when D₂O replaced H₂O. This verifies that the NH⁺ at 4.2 ppm and ⁻OH protons on the Iohexol molecule near 0.6 ppm are in exchange with the solvent. Note that the exact peak locations are not critical for obtaining our exchange estimates and that rapid proton exchange may have shifted the observed peak locations. The ⁻OH and NH⁺ peak assignments were made by comparison of the acquired spectrum to other published high-resolution ¹H spectra (8,26).

The Iohexol samples in Figure 2 show small increases in calculated exchange rate over the range of pH values studied. It is important to note that the calculated exchange rate estimates are apparent average rates and may reflect the combined effects of molecular motions and chemical exchange of several exchanging species in the phantom. No attempt has been made to separate the relative contributions of ⁻OH vs. NH⁺ (11). These species resonate with different relative chemical shifts and have been shown to exchange with water at different rates (2,16,27). At low exchange rates, the T_1ρ dispersion profile scales to higher frequency as the chemical shift of a species increases (19). This may contribute an error in the estimated exchange rates due to the assumptions listed in the methods section. However at the relatively rapid exchange rates reported here, especially for hydroxyl exchange, the effect on the estimates should be small. There is also a potentially important effect of the TRIS buffer solution where the primary amine (R-NH₂) may contribute to the overall T_1ρ dispersion profile (16). For this reason the buffer solution was explicitly included in Fig. 3.a. to demonstrate that its effect was also small.

BSA was chosen as a tissue phantom due to its well-studied proton relaxation properties and the ability to modulate the number of exchanging amide groups via glutaraldehyde (GA) cross-linking. The amount of GA used determines the approximate degree to which the protein matrix is cross-linked. For a 1% GA solution, the resulting gel should be nearly 100% linked (28), leaving only a few exchanging groups to conflict with Iohexol proton exchange.

Figure 3.a. shows the dramatic effect of the presence of the X-ray contrast agent Iohexol on the BSA tissue phantom. The addition of IO to the BSA phantom greatly alters its R_1ρ dispersion profile, where at low SLA the combined phantom has an R_1ρ near that of IO alone (~ 22 s⁻¹). This shift to much higher R_1ρ value at low locking field may be best thought of as a change in R₂. At high frequency the measured R_1ρ approaches that of BSA alone (~ 3 s⁻¹). The observed mean chemical exchange rate moves to lower frequencies by the addition of IO to BSA. This shift to lower frequencies is due to a corresponding shift in the average exchange rates, and it allows for contrast to be selected via locking field (within the limits of the imaging system) and it demonstrates a unique way to selectively modulate contrast based upon species exchanging at specific rates.

The potential contrast demonstrated as a large exchange-mediated R_1ρ dispersion in Figure 3 is consistent with other authors who report similar effects in image contrast with CEST techniques on Iopamidol (7,8). This technique may be improved by an optimized sampling scheme where sampling points in time and in locking field are more closely spaced around appropriate inflection points (29). For example, as shown in Fig. 3.b., the nearest time point to the point of maximal contrast is several tens of msec away.

We have presented two different approaches to use R_1ρ dispersion contrast. Either R_1ρ subtraction technique may be used to emphasize the presence of IO in the BSA phantom by appropriate selection of locking fields. For the method demonstrated in Eq. 2, the high SLA rate acts as an exchange rate filter, emphasizing contrast from species with large R_1ρ dispersions at rates slower than the selected maximum locking field. This phenomenon is demonstrated in Figure 4 where selective contrast enhancement of between 70 and 80% was achieved in the IO + BSA phantom due to the presence of the Iohexol. As the BSA phantom alone has much higher apparent exchange rates, the T_1ρ-weighted signal at low (250 Hz) and high (2800 Hz) SLA is essentially the same and the BSA phantom drops out of the subtraction image. However, the phantom of Iohexol alone was also greatly enhanced as it has a large R_1ρ dispersion at frequencies lower than the selected maximum locking field. This is contrasted to Figure 5, which uses the subtraction technique outlined in Eq. 3. Here the effect of the large T_1ρ dispersion shown in the IO phantom may be reduced by selectively choosing the locking field nearest to the exchange rate of the species of interest as illustrated in Fig. 5.b. and 5.c. This technique may therefore be thought of as exchange rate selective. This technique may be useful in distinguishing two substances with similar R₂ values but differing mean exchange rates.

The most significant drawback of either subtraction technique is the large SNR degradation suffered during image subtraction. The method outlined in Eq. 3 suffers a greater time- and ω₁-dependent degradation of image contrast as compared to the method outlined in Eq. 2 due to division by a squared signal difference. Therefore as mentioned in the methods section, a 5% threshold mask was applied to the images in Figure 5 before subtraction to reduce the effects of background noise. This measure was not necessary for the method outlined in Eq. 2, as the normalized subtraction still produced acceptable images.

For the Iohexol system studied here, the simultaneous contributions of ⁻OH vs. NH⁺ to overall image contrast and T_1ρ dispersion in spin-locking experiments highlights a potential weakness of the SL technique in comparison to CEST imaging. The CEST technique carries a few advantages in terms of power deposition and in spectral selectivity. Both CEST and SL techniques generate contrast with long saturation pulses, but the CEST saturation pulse is typically low-power and well off-resonance with respect to water. This allows for easier translation to in vivo and clinical imaging with respect to specific absorption rate (SAR) restrictions. CEST has been used clinically in a number of applications, and an excellent review of the technique has recently been published (30). Additionally, the spectral selectivity of CEST allows for the saturation of an exchanging species of choice, thus minimizing effects from other exchanging species. For example, previous studies of X-ray contrast agents typically use the amide peak, which is well separated from water, to generate image contrast (7). However, for spin locking, the contribution of exchanging ⁻OH groups may exceed the contribution of NH⁺ groups especially as typical hydroxyl exchange rates are generally an order of magnitude greater than amide exchange rates (2,8). Due to the small chemical shift of hydroxyl peaks, these are rarely used for quantitative CEST imaging due to conflation with the water peak. In addition, for rapidly exchanging species, CEST techniques are adversely affected by line broadening, while SL techniques may still be used to generate useful image contrast (17). Spin-locking techniques may be sensitive more to the rate of exchange than to the chemical shift, and thus the contribution of the slowly exchanging species to T_1ρ contrast is often ignored (31), which makes T_1ρ contrast complementary to the CEST sensitivity to slow amide exchange.

As demonstrated here, large exchange rate differences may be exploited to generate novel contrast. Spin-locking techniques have seen less adoption than CEST, presumably due to the multiple on- and off-resonance effects to which it is sensitive. The majority of applications reported to date have been in musculoskeletal imaging where changes in sugars such as chondroitin sulfate have been implicated in disease processes (32). A new method to separate the multiple contributions to T_1ρ may be the so-called “CESTrho” technique that combines off resonance CEST saturation of one spin population with subsequent on-resonance spin locking (33). However, the use of two long saturation pulses poses considerable problems for use in vivo due to SAR restrictions. Further study is required to illuminate the relative benefits and applications for each technique.

A strength of the T_1ρ technique is the ability to make dispersion measurements in an imaging context to reveal contrast at specific exchange rates. This is opposed to T₂ dispersion observed in the Carr-Purcell-Meiboom-Gill sequence, where the ability to string together 180 degree pulses is limited to a relatively low frequency. Spin-locking allows for ready translation to in vivo imaging, with the range of achievable locking fields being the primary limitation (9,10). Typically the lower limit of measurable exchange rates is given by the heterogeneity in the B₁ or B₀ fields generated in the tissue of interest. The upper limit is given by the stable cw-power achievable by the RF amplifier and specific absorption rate considerations. These rates are typically in the 20 kHz range on small animal systems and 2 kHz for human imagers. With most biological exchange processes in the kHz range (2,10,11,16,34), T_1ρ dispersion holds much promise for characterizing these processes in a variety of in vivo and ex vivo experiments.

In conclusion, spin locking may be used to enhance contrast in tissues due to the presence of an intrinsic or exogenous agent whose protons have specific exchange rates. For Iohexol, R_1ρ dispersion around 1 kHz is due to chemical exchange at one or more of the ⁻OH and NH⁺ sites on the Iohexol molecule with the surrounding water. The exchange seen in BSA alone occurs at higher rates, while the combined materials show intermediate exchange rates. By appropriate selection of the spin lock fields, maximal contrast can be derived from nuclei whose dispersion (exchange rate) occurs at the locking frequency.