More than one dynamic crossover in protein hydration water

Abstract

Studies of liquid water in its supercooled region have helped us better understand the structure and behavior of water. Bulk water freezes at its homogeneous nucleation temperature (approximately 235 K), but protein hydration water avoids this crystallization because each water molecule binds to a protein. Here, we study the dynamics of the hydrogen bond (HB) network of a percolating layer of water molecules and compare the measurements of a hydrated globular protein with the results of a coarse-grained model that successfully reproduces the properties of hydration water. Using dielectric spectroscopy, we measure the temperature dependence of the relaxation time of proton charge fluctuations. These fluctuations are associated with the dynamics of the HB network of water molecules adsorbed on the protein surface. Using Monte Carlo simulations and mean-field calculations, we study the dynamics and thermodynamics of the model. Both experimental and model analyses are consistent with the interesting possibility of two dynamic crossovers, (i) at approximately 252 K and (ii) at approximately 181 K. Because the experiments agree with the model, we can relate the two crossovers to the presence at ambient pressure of two specific heat maxima. The first is caused by fluctuations in the HB formation, and the second, at a lower temperature, is due to the cooperative reordering of the HB network.

Recent experiments have studied water in the first hydration shell of globular proteins (1–5). Unlike bulk water, this water does not freeze until the temperature T is well below 235 K (6), a property that may be essential to biological functioning (7). Although quasi-elastic neutron scattering investigations (1) and molecular dynamics simulations (8, 9) support the presence of a dynamic crossover at approximately 220 K, other experiments and simulations do not (2–4, 10). It has been demonstrated that the suggested crossover could be related to the anomalous behavior of water, but that it is independent of any possible liquid–liquid critical point at finite T (11).

Here, we show by experiments, simulations, and model calculations that the dynamic properties of the hydrogen bond (HB) network at the protein–water interface exhibit not one, but two dynamic crossovers in the one-phase region at low pressure. We show how the two crossovers are related to the thermodynamics of water. We investigate the dielectric relaxation time of water protons, due to charged defects—such as H₃O⁺—moving with a diffusive or hopping mechanism along the HB network (6, 12). These measurements are a sensitive probe for HB breaking and formation (13). We perform dielectric relaxation experiments on lysozyme powder with hydration level h = 0.30 g H₂O/g dry protein, over a broad frequency (10^-2 s^-1–10⁸ s^-1) and temperature range (150 K ≤ T ≤ 300 K). The experimental setup and the data analysis (14–18) are described in Methods and SI Text.

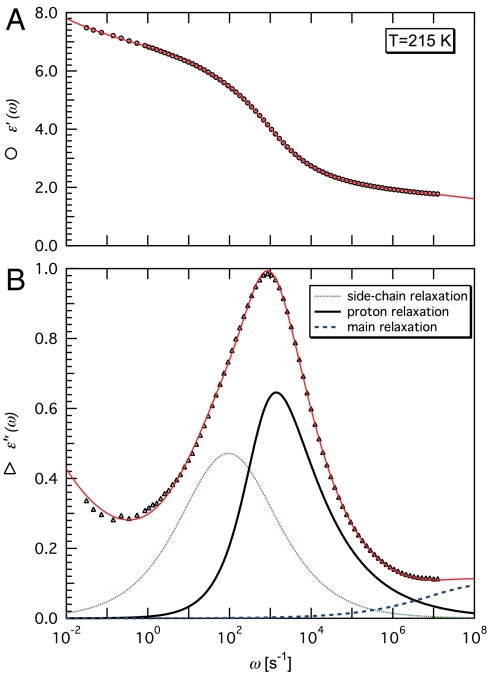
In the dielectric spectrum for lysozyme powder at 215 K (Fig. 1), we identify (i) a low-frequency tail, (ii) a relatively broad process at intermediate frequencies, and (iii) a small high-frequency relaxation. The low-frequency tail (i) is due to electrode polarization, to interfacial dispersion (also known as the Maxwell–Wagner effect), and to sample conductivity (see Methods). The high-frequency process (iii) has a relaxation time with a T dependence and absolute values identical to recent dielectric measurements on the same protein with the same water content h (3, 4). This process is labeled “main” in the literature cited above, and we will be using this terminology (see Methods and SI Text). This relaxation is undetectable at hydration levels below h ∼ 0.3 g H₂O/g dry protein, and we assign it to a local relaxation of protein hydration water (3), although its assignment and temperature dependence are controversial (19, 20).

Fig. 1.

Dielectric relaxation data for lysozyme powder at 215 K and hydration level h = 0.30 g H₂O/g dry protein. (A) ϵ^′ (◯) and (B) ϵ^″ (▵) are real and imaginary components, respectively, of the complex permittivity 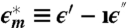, and ω is the angular frequency. Solid lines through symbols result from the fitting procedure in the complex plane (14–18), described in Methods and SI Text. As shown in B for ϵ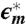^″, is resolved into (i) a low-ω tail (omitted for clarity), (ii) a broad process at intermediate ω deconvoluted into two relaxations (continuous and dotted lines), and (iii) a high-ω relaxation (dashed line).

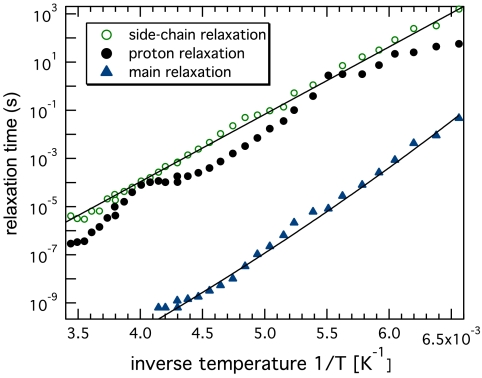
The broad relaxation process (ii), whose width at half maximum is about 3.5 frequency decades, can be resolved into two contributions (14), relatively close in frequency and largely overlapping but with a markedly different T dependence (Fig. 2). This decomposition has not been discussed in previous work (3, 4, 7), but a quantitative test for the presence of two relaxation processes is described in detail in ref. 14 (see Methods and SI Text). The quality of the two-relaxation fit, the T dependence, the h dependence, and the shape of each relaxation strongly suggest that two separate relaxations are present (see SI Text). Here, we label these processes “side-chain” relaxation and “proton” relaxation (Fig. 1). This labeling is based on previous studies of the T dependence and h dependence of the dielectric response of the same protein and of a similar globular protein (myoglobin). In particular, the side-chain process has a relaxation time in which the T dependence and absolute values agree with those measured by others for hydrated lysozyme powders (3) and hydrated myoglobin (7) (see Methods and SI Text). The side-chain relaxation has a symmetric shape over the entire temperature range investigated (see Fig. 3), in agreement with previous findings (3). This observation provides additional support for distinguishing the side-chain relaxation from the more asymmetric proton relaxation. Moreover, the wide temperature and frequency ranges investigated allow us to follow these two processes carefully and to identify them even when they are largely overlapping. The fitting parameters for each process, such as its relaxation time and shape parameters, change gradually with temperature, and this allows us to accurately distinguish between side-chain relaxation and proton relaxation at all temperatures.

Fig. 2.

Temperature dependence of the characteristic times of the relaxation processes shown in Fig. 1: side-chain relaxation (◯) and proton relaxation (•) of the intermediate-ω relaxation (ii), and “main” relaxation (▴) of the high-ω relaxation (iii). Solid lines are Arrhenius fits.

Fig. 3.

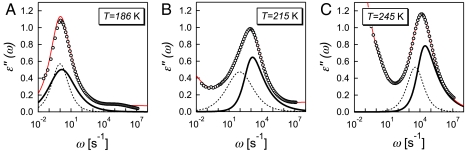
Imaginary component ϵ^″(ω) of the measured complex permittivity as a function of the angular frequency ω, at three temperatures, (A) T = 186 K, (B) T = 215 K, and (C) T = 245 K. Solid lines through the symbols are the result of the fitting procedure in the complex plane (see Methods and SI Text). Here, we show the results of the decomposition into two processes of the broad relaxation peak. Dashed lines represent the side-chain relaxation, and thick solid lines represents the proton relaxation. The fitting procedure yields a β₁ ≈ 1 (see Eq. 6) for the side-chain relaxation over the entire temperature range investigated, resulting in a symmetric relaxation process. Conversely, the same procedure gives a β₂ < 1 for the proton relaxation, resulting in a characteristic asymmetric shape. We omit for clarity the contributions due to sample conductivity and to electrode polarization at low frequency.

The proton relaxation that contributes to the broad peak in Fig. 1 is the focus of our work here, and it has been extensively studied (6, 14–18) at hydration h < 0.30 g H₂O/g dry protein. At these hydration levels, we find that the side-chain relaxation is indeed quite small and that it rapidly slows with dehydration, in agreement with ref. 3. The measured dielectric spectra for lysozyme at h < 0.30 g H₂O/g dry protein is thus dominated by the proton relaxation (6, 14–18). Its characteristic relaxation time and associated dc conductivity has been described in terms of percolation theory (6, 15). Its assignment to water-assisted proton displacements over the protein surface has been tested by measuring hydrogenated and deuterated samples (6, 16), and its quantum character has been checked experimentally using dielectric spectroscopy and deep inelastic neutron scattering (16, 21), and the results agree with theoretical models (22).

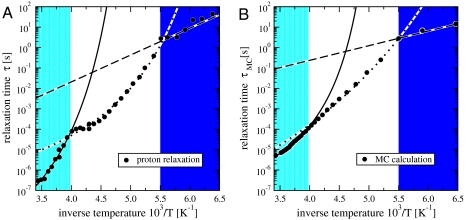
At hydration h < 0.30 g H₂O/g dry protein, the proton relaxation process has a characteristic relaxation time whose temperature dependence is well described by the Vogel–Fulcher–Tamman (VFT) equation τ(T) = τ₀ exp[B_T/R(T - T₀)], where τ₀, B_T, and T₀ are fitting parameters and R is the gas constant. Instead, for the sample water content, h = 0.30 g H₂O/g dry protein, the proton relaxation time τ at high T shows a VFT behavior, with a clear kink at T ≈ 252 K (Fig. 4A), where we find a crossover from one high-T VFT behavior to a second VFT behavior at a lower T. We associate the crossover at ≈252 K with a change in the diffusion regime of water protons, from subdiffusive at lower T to freely diffusive at higher T, which has been previously reported for a lysozyme sample at h = 0.26 g H₂O/g dry protein and 260 K (15). Note that the VFT description at high temperature of the water proton relaxation time is characterized by the same T₀ ∼ 200 K independent of the sample hydration (14–16). Moreover, τ would reach 100 s at approximately 220 K (Fig. 4A), which is often defined as the dielectric glass transition temperature. This value is in good agreement with the calorimetric glass transition temperature of the hydrated protein at the same hydration level (3, 4, 13, 15, 17, 18).

Fig. 4.

Two crossovers in the proton relaxation time τ of hydration water. We find a non-Arrhenius to non-Arrhenius crossover at T ≈ 252 K and a non-Arrhenius to Arrhenius crossover at T ≈ 181 K. (A) Experimental τ (•) vs. 1/T. Solid line is the VFT function with fitting parameters τ₀ = 7.8 × 10^-12 s, B_T = 9.4 kJ/mol, T₀ = 180 K. Dotted line is the VFT function with τ₀ = 6.5 × 10^-8 s, B_T = 6.2 kJ/mol, T₀ = 140 K. Dashed line is the Arrhenius function with fitting parameters τ₀ = 1.1 × 10^-7 s, A = 25.2 kJ/mol. The behaviors at high and low T intersect at about 232 K. Relative errors (not shown) on τ are about 0.2% for 1/T < 6 × 10^-3 K^-1 and are at least one order of magnitude larger for lower T (see SI Text for more details). (B) MC relaxation time τ_MC (•) vs. 1/T, for P = 0.1 MPa. Solid line is the VFT function with τ₀ = 1.61 × 10^-8 s, B_T = 5.2 kJ/mol, T₀ = 181.2 K. Dotted line is the VFT function with τ₀ = 7.5 × 10^-10 s, B_T = 15.9 kJ/mol, T₀ = 95.2 K. Dashed line is the Arrhenius function with τ₀ = 3.3 × 10^-4 s, A = 13.7 kJ/mol. See the text for the discussion about the quantitative differences between the numerical and the experimental results.

At T ≈ 181 K we observe a second crossover, as the T dependence of τ changes from the VFT above 181 K to Arrhenius τ(T) = τ₀ exp(A/RT) below 181 K, where τ₀ is a characteristic relaxation time and A a constant activation energy (Fig. 4A). To our knowledge, the crossover at approximately 181 K has not been previously reported. Here, we offer a possible interpretation based on the results of the model described below, and we attribute this crossover to a structural rearrangement of the HB network.

Neutron scattering experiments on the same hydrated protein have also revealed two dynamical transitions, one at 220 K and the other at 150 K (23). The transition at 220 K has been attributed to the rotational motion of interfacial water, and the one at 150 K has been attributed to proton dynamics on a very local scale (of the order of a few angstroms). The low temperature transition (150 K) has been attributed to a sudden increase in the configurational entropy of the system, linked to a significant change in the HB length (23). Deep inelastic neutron scattering experiments on the same hydrated protein do not support this claim because they do not find changes in the HB length or proton potential below 290 K (16, 21).

In order to study the microscopic mechanisms responsible for the dynamic crossovers observed at 252 K and 181 K, we use a coarse-grained model of a monolayer of water adsorbed on a generic inert substrate, which represents the low-hydrated protein powder. At this hydration level, the adsorption is such that water molecules are restricted to a surface geometry with a coordination number up to four (24). The temperature of their structural arrest is ≫250 K (25), hence they do not diffuse. Because water molecules do not crystallize (25), their positions and orientations fluctuate and they form and break HBs. These assumptions are based on the observation that, at the relatively low h value investigated, we have less than one monolayer of water molecules covering the protein surface, and the protein itself does not undergo any configurational transformation or large scale motion (6, 25). This model, originally proposed in ref. 26 and extensively studied, e.g., in refs. 11 and 27–32, reproduces the known properties of water at interfaces, including the shape of the locus of the temperatures of maximum density in the (T,P) plane, the anomalous behavior of thermodynamic response functions, the subdiffusive regime at low T for protein hydration water, and the occurrence of minima and maxima in diffusivity upon pressurization (33). It has also predicted behaviors for protein hydration water, successively verified by experiments (11, 34).

The model discretizes the coordinates of the water molecules in the monolayer into N cells, each containing one molecule, with a volume given by the inverse of the average water density and a height given by the monolayer thickness d. To take into account the change of configurational entropy upon HB formation, the model associates each molecule i with four variables σ_ij = 1,2,…,q with the index j running among the four neighbor molecules and with a discrete number of states q describing the bonding state of the molecule i with the neighbor molecule j. The model chooses q by adopting the standard convention that 30° is the maximum deviation of a HB from a linear bond (i.e., q ≡ 180°/30° = 6). For every molecule there are q⁴ = 6⁴ ≡ 1,296 total possible bonding states. The system is fully described by the average density V/N and the set of σ_ij.

The model separates the interactions among molecules into three components. The first is the sum of all isotropic interactions (e.g., van der Waals) between molecules at a distance r ≡ (V/Nd)^1/2, and is represented by a Lennard–Jones potential, U₀(r) = ϵ[(r/r₀)¹² - (r/r₀)⁶]. On the basis of previous experiments, the model uses attractive energy ϵ = 5.8 kJ/mol (35) and r₀ ≡ (v₀/d)^1/2 = 2.9 Å (36).

The second component is the directional component of the HB interaction. Neighboring molecules i and j form a HB when their facing bonding variables are in the same state (i.e., σ_ij = σ_ji). When a bond is formed, there is a J = 2.9 kJ/mol decrease in local energy, and a v_HB increase in local volume. Based on the change of density between tetrahedral ice Ih and the interpenetrating tetrahedral network in ice VI or ice VIII, the model uses v_HB/v₀ = 0.5. In real water the formation of HBs does not imply a larger separation between molecules but only a larger excluded volume per molecule. Therefore, in the model the increase v_HB does not affect the U₀(r) term but only the total enthalpy with a contribution -(J - Pv_HB)N_HB, where P is pressure and N_HB is the number of HBs in the system. N_HB is a function of the configuration of variables σ_ij

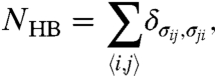[1]

where 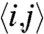indicates nearest neighbors and δ_a,b = 1 if a = b or δ_a,b = 0 if a ≠ b.

The final interaction is the cooperative (i.e., many-body) interaction among HBs, which gives rise to an O–O–O correlation (37) that drives the molecules toward a local ordered configuration. This is modeled using an interaction among the four σ_ij belonging to the same molecule, driving them toward the same state. For each molecule, there is a local energy decrease of J_σ = 0.29 kJ/mol for each of the six possible pairs of σ_ij in the same state.

The enthalpy of this model at pressure P is (26–28)

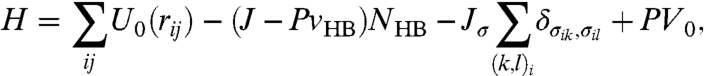[2]

where the first sum is over all pairs of molecules (i,j), the second sum is over all pairs of σ_ik belonging to molecule i, and V₀⩾Nv₀ is the water volume apart from the contribution of the HBs.

We perform Monte Carlo (MC) simulations at constant N = 10⁴, P and T, where V₀ fluctuates and the configuration of variables σ_ij changes, and therefore N_HB also changes. The result is a variable total volume V ≡ V₀ + N_HBv_HB. We explore the thermodynamics of the system in the P–T plane, confirming previous results (11, 26–31).

We next study the dynamic evolution of the system by adopting the single-spin flip Metropolis algorithm, which corresponds to Model A in the classification used by Hohenberg and Halperin (38). The most straightforward quantity to compare with the experiments considered here is the autocorrelation function

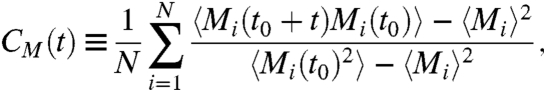[3]

where t is the time measured in MC steps, t₀ is a time larger than the equilibration time of the system, and 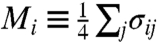quantifies the order of the four bond indices σ_ij of molecule i. Defining the MC relaxation time τ_MC from C_M(τ_MC) = 1/e, we observe two crossovers in the computed τ_MC, from VFT to VFT at T ≈ 252 K (in ref. 11 this crossover was estimated as VFT to Arrhenius due to the limited resolution at low T), and from VFT to Arrhenius at T ≈ 181 K (Fig. 4B) (to compare with experiments, MC T is offset of 134.5 K, MC P is rescaled by 5 and offset of -1 × 10^-4 GPa). Fig. 4 shows that the MC results agree well with the experimental data (with some difference at high T, which we will discuss below). The agreement suggests that the model is able to adequately describe the dynamics and connectivity of a real HB network and is thus a useful tool when investigating the thermodynamic origin of the crossovers.

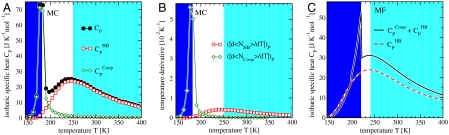
Next, we discuss the thermodynamic interpretation of the crossover in the model. Ref. 11 shows by direct calculations of the model in Eq. 2 that a maximum in isobaric specific heat, C_P(T) ≡ (∂H/∂T)_P, implies a crossover in the temperature dependence of τ. This result is consistent with the Adam–Gibbs theory (39). In the present work we find the C_P maximum observed in ref. 11, and also another maximum at a lower T, in a region not explored in ref. 11 (Fig. 5A). To understand the origin of the two C_P maxima, we write the enthalpy as the sum of two terms H = H^HB + H^Coop, where 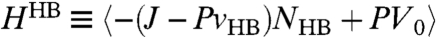and H^Coop ≡ H - H^HB. We define the HB contribution to the specific heat 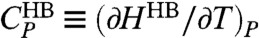, and the cooperative contribution 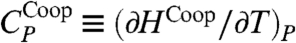. 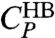is responsible for the broad maximum at higher T (Fig. 5A). To show that 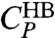captures the enthalpy fluctuations due to the HB formation, we calculate the locus of maximum fluctuation of 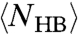, related to the maximum of 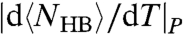. The temperatures of these maxima coincide with the locus of maxima of 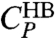(Fig. 5B).

Fig. 5.

Two maxima in the specific heat for the model. (A) The MC isobaric specific heat C_P (•), at P = 0.1 MPa has two maxima, decomposed into the components 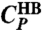(□) and 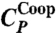(⋄) described in the text. (B) 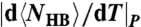(□) and 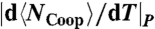(⋄) show maxima where 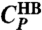and 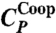, respectively, have maxima. (C) MF calculations at P = 0 for the case with cooperative interaction (J_σ/ϵ = 0.05, solid line labeled as 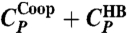) show two maxima for C_P, whereas for the case without cooperative interaction (J_σ = 0, dashed line labeled as 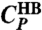) there is no low-T maximum that, hence, is due to the cooperativity.

The maximum of C_P at lower T is given by the maximum of 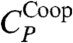(Fig. 5A). To confirm that 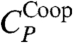corresponds to the enthalpy fluctuations due to the cooperative J_σ term in Eq. 2, we calculate 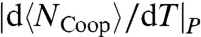, where 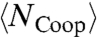is the average number of molecules with perfect local order of their bond indices. We find that the locus of maxima of |dN_Coop/dT|_P overlaps with the locus of maxima of 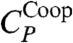(Fig. 5B). The same qualitative behavior for C_P is predicted from mean-field (MF) calculations (31) for the model (Fig. 5C).

The nonmonotonic behavior of 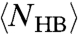and 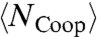explains the two crossovers in the HB correlation time. At very low T, both experimental τ and simulation τ_MC have an Arrhenius behavior with constant activation energy A, 25.2 kJ/mol in the experiments and 13.7 kJ/mol in the model. The quantitative difference between the two arises from the choice of the parameters J and J_σ. In both experiments and model, A is consistent with the average energy 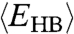necessary to break a HB in a locally ordered environment. The relation 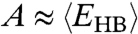in both experiments and model suggests that the dynamics is dominated by the breaking and formation of a single HB at low T. This is well understood in the model where the energies 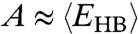are both functions of 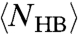and 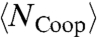(11). Therefore, the saturation of the HB network (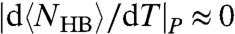) and its ordering (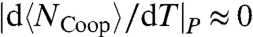) at low T imply constant A and an Arrhenius behavior for the HB correlation time.

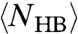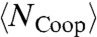At high T where C_P is monotonic, and increase for decreasing T. Hence, the activation energy and 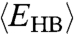also increase, implying a non-Arrhenius behavior.

At intermediate T, between the two maxima of C_P, the rate of change of 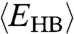is proportional to the decreasing 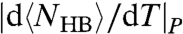and the increasing 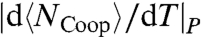, giving rise to another non-Arrhenius behavior down to the temperature of the maximum 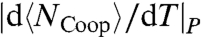and the crossover to Arrhenius behavior (in the model there is no water diffusion, hence the low-T crossover is not due to a bulk glass transition as hypothesized for fully hydrated cases in ref. 40). The difficulty to separate the large lysozyme contribution and the low-h water contribution from the total experimental C_P makes not possible a straightforward comparison of our C_P calculations with experimental data (23, 25).

The relaxation time calculated for the model is characteristic to the breaking and forming of H bonds, which is analogous to the proton relaxation measured by dielectric spectroscopy. We find good qualitative agreement between τ and τ_MC, but at high T the crossover for τ is more pronounced than that for τ_MC (Fig. 4). This difference arises from two factors.

1. The experiments are carried out at constant h, corresponding to a decreasing effective P (possibly negative due to the surface adsorption) acting on water for decreasing T, while the MC results are at constant P = 0.1 MPa. Our MF calculations predict that C_P displays two maxima along any path P(T) ≲ 0.1 MPa. 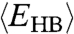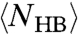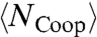Along a path such as in the experiments, in which P(T) decreases monotonically upon cooling, increases more rapidly by decreasing T, because and increase more rapidly when both P and T decrease (28, 29). This allows τ_MC to converge to the experimental τ at high T.

2. The fluctuations in the HB network and distance between water oxygens, predicted by the model, could enhance the probability for a proton to be delocalized between two first-neighbor oxygens, inducing shorter proton relaxation times than those predicted on the base of classical simulations at high T. Experiments (16) show that this effect is maximum around 250 K, approximately where the model predicts the maximum fluctuation of the HB network and the experimental τ shows a stronger cusp than τ_MC.

To conclude, in dielectric spectroscopy experiments on hydrated lysozyme at low hydration level, we observe a relaxation mode associated to water protons, with two crossovers, one at approximately 252 K and another at approximately 181 K. At the same time, we find that a coarse-grained model of an adsorbed monolayer of water shows in simulations two crossovers for the HB dynamics. In the model these two crossovers can be fully understood as the effects of two structural changes of the HB network. These two structural reorganizations are marked by two maxima in C_P, as well as in the compressibility K_T and the isobaric thermal expansion coefficient α_P (not shown here). The two structural changes are (i) at higher T, associated with the maximum fluctuations of the formation and breaking of the HBs, and (ii) at lower T, associated with the maximum fluctuation of the ordering of the local arrangement of the HBs. We argue that the model predictions provide an interpretation for our experimental findings.

Methods

Experimental Setup and Data Analysis.

We use an Alpha Analyzer dielectric apparatus (Novocontrol) to study crystallized and highly purified lysozyme powder from chicken egg white (Sigma-Aldrich), dialyzed and lyophilized to set its pH, then rehydrated (14). The capacitor containing the sample has blocking electrodes, coated by Teflon with thickness approximately 1/40th of the sample thickness. This choice of thickness eliminates the possibility of artifacts in our raw dielectric data, as discussed in a recent publication (41), and provides a “first check” of the reliability of the data analysis procedure adopted here.

Our measured complex admittance Y_m(ω) is directly related to the complex permittivity 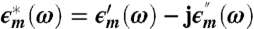given that

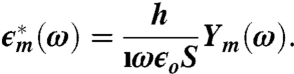[4]

Here, 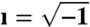; ϵ_o is the permittivity of free space; and S and h are, respectively, the electrode surface area and gap thickness. We extract the true sample permittivity from the measured frequency response by performing a complex function fit procedure that takes into account electrode polarization and capacity—that can be represented by a constant-phase-angle (CPA) element—interfacial dispersion, also known as the Maxwell–Wagner effect, along with relaxation processes due to the sample itself. Details about the deconvolution of the data are given in the SI Text.

We write the measured complex admittance 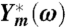as

[5]

where A and d characterize the ω-dependent fractal polarization due to the blocking electrode, as in ref. 42, and

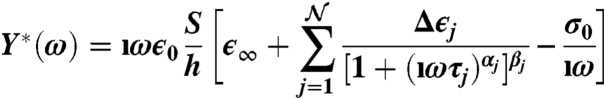[6]

is the admittance of the sample itself—expressed as a conductivity term plus a combination of Havriliak–Negami functions. Here, σ₀ is the sample conductivity; ϵ_∞ is the high-frequency limit of the permittivity; 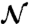is the number of relaxation processes (i.e., 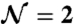for the broad peak in Fig. 3); Δϵ_j and τ_j are the dielectric strength and the relaxation time for the jth contribution, respectively; and α_j and β_j characterize the shape of the relaxation time distribution function.

The presence of blocking electrodes eliminates the dc conductivity across the bulk sample, but not the sample conductivity term Eq. 6, related to local displacement of protons along the protein surface (15). This sample “local” conductivity has the same temperature dependence as that measured in ref. 2. Because the experimental setup in ref. 2 does not use blocking electrodes, this observation provides a “second check” for the reliability of our data analysis. The check provides also a verification of our data decomposition, because in ref. 2 a different deconvolution of the data is used, but the results for the same relaxation mode are the same. See SI Text, section I, for a “third check” of our data analysis.

Quantitative Analysis of the Shape of the Relaxation Time Distribution Function.

Raicu (43) has proposed a phenomenological “universal dielectric response” function able to describe a single Debye-like relaxation, such as the Havriliak-Negami relaxation, combined with interfacial dispersion and electrode polarization. An important result of this work is that a distribution function for the relaxation times in the frequency domain can be directly calculated using parameters appearing in the universal response. We adapt an algorithm (44) to obtain, from raw data, a distribution function in the frequency domain, by means of an inverse Laplace transform with no a priori assumption on the kind and number of relaxation processes This approach has proven to be a reliable tool to obtain a distribution function of relaxation times (45, 46). Figure 2 of ref. 14 compares the two distribution functions, one based on a single relaxation, the other with no assumption on the number of relaxation processes, for the dataset of hydrated lysozyme powder at 270.4 K and h = 0.26 g H₂O/g dry protein. The analysis shows that the distribution function derived for a single relaxation process plus the effect of electrode polarization and interfacial dispersion does not totally account for the distribution calculated with no a priori assumptions. This implies that one or more additional relaxation processes are required to describe the raw dielectric data. We found that an additional relaxation is sufficient to completely account for the calculated distribution function. The addition of a third relaxation term results in unphysical negative Δϵ_i and therefore is not considered. We assume that a relatively small increase of water content from 0.26 to 0.3 g H₂O/g dry protein does not change the results of the approach described above.

Simulations.

We simulate N = 10,000 water molecules in the NPT ensemble. To equilibrate such a large system at approximately 180 K for 100 s is a task that cannot be accomplished with molecular dynamics simulations of any detailed model of water. To overcome this problem, we (i) adopt a coarse-grained model, as described in the main text, and (ii) use MC simulations. Depending on whether we want to study thermodynamic quantities or dynamic quantities, we implement two different MC techniques (see SI Text, section II).