Sparse linear modeling of next-generation mRNA sequencing (RNA-Seq) data for isoform discovery and abundance estimation

Abstract

Since the inception of next-generation mRNA sequencing (RNA-Seq) technology, various attempts have been made to utilize RNA-Seq data in assembling full-length mRNA isoforms de novo and estimating abundance of isoforms. However, for genes with more than a few exons, the problem tends to be challenging and often involves identifiability issues in statistical modeling. We have developed a statistical method called “sparse linear modeling of RNA-Seq data for isoform discovery and abundance estimation” (SLIDE) that takes exon boundaries and RNA-Seq data as input to discern the set of mRNA isoforms that are most likely to present in an RNA-Seq sample. SLIDE is based on a linear model with a design matrix that models the sampling probability of RNA-Seq reads from different mRNA isoforms. To tackle the model unidentifiability issue, SLIDE uses a modified Lasso procedure for parameter estimation. Compared with deterministic isoform assembly algorithms (e.g., Cufflinks), SLIDE considers the stochastic aspects of RNA-Seq reads in exons from different isoforms and thus has increased power in detecting more novel isoforms. Another advantage of SLIDE is its flexibility of incorporating other transcriptomic data such as RACE, CAGE, and EST into its model to further increase isoform discovery accuracy. SLIDE can also work downstream of other RNA-Seq assembly algorithms to integrate newly discovered genes and exons. Besides isoform discovery, SLIDE sequentially uses the same linear model to estimate the abundance of discovered isoforms. Simulation and real data studies show that SLIDE performs as well as or better than major competitors in both isoform discovery and abundance estimation. The SLIDE software package is available at https://sites.google.com/site/jingyijli/SLIDE.zip.

The recently developed next-generation mRNA sequencing (RNA-Seq) assay, with deep coverage and base level resolution, has provided a view of eukaryotic transcriptomes of unprecedented detail and clarity. Unlike microarrays, RNA-Seq data have novel splice junction information in addition to gene expression, thus facilitating whole-transcriptome assembly and mRNA isoform quantification. RNA-Seq data includes both single-end and paired-end reads, where a single-end read is a sequenced end of a cDNA fragment from an mRNA transcript, and a paired-end read is a mate pair corresponding to both ends of a cDNA fragment.

In the mRNA isoform discovery field, one of the most widely used software packages is Cufflinks (1). It builds a set of genes and exons solely from RNA-Seq data first, and subsequently uses a deterministic approach to find a minimal set of isoforms that can explain all the cDNA fragments indicated by paired-end reads. Cufflinks mainly uses qualitative exon expression and junction information in its isoform discovery, lacking a quantitative consideration of RNA-Seq data. Although Cufflinks gives very useful results, we note that the isoforms it discovers based on de novo assembled genes and exons can be heavily biased by different types of RNA-Seq data noise (2–5). Two recently published modENCODE (Model Organism Encyclopedia of DNA Elements) (6) consortium papers (7, 8) also raise concerns about relying solely on RNA-Seq reads in isoform discovery and have suggested using manual annotations to scrutinize the results.

In the mRNA isoform quantification field, the question is to estimate the abundance of isoforms in a given set. Available abundance estimation methods include direct computation (9, 10) and model-based approaches. Many model-based studies (1, 11–14) have used maximum-likelihood approaches to estimate isoform abundance. There are also efforts on formulating the abundance estimation problem as a linear model (15), where the independent and dependent variables are isoform expression levels and categorized RNA-Seq read counts, respectively. In particular, binary values have been used in the design matrix to relate categorized reads to different isoforms, but that design matrix misses the quantitative relationship between read quantities and isoform abundance.

In this study, we propose a statistical method called “sparse linear modeling of RNA-Seq data for isoform discovery and abundance estimation” (SLIDE) that uses RNA-Seq data to discover mRNA isoforms given an extant annotation of gene and exon boundaries, and to estimate the abundance of the discovered or other specified mRNA isoforms. The extant annotation can come from annotation databases [e.g., Ensembl (16) or UCSC Genome Browser (17)], can be supplemented by other transcriptomic data such as RACE or CAGE (18, 19), or can even be inferred from RNA-seq de novo assembly algorithms (1, 20). SLIDE is based on a linear model with a nonbinary design matrix modeling the sampling probability of RNA-Seq reads from mRNA isoforms. When modeling the design matrix, we considered the effects of GC content, cDNA fragment lengths, and read starting positions. This linear model, coupled with the carefully defined design matrix, gives SLIDE a stochastic property of making use of exon expression quantitatively in isoform discovery. The SLIDE model can also be easily extended to incorporate other transcriptomic data [e.g., RACE (18), CAGE (19), and EST (21)] with RNA-Seq to achieve more comprehensive results. The SLIDE software package is available at https://sites.google.com/site/jingyijli/SLIDE.zip.

Results

Linear Modeling for RNA-Seq Data.

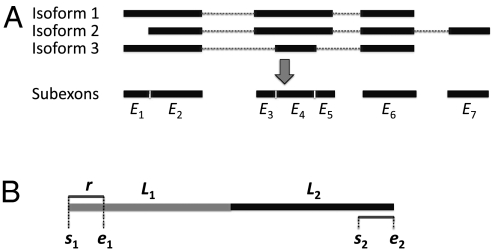
SLIDE is designed as a tool for discovering mRNA isoforms and estimating isoform abundance from RNA-Seq reads, on top of known information about gene and exon boundaries. For isoform discovery, SLIDE considers all the possible isoforms by enumerating exons of every gene. For example, a gene of n nonoverlapping exons has 2ⁿ - 1 possible isoforms, each composed of a subset of the n exons. However, because of the possible occurrence of alternative splicing within exons, isoforms of the same gene may have partially overlapping but different exons. Hence, for ease of enumeration, we define a subexon as a transcribed region between adjacent splicing sites in any annotated mRNA isoforms (Fig. 1A). With this definition, every gene has a set of nonoverlapping subexons, from which we can enumerate all the possible isoforms including annotated ones.

Fig. 1.

(A) Definition of subexons: transcribed regions between adjacent alternative splicing sites. (B) A two-exon mRNA transcript. s₁, e₁, s₂, and e₂, genomic positions associated with a paired-end read. r, the read end length; L₁ and L₂, the exon lengths.

We formulate the task of discovering isoforms for a given gene as a sparse estimation problem where the sparseness applies to the isoforms expected from RNA-Seq data. Because exon expression levels and the existence of possible exon–exon junctions are the key for isoform discovery and they can be inferred from the starting and ending positions of RNA-Seq reads mapped to a reference genome, we are motivated to transform RNA-Seq reads into a summary that captures the key information. For a paired-end read, we exact four genomic locations s₁, e₁, s₂, and e₂, where s₁ and e₁ are the starting and ending positions of its 5′ end, and s₂ and e₂ are the starting and ending positions of its 3′ end (Fig. 1B). Note that a paired-end read uniquely corresponds to a cDNA fragment with both ends sequenced, that is, s₁ and e₂ are the starting and ending positions of the fragment, respectively. We next categorize paired-end reads into paired-end bins defined as four-dimensional vectors: Bin (i, j, k, l) contains reads whose s₁, e₁, s₂, and e₂ are in subexons i, j, k ,and l, respectively (see Methods for details). For single-end reads, we can similarly categorize them into two-dimensional single-end bins. The so-defined bin counts provide all the exon expression and junction information.

SLIDE is built upon a linear model whose design matrix F models conditional probabilities of observing reads in different bins given an isoform. For paired-end data, modeling F requires distributional assumptions on the two ends (i.e., s₁, e₂) of a cDNA fragment in an mRNA transcript, or equivalently on the fragment’s 5′ end (i.e., s₁) and its length (i.e., e₂ - s₁). For s₁, uniform distribution assumptions have been widely used. However, after considering the high correlation observed between sequencing read coverage and genome GC content (2), we assume the density of s₁ is uniform within subexons and proportional to the GC content between subexons. We specify the distribution of the fragment length, e₂ - s₁, by assuming e₂ to follow a Poisson point process given s₁ fixed. Consequently, e₂ - s₁ is modeled as truncated Exponential after taking into account the size selection step in RNA-Seq protocols (see Methods). Another widely used fragment length distribution is Normal distribution (1), which is also implemented in SLIDE and compared with truncated Exponential (see SI Text).

We then use a linear model as approximation to the observed bin proportions,

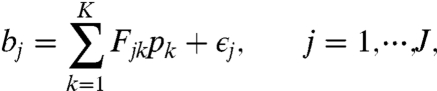[1]

where b_j is the observed proportion of reads in the jth bin, F_jk = Pr(jth bin|kth isoform) (i.e., the conditional probability of observing paired-end reads in the jth bin given that they are from the kth isoform), p_k is the proportion of the kth isoform to be estimated, and ϵ_j is the error term with mean 0. Besides, J and K are the numbers of bins and isoforms, respectively (see Methods). This is the core linear model used in SLIDE for both isoform discovery and abundance estimation of discovered isoforms. For isoform discovery, usually K > J, so the model is unidentifiable. But based on biological knowledge, we expect the model to be sparse and achieve sparse estimation by a modified Lasso (22) method (see Methods). For abundance estimation, only the proportions of discovered isoforms are parameters in the linear model, and their number is often far less than K, so there is no identifiability issue anymore. SLIDE then does the parameter estimation by nonnegative least squares. Compared with maximum-likelihood approaches used by other abundance estimation methods, SLIDE has the computational advantage of fitting a linear model as an intrinsic element.

Simulation Results.

A simulation study is used to assess the accuracy of SLIDE on isoform discovery and abundance estimation. We simulated reads from genes and true mRNA isoforms extracted from Drosophila melanogaster annotation (September 2010) of UCSC Genome Browser (17). For illustration purposes, we focus on the 3,421 genes on chr3R. Based on our defined subexons, those genes consist of 34.2% with 1–2 subexons, 57.6% with 3–10 subexons, and 8.2% with more than 10 subexons. Because the estimation for genes with 1–2 subexons is trivial due to their small numbers of possible isoforms, and genes with more than 10 subexons only constitute a small proportion and their estimation is computationally costly, we applied SLIDE to the subset of 3–10 subexons, 1,972 genes in total. We generated 500 × 50 (runs) paired-end reads for each gene from annotated isoforms of randomly defined proportions, and then we applied SLIDE to the simulated reads for isoform discovery and abundance estimation.

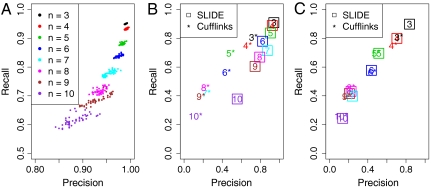
The isoform discovery results of all 50 runs are in Fig. 2A. We divided genes into groups by their numbers of subexons n (n = 3,⋯,10). For each gene, SLIDE returns a vector of estimated proportions of all its possible isofoms. We define isoforms whose estimated proportions exceed threshold 0.1 as discovered isoforms and evaluate them by the UCSC annotation. (Note that other thresholds 0.05 and 0.2 return similar results.) For each gene, the precision rate is defined as TP/(TP + FP), and the recall rate is TP/(TP + FN), where TP is the number of true positives (discovered isoforms that are also in the annotation), FP is the number of false positives (discovered isoforms that are not in the annotation), and FN is the number of false negatives (undiscovered isoforms that are in the annotation and have every exon observed). For each group of n-subexon genes, we calculated their average precision and recall rates as presented in Fig. 2A. The results show that SLIDE maintains high precision rates (> 80%) and good recall rates (> 60%) in all groups of genes. In particular, for genes with three and four subexons, the precision and recall rates are greater than 98% and 92%, respectively. As n increases, the precision and recall rates decrease, and the variance between different simulation runs increases. This observation is reasonable because with the increase of n, the number of possible isoforms increases exponentially, as does the difficulty of isoform discovery.

Fig. 2.

Isoform discovery results. (A) Precision and recall rates of SLIDE on 50 simulated datasets, with different colors for groups of genes with n subexons (n = 3,⋯,10) and every point representing the average precision and recall rates of every group on one dataset. (B) Precision and recall rates of SLIDE (using annotated genes/exons) and Cufflinks on dataset 1. Numbers, group indices of genes (i.e., numbers of subexons); squares/stars, SLIDE/Cufflinks results. (C) Precision and recall rates of SLIDE (using Cufflinks assembled genes/exons) and Cufflinks on dataset 1.

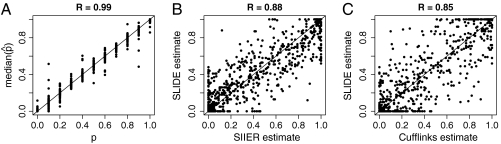
To illustrate the abundance estimation accuracy of SLIDE, we applied it to 317 multi-isoform genes on chr3R in the UCSC annotation (798 isoforms in total), with the same simulated paired-end reads. From reads of each simulation run, SLIDE estimates the 798 isoform proportions normalized by each gene. We calculated the Pearson correlation between the estimates and the true isoform proportions used in the simulation, and we found that the correlation coefficients of the 50 runs range from 0.92 to 0.95. We also illustrate the abundance estimation accuracy of SLIDE by a scatter plot of the median estimated isoform proportions over the 50 runs vs. true isoform proportions in Fig. 3A (R = 0.99).

Fig. 3.

Abundance estimation results. (A) p vs. median 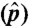of 798 isoforms on 50 simulated datasets. p, true isoform proportion; median 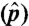, median of the 50 estimated isoform proportions. (B) SLIDE vs. SIIER estimates of the 798 isoforms on dataset 1. (C) SLIDE vs. Cufflinks estimates of the 798 isoforms on dataset 1.

This simulation study shows satisfactory performance of SLIDE in isoform discovery and abundance estimation. Further simulation studies with lowly expressed genes are in SI Text.

mRNA Isoform Discovery on modENCODE Data.

The main feature of SLIDE is discovery of mRNA isoforms from RNA-Seq data. Four modENCODE (6) D. melanogaster RNA-Seq datasets (Table 1) are used in the real data analysis. Again, for illustration purposes, we focus on the 1,972 genes with 3–10 subexons on chr3R of D. melanogaster. To avoid the effects of high false positive and negative rates of RNA-Seq data in lowly expressed genes (23), we applied SLIDE to genes with RPKM (number of reads per kilobase per million of mapped reads) (10) greater than 1.

Table 1.

modENCODE datasets used in the analysis

Dataset	Type	Sample	Read length	Total number of reads	Sequence Read Archive (http://www.ncbi.nlm.nih.gov/sra) numbers
1	paired-end	ML-DmBG3-c2	37 bp	25,094,224	SRX003838, SRX003839
2	paired-end	Kc167	37 bp	18,602,220	SRX003836, SRX003837
3	paired-end	Kc167	76 bp	20,118,748	SRR070261, SRR070269, SRR111873
4	paired-end and single-end	embryo 16-17h	76 bp	23,388,810 and 27,913,445	SRR023600, SRR035402, SRR023720, SRR023715, SRR023751, SRR023707, SRR023826

We compare SLIDE with Cufflinks (version 0.9.3) in terms of their isoform discovery precision and recall rates, evaluated by the UCSC annotation in a similar way to the simulation study (see SI Text). We note that SLIDE and Cufflinks target the isoform discovery problem from two different aspects. SLIDE discovers isoforms from given gene and exon structures, whereas Cufflinks contructs isoforms from its de novo assembled genes and exons. Hence, we carried out the comparison in two ways: (i) SLIDE with input genes and exons from the UCSC annotation vs. Cufflinks; (ii) SLIDE with input genes and exons assembled by Cufflinks vs. Cufflinks. The former is to evaluate the overall performance of the two methods under their default settings, whereas the latter is to specifically compare their isoform construction performance given the same set of genes and exons. The comparison results on dataset 1 (Table 1) are summarized in Fig. 2 B and C. (See SI Text for results on other datasets.)

Fig. 2B, corresponding to the first comparison, shows that SLIDE with input genes and exons from the annotation has significantly higher precision and recall rates than Cufflinks’. In the second comparison, with de novo genes and exons assembled by Cufflinks, SLIDE has better precision and recall rates than Cufflinks has for genes with three and four subexons, and for the rest of genes, the two methods have similar performance (Fig. 2C). We observe that the overall precision and recall rates in Fig. 2C are worse than those of SLIDE in Fig. 2B. These results remind us of the concerns voiced by other researchers about constructing isoforms based on de novo genes and exons built solely from RNA-Seq data (7, 8). We speculate that results of the second comparison are not enough to illustrate the isoform construction performance of SLIDE and Cufflinks, because the similarly low precision and recall rates observed in Fig. 2C might have been dominated by the disagreement between the de novo assembled genes/exons and the annotation. Hence, we performed an additional comparison on a smaller set of 246 genes whose de novo exons assembled by Cufflinks agree with the annotation. This comparison provides a direct evalulation on the isoform construction performance of SLIDE and Cufflinks. We found that isoforms discovered by SLIDE have an average precision rate of 93% and a recall rate of 96%, both higher than the average precision rate (89%) and recall rate (94%) of isoforms found by Cufflinks. This result demonstrates that SLIDE has higher acurracy than Cufflinks has in isoform construction from a given set of genes and exons. For more details, see SI Text.

By a detailed inspection of the isoforms discovered by Cufflinks, we find that many discovered isoforms are fragments of annotated isoforms in public databases. This is mainly due to the difficulty in de novo construction of gene boundaries. Cufflinks also has troubles in detecting lowly expressed genes de novo. By contrast, SLIDE can discover correct isoforms even with a small number of reads, based on existing gene boundary information. For instance, when applied to dataset 1, SLIDE has discovered isoforms in 1,084 genes (RPKM > 1) out of the total 1,972 genes, whereas Cufflinks has only found isoforms in 801 genes. These observations confirm again the importance of having correct gene boundaries in isoform discovery. Another advantage of SLIDE is the usage of a stochastic approach to simultaneously detect isoforms with alternative starts/ends [e.g., (1,2,3,4) and (2,3,4)], where Cufflinks will only discover the longest one (1). However, when there are significant RNA-Seq data biases in 5′ and 3′ ends of mRNA transcripts, the deterministic approach of Cufflinks may be more robust. In the future, with the continuing development of sequencing technology and promising improvement in RNA-Seq signal-to-noise ratios, we would expect the stochastic approach of SLIDE to be preferred.

There are other isoform discovery methods that use sparse estimation but with different methodology (15, 24). A numerical comparison between SLIDE and IsoLasso (15) shows that SLIDE has higher accuracy in isoform discovery. For detailed comparison information, please see SI Text.

mRNA Isoform Abundance Estimation on modENCODE Data.

Another feature of SLIDE is to estimate the abundance of mRNA isoforms discovered or other specified (e.g., annotated) from an RNA-Seq sample. Because of the lack of ground truth of isoform abundance in datasets 1–4 (Table 1), to evaluate the abundance estimation performance of SLIDE, we compare its estimates to those of two popular methods: statistical inferences for isoform expression in RNA-Seq (SIIER) (12) and Cufflinks (1). Note that SLIDE returns estimates of mRNA isoform proportions that are equivalent and convertible to the common abundance measure, isoform RPKMs (10) used in SIIER.

In the comparison between SLIDE and SIIER, both methods estimate the isoform abundance of the 317 chr3R genes with multiple isoforms in the UCSC annotation. In dataset 1, after removing 25 genes with high expression variance among exons (see SI Text), we obtain a scatter plot of the two sets of estimates in Fig. 3B (R = 0.88). A similar comparison is carried out between SLIDE and Cufflinks, and the results are in Fig. 3C (R = 0.85). The results show that SLIDE obtains estimates similar to those of SIIER and Cufflinks. For more discussions on the results, see SI Text.

Miscellaneous Effects on Isoform Discovery.

Using datasets 1–4 (Table 1), we study the following critical issues affecting isoform discovery from RNA-Seq data.

1. GC content variation. To study the usefulness of considering GC content variation in isoform discovery, we additionally implemented another version of F, assuming the cDNA fragment starting position s₁ as uniform across all subexons. Note that our default F assumes the density of s₁ as uniform within subexons but proportional to GC content between subexons, as motivated by observed high correlation between read coverage and GC content variation (2, 4) (see SI Text). Isoform discovery results on dataset 1 by SLIDE based on the two version of F are compared in Table 2. Recall rates are similar in both results, but precision rates are improved with the consideration of GC content. These results indicate that GC content can provide SLIDE with useful information in modeling F, and thus support various attempts of using GC content information to correct RNA-Seq data noise (3, 4).

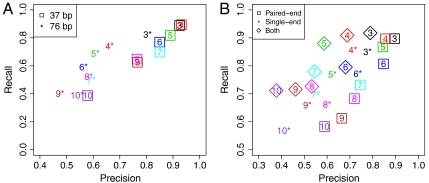
2. Read/fragment length effects. To explore the effects of RNA-Seq read lengths on isoform discovery, we applied SLIDE to datasets 2 and 3. The two datasets are generated from the same Kc167 sample of similar sequencing depth but with different read lengths: 37 bp (dataset 2) vs. 76 bp (dataset 3). We compare the isoform discovery results on both datasets in Fig. 4A. The precision and recall rates for genes with 3–9 subexons are surprisingly higher with the 37-bp data than the 76-bp data. This result contradicts our expectation that RNA-Seq data with longer read length would provide more information on exon junctions that are crucial to isoform discovery. Trying to find a plausible explanation, we checked the empirical distribution of cDNA fragment lengths in single-exon genes for both data, and found the distribution close to N(166,26²) and N(127,13²) for the 37-bp and 76-bp data, respectively. The fact that the 37-bp data contain more long fragments is a result of different experimental protocols, and is likely to be a reason for the observed unexpected comparison results. A simulation study with different read and fragment lengths reveals that the fragment length distribution has larger effects than the read length has on isoform discovery, and to some extent confirms our real data observation (see SI Text).

3. Paired-end vs. single-end RNA-Seq data. Compared with single-end RNA-Seq data, the more recent paired-end data provides more information on exon junctions and thus is expected to return isoform discovery results with higher precision rates. But if both single-end and paired-end data are available for the same RNA-Seq sample, the former can possibly complement the latter by providing more exon expression information, helping capture lowly expressed exons in rare isoforms, and thus resulting in isoform discovery results with higher recall rates. Because SLIDE has the flexibility of inputting both single-end and paired-end RNA-Seq data (see Methods), we tested these hypotheses by applying it to dataset 4, which has both single-end and paired-end data from the same sample and of similar numbers of reads (Table 1). We specifically compare the results of SLIDE on (i) paired-end data, (ii) single-end data, and (iii) both paired-end and single-end data in Fig. 4B. From the figure, we observe that using paired-end data alone has the highest precision rates for all the genes, whereas using both data has the best recall rates. These results confirm our intuitive hypotheses that paired-end data alone gives more precise information than single-end data does in isoform discovery; however, single-end data does provide extra exon expression information as well as noise when it is used in addition to paired-end data, hence resulting in higher recall rates and lower precision rates.

Table 2.

Comparison of isoform discovery results by SLIDE with two versions of F

n		3	4	5	6	7	8	9	10
without GC	precision	0.93	0.90	0.87	0.80	0.83	0.75	0.71	0.49
	recall	0.91	0.89	0.83	0.77	0.71	0.68	0.61	0.36
with GC	precision	0.94	0.92	0.90	0.82	0.87	0.79	0.74	0.56
	recall	0.91	0.89	0.84	0.78	0.71	0.67	0.60	0.38

Fig. 4.

Miscellaneous effects. (A) Precision and recall rates of SLIDE on 37 bp and 76 bp paired-end RNA-Seq data (datasets 2–3). (B) Precision and recall rates of SLIDE on dataset 4 with paired-end data only (squares), single-end data only (stars), and both (diamonds).

Discussion

We have proposed a sparse linear model approach (SLIDE) capable of discovering mRNA isoforms of given genes and estimating the abundance of discovered or other specified isoforms from RNA-Seq data. Compared to existing approaches (1, 12), SLIDE (i) discovers isoforms from all possible ones based on known gene and exon boundaries (e.g., from the UCSC annotation), (ii) uses a stochastic approach with a quantitatively modeled design matrix F (i.e., conditional probabilities of observing RNA-Seq reads from mRNA isoforms) in isoform discovery, (iii) uses the same linear model subsequently for abundance estimation on discovered or other specified isoforms, and (iv) can be used as a downstream isoform discovery tool of de novo gene and exon assembly algorithms. Other widely used isoform discovery methods (1, 20) find isoforms based on their own de novo genes and exons solely assembled from RNA-Seq reads, and thus their discovered isoforms are highly dependent on the accuracy of de novo assembly. SLIDE can avoid possible de novo assembly errors (2) by using known gene and exon boundaries; it can also integrate de novo assemblies with known ones to prevent the risk of missing isoforms involving novel exons. SLIDE will also benefit from ongoing efforts of improving D. melanogaster transcriptome annotations (6).

We have also explored various factors that may affect the performance of SLIDE on isoform discovery. Our results suggest that (i) the consideration of GC content variation in modeling F can improve the precision, (ii) the cDNA fragment size selection protocol and the resulting cDNA fragment lengths have larger effects than read lengths have on both the precision and recall, and (iii) paired-end RNA-Seq data provides more accurate information than single-end data does in isoform discovery, but the addition of single-end data would help with the discovery of rare isoforms.

As demonstrated by the isoform discovery and abundance estimation results, SLIDE shows great promise as a tool for handling the two tasks sequentially with a shared linear model. The modeled design matrix F is also shown to be a good quantitative representation of sampling RNA-Seq reads from mRNA isoforms, in contrast to the binary representation used in other isoform discovery methods (1, 11, 15, 20). We still lack the information to model irregular systematic RNA-Seq biases, such as low read coverage in transcript ends and significant read coverage variation unexplained by GC content. But we expect SLIDE to have increased power when such modeling becomes possible with the standardization of RNA-Seq protocols and the improvement of technology. Finally, SLIDE can be easily extended to incorporate mRNA isoform information from EST (21), CAGE (19), and RACE (18) data in addition to RNA-Seq data to refine its linear model and obtain more accurate isoform discovery results.

Methods

Linear Model Formulation and Identifiability Issue.

In the linear modeling of paired-end RNA-Seq data, we first categorize reads into paired-end bins. For an n-subexon gene, possible paired-end bins are {(i,j,k,l),1 ≤ i ≤ j ≤ k ≤ l ≤ n}, whose total number is 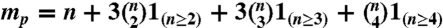. Then RNA-Seq data is transformed into bin counts (i.e., number of reads in each bin), which are further normalized as bin proportions b. Second, we enumerate all the possible isoforms of an n-subexon gene as I₁,⋯,I_2ⁿ-1, and denote p as the isoform proportions to be estimated. Third, we relate unknown p to observed b by a design matrix F, where F_jk = Pr(jth bin|kth isoform) (i.e., the conditional probability of observing reads in the jth bin given that the reads are from the kth isoform). (See next section for the modeling of F). Then, we write the following linear model:

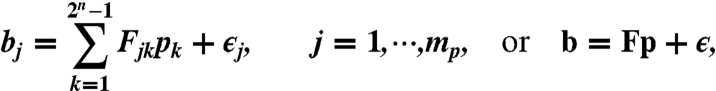[2]

where ϵ = (ϵ₁,⋯,ϵ_mp) is the random noise whose components are independent and have mean 0.

We note that the linear model (Eq. 2) becomes unidentifiable when m_p < 2ⁿ - 1 or equivalently n≥9. The model may also be unidentifiable when n < 9 due to possible collinearity of F. To solve this identifiability issue, we reduced the number of parameters dim(p) by adding a preselection procedure on isoforms. Also, given observed false zero bin counts of certain junction reads, we applied a preselection procedure on observations, too. (See SI Text for details.) We write the postselection linear model as

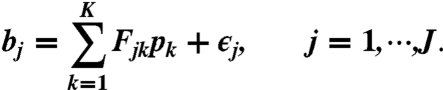[3]

We note that the unidentifiability issue still exists in many genes even after the preselection procedures, so sparse estimation is necessary (see SI Text).

For single-end data and the combination of both single and paired-end data, we can derive a similar linear model (see SI Text).

Modeling of Conditional Probability Matrix.

Modeling of the conditional probability matrix F = (F_jk), 1 ≤ j ≤ J, 1 ≤ k ≤ K is a key part in the estimation of p (Eq. 3). In paired-end RNA-Seq data, a mate pair represents ends of a cDNA fragment reversely transcribed from an mRNA transcript. In this sense, F_jk is the conditional probability that cDNA fragments with ends in the jth bin are reversely transcribed from mRNA transcripts in the kth isoform. With this interpretation, we model F with the following three assumptions.

1. The density of a cDNA fragment’s starting position (or the density of s₁ in Fig. 1), denoted by f, is uniform within subexons but proportional to GC content between subexons in an mRNA transcript.

2. The cDNA fragment length (ℓ = e₂ - s₁ in Fig. 1) distribution is modeled as truncated Exponential with density denoted by g. This modeling choice is based on empirical observations and Poisson point process approximations (see SI Text). SLIDE can also easily take other reasonable fragment length distributions.

3. Starting positions and fragment lengths are assumed to be independent.

In a two-subexon gene example (Fig. 1), suppose that the two subexons have boundaries [a₁,b₁] and [a₂,b₂]. Then, reads in bin j = (1,1,2,2) have s₁∈[a₁,b₁ - r + 1] and e₂∈[a₂ + r - 1,b₂]. For k = (1,2), we calculate .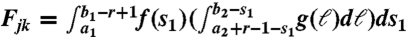

For single-end data and the combination of both single and paired-end data, F can be similarly calculated (see SI Text).

mRNA Isoform Discovery.

In isoform discovery, we expect sparse parameter estimation from the linear model (Eq. 3), because the number of mRNA isoforms for most D. melanogaster genes is below four (17) and far less than the number of possible isoforms K. L₁ penalization approach is widely used for sparse estimation and has applications in high-dimensional and potentially sparse biological data (25). We also observe that annotated isoforms often contain a large proportion of subexons, and thus expect isoform candidates with more subexons to be more likely true. Hence, we add an L₁ penalty term in the objective function below to limit the number of discovered isoforms as well as to favor the “longer isoforms”:

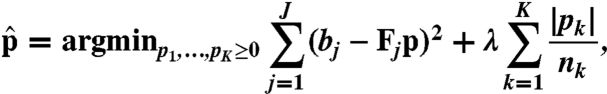[4]

where n_k is the number of subexons in the kth isoform and F_j is the jth row of F. With n_k in the penalty term, p_k would thus be favored if n_k is large. We note that this is a variant of Lasso, a regularization regression method for cases in which the number of parameters to be estimated exceeds the number of observations and most of the parameters are expected to be zeros (22). The difference between our penalty term and the one in standard Lasso is that the latter only aims to limit the number of discovered isoforms without favoring longer ones. Discussions about choosing L₁ over L₀ regularization and using different likelihoods in the linear model are in SI Text.

The selection of the regularization parameter λ (Eq. 4) is by a stability criterion that aims to return the most stable results over different runs of estimation (26). Because low signal-to-noise ratios in lowly expressed genes may significantly bias the λ selection and genes of the same number of subexons have similar dim(p) and dim(b) in Eq. 4, we group genes by their numbers of subexons n and select an optimal λ⁽ⁿ⁾ for each group from 16 candidate values 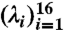(see Table 3). The selection procedure is described in SI Text, and the chosen λ⁽ⁿ⁾ values for datasets 1–4 and the simulation data are in Table 3.

Table 3.

λ⁽ⁿ⁾ selection results for different datasets

n	3	4	5	6	7	8	9	10
Datasets 1–2 (37 bp)	0.3	0.3	0.3	0.4	0.4	0.4	0.4	0.5
Datasets 3–4 (76 bp)	0.2	0.2	0.2	0.4	0.3	0.4	0.3	0.3
Simulation data (37 bp)	0.3	0.3	0.3	0.4	0.4	0.4	0.4	0.5
16 candidate λs: 10-6, 10-4, 10-3, 0.01, 0.04, 0.07, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1

R package “penalized” (27) is used in the implementation.

mRNA Isoform Abundance Estimation.

The SLIDE linear model (Eq. 3) can also be used for abundance estimation of discovered or other specified (e.g., annotated) isoform proportions. Because the number of discovered or annotated isoforms is smaller than the number of bin proportions, the linear model is identifiable. Thus, we use nonnegative least squares without a penalty term to estimate the isoform proportions. R package “NNLS” is used in the implementation (28).