Abstract
Molecular adaptation is typically assumed to proceed by sequential fixation of beneficial mutations. In diploids, this picture presupposes that for most adaptive mutations, the homozygotes have a higher fitness than the heterozygotes. Here, we show that contrary to this expectation, a substantial proportion of adaptive mutations should display heterozygote advantage. This feature of adaptation in diploids emerges naturally from the primary importance of the fitness of heterozygotes for the invasion of new adaptive mutations. We formalize this result in the framework of Fisher's influential geometric model of adaptation. We find that in diploids, adaptation should often proceed through a succession of short-lived balanced states that maintain substantially higher levels of phenotypic and fitness variation in the population compared with classic adaptive walks. In fast-changing environments, this variation produces a diversity advantage that allows diploids to remain better adapted compared with haploids despite the disadvantage associated with the presence of unfit homozygotes. The short-lived balanced states arising during adaptive walks should be mostly invisible to current scans for long-term balancing selection. Instead, they should leave signatures of incomplete selective sweeps, which do appear to be common in many species. Our results also raise the possibility that balancing selection, as a natural consequence of frequent adaptation, might play a more prominent role among the forces maintaining genetic variation than is commonly recognized.
Adaptation by natural selection is the key process responsible for the fit between organisms and their environments. The invasion of new adaptive mutations is an essential component of this process that fundamentally differs between haploid and diploid populations. In diploids, while a new mutation is still rare, natural selection acts primarily on the mutant heterozygote (1). As a result, only those adaptive mutations that confer a fitness advantage as heterozygotes have an appreciable chance of invading the population (“Haldane's sieve”). However, if the heterozygote of an invading adaptive mutation is fitter than the mutant homozygote, the mutation will not be driven to fixation but, instead, maintained at an intermediate, balanced frequency.
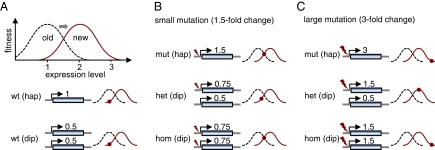
We argue that heterozygote advantage should be very common during adaptation in diploids if selection is stabilizing and at least some mutations are large enough to overshoot the optimum. Consider, for example, adaptation through changes in gene expression (Fig. 1A), which is an important, if not the dominant, mechanism of adaptation (2). Here, mutations of small effect (Fig. 1B) will be adaptive when they modify expression in the adaptive direction whether the organism is haploid or diploid. However, mutations of large effect (Fig. 1C) can be nonadaptive in haploids, because they overshoot the optimum, yet be adaptive in diploids, because their phenotypic effect is moderated when heterozygous. These mutations will have heterozygote advantage and lead to balancing selection in diploids.
Fig. 1.
Adaptation to a change in the optimal level of gene expression. (A) In both haploids (hap) and diploids (dip), the wild type (wt) is perfectly adapted to the original fitness function (dashed black curve). After an external change, the optimal expression level becomes twice the original level (solid red curve). Note that we are assuming phenotypic codominance; thus, the two individual gene copies in a diploid each contribute expression level 0.5, such that overall expression is 1. (B) Fitness effects of a small mutation that increases expression level by 1.5-fold. The mutant heterozygote (het) is less fit than both the haploid mutant (mut) and the mutant homozygote (hom). (C) Effects of a large mutation that increases expression by threefold. In this case, the mutant heterozygote effectively has only twofold increased expression, and thus lands right at the new fitness optimum. In contrast, both the haploid mutant and the mutant homozygote “overshoot” the optimum.
The components of the simple model in Fig. 1, stabilizing selection and availability of mutations of various sizes, are well established by empirical data in the case of gene expression. Pervasive stabilizing selection is indicated by the lack of large gene expression differences between and within species despite the abundance of mutations that change gene expression (3–7). In addition, expression-altering mutations are known to come in a variety of sizes ranging from subtle changes to dramatic ones of tens of fold or even hundreds of fold (4, 5, 8).
The model in Fig. 1, albeit instructive, may lack generality because it incorporates only a single trait. However, adaptation might often involve mutations that have complex pleiotropic effects in an effectively multidimensional phenotypic space. The classic model that incorporates this key feature of adaptation is Fisher's geometric model (9–13). In this single-locus model, phenotypes are vectors in an abstract geometric space (Fig. 2A), with the orthogonal axes representing different, independent traits, such as color and height. Mutations move phenotypes in a random direction, with the size of the step corresponding to the effect size of the mutation. The fitness landscape is peaked around a single optimal phenotype, capturing our intuition of stabilizing selection. Below, we extend Fisher's geometric model to diploidy and confirm the intuition from Fig. 1 that adaptation should generically lead to heterozygote advantage.
Fig. 2.
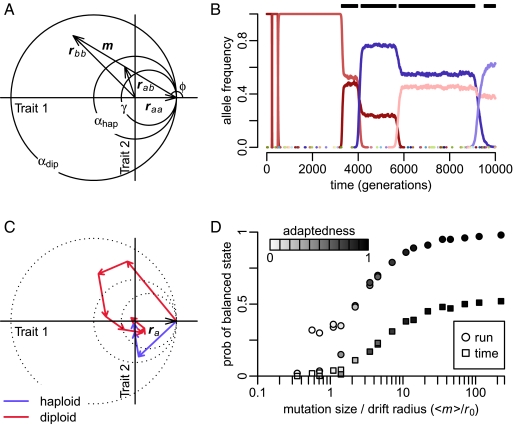
Fisher's geometric model of adaptation in two dimensions. (A) Two orthogonal axes represent independent character traits. Fitness is determined by a symmetrical Gaussian function centered at the origin. Consider a population initially monomorphic for the wild-type allele raa = (2,0). A mutation m gives rise to a mutant phenotype vector rbb = raa + m. The phenotype of the mutant heterozygote assuming phenotypic codominance (h = 1/2) is rab = raa + m/2. The different circles specify the areas in which mutations are adaptive in haploids (αhap), adaptive in diploids (αdip), and replacing in diploids (γ). (B) Frequency trajectories of all alleles present during a representative adaptive walk in a diploid population with N = 5⋅104, raa = (2,0), and <m> = σw = 1. Different colors represent different alleles. The black bars over the graph indicate the periods during which a balanced polymorphism was present. (C) Representative adaptive walks in a haploid population and a diploid population. Vectors depict the successive mutations that led to the prevalent allele at the end of the walk. The haploid walk consists of a single lineage of successive mutations, each conferring a selective advantage over the previous one. In the diploid walk, the first mutation overshoots the fitness optimum, generating a sequence of intermediate balanced states. Note that the areas αhap, αdip, and γ (dotted circles) from A apply only to the first mutation in the walk when the population is still monomorphic for ra. (D) Probability of observing balanced polymorphism during adaptive walks toward a fixed fitness optimum as a function of mutation sizes scaled by effective drift radius r0 (SI Text) for the various settings of N, σw, and <m> specified in Table S1. Circles show the probability of at least one balanced state arising over the course of a walk, and squares show the fraction of time during which balanced states were present. Coloration indicates the average “adaptedness” achieved during a walk, defined by the improvement in mean population fitness over the walk (<wend> − <wstart>) relative to the maximally possible improvement (1 − <wstart>).
Results
Consider an allele a with homozygous phenotype raa in Fisher's model. Mutations are modeled by adding a mutation vector m to the phenotype of the mutated allele (Fig. 2A). The direction of the mutation vector is chosen uniformly, and its size (m) is drawn from a specified distribution P(m). In diploids, the phenotype is determined by its two constituent alleles. The geometric nature of Fisher's model offers a straightforward mapping between the phenotype of the mutant heterozygote (rab) and the homozygote phenotypes (raa and rbb = raa + m) in terms of the weighted average: rab = raa + hm, where the weight h specifies the phenotypic dominance of the new mutation. For convenience, we assign the phenotype of a diploid homozygote to be equal to that of a haploid carrying the same allele (i.e., rii = ri).
Fitness w(r) decreases with the distance between the organismal phenotype and the phenotypic optimum. In haploids, adaptive mutations, w(rb) > w(ra), are those that bring the mutant allele closer to the optimum (i.e., the mutant falls inside the sphere αhap of radius ra centered at the optimum) (Fig. 2A). In diploids, it is the fitness of the mutant heterozygote rab that primarily determines the probability of successful invasion; therefore, we define the area in which mutations are adaptive in diploids (αdip) by the condition w(rab) > w(raa).
Let us first focus on the instructive case of strict phenotypic codominance, h = 1/2. Here, mutations in diploids have half the initial phenotypic effect that they would have in a haploid. Mutations of small effect thus have reduced initial selective effects in diploids compared with in haploids, but the area in which mutations are adaptive in diploids (αdip) is significantly enlarged (Fig. 2A). If the supply of mutations is restricted to those of small size compared with the distance to the optimum, adaptive mutations will invade a diploid population at a slower rate than they would a haploid population because of the reduced initial selection (SI Text and Figs. S1 and S2). In contrast, once mutations of large enough size are available, diploids start reaping the benefits of the larger space of adaptive mutants available to them. In this case, adaptive mutations will invade at a higher rate in diploids than in haploids, even after controlling for the difference in mutation rate that results from a diploid population having twice as many chromosomes as a haploid population of equal size (14).
The larger range of adaptive mutations available to diploids comes with a catch, however; many of these adaptive mutations display heterozygote advantage, and thus will not simply go to fixation. The fraction δu of adaptive mutations with heterozygote advantage [w(raa) < w(rab) > w(rbb)] in Fisher's model is the fraction of mutations that fall into the sphere αdip [w(rab) > w(raa)] but not the sphere γ [w(rbb) > w(rab) > w(raa)] (Fig. 2A). In the small-mutation limit, δu goes to zero because the nonoverlapping space between αdip and γ is not reachable by mutations that fall in the immediate neighborhood of ra. In the limit in which mutations of all sizes are equally likely, however, most adaptive mutations show heterozygote advantage (δu ≥ 1/2), except for the special cases of perfect dominance or perfect recessiveness (SI Text).
The crucial criterion determining the probability of heterozygote advantage during adaptation in diploids is the availability of “large” mutations. In Fisher's model, for heterozygote advantage to be common, the average size of mutations (<m>) has to be at least of order raa/√d, the distance to the optimum divided by the square root of the number of phenotypic dimensions (SI Text). However, even when mutations are initially small compared with this distance, during an adaptive walk, a population gradually approaches a fitness optimum via successive adaptations (11). Thus, at some point on the walk, this condition will be met; thereafter, heterozygote advantage will be likely.
We performed simulations of adaptive walks in Fisher's model to test these theoretical predictions and further investigate the consequences of frequent heterozygote advantage in such walks. Specifically, we simulated a single locus in a 2D phenotypic space under phenotypic codominance in a Wright–Fisher framework using an exponential distribution of mutation sizes and a symmetrical Gaussian fitness landscape (Materials and Methods).
We find that adaptive walks in diploids typically involve the succession of many intermediate balanced polymorphisms that tend to be ephemeral; they are quickly displaced by new adaptive alleles, themselves often displaying heterozygote advantage (Fig. 2 B and C). These dynamics contrast sharply to those in haploid populations, where adaptive walks proceed by successive sweeps of adaptive mutations and populations are generally monomorphic between sweeps (Fig. 2C).
We confirm that balanced states are likely during adaptive walks (Fig. S3), provided that mutation sizes meet our theoretical conditions and selection is strong enough to maintain balanced states despite the stochastic fluctuations arising from genetic drift (SI Text). Fig. 2D shows the probability of observing balanced states during adaptive walks under various parameter settings (Table S1). Note that the probability of observing balanced states correlates very strongly with the overall probability of observing successful adaptation. For example, in all our scenarios where the population eventually traversed at least 90% of the initial fitness distance to the optimum, balanced states were observed in ≥90% of the runs and were present ≥40% of the time during walks.
Simulated haploid populations approach the optimum faster, on average, than simulated diploid populations despite diploid populations generally containing the most fit individual (Fig. S4). This is because diploid populations suffer from a high genetic load, which can be identified as the segregation load attributable to pervasive heterozygote advantage. The balanced polymorphisms that result from the invasion of adaptive mutations with heterozygote advantage also cause high levels of standing variance in both phenotype and fitness to persist during the adaptive walk (Fig. S4).
The maintenance of genetic variation via heterozygote advantage during adaptation is a striking difference between the adaptive walks in haploids and diploids. Although the load resulting from the maintained variation is costly during adaptation to a constant environment, could this effect be advantageous in a changing environment? Environmental changes that displace the phenotypic optimum can convert dominance variance of fitness into additive variance, which would then fuel adaptation. To investigate this possibility, we incorporated a randomly moving optimum into our simulations (Materials and Methods). The optimum moves every generation in a random direction with step sizes sampled from a Gaussian distribution, the variance of which (σenv2) determines the speed of optimum movement.
Pervasive balanced polymorphism remains a feature of adaptation in diploid populations in the moving optimum scenario (typical trajectories are shown in Fig. S5). In simulations with a fast-moving optimum (σenv/σw = 10−2), polymorphisms at frequencies 0.05 < x < 0.95 are present around 30% of the time when averaged over replicate runs. More than 80% of these polymorphisms are balanced. Polymorphisms are observed less frequently (∼5%) when environmental change becomes very slow (σenv/σw = 10−5), because populations are well adapted most of the time. The fraction of polymorphisms that are balanced, however, remains substantial (∼58%) in this scenario. Table S2 shows the percentages of time during which polymorphisms were observed in our simulations and the fractions of those polymorphisms that were balanced for a wide range of values of σenv/σw. We also demonstrate that many of the balanced polymorphisms eventually fix such that a substantial proportion of substitutions (60–70%) pass through a balanced state (Fig. S6 and Table S2). These substitutions tend to be generated by larger phenotypic effect mutations than the substitutions that go to fixation without an intermediate balanced state (Fig. S6).
To evaluate how effectively populations followed the moving fitness optimum, we measured the mean population fitness averaged over a walk (<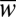 >). The difference, λ = 1 − <
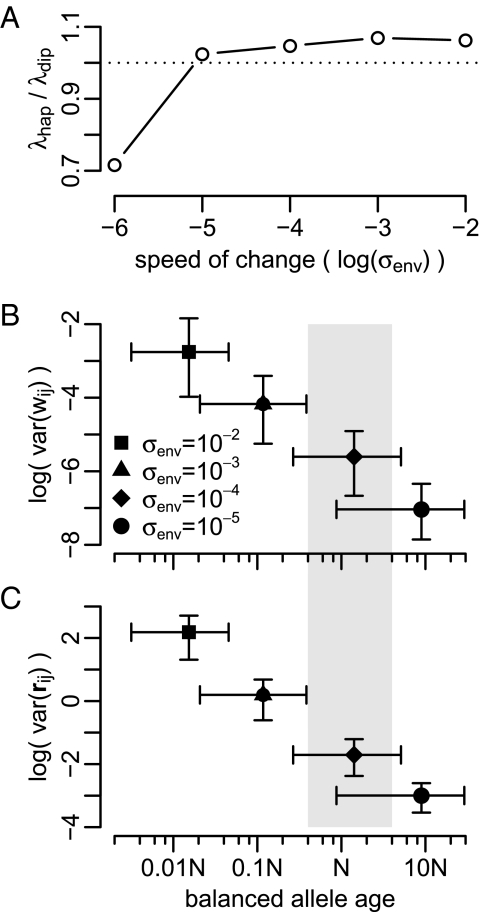
>). The difference, λ = 1 − <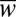 >, is then the average lag in fitness between the population and the optimum. Fig. 3A shows the ratio λhap/λdip between haploid and diploid populations for different values of σenv/σw. In slow-changing environments (σenv/σw < 10−4), haploids follow the moving optimum more closely than diploids, replicating the constant environment result. However, in fast-changing environments (σenv/σw > 10−4), it is diploids that prevail.
>, is then the average lag in fitness between the population and the optimum. Fig. 3A shows the ratio λhap/λdip between haploid and diploid populations for different values of σenv/σw. In slow-changing environments (σenv/σw < 10−4), haploids follow the moving optimum more closely than diploids, replicating the constant environment result. However, in fast-changing environments (σenv/σw > 10−4), it is diploids that prevail.
Fig. 3.
Statistics of adaptive walks under a moving fitness optimum. (A) Ratio of the average lag in fitness (λ) between the population and the optimum in haploids (hap) and diploids (dip) as a function of the speed of environmental change. In fast-changing environments, diploid populations follow the moving optimum more closely than haploids (λhap/λdip > 1). (B) Fitness variance attributable to balanced polymorphisms (frequency 0.05 < x < 0.95) and the age of the balanced polymorphism for different values of σenv. Both quantities are estimated from the balanced polymorphisms that were present at the end of simulation runs. The age of a balanced polymorphism is defined as the time since the most recent common ancestor of its constituent alleles. Data points are medians over 103 runs, and error bars specify the 10% and 90% quantiles. The gray-shaded area (0.04N < age < 4N) indicates the expected age range of common neutral polymorphisms at frequencies between 0.05 < x < 0.95. (C) Same as in B but phenotypic variance is shown instead of fitness variance.
The diversity advantage of diploid populations derives from the greater variation maintained during adaptation. Specifically, this greater variation should lead to an increased range of mutations starting from multiple balanced alleles as well as the ability of diploids to adapt by fast adjustment of the frequencies of balanced alleles without waiting for de novo mutations. Note that this diversity advantage of diploids is different in kind from the advantages based on the differences in number of chromosomes and the efficacy of selection in haploids and diploids discussed previously (14–16).
The characteristics of the genetic variation in diploid populations depend strongly on the speed of environmental change. Fig. 3 B and C show the joint distributions of allele age and the fitness or phenotypic variance of balanced polymorphisms at intermediate population frequencies as a function of σenv/σw. In slow-changing environments, balanced alleles generally persist over long periods of time, and thus tend to be much older than neutral alleles of comparable population frequencies. These old balanced alleles are similar phenotypically, and their segregation generates only limited variation in fitness (Fig. 3B) and phenotype (Fig. 3C). In contrast, in fast-changing environments, balanced alleles are much younger than comparably frequent neutral alleles. These young balanced alleles are often very distinct phenotypically, and thus produce high levels of standing variation in fitness (Fig. 3B) and phenotype (Fig. 3C).
Discussion
Our finding that heterozygote advantage emerges naturally in Fisher's geometric model if mutations are sufficiently large is very robust to the details of the model, such as the number of dimensions; the choice of phenotypic dominance rules, including under-, over-, and incomplete dominance; mutation rate and size distribution; population size; and flatness of the fitness function (SI Text, Figs. S1–S3, S7, and Table S1).
The features that underlie pervasive heterozygote advantage in Fisher's model are also likely to apply very generally in nature: (i) mutations in diploids should initially segregate as heterozygotes, (ii) selection should be stabilizing for some traits, and (iii) some invading mutations should be large enough to overshoot the local optimum. Indeed, rare mutations are generally heterozygous, except for cases of exceptionally strong inbreeding. It is also well established that stabilizing selection acts on many phenotypic traits (17, 18). Even if “more is always better” holds for certain traits, as long as adaptive mutations generally influence at least one trait under stabilizing selection, we still expect heterozygote advantage to be frequent. Finally, mutations of large phenotypic effect have been observed in many organisms, and it is becoming increasingly apparent that such large mutations do contribute to adaptation. For example, adaptive mutations of large effect have occurred in the domestication of maize (19) and dogs (20), the evolution of sticklebacks to fresh water habitats (21, 22), pesticide resistance in insects (8), coat color in mammals (23, 24), and several studies of experimental evolution (25, 26). Furthermore, analyses of mutation accumulation lines have demonstrated the availability of mutations causing multiple-fold changes in gene expression (4, 5). Because the expression of most genes is known to be constrained by stabilizing selection over much narrower ranges (3–7), we must conclude that gene expression mutations that overshoot the optimum are likely abundant.
The classic model of adaptation holds that adaption is driven by adaptive mutations that sweep quickly to fixation. Although our model also predicts such fast fixation events, it additionally predicts that many adaptive mutations will initially only sweep to intermediate frequencies, where they are then maintained for a period of time by balancing selection, before continuing on to either fixation or loss. Both models thus predict an elevated rate of fixation at functional sites compared with the neutral expectation and a local reduction of genetic diversity around adaptive sites, as have been observed in a range of organisms (27–30). However, in contrast to the classic model, we also expect the presence of many incomplete selective sweeps. Indeed, the genomic signatures of such incomplete sweeps appear to be plentiful in a number of organisms (31–33). Incomplete sweeps also appear to be common in experimental evolution in Drosophila, where virtually no classic sweeps have been detected after 600 generations of evolution despite abundant evidence of phenotypic adaptation over this period (34).
The abundance of incomplete sweeps in natural and experimental populations is consistent with but, unfortunately, not uniquely predictive of adaptation-driven balancing selection. Other scenarios, such as frequency-dependent selection, adaptation to specific subhabitats, and polygenic adaptation, also predict incomplete sweeps. The only way to test the hypothesis of heterozygote advantage explicitly is to measure fitness of the homozygotes and heterozygotes for the putatively balanced alleles directly. Such measurements are difficult but not impossible and can now be carried out systematically in laboratory systems of artificial selection, such as yeast or Drosophila (26, 34, 35).
However, in many other systems, direct fitness measurements are not feasible and balanced polymorphisms have to be identified by alternative approaches. The standard scans for balanced polymorphisms are inappropriate for our purposes because they typically search for very ancient balanced alleles (36–38), whereas the balanced alleles predicted by our model are often short-lived. To identify young balanced alleles specifically, one can search for polymorphisms that maintain their frequencies in the face of sharp bottlenecks (39). A particularly powerful system in this context is provided by human genetics because of the multiple recent bottlenecks associated with human migrations. Other opportune systems are island species recovering from natural disasters or man-made relocations of species to new but environmentally similar locations, such as the relocation of Euphydryas gillettii from Wyoming to Colorado (40).
Adaptive evolution is generally thought to be antithetical to the maintenance of genetic variation. In contrast, in our model, pervasive adaptation systematically generates genetic variation by promoting balanced polymorphisms. These balanced polymorphisms are expected to segregate at high frequencies yet can affect both phenotype and fitness substantially. This is very different from the common view that frequent polymorphisms should be neutral or subject to only weak selective forces.
We argue that adaptation-driven balanced polymorphisms can be an important source of consequential genetic variation. In particular, we believe that the balanced polymorphisms predicted by our model can be associated with human disease. Some of the common disease variants could be mutations that are maintained at high population frequencies because of strong heterozygote advantage, although they are very harmful as homozygotes.
Balancing selection and, specifically, the prevalence of heterozygous advantage was once considered the dominant force maintaining variation in natural populations (41–43). This view fell out of favor with the rise of the neutral theory in the 1960s (10). The neutral theory postulates that only a small proportion of substitutions are adaptive and that these substitutions are fixed very quickly; this, in turn, implies that practically all polymorphisms should be either neutral or slightly deleterious. However, recent genomic evidence has suggested that the rate of adaptation is substantial in some organisms, with, for example, ∼50% of all amino acid substitutions in Drosophila driven by positive selection (28). Here, we argue that such a high rate of adaptation in diploids should also lead to a high rate at which balanced polymorphisms are driven into the population. We thus advocate that the balance theory of genetic variation should be given new life and reassessed using all the modern genomic tools at our disposal.
Materials and Methods
Monte Carlo Simulations of a Single Adaptive Mutation in Fisher's Model.
We investigate the evolution of a single locus in Fisher's geometric model (9). Alleles are represented by vectors (r) in an abstract, d-dimensional Euclidean phenotype space. Mutant alleles are obtained by adding a mutation vector (m) to the parental allele: rb = ra + m. The directions of mutation vectors are distributed uniformly; mutation sizes (m) are distributed according to a probability distribution P(m) with an average mutation size <m>. We consider two such distributions in detail, the uniform distribution P(m) ∝ uniform(0,2<m>) and the exponential distribution P(m) ∝ exp(−m/<m>). Haploid organismal phenotypes are equal to the allelic phenotype. In diploids, the phenotype is a weighted average of its two constituent alleles. In the case of the heterozygous mutant, the phenotype can be expressed as rab = ra + hm, with h being the phenotypic dominance of the mutant allele.
The fitness of a phenotype is determined by its distance from the fitness optimum r*. Following precedent (10, 11), we use a Gaussian fitness function: w(r) = exp[−(r-r*)2/(2σw2)]. For convenience, we set the origin of the phenotype space to be at r* and choose the scale of the space such that σw2 = 1. We begin by considering mutations arising in a population that is monomorphic for the wild-type allele ra = (2,0,…,0). The invasion probability of new mutations is then approximately πhap(m) = 2[w(rb)/w(ra) − 1] in haploids (10). In diploids, we assume that mutants initially exist only as heterozygotes, therefore: πdip(m) = 2[w(rab)/w(ra) − 1].
Results in Figs. S1 and S2 were obtained from Monte Carlo simulations of the above model based on 107 randomly drawn mutations per data point. The ratios udip/uhap of the rates at which adaptive mutations occur in diploids vs. haploids were estimated by counting the overall numbers of mutations where rb ∈ αhap in haploids or, respectively, rab ∈ αdip in diploids. For the ratios vdip/vhap of the rates at which adaptive mutations invade the population, each adaptive mutation was additionally weighted by its respective invasion probability, πhap or πdip. Among successfully invading mutations, the expectation values, <w(rab) − w(ra)> in diploids and <w(rb) − w(ra)> in haploids, were measured to estimate the ratios <Δwdip>/<Δwhap>. Estimates of δu were obtained by counting the fraction of adaptive mutations with heterozygote advantage in the diploid scenario. For δv, each adaptive mutation was thereby additionally weighted by its respective invasion probability.
Simulation of Adaptive Walks Toward a Fixed Fitness Optimum.
To investigate adaptive walks toward a fixed fitness optimum, we simulated the full stochastic population dynamics in the above scenario under an infinite alleles assumption. We focused on the instructive case of a 2D Fisher's model with complete phenotypic codominance (h = 1/2). The phenotype of a heterozygous diploid is then always the coordinate-wise average of its two alleles: rab = (ra + rb)/2.
Mutations are modeled by a Poisson process with rate μ = 2.5⋅10−7 per individual and generation. Mutation directions are drawn uniformly, and mutation sizes are sampled from an exponential distribution with mean <m> = 1. Population sizes are Nhap = 105 for haploids and Ndip = 5⋅104 for diploids, ensuring that new mutations arise at equal overall rates in the two populations (Θ = 2cNμ = 0.05, where c is ploidy).
The state of the population at any given time point is specified by the set of alleles {ri} present in the population and their associated population frequencies {xi}. Allele frequency dynamics are modeled in a Wright–Fisher framework with selection (44). For haploids, we use the standard Wright–Fisher sampling procedure in which allele frequencies xi(t + 1) in the next generation are drawn from a multinomial distribution P(N,{pihap(t)}) with selection-adjusted probabilities: pihap(t) ∝ w(ri)xi(t). In the case of diploids, we first convert allele frequencies into genotype frequencies (assuming Hardy–Weinberg equilibrium) to calculate the selection-adjusted probabilities: pidip(t) ∝ ∑jw(rij)xi(t)xj(t). Allele frequencies xi(t + 1) are then drawn from P(2N,{pidip(t)}). In both cases, pi and xi are normalized such that ∑ipi = ∑ixi = 1.
As specified above, simulations start from a population that is monomorphic for the wild type ra = (2,0) with the optimal phenotype located at the origin, yielding an initial population average fitness of w(ra) ∼0.13. Populations are then evolved for 104 generations, which typically suffices to approach the fitness optimum closely (<w> > 0.96 at end of a run; Fig. S4A).
Simulations Under a Moving Fitness Optimum.
For the analysis of the moving optimum scenario, we adjust our simulation as follows. At the start of the simulation, the population is initialized to be monomorphic for the optimal phenotype: r*(t = 0) = ra = (0,0). In each subsequent generation, the optimum r*(t) moves one step in a random direction and the size of the mutation is sampled from the positive half of a Gaussian distribution with variance σenv2. In a single simulation run, the population is evolved for 107 generations (∼100N). We exclude the first 105 generations of each run from our analysis as a “burn-in” period so as to remove the influence of the initial state of the population.
Ascertainment of Balanced Polymorphisms During Adaptive Walks.
Balanced polymorphisms can consist of several alleles (45, 46). We determine the presence of a balanced polymorphism at a given time point in our simulation runs using Kimura's analytic conditions (47). Assume that n alleles {r1,…,rn} are present in the population with diploid fitness values given by w(rij). Let T be the matrix defined by Tij = w(rij) − w(rin) − w(rjn) + w(rnn) (i,j = 1,…,n). Let Δi be the determinant obtained when substituting all elements in the ith column of the fitness-matrix w(rij) (i,j = 1,…,n) with 1. The necessary and sufficient conditions for the existence of a stable equilibrium with all individual population frequencies xi of the alleles being nonzero are then that T is negative definite and that (−1)n − 1Δi > 0 for all i = 1,…,n. Geometrically, these first two conditions specify a peak in n-dimensional fitness space, and only one such peak is allowed for all alleles to coexist (47).
For heterozygote advantage to be consequential (i.e., to be capable of effectively stabilizing a balanced polymorphism against the stochastic fluctuations arising from random genetic drift), the fitness advantages of a heterozygote over its two homozygote have to be at least of order 1/N (10). Because we are only interested in such consequential cases of heterozygote advantage, we thus require, as a third condition, that for at least one pair of alleles in a balanced polymorphism, it holds that w(rij) > max[w(rii),w(rjj)] + 1/N.
In our simulations, we evaluate these three conditions for the fitness matrix of all alleles with frequencies 0.05 < xi < 0.95. Negative definiteness of T is tested by numerically calculating eigenvalues using symmetrical bidiagonalization with the QR reduction method (48) and checking for the negativity of all eigenvalues. Signs of determinants Δi are estimated using numerical LU decompositions (48).
All source code is openly available online at: http://sourceforge.net/projects/fgm. Simulations were run on the Bio-X2 cluster at Stanford University.
Supplementary Material
Acknowledgments
We thank members of the D.A.P. laboratory, Daniel Weinreich, Adam Eyre-Walker, Hunter Fraser, David Kingsley, Molly Przeworski, Matthew Stephens, Warren Ewens, Nick Barton, Kevin Bullaughey, Marc Feldman, Daniel Fisher, Daniel Hartl, Ward Watt, and six anonymous reviewers for helpful feedback. This research was supported by grants from the National Institutes of Health Grant GM 077368 and National Science Foundation Grant 0317171, CNS-0619926 (to D.A.P.). D.S. is a Stanford Graduate Fellow. P.W.M. was a Human Frontier Science Program postdoctoral fellow.
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1114573108/-/DCSupplemental.
References
- 1.Haldane JBS. A mathematical theory of natural and artificial selection, part V: Selection and mutation. Math Proc Camb Philos Soc. 1927;23:838–844. [Google Scholar]
- 2.Carroll SB. Evo-devo and an expanding evolutionary synthesis: A genetic theory of morphological evolution. Cell. 2008;134(1):25–36. doi: 10.1016/j.cell.2008.06.030. [DOI] [PubMed] [Google Scholar]
- 3.Lemos B, Meiklejohn CD, Caceres M, Hartl DL. Rates of divergence in gene expression profiles of primates, mice, and flies: Stabilizing selection and variability among functional categories. Evolution. 2005;59:126–137. [PubMed] [Google Scholar]
- 4.Denver DR, et al. The transcriptional consequences of mutation and natural selection in Caenorhabditis elegans. Nat Genet. 2005;37:544–548. doi: 10.1038/ng1554. [DOI] [PubMed] [Google Scholar]
- 5.Rifkin SA, Houle D, Kim J, White KP. A mutation accumulation assay reveals a broad capacity for rapid evolution of gene expression. Nature. 2005;438:220–223. doi: 10.1038/nature04114. [DOI] [PubMed] [Google Scholar]
- 6.Gilad Y, Oshlack A, Rifkin SA. Natural selection on gene expression. Trends Genet. 2006;22:456–461. doi: 10.1016/j.tig.2006.06.002. [DOI] [PubMed] [Google Scholar]
- 7.Bedford T, Hartl DL. Optimization of gene expression by natural selection. Proc Natl Acad Sci USA. 2009;106:1133–1138. doi: 10.1073/pnas.0812009106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Daborn PJ, et al. A single p450 allele associated with insecticide resistance in Drosophila. Science. 2002;297:2253–2256. doi: 10.1126/science.1074170. [DOI] [PubMed] [Google Scholar]
- 9.Fisher RA. The Genetical Theory of Natural Selection. Oxford: Clarendon; 1930. [Google Scholar]
- 10.Kimura M. The Neutral Theory of Molecular Evolution. Cambridge, UK: Cambridge Univ Press; 1983. [Google Scholar]
- 11.Orr HA. The population genetics of adaptation: The distribution of factors fixed during adaptive evolution. Evolution. 1998;52:935–949. doi: 10.1111/j.1558-5646.1998.tb01823.x. [DOI] [PubMed] [Google Scholar]
- 12.Hartl D, Taubes C. Towards a theory of evolutionary adaptation. Genetica. 1998;102–103:525–533. [PubMed] [Google Scholar]
- 13.Orr HA. The genetic theory of adaptation: A brief history. Nat Rev Genet. 2005;6(2):119–127. doi: 10.1038/nrg1523. [DOI] [PubMed] [Google Scholar]
- 14.Otto SP, Gerstein AC. The evolution of haploidy and diploidy. Curr Biol. 2008;18:R1121–R1124. doi: 10.1016/j.cub.2008.09.039. [DOI] [PubMed] [Google Scholar]
- 15.Goldstein DB. Heterozygote advantage and the evolution of a dominant diploid phase. Genetics. 1992;132:1195–1198. doi: 10.1093/genetics/132.4.1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Orr HA, Otto SP. Does diploidy increase the rate of adaptation? Genetics. 1994;136:1475–1480. doi: 10.1093/genetics/136.4.1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Haldane JBS. Natural selection. In: Bell PR, editor. Darwin's Biological Work. Cambridge, UK: Cambridge Univ Press; 1959. pp. 101–149. [Google Scholar]
- 18.Wright S. Evolution and the Genetics of Populations. Chicago: Univ of Chicago Press; 1977. [Google Scholar]
- 19.Doebley J, Stec A, Hubbard L. The evolution of apical dominance in maize. Nature. 1997;386:485–488. doi: 10.1038/386485a0. [DOI] [PubMed] [Google Scholar]
- 20.Sutter NB, et al. A single IGF1 allele is a major determinant of small size in dogs. Science. 2007;316:112–115. doi: 10.1126/science.1137045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Colosimo PF, et al. The genetic architecture of parallel armor plate reduction in threespine sticklebacks. PLoS Biol. 2004;2:E109. doi: 10.1371/journal.pbio.0020109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chan YF, et al. Adaptive evolution of pelvic reduction in sticklebacks by recurrent deletion of a Pitx1 enhancer. Science. 2010;327:302–305. doi: 10.1126/science.1182213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nachman MW, Hoekstra HE, D'Agostino SL. The genetic basis of adaptive melanism in pocket mice. Proc Natl Acad Sci USA. 2003;100:5268–5273. doi: 10.1073/pnas.0431157100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hoekstra HE, Hirschmann RJ, Bundey RA, Insel PA, Crossland JP. A single amino acid mutation contributes to adaptive beach mouse color pattern. Science. 2006;313:101–104. doi: 10.1126/science.1126121. [DOI] [PubMed] [Google Scholar]
- 25.Dunham MJ, et al. Characteristic genome rearrangements in experimental evolution of Saccharomyces cerevisiae. Proc Natl Acad Sci USA. 2002;99:16144–16149. doi: 10.1073/pnas.242624799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kao KC, Sherlock G. Molecular characterization of clonal interference during adaptive evolution in asexual populations of Saccharomyces cerevisiae. Nat Genet. 2008;40:1499–1504. doi: 10.1038/ng.280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Eyre-Walker A. The genomic rate of adaptive evolution. Trends Ecol Evol. 2006;21:569–575. doi: 10.1016/j.tree.2006.06.015. [DOI] [PubMed] [Google Scholar]
- 28.Sella G, Petrov DA, Przeworski M, Andolfatto P. Pervasive natural selection in the Drosophila genome? PLoS Genet. 2009;5:e1000495. doi: 10.1371/journal.pgen.1000495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cai JJ, Macpherson JM, Sella G, Petrov DA. Pervasive hitchhiking at coding and regulatory sites in humans. PLoS Genet. 2009;5:e1000336. doi: 10.1371/journal.pgen.1000336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Halligan DL, Oliver F, Eyre-Walker A, Harr B, Keightley PD. Evidence for pervasive adaptive protein evolution in wild mice. PLoS Genet. 2010;6:e1000825. doi: 10.1371/journal.pgen.1000825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Clark RM, et al. Common sequence polymorphisms shaping genetic diversity in Arabidopsis thaliana. Science. 2007;317:338–342. doi: 10.1126/science.1138632. [DOI] [PubMed] [Google Scholar]
- 32.Gonzalez J, Lenkov K, Lipatov M, Macpherson JM, Petrov DA. High rate of recent transposable element-induced adaptation in Drosophila melanogaster. PLoS Biol. 2008;6:e251. doi: 10.1371/journal.pbio.0060251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Coop G, et al. The role of geography in human adaptation. PLoS Genet. 2009;5:e1000500. doi: 10.1371/journal.pgen.1000500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Burke MK, et al. Genome-wide analysis of a long-term evolution experiment with Drosophila. Nature. 2010;467:587–590. doi: 10.1038/nature09352. [DOI] [PubMed] [Google Scholar]
- 35.Zhang M, Azad P, Woodruff RC. Adaptation of Drosophila melanogaster to increased NaCl concentration due to dominant beneficial mutations. Genetica. 2011;139:177–186. doi: 10.1007/s10709-010-9535-z. [DOI] [PubMed] [Google Scholar]
- 36.Asthana S, Schmidt S, Sunyaev S. A limited role for balancing selection. Trends Genet. 2005;21:30–32. doi: 10.1016/j.tig.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 37.Bubb KL, et al. Scan of human genome reveals no new loci under ancient balancing selection. Genetics. 2006;173:2165–2177. doi: 10.1534/genetics.106.055715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Andres AM, et al. Targets of balancing selection in the human genome. Mol Biol Evol. 2009;26:2755–2764. doi: 10.1093/molbev/msp190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Makinen HS, Cano JM, Merila J. Identifying footprints of directional and balancing selection in marine and freshwater three-spined stickleback (Gasterosteus aculeatus) populations. Mol Ecol. 2008;17:3565–3582. doi: 10.1111/j.1365-294X.2008.03714.x. [DOI] [PubMed] [Google Scholar]
- 40.Holdren CE, Ehrlich PR. Long range dispersal in checkerspot butterflies: Transplant experiments with Euphydryas gillettii. Oecologia. 1981;50:125–129. doi: 10.1007/BF00378805. [DOI] [PubMed] [Google Scholar]
- 41.Lerner IM. Genetic Homeostasis. New York: Wiley; 1954. p. 134. [Google Scholar]
- 42.Dobzhansky T. Heterosis: A Record of Researches Directed Toward Explaining and Utilizing the Vigor of Hybrids. Ames, IA: Iowa State College Press; 1952. Nature and the origin of heterosis; pp. 218–223. [Google Scholar]
- 43.Crow JF. Muller, Dobzhansky, and overdominance. J Hist Biol. 1987;20:351–380. [Google Scholar]
- 44.Ewens WJ. Mathematical Population Genetics: 1. Theoretical Introduction. New York: Springer; 2004. p. 417. [Google Scholar]
- 45.Hastings A, Hom CL. Pleiotropic stabilizing selection limits the number of polymorphic loci to at most the number of characters. Genetics. 1989;122:459–463. doi: 10.1093/genetics/122.2.459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Burger R, Gimelfarb A. Fluctuating environments and the role of mutation in maintaining quantitative genetic variation. Genet Res. 2002;80:31–46. doi: 10.1017/s0016672302005682. [DOI] [PubMed] [Google Scholar]
- 47.Kimura M. Rules for testing stability of a selective polymorphism. Proc Natl Acad Sci USA. 1956;42:336–340. doi: 10.1073/pnas.42.6.336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Galassi M. GNU scientific library: Reference manual. Bristol, UK: Network Theory; 2009. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.