Energy landscape of the reactions governing the Na⁺ deeply occluded state of the Na⁺/K⁺-ATPase in the giant axon of the Humboldt squid

Abstract

The Na⁺/K⁺ pump is a nearly ubiquitous membrane protein in animal cells that uses the free energy of ATP hydrolysis to alternatively export 3Na⁺ from the cell and import 2K⁺ per cycle. This exchange of ions produces a steady-state outwardly directed current, which is proportional in magnitude to the turnover rate. Under certain ionic conditions, a sudden voltage jump generates temporally distinct transient currents mediated by the Na⁺/K⁺ pump that represent the kinetics of extracellular Na⁺ binding/release and Na⁺ occlusion/deocclusion transitions. For many years, these events have escaped a proper thermodynamic treatment due to the relatively small electrical signal. Here, taking the advantages offered by the large diameter of the axons from the squid Dosidicus gigas, we have been able to separate the kinetic components of the transient currents in an extended temperature range and thus characterize the energetic landscape of the pump cycle and those transitions associated with the extracellular release of the first Na⁺ from the deeply occluded state. Occlusion/deocclusion transition involves large changes in enthalpy and entropy as the ion is exposed to the external milieu for release. Binding/unbinding is substantially less costly, yet larger than predicted for the energetic cost of an ion diffusing through a permeation pathway, which suggests that ion binding/unbinding must involve amino acid side-chain rearrangements at the site.

During each normal transport cycle of the Na⁺/K⁺-ATPase pump, three Na⁺ are exported from the cell in exchange for two K⁺ imported, a process driven by hydrolysis of one molecule of ATP. By establishing the Na⁺ and K⁺ gradients across cell membranes, the Na⁺/K⁺ pump enables action potentials, synaptic signaling, and most solute transport in and out of cells. Two consequences of the unequal transport stoichiometry of Na⁺ and K⁺ are that steady pumping produces an outwardly directed current (1), proportional in magnitude to the turnover rate (2), which can be monitored electrically (3–8), and that at least one step in the transport cycle must move charge through the membrane field (9). The latter implies that, under favorable conditions, charge relaxations following voltage jumps can be used to learn details about specific steps during the transport cycle (10–28).

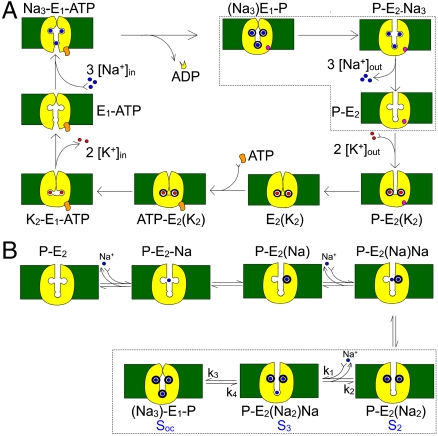
In the absence of internal and external K⁺, the nominal absence of internal ADP and presence of an ATP regenerating system, the Na⁺/K⁺ pump allows exchange of 3Na⁺ between their binding sites in a deeply occluded conformation and the external milieu (21, 29) (Fig. 1A; encircled by dotted lines). Under these conditions there is no steady pump current observed at any voltage. Nevertheless, sudden voltage steps produce pre-steady-state currents that can be recorded (12, 13, 16–18, 21, 23, 26). These currents allow direct measurements of the rates of partial reactions of the pump cycle. Using giant axons from the squid Loligo pealeii, we have characterized the kinetics of extracellular Na⁺ binding/release and Na⁺ occlusion/deocclusion and proposed mechanistic and structural hypotheses related to ion movement (18). The time course of the transient pump currents contains a fast, a medium-speed, and a slow component (see Materials and Methods and ref. 18). The temporal correlation between these components indicates that they occur in strict sequence (18), likely representing the binding/release and occlusion/deocclusion of individual Na⁺ (Fig. 1B). The charge distribution of each component can be described by a Boltzmann function with an apparent valence for the charge moved of approximately 1 for the medium (18) and slow (12, 13, 16–18, 21, 23, 26, 30) components but only approximately 0.2 for the fast component, indicating that it does not transport charge across a large portion of the electric field (26). Most importantly, the voltage dependence of the slow relaxation shifts with changes in external Na⁺ concentration, [Na⁺]_o, supporting the interpretation that Na⁺ ions must negotiate a high-field access channel as they travel back and forth between the external solution and their binding sites deep within the Na⁺/K⁺ pump (17, 18, 23).

Fig. 1.

Kinetic schemes. (A) Simplified Albers-Post model for the Na⁺/K⁺ pump cycle. E₁ and E₂ are the main Na⁺/K⁺ pump conformations with ion binding sites facing the intracellular and extracellular sides, respectively. Internal (0 ADP, 0 P, 0 K⁺, and an ATP regenerating system) and external solutions (0 Na⁺) were designed to force the pump to operate in a strictly forward direction (Fig. 3). (B) Explicit extracellular Na⁺ binding/release and occlusion/deocclusion model. Electrogenic binding and release of each Na⁺ is assumed to be independent and in strict sequence. Similarly, Na⁺ are occluded and deoccluded independently but with electroneutral transitions. States encircled by dotted lines represent the binding/release and occlusion/deocclusion governing the slow component of the transient currents. Here we have assumed that the deep occlusion and the E₁-P↔E₂-P transitions are the same reaction.

Giant axons from Loligo have provided unique advantages for studying Na⁺ translocation events mediated by the pump (18, 29). However, they too have limits. At low temperatures the amplitudes of the signals resulting from the binding/release of extracellular Na⁺ are too small to permit study of the thermodynamics of these steps. To overcome these biological limitations, we have performed experiments using the giant axons of the Humboldt squid (Dosidicus gigas). In Chile, where these experiments were conducted, these squid commonly reach lengths close to 2 m and weigh up to 40 kg. More importantly for the present purpose, their axons routinely surpass 1.2 mm in diameter (approximately twice the diameter of a large Loligo axon), providing a substantially larger membrane area, and hence a greater number of pumps, than comparable lengths of axons from Loligo. With the aim of characterizing the energetic landscape of the transitions associated with the extracellular release of the first Na⁺ from the deeply occluded state, in this study we have determined the thermodynamic parameters of the slowest component of Na⁺ translocation.

Results and Discussion

Na⁺/K⁺ Pump Turnover Rate Revisited.

The effectiveness with which the Na⁺/K⁺ pump exports Na⁺ is encapsulated by its turnover rate, which is a measure of how quickly the entire sequence of state transitions depicted in Fig. 1A is completed. To gauge the temperature sensitivity of the whole transport cycle, we characterized the Na⁺/K⁺ pump’s turnover rate (v_f) as a function of temperature. Pumps were constrained to cycle in the forward direction predominantly by withholding external Na⁺, as well as intracellular ADP, phosphate, and K⁺ (see Fig. 1A). The steady-state Na⁺/K⁺ pump current was then determined, at three different voltages (-70, 0, and +40 mV), as the component of membrane current abolished by a near-saturating concentration (100 μM) of dihydrodigitoxigenin (H₂DTG), a specific and reversible inhibitor of squid Na⁺/K⁺ pumps (2). Corresponding values of v_f at these voltages (Fig. 2) were obtained by dividing the pump current by an estimate of the total number of Na⁺/K⁺ pumps in the same axon, determined from pump charge movements (see Figs. 3 and 6 below; also see Materials and Methods). Under these conditions, in the absence of external Na⁺, v_f becomes essentially voltage independent (5), and for this reason we thought it reasonable to plot results obtained at different voltages together. In confirmation, v_f was similar across this potential range, with values of 20–23, 67–74, or approximately 106 s^-1 at temperatures of 15.2, 22.1, and 25.3 °C, respectively. Assuming that within these voltage and temperature ranges v_f reflects the same rate-limiting step, then on the basis of transition state theory the temperature dependence of v_f is given by

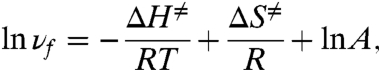[1]

where ΔH^‡ is the transition enthalpy, R is the molar gas constant, T is the absolute temperature, ΔS^‡ is the transition entropy, and A is the preexponential factor of the rate. A linear regression fit to a plot of ln v_f against 1/T yields the slope -ΔH^‡/R and intercept ΔS^‡/R + ln A. From the data in Fig. 2, we estimated ΔH^‡ to be approximately 24 kcal/mol, which corresponds to a Q₁₀ of approximately 4.3, similar to previous reports (31–33).

Fig. 2.

Activation energy of the Na⁺/K⁺ forward pumping rate. Forward pump rates were estimated from 16 axons (16 H₂DTG-sensitive steady-state determinations) at voltages of -70 (▪), 0 (●), and +40 mV (▴), with temperatures ranging from 13.2 to 25.3 °C. The solid line represents a linear fit in which the best fit parameter value for the slope and intercept were -12,103 and 45.2, respectively.

Fig. 3.

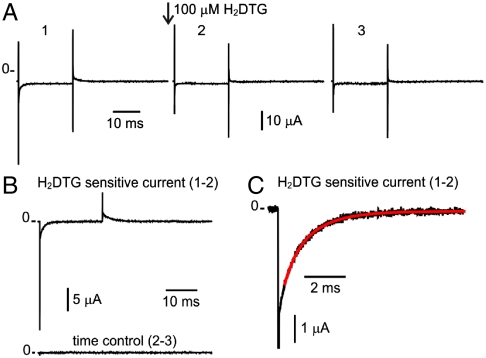
Na⁺ translocation by the Na⁺/K⁺-ATPase. (A) Current traces in response to a voltage step to -80 mV from a holding potential of 0 mV. Trace 1 was acquired immediately before the application of 100 μM H₂DTG to the external solution. Trace 2 was acquired after complete pump inhibition (approximately 25 s after H₂DTG application). Trace 3 was acquired approximately 25 s after trace 2. (B) Pump-mediated Na⁺ translocation (Upper) is obtained by subtracting the nonspecific membrane current of trace 2 from trace 1. The stability of the preparation was assessed by subtracting similar time-spaced acquisitions (Lower). (C) Expanded form of the On transient current in response to the voltage step to -80 mV. The solid line represents a two-component exponential fit to the current relaxation with best fit parameter values for the time constants of 0.56 and 1.44 ms.

Fig. 6.

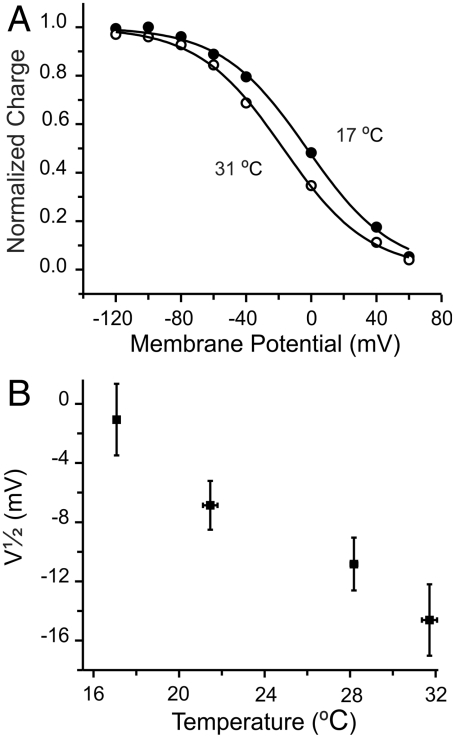
Influence of temperature on the voltage dependence of charge distribution. (A) Charge distributions. Normalized charge moved by the slow component from an axon exposed at 17 (●) and 31 °C (∘). Solid lines represent Boltzmann fits with midpoint values of -3 ± 1 (17 °C) and -17 ± 1 mV (31 °C). (B) Shift of voltage dependence with temperature. Data were grouped similarly as in Fig. 5.

The value of the transition entropy, ΔS^‡ = 89.8 - R ln A, necessarily requires a knowledge of the factor A, which for large molecules in aqueous solutions is largely unknown. For some protein conformational changes involved in protein folding or ion channel opening, however, experimental estimates have put the value of A at approximately 10⁶ s^-1 (34, 35). With this assumption, ΔS^‡ is approximately 62 cal/molK.

Given these estimates for ΔH^‡ and ΔS^‡, we can calculate the height of the free energy barrier (ΔG^‡) that determines the rate-limiting step of forward pumping under our experimental conditions: At 15 °C it is approximately 6.1 kcal/mol, and at 25 °C it is approximately 5.5 kcal/mol. This result means that, for a 10 °C increase in temperature, pump cycling encounters only a small reduction (< 1RT) in the barrier height. However, this small change in ΔG^‡ should not be taken to imply that the underlying structural changes are small. On the contrary, the values for ΔH^‡ and TΔS^‡ are both large, indicating large conformational changes, although the enthalpic and entropic terms largely cancel each other.

Na⁺ Translocation in Giant Axons from the Humboldt Squid.

Because temperature dependence provides information on the extent of structural changes, studying the thermodynamics of isolated transitions is particularly informative. We have been able to precisely restrict a subset of transitions from the Na⁺/K⁺ pump’s transport cycle that relate to the binding/release and occlusion/deocclusion of external Na⁺. We have been studying these signals in fine detail by using electrophysiological methods (18). The signal to noise ratio in Loligo axons had made it difficult to estimate the thermodynamic parameters at low temperatures, because, as the total charge is conserved, the amplitude of the transient currents become small as the temperature is decreased. We have solved this problem by using axons of the squid D. gigas that are much larger, giving transient pump currents about 3–5 times greater than those obtained by using the largest Loligo axons (see below).

A typical experiment that isolates transient pump currents is shown in Fig. 3A. This experiment was performed with 400 mM [Na⁺]_o (roughly the concentration of sea water) and at a temperature of 27.6 °C. Records 1–3, spaced at intervals of approximately 25 s, show averages of three traces, each in response to a 25 ms voltage step to -80 mV from a holding potential of 0 mV. Pump-mediated Na⁺ translocation (Fig. 3B, Upper) is isolated by subtracting the nonspecific membrane currents (record 2) from the total membrane current before the application of 100 μM H₂DTG (record 1). Subtraction of similar current records after complete H₂DTG inhibition (records 2–3) provides a time control to evaluate the stability of the preparation over the time interval needed to obtain records before and after arresting all the Na⁺/K⁺ pumps (Fig. 3B, Lower). Because we used K⁺-free Na⁺ solutions with high internal ATP and no ADP (see Materials and Methods), the transient currents shown in Fig. 3B reflect the kinetics of external Na⁺ interacting with phosphorylated conformations of Na⁺/K⁺ pumps (Fig. 1B). These transient currents have been studied in detail by using Loligo axons (18). They are composed of three distinct components, which have been proposed to represent the strict sequential binding/release and occlusion/deocclusion of the three Na⁺. The general features of the pump transient currents in Dosidicus are not different from those measured in Loligo (Figs. 3 B and C), but the amplitudes of the transient currents are substantially larger. The onset of the voltage step to -80 mV elicits a large, fast spike (Fig. 3B), which reflects the binding and occlusion of the first Na⁺ (18). The medium and slow components are represented by a two-exponential fit to the subsequent current decay (Fig. 3C, solid red line). The slower component (τ ∼ 1.4 ms) is derived from the pumps populating the deeply Na⁺ occluded state [Fig. 1B; (Na₃)E₁-P]. This component involves a voltage-dependent binding/release reaction through an access channel and an electroneutral conformational change associated with occlusion/deocclusion (18). From the reaction scheme, it is clear that the probability of entering into the deeply occluded state depends on the probability of finding the pump in the preceding state [P-E₂(Na₂)Na]. Therefore, assuming the Na⁺-binding reaction is at equilibrium with respect to the occluding reaction, the rate (1/τ_slow) is given by the relation (SI Text)

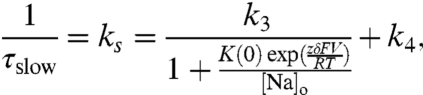[2]

where the Na⁺ binding/unbinding reaction parameters are the dissociation constant at 0 mV [K(0)], the Na⁺ valence (z) is 1, and δ represents the electrical distance that the Na⁺ must travel across the electric field along the access channel, whereas k₃ and k₄ denote the occlusion and deocclusion rates, respectively.

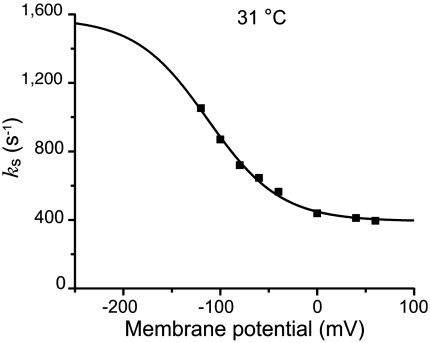
Both the forward and backward rate constants can be extracted by extending the model to extreme voltages. At very negative potentials the model predicts an asymptote given by k_s = k₃ + k₄ and at very positive voltages an asymptote given by k_s = k₄. Fig. 4 shows that as predicted a constant value for k_s is reached at voltages ≥0 mV. In this experiment, performed at 31 °C, k_s reaches a value of approximately 390 s^-1 at voltages ≥0 mV. The asymptote at negative potentials (k₃ + k₄) can only be estimated, because these data would require voltage steps far beyond what the axon’s membrane can withstand without damage (≤ -200 mV). The solid line shows a fit of the k_s vs. V data to Eq. 2 in which δ has been constrained to 0.7, a rather robust value that has been obtained by using different approaches and preparations (12, 13, 17, 18, 26, 29, 30). Fixing δ allows us estimate k₃ to be approximately 1,180 s^-1 at 31 °C.

Fig. 4.

Voltage dependence of the relaxations of the slow charge translocation component. The solid line represents a fit of the data to Eq 2. The best fit parameter values for k₃, k₄, and K(0) were 1,185 s^-1, 393 s^-1, and 8.16 M, respectively.

Global Fit of k_s vs. Voltage at Different Temperatures.

Our aim is to determine the thermodynamic parameters that characterize the slow component, because it represents the rate-limiting transition for external Na⁺ translocation. The temperature dependence of k_s (Eq. 2) may be obtained on the basis of transition state theory for k₃ and k₄ and by assigning enthalpic and entropic components to the binding/unbinding reactions to give (see SI Text)

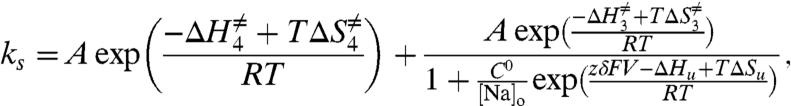[3]

where ΔH^≠ and ΔS^≠ correspond to the activation enthalpies and entropies for the deocclusion (subindices 4) and occlusion (subindices 3), respectively, A is the preexponential term, which has been set to be 10⁶ s^-1 (34, 35) and assumed to be the same for the slow deocclusion and occlusion reactions, C⁰ is the standard state concentration of 1 mol/L (= 1/1661 Å³; see ref. 36), and ΔH_u and ΔS_u are the total enthalpy and entropy, respectively, of the adjacent binding reaction (binding of the third Na⁺ and unbinding of the first Na⁺ released).

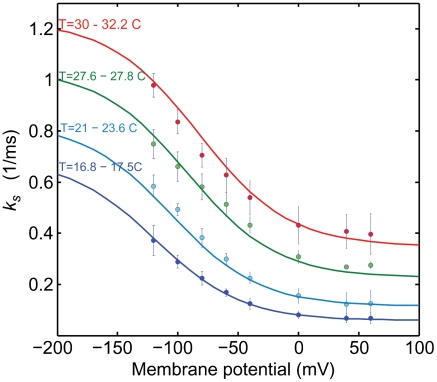
To determine the parameters of Eq. 3, we first measured the slow time constant (τ_slow) of 151 H₂DTG-sensitive pre-steady-state currents obtained from voltages between -120 and +60 mV and temperatures ranging from 16.8 to 32.2 °C. Second, the reciprocals of the experimental time constants (k_s = 1/τ_slow) were globally fitted to Eq. 3 to extract the entropies and enthalpies of the third Na⁺ binding/unbinding and the occlusion/deocclusion reactions. All the experiments were performed with 400 mM [Na]_o. As before, δ was the only fixed parameter. Because the fit was made by using every relaxation rate at a given temperature and membrane potential, it is difficult to present all the data, together with the fits, in a single panel. For presentation purposes, Fig. 5 shows the data binned in four temperature ranges, each spanning less than about 2 °C (as indicated in Fig. 5). The average experimental rates at each potential, in each temperature bin, are shown with their standard deviation. The curves in Fig. 5 were generated by assigning the fitted parameters to Eq. 3 and using temperature values representing the average of each bin.

Fig. 5.

Global fit of the slow rate constant k_s, as a function of voltage. A total of 151 reciprocal slow time constants that spanned 8 voltages and 15 temperatures were fitted to Eq 3. The data have been grouped at four temperatures, and the points represent averages with their standard deviation. The continuous curves were generated with the fitted parameters at the average value of each group of temperatures. The range of temperatures of each group is indicated at the left of the graph.

The results from the fit are summarized in Table 1 (bold) along with the derived parameters. These results provide insights into the energy landscapes of the transitions involving the deeply occluded conformation. The occlusion/deocclusion transition of the first Na⁺ to be released from the pump involves large enthalpic and entropic changes (Net ΔH = 19.6 kcal/mol and net ΔS = 62.4 cal/mol K). From the occlusion/deocclusion net enthalpy, it is expected that this transition would have a Q₁₀ value of 3.3 (18, 22), characteristic of transitions involving protein conformational changes. Of note is the fact that it is smaller than the value obtained for the rate-limiting step (v_f) when Na⁺/K⁺ pumps are exchanging Na⁺ for K⁺ (Fig. 2) in their normal mode of operation, indicating that release of the deeply occluded Na⁺ is not the step that rate limits the pump cycle. Likely, completion of the entire transport cycle is limited by transitions associated with dephosphorylation and deocclusion of K⁺ to the intracellular side, which involve large conformational changes of intracellular domains that are accelerated by low-affinity binding of ATP (37). In addition, the thermodynamic analysis of the Na⁺ occlusion/deocclusion step indicates that the energetic landscape of this transition is not symmetrical. Thus, assuming that the transition state is the same for the deep occlusion and deocclusion reactions, considerably more activation energy seems required to leave the deeply occluded state (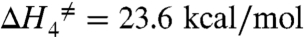; Q₁₀ = 4.2) than to return (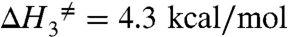; Q₁₀ = 1.3). In spite of this fact, the heights of the free energy barriers are not very different in the two directions. If anything, the deeply occluded state [P-E₁(Na₃)] is slightly more stable than the P-E₂(Na₂)·Na state. The increase in net entropy of the occlusion/deocclusion transition indicates that the deeply occluded state is also more ordered than the P-E₂(Na₂)·Na state.

Table 1.

Thermodynamic parameters describing the reactions governing the Na⁺ deeply occluded state

		ΔH≠ kcal/mol	ΔS≠ cal/molK	ΔG≠ kcal/mol	Net ΔH kcal/mol	Net ΔScal/mol K	Net ΔG kcal/mol
Soc↔S3	deocclusion	23.6 ± 1.5	61.8 ± 5.1	5.5 ± 1.7	19.6	62.4	1.2 ± 1.5
	occlusion	(4.1 ± 1.3)	(−0.6 ± 4.5)	4.3 ± 0.1
Binding/unbinding S3↔S2K(0) = 7.74 ± 0.6					−11.4 ± 3.5	−34.7 ± 12	−1.2 ± 3.5
Combined Soc↔S2					8.4	27.7	0 ± 3.8

The adjacent Na⁺ binding/release transition has a smaller enthalpy (net ΔH = -11.4 kcal/mol), which corresponds to a Q₁₀ of only 2.0. Such levels of enthalpic activation energy are consistent with processes that do not require conformational changes as substantial as those associated with occlusion/deocclusion reactions, as might be expected for a Na⁺ traveling through an access channel and interacting with its binding site. For comparison, in open voltage-gated Na⁺ channels, Na⁺ permeation causes even smaller changes in enthalpy (6.25 kcal/mol; Q₁₀ = 1.53) (38) or K⁺ binding to the Na⁺/K⁺-ATPase where values of Q₁₀ are approximately 1.3 (22, 39). This smaller value, in turn, suggests that the binding and unbinding reaction of this Na⁺ to the Na⁺/K⁺-ATPase itself involves amino acid rearrangements. Interestingly, the decrease in entropy upon unbinding implies that the unbound state [P-E₂(Na₂)] is more ordered than the bound state [P-E₂(Na₂)·Na]; possibly, release of that Na⁺ might allow ordered binding of water molecules, thus lowering the electric field for subsequent release of the two remaining Na⁺ (9, 18, 26, 28).

The overall net change in free energy over the two coupled transitions (S_oc↔S₂) is essentially zero, indicating that under the conditions of these experiments the occluded (Na₃)E₁-P and partly deoccluded P-E₂(Na₂) states are energetically equivalent. The net ΔH and ΔS values of these combined transitions (Table 1) are poorly determined, because the confidence in the ΔH and ΔS values is low. However, we extract from the net ΔH a Q₁₀ of 1.6 for the overall reaction on the basis of the enthalpic change. Of more interest is that the effect of temperature on the voltage dependence of the charge moved between (Na₃)E₁-P and P-E₂(Na₂) states can be predicted and checked against the Q-V curves. The shift of the midpoint of the distribution of the charge vs. potential with temperature is a direct indication of an entropic change in the overall reaction (38). When we consider only the net changes in entropy and enthalpy, we derive the midpoint of the distribution (V_1/2) of the charge vs. potential curve from a two-state model (see SI Text) as

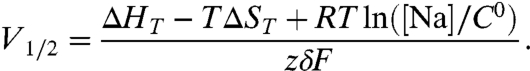[4]

From the net ΔS obtained from the global fit (see Table 1), increasing the temperature by 10 °C is expected to shift the charge distribution by approximately 17 mV toward negative voltages. Indeed, we did observe a small negative shift of V_1/2 upon increasing the temperature (Fig. 6). The measured shift, however, is somewhat smaller than predicted. It should be noted that the midpoints of Q-V relationships under our experimental conditions are difficult to determine with precision, because charge movement at voltages near the holding potential cannot be accurately measured. With this difficulty in mind, it is significant that the direction of the predicted shift is fulfilled by the direct measurements of the charge distribution vs. potential. Although the direction of the Q-V curve displacement with temperature might appear counterproductive for a squid neuron subjected to a decrease in temperature, because Na⁺ release would then be hindered, our results indicate that the effect is too small to have any real consequences for intracellular ion homeostasis.

Conclusions.

Electrophysiological studies of external Na⁺ translocation by the Na⁺/K⁺-ATPase have deepened our understanding of how external Na⁺ are bound and released (10, 11, 13–19, 21, 23–27, 29, 30), and they have provided a picture of the general architecture of the path through which Na⁺ move between their binding sites and the external milieu: the access channel model (9, 17, 18, 23, 26, 29). The energetic landscape of the transitions associated with the extracellular release of the first Na⁺ from the deeply occluded state revealed that the occlusion/deocclusion transition involves large changes in enthalpy and entropy as the ion is exposed to the external milieu for release. Clearly, ion unbinding must carry some amino acid side-chain rearrangements at the site, because the enthalpic activation energy of the binding/unbinding reaction was substantially larger than expected for an ion diffusing through a permeation pathway. This study provides the initial framework for further investigations on the energetic landscape for the release of the second and third Na⁺, to begin building a precise description of the molecular events that accompany the translocation of Na⁺ by the Na⁺/K⁺-ATPase.

Materials and Methods

Squid Collection and Axon Preparation.

Humboldt squid (D. gigas) were caught by local fishermen using traditional methods. Once a large specimen was brought on the boat, a large section of the mantle containing the stellate ganglion and giant axons of both sides was immediately excised and transferred to an insulated container filled with chilled sea water. Within 30 min, axons were removed from the mantle, separated, and kept in filtered sea water in a refrigerator at 4 °C. Healthy axons could be kept up to 2 d. As needed, axons were cleaned prior to experiments.

Experimental Solutions.

Giant axons were internally dialyzed and externally superfused with solutions designed to allow the Na⁺/K⁺-ATPases either to cycle at maximum speed in the forward direction (Fig. 1A) or to distribute themselves among conformations connected by reversible transitions involving the binding/unbinding and occlusion/deocclusion of external Na⁺ (Fig. 1B). In both cases, the dialysis solution was prepared from stock solutions (pH 7.6, adjusted with Hepes) and contained (in millimoles): 85 Na-Hepes, 80 N-methyl-d-glucamine (NMDG)-Hepes, 50 glycine, 50 phenylpropyltriethyl-ammonium sulfate [to block potassium channels (40)], five DTT, 2.5 1,2-bis(2-aminophenoxy)ethane-N,N,N^′,N^′-tetraacetate, 10 Mg-Hepes, 5 Mg-ATP, five phospho(enol) pyruvate tri-Na⁺ salt, and five phospho-l-arginine mono-Na⁺ salt. Turnover rate experiments were performed with external solutions containing (in millimoles): 400 tetra methylammonnium (TMA)-sulfamate, 10 KCl, 75 Ca²⁺-sulfamate, 1 3,4-diaminopyridine, 2 × 10^-4 TTX, 5 Tris-Hepes, and 0.05 EDTA (pH 7.7, adjusted with NMDG or sulfamic acid). In experiments to study external Na⁺ charge translocation, the external solutions had 400 Na-sulfamate instead of TMA-sulfamate and were devoid of KCl. During the last experimental season in Chile, external solutions contained chloride instead of sulfamate as the anion. These changes did not cause detectable differences either in the electrical leak of the preparation or in the kinetics of the Na⁺ translocation. The osmolality of all solutions was adjusted to approximately 950 mOsmol kg^-1.

Axon Preparation and Electrophysiology.

Freshly dissected giant axons (950- to 1,200-μm diameter) were threaded through a chamber that contained a central test pool flanked by two guard pools. The three pools have independent inlet and outlet perfusion systems. A peltier block controls the temperature of the solution before it enters the chamber, and the block is also in thermal contact with the three chamber pools. A thermocouple within the block feeds back to a temperature regulation system on the basis of an Omega controller. A microthermocouple measures the temperature in the test pool near the axon. Once the axon is mounted, it is cut at both ends, and the dialysis system comprising two 210-μm porous capillaries, each containing a 100-μm platinized platinum wire, is inserted and advanced along the entire axon length. The internal voltage electrode (a 120-μm glass capillary filled with 0.6 M KCl solution and containing an electrically floating platinum wire) is inserted as far as the middle of the axon (i.e., within the central pool). The external reference electrode, a 3M KCl/agar-filled glass capillary that also contains a floating platinum wire, is placed in the central pool just outside the axon and near the solution outflow. The current is collected in the central chamber by a large platinized platinum plate connected to a current-to-voltage converter that keeps the compartment at virtual ground, whereas the guard chambers are connected directly to ground through two additional large platinized platinum plates (41). Voltage steps were generated, and currents recorded, by using a 14-bit high speed analog-digital–digital-analog conversion board (A4D1; Innovative Integration) driven by a SB6711 board (Innovative Integration) with software developed in house. Currents were filtered at 100 kHz with an eight-pole Bessel filter (Frequency Devices 90IP or Krohn-Hite 3382) and then sampled at 3 μs intervals. The pump-mediated currents were isolated by using H₂DTG to specifically and reversibly inhibit squid Na⁺/K⁺ pumps (2). H₂DTG-sensitive currents were analyzed with in-house software and OriginLab v8. Global fits were carried out with programs written in Matlab utilizing their fit library.

Turnover Rate Estimations.

Steady-state Na⁺/K⁺ pump currents, and the number of Na⁺/K⁺ pumps generating them, were determined independently in each axon. Na⁺/K⁺-ATPase density was estimated from the total amount of charge moved during Na⁺ translocation transitions between -120 and +60 mV, at room temperature, assuming that the equivalent of a single charge moves through the entire membrane electric field. Under the conditions of these recordings, > 90% of the total amount of charge is moved (18). Steady-state pump currents were measured at voltages of -70, 0, and +40 mV, in the presence of 10 mM external K⁺ and the nominal absence of external Na⁺. Each steady-state pump current measurement was bracketed with two estimates of pump density assessed by the maximum amount of Na⁺ translocation charge. The pump density at the time of the steady-state current measurement was interpolated when necessary. The turnover rate is simply the steady-state pump current divided by the total amount of Na⁺ translocation charge.