Reconciling molecular regulatory mechanisms with noise patterns of bacterial metabolic promoters in induced and repressed states

Abstract

Assessing gene expression noise in order to obtain mechanistic insights requires accurate quantification of gene expression on many individual cells over a large dynamic range. We used a unique method based on 2-photon fluorescence fluctuation microscopy to measure directly, at the single cell level and with single-molecule sensitivity, the absolute concentration of fluorescent proteins produced from the two Bacillus subtilis promoters that control the switch between glycolysis and gluconeogenesis. We quantified cell-to-cell variations in GFP concentrations in reporter strains grown on glucose or malate, including very weakly transcribed genes under strong catabolite repression. Results revealed strong transcriptional bursting, particularly for the glycolytic promoter. Noise pattern parameters of the two antagonistic promoters controlling the nutrient switch were differentially affected on glycolytic and gluconeogenic carbon sources, discriminating between the different mechanisms that control their activity. Our stochastic model for the transcription events reproduced the observed noise patterns and identified the critical parameters responsible for the differences in expression profiles of the promoters. The model also resolved apparent contradictions between in vitro operator affinity and in vivo repressor activity at these promoters. Finally, our results demonstrate that negative feedback is not noise-reducing in the case of strong transcriptional bursting.

Gene expression and regulation exhibit a high degree of stochasticity when studied at the level of individual cells. Even in genetically identical cell populations exposed to a uniform environment, gene activity levels and their phenotypic consequences are subject to random fluctuations that generate cell-to-cell variations and eventually lead to alternative cell fates. This stochastic “noise” in gene expression is thought to be a critical, biologically relevant property of genetic circuits in both microbial and eukaryotic cells (1–3). Noise in gene expression primarily originates from bursting of mRNA production and mRNA translation into proteins. Gene promoters stochastically switch between “off” states with no mRNA produced and sharp production during “on” states. The burst size and frequency are thus two key parameters of stochastic protein expression at the single cell level (4–6). At the molecular level, the specific mechanisms of transcription and translation and, if relevant, the associated regulatory mechanisms, generate different patterns and levels of noise. Gene expression noise patterns are thus expected to be under selection by evolution. Several indirect and direct lines of evidence for counterselection of noise in expression of genes important for cell growth have been reported (7, 8), and a quantitative estimation of the general deleterious effect of noise has been recently proposed (9). However, elevated expression noise is advantageous in the context of particular biological processes such as development (10) or for specific classes of genes (11). In the context of environmental changes, expression noise enabling stochastic phenotype switching can be used by cells or cell populations as effective adaptation strategies (12, 13). Expression noise can also provide insights into gene function (14) or critical aspects of the molecular mechanism that control the expression of a particular gene.

In the present work we investigated gene expression noise patterns in a natural coherent genetic system in bacteria and a simple adaptation process—namely, the central carbon metabolism (CCM) in the model Gram positive bacterium Bacillus subtilis and a switch in carbon source. At the molecular level, we focused on the transcription initiation step of the genetic expression process. Within the CCM network, we characterized promoter activity at main control points in the physiological switch between glycolysis and its reverse pathway, gluconeogenesis, which allows for growth on noncarbohydrate carbon sources. In B. subtilis, this switch involves two glyceraldehyde 3-phosphate dehydrogenases, GapA and GapB, that catalyze opposite reactions, and the phosphoenolcarboxykinase, PckA, that catalyses another irreversible gluconeogenic reaction under physiological conditions (Fig. 1A) (15, 16). The auto-repressed gapA operon, encoding its repressor CggR, GapA as well as four other central glycolytic enzymes, is induced under glycolytic conditions upon binding of fructose-1,6-bis-phosphate (FBP), a metabolite of glucose, to CggR (17). The operator site for CggR is located downstream of the transcription start site and upstream of the translation initiation region (RBS), and hence CggR is thought to function as a roadblock to the transcribing RNA Polymerase (RNAP) (17, 18). The GapB and PckA enzymes are both required for the utilization of gluconeogenic carbon sources, such as malate, but their expression is deleterious under glycolytic regimes (15, 16, 19). CcpN is the repressor responsible for the very strong catabolite repression of the gapB and pckA promoters in the presence of glucose or other glycolytic substrates (16). It plays a dominant role in the control of carbon fluxes through central metabolic pathways in B. subtilis and is obligate for optimal growth under glycolytic conditions (16, 19). CcpN activity is linked to the energy charge of the cell (20) and is also negatively controlled by the coexpressed regulatory protein, YqfL (16). The CcpN operator site overlaps the promoter region of the gapB gene, but the bound repressor does not hamper RNAP binding. Rather, CcpN is thought to act on transcription initiation by preventing promoter escape by RNAP (20, 21).

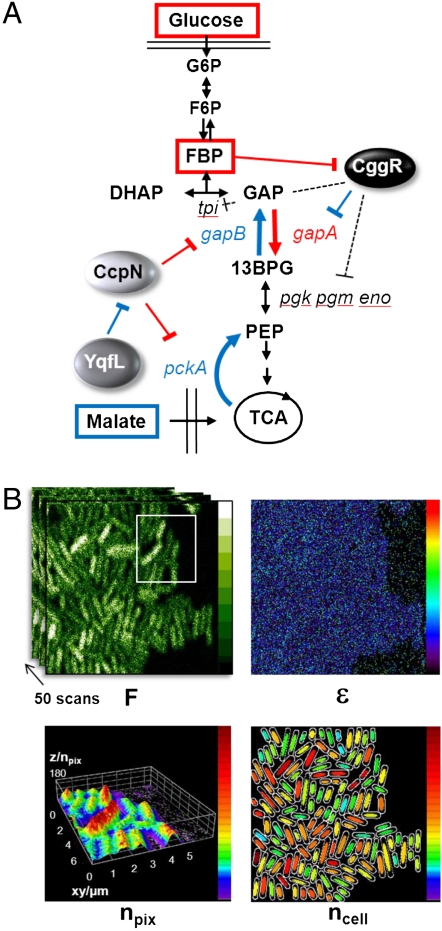
Fig. 1.

(A) Schematic of the central carbon metabolism showing the switch between glycolysis and gluconeogenesis controlled by the repressors CggR and CcpN. Important metabolites are in squares, regulatory proteins are ellipses, and the genes coding for the enzymes are in small italic letters. When glucose is available for cell growth, fructose-1,6-biphosphate (FBP) accumulates and blocks the repressive action that CggR exerts on the transcription of gapA and four other central glycolytic genes (pgk, pgm, eno, and tpi). Because CggR is transcribed from the same gapA operon that it represses, it is also an autorepressor. Inversely, when cells are grown on malate or other nonglycolytic carbon sources, the CcpN repressor is inhibited by an unknown mechanism involving YqfL, allowing expression of the essential gluconeogenic genes gapB and pckA. (B) Schematic of 2psN&B experiments. A stack of 50 raster scans of agarose immobilized live cells of B. subtilis expressing gfpmut3 are recorded using infrared (930 nm) laser excitation and a dwell time of 50 μs at each pixel (faster than GFP diffusion); full scale of fluorescence intensity (F) is 10 photon counts/pixel/50 μs laser dwell time. The fluorescence fluctuations relative to the mean at each pixel are used to calculate the pixel-based maps of the true (shot noise corrected) molecular brightness (ϵ, full scale 1 photon/molecule/50 μs dwell time) and the number (n_pix) of the fluorescent particles detected in the 2-photon excitation volume (vol_ex = 0.07 fL inside B. subtilis); a 3D surface plot of n_pix is shown for the white-delineated area of the above intensity panel. Bottom right: Cartoon representation of the individual cells auto-detected using PaTrack (40) and showing the 50% central pixels used for averaging the particles number in each cell (n_cell); the full scale for the n_pix and n_cell maps is 180 molecules/vol_ex.

Assessing noise in gene expression in order to obtain molecular mechanistic insights concerning its physical origins requires accurate quantification of expression levels in hundreds of individual cells over a large dynamic range, under repressing as well as inducing conditions, and in particular at very low levels of expression where stochastic effects are expected to be most prominent. The fluorescent protein intensity measurements provided by the standard approaches typically used in such studies yield only fluorescence intensity values which are related to concentration by an unknown scaling factor. Moreover, the sensitivity of such measurements is restricted by the relatively high auto-fluorescence of the bacterial cell cytoplasm. Hence, measuring the activity of weakly transcribed genes using fluorescent protein reporter systems is usually not possible (2). Although recent approaches extend the range of the intensity-based methods to the single-molecule level (22–24), they remain indirect and suffer from uncertainty in molecular brightness and background fluorescence. Here we applied a modified version of two-photon scanning (true) number and brightness (2psN&B) (25, 26), in which the intensity fluctuations at each pixel in a series of rapid raster scanned images of bacteria are used to deconvolve the average intensity (counts/s) into the molecular brightness (counts/s/molecule) and absolute number (molecules) of fluorescent proteins diffusing inside individual bacterial cells (Fig. 1B) (27). Thus unlike standard imaging techniques, which yield fluorescence intensity, sN&B provides absolute concentrations and can be carried out using confocal microscopy, although with more auto-fluorescence and photo-bleaching (Fig. S1) than with the 2-photon excitation used here.

Using this approach, our primary objective was to focus on promoter activity. We sought to directly measure in single cells transcriptional activity of key regulated promoters in their repressed and derepressed states to characterize any heterogeneity among the cell population and to understand how cells are prepared for environmental changes. Moreover we sought to measure transcriptional bursting and to reveal how control mechanisms at these different promoters affect the frequency and the size of the transcriptional bursts during the switch between inactive and active states. Finally, we asked whether, using stochastic models of the molecular control mechanisms of the studied promoters, we could correlate the operative mechanistic physical features with specific characteristics of the noise patterns.

Results

Absolute Quantification of Expression Levels Under Permissive and Repressing Conditions.

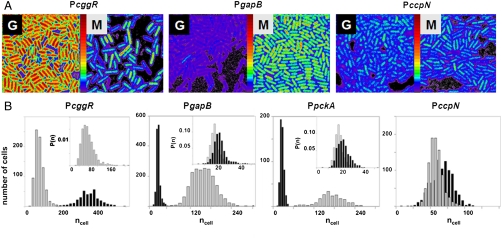
Using N&B analysis we measured the absolute concentration of green fluorescent protein (GFP) in individual cells expressing gfpmut3 (encoding a very bright, fast-maturing and stable GFP variant) (28) from four promoters of interest, P_cggR (gapA operon), P_gapB, P_pckA, and P_ccpN, (Fig. S2) grown at steady state under glycolytic (glucose) or gluconeogenic (malate) conditions. Fluorescent particles number maps and histograms of the distributions in the bacterial populations (Fig. 2 A and B) were calculated as described in detail elsewhere (27) (SI Text). Large differences in the expression levels and cell-to-cell variations were observed for the different strains depending on the carbon source used for growth. The P_cggRgfp fusion was strongly expressed on glucose but poorly repressed on malate, exhibiting an induction level of only sevenfold, in good agreement with bulk population measurements using gfpmut3 (Fig. S3) or other reporter systems (17). Expression from the P_cggR promoter was visibly heterogeneous for the cell population grown on malate (Fig. 2A). The number of fluorescent particles detected in our 2p excitation volume inside the bacterial cell, vol_ex (approximately 0.07 fL) ranged from 30 to over 250 (Fig. 2B). In contrast, transcription from both P_gapB and P_pckA was very strongly repressed on glucose and induced over 40-fold on malate (Fig. 2 A and B, middle panels). For these promoters under repressing condition, we were able to determine a population average of approximately 3.5 GFP molecules (per vol_ex) above the background of dim fluorescent particles observed in the reference BSB168 receiver strain (Fig. 2B, insets of panel 2 and 3). This corresponds to a population average concentration of approximately 80 nM or around 30–50 total GFP molecules in the bacterial cells, depending upon their size. For the strain carrying the gfpmut3 fusion with the weak and constitutive P_ccpN promoter we measured rather low GFP concentrations, averaging approximately 1 μM on both carbon sources.

Fig. 2.

Cell-by-cell quantification of catabolite regulation in B. subtilis by 2psN&B. (A) Pixel-based fluorescent particles number maps of B. subtilis cells expressing gfpmut3 transcriptional fusion from P_ccgR, P_gapB (results are similar for P_pckA; not shown), and P_ccpN. Cells harvested from liquid cultures containing 0.5% glucose (G) or 0.5% malate (M) as the sole carbon source were immobilized on agarose pads for 2psN&B analysis as described in Fig. 1B. The full scale is 360 molecules/vol_ex. (B) Cell-based particles number (n_cell) distributions for the indicated promoter-gfpmut3 fusion strains grown on glucose (black) or malate (gray). Inset in the first panel shows the expanded histogram of the probability density function P(n_cell) measured in malate for P_cggR. Insets in panel 2 and 3 show the expanded histogram of the probability density function P(n_cell) observed in glucose for the P_gapB and P_pckA promoters in black, and that observed for the background BSB168 strain in gray.

Changes in Noise Pattern Parameters During Nutrient Shifts.

The coefficient of variation (COV), one of the metrics used for quantifying noise in gene expression, is the ratio of the standard deviation in the number of proteins (/vol_ex) over the mean, 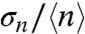, for distributions in a population of bacteria (i.e., Fig. 2B). For all three regulated promoters (P_cggR, P_gapB, and P_pckA), the COV is very large (approximately 60–100%) for the repressed promoters. The increase in the average number of GFP molecules under permissive conditions is accompanied by a drastic decrease in 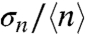(Fig. 3A) but remains above the experimental uncertainty inherent to our method (approximately 0.05) (27). For the unregulated P_ccpN promoter, we observed no significant change in the 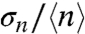value upon the shift of carbon source. We note that a small coefficient of variation does not necessarily mean that the noise is small; this is particularly true for skewed and leptokurtic histograms, such as that observed for P_cggR, and which are usually associated with bursting (2, 5, 29).

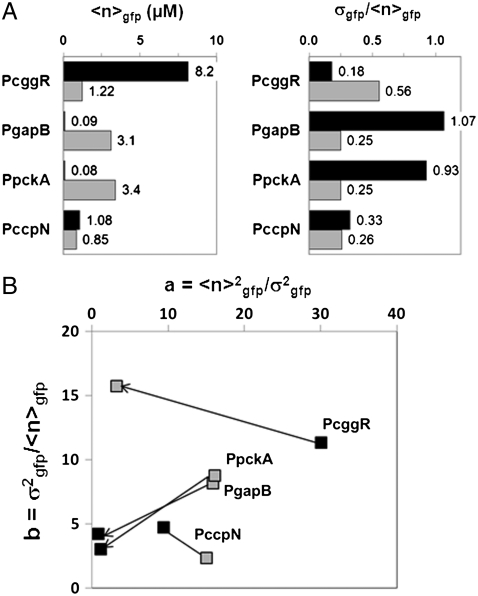
Fig. 3.

Changes in promoter activity levels and noise patterns upon a switch of carbon source. (A) The average number of GFPmut3 molecules per vol_ex (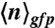 expressed in micromolar concentration) and its coefficient of variation (the standard deviation over the mean, 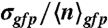) in the cell populations grown on glucose (black bars) or malate (gray bars), estimated from the cell-based particles number distributions shown in Fig. 2B and considering a fixed auto-fluorescence background contribution as determined in the BSB168 receiver strain under identical experimental conditions. (B) Effect of nutrient switch on promoter activity noise patterns. The parameter of stochastic gene expression, the Fano factor b 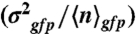, related to GFP production burst size is plotted against a 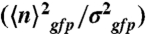related to the GFP production burst frequency for the activity of the indicated promoters on glucose (black square) or malate (gray diamonds). The single arrows indicate the sense of repression for the regulated promoters.

Two other key parameters of stochastic gene expression can be extracted from the average and variance of GFP molecules in the cell population histograms: the apparent frequency of protein production burst per cell cycle (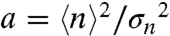) and the average number of protein molecules produced per burst, related to the Fano factor (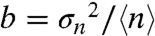) (5). Thus, for a repressible promoter, the mean expression level, 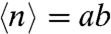, can be decreased by reducing a or b or both. We note that in our system, differences in bursting characteristics from one promoter fusion to another and from one condition to another only emanate from transcriptional bursting. Indeed, in all our constructions, the gfpmut3 gene is under identical translational signal, insensitive to the different physiological conditions examined here. As expected for the constitutive promoter, P_ccpN, little variation is observed in either the values of a or b upon a switch in carbon source. In contrast, examination of the variations in these parameters for the glycolytic and gluconeogenic promoters on different carbon sources (Fig. 3B) reveals dramatic differences between their noise patterns. Indeed the parameters, a and b, are very dynamic and discriminative of the behavior of the two types of promoters, providing strong evidence that the major contribution to the observed cell-to-cell fluctuations is intrinsic to the regulatory circuitry. The gluconeogenic promoters (P_gapB and P_pckA) show a strong relative decrease of both burst size and frequency upon repression under glucose, whereas upon repression of P_cggR under malate, a decreases significantly while b actually increases slightly. Large bursts under repression by CggR are thus responsible for the heterogeneity observed in this population (Fig. 2A). Our findings reveal two distinct noise signatures associated with the glycolytic as opposed to gluconeogenic promoters.

Modeling the Expression Patterns of P_cggR and P_gapB During the Nutrient Shift.

We modeled the kinetics of the transcription events from the P_cggR and P_gapB promoters with a unique realistic scheme inspired from a generic model for prokaryotic gene expression (30) (Fig. 4 A–B and Table S1). An in-depth justification for fixed parameter values and fitting procedure is given in SI Methods. Our model included repressor binding and dissociation from the operator DNA, 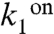and 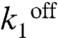, respectively. The main contribution to the fluctuations of mRNA production and of the other downstream variables arose from dissociation of the repressor, which justifies a two-state operator model. Transcription initiation was assigned rate constants k₂ or 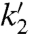, and the transcribing polymerase (tRNAP) was considered to synthesize the mRNA leader region containing the RBS with rate constants k₃ (30, 31) or 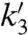, depending on whether the operator DNA is free or bound by repressor. A switched, first order reaction of rate constant k₄ was used to model dissociation of the elongation complex, thus reducing jamming of stalled polymerase molecules in the repressor-bound operator state for P_cggR. We pooled several states (29, 31, 32) related by rapid transitions and consider that RBS gives rise directly to the ribosome elongating the protein chain (ElRib) then to the matured GFP (MdGFP). All reactions past RBS synthesis are considered to be identical for the promoters under study. We adjusted the parameters of the model to fit the experimental expression histograms.

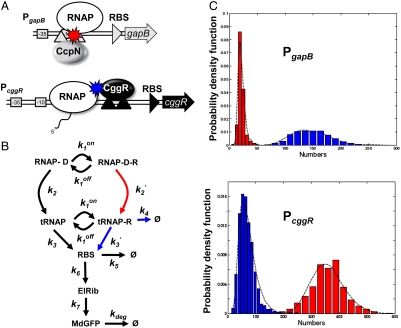
Fig. 4.

Model of gene regulation by CggR and CcpN. (A) Scheme describing the architecture of the B. subtilis P_ccgR and P_gapB promoter region (boxed -10 and -35 RNAP recognition sequences) and tandem operator sites (black or gray upward triangles) for the CggR or CcpN repressors. Under glycolytic conditions, CcpN is thought to prevent promoter clearance by the RNA polymerase whereas under gluconeogenic conditions CggR acts as a roadblock to the transcribing polymerase when bound as a compact tetramer. (B) General model of prokaryotic gene expression and regulation applied to both repressors. RNAP-D is the RNAP-bound DNA, R the active repressor, tRNAP the elongating transcription complex, RBS the ribosome binding site on the transcribed mRNA, ElRib the elongating translation complex, and MdGFP the folded and matured green fluorescent protein. According to the above mechanistic models of regulation, besides changes in DNA affinity constants (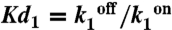), CcpN repression affects primarily k₂, the rate at which the elongation complex is formed, whereas CggR would affect the transcription rate in the mRNA leader region (k₃), thereby increasing the dissociation rate of the (paused) polymerase (k₄). In the gfpmut3 reporter system used in this study, all steps past RBS production are identical for all promoter constructs and all conditions. The GFPmut3 variant has been shown to be fast-maturing (within a few minutes) and slow degrading (stable for several hours) in B. subtilis (3), therefore the degradation rate k_deg corresponds to slow dilution whereas the lifetime of the mRNA is much shorter (i.e., k₅≫k_deg). (C) Results of the model compared to the experimental data for the stochastic expression of P_gapBgfp and P_cggRgfp transcriptional fusions under glucose (red) or malate (blue). Lines correspond to the continuous distributions obtained from the model parameters reported in Table S1. The histogram from the P_gapBgfp promoter fusion data was not corrected for the BSB168 background contribution, as the deconvolution cannot be done reliably for experimentally reasonable dataset sizes; instead, a Gamma random variable having the same first two moments as the background contribution has been added to the model predictions.

The model reproduces well the observed behavior of P_gapB and P_cggR (Fig. 4C and Table S1). Testing key parameters for their uniqueness revealed significant constraints on their values (SI Methods and Fig. S4). The promoters function in a regime where 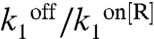is small for all conditions and promoters; the probability, 1 - p, that the repressor, R, is bound to the DNA remains large, and repression does not vanish even under permissive conditions, in good agreement with genetic data showing constitutive overexpression of these promoters in repressor knockout strains (15, 16). The nutrient switch affects repression mainly at two levels: affinity of the repressor for the DNA (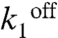) in the case of P_cggR and concentration of active repressor and hence the burst duration and size (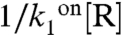) in the case of P_gapB. Good fits for these two promoters were constrained by the modification of these two parameters, respectively. At P_gapB, a decrease in the concentration of active repressor is consistent with the proposed sequestration of CcpN by YqfL under malate, although the total CcpN concentration is not thought to change (16). The change of 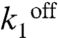is minimal upon induction, and hence K_D values are constant and in the range of 0.8 nM, in reasonable agreement with the 8 nM affinity measured in vitro (33, 34). For CggR, operator affinity is high under repression, K_D = 0.1 nM, and decreases about 10-fold upon induction ( 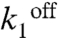increases), in reasonable agreement with the in vitro operator affinity (< 0.5 and 10 nM) of CggR in absence and presence of inducer (35, 36). The model reconciles as well this high in vitro affinity with moderate repression by CggR in vivo (15). The position of the CggR operator site between the promoter and the RBS allows unhindered RNAP binding and initiation and hence passage of multiple polymerase molecules while the repressor is dissociated, leading to large amplitude bursts. Indeed, the large bursts for P_cggR under repression cannot be modeled otherwise. Moreover, the enzymes of the CCM must be produced in large quantities when needed, and hence we must assume strong promoters in order to insure this strong production in the derepressed state. The price to pay is that strong promoters favor transcriptional bursting. In addition, strong bursting under repression for P_cggR is favored by the fact that CggR is a self-repressed promoter, and hence the concentration of repressor is lower under repressive, relative to permissive, conditions.

Discussion

Our N&B data provide reliable measurements of absolute gene expression levels and fluctuations from metabolic promoters implicated in catabolite repression under both permissive and repressive conditions. The activity of the strongly repressed gluconeogenic promoters has been undetectable at the single cell level by other methods. Indeed, combined two-photon excitation and raster scanning considerably reduce both the auto-fluorescence from the bacterial cytoplasm and photo-bleaching of the GFP molecules, thereby achieving the single-molecule detection limits required for single cell quantification of gene expression levels from these strongly repressed promoters. Moreover, fluorescence fluctuation-based methods such as N&B analysis do not require calibration of the light intensity signal and therefore allow for the direct counting of fluorescent reporter proteins diffusing in the excitation volume.

Our measurements, due to their absolute nature, reveal distinct noise patterns for the glycolytic and gluconeogenic promoters, which inform on the adaptive strategy selected by evolution. For P_cggR, 2psN&B allowed us to demonstrate significant cell-to-cell heterogeneity, in particular the existence of a subpopulation of cells expressing GFP under the repressed state at levels as high as half the average level of induced cells. This heterogeneity does not correspond to bistability that would provoke a bimodal distribution of the expression levels as reported for other bacterial regulation systems (37), instead of the skewed unimodal distribution observed here. Rather it arises from strong transcriptional bursting from this promoter under repression, which itself has two origins. First, P_cggR is intrinsically a strong promoter, a required feature for the enzymes of the central carbon metabolism which must be produced in large quantity in the induced state. Secondly, the repressive mechanism of CggR, rather than competing with RNA polymerase for promoter binding, as in the case of the lactose repressor for example, acts as a roadblock to elongation. Hence multiple RNAP molecules can accomplish transcription during repressor dissociation episodes. While the affinity of CggR for its operator is quite high in vitro (35, 36), it exhibits moderate repressor activity in vivo (17), as it is subject to strong transcriptional bursting. Although transcriptional bursting has been observed, albeit rarely, in prokaryotes (2, 38), quantitative and mechanistic insights into the process, such as those presented here, have been lacking. Significant activity for the P_cggR promoter in a subpopulation of cells grown on malate enables them to respond more rapidly when glucose becomes available, thereby conferring a competitive advantage to the clonal population. The high level of noise for this promoter may have been selected for implementing such a bet-hedging adaptation strategy.

As often invoked (39) one is inclined to expect that negative feedback reduces noise. Our results provide the experimental demonstration that this property is not valid in the strong bursting regime of the self-repressed P_cggR promoter. Indeed, the burst size scales with the lifetime of the active state of the operator, which for a self-repressed promoter, scales inversely with the concentration of repressor and is smaller under permissive conditions when the feedback is weak. In contrast to the strong transcriptional bursting observed for the glycolytic promoter, in the case of the gluconeogenic promoters, because derepression under glycolytic conditions greatly impairs growth (16, 19), strict control by CcpN and limited noise are essential. Hence, the repressive mechanism of CcpN has evolved to limit bursting in the repressed state by impairing promoter escape by the RNAP, leading to very strong catabolite repression.

In conclusion, our study demonstrates that N&B analysis can be applied for direct and absolute quantification of promoter activity and noise in bacterial populations upon changes in conditions. The highly quantitative nature of our approach, coupled with its sensitivity and broad dynamic range render 2psN&B particularly well suited to the study of promoter activity. Here it allowed us, in a natural bacterial system, to associate expression noise patterns with specific features of molecular mechanisms of transcriptional repression, to demonstrate transcriptional bursting and to show that negative feedback control does not necessarily reduce noise. Hence, 2psN&B offers broad perspectives for the quantitative characterization of a wide range of gene regulatory networks in both prokaryotes and eukaryotes.

Materials and Methods

Bacterial Strains, Cultures, and Sample Preparation.

Strains of Bacillus subtilis carrying transcriptional fusions with the gfpmut3 reporter gene were constructed using the pBaSysBioII plasmid designed for high throughput analysis of promoter activities by Live Cell Arrays (3) (http://www.basysbio.eu). (See Fig. S2 and SI Text for more details.) Microscopy samples were prepared with cells from exponentially growing cultures and immobilized on 1.5% agarose pads as described in SI Text and in ref. 27.

Two-Photon Scanning Microscopy.

In scanning N&B analysis the number and molecular brightness of the diffusing fluorescent molecules are calculated from the fluctuations in fluorescence intensity at each pixel in a series of raster scanned images, in which the laser dwell time is small with respect to the diffusion time of the molecule. Fluorescence fluctuations from the average intensity arise from Brownian diffusion into and out of the very small two-photon excitation volume (vol_ex = 0.07 fL) focused inside the bacterial cells. The pixel-based temporal average and variance images were calculated from 50 raster scans, then the true (shot noise corrected) molecular brightness, ε, was determined at each pixel. The average true molecular brightness 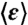was determined for all of the cells in the field of view using only those central pixels for which the vol_ex is encompassed within the cells. This spatially averaged true molecular brightness for each field of view allowed for the calculation of the number of molecules, n_pix(/vol_ex), at each pixel. Then for each cell in the field of view, n_pix was averaged over the pixels situated in an ellipse representing the central 50% of the cell area, yielding n_cell. The averaged intracellular concentration of GFPmut3 molecules (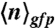) and their intrinsic brightness (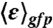) for a population of cells under a particular set of conditions were obtained by correcting the average values obtained from the distribution for background fluorescence from the BSB168 receiver strain bearing no gfp. More details on our 2psN&B method are given in SI Text and ref. 27.

Modeling.

The model of stochastic gene expression is described by the set of biochemical reactions given in Fig. 4B and Table S1. We used Gillespie direct simulation accelerated by cycle averaging (29) to compute the stationary solutions of the chemical master equation. The model predictions were compared to the experimental histograms for the cggR and gapB promoters, under two nutritional conditions, glycolytic (glucose) and gluconeogenic (malate). Parameter values were approximated using analytical approximations for the first two moments of the predicted expression distribution and then refined by minimizing the distance between predicted and observed histograms. Further description of the genetic switch modelling is available in SI Text.