Population rate coding in recurrent neuronal networks with unreliable synapses

Abstract

Neuron transmits spikes to postsynaptic neurons through synapses. Experimental observations indicated that the communication between neurons is unreliable. However most modelling and computational studies considered deterministic synaptic interaction model. In this paper, we investigate the population rate coding in an all-to-all coupled recurrent neuronal network consisting of both excitatory and inhibitory neurons connected with unreliable synapses. We use a stochastic on-off process to model the unreliable synaptic transmission. We find that synapses with suitable successful transmission probability can enhance the encoding performance in the case of weak noise; while in the case of strong noise, the synaptic interactions reduce the encoding performance. We also show that several important synaptic parameters, such as the excitatory synaptic strength, the relative strength of inhibitory and excitatory synapses, as well as the synaptic time constant, have significant effects on the performance of the population rate coding. Further simulations indicate that the encoding dynamics of our considered network cannot be simply determined by the average amount of received neurotransmitter for each neuron in a time instant. Moreover, we compare our results with those obtained in the corresponding random neuronal networks. Our numerical results demonstrate that the network randomness has the similar qualitative effect as the synaptic unreliability but not completely equivalent in quantity.

Introduction

Neuron is a powerful nonlinear information processor in the brain. By sensing its surrounding inputs, neuron continually generates appropriate discrete electrical pulses termed as action potentials or spikes. These spikes are transmitted to the corresponding postsynaptic neurons through synapses, which serve as the communication bridges between different neurons. It is known that the information processing in the brain is highly reliable. However, some biological experiments have demonstrated that the microscopic mechanism of synaptic transmission displays the unreliable property (Abeles 1991; Friedrich and Kinzel 2009; Raastad et al. 1992; Smetters and Zador 1996). Such unreliability is attributed to the probabilistic neurotransmitter release of the synaptic vesicles (Allen and Stevens 1994; Branco and Staras 2009; Katz 1966; Katz 1969; Trommershauser et al. 1999). For real biological neural systems, the successful spike transmission rates between 0.1 and 0.9 are widely reported in the literature (Abeles 1991; Allen and Stevens 1994; Rosenmund et al. 1993; Stevens and Wang 1995). In the past decades, several works, though not many, have investigated the dynamics and information transmission capability of unreliable synapses. Researchers especially paid close attention to the functional roles of unreliable synapses on the information transmission of neuronal systems. It has been demonstrated that the synapses with suitable successful transmission probability are able to improve information transmission efficiency (Goldman 2004), filter redundant information (Goldman et al. 2002), enhance synchronization (Li and Zheng 2010), as well as enrich dynamical behaviors of neuronal networks (Friedrich and Kinzel 2009; Kestler and Kinzel 2006). It has been also found that the unreliability of synaptic transmission may be viewed as a useful tool for analog computing, rather than as a “bug” in neuronal networks (Maass and Natschlaeger 2000; Natschlaeger and Maass 1999). Moreover, a very recent study has clearly uncovered that the depressing synapses with a certain level of facilitation allow recovering the good retrieval properties of networks with static synapses while maintaining the nonlinear characteristics of dynamic synapses, convenient for information processing and coding (Mejias and Torres 2009). All above findings indicate that the unreliability of synaptic transmission might play important functional roles in the information processing of the brain.

One of the most significant challenges in the field of computational neuroscience is to understand how neural information is represented by the activities of neuronal ensembles. So far many neural encoding mechanisms have been proposed, including the population rate coding (Dayan and Abbott 2001; Gerstner and Kistler 2002), synchrony coding (Dayan and Abbott 2001; Gerstner and Kistler 2002), transient coding (Friston 1997), time-to-first-spike coding (Thorpe et al. 1996; Thorpe et al. 2001), and so on. Among these encoding mechanisms, the population rate coding is an elegant theoretical hypothesis, assuming that the neural information about the external stimuli is contained in the population firing rate. Actually, this encoding mechanism is based on the experimental observation that the firing rates of most biological neurons correlate with the intensity of the external stimuli (Gerstner and Kistler 2002; Kandel et al. 1991). In recent years, the population rate coding has been widely examined in different neuronal network models, e.g. (Masuda and Aihara 2003; Masuda et al. 2005; Rossum et al. 2002; Wang and Zhou 2009). However, to the best of our knowledge, the dynamical behaviors of synapses in these studies are typically simulated by using the deterministic synaptic interaction model. Since the communication between real biological neurons indeed displays the unreliable property, a naturally arising question to be tackled is how the unreliable synapses influence the performance of the population rate coding. In reality, such question is more complicated when the topology of the considered neuronal network has the recurrent structure. This is because the intrinsic recurrent currents due to synaptic interactions will also affect the encoding performance of the neuronal network.

To answer the aforementioned question, we systematically investigate the population rate coding in a recurrent neuronal network by computational modelling. The recurrent network model considered in this paper is an all-to-all neuronal network consisting of both the excitatory and inhibitory neurons connected with unreliable synapses, which can be roughly regarded as a local cortex. Here we mainly examine the effects of the synaptic unreliability as well as some other important synaptic parameters, such as the synaptic strength and synaptic time constant on the performance of the population rate coding under different levels of noise. Furthermore, in order to clarify the differences between the synaptic unreliability and the network randomness, we also make comparisons on the encoding performance between our considered neuronal network model and the corresponding random neuronal network (the meaning of “corresponding” will be given in detail in “Comparison with the corresponding random neuronal networks” section).

The rest of this paper is organized as follows. In “Model and method” section, we introduce the computational model and the measurement of the population rate coding. In “Simulation results” section, we present the mainnumerical simulation results of this work. In “Conclusion and discussion” section, we discuss our findings and their implications in detail, and summarize the conclusion of the present work.

Model and method

In this section, we introduce the computational model and the measurement of the population rate coding used in this work. We first consider an all-to-all neuronal network totally containing N = 100 spiking neurons coupled by unreliable synapses. We assume that the larger fraction of neurons in the considered network (N_exc = 80) is excitatory and the rest (N_inh = 20) is inhibitory, as the ratio of excitatory to inhibitory neurons is approximate to 4:1 in mammalian neocortex. It should be noted that we do not allow a neuron to be coupled with itself. Spiking dynamics of each neuron is simulated based on the integrate-and-fire (IF) neuron model. Let 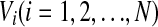denote the membrane potential of neuron i. The subthreshold dynamics of the membrane potential for a single IF neuron can be expressed as follows (Dayan and Abbott 2001; Gerstner and Kistler 2002):

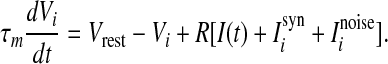1

In this equation, the IF neuron is characterized by a membrane time constant τ_m, a resting membrane potential V_rest, and a membrane resistance R. Throughout our simulations, we let the values of these parameters be: τ_m = 20 ms, V_rest =  −60 mV, and 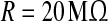. I(t) is a time-varying external input current injected to all neurons, I^syn_i denotes the total synaptic current of neuron i, and 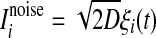represents the noise current of neuron i, where ξ_i(t) is a zero-mean Gaussian white noise with unit variance and D is referred to as the noise intensity. A neuron fires a spike whenever its membrane potential exceeds a fixed threshold value V_th =  −50 mV, and then its membrane potential is reset to the resting membrane potential at which it remains clamped for a 5 ms refractory period.

For each simulation, we use the time-varying external input current I(t) generated according to an Ornstein-Uhlenbeck process η(t) whose dynamics is represented by

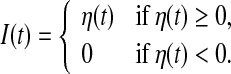2

with

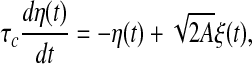3

where ξ(t) is a Gaussian white noise with zero mean and unit variance, τ_c is a correlation time constant, and A is a diffusion coefficient used to denote the intensity of the external input current. In the following studies, we choose A = 200 and τ_c = 80 ms. It should be noted that the external input current I(t) corresponds to a Gaussian noise low-pass filtered at 80 ms and half-wave rectified. In the literature, this type of external input current is widely used in studying the population rate coding (Rossum et al. 2002; Wang and Zhou 2009).

The total synaptic current onto neuron i is the linear sum of currents of all incoming synapses, I^syn_i = ∑_j I^syn_ij, where the individual synaptic currents are modeled by a modified version of the traditional conductance-based model as in our previous work (Guo and Li 2011),

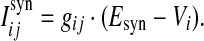4

Here g_ij is the conductance of the synapse from neuron j to neuron i, and E_syn is the reversal potential. In our study, the value of E_syn is fixed at 0 and −75 mV for excitatory and inhibitory synapses, respectively. Whenever apresynaptic neuron j fires a spike, the corresponding postsynaptic conductances are increased instantaneously after a 1 ms spike transmission delay

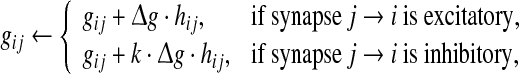5

where 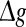is the relative peak conductance of the excitatory synapses (also called “excitatory synaptic strength” in this paper), k is the scale factor used to control the relative strength of inhibitory and excitatory synapses, and h_ij is the synaptic reliability variable. In other time, g_ij decays exponentially with a fixed synaptic time constant τ_s. In our model, a stochastic on-off process is introduced to mimic the probabilistic transmitter release of the real biological synapses. When a presynaptic neuron j fires a spike, we let the corresponding synaptic reliability variables h_ij = 1 with probability p and h_ij = 0 with probability 1 − p, where parameter p represents the successful transmission probability of spikes. Here we use the above stochastic process describes whether the neurotransmitter is successfully released or not. It should be noted that the synaptic transmission in real biological neural systems is much more complex than our model. For instance, it has been found that there exists an increased release probability for the second spike within a short time interval after the first spike has arrived a synapse (Stevens and Wang 1995). However, in modelling studies, we should accept that there are no exact mathematical descriptions of processes in nature, and have to search for approximations that capture all aspects of interest as accurately as feasible and at the same time allow us to gain insight from the analysis. In this work, we choose the above stochastic on-off process as an intermediate level between the deterministic synaptic interaction and real biological synaptic interaction, allowing us to build effective simulations while capturing the basic properties of biological neuronal networks.

In the present work, the performance of the population rate coding is quantified by determining the correlative property between the output of the network and the time-varying external input current I(t) (Masuda and Aihara 2003; Masuda et al 2005; Wang and Zhou 2009; Vogels and Abbott 2005). To do this, we use a 5 ms moving time window with 1 ms sliding step to compute both the population firing rate r(t) and the smooth version of the external input current I_s(t). In our study, the population firing rate r(t) means the average of the firing rates of all neurons for the time bin centered at time t, and is employed to represent the output of the considered neuronal network. The cross-correlation coefficient between r(t) and I_s(t) is therefore given by (Masuda and Aihara 2003; Masuda et al 2005; Wang and Zhou 2009; Vogels and Abbott 2005):

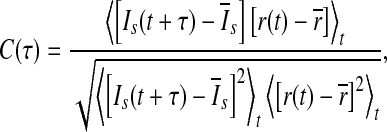6

where 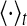stands for the average over time. The maximum cross-correlation coefficient Q = max{C(τ)} is used to measure the performance of the population rate coding, where Q is a normalization measure and a larger value corresponds to a better encoding performance. This measure determines how well the input signal is encoded by the network in terms of the population firing rate of neurons, which has been widely used both in feedforward (Masuda and Aihara 2003; Masuda et al 2005; Vogels and Abbott 2005) and all-to-all (Wang and Zhou 2009) neuronal networks. Note that the maximum cross-correlation coefficient might be largely influenced by the bin size chosen for analysis. Bin sizes in the range 1 to 10 ms are widely used for evaluating the dynamics of the neuronal networks composed of integrate-and-fire neurons (Vogels and Abbott 2005; Tetzlaff et al. 2008; Kumar et al. 2008; Guo and Li 2011). As we mentioned above, bin size of 5 ms is used in the present work. In additional simulations, we have also checked other bin sizes and found that our results are valid for the bin sizes within the range 1–10 ms.

The aforementioned stochastic differential equations are solved numerically by the standard Euler-Maruyama integration scheme (Kloeden et al. 1994). To ensure the stability of the IF neuron model, the integration step is taken as 0.1 ms. For each simulation, the initial membrane potentials of the neurons are chosen randomly from a uniform distribution on (V_rest, V_th), and the initial values of g_ij are chosen randomly from a uniform distribution on (0, 0.5). We perform all simulations up to 5,000 ms to collect enough spikes for statistical analysis. It should be emphasized that we realize at least 100 independent runs with different random seeds for each group of experimental conditions and report the average value as the final result in the present work (except for the data shown in Fig. 2).

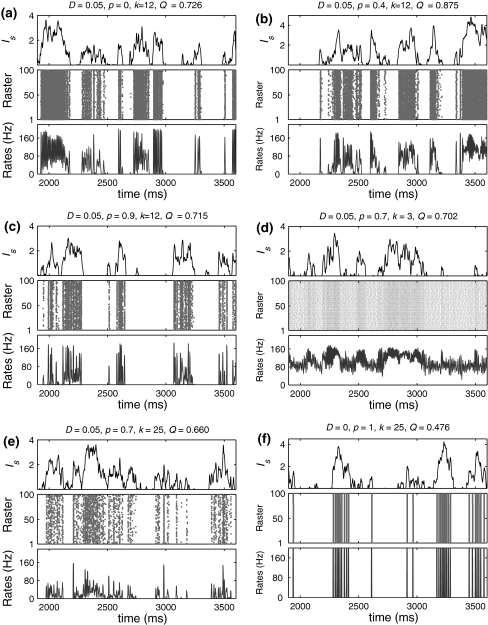
Fig. 2.

Examples of several typical network activity. In each subfigure, the upper panel shows the smooth version of the external input current I_s(t); the middle panel depicts the spike raster diagram; and the lower panel presents the population firing rate. We set τ_s = 5 ms and 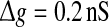in all cases

Simulation results

In this section, we first study the effects of synaptic unreliability as well as several other important synaptic parameters on the performance of population rate coding in our considered neuronal network. Then, we compare the encoding performance in our considered network with that in the corresponding random neuronal network.

Roles of the unreliable synapses

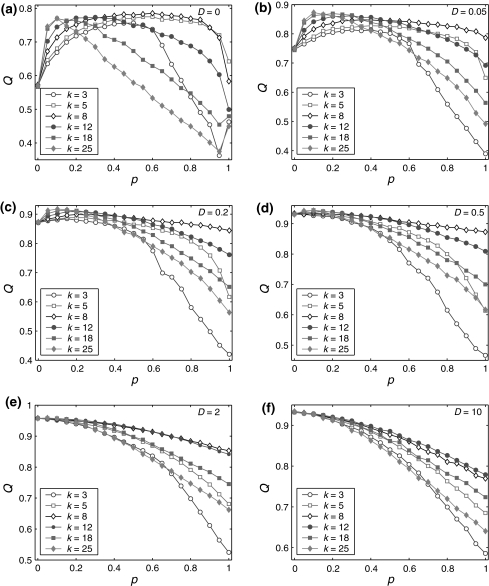
Let us systematically investigate how unreliable synapses influence the performance of the population rate coding in the considered neuronal network under different parameter conditions. As a starting point, we examine the dependence of the performance of the population rate coding Q on the successful transmission probability p and the scale factor k at different levels of noise. To this end, we let the other synaptic parameters be 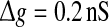and τ_s = 5 ms. The numerically obtained results are shown in Figs. 1 and 2, respectively. It is clear that several interesting features can be extracted from these two figures.

Fig. 1.

Effect of the successful transmission probability and the scale factor on the performance of the population rate coding at different noise levels. Results are obtained for D = 0 (a), D = 0.05 (b), D = 0.2 (c), D = 0.5 (d), D = 2 (e), and D = 10 (f), respectively. We choose 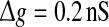and τ_s = 5 ms in all cases

Our first finding is that, for a fixed scale factor, the population rate coding achieves the best performance at a corresponding intermediate successful transmission probability, provided that the intensity of the additive Gaussian white noise is small (Fig. 1a–c). This result indicates that the synapses with suitable successful transmission probability can enhance the encoding performance in our considered neuronal network in the weak noise regime. For a sufficiently small p, due to weak noise, the firing activities of the network are dominated by the external input current. This reason makes neurons in the considered network fire spikes almost synchronously, thus resulting that the information of the external input current is poorly encoded by the population firing rate (see Fig. 2a) (Mazurek and Shadlen 2002; Kumar et al. 2010). With the increasing of p, the synaptic currents from other presynaptic neurons start to influence the firing dynamics of the postsynaptic neuron. For a suitable intermediate p, due to the sparse active synaptic connections taking part in transmitting spikes in a time instant, the synaptic currents act as a source of noise (Gerstner and Kistler 2002; Brunel et al. 2001; Destexhe and Contreras 2006). Such “noise” effect of synaptic currents makes neurons encode different aspects of the external input current through the desynchronization process. As a result, a suitable level of information exchange between neurons is able to facilitate the encoding performance in the case of weak noise (Fig. 2b). Further increasing the successful transmission probability will just deteriorate the performance of the population rate coding. This is at least due to the following two reasons: (i) for too small or too large k, a high synaptic reliability tends to evoke bursting firings or excessively firing suppression (see Fig. 2d, e), respectively. (ii) For an intermediate k, although excitation and inhibition is balanced to a certain degree, the unavoidable overlap of input populations for different neurons introduces strong correlations of network activity. The synaptic currents therefore have the tendency to drive neurons fire spikes synchronously in this case (Fig. 2c). Accordingly, the neural information of the external input current cannot be well read from the population firing rate for large p. For simplicity, we call the optimal encoding performance occurring at an intermediate parameter value (here the parameter is the successful transmission probability) the encoding enhancement phenomenon in the following studies.

Second, in the case of D = 0, we observe that there exists the encoding rebound phenomenon occurring at p = 1 for both too small and too large scale factors (see k = 3 and 25 in Fig. 1a). The underlying mechanism can be interpreted as follows. In the absence of noise, the firing activities of the network are purely determined by the external input current as well as the synaptic currents. Based on the above discussion, for too small or too large k, a high synaptic reliability (in this case, p ≠ 1) tends to evoke bursting firings or excessively firing suppression, respectively. When p = 1, due to the same synaptic currents (without noise current), all neurons in the considered network are easy to be driven to the synchronous state. Although the total synaptic current for each neuron is also very large (its absolute value) in this case, due to refractory period the total synaptic current will decay to a small value before the membrane potential of the neuron can be excited again. This will reduce the effects of synaptic currents and avoid both the occurrence of the bursting firings and excessive firing suppression (Fig. 2f). It should be emphasized that even a weak noise may destroy the synchronous state of neurons at p = 1, indicating that the encoding rebound phenomenon might not be observed for D > 0.

As the third observation, we find that the so-called encoding enhancement phenomenon is largely influenced by the intensity of the additive Gaussian white noise. As we see from Fig. 1a–c, increasing the parameter D from 0 to a slightly larger value can suppress the encoding enhancement phenomenon. This may be partially because with the help of slightly stronger noise, the population firing rate will reflect more accurate temporal structural information (i.e., temporal waveform) of the external input current. In this case, the encoding performance of the considered network is promoted in the whole parameter regime from 0 to 1. Because of the bottleneck effect of coding,1 the above reason leading to the tuning of the synaptic transmission probability cannot further enhance the encoding performance in a significant way, at least not as in the case of D = 0. Once the noise intensity exceeds a critical value slightly larger than 0.5, we observe that the optimal encoding performance is obtained at p = 0. In this situation, each Q curve basically decreases from a corresponding large initial value as the successful transmission probability grows, implying that the synaptic unreliability induced encoding enhancement phenomenon disappears (Fig. 1e, f). That is to say, the intrinsic synaptic interactions between neurons will disturb their firing behaviors and purely deteriorate the accuracy of neural information for strong noise. This is possible because strong noise can cause some neurons to fire an amount of “false” spikes, and the intrinsic information exchange from these false spikes will reduce the encoding performance.

Moreover, the numerical results shown in Fig. 1a–f also suggest that the relative strength between inhibitory and excitatory synapses (i.e., scale factor) plays an important role in the performance of the population rate coding for both the weak and strong noise. When the noise intensity is small, the optimal encoding performance is found to increase gradually as the scale factor grows at first, and then almost reaches a saturation value at around k = 18. With the increasing of k, it is observed that the peak position of the Q curve moves toward the left direction. At the same time, our simulation results show that the top plateau region of the Q curve becomes narrower during this process. Therefore, there exists a “compromising” scale factor regime (between about 8 and 12), and when parameter k falls into this special regime, the considered network undergoes better encoding performance within a wide range of the successful transmission probability. It should be noted that the similar effect of scale factor can be observed even for the case of strong noise, but becomes less and less marked as the noise intensity is increased. These findings tell us that the turning of scale factor is critical for the population rate coding, and the benign competition between excitation and inhibition can help the considered neuronal network maintain better information processing capability with different levels of synaptic unreliability.

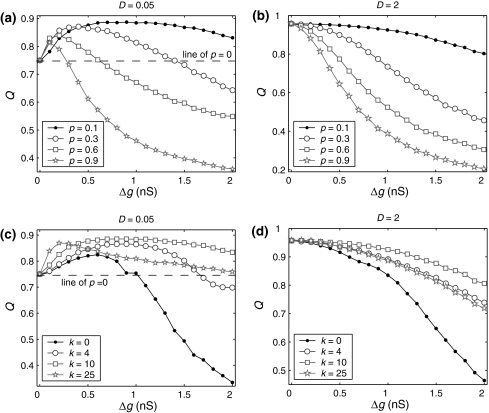
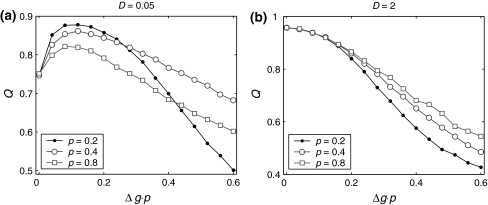
Next, to examine what happens when the synaptic strength changes in our considered neuronal network, we manually set τ_s = 5 ms. First, we study the effects of the excitatory synaptic strength on the encoding performance for both the weak and strong noise. For simplicity, we fix the scale factor k at 10, and calculate the value of Q as a function of 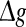for various successful transmission probabilities with noise intensities D = 0.05 and 2. The corresponding results are plotted in Fig. 3a, b, respectively. In the case of weak noise, the Q curves all first rise and then drop with the increasing of the excitatory synaptic strength, indicating that there exists an optimal intermediate excitatory synaptic strength to best support the population firing rate coding for each value of p   (p > 0). In fact, it is not surprising that the excitatory synaptic strength induced encoding enhancement phenomenon can be observed for weak noise, because increasing 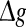with p fixed has similar effect as increasing p while keeping 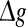fixed (see also the discussion in the last paragraph of this subsection). Furthermore, we find that such encoding enhancement phenomenon largely depends on the successful transmission probability. With a suitable small p, our considered neuronal network is able to support the encoding enhancement phenomenon within a wide range of the 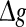(for comparison, see p = 0.1, p = 0.3, and the line of p = 0 in Fig. 3a). For a quite high synaptic reliability, a slightly larger 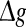might evoke more synchronized or burst firings, resulting that the value of Q rapidly decreases with the excitatory synaptic strength after an insignificant encoding enhancement in the weak 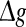regime. In the case of strong noise, we find that the encoding enhancement phenomenon vanishes, which is in agreement with the conclusion drawn from Fig. 1e, f. In this case, the intrinsic information exchange just deteriorates the performance of the population rate coding in our considered neuronal network (Fig. 3b). Second, to investigate the effects of inhibitory synaptic strength, we set p = 0.1, and calculate the value of Q versus 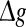for different scale factors with noise intensities D = 0.05 and 2. The corresponding results are present in Fig. 3c, d, respectively. Similar to Fig. 1, a compromising scale factor is also found to better support the performance of the population rate coding for both the weak and strong noise. Theoretically, it is also because too small k will lead to burst firings and too large k will suppress firings excessively. The results shown here further reveal that the inhibition has significant effects on the performance of the population rate coding in our considered network.

Fig. 3.

Effects of the synaptic strength on the performance of the population rate coding. The value of Q as a function of 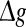for different values of p, with noise intensities D = 0.05 (a) and D = 2 (b). We choose the scale factor k = 10 for a and b. The value of Q as a function of 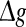for different values of k, with noise intensities D = 0.05 (c) and D = 2 (d). The successful transmission probability p is fixed at 0.1 for c and d. The synaptic time constant is τ_s = 5 ms in all cases

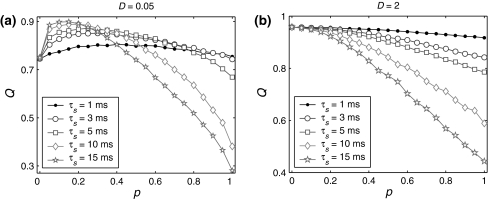
We further evaluate the effects of the synaptic time constant, which is also a very important parameter for synapses, on the encoding performance. Figure 4a illustrates Q versus the successful transmission probability p for different values of τ_s at the weak noise level. For the case of τ_s = 1 ms, the performance of the population rate coding has no significant change as p is increased from 0 to 1. During this process, the value of Q keeps between 0.75 and 0.8, and only weak encoding enhancement phenomenon can be observed. With the increasing of τ_s, the maximum of Q becomes larger, and at the same time, the peak position of the Q curve moves toward left and the top region becomes narrower. When τ_s = 10 ms, the maximal Q achieves a quite large value, and due to the bottleneck effect of coding, further increasing the synaptic time constant cannot enhance the encoding performance significantly. One possible candidate mechanism for these behaviors can be elucidated as follows. For a fixed p, slower synapses will provide neurons with more correlated inputs (Tetzlaff et al. 2008), which drive these neurons to fire more synchronously. The network therefore needs a relatively smaller p to generate appropriate randomness to maintain the best encoding performance for a larger τ_s. On the other hand, a long synaptic time constant with suitable small p also means that the synaptic currents have enough intensity and suitable randomness, which are able to accelerate the response speed of the network to the external input current (Gerstner 2000). To a certain extent, this will enhance the correlation between the inputs and outputs of the network. For a high synaptic reliability, a larger τ_s tends to evoke more synchronized or burst firings. In this situation, the neural information cannot be better read from the population firing rate. In Fig. 4b, we present the numerical simulation results corresponding to the case of strong noise (D = 2). Again, we observe that the encoding enhancement phenomenon disappears. For a fixed p, increasing the synaptic time constant can enhance the propagation of false spikes, which are caused by strong noise. As a result, the performance of the population rate coding reduces as the synaptic time constant grows in this case. Our above findings indicate that: (i) for weak noise, fast synapses support ordinary encoding performance in the whole parameter region, while slow synapses can support high level of encoding performance but in narrow parameter region; (ii) for strong noise, slow synapses have the tendency to purely reduce the encoding performance.

Fig. 4.

Effects of the synaptic time constant on the performance of the population rate coding. Results are obtained for D = 0.05 (a) and D = 2 (b), respectively. In all cases, other synaptic parameters are 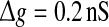and k = 10

Some persons might postulate that the encoding dynamics in neuronal networks with unreliable synapses can be simply determined by average amount of received neurotransmitter for each neuron in a time instant, which can be reflected by the produce of 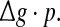To check whether this is true, we calculate the value of Q as a function of 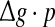for different successful transmission probabilities at different levels of noise. For a fixed D, it is obvious that such postulate is true if all Q curves coincide with each others. The numerically obtained results are plotted in Fig. 5a, b, respectively. As we see, although the Q curves exhibit the similar trend with the increasing of 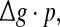they do not superpose in most parameter region for both strong and weak noise. The results shown here clearly demonstrate that the encoding performance of our considered network can be not simply determined by the produce 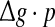or, equivalently, by the average amount of received neurotransmitter for each neuron in a time instant. This may be because the unreliability of the neurotransmitter release will add randomness to the system. Since different values of successful transmission probability will introduce different levels of randomness, and this randomness might affect the spiking dynamics of neurons, therefore the network may show different encoding performance for different values of p at a fixed 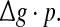It should be emphasized that this result does not contradict our previous discussion, that is, increasing 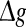with p fixed has similar effect as increasing p while keeping 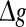fixed. This is due to the fact that the Q curves for different successful transmission probabilities show the similar trend as 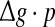is increased (see Fig. 5a, b).

Fig. 5.

Dependence of the encodingperformance Q on the produce 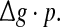Results are obtained for D = 0.05 (a) and D = 2 (b), respectively. In all cases, other synaptic parameters are τ_s = 2 ms and k = 10

Comparison with the corresponding random neuronal networks

Up to now, we have systematically examined how unreliable synapses influence the performance of the population rate coding in an all-to-all neuronal network consisting of both the excitatory and inhibitory neurons connected with unreliable synapses. We have also shown that, for different levels of synaptic unreliability, the considered neuronal networks with unreliable synapses may display different encoding performance (but have the similar trend), even when their average amount of received neurotransmitter for each neuron in a time instant remains unchanged. In order to further clarify the differences between the synaptic unreliability and network randomness, we make comparisons on the encoding performance between our considered neuronal network model (unreliable model) and a corresponding random neuronal network (random model) in this subsection.

We first introduce how to generate a corresponding random neuronal network. Assume that there is an all-to-all neuronal network consisting of N neurons coupled by unreliable synapses with successful transmission probability p. A corresponding random neuronal network is constructed by using the connection density p (on the whole), that is, a unidirectional synapse exists between each directed pair of neurons with probability p. As mentioned above, we also do not allow a neuron to be coupled with itself. It is obvious that parameter p has different meanings in these two different neuronal network models. From the viewpoint of mathematical expectation, the numbers of active synaptic connections taking part in transmitting spikes in a time instant are the same in these two different neuronal network models. In the corresponding random neuronal network, neurons are also simulated by using the IF neuron model, whereas the synaptic interactions are implemented by using the traditional conductance-based model, i.e., removing the constraint of the synaptic reliability parameter from Eq. 5.

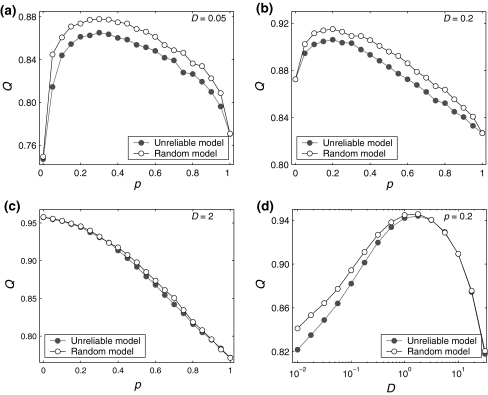
In Fig. 6a–c, we show several comparisons on the encoding performance between our considered neuronal network model and the corresponding random neuronal network model for different noise intensities. Here we manually set 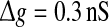, τ_s = 5 ms, k = 10, and choose D = 0.05, 0.2 and 2 for Fig. 6a–c, respectively. As we see, changing the value of connection density in the random model has the similar qualitative effect on the encoding performance as changing the value of successful transmission probability in the unreliable model. However, we find some interesting results in the weak noise regime. In this case, the corresponding random neuronal network obviously undergoes a slightly better encoding performance, although the two different Q curves exhibit the similar trend with the increasing of p. This is possible because the long-time averaging effect of unreliable synapses tends to make neurons fire more synchronous spikes. With the increasing of D, we observe that the encoding difference between these two neuronal network models becomes smaller and smaller. For a sufficiently large noise intensity, the difference becomes so small that the two Q curves almost coincide with each other (for example D = 2, see Fig. 6c). Theoretically, this is due to the fact that the information from weak excitatory synaptic interaction is almost drowned in strong noise in this case. Our results are further demonstrated by the data shown in Fig. 6d.

Fig. 6.

Comparisons on the encoding performance between our considered neuronal network (unreliable model) and the corresponding random neuronal network (random model). (a–c): The value of Q versus p for three typical noise intensities. Here D = 0.05 (a), D = 0.2 (b), and D = 2 (c). d The value of Q as a function of D, with p = 0.2. In all cases, we set 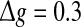nS, τ_s = 5 ms, k = 8

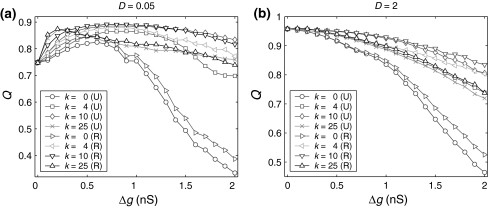
On the other hand, we also find that the encoding difference between the unreliable model and random model are largely influenced by the excitatory synaptic strength and scale factor. For sufficiently strong network excitation (large 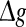and small k), it is observed that the encoding difference between these two different neuronal network models becomes significant (see k = 0 in Fig. 7a, b). This is because strong excitation will lead to high firing rate of neurons, thus resulting in much more different spiking dynamics and encoding performance. Moreover, compared to the case of weak network excitation shown in Fig. 7, we see that there also exists significant encoding difference between these two different network models in the strong network excitation region even for strong noise intensity. This is of no surprise, since for sufficiently strong network excitation, the information due to strong excitatory synaptic interaction has also great effect on the spiking dynamics of neurons, thus leading to different encoding performance.

Fig. 7.

Effect of the successful transmission probability and scale factor on the encoding difference for the unreliable model and random model. Here ‘U’ denotes the unreliable model and ‘R’ denotes the random model. System results are obtained for D = 0.05 (a) and D = 2 (b), respectively. In all cases, other system parameters are τ_s = 5 ms, k = 10 and p = 0.1

Although form the above results we cannot conclude that unreliable synapses have advantages and play specific functional roles in encoding performance, at least it is shown that the encoding performance in these two different neuronal network models is different to a certain degree. In reality, the neuronal network model considered in our work can be roughly regarded as a local cortex. As we know, signal propagation is a widespread phenomenon in the brain and many higher cognitive tasks involve signal propagation through multiple brain regions. Such encoding difference for these two different network models should be further accumulated and enlarged through the process of neural activities transmission. According to above discussions, we feel that it should be better not to simply use the random connections to replace the unreliable synapses in modelling research, especially when considering the network has feedforward structure (Guo and Li 2011).

Conclusion and discussion

Information processing in biological neuronal networks involves the process of spike transmission through synapses. Thus, the synaptic dynamics will, at least to a certain degree, determine how well the neural information is encoded by the output of the neuronal network. So far, most relevant computational studies only considered that neurons transmit spikes based on the deterministic synaptic interaction model. However, some experiments have revealed that the communication between neurons more or less displays the unreliable property (Abeles 1991; Friedrich and Kinzel 2009; Raastad et al. 1992; Smetters and Zador 1996). The question as to what roles the unreliable synapses play in the neural information encoding is still unclear and requires investigation. It is reasonable and worthwhile to use a heuristic unreliable synaptic model to study this type of question.

In the present work, we investigated the population rate coding in an all-to-all coupled neuronal network consisting of the excitatory and inhibitory neurons connected with unreliable synapses. By introducing a stochastic on-off process to explicitly simulate the unreliable synaptic transmission, we systematically examined how the synaptic unreliability and other important synaptic parameters influence the encoding performance in our considered neuronal network. Interestingly, we found that a suitable level of synaptic unreliability can enhance the performance of the population rate coding for weak noise. While in the case of strong noise, the synaptic interactions between neurons purely have negative effects on the encoding performance. Further simulation results indicated that the encoding performance of our considered network depends on several other important synaptic parameters, such as the synaptic strength, scale factor, and synaptic time constant. Better choosing the values of these synaptic parameters can help our considered neuronal network maintain high levels of encoding performance. The heuristic reasons for these behaviors have been discussed in the present work. Moreover, it was also found that encoding dynamics in neuronal networks with unreliable synapses cannot be simply determined by the average amount of received neurotransmitter for each neuron in a time instant. For different levels of synaptic unreliability, our considered networks may display different encoding performance, even when their average amount of received neurotransmitter for each neuron in a time instant remains unchanged. On the other hand, we compared the encoding performance in our considered network with that in the corresponding random neuronal network. Our simulation results suggested that the network randomness has the similar effect as the synaptic unreliability on the performance of the population rate coding, but they are not completely equivalent in quantity. This result tells us that it is better (or more safe) not to simply use the random connections to replace the unreliable synapses in modelling research, especially if we consider the network having feedforward structure.

In reality, our main finding that synapses with suitable successful transmission probability can improve the encoding performance of the considered neuronal network in the weak noise region might be related to a well known phenomenon called stochastic resonance (SR) (Collins et al. 2002; Wenning and Obermayer 2003; Destexhe and Contreras 2006; Guo and Li 2009). Theoretically, SR refers to a phenomenon that an appropriate intermediate level of noise makes a nonlinear dynamical system reach its optimal response to external inputs. As we discussed above, the unreliability of neurotransmitter release will add a certain of randomness to the neural system. Therefore, in the case of weak noise, suitable synaptic transmission probability might provide appropriate additional randomness to help the considered system trigger the SR mechanism and enhance its encoding performance. Notice that it is not surprised that we could not observe the similar result in the strong noise region, because in this case the noise current itself has already exceeded the optimal noise level for triggering SR.

The neuronal network model we considered in this work is an all-to-all coupled recurrent network model used to study the population rate coding. In fact, such model can be roughly regarded as a local cortex. We have shown that, in principle, the unreliable synapses might have significant effects on the performance of the population rate coding. In additional simulations, we have demonstrated that the similar results can be also observed in large scale neuronal networks. Since the communication between real neurons indeed exhibits the unreliable property, we believe that these results are able to improve our understanding about the effects of biological synapses on the population rate coding. In real neural systems, we anticipate that neurons may make full use of the properties of unreliable synapses to enhance the encoding performance in the weak noise region, and also suggest physiological experiments to test the results. Further work on this topic includes studying the effects of unreliable synapses on other types of neural coding, for example the synchrony coding, examining the information transmission capability of neuronal networks with unreliable synapses through the information-theoretic analysis (Zador 1998; Manwani and Koch 2000), as well as considering the roles of unreliable synapses in neuronal networks with complex topology structures, such as the random neuronal networks, small-world neuronal networks (Watts and Strogatz 1998; White et al. 1986; Sporns et al. 2004; Stam 2004; Humphries et al. 2006; Guo and Li 2010), and neuronal networks with community structure.