Unsymmetrical hot electron heating in quasi-ballistic nanocontacts

Abstract

Electrons are allowed to pass through a single atom connected to two electrodes without being scattered as the characteristic size is much smaller than the inelastic mean free path. In this quasi-ballistic regime, it is difficult to predict where and how power dissipation occurs in such current-carrying atomic system. Here, we report direct assessment of electrical heating in a metallic nanocontact. We find asymmetric electrical heating effects in the essentially symmetric single-atom contact. We simultaneously identified the voltage polarity independent onset of the local heating by conducting the inelastic noise spectroscopy. As a result, we revealed significant heat dissipation by hot electrons transmitting ballistically through the junction that creates a hot spot at the current downstream. This technique can be used as a platform for studying heat dissipation and transport in atomic/molecular systems.

Understanding and control of heat dissipation in nanoscale structures is one of the key issues in development of atomic- and molecular-scale electronics¹,²,³,⁴. Unlike diffusive electron transport in macroscopic systems, electronic charges are allowed to transmit through conductors without being scattered by phonons or defects when the characteristic size is much smaller than the inelastic mean free path. Energy dissipation in this quasi-ballistic regime is still non-negligible because of the huge current density that leads to relatively high electron-phonon scattering rates in the microstructures⁵,⁶,⁷,⁸,⁹,¹⁰. This has been elucidated by recent experiments that report substantial local heating in current-carrying atomic and molecular junctions¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶.

In contrast, little attention has been paid to power dissipation via hot electrons escaping through a quasi-ballistic contact under high field³,¹⁷, which is of practical importance from viewpoint of assessing energy efficiency and current carrying capacity of atomic/molecular electronic devices. In the present work, therefore, we developed a micro-fabricated temperature sensing system for exploring electrical heating in Au single atom contacts. The operational principle is based on a mechanically-controllable break junction (MCBJ), a well-established method widely used for forming stable atom-sized junctions¹⁸,¹⁹. Our idea here is to embed a lithographically-defined resistance thermometer²⁰ in MCBJs and utilize it to measure the local temperature at the banks of the free-standing single-atom contact under a current flow.

Results

The configuration of a temperature-sensor-integrated MCBJ is shown in Fig. 1 a–d (see also Methods). It consists of a free-standing Au nano-junction and adjacent Pt coils that serve as a resistance thermometer. The device architecture is designed to achieve a high sensitivity for local temperature measurements. The Pt sensing elements are thermally coupled to the junction via the underlying Al₂O₃ layer. Furthermore, Pt and Au leads were made partially free-standing for the sake of minimizing heat escape from the square Al₂O₃ regions. The whole structure was fabricated on a thick polyimide layer possessing excellent thermal insulating characteristics (thermal conductivity is about 0.3 W/mK, two orders of magnitude lower than that of Al₂O₃) to prevent heat leakage to the substrate.

Figure 1. Structure and operational principle of a micro-thermometer-embedded mechanically-controllable break junction (MCBJ).

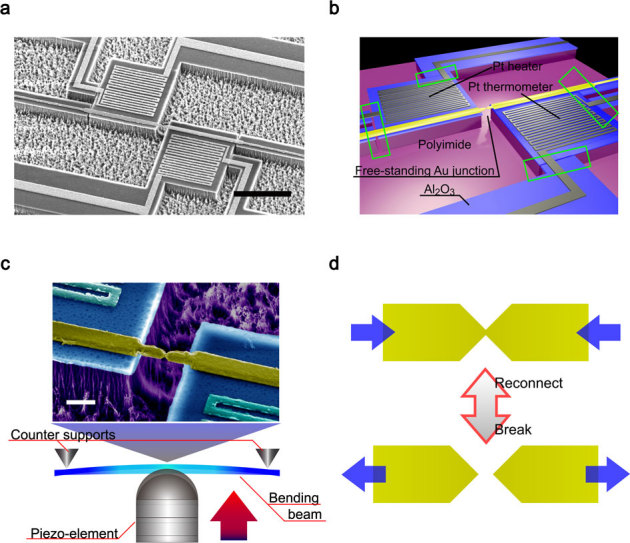
(a,b) A scanning electron microscopy image (a) and a schematic layout of a thermometer-integrated MCBJ (b). The device consists of a free-standing Au nano-junction and two adjacent Pt coils that function as a heater and a resistance thermometer. The alumina layers thermally connect the junction and the Pt coils. Regions marked by green rectangles possess free-standing structure. Scale bar is 10 μm. (c) A three-point bending configuration used for break junction experiments. Scale bar in the magnified view of a Au nanobridge is 1 μm. (d) The Au contact can be broken and re-formed by manipulating the beam bending.

The sensitivity of the micro-thermometers was evaluated by examining Joule heating at the Pt coil heater and characterizing the temperature change using the Pt thermometer on the other side of the Au nano-junction exploiting the temperature response of the resistance R_h and R_t of the heater and the thermometer, respectively (Fig. 2 a) and the calibration curve (Fig. 2 b) for converting R_h(t) to T_h(t) of the heater (thermometer) through the temperature coefficient r (see Methods for calibration of Pt resistance thermometer). Specifically, we measured R_h under a linear voltage sweep from V_h = −0.8 V to 0.8 V applied to the heater at a rate of 2 mV/s and simultaneously recorded R_t using the lock-in technique with the ac voltage V_ac of 2 mV at 1 kHz for a closed Au junction at T₀ = 150 K. The R_h – V_h as well as R_t – V_h characteristics reveal a parabolic feature (Fig. 2 c and e). We deduced a temperature rise at the heater ΔT_h and the thermometer ΔT_t from the Joule heating-induced increase in the resistivity through ΔT_h(t) = (R_h(t) - R₀) / r (R₀ is the residual resistance estimated by extrapolating the R_h(t)-T₀ curve to T₀ = 0 K), which is valid in the present condition wherein f ≫ 2πτ where f = 1 kHz is the voltage modulation frequency and τ is the thermal time constant, and plotted as a function of the dissipated power in the Pt heater P_h = V_h²/ R_h (Fig. 2 d and f). We see that ΔT_h and ΔT_t scale linearly with P_h. This suggests steady-state power dissipation and a certain level of heat diffusion from the heater to the thermometer via the Au junction²¹. The fact that ΔT_h is more than one order of magnitude higher than ΔT_t infers only a limited amount of heat transfer across the free-standing nano-junction due to the relatively small thermal conductance compared to that of the Au and Pt micro-leads.

Figure 2. Detection of Joule heat generated at a micro-heater.

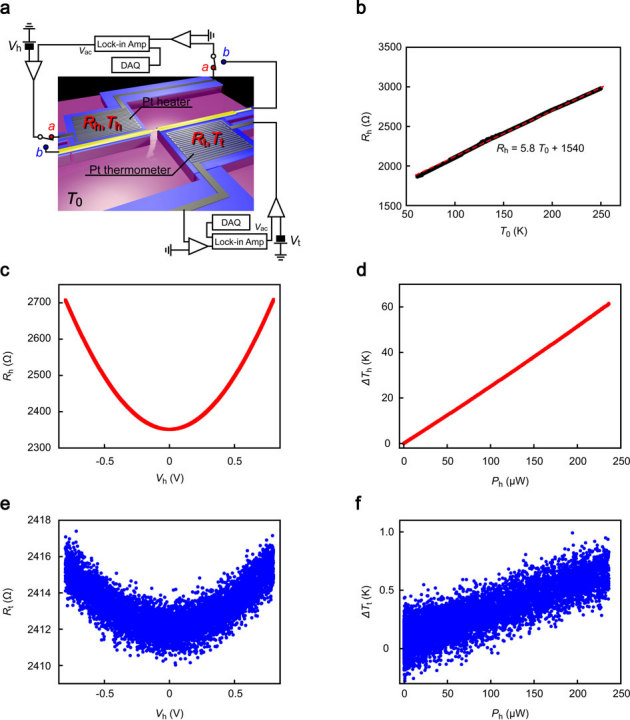
(a) A circuit used for the local temperature measurements. The lock-in amplifiers are employed to measure the resistance of the Pt coils. The circuit can also be utilized for measuring the resistance of the Au junction by turning the switch from a to b. (b) A calibration curve of the Pt thermometer. (c,d) Increase in the resistance of Pt heater R_h during a bias ramp plotted as a function of the applied dc voltage V_h (c) and corresponding temperature rise ΔT_h depicted as a function of power P_h consumed by the heater (d). (e,f) A concomitant change in the Pt thermometer resistance R_t (e) and corresponding temperature rise ΔT_t depicted as a function of power P_h that indicates an increase of the local temperature at the thermometer by heat transfer from the heater via the Au nanobridge (f).

The local temperature measurements were applied to detect Joule heat generated in a Au nano-junction at T₀ = 150 K. The wire resistance R_Au was obtained by the ac method utilizing the ac voltage V_ac of 2 mV at 1 kHz in a voltage range from V_Au = −0.05 V to 0.05 V (Fig. 3 a). We observed a non-linear increase in R_Au with |V_Au| associated with electrical heating (Fig. 3 b). It is noticeable that R_Au – V_Au characteristics is asymmetric with respect to the bias polarity. This behavior is ascribed to annealing effects on the microstructure such as grain size and defect density and accompanied irreversible change in the electrical conductivity by Joule heating²². Heat dissipation in the Au bridge led to concurrent rise in the resistance of the adjacent Pt thermometer as presented in Fig. 3 c. In accordance to the R_Au – V_Au characteristics, R_t (and equivalently the local temperature at the thermometer) demonstrated irregular increase with V_Au, further suggesting structure deformation in the Au contact during electrical heating²². Meanwhile, T_t – P_Au plots reveal linear feature that manifests diffusive transport in the Au nano-contacts and Joule heating origin of the local temperature increase at the thermometer, where P_Au = V_Au²/R_Au is the power dissipated in Au nano-junctions (Fig. 3 d)²¹.

Figure 3. Electrical heating of a Au nano-junction at T₀ = 150 K.

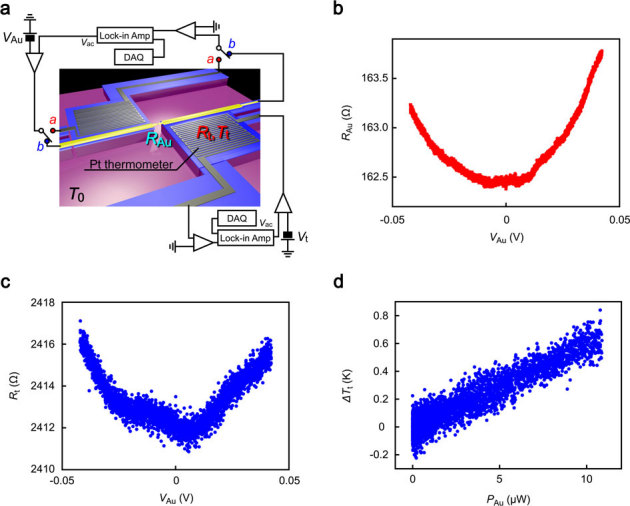
(a) A measurement circuit utilized for characterization of Joule heat generated in a Au nano-junction. Bias voltage V_Au was applied to the Au nano-constriction and the resistance of the junction R_Au as well as that of the thermometer R_t was measured simultaneously. (b) The junction resistance R_Au increases with V_Au by Joule heating. (c) At the same time, the thermometer resistance R_t also increases. The irregular behaviour of R_t is presumably due to annealing effects on the Au contact microstructure. (d) The local temperature change at the thermometer ΔT_t scales linearly with the power P_Au consumed by the junction.

Having verified the adequate sensitivity of the micro-thermometer for detecting Joule heat occurring in the Au nano-bridge, we extended the power dissipation characterization to a single-atom chain (Fig. 4 a). After forming and holding a Au single atom contact at T₀ = 80 K (Fig. 4 b, see also Methods), we performed simultaneous measurements of I – V_Au characteristics and the thermometer resistance. As the atomic contact tend to become unstable under elevated field by the local heating and current-induced forces, a small bias ramp of V_Au ≤ 0.1 V was used (Fig. 4 a). Furthermore, we collected 10 points of I and R_t at each 0.2 mV step of V_Au for better resolution of the temperature sensor in the low-power regime. The resulting ramp rate was 0.2 mV/s. We calculated the average current <I> and the thermometer resistance <R_t> from the 10-point data. A linear <I> – V_Au curve was obtained reflecting ballistic electron transport through the Au single-atom chain (Fig. 4 a, inset)¹⁰,²³. At the same time, <R_t> exhibited monotonic increase by about 1 Ω with |V_Au| corresponding to the temperature rise of up to about 0.3 K above T₀ (Fig. 4 c). The <R_t> – V_Au was reproduced in the consecutive sweeps in positive and negative directions indicating stable heat dissipation and diffusion under the relatively slow voltage sweep rate.

Figure 4. Characterization of power dissipation in a quasi-ballistic single-atom contact.

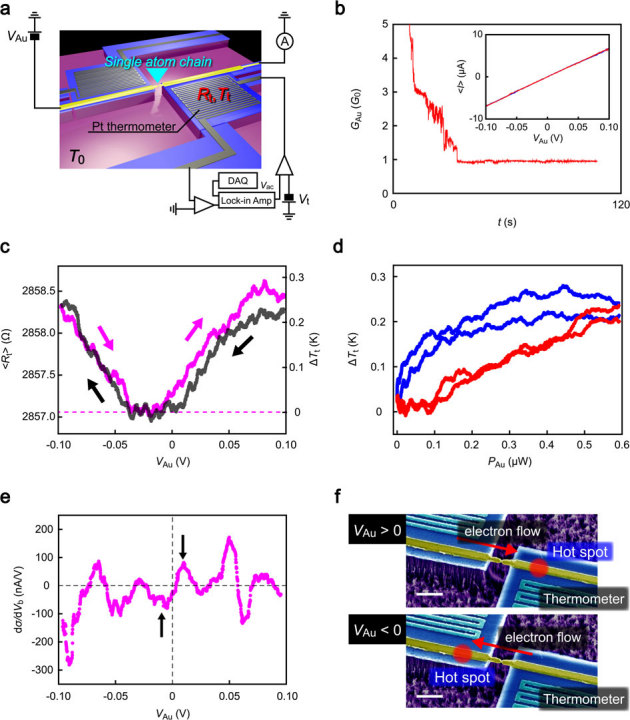
(a) The measurement set up used for detection of local electrical heating in a Au single atom contact. Bias voltage V_Au was swept in a range from −0.1 V to 0.1 V and the resistance R_t of the thermometer was simultaneously recorded. (b) Formation of a Au single-atom wire using the self-breaking technique at T₀ = 80 K under V_Au = 0.05 V. The contact conductance G_Au ( = 1/R_Au) exhibits a flat plateau at about 1 G₀ during mechanical stretching signifying junction thinning to a single-atom size. Inset is the average current-voltage (<I> – V_Au) characteristics measured for a Au single-atom contact. (c) The local temperature change ΔT_t at the thermometer during the voltage sweep on the single-atom junction estimated from the average Pt coil resistance <R_t>. (d) Plots of ΔT_t with respect to P_Au = V_Au²/ R_Au. Red (blue) dots correspond to ΔT_t at V_Au < 0 V (V_Au > 0 V) in (b). (e) The noise spectrum of Au single atom wire. Dashed lines are a guide to the eyes. Arrows point to the lowest peak that represents an onset of local ionic heating in the atomic bridge. (f) Hot electron heating mechanism. A hot spot is generated at the different side of the junction depending on the bias polarity. Scale bars denote 1 μm.

Discussion

It is of interest to explore the underlying physics of the temperature rise at the Pt coil thermometer detected in response to a current flow through a single-atom junction. The positive response of ΔT_t to V_Au implies non-negligible heat dissipation in the Au junction. However, unlike the typical Joule heating characteristics observed for the nano-contact shown in Fig. 3 d, ΔT_t – P_Au plots for the single-atom chain reveal nonlinear temperature increase against the input power and an asymmetry with respect to the bias polarity (Fig. 4 c,d). In order to shed light on this peculiar feature, we investigated the onset of the electron-phonon-interaction-derived local heating in the single-atom contact by conducting an inelastic noise spectroscopy²³,²⁴,²⁵. Current noise is characterized here by the standard deviation 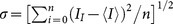calculated from the set of n-point I data acquired at each V_Au step during a voltage sweep. Although the feature as a whole is broadened by thermal smearing, we can find stepwise increase of with V_Au as shown in Fig. S3. The corresponding d/dV_Au – V_Au curve shows peaks at around |V_Au| = 0.01 V (Fig. 4 e). This inelastic spectrum thus suggests an onset of electron-phonon interactions at |V_Au| ∼ 0.01 V, the corresponding excitation energy of which corresponds to the acoustic phonon modes of Au single-atom chains¹⁰,²⁶.

The above results manifest non-negligible local heating in the current-carrying quasi-ballistic single-atom contact that can be a possible cause of the local temperature increase detected by the thermometer. There are two distinct mechanisms responsible for the local heating in atom-sized junctions: electron-phonon and electron-electron scattering. Among these, local ionic heating via electron-phonon scattering fails to explain the bias polarity asymmetry of the ΔT_t – V_Au dependence: T_t starts to increase from 0 V in positive V_Au region whereas the temperature rise is suppressed in the low voltage range of −0.04 V ≤ V_Au ≤ 0 V at negative bias side, while on the other hand, there is no conspicuous bias polarity dependence of electron-phonon interactions confirmed in the noise spectrum (Fig. 4 e). For electron-electron scattering, it serves to heat up electrons appreciably in a quasi-ballistic nanoscale conductor by the huge current density and affect the bias dependence of the local junction temperature⁴,⁸,²⁷. This local electron heating has been predicted theoretically to originate a larger current density at the electron flow downstream and accompanied significant electron-phonon scattering there that causes a hot spot at one side of the junction. The asymmetric ΔT_t – V_Au dependence can thus be explained qualitatively by the contribution of this electron heating. However, it is also anticipated that the electron heating effect is less significant compared to the local ionic heating and not detectable in metallic nanocontacts⁴,⁸,²⁷. Therefore, although we cannot rule out the possibility, the asymmetric heating in the Au single-atom chain found in the present study may not be attributed to the local electron heating mechanism.

On the other hand, it is more likely that power dissipation by hot electrons is responsible for the electrical heating phenomenon identified through the local temperature measurements here. The accelerated electrons transmit ballistically through Au single-atom junctions and become scattered by phonons at a distance defined by the inelastic mean free path (typically several hundreds of nanometer under low field) and release the kinetic energy there¹⁷. This hot electron heating is thus directional along the electric field; a hot spot is created close to (away from) the thermometer at the electron flow downstream under positive (negative) V_Au (Fig. 4 f). As a consequence, the heating effects became too weak to cause a detectable change in T_t at small negative V_Au where power dissipation of hot electrons took place at the opposite side of the single-atom contact, since heat transfer to the thermometer becomes less efficient due to the relatively large thermal resistance at the atomic-scale constriction. Meanwhile, the asymmetry of ΔT_t – V_Au curve is becoming less obvious at the high voltage regions (Fig. 4 c). It is anticipated that inelastic scattering length of hot electrons diminishes with V_Au because of enhanced probability of multiphonon scattering²⁸,²⁹, thereby shifting the hot spot closer to the junction. As a result, a hot spot generated near the thermometer under positive V_Au tends to move away from the thermometer as V_Au increases and gives rise to the saturation-like local heating effects at the high biases. In contrast, the hot spot moves closer to the thermometer when sweeping V_Au from 0 to −0.1 V, which leads to more pronounced heating effects at high |V_Au| in the negative bias regime. Eventually, asymmetry of the hot electron heating effects disappears under high field as hot spot emerges at the vicinity of the Au single atom contact under high field irrespective of the bias polarity, which explains the high-bias ΔT_t behavior in Fig. 4 c. In fact, quantitatively, fraction of the power dissipated in the single-atom chain should be marginal considering the ballistic nature of electron transport³. Therefore, predominant portion of the power is dissipated via inelastic scattering of hot electrons at the current downstream side of the contact bank.

Methods

Fabrication of micro-thermometer-embedded mechanically-controllable break junctions

Micro-thermometer-embedded MCBJs were fabricated as follows (see also Fig. S1). First, a polyimide layer (Pyre-Ml, Industrial Summit Technology Co.) of 4 μm thick was spin coated on one side of a phosphorous bronze substrate. Micro-electrodes were fabricated on the polyimide surface using a photo-lithography technique followed by metal deposition (Cr/Au = 2 nm/20 nm) with a radio-frequency magnetron sputtering method and subsequent lift-off (Fig. S1 (a)). Al₂O₃ films of 20 nm thick were then rendered using an electron-beam lithography, radio-frequency magnetron sputtering, and lift-off processes. Subsequently, Au junctions having a narrow constriction with a cross-section of about 100 nm×100 nm was formed (a thin Cr layer of 1 nm thick was used for adhesion). After that, Pt coils were prepared, whose thickness and width were 30 nm and 300 nm, respectively. Finally, the sample was exposed to isotropic reactive ion etching with a mixture gas of CF₄/O₂. As a result, polyimide underneath was removed making the Au and Pt electrodes partially free-standing (Fig. S1 b).

Mechanical break junction system configuration

The micro-thermometer-embedded MCBJ was mounted on the stage of a cryostat in a three-point bending configuration. A piezo-actuator-driven pushing rod was placed at the back of the sample to mechanically bend the phosphorous bronze beam (Fig. 1 c). By doing so, we could narrow the constriction of the Au nanobridge by the necking and form a stable atom-sized contact (Fig. 1 d)³⁰. After evacuating the chamber to below 10⁻⁵ Torr, we introduced liquid coolant and cooled the junction.

Pt heater and thermometer calibrations

The platinum thermometers were calibrated by checking the resistance change R_h and R_t of the Pt heater and the Pt resistance thermometer during the cooling process²¹,³¹. For this, ac voltage of V_ac = 2 mV at 1 kHz was applied to the Pt coils and the differential resistance R_h(t) was acquired using two lock-in amplifiers (SR830, Stanford Research Systems Co.) while monitoring the substrate temperature T₀ with a temperature sensor/controller (Scientific Instruments Model 9700) as schematically depicted in Fig. 2 a. We observed linear decrease of R_h with decreasing T₀ from 300 K to 60 K at a rate of r = 5.8 Ω/K (Fig. 2 b), which is attributed to mitigated electron-phonon scattering at the low temperatures. Among the samples we fabricated, r as well as the room temperature resistance varied in a range of 4 to 7 Ω/K and 2500 to 3500 Ω, respectively. The scattering of these sensor parameters stem most likely from a difference in the coil geometries and microstructures. We note that this temperature coefficient agrees with the previous experimental reports²¹.

Single-atom contact formation

We imposed a tensile stress on the Au nano-bridge by mechanically bending the MCBJ substrate. By doing so, the junction was elongated by d = r_MCBJ L, where d and L are the displacements of the contact and the piezo-element that bends the phosphor bronze beam, respectively. The attenuation factor r_MCBJ was ∼3×10⁻⁴ estimated by examining an exponential decay of tunnelling current flowing through the vacuum gap between the two MCBJ electrodes¹⁸. As a result, we could break and form a Au junction repeatedly by controlling the substrate bending through manipulation of the piezo-actuator driving voltage. Formation of a single-atom contact was implemented via a resistance-feed-back control of the junction thinning processes³⁰. In this procedure, a fused contact was elongated under a constant voltage of V_Au = 0.05 V at a predefined stretching rates ranging from 6 nm/s to 6 pm/s while monitoring the conductance G = 1/R_Au¹¹. We observed a gradual decrease of G indicating narrowing of the junction by stress concentration at the constriction and concomitant necking deformation. The conductance trace revealed a staircase-like feature when G is further lowered to below 10 G₀, and finally demonstrated a flat plateau at around 1 G₀ right before dropping to zero, where G₀ = 2e²/h ∼ 77.5 μS is the conductance quantum (Fig. 3 a). At this stage, the atom-sized junction undergoes mechanical thinning via atom rearrangements and eventually evolved into a single-atom chain that possesses one fully opened channel for electron transmission¹⁹.

Author Contributions

M. Tsutsui, T. K., and M. Taniguchi planned and designed experiments. M. Tsutsui and M. Taniguchi fabricated MCBJ devices, exhibited single-molecule conductance measurements, and performed data analyses. M. Tsutsui, T. K., and M. Taniguchi co-wrote paper.

Supplementary Material

Supplementary Information

Supplementary Information