Bayesian Time-Series Analysis of a Repeated-Measures Poisson Outcome With Excess Zeroes

Abstract

In this article, the authors demonstrate a time-series analysis based on a hierarchical Bayesian model of a Poisson outcome with an excessive number of zeroes. The motivating example for this analysis comes from the intensive care unit (ICU) of an urban university teaching hospital (New Haven, Connecticut, 2002–2004). Studies of medication use among older patients in the ICU are complicated by statistical factors such as an excessive number of zero doses, periodicity, and within-person autocorrelation. Whereas time-series techniques adjust for autocorrelation and periodicity in outcome measurements, Bayesian analysis provides greater precision for small samples and the flexibility to conduct posterior predictive simulations. By applying elements of time-series analysis within both frequentist and Bayesian frameworks, the authors evaluate differences in shift-based dosing of medication in a medical ICU. From a small sample and with adjustment for excess zeroes, linear trend, autocorrelation, and clinical covariates, both frequentist and Bayesian models provide evidence of a significant association between a specific nursing shift and dosing level of a sedative medication. Furthermore, the posterior distributions from a Bayesian random-effects Poisson model permit posterior predictive simulations of related results that are potentially difficult to model.

Conducting an observational, clinical study of medication use among older patients in a medical intensive care unit (ICU) is complicated by both clinical and statistical issues (1). First, the patients are critically ill, and treatments they receive may include measures such as intubation and administration of sedative hypnotic medications (2). Second, because patients are admitted to the ICU around the clock, their medication dosing is potentially influenced by circadian rhythms, as well as changes in medical staff. Lastly, some patients will inevitably die during their stay in the ICU (3). An important statistical concern is that for some drugs, the great majority of doses given over time will be at the zero level. Other statistical challenges include potential periodicity in dosing and autocorrelation among within-subject measurements.

Owing in part to these analytical concerns, there is a paucity of clinical evidence regarding the temporal patterns of medication dosing in the medical ICU across a 24-hour day. However, in one non-ICU study, Baker et al. (4) suggested that there is a tendency for clinicians to more frequently prescribe psychotropic medications in the late evening. Instead of analyzing medication doses, Baker et al. used a count of the number of times that certain drugs were delivered to patients within work shifts (4). Although a valid statistical test of shift-based dosing levels will yield more directly interpretable quantitative results—that is, rates of medication usage corresponding to shift—it must also contend with the above-mentioned statistical concerns while adjusting for important clinical covariates. For these reasons, the analysis proposed here is significantly more complex.

Although there have been many applications of time series to clinical studies (5–7) and a growing number of case studies using Bayesian methods (8, 9), to our knowledge there are few examples of time-series analysis of clinical data within the Bayesian context. Our objective in this article is to emphasize the advantages of applying a Bayesian random-effects Poisson model in the evaluation of differences in shift-based dosing of a medication characterized by an extremely high proportion of zero-level doses. To achieve that objective, we have organized the article as follows. In Materials and Methods, we define the study sample, explore the periodicity and autocorrelation of the data, present graphical trajectories of average medication doses, and describe the advantages of a Bayesian approach for this situation. In Results, we present results from both frequentist and Bayesian models and demonstrate how the posterior distributions of model coefficients afforded by the Bayesian framework enable posterior predictive simulations that can provide estimates of related findings not easily modeled. In the Discussion, we review strengths and limitations of the analysis and offer concluding remarks.

MATERIALS AND METHODS

Analytical sample and related statistical concerns

The original cohort of study participants consisted of 309 patients aged 60 years or older who were admitted to the medical ICU at Yale-New Haven Hospital from September 2002 through September 2004. As described elsewhere (10, 11), proxy respondents served as the primary source of baseline information for critically ill patients. Hospital medical records were reviewed to obtain demographic information, admission diagnoses, laboratory data, and shift-based medication dosing.

In this study, we analyzed the dosing levels of a common benzodiazepine, midazolam, that is specified on the formulary for sedation in this ICU. Its use was diligently recorded during every shift, including all routes of administration. Also recorded was the use of other psychoactive medications, including typical and atypical antipsychotic agents, seizure medications, and antidepressants. All prescriptions of medication were made at the discretion of the treating physician. A research nurse performed the chart reviews and recorded the medication data from both nursing flow sheets and the pharmacy’s electronic database.

The formal model of our analysis, designed to evaluate the dosing of the benzodiazepine midazolam across a potential maximum time period of 5 days (i.e., 15 consecutive 8-hour nursing shifts in the ICU), was restricted to those patients with ICU stays spanning a minimum of 3 calendar days and who received midazolam during their stay. The choice of patients who spent 3 or more days in the ICU was guided by our desire to obtain a sample size that would enable us to analyze dose levels with full adjustment for linear trend, periodicity, autocorrelation, and clinical covariates. The nursing shifts were defined as night (midnight–8 AM), day (8 AM–4 PM), and evening (4 PM–midnight). Because 79% of the participants had data for at least 15 shifts, we decided to make use of this additional clinical information (i.e., additional repeated measures) across different patients to detect any potential difference in the medication doses during the night shift with respect to the day and evening shifts.

Whereas the constraints on our study population, referent to an observational study that does not impose restrictions on the basis of the outcome and duration of ICU stay, might seem arbitrary, they did provide the best study sample with which to address our clinical hypothesis. The clinical question was whether there was an association between the night nursing shift and the dose of midazolam given to patients. In terms of risk of exposure, a person who never receives midazolam in the ICU is not truly at risk for the outcome of interest, that is, a night-related change in dose. In like manner, if a person is not in the ICU for at least 3 days, there is not adequate information to detect the temporal shift of interest. For these reasons, the restrictions on our study population provided the most appropriate sample with which to evaluate our clinical hypothesis. These same restrictions also imply that results of this study are generalizable only to older ICU patients in this hospital who take midazolam during an ICU stay lasting for 3 days or longer.

Table 1 presents information on the entire cohort, as well as the analytic sample. Of the 309 patients in the full cohort, only 114 (37%) received midazolam and spent 3 or more days in the ICU. The one person missing data on the dementia covariate was excluded from the analysis, because we were not convinced that the Bayesian model would adequately impute this missing dichotomous value based on the other model terms. There were no missing data on the outcome or on the other covariates used in the model. Web Figure 1, which appears on the Journal’s Web site (http://aje.oxfordjournals.org/), is a bar chart with color coding that indicates the number of specific nonzero person-doses given to patients in each of the 15 shifts. It is evident that in 3 of the night shifts (i.e., shifts 1, 7, and 10), there are fewer nonzero doses administered to patients relative to their corresponding day (shifts 2, 8, and 11) and evening (shifts 3, 9, and 12) shifts, respectively.

Table 1.

Characteristics of Persons Aged ≥60 Years Admitted to the Intensive Care Unit (ICU) of Yale-New Haven Hospital and of Patients Receiving Midazolam With ICU Stays Spanning At Least 3 Calendar Days, New Haven, Connecticut, 2002–2004

Characteristic	Entire Cohort (n = 309)a				Patients Receiving Midazolam and Staying ≥3 Days in ICU (n = 114)b
	No.	%	Mean (SD)	Median (IQR)	No.	%	Mean (SD)	Median (IQR)
Demographic factors
Age, years			74.7 (8.5)				73.4 (8.8)
Male gender	145	47			63	55
Education, years			12.5 (2.8)				12.5 (2.9)
Nonwhite race	51	17			19	17
Admitted from homec	241	78			96	84
Baseline medical status
APACHE II score (18)			23.5 (6.4)				24.3 (6.7)
Charlson comorbidity index (29)			1.8 (1.9)				1.6 (2)
Evidence of depressiond	85	28			33	29
Dementiae	95	31			34	30
Any impairment in Activities of Daily Living (30)	111	36			41	36
Admitting diagnosis
Sepsis	51	17			18	16
Respiratory	156	51			56	49
Neurologic	5	2			1	<1
Gastrointestinal hemorrhage	52	17			31	27
Other	45	15			8	7
ICU factors
Intubation	167	54			86	75
No. of days of ventilationf				6 (8)				7 (8)
Length of stay, daysf				4 (5)				6 (8)

Abbreviations: APACHE, Acute Physiology and Chronic Health Evaluation; ICU, intensive care unit; IQCODE, Informant Questionnaire on Cognitive Decline in the Elderly; IQR, interquartile range; SD, standard deviation.

^aData were missing for some subjects (1 for Charlson comorbidity index, 9 for education, 3 for dementia, and 4 for weight).

^bData were missing for some subjects (1 for Charlson comorbidity index, 1 for education, 1 for dementia, and 2 for weight).

^cAdmitted from home as opposed to a skilled nursing facility or rehabilitation center.

^dEvidence obtained by surrogate or chart.

^eIQCODE score (31) > 3.3.

^fDuring entire ICU stay (includes first admission and, if applicable, readmissions to ICU).

Note the 4 noninteger dose values in Web Figure 1: 0.5, 1.5, 2.5, and 3.5 mg. Because the probabilistic properties of the Poisson distribution are defined only for nonnegative integers, in our analysis we rounded up each noninteger dose to the next integer value.

Outcome and hypothesis of interest

Our outcome was the dose of midazolam, in milligrams, administered to that subset of patients who received at least 1 dose of midazolam and whose stay in the ICU spanned at least 3 calendar days. Our hypothesis was that the doses corresponding to the night shift (midnight–8 AM) would be lower than the doses administered during the evening and day shifts. Even within this restricted study population, 88% of all of the person-doses recorded were zeroes. This situation was appropriate for testing the utility of an approach that proactively accounts for excess zeroes in a Poisson model.

Why Bayesian analysis?

There are 3 well-documented advantages to using Bayesian methods for zero-inflated outcomes. First, Bayesian zero-inflated regression models have been shown to possess better small-sample performance with tighter intervals and better coverage probabilities than frequentist methods (12). Second, Bayesian methods allow for seamless integration of information from other sources, such as pilot data (13). Lastly, Bayesian methods yield posterior distributions of the model coefficients that facilitate posterior predictive simulations of related findings that are often difficult to model (see section 8.4 of Gelman and Hill (14)). We demonstrate the latter property in our example.

Analysis of time-series data

Time-series data are routinely analyzed in business and engineering with models based on the seminal text of Box and Jenkins (15). The key assumption in these models is that the process generating the time-series data is weakly stationary (16). Weak stationarity is typically demonstrated by showing that both the mean and the variance of the time-series data are relatively constant over the period of measurement. A relatively constant mean is often achieved by adjusting for linear trend and periodicity, whereas constant variance is typically obtained by adjusting for autocorrelation. Significant autocorrelation means that data values closer to each other in time are more similar than those further away in time and thereby contradicts the crucial assumption of constant variance over time for any regression model. For this reason, terms that adequately capture the autocorrelation must be present in the time-series model.

Evidence of periodicity and linear trend in shift-based doses of midazolam

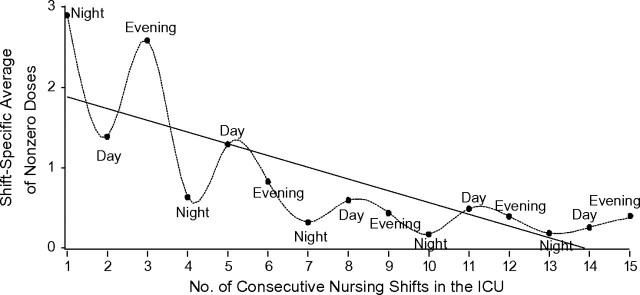
Figure 1 depicts the average dose of our data cohort across their first 15 shifts in the ICU. In order to perform analyses that accounted for the periodicity of nursing shifts, we had to temporally align each person-shift in the ICU with its corresponding nursing shift (night, day, or evening). For this reason, each patient’s first shift in the ICU was recorded as either shift number 1, 2, or 3 (per Figure 1), corresponding to the person’s admission during either the night, day, or evening shift, respectively, on the calendar day of admission. Consequently, each participant contributed 7–15 person-shifts to the analytical sample. Because people were admitted across all 3 shifts, the doses contributing to each of the plotted points did not necessarily pertain to the same persons as in previous or subsequent shifts.

Figure 1.

Average number of nonzero doses of midazolam given over the course of patients’ first 15 nursing shifts in the intensive care unit (ICU) at Yale-New Haven Hospital, New Haven, Connecticut, 2002–2004. Results are shown for persons who stayed in the ICU for ≥3 days and received midazolam, with spline-based interpolation.

Figure 1 emphasizes the temporal patterns in the data in two ways. The wavy plot was generated using cubic splines that form the continuous curves between each pair of consecutive dots (17), that is, the shift-based average doses among persons receiving the drug. The shape of the spline-based plot suggests a periodicity wherein higher average doses, relative to night shifts, appear to collectively correspond to both day and evening shifts. The second plot is a simple linear regression of the average dose on shift number that provides evidence of a negative trend over time. Although this simple linear regression of the average dose on shift number provides evidence of a negative trend over time, the mathematical properties of the Poisson model in which it resides do not allow for the prediction of negative doses. This exploratory graph, which plots shift-based averages for only those persons receiving midazolam in each specific shift, speaks to the need for model terms that account for periodicity and linear trend.

Evidence of autocorrelation in shift-based doses of midazolam

We examined the shift-based averages for autocorrelation to verify compliance with the assumption of stationarity. Figure 2 presents 3 ways of examining autocorrelation that are calculated by means of the SAS procedure ARIMA (SAS Institute Inc., Cary, North Carolina). The 3 panels present different ways of considering autocorrelation for different temporal lags between data points. From top to bottom, the 3 measures are the autocorrelation function, the partial autocorrelation function, and the inverse autocorrelation function. With the exception of lag 2 on the inverse autocorrelation function, none of the measures of autocorrelation were significant at α = 5%. These graphs tell us that the variance of the time-series data remains relatively constant over time.

Figure 2.

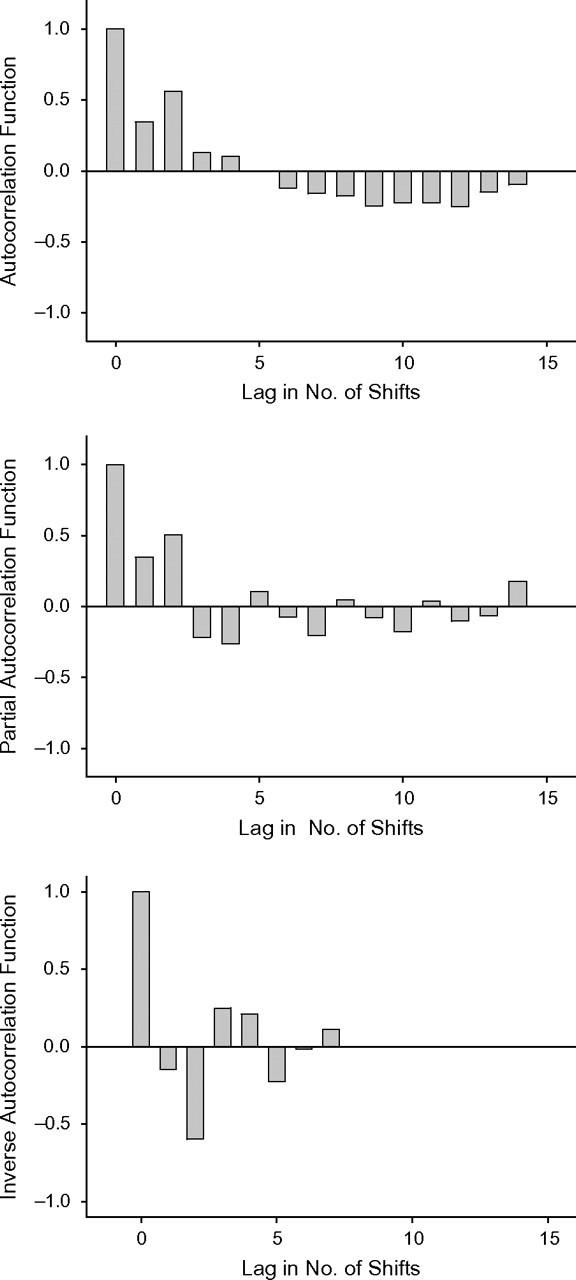
Correlation analysis of the average number of midazolam doses given over the course of patients’ first 15 nursing shifts in the intensive care unit at Yale-New Haven Hospital, by shift, New Haven, Connecticut, 2002–2004. The 3 panels present different ways of considering autocorrelation for different temporal lags between data points. From top to bottom, the 3 measures are the autocorrelation function, the partial autocorrelation function, and the inverse autocorrelation function. The lag represents the temporal difference between shifts for which serial autocorrelation was estimated. With the inverse autocorrelation function, autocorrelation exceeded the 95% confidence interval for lag 2.

Because stationarity requires, in addition to a stable variance, a temporally constant mean, it is more comprehensive than a simple examination of autocorrelation. The ARIMA procedure also conducts a χ² test of autocorrelation for different lag values. For the midazolam data, this test resulted in a P value of 0.15 for lags up to 6 and a P value of 0.015 for lags greater than 12. This is due to the strong, negative linear trend evident in Figure 1, which induces a negative correlation between longer gaps. This means that over time periods of 12 shifts or longer, the negative linear trend violates the constant mean required to satisfy stationarity. Whereas the bar graphs of Figure 2 affirm the need for model terms that account for autocorrelation, the P values of the χ² test for lags of 12 emphasize the need to adjust for linear trend.

Two Poisson models for midazolam that adjust for excess zeroes

We consider 2 distinct Poisson models for the midazolam doses. The first is the traditional zero-inflated Poisson (ZIP) model, where the outcome is assumed to be a mixture of 2 stochastic processes, one that generates Poisson-distributed values and a second Bernoulli process that generates the excess zeroes. This mixed distribution is

which implies

(1)

where the tilde (∼) denotes a probability distribution, j(t) indicates person j at shift t, and p_j is the probability of an excess zero dose from the Bernoulli process. The linear model of the natural logarithm of the mean parameter μ_j(t) is defined as

(2)

where all terms on the right-hand side of equation 2, except φ_j, are fixed effects common to each submodel of equation 1. Here, μ is an intercept, N_t indicates whether time t is the night shift referent to either the day or evening shift (1 for night shift, 0 otherwise), and time t (shift 1, …, 15) is multiplied by the slope of the linear trend (β). X_j is a vector of the following important clinical covariates: age in years, APACHE II (Acute Physiology and Chronic Health Evaluation) score for severity of illness (18), an indicator for death in the ICU, an indicator for dementia based on an IQCODE (Informant Questionnaire on Cognitive Decline in the Elderly) score greater than 3.3 (19, 20), an indicator for mechanical ventilation, an indicator for male gender, an indicator for nonwhite race, and an indicator for whether the person did not remain in the ICU for 5 days. The indicators for death in the ICU and an ICU stay less than 5 days accounted for potential selection effects introduced by persons with shorter stays. The random effect φ_j is person-specific and, in combination with μ, represents each person’s individual intercept. We present results obtained from both the frequentist and Bayesian formulations of equation 2.

The second model assumes that the outcome follows a regular Poisson distribution, midazolam dose_j(t) ∼ Poisson (μ_j(t)), where the natural logarithm of the mean parameter μ_j(t) is modeled as

(3)

The last two terms on the right-hand side of equation 3 are random effects that account for the overdispersion created by the high number of zero doses and autocorrelation, respectively. Here θ_j(t) is a unique random effect for each person-shift, providing comprehensive treatment of autocorrelation. Because a large number of random effects makes model convergence difficult to achieve in the frequentist framework, this second model is fitted in the Bayesian context only and can be seen as a Bayesian enhancement of the generalized linear mixed model approach used by Breslow and Clayton (21).

For all formulations of equations 2 and 3, the fixed model coefficients were given widely dispersed normal priors of mean zero, and the precision terms corresponding to the random effects φ_j and θ_j(t) were given gamma priors whose parameters were assigned mildly informative values to expedite Markov chain Monte Carlo convergence. For all Bayesian formulations, 3 Markov chains initialized at disparate values were each cycled for 20,000 iterations, with convergence confirmed by the Gelman-Rubin statistic as modified by Brooks (22, 23). Following burn-in, each chain was cycled for an additional 5,000 iterations to obtain estimates of posterior distributions of all model parameters. Model fit was checked with the posterior predictive evaluations described in chapter 8 of Gelman and Hill (14) and demonstrated elsewhere (24). The posterior distributions of the model coefficients were also used to calculate a related statistic in this study (discussed in Results). Exploratory analysis was performed using SAS, version 9.2 (25); models were evaluated with WinBUGS 1.4 (26); and posterior predictive simulations were conducted in the R language, using the “arm” package (27, 28). Significance for all parameters was interpreted as a 95% credible interval that excluded the null value of 1.

Sample code for all models discussed is available in the Web Appendix.

RESULTS

Table 2 presents the posterior estimates of the risk ratios from the ZIP mixture models with their corresponding 95% confidence (frequentist) and credible (Bayesian) intervals. Because the linear models in equations 2 and 3 are models of the log of the Poisson parameter, the resultant model coefficients are not directly interpretable until they are exponentiated to yield the corresponding risk ratios. The “risks” are the effect of the covariates in either reducing or increasing the dose with respect to the average. Any risk ratio whose credible interval ranges exclusively below or above the null value of 1 signifies that the corresponding model term is associated, respectively, with a reduction or increase in dose.

Table 2.

Risk Ratios and 95% Confidence/Credible Intervals From Models for Midazolam Dose That Accommodate Excess Zeroes, New Haven, Connecticut, 2002–2004

Model Term	Notation	Frequentist ZIP Mixture With Random Intercept		Bayesian ZIP Mixture With Random Intercept		Bayesian Random–Effects Poisson Model
		RR	95% Confidence Interval	RR	95% CrI	RR	95% CrI
Night shift	1 = night, 0 = day or evening	0.78*	0.63, 0.97	0.83*	0.67, 0.98	0.63*	0.44, 0.90
Shift no.	1, 2, …, 15	0.89*	0.87, 0.92	0.88*	0.85, 0.99	0.85*	0.78, 0.92
Age, years	Continuous	0.97	0.53, 1.75	0.98	0.95, 1.01	1.01	0.96, 1.05
Severity of illnessa	Continuous	0.99	0.95, 1.02	0.99	0.95, 1.01	1.01	0.96, 1.07
Death in ICU	1 = decedent, 0 = survivor	1.51	0.88, 2.59	1.59	0.97, 2.75	0.94	0.42, 2.14
Intubation	1 = yes, 0 = no	1.60	0.84, 3.04	1.50	0.78, 2.71	0.96	0.46, 1.97
Dementiab	1 = yes, 0 = no	1.23	0.79, 1.92	1.28	0.81, 1.93	1.34	0.69, 2.80
ICU stay <5 days	1 = yes, 0 = no	0.99	0.96, 1.01	0.95	0.49, 1.67	1.51	0.73, 3.13
Male gender	1 = male, 0 = female	1.38	0.91, 2.09	1.28	0.81, 1.93	1.30	0.69, 2.65
Nonwhite race	1 = yes, 0 = no	1.52	0.87, 2.67	1.54	0.99, 2.64	2.05*	1.03, 5.16

Abbreviations: APACHE, Acute Physiology and Chronic Health Evaluation; CrI, credible interval; ICU, intensive care unit; IQCODE, Informant Questionnaire on Cognitive Decline in the Elderly; RR, risk ratio; ZIP, zero-inflated Poisson.

^*P < 0.05.

^aAPACHE II score for severity of illness (18).

^bIQCODE score (31) > 3.3.

Referent to the zero value used for day and evening shifts, and after adjustment for linear trend and important clinical factors, the night shift is associated with lower doses of midazolam, that is, 78% and 83% as large in the frequentist and Bayesian ZIP paradigms, respectively. Because of the pronounced negative trend depicted in Figure 1, the dose of any subsequent shift is only about 88% as large as that preceding it. No other covariates show a significant association with shift-based doses of midazolam in either the frequentist or Bayesian ZIP formulation.

Table 2 also presents posterior estimates of the risk ratio and 95% credible interval from the Bayesian random-effects Poisson model of equation 3. Owing to the use of random effects for each person-shift, the credible intervals are generally wider. Here the effect of the night shift is even smaller (risk ratio = 0.63) and nonwhite race has a significant positive association (risk ratio = 2.05). All other associations are of a magnitude proximate to that in the ZIP models.

The statistically smaller dose level for the night shift in our analysis is attributable to the fact that the average person-dose across the night shifts (0.45 mg) was smaller than those of both the day (0.66 mg) and evening (0.89 mg) shifts. This is at least partially due to the fact that only 37 patients (32%) received nonzero doses during at least 1 night shift, as compared with 66 patients (58%) and 63 patients (55%) in at least 1 day or evening shift, respectively. Because the average dose of midazolam was so low (0.66 mg over any given 8-hour shift), the statistically significant association with the night shift is not clinically meaningful. For the same reason, the significantly positive effect of nonwhite race is also not of clinical concern. We use the demonstrated association of nonwhite race, however, to illustrate the potential of posterior predictive simulation enabled by the Bayesian approach.

The Bayesian random-effects Poisson model is based on a simple Poisson distribution, and given the posterior distributions of all model coefficients, provides a direct way to calculate related statistics that may inform the question at hand. Suppose we were interested in knowing the probability of someone’s receiving a clinically high dose of midazolam in their first shift. By making 1,000 random draws from the posterior distributions of the model coefficients, we can simulate 1,000 doses for any combination of covariates in a given shift. For example, noting that the covariates nonwhite race, male gender, dementia, and ICU stay <5 days each have risk ratios greater than 1, we make 1,000 Poisson draws of random combinations of these model coefficients, while setting the intercept and shift covariate to values of 1 and the other covariates to 0. This simulates 1,000 predicted doses for this combination of covariates in the first shift, and for illustrative purposes we will interpret doses ≥3 mg as clinically high. Using the percentiles of the simulated dose values, we can readily provide a credible interval for the probability of receiving a dose at this level in the first shift, conditional on having the covariates male gender, nonwhite race, dementia, and ICU stay <5 days. In the first shift of our recorded data, only 0.9% of all midazolam doses received by persons with these covariates were ≥3 mg, which resides within the credible interval yielded by the corresponding posterior simulation (95% credible interval: 0%, 1.8%). Regardless of whether or not the nonwhite covariate has a positive association with midazolam, there is a very low probability that a nonwhite male with dementia and an ICU stay less than 5 days (among the scenarios for highest predicted doses of midazolam) will receive a dose of ≥3 mg in his first shift. This sort of result is often difficult to model directly but is easily obtained by sampling from the posterior distributions of the model coefficients from the Bayesian random-effects Poisson model.

The results presented here provide neither strong agreement nor disagreement with the previously mentioned non-ICU study in which Baker et al. (4) reported a higher number of prescriptions of psychotropic medication in the evening. That study was largely descriptive, and Baker et al. did not analyze specific dose levels.

DISCUSSION

Strengths

For clinical researchers, the ability to accurately estimate important clinical effects in statistically complicated circumstances is a valuable research asset. In this time-series analysis of the dosing of medications for a critically ill population, the chief clinical predictor was an indicator variable representing the night shift, relative to the day and evening shifts. Using Bayesian and frequentist formulations of the ZIP mixture model, we were able, with a small sample, to analyze a longitudinal outcome for linear trend, periodicity, and within-person autocorrelation while adjusting for excess zeroes and key clinical covariates. Because simulation studies have shown the Bayesian approach to be more precise for zero-inflated regression models and because the simpler Poisson distribution of the second model facilitates posterior predictive simulations, we emphasize the Bayesian random-effects Poisson model. Detailed exposition of this generalized Bayesian time-series analysis is the focus of this article. The exposited method has potential application in studies of the effects of drug dosing on sleep patterns and delirium among older persons hospitalized in the ICU.

Limitations

These data did not include a term for the specific physicians who prescribed doses in any given shift, which was probably a substantive source of variability in the dosing patterns. From a clinical perspective, this was a small, observational sample from a single, urban medical ICU, so findings from this study may not be easily generalizable. As we noted above, the constraints on data collection raise concern about the proper inferential population for these results. Lastly, because the data came from an observational study, there was potential for an imbalance of unmeasured covariates across the nursing shifts that may have introduced bias into the estimates. While this might be protected against with a randomized trial, conducting trials in the ICU is expensive and complicated and would, in any case, need to be justified with rigorous observational results like those presented here.

Conclusion

In many clinical circumstances, such as a medical ICU, data analysis is complicated by statistical concerns like excess zeroes, periodicity, and autocorrelation. While these issues can often be resolved using frequentist techniques, in some cases Bayesian analysis may be the preferred option because of its greater precision in small samples, its systematic accommodation of complementary data sources in the prior distribution, and its easy provision of related results based on posterior predictive simulations. We have demonstrated here how the Bayesian random-effects Poisson model can flexibly integrate elements of time-series analysis and how it facilitates estimation of related findings that are potentially difficult to model.

Glossary

Abbreviations

ICU

intensive care unit

ZIP

zero-inflated Poisson