Analysis of a simulation algorithm for direct brain drug delivery

Abstract

Convection enhanced delivery (CED) achieves targeted delivery of drugs with a pressure-driven infusion through a cannula placed stereotactically in the brain. This technique bypasses the blood brain barrier and gives precise distributions of drugs, minimizing off-target effects of compounds such as viral vectors for gene therapy or toxic chemotherapy agents. The exact distribution is affected by the cannula positioning, flow rate and underlying tissue structure. This study presents an analysis of a simulation algorithm for predicting the distribution using baseline MRI images acquired prior to inserting the cannula. The MRI images included diffusion tensor imaging (DTI) to estimate the tissue properties. The algorithm was adapted for the devices and protocols identified for upcoming trials and validated with direct MRI visualization of Gadolinium in 20 infusions in non-human primates. We found strong agreement between the size and location of the simulated and gadolinium volumes, demonstrating the clinical utility of this surgical planning algorithm.

1. Introduction

Achieving robust drug distribution is critical to the efficacy of neurotherapies. For many therapies, such as toxic agents used in chemotherapy or viral vectors used in gene therapy, it is also critical to minimize off-target distribution. Direct transcranial pressure-driven infusion through a small cannula, often called Convection-Enhanced Delivery (CED), meets these criteria (Bobo, Laske et al. 1994). However, it can be technically challenging to predict the exact shape of the distribution pattern because the shape is affected by infusion parameters such as the geometry of the cannula and flow rate as well as by the underlying tissue structure (Raghavan, Brady et al. 2006). As a result, clinical trials have achieved poor drug distribution. This failure to adequately cover the target structure has been identified as a primary contributor to the failure of the trials of glial-derived neurotrophic factor for Parkinson’s disease (Lang, Gill et al. 2006; Salvatore, Ai et al. 2006), neurturin gene therapy for Parkinson’s disease (Marks and Stacy 2009) and anti-tumor drugs in glioblastoma multiforme (Sampson, Archer et al. 2009).

The theoretical groundwork describing how infusion and tissue parameters affect infusate distribution has been previously described (Morrison, Chen et al. 1999). This theory was realized in software (iPlan^® Flow; Brainlab AG, Feldkirchen, Germany) that uses magnetic resonance imaging (MRI) data to simulate the infusate distribution by estimating the tissue geometry from diffusion tensor imaging (DTI) (Sampson, Raghavan et al. 2007). This software was initially validated in a malignant glioma study by comparing the simulated distribution to the distribution detected with SPECT after co-infusing ¹²³I-HSA in eight patients receiving tumoral infusions of cintredekin besudotox.

The purpose of this study was to refine the simulations for infusion techniques that will be used in upcoming clinical trials and to do a highly accurate validation of the predictability of distributions. The validation data was a large series of infusions in non-human primates (NHP) conducted with real-time MRI visualization of gadolinium distribution. Quantification of the distribution with MRI provided sub-millimeter resolution with high signal contrast due to the T1-shortening effects of the gadolinium.

These datasets were collected as part of safety and efficacy studies co-infusing gadolinium with gene therapy agents and, hence, followed the protocols of planned clinical studies. The infusions used a cannula with a stepped design at the tip that will be used in upcoming trials. Modeling the infusate distribution around this stepped tip required modifying the previously published simulation algorithms. The stepped tip has previously been shown to reduce back flow along the cannula and thus improve the distribution of therapy in the surrounding parenchyma (Krauze, Saito et al. 2005).

The simulation algorithm was validated by comparing the simulated volume of distribution to the distribution of gadolinium observed in the MRI images. The goal was to inform clinicians’ expectations for how much infusate will reach the target or leak outside the simulated distribution.

2. Materials and Methods

2.1. Data Acquisition

2.1.1. Subjects and Infusion Procedure

Ten NHP (Macaca Mulata) received a total of 20 direct transcranial CED infusions in an MRI. NHP were selected because they most closely resemble the anatomical features and size of the human brain.

The infusion cannula (MRI Interventions, Irvine, CA) was a rigid cannula with a narrow 0.2 mm inner diameter and a step from 0.36 mm to 0.67 mm at 3 mm from the tip to prevent reflux (Krauze, Saito et al. 2005). The cannulae were primed with saline containing 1 mM gadolinium (Gd-DTPA, Prohance^®; Bracco Diagnostics, Princeton, NJ). The gadolinium was co-infused with gene therapy vector as previously described (Su, Kells et al. 2010). Gene therapy vectors included AAV2-GDNF (N=15), AAV2-AADC (N=2), AAV2-hASM (N=1) and AAV2-Tor1A mutant (N=2). The infusion cannula was positioned intraoperatively in the MRI with either a modified stereotactic DBS placement system (Clearpoint; MRI Interventions, Irvine CA) or a polyethylene array (Rosenbluth, Luz et al. 2010).

The infusions volumes ranged from 30 to 300 μL and included targets in the thalamus (N=9, 220 ± 78 μL), putamen (N = 10, 54 ± 6 μL) and caudate (N = 1, 30 μL). The infusion volumes were measured on the infusion pump (Harvard Apparatus Inc, Holliston MA). The infusion durations ranged from 18 to 86 min. Infusion rates started at 1 μL/min and ramped approximately every 5 min by 0.5 μL/min to a final infusion rate of 3 μL/min.

2.1.2. MRI Acquisition

All procedures were conducted in a 1.5 Tesla MRI (Avanto; Siemens Medical Solutions, Erlangan, Germany) with an MRI-compatible head-frame and an MRI surface-coil (MR Instruments Inc, Minnetonka, MN). Prior to the infusion, high-resolution anatomical MPRAGE and DTI images were acquired. The MPRAGE was used to visualize the anatomy and the DTI was used for the simulation. The MPRAGE was acquired with an in-plane spatial resolution of 0.7 mm and a slice thickness of 1 mm at TE 3.76 ms, TR 2170 ms and flip of 15°. The DTI was a 14 min echo-planar spin echo (EPSE) acquired with 6 directions at a b-value of 750, 1 shot, a bandwidth of 1502 Hz/px, a TE of 110ms, a TR of 7300 ms, 16 repetitions, a 1.4 mm in-plane resolution and slices 1.8 mm thick. The field of view on all acquisitions was 180 mm. DTI datasets were corrected for eddy currents and fused to the undistorted MPRAGE images by an affine transformation including translation, rotation, dilatation and shear correction (iPlan^® Flow). Apparent Diffusion Coefficient (ADC, Figure 1B) and Fractional Anisotropy (FA, Figure 1C) were evaluated on a pixel-by-pixel basis (iPlan^® Flow).

Figure 1. Sample MRI dataset and analysis.

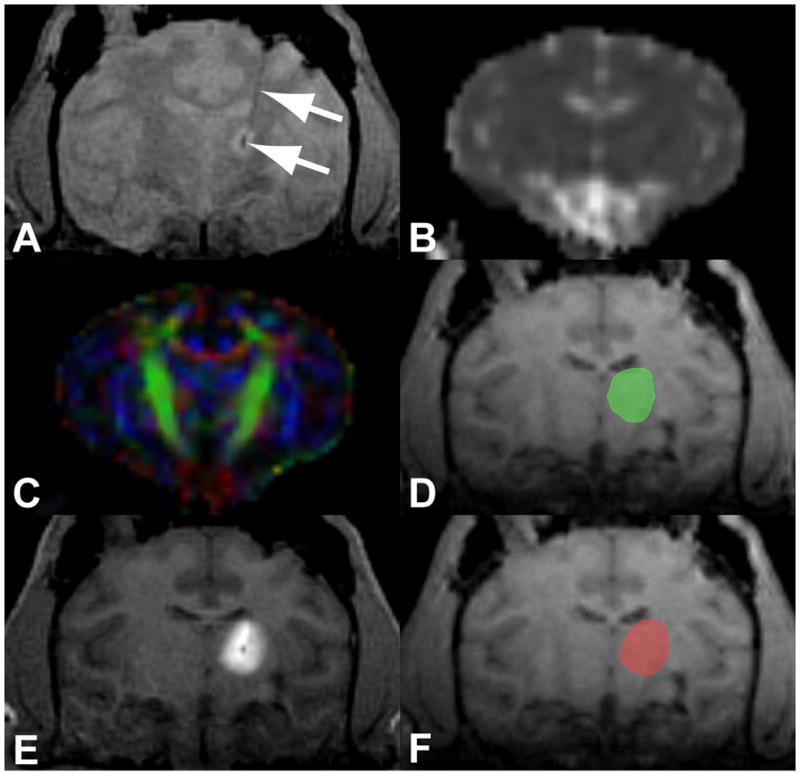
(A) Proton-density weighted FLASH image used to segment the cannula trajectory and cannula tip (arrows). (B) ADC and (C) FA map calculated from the DTI image. (D) Simulated volume of distribution from A, B and C displayed on the MPRAGE. (E) T1-weighted FLASH image used to measure the gadolinium volume of distribution. (F) Measured volume of gadolinium distribution from E displayed on the MPRAGE.

After the start of the infusion, repeated T1-weighted image volumes were acquired every 5 minutes to visualize the distribution of gadolinium (Figure 1E). The sequence was a fast low angle shot (FLASH) scan acquired with TE 4.49 ms, TR 17 ms, flip 40°, 2 repetitions, 0.7 mm in-plane resolution, 180 mm field of view and 1 mm slices. The infusate appeared bright on these scans due to the T1-shortening effects of the gadolinium. One iteration of the scan was acquired prior to the appearance of infusate with a low flip angle of 4° to achieve proton-density weighting for visualization of the cannula tip position and trajectory (Figure 1A).

2.2. Algorithm for simulating infusate distribution

The algorithm for simulating the infusate distribution has been previously described (Raghavan, Brady et al. 2006; Raghavan, Mikaelian et al. 2010) and is summarized only briefly here to highlight the modifications made to adapt the existing implementation for this validation and upcoming trials.

The distribution of infusate was calculated in four sequential steps described below. First, the boundary values for pressure and concentration along the cannula were estimated from a calculation of the backflow. Second, these values were used to estimate the three-dimensional (3D) pressure field around the cannula. Third, the Darcy flux was used to calculate the distribution of infusate into the tissue for this pressure field. Fourth, a threshold was used to segment the simulated region of infusion.

Baseline values for the hydraulic conductivity tensor (K) and the pore fraction (ϕ) were set to 1.7e⁻⁸ cm⁴/dyn s and 0.2 (Morrison, Chen et al. 1999). The DTI image was used to scale K and ϕ and to estimate the diffusion tensor of molecules in the interstitial fluid (D_e) from the water self-diffusion coefficient (Basser, Mattiello et al. 1994) with cross-property relations (Torquato 2000).

2.2.1. Backflow calculation

The backflow calculation was based on the work of (Morrison, Chen et al. 1999) with modifications to account for the step in the cannula dimension. Backflow was modeled as the growth of a fluid-filled region around the cannula, referred to as the annulus. The annulus was assumed to start at the cannula tip and to progress along the cannula in the distal direction during the infusion.

Backflow was calculated in one-dimension with the assumption that the annulus was rotationally symmetric around the axis of the cannula. The backflow equation was solved by a set of differential equations describing the growth of the annulus, the flow of fluid in the annulus and the loss of fluid into the surrounding tissue. This system of differential equations was solved numerically by discretizing it along the cannula track and iteratively minimizing the error in a finite differences scheme.

The Stokes equation was used to find the fluid velocity in the annulus:

$$0=-\frac{\partial p(z)}{\partial z}+\mu \cdot \frac{{\partial }^2{u}_z}{\partial r^2}$$ Equation 1

where z is the direction along the cannula, r is the radial distance from the cannula, p(z) is the hydrostatic pressure along the cannula, μ is the viscosity of the infusate and u_z is component of the fluid velocity along the cannula. The Stokes equation reasonably describes CED since the inertial flow is small compared to the viscous flow at the flow rates typically employed in CED and the fluid is incompressible.

The volumetric flow was obtained by integrating u_z over the thickness h(z) of the annulus:

$$Q(z)=\int u_{z}dz$$ Equation 2

The loss of fluid into the surrounding tissue was described by Darcy’s law:

$$Q(z)=-\phi \kappa \frac{\partial p(z)}{\partial r}$$ Equation 3

where φ is the tissue pore fraction and κ is the hydraulic conductivity. Darcy’s law describes the flow of fluid through a porous medium like the brain.

Finally, the growth in the thickness of the annulus h(z) was described through a derivation of Hooks’s law developed by (Morrison, Chen et al. 1999) for an elastic, cylindrical deformation of tissue:

$$p(z)=\left(\frac{2G}{r_c}\right)\cdot h(z)$$ Equation 4

where G is the shear modulus. The shear modulus G was increased from 10⁵ dyne/cm² proximal to the step (Morrison, Chen et al. 1999) to 10⁹ dyne/cm² distal to the step to simulate the effect of the step. This implementation attributes the restriction of initial backflow along the cannula observed experimentally (Krauze, Saito et al. 2005) to the compression of tissue distal to the step. This compression would effectively increase the local shear modulus because it is more difficult to compress the tissue further.

2.2.2. Infusate distribution calculation

The boundary conditions calculated above were used to estimate the pressure field by assuming that the pressure reaches its steady state value everywhere in a short time compared to the total infusion time. The continuity equation for the drug assumes it can either leak into the capillaries or accumulate and increase interstitial pressure:

$$\nabla \cdot \overrightarrow{v}(x)=\frac{L_{P}S}{V}$$ Equation 5

where L_p is the hydraulic conductivity of the capillary walls and S/V is the capillary area per unit of tissue volume. Combining the continuity equation with Darcy’s law:

$$\overrightarrow{v}=-K\cdot \nabla p$$ Equation 6

produces the following differential equation for the pressure:

$$\nabla \cdot [K(\overrightarrow{x})\cdot \nabla p]=\frac{L_{P}S}{V}\cdot p$$ Equation 7

The Feynman-Kac formalism was used to turn this equation into a stochastic PDE that was then solved with a random walk scheme (Friedman 1976; Freidlin 1985). A step size of 1.5 mm with 5000 particles was experimentally found to provide a suitable tradeoff between accuracy and computing time.

The Darcy flux calculated from the pressure field (Equation 6) was used to estimate the concentration profile:

$$\frac{\partial (\phi c)}{\partial t}=-\nabla \cdot (\overrightarrow{v}c)+\nabla \cdot (\phi D\cdot \nabla c)-kc$$ Equation 8

where c is the concentration of the drug in interstitial space, D is the diffusion tensor and k is the loss rate describing the losses due to leakage or metabolic processes. The solution of this equation was again computed by a random walk at a step size of 1.5 mm with 5000 particles.

Finally, the gadolinium concentration field was thresholded at 0.006 mM. This threshold was identified by comparing the gadolinium distribution in the MRI to the simulation distribution profile in two training data sets.

2.3. Generation of Simulated and Gadolinium Volumes

A reviewer used the proton-density weighted FLASH image to identify the cannula tip location and trajectory (Figure 1A). When the tip was not clearly defined, the reviewer used the first observation of infusate in the T1-weighted FLASH image series.

The tip location and trajectory were passed to a second reviewer who used the average infusion rate and total infusion time to run the simulation described in Section 2.2. The average infusion rate was calculated by dividing the final infusion volume by the total infusion time. The resulting predicted distribution was referred to as the “simulated volume” (S) (Figure 1D, green volume).

A third reviewer segmented the enhancing region on the T1-weighted FLASH images with a standard semi-automated segmentation technique (iPlan^® Smartbrush). This region was referred to as the “gadolinium volume” (G) (Figure 1F, red volume).

This workflow ensured that the reviewer identifying cannula location or running the simulations was blinded to the T1-weighted images of the gadolinium distribution and the reviewer segmenting the gadolinium distribution was blinded to the cannula tip image or simulation results.

A fourth reviewer repeated a blinded gadolinium segmentation of the T1-weighted FLASH images to evaluate the inter-operator variability.

2.4. Comparison of Simulated and Gadolinium Volumes

Students’ t-test was used to compare simulated and gadolinium volumes. A p value of 0.05 or less was considered significant. The volumes were normalized by calculating the Vd/Vi ratio of the final volume of distribution (Vd) to the volume of infusion (Vi) (Krauze, McKnight et al. 2005). Inter-operator variability was reported through Pearson’s correlation coefficient.

The shape and overlap of the simulated and gadolinium volumes were quantitatively compared in Matlab (Mathworks, Natick MA). Coverage and leakage were used to measure the spatial overlap of the volumes. Coverage was defined as the percentage of the simulated volume that was found experimentally to have received gadolinium (Figure 2C). Leakage was defined as the percentage of gadolinium that was found experimentally to be outside the simulated volume (Figure 2D). A simulation was defined as being “clinically useful” if it produced greater than 50% coverage and less than 50% leakage. Mathematically, coverage and leakage were described by set theory as:

$$\mathit{Coverage}=\frac{\text{S}\cap \text{G}}{S},\mathit{Leakage}=\frac{\text{G}-\text{S}}{G}$$ Equation 9

Figure 2. Geometric parameters used to characterize the shape and location of the (A) gadolinium volume and (B) simulated volume.

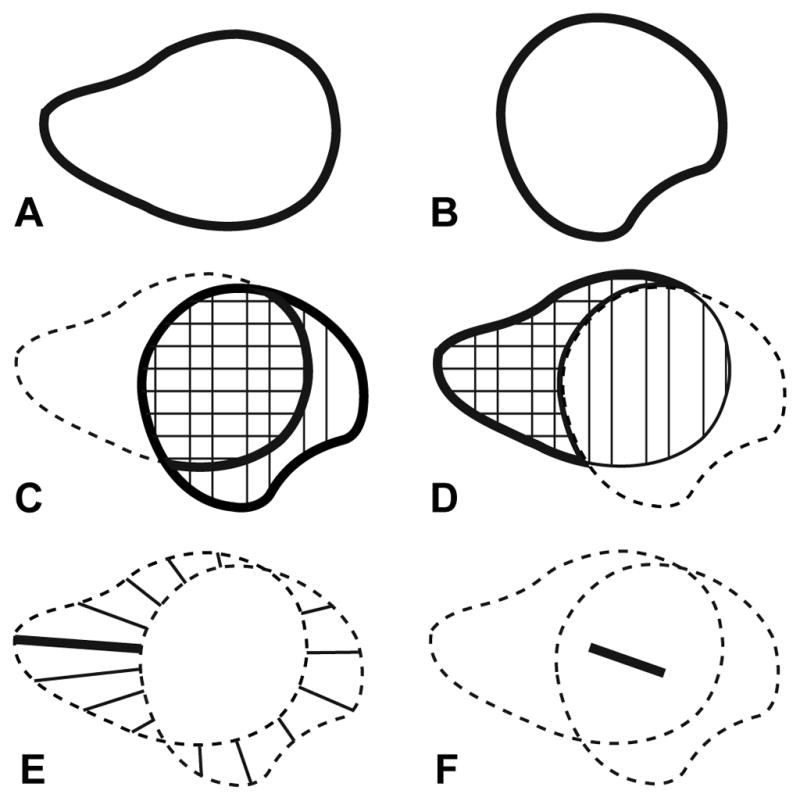
(C) Coverage was defined as the percentage of the simulated volume (vertical hatch) covered by the gadolinium (cross-hatch). (D) Leakage was defined as the percentage of the gadolinium volume (vertical hatch) that was outside the simulated volume (cross-hatch). (E) The mean and maximum edge distances were measured between the outer edges and the overlap of the gadolinium and simulated volumes. (F) The centroid shift was defined as the distance between the centroids of the gadolinium and simulated volumes.

The mean and maximum distances between the simulated and gadolinium volumes were evaluated to characterize the shape differences (Figure 2E). Edge distance (ED) was measured as the Euclidean distance from the edge of each volume to the intersection of the two volumes:

$$ED(x,y,z)=\sqrt{{(x-x_{\text{S}\cup \text{G}})}^2{(y-y_{\text{S}\cup \text{G}})}^2{(z-z_{\text{S}\cup \text{G}})}^2}$$ Equation 10

The centroid shift (CS) between the simulated and gadolinium volumes was calculated to measure the net displacement of the two volumes (Figure 2F):

$$CS=\frac{\sqrt{{(\sum x_{\mathit{Gad}}G-\sum x_{\mathit{Sim}}S)}^2+{(\sum y_{\mathit{Gad}}G-\sum y_{\mathit{Sim}}S)}^2{(\sum z_{\mathit{Gad}}G-\sum z_{\mathit{Sim}}S)}^2}}{\sum \text{S}\cup \text{G}}$$ Equation 11

To emulate the clinical use of the software for predicting coverage of a desired target, the simulated and gadolinium coverage of the target structures was also measured. As in Equation 9, coverage was defined as the ratio between the overlap of the simulated (or gadolinium) volume and the volume of the putamen, thalamus or caudate. The putamen, thalamus and caudate were auto-segmented in the software by a custom-built registration atlas for rhesus macaques.

3. Results

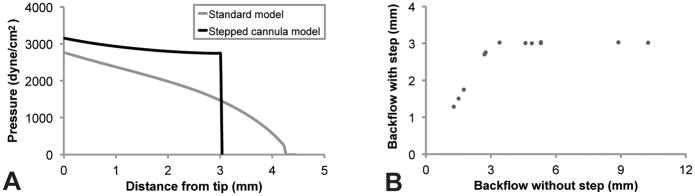
The backflow simulation adequately restricted the backflow to the step. At the step, the pressure profile dropped abruptly due to the restriction caused by the increased shear modulus (Figure 3A). As a result, backflows smaller than the step-length of 3 mm were unaffected by the modifications to the simulation, whereas larger backflows were restricted to the 3 mm step (Figure 3B). The pressure profile shown in Figure 3A demonstrates a typical flow rate of 2.5 μL/min. It shows that the stepped model slightly increased the pressure at the cannula tip relative to the un-stepped model. This behavior was physically reasonable and further validated the model.

Figure 3. Performance of the stepped cannula model.

The model effectively restricted backflow to the 3 mm step length. (A) Comparison of the original backflow model (grey) to the stepped model (black) in a simulation with a typical flow rate of 2.5 μL/min. Without the step model, the backflow would have passed the step, contrary to experimental evidence. (B) All simulations found to have backflow larger than 3 mm in the original backflow model were restricted to 3 mm by increasing the effective shear modulus at the step.

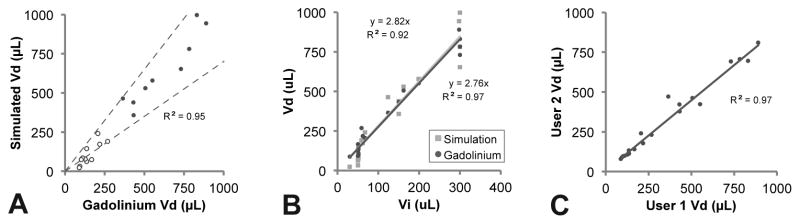
As shown in Figure 4 and Figure 5, there was good agreement between the simulated and gadolinium volumes. There was a strong linear relationship (R² = 0.95) between the volumes (Figure 4A). Both the simulated and gadolinium volumes scaled linearly with the infusion volume (R² > 0.90) with Vd/Vi slopes of approximately 2.8 (Figure 4B).

Figure 4. Comparison between the simulated and gadolinium distribution volumes.

(A) There was strong correlation between the volumes. The dotted lines are drawn at ±30% and open dots show the very small infusion volumes <100 μL. (B) Both the simulated and measured volumes scaled linearly with the infusion volume. (C) There was low variability between the two reviewers segmenting the gadolinium volumes.

Figure 5. Screenshots of the simulation software.

(A) Thalamus infusion of 298 μL with 80% coverage and 17% leakage. (B) Putamen infusion of 51 μL with 56% coverage and 43% leakage. (Top) 3D-cutaway and 3-plane views with an overlay of the simulated (green) and gadolinium (red) distribution volumes. (Bottom) Higher magnification views of the overlay.

Both the gadolinium segmentation and simulation were robust and showed low variability. The inter-operator variability for repeat gadolinium segmentations was low with a Coeffiecient of Variance (CoV) of only 13% (Figure 4C) as was the variability for 10 repeat simulations of a sample data set (CoV 7%).

Figure 5 shows sample screen captures of the software. The thalamic example was a 298 μL infusion performed over 86 min. The simulation produced a volume (944 μL) similar to the measured gadolinium volume (890 μL) with excellent spatial overlap (93% coverage, 20% leakage). The putaminal example was a 51 μL infusion performed over 29 min that barely met the criteria for clinical usability (56% coverage, 43% leakage).

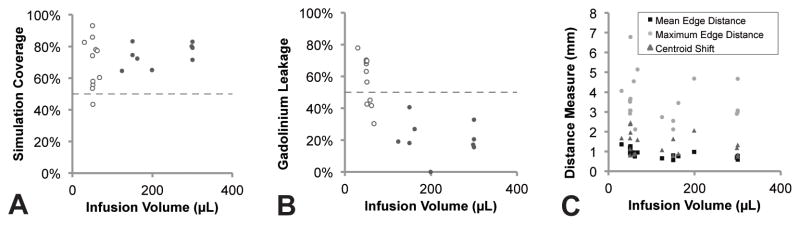
Figure 6 and Table 1 characterize the spatial overlap of the simulated and gadolinium distribution volumes. Overall, 72 ± 13% of the simulated volume was found experimentally to have been infused with gadolinium (Figure 6A) and 41 ± 23% of the infused gadolinium was found outside the simulated volume (Figure 6B). The distances between the volumes were on the order of the MRI pixel resolution (Figure 6C).

Figure 6. Spatial overlap of the simulated and gadolinium distribution volumes.

(A) The simulation coverage was consistently over 50%. (B) The leakage of gadolinium outside the simulated volume was significantly higher for infusion volumes smaller than 100 μL (open dots) than infusion volumes larger than 100 μL (56% vs. 21%, p<0.05). (C) The distance measures did not scale with infusion volume.

Table 1.

Parameter	All Infusions	Infusions >100 μl	Infusions <100 μl	p value*
Coverage	72 ± 13 %	75 ± 7%	69 ± 16%	0.31
Leakage	41 ± 23 %	21 ± 11%	58 ± 15%	<0.05
Mean edge distance	0.91 ± 0.23 mm	0.73 ± 0.12 mm	1.06 ± 0.19 mm	<0.05
Maximum edge distance	3.60 ± 1.13 mm	3.24 ± 0.89 mm	3.86 ± 1.27 mm	0.22
Mean centroid shift	1.41 ± 0.59 mm	1.17 ± 0.44 mm	1.62 ± 0.63 mm	0.08
Ratio of volumes**	0.84 ± 0.29	1.04 ± 0.14	0.69 ± 0.28	<0.05
Ratio of target coverage**	0.75 ± 0.34	1.00 ± 0.21	0.55 ± 0.30	<0.05

^*Significance of the difference between infusions >100 μL and <100 μL (Students’ t-test)

^**Ratio of simulated to gadolinium parameters

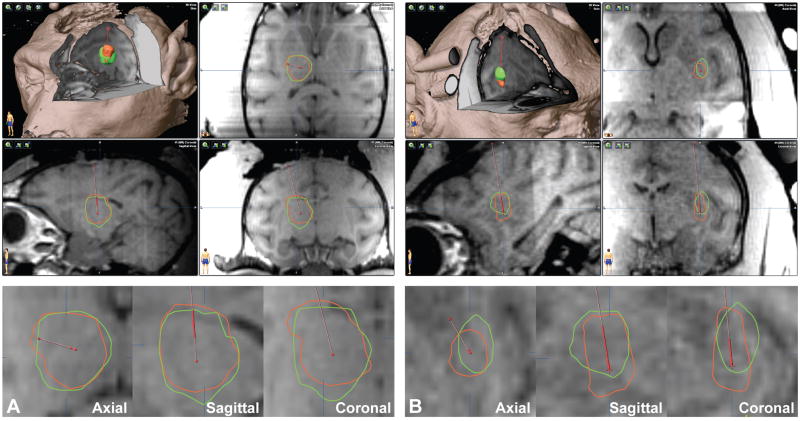
Figure 7 shows representative examples of infusions in the caudate, putamen and thalamus. There was strong agreement between the simulated and gadolinium coverage of the target structures (R² = 0.90).

Figure 7. Coverage of the target structure.

A through C show the target (yellow), simulated (green) and gadolinium (red) volumes in infusions in the (A) caudate, (B) putamen) and (C) thalamus. The MRI images are the T1-weighted FLASH images showing the distribution of gadolinium. (D) There was strong agreement between the simulated and gadolinium coverage of the target structure. The dotted lines are drawn at ±30% and open dots show the very small infusion volumes <100 μL.

It was obvious from the plots that the smallest infusion volumes produced the most erroneous simulations. The simulation often underestimated the volume (Figure 4A and B) and target coverage (Figure 7D) in very small infusions, which consistently also had high leakage (Figure 6B). All infusions over 100 μL met the criteria for clinical usability, while only 4 of the 11 infusions smaller than 100 μL did so. The remaining 7 had leakage over 50% and one additionally had coverage below 50%. All clinically useful simulations had Vd/Vi ratios greater than 2.5 and all non-clinically useful simulations had Vd/Vi ratios greater than 2.5, reflecting the underestimation of the small distribution volumes.

Table 1 presents a subgroup analysis of infusion volumes larger or smaller than 100 μl. The significantly higher leakage in the small volumes (56% vs. 21%) was attributable to the fact that the simulation significantly underestimated the gadolinium volume by 31% in small infusions. Similarly, the simulation underestimated the target coverage by 45% in the small volumes. In the large volumes, the simulation accurately predicted the distribution volume and target coverage within 5% of the gadolinium volume. The small infusions were shown as open dots in Figure 4A, Figure 6A, Figure 6B and Figure 7D.

4. Discussion

4.1. Clinical Utility

This study showed that the simulation adequately predicted the measured gadolinium distribution volume. It produced clinically useful estimations of the coverage and leakage, particularly for the large infusions (>100 μl) comparable in size to the infusions planned for upcoming clinical trials. To put these numbers in perspective, the average coverage of 72% by volume means that the diameter of a spherical distribution only varies by about 10%. For infusions of 300 μL as proposed in upcoming human gene therapy trials with putaminal infusions (Richardson, Kells et al. 2011), this corresponds to a shift of only 0.5 mm or about one typical MRI pixel.

Incorporating this surgical planning algorithm into both preclinical large animal studies and clinical trials will improve the effectiveness, reproducibility and ease-of-use of CED. Accurate prediction of the shape of the infusion is critical to achieving robust coverage of the target structure. The failures of numerous previous trials (Lang, Gill et al. 2006; Salvatore, Ai et al. 2006; Marks and Stacy 2009; Sampson, Archer et al. 2009) have been attributed to ineffective target coverage, reducing efficacy of the therapy and causing significant off-target exposure. The algorithm and results of this study are directly applicable to upcoming clinical trials targeting the striatum for CED including GDNF protein, AAV2-GDNF and AAV2-AADC. Similar to this study, these trials will target cytoarchitecturally homogeneous deep gray matter structures.

Applying the simulation from this study to CED protocols with significantly different infusion parameters, target structures and imaging agents may require modifications to the algorithm. For example, the Gadolinium threshold may need to be adjusted for studies with different flow rates or infusion volumes due to efflux and diffusion of the tracer. Alternatively, infusions into white matter or heterogeneous brain tumors might require higher spatial resolution of the DTI or a denser grid for the random walk scheme to incorporate smaller anatomical features. Previous research has demonstrated the decline in the Vd/Vi ratio at ependymal and pial surfaces due to ventricular or cisternal fluid loss (Jagannathan, Walbridge et al. 2008). Measuring these surfaces in the anatomical images and incorporating them in the simulation may enhance the performance of this DTI-based algorithm.

Further, this study only investigated infusions in relatively homogeneous striatal tissue. Disease conditions such as edematous brain tumors or ischemia could dramatically affect flow of infusate in the extracellular space (Equation 3). This algorithm used the fluid diffusivity to scale literature values for the porosity and hydraulic conductivity as described in the Methods, however its ability to simulate dramatic changes due to disease pathology was not evaluated.

Similarly, studies using an imaging agent other than 1 mM Gd-DTPA may require modifications of the algorithm. However, numerous publications have shown that the distributions of both the drug and imaging agent achieved by CED closely match the distribution of the carrier fluid (Saito, Krauze et al. 2005; Fiandaca, Varenika et al. 2009; Su, Kells et al. 2010; Richardson, Kells et al. 2011). We believe these particles of very different sizes achieve the same distribution because both are carried by the bulk flow of infusate through the tissue. The most relevant clinical information is whether the algorithm accurately predicts the therapeutic distribution. The imaging agent itself is only relevant as a surrogate marker for the therapeutic that enables in-vivo, real time monitoring of the distribution.

Ultimately, the algorithm should be adjusted for the specific parameters of each trial and confirmed in a prospective experimental manner. The careful blinding in this retrospective study was designed to replicate the workflow of a prospective study by providing the user with only information about the cannula location and infusion parameters. However, future studies should prospectively validate how well a patient’s final drug distribution matches the plan from the pre-surgical baseline images by integrating the algorithm with a stereotactic cannula placement system.

4.2. Sources of error

Although the simulation software accurately predicted distribution in most infusion volumes, it did underestimate the distribution volume for very small infusions (<100 μL). These errors may be attributable to the MRI resolution or steady state assumption.

A major challenge for this study was the accuracy of the gadolinium detection. Because the image resolution was large compared to the diameter of the infusion volume, even small shifts had drastic effects on the geometric overlap of the volumes. In most cases the edge distances between the volumes were comparable to the in-plane resolution of the MRI. Further, the smaller size of primate brains relative to human brains provided relatively higher distortion and larger voxel sizes in the DTI. Since the hydraulic conductivity is estimated from DTI data, the quality of the simulation is heavily dependent on the quality of the DTI. The DTI may have also biased the simulation in the z-direction since it was acquired with non-isotropic voxels. In the future, it would be preferable to acquire all scans isotropically.

The underestimation of very small infusion volumes may further be attributable to the assumption that a steady state of pressure is reached in a short time compared to the infusion duration. Depending on the choice of parameters (Basser 1992) the consolidation time until steady state is reached can be several minutes (5 min 35 seconds in example from Figure 3A). During this period the infusate flux is higher, explaining the underestimation of the distribution volume. The relatively worse concordance in the shorter infusions is a logical consequence of this effect. The consolidation period could be addressed by a time dependent pressure calculation, however this would pose formidable implementation challenges.

Another challenge for this study was that the agreement between the simulated and gadolinium volumes was similar to the interoperator variability, suggesting that the reported accuracy reached the detection limit of our system. At this limit, it was impossible to ascertain whether the observed variability came from errors in the simulation software or errors in the gadolinium segmentation. It is reasonable to assume that acquiring data at higher field strengths or in humans would improve the relative spatial resolution and hence improve the accuracy of the simulation. Use of an automated segmentation algorithm would further alleviate user bias in the gadolinium segmentation.

4.3. Towards a comprehensive CED platform

This software fills a critical step in delivering a comprehensive technology platform for achieving reliable direct brain infusions in the clinic. The ultimate goal is to achieve the same drug distribution in the clinic as planned on the patient’s pre-surgical baseline MRI.

Achieving this goal requires accuracy of the surgical planning, accuracy of the cannula placement and accurate MRI monitoring of the drug distribution. This study addresses the first requirement. Complementary developments discussed below converge with this work to produce a complete package for direct brain drug delivery.

The recent development of MRI-guided stereotactic systems addresses the requirement for accurate cannula placement. These systems have shown impressive accuracy and integrate seamlessly into clinical workflows that sequentially acquire a baseline MRI, place the cannula and use MRI for monitoring the infusion. For example, we recently published a validation of an MRI-guided system (Clearpoint®; MRI Interventions, Irvine, CA) with 0.8 mm accuracy (Richardson, Kells et al. 2011) that subsequently received FDA approval.

Numerous studies have addressed the requirement that MRI accurately depict the distribution of drugs delivered by CED. These studies include our recent publications comparing the distribution of liposomal CPT11 infusions seen on MRI to fluorescence (Dickinson, LeCouteur et al. 2008) and comparing the distribution of gadolinium tracer visualized by MRI to subsequent immunohistochemical analysis of viral vector transduction (Fiandaca, Varenika et al. 2008; Richardson, Varenika et al. 2009).

Ultimately, achieving reproducible and effective CED will require thoughtful integration of these software, hardware and medical imaging technologies. The next critical study is to evaluate the clinical reproducibility of the entire integrated infusion system in a prospective study.

5. Conclusions

This study demonstrated the algorithm’s ability to predict the infusate distribution from a known cannula tip position. Accurate prediction is critical to allow a physician to plan optimal cannulae positioning on a patient-by-patient basis. The next step will be to incorporate a stereotactic navigation system and evaluate the ability to predict the infusate distribution prior to cannula placement.

Research Highlights.

• Analysis of a DTI-based simulation algorithm for direct drug delivery to the brain.

• Adaptation of the algorithm for stepped infusion cannulae.

• Validation by intra-operative MRI of gadolinium infusions in non-human primates.

• Shows strong similarity between simulated and experimental infusions.

• Clinical relevance for upcoming convection-enhanced delivery (CED) trials.