Metabolic networks evolve towards states of maximum entropy production

Abstract

A metabolic network can be described by a set of elementary modes or pathways representing discrete metabolic states that support cell function. We have recently shown that in the most likely metabolic state the usage probability of individual elementary modes is distributed according to the Boltzmann distribution law while complying with the principle of maximum entropy production. To demonstrate that a metabolic network evolves towards such state we have carried out adaptive evolution experiments with Thermoanaerobacterium saccharolyticum operating with a reduced metabolic functionality based on a reduced set of elementary modes. In such reduced metabolic network metabolic fluxes can be conveniently computed from the measured metabolite secretion pattern. Over a time span of 300 generations the specific growth rate of the strain continuously increased together with a continuous increase in the rate of entropy production. We show that the rate of entropy production asymptotically approaches the maximum entropy production rate predicted from the state when the usage probability of individual elementary modes is distributed according to the Boltzmann distribution. Therefore, the outcome of evolution of a complex biological system can be predicted in highly quantitative terms using basic statistical mechanical principles.

Introduction

Mutations and genetic rearrangements enable an organism to adapt to environmental conditions. A cell with optimal performance is expected to emerge from an evolutionary process in which fittest cells are selected by the given cell environment (Ibarra et al., 2002; Fong et al., 2003; Teusink et al., 2009). The optimality of a cell is achieved through a redistribution of the flux pattern through the metabolic network by adjusting the expression pattern of catalytic and regulatory proteins. A fundamental question in evolution is how the flux distribution of a cell changes in response to selection conditions imposed by the environment. Understanding the evolutionary optimization of cell metabolism requires knowledge of the steady-state metabolic flux distribution. Such knowledge can be obtained through Elementary Mode Analysis (EMA) which decomposes the overall metabolism of a cell into a set of unique, indivisible pathway fluxes called elementary modes (Pfeiffer et al., 1999; Schuster et al., 2000). These pathway fluxes operate based on minimal sets of enzymes and are considered the fundamental components determining cell physiology. The functioning metabolism can be expressed as a weighted, linear combination of elementary modes. Thus, analysis of elementary modes permits a quantitative evaluation of the structure, capability and robustness of cell metabolism (Carlson and Srienc, 2004; Papin et al., 2002; Stelling et al., 2002; Trinh et al., 2008; Unrean et al., 2010). A steady-state flux distribution corresponding to the state of cellular metabolism can be reconstructed using a combination of elementary modes and their usage probabilities (Srienc and Unrean, 2009; Wlaschin et al., 2006). A cell’s metabolism is expected to adapt to a given condition by varying the probabilities of these elementary modes to result in optimal fitness.

We previously developed a theoretical framework (Srienc and Unrean, 2009)to describe the cell metabolism according to the principle of maximum entropy production (Martyushev and Seleznev, 2006). Identical theoretical results can be obtained on the basis of statistical thermodynamics when the set of elementary modes operating at steady state conditions is viewed as a canonical ensemble of metabolic states analogous to an ensemble of quantum states of a macroscopic system (for a detailed derivation see supplementary file). The theory suggests that the cell metabolism operates at the most likely distribution of usage probabilities of elementary modes when entropy production is distributed according to the principle of ‘fair apportionment of outcomes’ in which the usage probabilities of individual elementary modes are distributed according to the Boltzmann distribution law. We therefore hypothesize that evolving cells would spontaneously redistribute their pathway fluxes by optimizing the usage probabilities to reach the state where the total rate of entropy formation of the cell is maximized. In such state, which represents the fully evolved metabolism, the occupation number (usage probability) of the entropy contribution of individual elementary modes is distributed according to the Boltzmann distribution law analogous to the distribution of discrete energy states in a physical system. Thus, the redistribution of the rate of entropy production represents a critical objective in the evolution of metabolic pathways supporting cell function.

We validate here the theoretical predictions by analyzing the changes in metabolic flux distributions of the metabolism of Thermoanaerobacterium saccharolyticum during adaptive evolution in a serial dilution experiment in which the cell culture has been maintained at exponential growth conditions for extended numbers of generations. We show that the evolving mutant of T. saccharolyticum adjusts the metabolic flux distribution during adaptive evolution in a direction of increasing rate of entropy production supporting the previously proposed assertion that a metabolic network naturally evolves by redistributing its fluxes to maximize the rate of total entropy production.

Materials and Methods

Bacterial strains and plasmids

A knockout mutant of T. saccharolyticum was constructed by homologous recombination with a non-replicative knockout plasmid (Desai et al., 2004). The knockout plasmid which contained upstream and downstream homology regions of targeted gene and the kanamycin marker inserted between the homologous regions was made by in vivo recombination in S. cerevisiae (Shanks et al., 2006). A T. saccharolyticum host cell was transformed with the plasmid which integrated into the genome at the regions upstream and downstream of the target gene. The knockout cell with the target gene being replaced by the resistance marker was selected on kanamycin. The marker in the knockout was later removed by transforming the cell with the two homologous flanking regions upstream and downstream of the target gene without selection marker. Markerless gene deletion was confirmed by PCR and gel electrophoresis (Trinh et al., 2006).

Metabolic evolution

Evolution experiments were conducted in anaerobic shake tubes containing MTC medium and 20 g/l of glucose. The evolution was carried out in an extended exponential growth experiment accomplished through serial dilution where the seed culture was started from frozen stock. The culture was allowed to grow exponentially to an OD₆₀₀ of 0.8–1.0 before being transferred to fresh medium using a 40 fold dilution. At each dilution step, cell growth was monitored via optical density measurement. Two to three serial dilutions were performed every day. Serial dilution was continued for 68 culture transfers.

Growth in bioreactors

Batch growth kinetics was measured in a 2l Braun bioreactor (Biostat MD, B. Braun Biotech International, Melsungen, Germany) with a working volume of 1l. The temperature was kept at 55°C and pH was controlled at 6.0 using N₂-flushed 6M NaOH (Sigma, St. Louis, MO). Agitation speed was set at 100 rpm. The fermentor was made anaerobic by sparging with nitrogen for 6 hours or until the culture medium became colorless. The fermentation contained MTC medium (10 g/l yeast extract, 5 g/l tryptone, 2 g/l C₆H₅O₇K₃·H₂O, 1.25 g/l C₆H₈O₇·H₂O, 1 g/l Na₂SO₄, 1 g/l KH₂PO₄, 2.5 g/l NaHCO₃, 5 g/l CH₄N₂O, 1 g/l MgCl₂·6H₂O, 0.2 g/l CaCl₂·2H₂O, 0.1 g/l FeCl₂·4H₂O, 1 g/l cysteine-HCl, 1 mg/l resasurin) supplemented with 20 g/l sugar. The cell inoculum was an overnight culture grown in the same medium. The batch bioreactor was inoculated with seed culture at initial OD_600nm of approximately 0.1. The culture samples and supernatants were periodically collected for analysis.

Analytical techniques

Cell concentration was monitored via optical density at a wavelength of 600 nm in a 1 cm cuvette using a Hewlett Packard 8453 Diode Array spectrophotometer (Palo Alto, CA). Metabolite concentrations including glucose and other secreted byproducts were determined using a HPLC system (Shimadz10A, Shimadzu, Columbia, MD) equipped with an autosampler (SIL-10AF), a cation exchange column (HPX-87H, Biorad Labs, Hercules, CA) and a UV–vis detector (SPD-10A) and a refractive index detector (RID-10A) in series. The column was run in an isocratic mode at 65°C at a flow rate of 0.5 ml/min with 5 mM H₂SO₄ as the mobile phase. A calibration curve correlating peak area to concentration of metabolites was used to determine the quantity of metabolites in the sample.

Elementary Mode Analysis

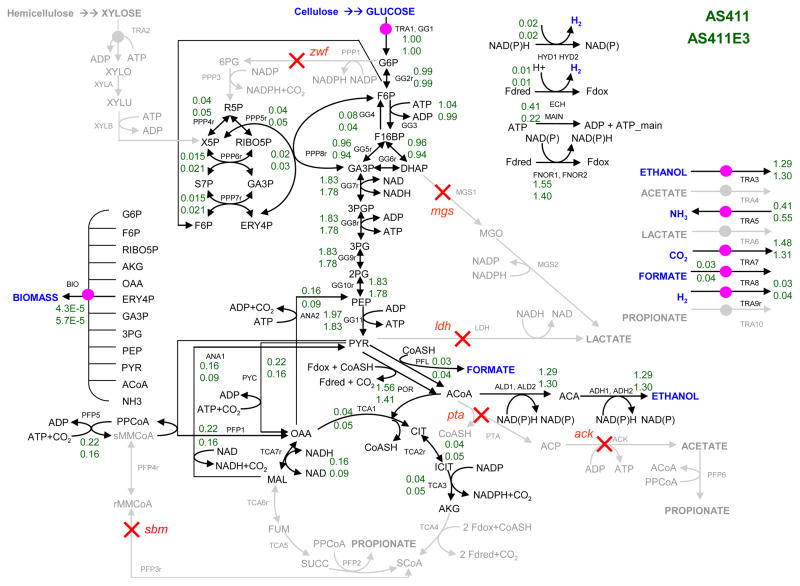
A T. saccharolyticum metabolic network was constructed as shown in Fig. 1. The model was based on utilizing glucose or xylose as the carbon source. Cell growth in the metabolic network is described through the production of biomass with a composition as previously determined experimentally for thermophilic bacteria (Tang et al., 2009). The biomass composition determines then the connection with the precursors in the central metabolism (Carlson and Srienc, 2004). Elementary mode analysis has been carried out using METATOOL software version 5.0 (von Kamp and Schuster, 2006).

Figure 1.

Metabolic map of Thermoanaerobacterium saccharolyticum central metabolism. The suggested targets gene deletions (indicated by the symbol X) in the designed strain AS411 are PPP1 (zwf), MGS1 (mgs), LDH (ldh), PFP3r (sbm), and PTA and ACK (pta-ack). The sbm gene is assumed inactive in AS411 based on experimental measurements of fermentation products. Metabolic fluxes in AS411 (Top) and in AS411E3 (Bottom) are listed next to reactions. The fluxes are determined from the sum of the products of the probabilities and the fluxes of the 4 families shown in Table 1. All metabolic fluxes are normalized to the uptake rate of glucose. The zero fluxes are shown in grey.

Non-equilibrium Thermodynamics of open systems

Consider an open system such as a CSTR with constant volume V and operating at constant temperature T and pressure p. The entering and outflowing material streams contain i components. The variables associated with the incoming stream are marked with the suffix ‘in’. The outgoing stream is of the composition of the system since it is well mixed and homogeneous. Heat can be exchanged through the surface of the system. To simplify the balances we assume that the entering stream has the same temperature as the system. In this system cell growth occurs, and the incoming stream contains all the required nutrients and the outgoing stream contains unreacted nutrients, cells and secreted products.

Material Balance

The material balance for such open system can be written for each component as follows

$$\frac{{dn}_i}{dt}=({\stackrel{.}{n}}_{i,in}-{\stackrel{.}{n}}_i)+{V\nu }_i\stackrel{.}{\xi }$$ (1)

where ṅ_i are the molar flow rates of each component i, ξ̇ (moles/l sec) is the extent of reaction and ν_i is the stoichiometry coefficient of each component as it appears in the growth equation, and V is the reactor volume. Note that cells or biomass represent one of the components in the system. They contain many metabolites that never cross the cell membrane. These do not have to be explicitely accounted for since they are included in the biomass. Only nutrients that are taken up by cells and products that are secreted by the cells have to be considered in the balance to completely describe the system. This makes for a convenient simplification since much of the complexity of the metabolism disappears as it is contained within the cells.

Energy Balance

To obtain an expression for the enthalpy of reaction we can multiply Equ. (1) with the molar component enthalpies h_i and obtain for steady state conditions the expression

$$0=h_i({\stackrel{.}{n}}_{i,in}-{\stackrel{.}{n}}_i)+V\stackrel{.}{\xi }{\nu }_i{h}_i$$ (2)

If we sum up all component balance equations we obtain

$$0=\sum _i{h}_i({\stackrel{.}{n}}_{i,in}-{\stackrel{.}{n}}_i)+V\stackrel{.}{\xi }\sum _i{\nu }_i{h}_i$$ (3)

We can define the enthalpy of reaction ΔH_R

$$\mathrm{\Delta }{H}_R\equiv \sum _i{\nu }_i{h}_i$$ (4)

and substitute in (3) to obtain after rearrangement

$$\sum _i{h}_i({\stackrel{.}{n}}_{i,in}-{\stackrel{.}{n}}_i)=-V\stackrel{.}{\xi }\mathrm{\Delta }{H}_R$$ (5)

This relationship defines the enthalpy of reaction as the difference of component enthalpies of component flows in and out of the system.

The energy balance under the assumed simplifying conditions can be written as

$$\frac{dH}{dt}=\sum _i{h}_i({\stackrel{.}{n}}_{i,in}-{\stackrel{.}{n}}_i)-\stackrel{.}{Q}$$ (6)

where H is the enthalpy content of the system, h_i are the molar enthalpies of the individual components, ṅ_i,in and ṅ_i are the molar flow rates in and out of the system and Q̇ is the rate of heat transfer to the environment. If we substitute (5) in (6) we obtain at steady state

$$\stackrel{.}{Q}=-V\stackrel{.}{\xi }\mathrm{\Delta }{H}_R$$ (7)

Entropy Balance

To obtain an expression for the entropy of reaction we can multiply the steady state material balance (1) with the molar component entropy s_i

$$0=s_i({\stackrel{.}{n}}_{i,in}-{\stackrel{.}{n}}_i)+V\stackrel{.}{\xi }{\nu }_i{s}_i$$ (8)

If we sum up all component equations we obtain

$$0=\sum _i{s}_i({\stackrel{.}{n}}_{i,in}-{\stackrel{.}{n}}_i)+V\stackrel{.}{\xi }\sum _i{\nu }_i{s}_i$$ (9)

We can define the entropy of reaction ΔS_R

$$\mathrm{\Delta }{S}_R\equiv \sum _i{\nu }_i{s}_i$$ (10)

and substitute in (2) to obtain

$$\sum _i{s}_i({\stackrel{.}{n}}_i-{\stackrel{.}{n}}_{i,in})=V\stackrel{.}{\xi }\mathrm{\Delta }{S}_R$$ (11)

We can subtract on both sides the total entropy flowing with the material into the system and obtain after rearrangement

$$\sum _i{s}_{i,in}{\stackrel{.}{n}}_{i,in}-\sum _i{s}_i{\stackrel{.}{n}}_i=-\sum _i{\stackrel{.}{n}}_{i,in}(s_i-s_{i,in})-V\stackrel{.}{\xi }\mathrm{\Delta }{S}_R$$ (12)

This relationship can be interpreted as the contributions to the entropy balance due to material transport and conversion in the system. The left side of the equation represents the difference between total entropy flowing in and out of the system, i.e the amount of entropy accumulated in the system due to material flow. This amount is equal to the right side which has two contributions. The first is the amount of entropy generated due to the dilution of the concentration in the incoming process stream to the concentration in the reactor. The second is the amount due to material conversion in the reaction.

We can formulate a balance for entropy in a similar way as previously for the other extensive quantities, except we have to consider that entropy of a component depends also on its concentration. To account for this we can write

$$\frac{dS}{dt}=\sum _i(s_{i,in}{\stackrel{.}{n}}_{i,in}-s_i{\stackrel{.}{n}}_i)-\frac{\stackrel{.}{Q}}{T}+{\stackrel{.}{S}}_{\mathit{prod}}$$ (13)

Here s_i,in (s_i) are the molar entropies of the individual components at the corresponding concentrations transported in (out) of the system; Q̇ is the rate of heat transfer through the walls and Ṡ_prod is the rate of internal entropy production of the system due to the irreversibility of the process. The first two terms on the right hand side represent the entropy transported to the surroundings due to material transport and due to heat transfer, respectively. From this expression one can see that in a steady state situation with zero entropy accumulation, the internal entropy production term must be balanced by the transport of entropy to the surroundings. Due to the second law, the internal entropy production term must always be larger or equal to zero.

If we substitute in the entropy balance (13) the entropy transport term with (12) and the heat transfer term with (7) we obtain at steady state the following expression for the rate of entropy production

$${\stackrel{.}{S}}_{\mathit{prod}}=\sum _i{\stackrel{.}{n}}_{i,in}(s_i-s_{i,in})-V\stackrel{.}{\xi }\frac{\mathrm{\Delta }{H}_R}{T}+V\stackrel{.}{\xi }\mathrm{\Delta }{S}_R$$ (14)

Thus, the rate of entropy production, reflecting the irreversibility of the process, consists of three contributions. The first is due to the mixing of the incoming process stream with the content of the system, the second is due to the heat of reaction, and the third is generated by the chemical material conversion of the reaction.

If we substitute in the entropy balance (13) the rate of heat transfer with (7) and the rate of entropy production with (14) the balance at steady state reduces to

$$0=\sum _i{s}_i({\stackrel{.}{n}}_{i,in}-{\stackrel{.}{n}}_i)+V\stackrel{.}{\xi }\mathrm{\Delta }{S}_R$$ (15)

Note that the entropy generated by the heat of reaction and the entropy transported by heat transfer to the environment cancel each other in the entropy balance of the open system. Furthermore, the entropy of mixing is inherently incorporated in this formulation of the transport term in which only molar entropies of components in the system appear. Thus the steady state of an open system is governed only by the molar component entropies of the system involved in the entropy transport to the surroundings with the material flow and the rate of internal entropy production due to the entropy of reaction. This result is derived here from the entropy balance and is identical to (11) which has been obtained above based on the material balance.

The obtained relationships represent important results as they show that the open system can operate isothermally at a steady state without accumulating any entropy. Furthermore, the system is completely defined by the rate of entropy production due to the chemical transformation, the entropy of reaction, which characterizes the irreversibility of the system. The entropy production due to the heat of reaction does not appear in this expression and thus does not appear to contribute to the amount of entropy transported to the surroundings by material flow. To express it more directly, the system at this state does not ‘know’ that heat is produced or transferred during this state of operation. The only thing that matters is the entropy of reaction.

Statistical Thermodynamics of Metabolic Networks

The rate of internal entropy production of the open system at steady state can be viewed as a weighted, linear combination of entropies of reaction of individual elementary modes defining the metabolic network

$$\stackrel{.}{\xi }\mathrm{\Delta }{S}_R={\nu }_g\stackrel{.}{\xi }\mathrm{\Delta }{S}_R=r_g\mathrm{\Delta }{S}_R=r_g\mathrm{\Delta }{S}_{\mathit{TOT}}=r_g\sum _{i=1}^n{p}_i\mathrm{\Delta }{s}_i$$ (16)

Here, ν_g is the stoichiometry coefficient of glucose in the growth reaction (we assume glucose is the carbon and energy source), r_g is the rate of glucose consumption. ΔS_TOT is identical with the entropy of reaction, but the new subscript indicates now that it represents the total reaction entropy composed of reaction entropies Δs_i of all n elementary modes contributing with probabilities (or weights) p_i.

We have previously shown that the entropy of reaction ΔS_TOT is maximized when probabilities are assigned such that the contributing elementary mode entropies are distributed according to the Boltzmann distribution law (Srienc and Unrean, 2010). The same result is obtained based on a standard statistical thermodynamics derivation which is included as a supplementary file. It is shown that usage probabilities of elementary modes are related to their entropies of reaction according to

$$p_i=e^{-\frac{\mathrm{\Delta }{s}_i}{b}}$$ (17)

such that

$$\mathrm{\Delta }{S}_{\mathit{TOT}}=-b\sum _i{p}_{i}ln{p}_i$$ (18)

Since reaction entropies of individual elementary modes can be computed, the constant b can be evaluated form the requirement that probabilities have to sum up to unity:

$$1=\sum _{i=1}^n{e}^{-\frac{\mathrm{\Delta }{s}_i}{b}}$$ (19)

Thus, the metabolic flux distribution in a metabolic network can be predicted based on the knowledge of elementary modes. In the experimental part of this work it is shown that cells indeed evolve towards such a predictable state.

Results and Discussion

T. saccharolyticum is an anaerobic, thermophilic, saccharolytic bacterium that is known to ferment various biomass-derived sugars into ethanol (Desai et al., 2004; Shaw et al., 2008). A metabolic network model of T. saccharolyticum for anaerobic growth on glucose or xylose was constructed (Fig. 1), and was analyzed by elementary mode analysis to determine all balanced pathways that are inherent in the cell metabolism. There exist 4,336 elementary modes for growth on glucose and 4,714 elementary modes for growth on xylose. Multiple gene knockouts were implemented to limit the metabolic functionality of T. saccharolyticum growing on glucose to a set of only 4 classes (families) of efficient ethanol-producing pathways representing 42 elementary modes. Each family of modes has the same overall reaction stoichiometry (Table 1). The targeted gene knockouts are PPP1 (zwf), MGS1 (mgs), LDH (ldh), PFP3r (sbm), and PTA and ACK (pta-ack) which were identified using a selection algorithm as previously described (Trinh et al., 2006).

Table 1.

Stoichiometric equations and standard reaction entropies of the remaining elementary modes in AS411. All remaining biomass-producing modes have cell growth and ethanol production coupled. The 42 elementary modes can be grouped into 4 families of modes that have the same overall reaction stoichiometry.

Family	Reaction stoichiometry	No. of EMs	YETOH1	YBIO1	ΔS2
Xylose substrate
1	Xylose → 1.67 Ethanol + 1.67 CO2+ 1.67 ATP	3	0.51	0	0.363
2	Xylose → 1.67 Ethanol + 1.67 CO2	15	0.51	0	0.327
3	Xylose + 0.59 NH3 → 2.40 Biomass + 0.09 H2 +0.92 Ethanol + 0.98 CO2	18	0.28	0.41	0.302
4	Xylose + 0.59 NH3 → 2.40 Biomass + 0.09 Formate + 0.92 Ethanol + 0.89 CO2	6	0.28	0.41	0.285
Glucose substrate
1	Glucose → 2 Ethanol + 2 CO2+ 2 ATP	3	0.51	0	0.547
2	Glucose → 2 Ethanol + 2 CO2	15	0.51	0	0.503
3	Glucose + 0.70 NH3 → 2.88 Biomass + 0.11 H2+ 1.10 Ethanol + 1.18 CO2	18	0.28	0.41	0.473
4	Glucose + 0.70 NH3 → 2.88 Biomass + 0.11 Formate + 1.10 Ethanol + 1.07 CO2	6	0.28	0.41	0.453

¹Yield is shown in g-product produced per g-sugar consumed.

²The standard entropy of reaction per mole glucose of each family (kJ/K-mole) is calculated using Gibbs equation and correlations with the degree of reduction given in Sandler and Orbey (1991).

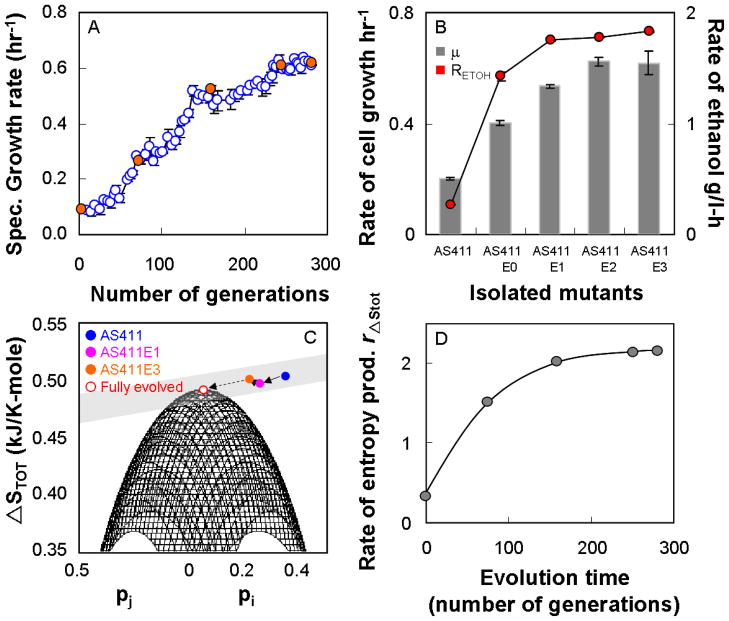
The mutant strain AS411 which contained the predicted gene deletions was constructed using previously described methods (Desai et al., 2004; Mai and Wiegel, 2000). The predicted target gene sbm, which is part of the propionic acid synthesis pathway, is assumed to be inactive because propionic acid has not been detected in the fermentation medium of AS411. Therefore it has not been deleted. Gene knockouts in AS411 were verified via PCR amplification using the wild type as a positive control (data not shown). The constructed strain which can operate within the set of 4 pathway groups was allowed to evolve in a serial dilution experiment for approximately 280 generations equivalent to 650 hrs of anaerobic growth on glucose. Faster-growing mutants are expected to be selected during the evolution experiment since strains with faster growth rate will eventually dominate the culture replacing the slower-growing strains. This can be seen by a continuous increase in the specific growth rate of the culture over the number of generations (Fig 2A). The specific growth rate of the evolved mutant AS411E3 isolated after 280 generations of evolution, was at 0.61 hr⁻¹ compared to the growth rate of 0.11 hr⁻¹ of the parent AS411 under identical conditions. Due to the strong link between cell growth and ethanol synthesis in the 4 remaining pathways operating in AS411, the evolved mutant with an increased growth rate also produced ethanol at a faster rate (Fig. 2B). AS411E3 converted glucose into ethanol within 8 hr, while the original parent, AS411, fermented the same amount of glucose to ethanol at around 36 hr (data not shown). The strict coupling between the two products is in part due to redox constraints since the reducing and oxidizing equivalents NAD/NADH and NADP/NADPH generated for growth of AS411 can only be disposed through ethanol synthesis.

Figure 2.

Metabolic evolution of AS411 during anaerobic growth on glucose. (A) Change in specific growth rate over evolution time during serial dilution. Filled symbols represent cultures that have been evaluated in controlled bioreactor experiments. (B) Performance of the evolved cells after an evolution time of 329 hrs (AS411E0); 487 hrs (AS411E1); 600 hrs (AS411E2); 642 hrs (AS411E3). Evolved cells have higher specific growth rates and ethanol production rates in comparison to their parent, AS411. (C) Total reaction entropy for AS411 ( ) and the evolved cell cultures ( AS411E1; AS411E3) as a function of probabilities of elementary modes. The plot shows the shift in metabolic state of cells towards the predicted state of a fully evolved system where the entropy is maximized and the usage probabilities are according to the Boltzmann distribution law. The symbol represents the fully evolved system estimated from the asymptotic value of the fitting functions of probabilities shown in Fig. 3 at infinite evolution time. (D) Change in rate of entropy generation, computed from the product of the total reaction entropy and the uptake rate of glucose, as a function of evolution time. Circles represent the experimentally determined rate of entropy production while the line represents the rate of entropy production calculated from the fitting functions of probabilities given in Fig. 3. The plot suggests that the cell system has a natural tendency to evolve with time towards an asymptotic state with maximum rate of entropy production.

The minimized metabolic functionality of AS411 permits convenient metabolic flux estimations of the strain from experimentally determined metabolite secretion patterns. The probability for each set of pathways contributing to the overall metabolism of the strain was computed from a completely determined algebraic system of mass balance equations based on the measured secretion or consumption fluxes of glucose, ethanol and biomass and the summation constraint of the probabilities. Analysis of the associated usage probabilities of pathway groups for AS411 and the evolved strain AS411E3 suggests an increase in the probabilities of the biomass-ethanol coproducing modes during the directed evolution. The overall flux distribution for both mutants (Fig. 1), which was determined from the sum of the products of the 4 family modes and the usage probabilities, reveals the adaptation capability in the cell metabolism during evolution. The metabolism of AS411E3 has an increase in pentose phosphate pathway (PPP) flux which could be one of the main reasons for improved cell growth observed in the evolved strain since the PPP is important for the synthesis of several biomass precursors.

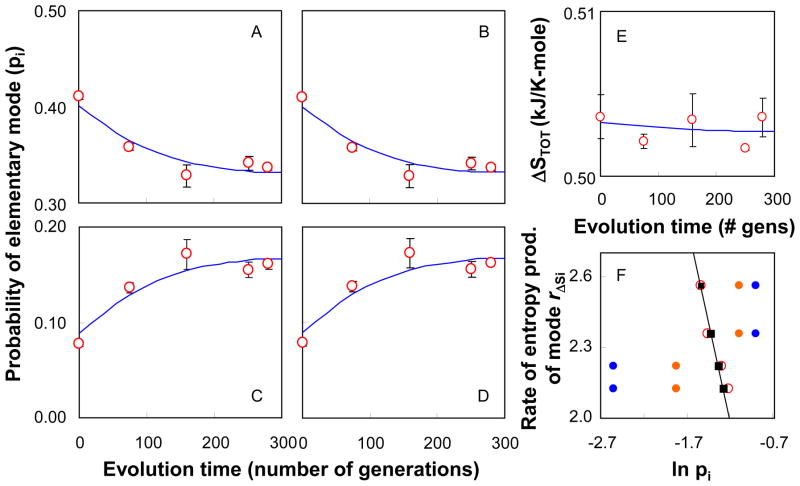
Analysis of the experimentally determined pathway probabilities of the evolving cells suggests that the strain evolved by redistributing the probabilities of family modes towards the state where the total entropy production is maximized and the usage probabilities are according to the Boltzmann distribution law (Fig. 2C). Likewise, The total rate of entropy production, which was calculated from the product of the uptake rate of glucose and the total reaction entropy revealed a shift in the metabolic functional state of the evolving cells in a direction of increasing rate of entropy generation (Fig. 2D). As shown in the Fig. 2C, the metabolism of the evolved strain AS411E3 has not yet reached the predicted state of a fully evolved metabolism. Hence, to verify that the predicted state of maximum entropy production represents the metabolic state of a fully evolved cell, we fitted an exponential function to the experimentally determined probabilities over evolution time and estimated the asymptotic values of these probabilities from the fitting function (Fig. 3). These asymptotic values represent the probabilities that the cell would ultimately reach at an infinite evolution time. Thus, they represent the usage probabilities of the pathway families in the fully evolved cell system. The asymptotic probabilities agree well with the predicted probabilities (Table 2) suggesting that the fully evolved cell system functions at the state of maximum entropy production where the distribution of the metabolic pathways follows the distribution law. In addition, the fitting functions of probabilities can accurately predict the entropy generation per mole of glucose and the total entropy production rate over evolution time (Fig. 2D and 3). Based on the values of asymptotic probabilities, we computed the total reaction entropy for the fully evolved strain to be 0.50 kJ/K-mole, which is in excellent agreement with the predicted maximal entropy production value of 0.49 kJ/K-mole (Table 2).

Figure 3.

Change in usage probabilities of elementary mode families and total reaction entropy production during metabolic pathway evolution. The probabilities of family mode 1 (A), family mode 2 (B), family mode 3 (C), and family mode 4 (D) change over evolution time. Circles represent the experimental values, while the lines represent the exponential fitting functions. The parameters of the function have been determined by a least square method. The fitting functions are W₁ = 0.188·e^{(−0.001·t)} + 0.214; W₂ = 0.169·e^{(−0.001·t)} + 0.233; W₃ = −0.186·e^{(−0.001·t)} + 0.273; W₄ = −0.212·e^{(−0.001·t)} + 0.298. The total reaction entropy (kJ/K-mole of glucose) over evolution time (E) is computed as a weighted sum of the probabilities and the reaction entropies of individual modes. (F) The production rate of entropy of individual modes as a function of the natural log of the usage probabilities of modes. The rate of entropy production is computed from the product of reaction entropy of individual modes and the asymptotic rate of glucose uptake (see supplementary information for detail). The experimentally determined usage probabilities of elementary modes after an evolution time of zero generations ( ), of 280 generations ( ), and the asymptotic values at infinite evolution time ( ) are compared to the predicted probabilities based on the Boltzmann distribution law (■). Over the evolution time the probabilities approach the predicted values.

Table 2.

Usage probabilities of elementary modes and reaction entropy for a fully evolved metabolism of AS411. The p_Fi and p_Ei represent the probabilities of family modes and of individual modes within the corresponding families respectively. The p_Ei value is computed from the p_Fi value by dividing by the number of elementary modes in the family. The predicted probabilities are determined from the Boltzmann distribution law (see supplementary file for detail). The asymptotic probabilities are estimated from experimental data using the fitting functions given in Fig. 3. Total reaction entropy (kJ/K-mole) is determined from the weighted sum of the probabilities and the reaction entropies of individual modes.

Family	Predicted pFi	Predicted pEi	Asymptotic pFi	Asymptotic pEi
1	0.214	0.071	0.214	0.071
2	0.242	0.016	0.233	0.016
3	0.264	0.015	0.273	0.015
4	0.279	0.047	0.298	0.050
ΔSTOT (kJ/K-mole)	0.49		0.50

We have demonstrated here that the steady-state flux distribution obtained through elementary mode analysis provides a quantitative measure in the evolutionary optimization of cell metabolism. The presented results suggest that a metabolic network evolves by redistributing its metabolic pathway fluxes in order to maximize the rate of entropy production. Thus, for a cell system that is not at the fully evolved state, the evolutionary path towards the maximum entropy generating state can be predicted. The present work suggests that the evolution of metabolic pathways is driven by the rate of entropy generation and that the Boltzmann distribution law predicts the optimal metabolic flux distributions of the fully evolved metabolism. The presented approach should be of considerable value in systems biology as it relates physiological activities to basic thermodynamic principles. It is interesting to note that a similar approach has been recently proposed to describe stochastic fluctuations in biochemical reactions caused by a small number of molecules undergoing observable transition trajectories (Pressé et al., 2010).

The total rate of entropy production σ = r_gΔS has two contributions: the glucose uptake rate and the amount of entropy produced per unit glucose consumed. The presented data suggest that during evolution the total rate of entropy production approaches a maximum value. During this process, the change in the rate of entropy production has clearly two distinct contributions:

$$\frac{d\sigma }{dt}=r_g\frac{\partial \mathrm{\Delta }S}{\partial t}+\mathrm{\Delta }S\frac{\partial r_g}{\partial t}$$

The first term on the right hand side expresses the change due to the adjustment of the metabolic network structure to reach the most likely distribution when the Boltzmann distribution law for the pathway usage is satisfied. In this situation the entropy generation of the network is maximized while complying with the principle of fair apportionment of outcomes. The second term expresses the change in the glucose uptake rate. This rate is proportional to the growth rate. Thus, this term reflects the selection process. It is expected to be always positive because only faster growing cell variants can overtake a cell population. The upper limit of the rate of glucose uptake is likely reached when some other process such as perhaps the external mass transfer or internally a step such as DNA replication, limits a further increase in the metabolic rates. The fully evolved state is then reached when the two terms balance each other and the entropy production rate is maximized.

The cellular metabolic flux distribution can be computed from nutrient uptake and metabolite secretion rate data if the system of algebraic equations, defined by the molar balances of internal and external metabolites, is completely determined. However there are usually many more unknown intracellular reactions present than measurable reactions resulting in underdetermined systems. In such cases an optimal flux distribution can be estimated using linear programming assuming maximization of the growth yield as the constraining objective function. While intuitively plausible, to our knowledge a theoretical justification for the choice of such objective function has never been established. Alternately, the metabolic flux distribution of a metabolic network can be computed as a weighted average of all elementary modes defined by the network. Since elementary modes can be exactly computed the problem is reduced to finding the unknown weights. In the present work these weights (or probabilities) could be calculated from a completely determined algebraic system of equations from the measured metabolite secretion and nutrient uptake rates. And it is shown that the estimated weights converge during evolution towards an optimal state predicted by the presented theory. Thus, the optimal metabolic state can be directly computed from thermodynamic data without any constraints. While the linear programming approach results in a single optimal flux distribution that maximizes growth yield, in the presented approach such optimal solution is favored. However, contributions from less efficient elementary modes choices are also included in the solution since they are part of the most likely elementary mode distribution that the system attempts to reach. But validation of these conclusions will require further research.