Abstract
The research into kinetics of styrene biodegradation by bacterial strain Pseudomonas sp. E-93486 coming from VTT Culture Collection (Finland) was presented in this work. Microbial growth tests in the presence of styrene as the sole carbon and energy source were performed both in batch and continuous cultures. Batch experiments were conducted for initial concentration of styrene in the liquid phase changed in the range of 5–90 g m−3. The Haldane model was found to be the best to fit the kinetic data, and the estimated constants of the equation were: μ
m = 0.1188 h−1, K
S = 5.984 mg l−1, and K
i = 156.6 mg l−1. The yield coefficient mean value
Keywords: Styrene, Pseudomonas, Kinetics, Chemostat, Batch experiment
Introduction
The starting point for quantitative description of the phenomena occurring in bioreactors is the material balance expressed for any reactant or product. In such equations, there is a term determining the rate of loss/formation components which are the growth substrates for microorganisms/products of microorganism metabolism. Therefore, in mass balances of reactors, this term will play the role of an expression defining mass sink/source of a given component in the considered element of the reactor.
The subject of analysis which is presented in this study is kinetics of styrene biodegradation by bacteria from genus Pseudomonas. Styrene, the simplest alkenylbenzene, is employed as both a starting material for synthetic polymers and a solvent in the polymer processing industry. In 2008, 30 million tons of styrene was produced (EC DG ENV 2011), and the demand for it still increases, on average, by 2–3% a year. Such common and quantitatively big consumption of styrene, belonging to the group of volatile organic compounds (VOCs), significantly affects the amount of its emission into the atmosphere (it has been estimated to be in the range of 25,000 t per year) (US EPA 1994). Styrene gets into the human body mainly through the respiratory system and, to a lesser extent, through the skin, and it is stored in the fatty tissue. Metabolism of styrene in a human body is diversified. One way is oxidation to an active intermediate product, 1,2-epoxyethylbenzene, which may also have immunomodulatory effects on workers exposed to gaseous emission of the component (Vodicka et al. 2006). Irritation of mucous membranes of the respiratory system, eyes and nose is observed among people exposed to the vapor of styrene. Chronic contact causes a variety of discomforts such as headache, fatigue, weakness, depression, and peripheral neuropathy. Styrene has been listed among the 189 hazardous and toxic atmospheric contaminants under EPA, whereas the International Agency for Research and Cancer classified styrene as a potential carcinogenic factor (US EPA 1999).
Taking the above into consideration, the necessity to remove styrene from waste gasses of the installations using this monomer has become a very important task connected with the protection of the environment. One of the possibilities is to use the biological methods which are especially favorable in case there is the necessity to purify large streams of air containing small amounts of pollutants. Pollutant as the only source of carbon and energy for the microorganism is decomposed to carbon dioxide and water if the process parameters are properly selected. In literature, one can find a lot of studies whose authors examined the process of purifying the air from styrene in biofilters or biotrickling filters. Various microorganisms were used in the research: Pseudomonas sp. (Das et al. 2008; Jang et al. 2004, 2005, 2006; Okamoto et al. 2003; Ryu et al. 2004), Brevibacillus sp. (Hwang et al. 2008), Rhodococcus pyridinovorans PYJ-1 (Jung and Park 2005), Exophiala jeanselmei yeast (Cox et al. 1997), Sporothrix variecibatus fungus (Rene et al. 2010), or mixed bacteria cultures obtained from soil or activated sludge (Arnold et al. 1997; Babaee et al. 2010; Djeribi et al. 2005; El Aalam et al. 1993; Jorio et al. 2000; Lu et al. 2001; Novak et al. 2008; Pol et al. 1998). In the research, the maximum removal rates from 91 (Cox et al. 1997) to 635 g m−3 h−1 (Ryu et al. 2004) were obtained depending on the used microorganisms, bed load with pollution, and empty bed resistance time. It is worth emphasizing that numerous studies focusing on the biochemical and genetic bases of styrene degradation by other species, mainly from genus Pseudomonas, are also described in literature (Marconi et al. 1996; Panke et al. 1998; Velasco et al. 1998).
The research into microbiological styrene biodegradation indicates that the amounts of formed biomass, carbon dioxide, and intermediates depend on the examined strain. Arnold et al. (1997) isolated a few bacterial strains from the microflora of active peat filter material after an enrichment period of 2 months. The isolated strains varied significantly not only with regard to styrene degradation efficiency, but also in how they utilized this carbon source. At high concentration of styrene (∼0.2% v/v), only Pseudomonas sp. E-93486, Pseudomonas chlororaphis DSM 6508, and the co-culture of seven isolates were able to grow and produce carbon dioxide. One of them, Pseudomonas sp. E-93486, was chosen for further research whose final aim was to determine the usefulness of this strain in technical applications. The first stage of the research, presented in the work, was to define the kinetics of styrene biodegradation reaction by the selected strain and to compare the determined rate of styrene biodegradation with the data available in literature.
As for the kinetics of styrene biodegradation, the literature data are very limited (Babaee et al. 2010; Cox et al. 1997; Das et al. 2008; Jorio et al. 2005; Jung and Park 2005), and the presented findings are often debatable. The works will be discussed in detail in the further part of the study, and the values of the kinetic parameters determined by the authors were set in Table 1.
Table 1.
The values of kinetic parameters for styrene biodegradation in different studies
| Strain | q m (gS g−1biomass h−1) | K S (mg l−1) | K i (mg l−1) | T (°C) | pH | References |
|---|---|---|---|---|---|---|
| Pseudomonas sp. E-93486 | 0.165 | 5.984 | 156.6 | 30 | 7.0 | This study |
| Industrial activated sludge | 0.160 | 13.8 | 21.57 | 32 | 7.0 | Babaee et al. (2010) |
| Mixed culture | 0.02322 | 3.49 | 26.55 | 25 | Jorio et al. (2000) | |
| Exophiala jeanselmei | 0.630 | 0.78 | 21.8 | 25 | 5.7 | Cox et al. (1997) |
| Rhodococcus pyridinovorans PYJ-1 | 0.210 | 858.7 | 1,033.3 | 32 | 7.0 | Jung and Park (2005) |
Kinetics of bacterial growth
Batch experiments
The kinetic model parameters are usually obtained from batch experiments by observing the biomass growth rate with time at a different initial concentration of substrate. For the exponential growth phase, where the specific growth rate of biomass (μ net) remains constant and its value depends only on the initial substrate level, the growth rate of biomass is first order and can be defined as:
| 1 |
where μ net is net specific growth rate (per hour) and X is biomass concentration (milligrams per liter).
Integration of Eq. 1 with boundary condition X = X 0 at t = 0 yields:
| 2 |
For every experimental point, that is, for every initial dose of substrate, the graph representing the dependence lnX as a function of time is expected to take the form of a straight line whose slope is μ net. By changing the initial concentration of the growth substrate in the solution μ net = f(S 0), data base can be obtained making it possible to select the form and estimation of the kinetic equation constants. When substrate inhibition takes place, the Haldane model is frequently applied:
| 3 |
where S 0 is initial styrene concentration in gas or liquid phase (milligrams per liter), q is specific styrene degradation rate (milligrams per milligram protein per hour), q m is the maximum value of q, and K S and K i are the half velocity constant (milligrams per liter) and substrate inhibition constant (milligrams per liter), respectively.
To better describe the growth kinetics, we define some stoichiometrically related parameter such as the observed yield coefficient, defined as the ratio of the biomass formed to the mass of substrate utilized, measured during any finite period of exponential growth. Since the growth substrate (styrene) is a volatile chemical compound, therefore, thermodynamic equilibrium is set after the injection of a given dose of the substance to the solution. Styrene concentrations in each phase change according to Henry's law:
| 4 |
where H
* is Henry's constant (dimensionless). For styrene,
Assuming that the equilibrium between gas and liquid phases is established instantaneously, the total mass of styrene in agitated batch reactor (m S) in both liquid and gaseous phases can be expressed as (Jorio et al. 2005):
| 5 |
where V L and V g (liters) are the volumes of liquid and gas phases in the biostat.
The substrate mass loss as a result of biodegradation can be connected with the biomass growth via the following relationship:
| 6 |
Integrating Eq. 6 over the test period, from time 0 to time t, we obtain:
| 7 |
where
| 8 |
and m S0 is the mass of styrene initially introduced into the reactor.From the above equation, the yield coefficient can be calculated as:
| 9 |
If the process is conducted until the substrate is completely consumed, then S L = 0, and Eq. 9 is simplified to the form of:
| 10 |
Growth in continuous culture
The essential feature of the continuous culture of microorganism technique is that microbial growth occurs under steady-state conditions, that is, at a constant rate and in a constant environment. Such a technique is usually used to determine the maintenance coefficient (m
S), maximum value of the yield coefficient
In an ideal chemostat, fresh sterile nutrient medium is continually supplied to the well-stirred volume of a reactor and products, and cell suspension is removed at the same rate. So, liquid volume in the reactor (V R) is kept constant. The specific growth rate of microorganisms is characterized by the net specific growth rate (Moser 1988):
| 11 |
where:
| 12 |
μ g (per hour) is gross specific growth rate, and k d (per hour) is the rate of the loss of cell mass due to endogenous metabolism.
The material balance for the biomass around the chemostat yield can be described as (Schuler and Kargi 2002):
| 13 |
where
The rate of growth of microorganisms can be written as:
| 14 |
Substituting the dependence (12) to the Eq. 14 yields:
| 15 |
Taking into account Eq. 15, Eq. 13 can be rearranged to the form of:
| 16 |
where
Usually the feed media are sterile, so X 0 = 0. If the system is at steady state (dX/dt = 0), then:
| 17 |
and
| 18 |
A material balance on the limiting substrate (assuming no extracellular product formation) can be described as:
| 19 |
When the system is at steady state (dS/dt = 0), then Eq. 19 can be rearranged to:
| 20 |
where M denotes maximum value of the yield coefficient.
Taking into account Eq. 17, we can rearrange Eq. 20 to the form:
| 21 |
or
| 22 |
where
It is assumed that
If the steady-state conditions are known for several dilution rates, but S
L0 = const., then the values of
The slope of the linear regression line in the plot is m
d, and the intercept represents 1/
The maximum specific growth rate of a continuous culture was estimated using the wash-out method. Since the results of the experiments require more thorough analysis, they will be presented in the next study.
Materials and methods
Microorganism
The gram-negative bacterium used in this study, coming from VTT Culture Collection (Finland), showed 97% homology with Pseudomonas putida and 97% with Pseudomonas stutzeri from 16S rDNA analysis. The strain marked as E-93486, oxidase- and catalase-positive, was isolated from the activated sludge enriched with styrene (Arnold et al. 1997). The strain was kept on nutrient agar slopes at 4°C and transferred to the new ones every month.
Preparation of inoculum
Before inoculating into the reactor, a few colonies of Pseudomonas sp. E-93486 pre-grown on the nutrient agar were introduced to 5 ml of LB medium and incubated for 24 h. Next, the cell suspension was poured into 5 ml of mineral medium supplemented with 9 g m−3 styrene. The composition of the mineral medium used for the cultivation was as described previously (Greń et al. 2009). After another 24 h, the suspension was carried to a hermetic bottle replenished with mineral medium to 100 ml, and 45 g m−3 of styrene was added. In subsequent days, the absorbance was measured, and 45 g m−3 of substrate was added every day. After 7 days, new cultures were set, and concentration of substrate increased to 90 g m−3. Cultures were renovated every week. The adaptation of E-93486 strain to styrene lasted ∼5 weeks. The cultures of the adapted bacteria were conducted in hermetic 500-ml flasks containing 100 ml of the suspension. Steady-state conditions of the culture were kept: temperature of 30°C and shaking at 130 rpm. A dose of styrene corresponding to 90 g m−3 was fed into the culture every 24 h.
Batch experiments
Experiments were conducted in Biostat B fermenter (Sartorius, USA) with working volume of 2 l. The tests were conducted at 30°C, oxygenation was maintained at the level of 5 mg dm−3, pH 7, and stirrer speed was 300 rpm. A constant value of pH was maintained by feeding a 10% solution of KOH or KH2PO4, whereas a constant concentration of oxygen by dosing 0.75% solution of H2O2 according to the indication on the pO2 electrode.
The following procedure was performed before every experiment. The sterile biostat was filled with the mineral medium, centrifuged, and washed out with deionized water. Styrene grown cells were inoculated into the biostat in the amount which enabled the start of each culture at a similar concentration of cells in the solution, equaling 5.31 × 10−5 gdry cell weight ml−1 of suspension which corresponded to the 0.1 absorbance at λ = 550 nm. After the process parameters had been stabilized, a proper dose of liquid styrene (S L0), as the only source of carbon and energy for bacteria, was introduced into the solution. During the experiment, at regular intervals, biomass concentration and growth substrate concentration were determined. The experiments were performed for the initial styrene concentration changed within the range of 5–50 mg l−1 by 5 mg l−1, however, in the subsequent experiments within the range of 50–90 mg l−1 by 10 mg l−1. The range of changes in the styrene concentration used in the experiments was the same as during the adaptation of the microorganisms.
Continuous culture
Continuous culture was started with a batch culture at styrene concentration in a solution corresponding to the concentration of this compound in a fed later on nutrient medium. After reaching the logarithmic growth phase, feeding with the nutrient and removal of excess culture liquid were started. After the steady state had been established, the process was conducted for a period corresponding to a minimum of seven exchanges of reactor working volume. Styrene concentration was determined both in the feed and outlet solutions.
Analytical methods
The concentration of biomass was determined by measuring the optical density (OD) of the fluid culture (λ = 550 nm). Next the suspension absorbance was converted into grams of dry mass of microorganisms according to the calibration which was performed earlier.
Styrene concentration was determined by gas chromatography using Varian 38009 (USA) chromatograph with a 30-m length CP-wax 52CB column and a flame ionization detector (FID). Helium was used as the carrier gas. Separation was achieved with a temperature program (120°C was maintained for 5 min; then, temperature was increased to 210°C, 30°C min−1), while the temperature of the injector and the FID was 250°C. Every experimental point was repeated twice in identical conditions, and the values were averaged to get the true experimental value.
Results
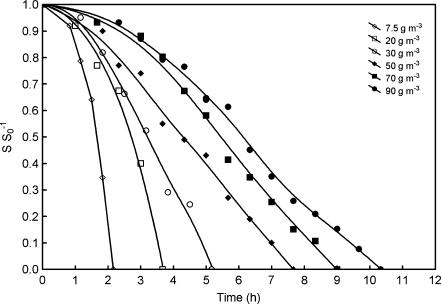
Figure 1 shows the curves representing the rate of substrate utilization for different initial styrene concentrations. It has to be stressed that in every experiment, no measurable amounts of styrene biodegradation intermediates in the culture liquids were found, which seems to perform a complete mineralization of aromatic substrate.
Fig. 1.
Styrene concentration in the liquid phase versus time for different initial styrene concentrations (S L0)
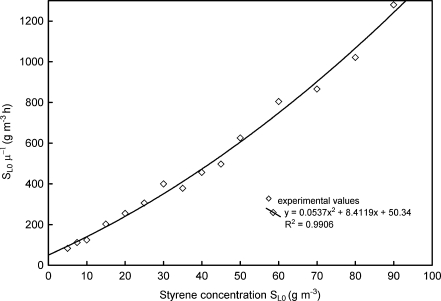
A lnX = f(t) graph was plotted for every experimental point. In the logarithmic growth phase, the dependence is a straight line whose slope determines the value of the specific growth rate (μ net). The data base compiled in this way was shown in Fig. 2 in the form of a S L0/μ = f(S L0) dependence which enables the choice of a kinetic model equation. The highest correlation coefficient (R 2 = 0.9906) was obtained by approximating the experimental data with a quadratic equation. It confirms the earlier suggestions about an inhibitory effect of styrene. Therefore, the Haldane model was used to describe Pseudomonas sp. E-93486 strain growth kinetics on styrene, and kinetic equation parameters were estimated using the least-square error method with the help of NLREG—nonlinear regression analysis program (Sherrod 1997) yielding the dependence:
| 23 |
which with the mean percentage error not exceeding 7% approximates the experimental data. The high value of substrate inhibition constant K
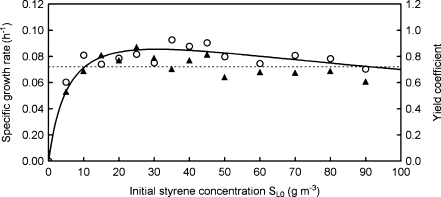
i = 156.6 mg l−1 shows a great resistance of Pseudomonas sp. E-93486 to inhibitory activity of styrene, which is noticeable only at concentrations higher than 30 mg l−1. The conducted experiments made it possible to determine the value of the biomass yield coefficient. Since the batch cultures were always performed to the moment of using up the substrate, then
Fig. 2.
Plot of function
Fig. 3.
Specific growth rates (circles) and observed yield coefficients (triangles) as a function of initial styrene concentration (S
L0); the dashed line corresponds to yield coefficient mean value
Continuous culture
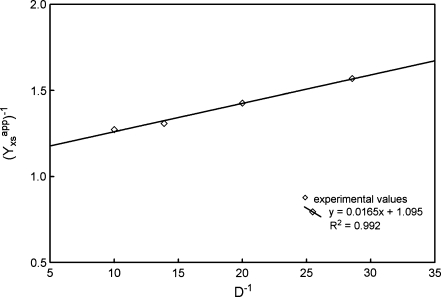
The presence of styrene was not noticed in the liquid leaving the chemostat for the values of the process parameters (D, S
L0) used in the measurements. The first series of experiments was performed for a steady (25 mg l−1) styrene concentration in a solution fed into the reactor changing, in the successive cultures, the dilution rate (D = 0.035–0.1 h−1). The obtained experimental data base made it possible to plot a graph 1/
Fig. 4.
A plot of 1/
Another series of measurements was performed at a constant dilution rate but at different styrene concentrations in the fed to the reactor mineral medium (S
L0). Their aim was to check the influence of changes of S
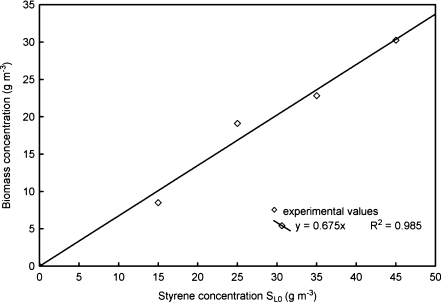
L0 on the amounts of the formed biomass and, as a result, on the biomass yield coefficient. Figure 5 shows the results of one measuring series for D = 0.072 h−1 and styrene concentration in the fed solution changed within the range of 15–45 g m−3. The slope of a straight line correlating the experimental data is the looked for
Fig. 5.
Plot of function X = f(S L0) for D = 0.072 h−1
Discussion
As a result of the conducted research, the parameters of the equation describing the rate of the biological reaction of styrene oxidation by Pseudomonas sp. E-93486 bacteria were determined. The conducted experiments showed that this strain is able to degrade styrene in solutions containing this component at the concentration up to 90 g m−3 .The tested microorganisms also showed great resistance to inhibition of their growth by styrene.
Literature data referring to the kinetics of styrene biodegradation were analyzed to compare the activity of the tested strain with the activity of other microorganisms. As it has been mentioned, the number of such works is very limited. In the work of Das et al. (2008), one can find a very short description of experiments whose aim was to determine the biomass growth kinetics during styrene biodegradation by P. putida strain from the Indian NCJM Collection. Dependence of the specific growth rate (μ) on the initial concentration of the substrate was described by the Monod kinetic equation with the estimated constants: μ m = 45 h−1 and half velocity constant K S = 0.8 g m−3. The maximum growth rate, suggested by the authors, seems to be very unlikely. Therefore, that equation is not taken into consideration in the further part of the study.
Jung and Park (2005) examined the biodegradation kinetics of styrene by R. pyridinovorans PYJ-1. The strain was isolated from a compost-packed biofilter which had been operated for 100 days to remove a mixture of VOCs including styrene. Batch experiments were conducted at 32°C, pH 7, and initial styrene gas concentrations changed within the range of 0–400 mg l−1. The specific styrene degradation rate followed a typical substrate inhibition kinetic expression (Eq. 3) in which S0 is the initial styrene concentration in gas phase. For R. pyridinovorans PYJ-1 q m = 0.42 (milligrams per milligram protein per hour), K S = 129 (milligrams per liter), and K i = 155 (milligrams per liter) were estimated. The authors claim that the bacterial strain used in the experiments was three times less active than yeast used by Cox et al. (1997). Attention is drawn to K S and K i constant values suggested by Jung and Park (2005) and used in the experiments' range of changes of styrene concentration in the gas phase corresponding to equilibrium styrene concentration in the liquid phase considerably exceeding the solubility of this component in a mineral salt solution. Babaee et al. (2010), quoting the findings of that study, assumed that each concentration of styrene in the gas phase is given in parts per million and not in milligrams per liter, assuming that one obtains a range of changes in the styrene concentration in the gas phase amounting to 0.006–0.5 mg l−1. It corresponds to changes in the styrene concentration in the liquid phase in the range of 0.04–3.33 mg l−1, which is far below the range of changes used in the studies by Babaee et al. (2010), Cox et al. (1997), Jorio et al. (2005), and this study.
Cox et al. (1997) showed a very high activity of the E. jeanselmei yeast in the process of degradation of low doses of styrene and at the same time their high sensitivity to the inhibitory influence of styrene at higher concentrations in the solution. The dependence of the specific degradation rate (q) on the initial styrene concentration in the solution was described by the Haldane equation, and the estimated constants of the equation were q m = 21 μg mg−1protein min−1, K s = 7.5 μmol l−1 (0.78 mg l−1), and K i = 0.215 μmol l−1 (0.02184 mg l−1).
A novel procedure for the study of biodegradation kinetics of styrene was proposed by Jorio et al. (2005). Microbial growth tests were performed using suspensions of microorganisms prepared from samples of filter bed material. Biomass yield coefficients and kinetic equation coefficients were determined on the base of the analysis of the composition of the gas phase over the solution in which styrene biodegradation took place. Variations of styrene and carbon dioxide concentration in the gas phase with time were measured for the initial concentration of styrene in the liquid phase changed within the range of 4.5–36 g m−3. Specific biomass growth rate was described by the Haldane model with the following values of kinetic parameters: μ m = 0.388 day−1, K S = 3.49 g m−3, and K i = 26.55 g m−3. The mean value of the biomass yield coefficient, determined in the experiments, was Y X/S = 0.696 gbiomass (gstyrene)−1.
Babaee et al. (2010) used two kinds of activated sludge, municipal and industrial, to styrene biodegradation. The culture was conducted in sterile serum bottles of 118-ml volume containing 16 ml of the mineral medium at the biomass concentration of 650 mg l−1. Such a great biomass concentration shortened the time needed for styrene biodegradation and, as a consequence, eliminated the possibility of mutation to occur. The initial styrene concentration was changed within the range of 8.5–123.4 mg l−1. The research showed that at concentration in the solution exceeding ∼17 mg l−1, styrene begins to act as an inhibitor of bacterial activity. Specific degradation rate of styrene was, therefore, described with the Haldane kinetic model, and the estimated, on the basis of experimental data, constants of the equation were: q m = 160.13 mg (gbiomass h)−1, K S = 13.8 mg l−1, and K i = 21.57 mg l−1.
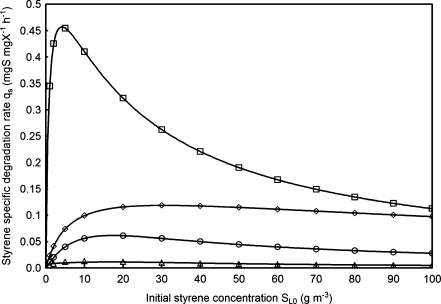
The comparison of these and other previously reported data (see Fig. 6) reveals that the rate of styrene biodegradation by Pseudomonas sp. E-93486 strain is much higher than the rates determined in the studies of other authors. Only yeast E. jeanselmei used by Cox et al. (1997) surpassed with their activity Pseudomonas sp. E-93486. However, it has to be noticed that their activity decreased rapidly with the increase of styrene concentration in a solution, and for S 0 ∼90–100 g m−3, both microorganisms biodegraded the substrate at the same rate. Due to such features, the examined microorganism may be recommended as biological material in the processes of removing styrene from gasses and liquids. High values of biomass yield coefficient were obtained both in batch and continuous cultures. A problem may occur, however, if the strain is used in the form a biofilm immobilized on bed in a biofilter or biotrickling filter. The next stage of the work is research into purifying process of the air from styrene in a biotrickling filter using Pseudomonas sp. E-93486. Kinetic data determined in the presented work will be used in the mathematical model of the reactor.
Fig. 6.
Comparison of styrene biodegradation rate obtained in the studies of other authors. Circles Babaee et al. (2010), squares Cox et al. (1997), triangles Jorio et al. (2000), and diamonds this study
Acknowledgments
The present work is financially supported by the National Centre for Research and Development (NCBiR), grant 1066/R/T02/2010/10.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Contributor Information
Agnieszka Gąszczak, Email: gaszczak@iich.gliwice.pl.
Izabela Greń, Email: izabela.gren@us.edu.pl.
References
- Arnold M, Reittu A, von Wright A, Martikainen PJ, Suihko M-L. Bacterial degradation of styrene in waste gases using a peat filter. Appl Microbiol Biotechnol. 1997;48:738–744. doi: 10.1007/s002530051126. [DOI] [PubMed] [Google Scholar]
- Babaee R, Bonakdarpur B, Nasernejad B, Fallah N. Kinetics of styrene biodegradation in synthetic wastewaters using an industrial activated sludge. J Hazard Mater. 2010;184:111–117. doi: 10.1016/j.jhazmat.2010.08.012. [DOI] [PubMed] [Google Scholar]
- Cox HHJ, Moerman RE, van Baalen S, van Heiningen WNM, Doddema HJ, Harder W. Performance of a styrene-degrading biofilter containing the yeast Exophiala jeanselmei. Biotechnol Bioengin. 1997;53:259–266. doi: 10.1002/(SICI)1097-0290(19970205)53:3<259::AID-BIT3>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- Das C, Chowdhury R, Bhattacharya P. Three phase biofilter model for the removal of styrene through the microbial route. Inter J Chem Reactor Eng. 2008;6:A6. [Google Scholar]
- Djeribi R, Dezenclos T, Pauss A, Lebeault J-M. Removal of styrene from waste gas using a biological trickling filter. Eng Life Sci. 2005;5(5):450–457. doi: 10.1002/elsc.200520092. [DOI] [Google Scholar]
- El Aalam S, Pauss A, Lebeault JM. High efficiency styrene biodegradation in a biphasic organic/water continuous reactor. Appl Microbiol Biotechnol. 1993;39:696–699. doi: 10.1007/BF00164452. [DOI] [Google Scholar]
- European Commission DG ENV (2011) Plastic waste in the environment-Final Report. At http://ec.europa.eu/environment/waste/studies/pdf/plastics.pdf. Accessed 05 May 2011
- Greń I, Gąszczak A, Szczyrba E, Łabużek S. Enrichment, isolation and susceptibility profile to the growth substrate of bacterial strains able to degrade vinyl acetate. Polish J of Environ Stud. 2009;18(3):383–390. [Google Scholar]
- Hwang JW, Choi CY, Park S. Biodegradation of gaseous styrene by Brevibacillus sp. using a novel agitating biotrickling filter. Biotechnol Lett. 2008;30:1207–1212. doi: 10.1007/s10529-008-9670-0. [DOI] [PubMed] [Google Scholar]
- Jang JH, Hirai M, Shodai M. Styrene degradation by Pseudomonas sp. SR-5 in biofilters with organic and inorganic packing materials. Appl Microbiol Biotechnol. 2004;65:349–355. doi: 10.1007/s00253-004-1628-0. [DOI] [PubMed] [Google Scholar]
- Jang JH, Hirai M, Shodai M. Performance of a styrene-degrading biofilter inoculated with Pseudomonas sp. SR-5. J Biosci Bioengin. 2005;100:297–302. doi: 10.1263/jbb.100.297. [DOI] [PubMed] [Google Scholar]
- Jang JH, Hirai M, Shodai M. Enhancement of styrene removal efficiency in biofilter by mixed cultures of Pseudomonas sp. SR-5. J Biosci Bioengin. 2006;102:53–59. doi: 10.1263/jbb.102.53. [DOI] [PubMed] [Google Scholar]
- Jorio H, Bibeau L, Leheitz M. Biofiltration of air contaminated by styrene: effect of nitrogen supply, gas flow rate, and inlet concentration. Environ Sci Technol. 2000;34:1764–1771. doi: 10.1021/es990911c. [DOI] [Google Scholar]
- Jorio H, Brzezinski R, Heitz M. A novel procedure for the measurement of the kinetics of styrene biodegradation in a biofilter. J Chem Technol Biotechnol. 2005;80:796–804. doi: 10.1002/jctb.1245. [DOI] [Google Scholar]
- Jung I-G, Park C-H. Characterization of styrene degradation by Rhodococcus pyridinovorans isolated from a biofilter. Chemosphere. 2005;61:451–456. doi: 10.1016/j.chemosphere.2005.03.007. [DOI] [PubMed] [Google Scholar]
- Lu C, Lin M, Lin J. Removal of styrene vapor from waste gases by a trickle-bed air biofilter. J Hazard Mater. 2001;B82:233–245. doi: 10.1016/S0304-3894(00)00347-2. [DOI] [PubMed] [Google Scholar]
- Marconi AM, Beltrametti F, Bestetti G, Solinas F, Ruzzi M, Galli E, Zennaro E. Cloning and characterization of styrene catabolism genes from Pseudomonas fluorescens ST. Appl Environ Microbiol. 1996;62:121–127. doi: 10.1128/aem.62.1.121-127.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moser A. Bioprocess technology, kinetics and reactors. New York: Springer; 1988. [Google Scholar]
- Novak V, Paca J, Halecky M, Soccol CR. Styrene biofiltration in a trickle-bed reactor. Braz Arch Biol Technol. 2008;51:385–390. doi: 10.1590/S1516-89132008000200019. [DOI] [Google Scholar]
- Okamoto K, Izawa M, Yanase H. Isolation and application of a styrene-degrading strain of Pseudomonas putida to biofiltration. J Biosc Bioeng. 2003;95(6):633–636. [PubMed] [Google Scholar]
- Panke S, Witholt B, Schmid A, Wubbolts MG. Towards a biocatalyst for (S)-styrene oxide production: characterization of the styrene degradation pathway of Pseudomonas sp. strain VLB120. Appl Environ Microbiol. 1998;64:2032–2043. doi: 10.1128/aem.64.6.2032-2043.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pol A, van Haren FJJ, Op den Camp HJM, van der Drift C. Styrene removal from waste gas with a bacterial biotrickling filter. Biotech Let. 1998;20:407–411. doi: 10.1023/A:1023438517772. [DOI] [Google Scholar]
- Rene ER, Veiga MC, Kennes C. Biodegradation of gas-phase styrene using the fungus Sporothrix variecibatus: impact of pollutant load and transient operation. Chemosphere. 2010;79:221–227. doi: 10.1016/j.chemosphere.2010.01.036. [DOI] [PubMed] [Google Scholar]
- Ryu HW, Kim J, Cho KS, Jung DJ, Lee TH (2004) Biological treatment of air contaminated with styrene. In: Proceedings of Better Air Quality (BAQ) 2004, Agra, India, 6–8 December 2004. At www.clearairnet.org/baq2004/1527/article-59320.html. Accessed 12 March 2009
- Schuler ML, Kargi F. Bioprocess engineering. New Jersey: Prentice Hall, PTR; 2002. [Google Scholar]
- Sherrod PH (1997) Nonlinear regression analysis program (NLREG). Nashville, TN
- US Environmental Protection Agency (1994) OPPT chemical fact sheets. At http://www.epa.gov/chemfact/styre-sd.pdf Accessed 12 March 2009
- US Environmental Protection Agency (1999) Integrated risk information system (IRIS) on styrene (CASRN 100-42-5). At http://www.epa.gov/iris/subst/0104.htm. Accessed 12 March 2009
- US EPA (2011) EPA on-line tools for site assessment calculation. www.epa.gov./athens/learn2model/part-two/onsite/esthenry.html. Accessed 12 July 2009
- Velasco A, Alonso S, Garcia JL, Perera J, Diaz E. Genetical and functional analysis of the styrene catabolic cluster of Pseudomonas sp. strain Y2. J Bacteriol. 1998;180:1063–1071. doi: 10.1128/jb.180.5.1063-1071.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vodicka P, Koskinen M, Naccarati A, Oesch-Bartlomowicz B, Vodickova L, Hemminki K, Oesch F. Styrene metabolism, genotoxicity, and potential carcinogenicity. Drug Metab Rev. 2006;38(4):805–853. doi: 10.1080/03602530600952222. [DOI] [PubMed] [Google Scholar]