Growth, metabolic partitioning, and the size of microorganisms

Abstract

Population growth rate is a fundamental ecological and evolutionary characteristic of living organisms, but individuals must balance the metabolism devoted to biosynthesis and reproduction against the maintenance of existing structure and other functionality. Here we present a mathematical model that relates metabolic partitioning to the form of growth. The model captures the observed growth trajectory of single cells and individuals for a variety of species and taxa spanning prokaryotes, unicellular eukaryotes, and small multicellular eukaryotes. Our analysis suggests that the per-unit costs of biosynthesis and maintenance are conserved across prokaryotes and eukaryotes. However, the relative metabolic expenditure on growth and maintenance of whole organisms clearly differentiates taxa: prokaryotes spend an increasing fraction of their entire metabolism on growth with increasing cell size, whereas eukaryotes devote a diminishing fraction. These differences allow us to predict the minimum and maximum size for each taxonomic group, anticipating observed evolutionary life-history transitions. The framework provides energetic insights into taxonomic tradeoffs related to growth and metabolism and constrains traits that are important for size-structured modeling of microbial communities and their ecological and biogeochemical effects.

Understanding the fundamental principles that underpin the rates of growth and reproduction of organisms is of central ecological importance, ultimately affecting long-term evolutionary trajectories of populations and communities. The growth of an individual, including single cells, depends on multiple metabolic, biochemical, and physiological processes (e.g., refs. 1–6). Microbes exhibit a diversity of biochemical and metabolic strategies, making it difficult to evaluate and synthesize the associated fitness tradeoffs between species. How do different organisms allocate and manage internal metabolic resources to govern the complicated process of reproduction? Here we combine basic cellular bioenergetics with macroecological perspectives to produce a framework that is useful for examining and interpreting the growth trajectory of a single cell and also provides insight into major evolutionary patterns in population growth rates. The model is general and can be applied across a broad spectrum of species spanning two of the three domains (Eukarya and Bacteria) and four kingdoms (Bacteria, Fungi, Plantae, and Animalia).

Metabolic Perspectives

In general the growth and metabolism of organisms have been investigated at multiple levels of organization. At one end of this spectrum, experimental techniques are expanding our ability to track single cells through a division cycle, revealing the growth trajectories of individual organisms even at the microbial scale (Fig. 1) (7–12). At the population scale, single-species culture studies have been used to understand the relationship between resource use and growth rate (13–18). At the largest scale ecologists have looked across many species and taxa of organisms to characterize general power law relationships between body size and growth rate, metabolism, or other traits (e.g., refs. 19–21). Here we present a model that combines these three perspectives to understand the form for growth of single cells and populations of individuals for diverse organisms.

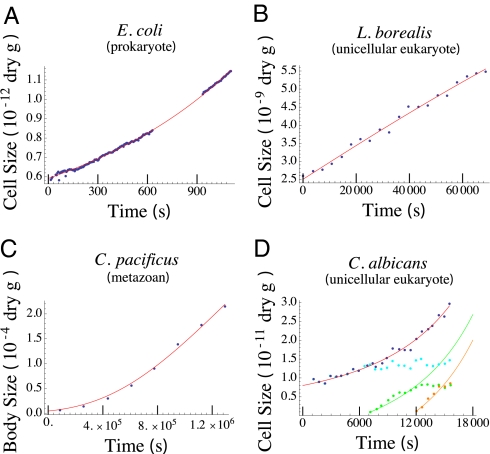
Fig. 1.

Growth curve of (A) E. coli data from refs. 8 and 9, (B) L. borealis from ref. 10, (C) C. pacificus from ref. 12, and (D) C. albicans from ref. 11. Dots indicate the cell mass as a function of time from the experiments in refs. 8–12. The red lines are the best fit of Eq. 8. The values of α, γ₀, and b that provide this best fit are given in SI Appendix, Table S4. For C. albicans (D) the red curve tracks the fitted growth of the total budding complex of yeast (blue points), whereas the green and orange points and curves represent the growth of individual daughter buds. The orange and green curves are predictions assuming that all growth energy from the entire complex is devoted to a bud as it forms (details in SI Appendix). The cyan points represent the growth of the mother cell, which is identical to the total complex until the formation of daughter buds. Data and model fits for additional individual cells are provided in SI Appendix, Figs. S4–S10.

Community Metabolism and Energetics.

We begin at the population scale, for which numerous continuous culture studies have been used to characterize microbial energetics. Typically, they reveal a linear relationship between biomass weighted resource consumption and growth (dilution) rate (13–18). The Pirt model (13) interprets this relationship in terms of a partitioning between growth and maintenance:

where Q is a consumption rate per unit mass of a limiting resource (mol resource⋅s⁻¹⋅g cells⁻¹), μ is the specific growth rate (s⁻¹), Y is a yield coefficient (g cells⋅mol resource⁻¹), and P is a maintenance term (mol resource⋅s⁻¹⋅g cells⁻¹) (a list of symbols is given in SI Appendix, Table S5). Maintenance metabolism is defined as the consumption rate at zero growth, or the minimal requirement for survival. The total consumption rate, Q, can be measured by oxygen use (14–16), light absorption (17), prey ingestion (18), or any other resource consumption rate that is assumed to be proportional to the total metabolic rate of the organism.

This perspective of cellular energetics has broad-ranging applications, from interpreting the metabolic drivers of food or biofuel production efficiency to understanding the energetics of human pathogens (22). Here we will use the Pirt model to phenomenologically motivate a relationship between single-cell growth and metabolic allocation, drawing analogies with population studies.

Interspecific Metabolism.

In a complementary view, power law relationships between body size and numerous organisms traits, including total metabolism, have been identified for organisms ranging from microbes to mammals (19, 20, 23). Recent theoretical work suggests mechanisms that underpin these scalings for multicellular organisms (e.g., refs. 21, 20, and 24). Total metabolic rate, B (W), is typically measured over several orders of magnitude and is expressed as

where B₀ (W g^−α) is a parameter reflecting the size-normalized metabolism and accounts for metabolic differences between organisms that are not related to size, including temperature dependence (SI Appendix). The exponent α describes how quickly total metabolism changes with body mass. There has been much debate over the value of the exponent of these scalings and its interpretation (e.g., refs. 25 and 26). Recent work shows that different broad groups of organisms follow characteristically different power relationships (27, 26), with α ranging from 1.96 for prokaryotes to 0.79 for metazoans (27).

Growth Trajectories of Single Cells and Individuals.

Models of cellular division have traditionally focused on the interconnected fluxes of available resources into the cell and between different internal physiological processes or partitions (e.g., refs. 3, 5, and 6) or on the kinetics of regulatory proteins (e.g., ref. 4). We consider a growth model for unicellular organisms that incorporates the basic energetic partitioning of the Pirt model along with metabolic scaling principles. The mass-specific consumption rate (Eq. 1) from the Pirt model of an entire population of cells can be related to the metabolic rate of an average single cell by

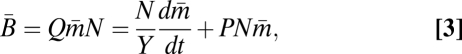where N is a conversion between resource use and energy production (J mol resource⁻¹). 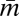and 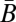are, respectively, the population average per-cell mass and metabolic rate. Eq. 3 implies that maintenance costs scale linearly with mass and that the unit cost of biomass production is constant (consistent with refs. 26 and 28–30). We also assume that the total metabolism of a single cell follows this relationship and is divided between the growth of new biomass and the maintenance of existing biomass, leading to the following single-cell model of metabolic partitioning:

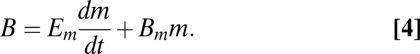Here B_m (W g⁻¹) is the metabolic expenditure to support an existing unit of mass, E_m (J g⁻¹) is the metabolic energy needed to synthesize a new unit of biomass, m (g) is the current mass of the organism, and dm/dt (g s⁻¹) is the growth rate of an individual. When B follows a power law with mass (Eq. 2) and is combined with Eq. 4, this set of assumptions is termed the ontogenetic growth model (e.g., refs. 26 and 28–30), which has previously been applied to multicellular organisms assuming a fixed value of α. Here we will treat α as a free parameter that might differ between species.

Normalizing by B, this single-cell budget can be expressed as the fraction of total metabolism being used for growth and maintenance

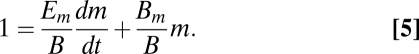Substituting B from Eq. 2, we can define the time-dependent fraction of metabolism devoted to growth and maintenance respectively as

Rearranging for dm/dt and integrating, we can describe the growth trajectory of an individual cell, with initial mass m₀, by

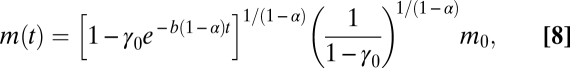(e.g., ref. 31), where b = B_m/E_m (s⁻¹) is the ratio of the maintenance metabolic rate to biosynthetic cost, and 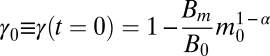is the fraction of metabolism devoted to growth for a cell at this initial mass (details in SI Appendix). Thus, given an initial mass, the growth trajectory m (t) depends on only three parameters: γ₀, b, and α. These parameters simply combine the fundamental biological quantities of E_m, B_m, B₀, and α.

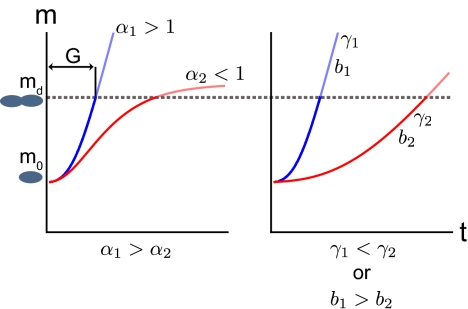
This solution for m (t) suggests a variety of possible forms for the growth trajectory of an individual, as shown schematically in Fig. 2 and for individual growth data in Fig. 1. The bioenergetic parameters α, b, and γ₀ exert a strong influence on the growth of an individual to division. A shorter generation time (faster division rate) is the result of increasing the metabolic scaling exponent α, increasing the initial percentage of metabolism devoted to growth γ₀, or increasing b, the ratio of the unit maintenance metabolism to the unit biosynthetic cost (illustrated in Fig. 2 A and B). Increasing α yields a greater total metabolism, and increasing the growth fraction γ₀ implies a greater fraction of metabolism devoted to biosynthesis. Similarly, increasing b alone requires decreasing the biosynthetic cost E_m (increasing B_m will simultaneously decrease γ₀), and this implies more efficient biosynthesis.

Fig. 2.

Schematic of the growth trajectories predicted by Eq. 8; the mass of an individual is plotted against time. Division occurs when the mass of the organism crosses the division mass, m_d. The relative contribution of the three metabolic parameters α, b, and γ₀ to division time are illustrated. In each panel species 1 (blue) is compared with a species (red), which is identical except for a change to one of the three parameters. Organisms will divide more quickly if the metabolic scaling exponent, α, or the ratio of the unit maintenance metabolism to unit biosynthetic cost, b, are increased or if the initial percentage maintenance, γ₀, is decreased. For α < 1, organisms grow toward an asymptotic mass, whereas for α > 1, organisms do not.

Previously, growth trajectories of single cells have been considered to follow either an exponential or linear relationship (e.g., refs. 7–9). The model described in Eq. 8 indicates additional forms for growth where an exponential is a special case of Eq. 4 with α = 1. For α > 1 the growth rate of an individual, and the fraction of metabolism devoted to biosynthesis, continues to increase with mass until division. For α < 1 an organism will grow toward an asymptotic mass (Fig. 2A), with growth rate initially increasing for young cells but decreasing as they approach division, and with the biosynthesis fraction decreasing over the entire life cycle.

Growth of Populations.

A common measure of fitness in an ecosystem is the population growth rate, μ, of a species. The single-cell (or single-individual) model of Eq. 8 can be evaluated to provide the generation time G (28), the time for one organism to reach reproductive mass, M_d ≡ εm₀,

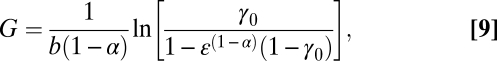where for simple fission ε ∼ 2. Following ref. 32, the population growth rate, μ, is given by this generation time along with the average fecundity, f, and percentage of the population to reach the age of reproduction, L:

Considering simple fission one could assume that μ_max ∼ ln(2)/G.

Bioenergetics of Species and Taxa

Here we fit the framework outlined above to observed growth trajectories of single cells (or single individuals) and to data relating population growth rate to body size. We compare the underlying bioenergetics of different species, as represented by the parameters of our framework, using these fits along with separate estimates obtained from growth-resource consumption data for populations of cells.

We compiled published measurements of the size of single cells as they grow through a division cycle for five species, including the heterotrophic bacteria Escherichia coli (8, 9) and Bacillus subtilis (7), two photo-autotrophic marine diatoms (Thalassiosira weissflogii and Lauderia borealis) (10), as well as budding yeast Candida albicans (11). In addition, we used growth data for individuals from two small (submillimeter), multicellular marine copepods (Calanus pacificus and Pseudocalanus sp.) (12). Fitting model Eq. 8 to the time-changing size of each individual, we infer the values for b, γ₀, and α (SI Appendix, Table S4).

We found that Eq. 8 was able to accurately describe the growth trajectories of unicellular and small multicellular individuals from two of the three domains (Eukarya and Bacteria) and four kingdoms (Bacteria, Fungi, Plantae, and Animalia) (Fig. 1 and SI Appendix, Figs. S4–S10).

We were able to estimate a single interspecific value of α and the bioenergetic parameters by fitting Eq. 10 to compiled measurements (27) of population growth rate and body size. We also compiled continuous culture experiments to estimate the bioenergetics of a single species at the population scale. Combining Eqs. 1, 3, and 4, the population average value for b can be evaluated from continuous culture data as 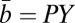, summarizing all of the information of a standard “Pirt plot.” Similarly, the average fraction of metabolism devoted to growth is given by

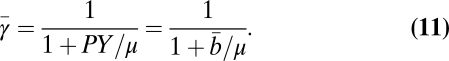Here the fraction of metabolism devoted to growth has a simple meaning in terms of the dimensionless parameter 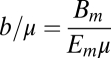, rep-resenting the ratio of maintenance and biosynthesis rates per unit mass.

Variation in α, the Metabolic Exponent.

Metabolic considerations of ecology often emphasize the scaling exponent α, with macroecological compilations revealing relatively constant values for α over large ranges of body size. Here, our evaluations of α from individuals reveal considerable variation at both the species and single-cell level (Fig. 3C and SI Appendix, Table S4). For individual E. coli cells the exponent varies between 0.57 and ≈3, although all have a similar form to their growth trajectory (Fig. 1A and SI Appendix, Fig. S4) because of the short timescale for division.

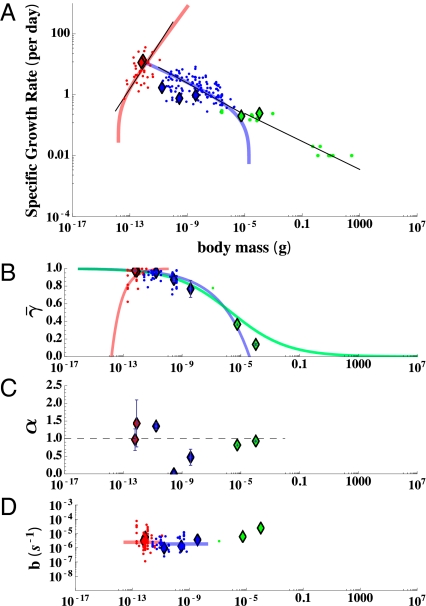
Fig. 3.

(A) Interspecific plot of specific growth rate (day⁻¹) against size along with the metabolic constants (B−D) inferred from fits of our model to individual growth trajectories all plotted against organism mass. The prokaryotes are colored red, the eukaryotes blue, and the small metazoans green. In each panel diamonds represent the results for single individuals, whereas the points are estimates from compiled population studies (ref. 27 for A; our own compilation for C and D). In A the colored curves represent the best fit of the framework to interspecific growth using Eqs. 9 and 10, whereas the black curves are the best fit power law relationships (27). The asymptotes illustrate the size limitations of prokaryotes and unicellular eukaryotes. (B) The average percentage of metabolism devoted to growth, 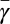, illustrates the differences in metabolic partition across the three major taxonomic groups (for prokaryotes there is a dense clustering of points near 1 that is not visible). The colored curves are predictions based on fits from A. (C) The metabolic scaling exponent, α, shows variation at the species and taxonomic levels where the dashed line represents α = 1. (D) The maintenance to biosynthesis cost ratio, b, is on average constant across species and major evolutionary transitions, and the colored curves represent the mean value for each taxon. Error bars represent the SD from the mean of each parameter but do not include the statistical confidence of each nonlinear fit (SI Appendix).

The cell-to-cell variation in the exponent could be the result of a variety of physiological effects at the individual scale, including natural phenotypic variability, fine-scale differences in experimental conditions, or the prior history of each cell. As well as variation within a species we also find that the average exponent for a species often deviates significantly from the interspecific value for each of the three major taxonomic groups. For example, for the prokaryote B. subtilis α = 0.98 ± 0.30, significantly different from the interspecific value of 1.96 ± 0.18 based on a range of prokaryotes (27). We thus illustrate that the general constraints that are hypothesized to organize allometric scalings at the taxonomic level can be substantially violated at the single-species level. This is perhaps least surprising for prokaryotic organisms (Discussion), but it should be noted that deviations of this magnitude may be significant when attempting to apply uniform scalings and parameterizations in ecological models.

We also obtain an interspecific estimate of the metabolic exponent, α, by fitting our population model (Eq. 10) to the data for growth rate against body size for many species (SI Appendix). We find that that the fitted values of α agree with the compiled data (27) for metabolic rates (we find 1.66 for prokaryotes and 0.80 for eukaryotes). The fitted curves accurately capture the interspecific form for growth (Fig. 3A), which is normally fit by a power law (also drawn in Fig. 3A). The model fitted here is more complicated than a simple power law, but it brings to bear additional information in the form of fundamental bioenergetic constraints (i.e., unit biosynthetic costs), discussed in detail below. The model approximates a simple power law over much of the size range of the organisms under examination.

Common Energetic Costs.

From the fits to individual cells we find that b, the ratio of the unit maintenance metabolism to biosynthetic cost, ranges between ≈10⁻⁶ and ≈10 ⁻⁵ s⁻¹ but exhibits no trend with body size (Fig. 3D and SI Appendix, Table S4 and Datasets S1 and S2) nor any clear distinction between the three major evolutionary life-history groups (prokaryotes, single-cell eukaryotes, metazoans). Compiled population-based estimates, 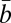, covering a variety of prokaryotic and eukaryotic species, also show no trend with size or taxonomic grouping (Fig. 3D) but have a greater variance (more than an order of magnitude) owing to the range of culture conditions and growth on different substrates (SI Appendix, Fig. S1 and Table S2). Although noisy, the relative constancy of b across cell size and between taxa suggests a fundamental bioenergetic commonality (Discussion).

Variations in Metabolic Partitioning.

Given Eq. 7, the metabolic partitioning should follow a relationship that depends on the size of an organism, the unit bioenergetic costs (represented by b), and the value of α. Because b is on average constant, this implies that we should see changes in the partitioning across taxa based on changes in the metabolic scaling exponent α. Using Eq. 11 and the interspecific fit for μ (Fig. 3A) it is possible to predict the interspecific dependence of 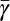on mass for each species and taxa. In Fig. 3B we provide the predicted curves for the metabolic partitioning of prokaryotes, unicellular eukaryotes, and small multicellular organisms. For prokaryotes the percentage of metabolism devoted to growth is constantly increasing with increasing body size, whereas for eukaryotes it is constantly decreasing. This is associated with the change in the interspecific value of α, which is >1 for prokaryotes and <1 for eukaryotes. The fits to single-cell growth trajectories provide an estimate for the average metabolic partitioning, 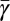. These species-specific points generally follow the predicted curve (Fig. 3B). For population-based estimates we used the compilation of continuous culture data to estimate 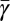for each species; these also fall generally along the predicted curve.

This analysis reveals that large prokaryotes and small eukaryotes devote the highest fraction of total metabolism to growth, and there is a size range for which the two classes have similar metabolic partitioning. Here we infer a tradeoff between devoting resources to maintenance purposes and dividing quickly, which is most easily seen by normalizing each growth trajectory (SI Appendix, Fig. S2).

Bioenergetic Limitations and Differing Reproductive Strategies.

Given a set of bioenergetic parameters, the model presented here predicts some general limitations and constraints facing different classes of organism. First we note that a viable organism must allocate metabolic resources to growth at its initial size, that is, γ₀ > 0. This implies a limitation on the initial mass dependent on the metabolic scaling:

This gives a lower bound on size if α > 1 and an upper bound on size if α < 1. These limitations appear as the asymptotes in Fig. 3A for our fitted population growth equation. For prokaryotes this model predicts a lower bound on size of 1.59 × 10⁻¹⁴ g, which is close to the mass of the smallest observed prokaryotes, of the genus Mycoplasma, which are between 1.2 and 4 × 10⁻¹⁴ g (27, 33). For unicellular eukaryotes we predict an upper bound on size at 3.89 × 10⁻⁵, which corresponds to the general scale at which there is a major evolutionary life-history transition to multicellularity.

As prokaryotes grow larger, and as eukaryotes grow smaller, they move away from the limit where all energy is devoted to maintenance. In doing so the fractional allocation of metabolism devoted to growth approaches unity for large prokaryotes and small eukaryotes (Fig. 3B), and this imposes a different limitation: at some point the increasing biosynthetic rates cannot be sustained by the fundamental processes of the cell (Discussion). The transition from prokaryotes to eukaryotes shifts the metabolic exponent such that the unit biosynthesis rates begin to decrease with increasing body size, allowing eukaryotes to grow larger.

In summary, the minimum size for prokaryotes is bounded by the limit at which all energy is devoted to maintenance, whereas the maximum size is bounded by the demand for unsustainable biosynthesis rates. The transition to unicellular eukaryotes is accompanied by shifts in physiology and metabolic scaling, which allow them to devote an increasing fraction of total metabolism to maintenance with increasing size. Hence their lower size limit is bounded by unachievable biosynthesis rates, whereas the largest unicellular eukaryotes face a limit at which they cannot allocate any metabolic energy to biosynthesis, setting the stage for the transition to multicellularity. Here there is not a dramatic shift in the metabolic scaling, rather the more advanced body plans of multicellular organisms afford more complicated reproductive strategies, such as internal gestation and individuals hatched from an egg, resulting in various alterations to the generation time as represented by Eq. 9.

The importance of reproductive strategy in the eukaryotes is illustrated by the budding yeast C. albicans, which reproduces in a manner that differs from the standard fission of unicellular eukaryotes. For a complex of budding yeast, as new buds form other parts of the complex reach an asymptotic size (Fig. 1D), which would suggest that α < 1. However, fits of the model (Eq. 8) to the entire complex yield α = 1.14 ± 0.07. The asymptotic size reached by each bud is not the result of a metabolic limit but is rather due to the entire complex sharing metabolic resources. The growth of the buds can be predicted by assuming that the bud is using all of the growth energy of the entire complex (SI Appendix). Buds grow more rapidly because of the assistance of the entire complex than if growing in isolation. This strategy illustrates how the upper bounds proposed by our model can be overcome and how they could lead to the transition to multicellular life because of the corresponding growth advantage.

Discussion

Simplified models of cellular growth and metabolism are widely applied in laboratory and ecological contexts. Macroecological descriptions generally capture broad trends across many species and highlight major patterns in biology but often lack the ability to interpret differences between species or describe detailed cellular processes. At the other end of the spectrum, explicit models of cell division attempt to capture the interconnected dynamics of internal biochemistry, external resources, and/or physiological regulation (e.g., refs. 3 and 4), often using metabolic reconstructions from whole genomes (e.g., refs. 6 and 34). Here we have developed and applied a relatively simple framework that combines macroecological and energetic perspectives. It provides insight into single-cell growth dynamics and is also useful for considering interspecific and taxonomic trends in population growth. We have used the model to show how organisms in different taxonomic groups are subject to different constraints on metabolic expenditure at the individual scale, allowing the model to anticipate and interpret three major evolutionary life-history transitions from a metabolic partitioning perspective.

Many macroecological studies (e.g., refs. 21 and 25) have found a single value (2/3 or 3/4) for the scaling exponent for metabolism with body size, α. However there is recent empirical evidence for taxonomic specific α (27). In this study, it was critical to allow α to be a free parameter to accurately interpret the bioenergetics of individual microbial species (SI Appendix). We find that α not only varies between taxa (27) but also between cells of an individual species and between species of the same taxonomic group. The averages over many species and individuals (i.e., the interspecific values) of α reveal the broad physiological organization of different taxa. Variation around these values illustrates that individual species can modify their physiology away from the general constraints facing a class of organisms.

In contrast to the taxonomic variations in α, we find that the average value of b (the ratio of unit maintenance metabolism to biosynthesis cost) is unchanging across major evolutionary transitions and has no significant trend with body mass within or between taxa. This suggests that the basic, per-unit mass costs of biosynthesis and maintenance are common across broad taxonomic divides; these energetic costs are likely related to highly conserved, common metabolic machinery and function (27, 35). This is consistent with the success of thermodynamic interpretations of the yield, Y, which is a predictable function of the substrate in heterotrophic microbes (36, 37). However, b also requires an understanding of the maintenance metabolism P, whose fundamental meaning still requires future investigation.

The framework developed here is broad and flexible and can capture the interspecific relationship between growth rate and body mass in microorganisms using the interspecific value of α for each taxon and a single average value of b. Because b is, on average, a constant value, the interspecific trend in metabolic partitioning (represented by γ) is also dictated by body size and α (e.g., Eq. 11). By compiling laboratory data within this framework, we have a vehicle to interpret and hypothesize the taxon-specific energetic limitations to population growth and their relationship to body size (Fig. 3A and Eq. 9). We can anticipate the minimum and maximum size of prokaryotes and eukaryotes and suggest the body size at which shifts between evolutionary life-histories occur.

Prokaryotes are bounded by a minimum size below which they are unable to conduct biosynthesis because all metabolism must be devoted to maintenance. As they become larger, growth rate continually increases up to a maximum size at which higher biosynthesis rates are not achievable.

The smallest known prokaryotes are similar in size to the predicted lower bound and also possess the smallest observed genomes, which are assumed to be close to the minimum required to live alone in culture (33). Our framework therefore suggests that the minimal genome is defined by the limit at which biosynthesis is just viable. We hypothesize that larger prokaryotic genomes allocate an increasing fraction of genes to biosynthesis, corresponding to an increase in the fraction of metabolism devoted to growth. This is consistent with the argument that the interspecific scaling of prokaryotic metabolism is due to a relationship between body size, genome length, the overall metabolic complexity of prokaryotes, and their ability to encode for a diverse set of enzymes (27). However, genome length does not change over the life cycle of an individual cell, and thus it is unclear what sets the scaling of metabolism at the single-cell scale.

Many other factors may contribute to metabolic scaling at the single-species level. New techniques to track the transcriptional composition of a population have revealed that prokaryotic cells can maximize growth rate by adjusting the partitioning of transcriptional resources between producing basic components for protein synthesis (amino acids) or building more ribosomes to construct them (38). Faster-growing cells are observed to allocate a greater proportion of promotor activity to ribosomes than to metabolism (38). Our finding that population growth rate increases as the fraction of total metabolic resources devoted to growth increases is consistent with this observation (Eqs. 6 and 11). Further experiments could be designed to seek correlations between transcriptional partitioning or the number of ribosomes and variations in metabolic scaling, bioenergetic parameters, and metabolic partitioning of particular prokaryotic species.

We hypothesize that the maximum size for prokaryotes is determined by a point at which the overall biosynthesis rates cannot be met by basic cellular processes. For example, prokaryotic genome length increases with body size following a power law (27), whereas the generation time decreases with body size according to Eq. 9, and this predicts that at some point the time to replicate the genome will be slower than the generation time (e.g., the maximum nucleotide copying rate is insufficient). Another possibility is that at some point the number of ribosomes required for protein synthesis cannot fit within the cell because cell volume scales more slowly than biosynthesis rates.

The framework developed here suggests that eukaryotes, in contrast to prokaryotes, exhibit a decrease in metabolism and population growth rate with body size, also consistent with ref. 27. Smaller eukaryotes allocate all of their metabolism to growth and cannot be any smaller and still achieve the required rate of biosynthesis (eukaryotes moving towards smaller size is analogous to prokaryotes moving toward larger size). As cell size increases, expenditure on maintenance is enhanced. Eventually, the single-celled eukaryotes reach a size at which they are devoting all metabolism to maintenance and, with no energy for biosynthesis, they are no longer viable. Beyond this upper size limit, other strategies come into play, including multicellularity.

It seems that the transition between prokaryotes and eukaryotes is accompanied by a fundamental shift in strategies for metabolic partitioning, consistent with significant differences in their basic physiology. For example, the average number of proteins made per mRNA is an order of magnitude higher in eukaryotes than in prokaryotes (39), implying that eukaryotes are able to produce far more proteins for the same amount of transcriptional resources. Eukaryotes are also able to expend an order of magnitude greater metabolic power on each gene, regardless of function, compared with prokaryotes (40), which may alleviate genome length or transcription-related constraints. The increased metabolic power for eukaryotes has been hypothesized to be the result of the presence of mitochondria, which create a greater internal surface area for ATP production (40). Similarly, the metabolic exponent for unicellular eukaryotes is hypothesized to be the result of the linear scaling between mitochondrial volume and overall cell volume (27). These hypotheses could potentially be tested by correlating estimates of α with concurrent measurements of the total mitochondrial volume in a cell.

Our framework suggests that the bioenergetic limitations of binary fission faced by the simplest unicellular eukaryotes may be overcome by the development of more-complicated reproductive strategies. This is consistent with the transition to more-elaborate body plans and the increasing presence of internal distribution networks that are argued to underpin the metabolic scaling (i.e., value of α) observed across a vast range of multicellular body sizes (27). Although the basic metabolic framework outlined here can be expanded to account for altered reproductive strategies (e.g., budding yeast), certain reproductive strategies, such as resting or dormant phases, highlight the limitations of this framework when trying to estimate metabolic scalings from the growth trajectories of individuals alone (e.g., T. weissflogii; see SI Appendix). To better constrain α and to test the role of reproductive strategy, simultaneous determinations of body size and resource consumption could provide critical information.

Conclusion

We have developed a framework to characterize the growth and division of individual cells. We have used it to interpret the metabolic scaling, bulk bioenergetics, and metabolic partitioning of diverse species using the growth trajectory of individuals and laboratory populations. We find that the relative per-unit metabolic costs of biosynthesis and maintenance are the same for prokaryotes, unicellular eukaryotes, and small metazoans, cutting across major evolutionary life-history transitions. In contrast, prokaryotes and eukaryotes have fundamentally different strategies and limitations in the allocation of their metabolic resources, which coincide with the observed evolutionary transitions. The allocation of all metabolic resources to maintenance purposes limits the size of the smallest prokaryotes and largest unicellular eukaryotes, whereas an inability to meet the ever-increasing biosynthesis rates limits the largest prokaryotes and smallest unicellular eukaryotes. Metabolic constraints for larger eukaryotes are relieved by alternative reproductive strategies and multicellularity.

The metabolic theory has traditionally focused on average values and general principles across many species; here we illustrate strong variation of the metabolic size-scaling exponent at the individual species level. This framework provides avenues for connecting metabolic scaling to cellular characterizations such as genome length, or the partitioning of transcriptional resources, which may help to further elucidate the fundamental factors driving the evolutionary shifts discussed in this article. This framework connects ecological fitness with basic bioenergetics, and it may provide a mechanistic strategy for incorporating taxonomic differences into size-based approaches for modeling microbial systems (e.g., refs. 41 and 42) to better understand complex microbial communities and their role in biogeochemical cycles.