Abstract
Allostery has been studied for many decades yet it remains challenging to determine experimentally how it occurs at a molecular level. We have developed an approach combining isothermal titration calorimetry, circular dichroism, and nuclear magnetic resonance spectroscopy to quantify allostery in terms of protein thermodynamics, structure, and dynamics. This strategy was applied to study the interaction between aminoglycoside N-(6′)-acetyltransferase-Ii and one of its substrates, acetyl coenzyme A. It was found that homotropic allostery between the two active sites of the homo-dimeric enzyme is modulated by opposing mechanisms. One follows a classical KNF paradigm while the other follows a recently-proposed mechanism in which partial unfolding of the subunits is coupled to ligand binding. Competition between folding, binding, and conformational changes represents a new way to govern energetic communication between binding sites.
Allostery is a key feature of biological systems in which covalent modification or ligand binding at one site influences the activity at distant sites in a macromolecule or macromolecular assembly. Allosteric regulation plays a central role in metabolism and cell signaling, and has been identified as a source of new drug targets1–5. Thus detailed descriptions of allostery have far reaching implications. A number of systems have been explained in terms of mechanistic models, yet allostery takes a variety of forms and many details of this phenomenon remain unresolved6–9. Homotropic allostery (or homotropic cooperativity) involves interactions between a macromolecular system and two or more identical ligands. Cooperativity implies that binding depends on the ligation state, i.e. the first ligand is bound with a different affinity than the second, etc. This occurs frequently in oligomeric proteins and many theoretical models have focused on such systems. For example, in the Monod-Wyman-Changeux (MWC) model, ligand binding leads to simultaneous conformational changes in all subunits of an oligomeric protein, thereby altering their binding affinities for the next ligand(s)2. In the Koshland-Nemethy-Filmer (KNF) model, free and bound subunits adopt different conformations, and cooperativity results from inter-subunit interactions5. Recently, Hilser and Thompson (HT) have proposed a model in which allostery is mediated by coupled folding and binding of adjacent protein domains or subunits10. A key difference between these last two paradigms is that the KNF model assumes that conformational changes occur only upon ligand binding, while the HT model explicitly includes conformational equilibria in the unbound subunits. The MWC, KNF, and HT models are illustrated schematically in Figure 1. Other allosteric models have also involved coupled folding and binding11, invoked changes in protein flexibility12–14, or networks of interacting amino acid residues15–16, and emphasized the role of shifting populations within conformational ensembles17–23.
Figure 1.
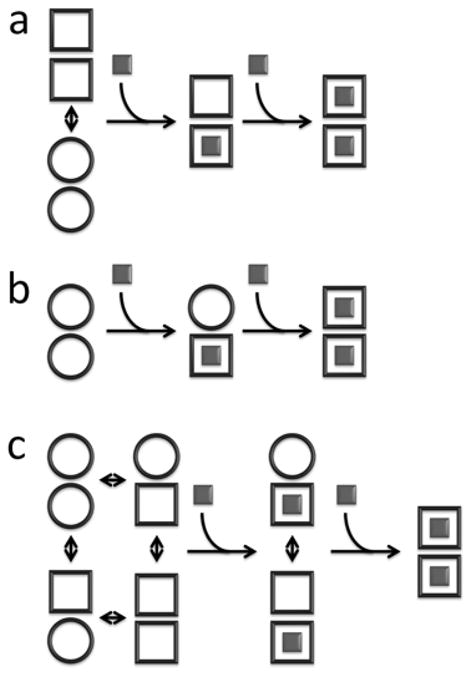
Schematic representation of homotropic allosteric models for a dimeric protein. ○ and □ correspond to subunits in binding-incompetent, and binding-competent states, respectively. (a) Monod-Wyman-Changeux (MWC): The symmetry of the dimer is preserved, so that only ○○ and □□ states are permitted. In the absence of ligand, both states are populated, while ligand binding forces the dimer into the □□ state. If the initial equilibrium favors the ○ ○ state, binding is positively cooperative, since the energetic cost of the ○ ○ to □ □ transition is paid by binding the first, but not the second ligand. Note that in the standard MWC model, both ○ ○ and □ □ bind ligand, but with different affinities. For the sake of simplicity we have shown the limiting case where ○ ○ is binding-incompetent. (b) Koshland-Nemethy-Filmer (KNF): Each subunit converts from the ○ to the ○ state only upon binding ligand. Cooperativity is explained in terms of the strengths subunit-subunit interactions. If the transition from the ○ ○ to ○ □ interface is energetically more favorable than from the ○ □ to □ □, binding is negatively cooperative, and the first ligand is bound more strongly than the second. If the transition from the ○ ○ to ○ □ interface is less favorable than from the ○ □ to □ □, binding is positively cooperative, and the second ligand is bound more strongly than the first. (c) Hilser-Thompson (HT): In this case, ○ and □ correspond to the unfolded and folded states, respectively. Each unbound subunit can populate either the folded or unfolded state, and the folding equilibrium is influenced by the state of the adjacent monomer. If folding (□) of one subunit promotes folding (□) of the adjacent subunit, binding is positively cooperative. Conversely, if folding (□) of one subunit promotes unfolding (○) of the adjacent subunit, binding is negatively cooperative.
We have used a combination of nuclear magnetic resonance (NMR), isothermal titration calorimetry (ITC), and circular dichroism (CD) spectroscopy to characterize the allosteric mechanism of acetyl coenzyme A (AcCoA) binding to aminoglycoside N-(6′)-acetyltransferase-Ii (AAC(6′)-Ii) from Enterococcus faecium. This homo-dimeric enzyme confers bacterial resistance to aminoglycoside antibiotics by transferring an acetyl group from AcCoA to the 6′-N position of the drugs24. The structure of AAC(6′)-Ii has been solved by X-ray crystallography, with CoA, AcCoA25–27, or inhibitors28 bound in the two active sites of the homo-dimeric enzyme. It has recently been shown that AAC(6′)-Ii binds two molecules of AcCoA with positive cooperativity, likely reflecting energetic coupling between the active sites29. We find that this interaction varies unexpectedly with temperature, shifting from positive to negative cooperativity as the temperature is raised. This behavior can be quantitatively explained in terms of a novel arrangement in which an HT-type coupled folding and binding mechanism is superposed on a classical KNF-type interaction. This finding provides experimental validation for the recently-proposed HT paradigm, and to our knowledge represents the first example in which it appears in the context of a hybrid allosteric mechanism.
Results
Isothermal Titration Calorimetry
A total of 28 ITC experiments were performed at 8 temperatures ranging from 10 to 40°C, titrating AcCoA into solutions of AAC(6′)-Ii (Supplementary Fig. 1 online). All ITC data were fitted simultaneously to a sequential two-site binding model, using a global strategy that exploits the van’t Hoff relationship to improve the accuracy of extracted binding parameters (see Supplementary Methods online). This method yields apparent equilibrium association constants (KA1app, KA2app) and enthalpy changes (ΔHA1app, ΔHA2app) for binding of the first and second molecules of AcCoA to the enzyme as a function of temperature (Fig. 2a,b, Supplementary Table 1 online). At 10°C, KA2app > KA1app, indicating that the second molecule of AcCoA binds more tightly than the first and the interaction is positively cooperative. The difference between KA2app and KA1app decreases as the temperature increases and the situation reverses to negative cooperativity, KA2app < KA1app, starting at around 37°C.
Figure 2.
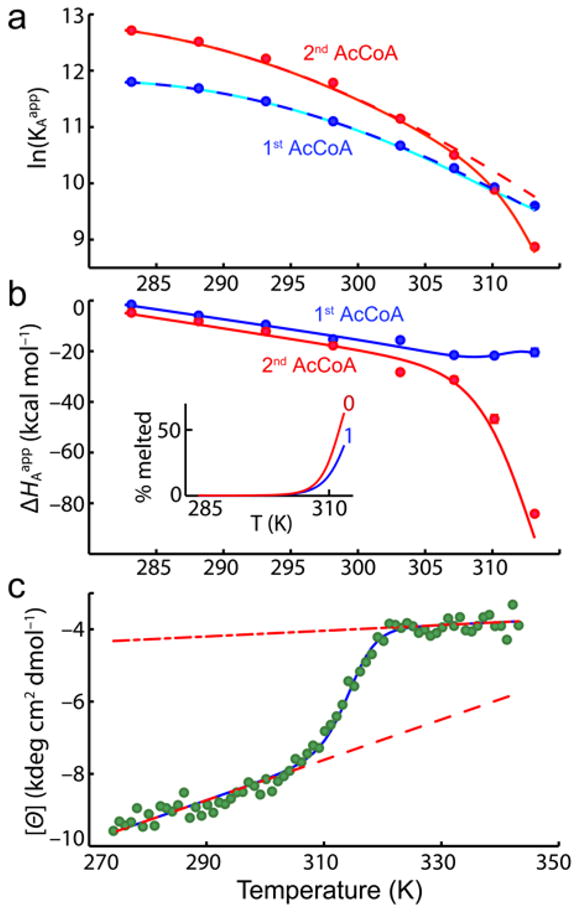
Temperature dependence of AAC(6′)-Ii binding thermodynamics and secondary structure. (a) Equilibrium association constants for the first and second molecules of AcCoA, plotted as a function of temperature. Solid lines correspond to the best fit obtained with Eqs. 2 to 9. Dashed lines indicate the predicted affinities in the absence of thermal melting of the subunits. (b) Binding enthalpies of the first and second molecules of AcCoA. Inset shows the fraction of free subunits that are melted in the 0-bound and 1-bound forms. (c) Molar ellipticity (222 nm) of AAC(6′)-Ii as a function of temperature. Dashed and dash-dot lines correspond to the pre- and post-transition baselines, respectively.
In many systems, the binding enthalpy depends linearly on temperature with a slope equal to the difference in heat capacity between the bound and free forms. In contrast, for AAC(6′)-Ii, the binding enthalpies for the first and second molecules of AcCoA (ΔHA1app, ΔHA2app) exhibit curvature above about 30°C. ΔHA1app deviates slightly upwards, while ΔHA2app exhibits a sharp decrease. Curved enthalpy profiles of this sort are characteristic of systems that populate both an active free form (F) and an inactive partly unfolded or fully unfolded form (U) that is higher in enthalpy, within the temperature range studied30–32. At low temperatures (Fig. 2a,b), almost all protein molecules are in the active F state and ITC detects the intrinsic heat of binding, i.e. the difference in enthalpy between the bound (B) and F states. At high temperatures, free proteins populate the inactive U state. When ligand is added, the proteins must both fold and bind (U→F→B) and ΔHAapp contains contributions from both folding and the intrinsic binding enthalpy. We show below that the curvature in both the ΔHA1app and ΔHA2app profiles can be quantitatively explained by a model involving multiple states with coupled partial unfolding of the two enzyme subunits.
Circular Dichroism Spectroscopy
The CD spectrum of AAC(6′)-Ii was monitored at 222 nm, from 0.1 to 71°C in the absence of AcCoA. The molar ellipticities of both alpha-helices and beta-sheets are large and negative33–34, while those of unstructured polypeptides are close to zero or slightly positive at this wavelength33–35. The CD data show a sigmoidal decrease in the absolute molar ellipticity from about 35 to 45 °C (Fig. 2c). Curvature of the ITC-derived binding enthalpies is observed within the same temperature range. These data are thus consistent with an endothermic transition from the native free F state to a partly or fully unfolded U state that is unable to bind AcCoA, at around 40°C. We investigated whether the AAC(6′)-Ii dimer fully dissociates when subunits are in the U state by repeating the CD experiments with the enzyme concentration reduced by about a factor of three. If unfolding and dissociation are concurrent, then lowering the concentration by a factor of 3 would be expected to reduce the melting temperature by approximately , where ΔHU is the enthalpy of the transition at the midpoint temperature, TU. Using the values obtained from the joint ITC/CD fitting described below, this predicts a reduction in the midpoint temperature of 2.7°C. The two CD traces are nearly superimposable and yield midpoints that differ by only about 0.1°C (Supplementary Fig. 2 online).
We therefore conclude that the transition to the U state does not involve the complete loss of structure and dissociation of the subunits, but rather involves partial unfolding that leaves the dimer intact. This is supported by the observations that the enzyme elutes from size-exclusion chromatographic columns as a dimer, even in dilute solutions, and that binding cooperativity is not affected by protein concentration29.
Nuclear Magnetic Resonance Spectroscopy
Two dimensional 1H/15N NMR correlation spectra of AAC(6′)-Ii in the free (apo) and ligand-saturated (holo) forms provide evidence that large structural and dynamical changes accompany AcCoA binding (Fig. 3a,b). The apo-spectrum contains only about 137 distinguishable backbone amide peaks, 60 of which are baseline-separated, while 172 signals are expected (Fig. 3a). The remainder of the signals are either located in a highly overlapped region in the center of the spectrum, or are absent altogether, possibly due to dynamical broadening or rapid hydrogen exchange with water. In contrast to the free form, the spectrum of the AcCoA-saturated enzyme is typical of a folded globular protein, containing about 166 well-resolved backbone amide resonances, 89 of which are baseline-separated (Fig. 3b). This suggests that in the absence of AcCoA, much of the protein is highly mobile or partially disordered, while a few ordered regions give rise to a number of well-dispersed signals. As a result, it was not possible to assign the apo spectrum directly. Nevertheless, we were able to transfer 32 assignments from the holo to the apo spectrum, based on 2D exchange spectroscopy (EXSY) experiments36 and the superposition of some peaks in both spectra. On average, one in every 6 residues in the apo spectrum of AAC(6′)-Ii has been assigned. Therefore it is notable that a stretch of about 46 residues, from 105 to 150, gives rise to no assigned peaks (Fig. 3c (red), and Supplementary Fig. 3 online). This region is implicated in undergoing extensive dynamical broadening in the free form of the enzyme. The NMR measurements were performed under stabilizing conditions where free subunits are almost entirely in the F state. The U state, which predominates at higher temperatures, is presumably even less structured.
Figure 3.
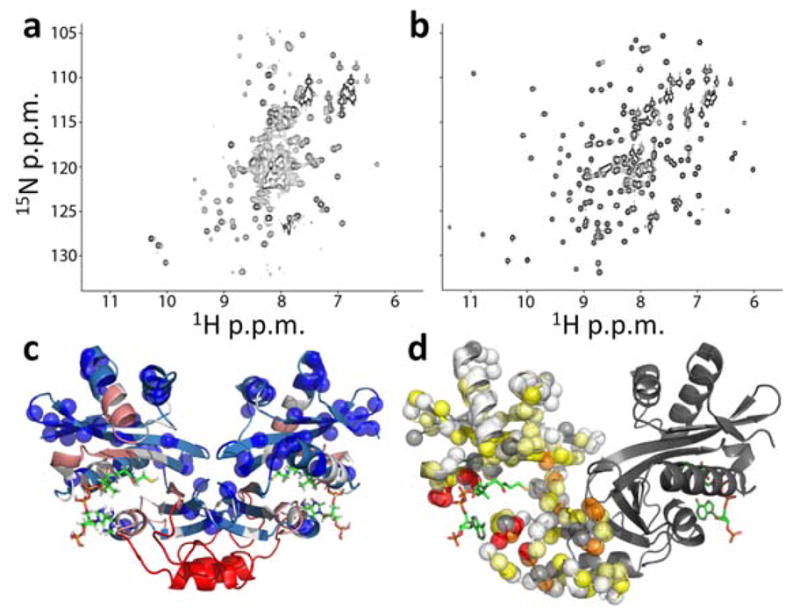
Changes in AAC(6′)-Ii NMR spectra produced by AcCoA binding. (a,b) 1H/15N correlation spectra of AAC(6′)-Ii free (a) and saturated with AcCoA (b). (c) X-ray crystal structure of the enzyme (PDB 2A4N25) bound to CoA (sticks) with blue spheres indicating the locations of residues with assigned cross-peaks in apo spectra. The backbone is color-coded according to the distance in the 1° sequence (n) from the nearest assigned residue according to 1≤n≤2 (light blue), 3≤n≤5 (white), 6≤n≤10 (pink), n>10 (red) (d) Apparent minimal chemical shift differences ( ) between the free and bound states, mapped onto the X-ray crystal structure (PDB 2A4N25). Backbone amide nitrogen atoms are indicated with spheres for one subunit of the dimer and colored according to Δδapp<0.5 ppm (white), 0.5≤Δδapp<1 (light yellow), 1≤Δδapp<2 (yellow), 2≤Δδapp<4 (orange), 4≤Δδapp (red). Unassigned residues, including prolines, are indicated with gray spheres. Structures were generated using PyMOL.
Information on the conformational transition from the active free (F) to the bound (B) states can be obtained from a comparison of the apo and holo spectra. Several of the well-resolved apo-peaks due to F disappear upon addition of AcCoA (for example Leu56, located 15 Å from the active site). This strongly suggests that the free enzyme adopts a distinctly different configuration than that of the bound enzyme. It is unlikely that dynamical broadening in the unbound enzyme is due to excursions between the “free” and “bound” conformations in the absence of AcCoA. Millisecond-timescale exchange between F-type and B-type configurations would preferentially broaden signals whose chemical shifts change the most upon AcCoA binding. This is not apparent. Furthermore, no holo signals are observed when AcCoA is not present. We therefore conclude that the population of B-type conformations in the absence of AcCoA is below our detection limit (≈1%). As discussed above, only a relatively small number of spectral assignments could be obtained for the unbound enzyme. Thus in order to map ligand-induced changes onto the protein structure, we calculated minimum chemical shift differences (Δδapp)37, which are defined as the distance between each holo-peak and the nearest signal in the apo-spectrum. All residues with large values of Δδapp either have very different chemical shifts in the free and bound forms, or are broadened beyond detection in the free form of the protein. Large values of Δδapp are obtained throughout the protein, notably including residues located at the interface between the two subunits and near the bound AcCoA (Fig. 3d). This suggests that binding AcCoA leads to remodeling of subunit interactions, and provides some insight into the mechanism for allosteric communication between the two active sites, as discussed below.
A series of two-dimensional protein NMR spectra were recorded as AcCoA was titrated into a sample of AAC(6′)-Ii. In what follows, apo and holo are used to describe peaks appearing in NMR spectra of the AcCoA-free and AcCoA-saturated protein, and 0-bound, 1-bound, and 2-bound to describe the various ligated states of the enzyme. Binding occurs slowly on the NMR chemical shift timescale therefore both apo and holo peaks are simultaneously visible in spectra collected midway through the titration (Supplementary Fig. 4 online). The expected fraction of enzyme in the 0-bound (f0), 1-bound (f1), and 2-bound (f2) forms may be calculated based on the concentrations of AcCoA used in the titration and the binding parameters determined by ITC (Fig. 4a). The value of f1 is predicted to increase to about 30% at partial AcCoA saturation, before decreasing at higher ligand concentrations. Notably, we do not observe any signals in the spectra that follow this pattern of intensities. We conclude that all signals from the 1-bound form are either coincident with those of the 0-bound and 2-bound states (i.e. contribute to the apo and holo peaks or are located in overlapped regions) or are dynamically broadened beyond detection. In order to discriminate between these two possibilities on a peak-by-peak basis, we developed a joint analysis of the NMR and ITC data. The intensity profile of each well-resolved apo and holo peak was fitted using the sets of ITC-derived f0, f1, and f2 values, adjusting only the relative contribution of the 1-bound state to the apo or holo peak as follows: the initial intensity of each apo peak was normalized to 2, and the final intensity of each holo peak was normalized to 2. Peak intensities throughout the titration were calculated as Itotapo = 2×f0 + f1I1apo and Itotholo = f1I1holo + 2×f2. The values of I1apo and I1holo were optimized for each apo and holo peak, respectively. Excellent agreement was obtained with all NMR titration data (Fig. 4b and Supplementary Fig. 5 online). The value of I1apo or I1holo thus quantifies the contribution of the 1-bound form to each signal, relative to that of a single subunit of the 0-bound or 2-bound form, respectively. The 62 values of I1holo cluster about a value of 1 (Fig. 4c). This strongly suggests that a single subunit of the 1-bound enzyme resembles those of the 2-bound state, and produces a set of signals coincident with the holo spectrum. The 10 values of I1apo are more heterogeneous, ranging from 0 to 1. The presence of five peaks with I1apo much greater than zero suggests that the unbound subunit in the 1-bound enzyme may somewhat resemble those of the 0-bound form, and produces some signals coincident with the apo spectrum. The five values of I1apo close to zero could result from increased dynamical broadening, hydrogen exchange with solvent, or movement of peaks to overlapped regions of the spectrum. Due to the lack of unequivocal data, we hesitate to propose a specific model for the unbound subunit of the 1-bound enzyme, and will refer to it as the F′ state, to distinguish it from the F subunits of the 0-bound state. This analysis provides a basis for discriminating between the classical KNF5 and MWC2 paradigms (Fig. 1a,b). The KNF model predicts that the 1-bound enzyme contains one B-type subunit and one F-type subunit. Values of I1apo and I1holo should thus both be close to 1. This corresponds closely to what is observed experimentally, although some values of I1apo are smaller. In contrast, the MWC model predicts that the 1-bound enzyme contains two B-type subunits and no F-type subunits. Values of I1apo should be 0, while values of I1holo should be close to 2. This is not observed.
Figure 4.
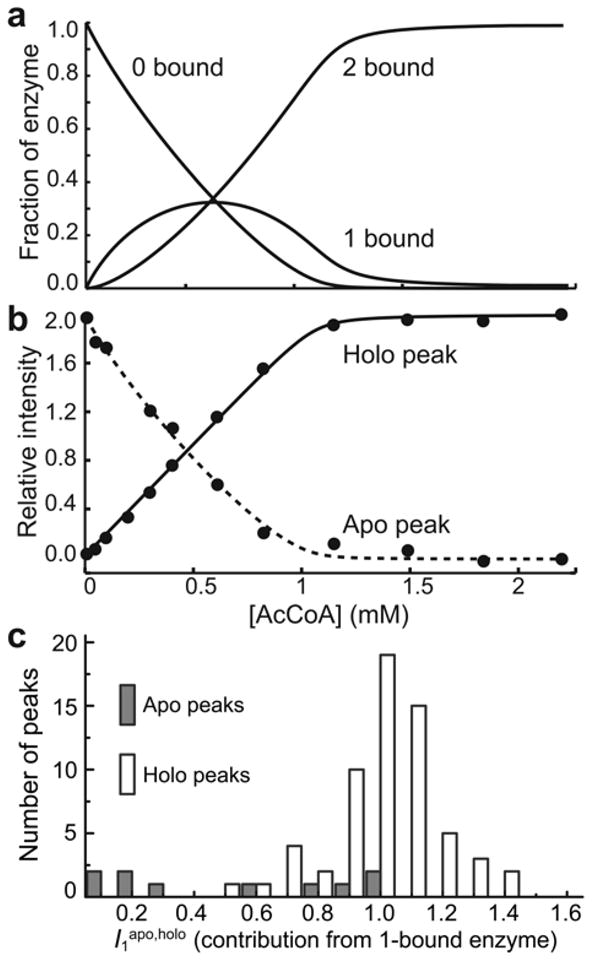
Analysis of NMR titration data. (a) Fraction of the enzyme in the 0-bound, 1-bound, and 2-bound states determined by ITC. (b) Intensities of the apo (dashed line) and holo (solid line) peaks for Leu56 as a function of [AcCoA]. The intensities were analyzed to extract the relative contribution of the 1-bound enzyme to the signals (I1apo,holo) as described in the text. The lines correspond to the optimized theoretical intensities. (c) Histograms of the relative contribution of the 1-bound enzyme to apo (I1apo) and holo (I1holo) peaks in titrations of AAC(6′)-Ii with AcCoA.
Given the large conformational changes exhibited by AAC(6′)-Ii, it is of interest to understand the binding reaction pathways, or the sequences of events that occur as AcCoA is taken up by the enzyme. This process has historically been described by an “induced-fit” model, in which ligands bind weakly to F-type molecules, which subsequently convert to the tightly-bound B form38. More recent work has focused on a “conformational selection” model, in which ligands bind directly to a small, pre-existing population of unbound, high-affinity B-type molecules17,39. It has been noted that the conformational selection and MWC models are similar, since both models invoke small pre-existing populations of unbound B-type molecules40. As well, the induced fit and KNF paradigms are similar, and KNF is sometimes referred to as an “induced-fit” model41. However, our identification of a KNF-type allosteric mechanism in AAC(6′)-Ii does not necessarily imply that ligands are taken up through an induced-fit pathway. The KNF paradigm describes binding purely in terms of thermodynamics and ligands can be taken up by either induced fit or conformational selection pathways5. The contributions of the two pathways are governed by the microscopic rate constants for binding and conformational transitions5,40,42–44 and also by protein and ligand concentrations43–44. Thus it is quite challenging to determine the extent to which a particular system follows the conformational selection or induced-fit binding pathway. We cannot confidently assign either model to AAC(6′)-Ii, given the data at hand. Discriminating between the KNF and MWC allosteric models is more straightforward than identifying the binding pathway. According to the MWC model, the 1-bound enzyme exists in a BB-type conformation (Fig. 1a), while according to the KNF model, the 1-bound enzyme exists in a BF-type conformation (Fig. 1b), irrespective of ligand concentration or the rates of binding or conformational transitions. Based the on the NMR titration data and this criterion, we can confidently assign a KNF-type model to the interaction of AcCoA with native AAC(6′)-Ii.
Thermodynamic Description of Allostery
Temperature-dependent allostery in AAC(6′)-Ii can be explained by a model comprising a hybrid of the KNF and HT paradigms (Fig. 5). The ITC, CD, and NMR data indicate that each subunit of the enzyme can exist in at least 3 (likely more) distinct conformational states. The enzyme loses structure and binding activity as the temperature is raised, although a dimeric form is retained. We have represented this as the transition of each subunit from a native free (F) form to a partially unfolded (U) form. The free enzyme can therefore exist as a mixture of FF, FU, UF, and UU states. Under stabilizing conditions where the enzyme is entirely in the FF state, subunits undergo large conformational changes when AcCoA is bound. This can be represented as transitions from the F state to a bound (B) state (we assume that this conformational change does not occur to a detectable extent in the absence of AcCoA, as discussed above). Under stabilizing conditions, the 1-bound enzyme contains one subunit in the B form, and another that somewhat resembles the 0-bound state, i.e. BF′ and F′B. The free subunit (F′) also melts, since the temperature profile of ΔHA2app is curved. For the sake of generality, we will refer to the partially unfolded subunit in the 1-bound enzyme as U′ to distinguish it from partly unfolded subunits of the 0-bound enzyme. Therefore a full description of the 1-bound enzyme includes the states BF′, BU′, F′B, and U′B. The 2-bound enzyme exists simply as BB. The ITC data show that the thermal unfolding transition depends upon the conformational state of the adjacent subunit (i.e. FF→FU ≠ BF′→BU′ ). This conclusion is based on the observation that if the thermal transition of each subunit were unaffected by its neighbor, both ΔHA1app and ΔHA2app would exhibit identical curvature, which is not the case (Fig. 2b). We therefore employed a model in which all thermal transitions of the 0-bound state are thermodynamically equivalent but differ from those of the 1-bound state. The assumption that subunits partially unfold independently in the 0-bound enzyme (FF→FU = UF→UU) is almost certainly an over-simplification. However a more realistic description of subunit unfolding would require additional adjustable parameters. This simple model provides excellent agreement with the data (see below). Any additional folding parameters would therefore be ill-defined by the data. Thus parameters extracted using this model provide effective measures of subunit unfolding, even though the process is likely more complex in reality.
Figure 5.
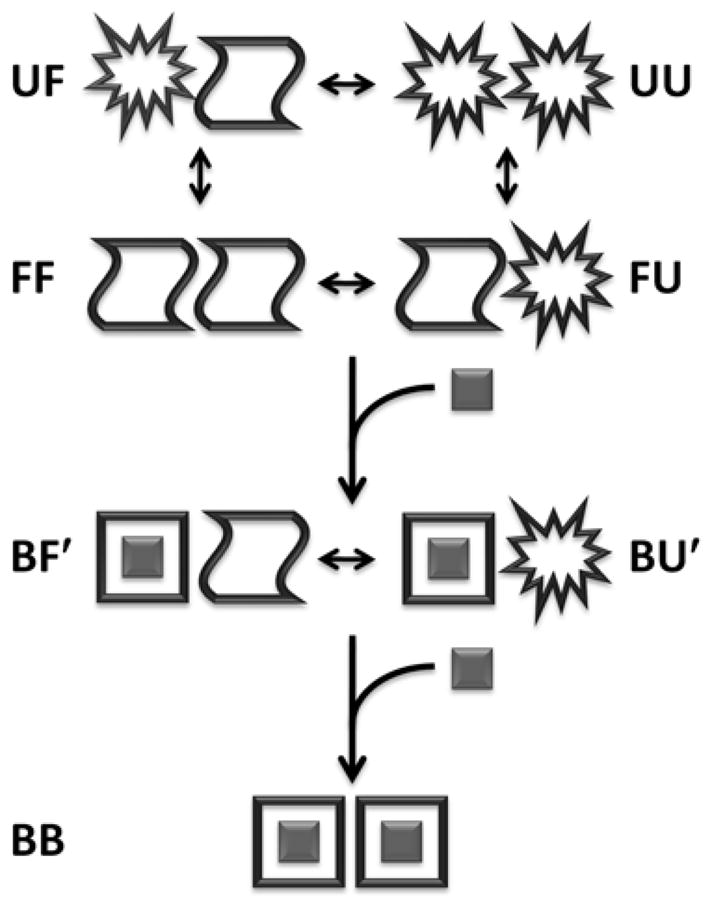
Schematic representation of the allosteric binding model. B corresponds to the bound state. F(F′) and U(U′) correspond to the free folded and partially unfolded states that are adjacent to a free (bound) subunit, respectively. Transitions involving the symmetry-related F′B and U′B states are not shown.
Temperature-dependent allostery in this protein is described by 12 microscopic thermodynamic parameters. Equilibrium constants, enthalpy and heat capacity changes are associated with the first (FF→ F′B, FF→BF′) and second (F′B→BB, BF′→BB) binding events, as well as thermal transitions in the 0-bound (FF→FU, FF→UF, FU→UU, UF→UU) and 1-bound states (BF′→BU′, F′B→ U′B). In addition, the linear CD baselines of the F and U states are each described by two parameters (slopes and vertical positions). We fitted these parameters to the combined ITC and CD dataset, as reported in Table 1. The lines in Fig. 2 are derived from these optimized thermodynamic parameters, and show excellent agreement between the model and all experimental data, even capturing the slight upward curvature of ΔHA1app.
Table 1.
Thermodynamic parameters describing allostery in AAC(6′)-Ii
| K′A1 (×104 M−1)a | 2.1 | ±0.1 |
| K′A2 (×104 M−1)b | 2.8 | ±0.1 |
| K′U0c | 0.20 | ±0.06 |
| K′U1d | 0.38 | ±0.07 |
| ΔG′A1 (kcal mol−1)e | −6.13 | ±0.03 |
| ΔG′A2 (kcal mol−1)f | −6.32 | ±0.02 |
| ΔG′U0 (kcal mol−1)g | 1.0 | ±0.2 |
| ΔG′U1 (kcal mol−1)h | 0.6 | ±0.1 |
| ΔH′A1 (kcal mol−1)i | −22.9 | ±0.8 |
| ΔH′A2 (kcal mol−1)j | −28.1 | ±0.8 |
| ΔH′U0 (kcal mol−1)k | −71 | ±7 |
| ΔH′U1 (kcal mol−1)l | −93 | ±6 |
| ΔCp,A1 (cal mol−1 K−1)m | −790 | ±40 |
| ΔCp,A2 (cal mol−1 K−1)n | −820 | ±30 |
| ΔCp,U0 (cal mol−1 K−1)o | 2100 | NA |
| ΔCp,U1 (cal mol−1 K−1)o | 2100 | NA |
| [⊝] ′F (deg cm2 dmol−1)p | −7600 | ±200 |
| [⊝] ′U (deg cm2 dmol−1)q | −4040 | ±20 |
| mF (deg cm2 dmol−1 K−1)r | 54 | ±3 |
| mU (deg cm2 dmol−1 K−1)s | 8 | ±2 |
T′=37°C
Equilibrium association constant for the native (non-melted) enzyme and the first AcCoA molecule at T′
Equilibrium association constant for the native (non-melted) enzyme and the second AcCoA molecule at T′
Equilibrium constant for subunit melting in the 0-bound enzyme at T′
Equilibrium constant for melting of the unbound subunit in the 1-bound enzyme at T′
Free energy change upon binding of one molecule of AcCoA to the native (non-melted) 0-bound enzyme at T′
Free energy change upon binding of one molecule of AcCoA to the native (non-melted) 1-bound enzyme at T′
Free energy change upon melting of a single subunit in the 0-bound enzyme at T′
Free energy change upon melting of the unbound subunit in the 1-bound enzyme at T′
Enthalpy change upon binding of one molecule of AcCoA to the native (non-melted) 0-bound enzyme at T′
Enthalpy change upon binding of one molecule of AcCoA to the native (non-melted) 1-bound enzyme at T′
Enthalpy change upon melting of a single subunit in the 0-bound enzyme at T′
Enthalpy change upon melting of the unbound subunit in the 1-bound enzyme at T′
Heat capacity change upon binding of one molecule of AcCoA to the native (non-melted) 0-bound enzyme
Heat capacity change upon binding of one molecule of AcCoA to the native (non-melted) 1-bound enzyme
Heat capacity change upon subunit melting. These values were fixed at the value obtained for a monomeric mutant of AAC(6′)-Ii
CD molar ellipticity of a native (non-melted) subunit at T′
CD molar ellipticity of a melted subunit at T′
Temperature dependence of the molar ellipticity of a native subunit
Temperature dependence of the molar ellipticity of a melted subunit
Discussion
The energy of AAC(6′)-Ii binding to AcCoA can be separated into two distinct contributions, based on the parameters extracted in the global fit of ITC and CD data (Fig. 2 and Table 1). The first component corresponds to the intrinsic binding affinity of the native dimer for AcCoA, while the second arises from partial unfolding of the subunits. In order to address the first component, the intrinsic ability of the dimer to bind AcCoA in the absence of F→U and F′→U′ transitions can be predicted based on the model parameters, even for temperatures where the U and U′ states are prevalent (dashed lines in Fig. 2a) The calculations show that the native dimer binds with intrinsically positive cooperativity across the entire temperature range studied (although the intrinsic positive cooperativity should disappear at about 48°C due to the temperature dependences of KA1 and KA2). According to the NMR data, when the 0-bound enzyme binds a single molecule of AcCoA, a single subunit converts from the F to the B state. This is consistent with a classical KNF explanation of allostery5. We hypothesize that binding of the first ligand (FF→BF′) is opposed by disruption of the FF interface, while binding of the second (BF′→BB) is promoted by formation of the BB interface; the symmetry of the FF and BB interfaces likely make them more stable than the F′B interface of the 1-bound state.
The low intensities of some NMR signals for the free subunit in the 1-bound enzyme (F′) suggest that it may undergo additional dynamics beyond those already present in the F state. In fact, modulation of protein dynamics can provide a powerful driving force for protein allostery12–14. It is possible that the intrinsic positive cooperativity of the AAC(6′)-Ii dimer derives from a combination of these two effects. This idea is supported by the extracted thermodynamic parameters (Table 1). Compared to binding the first molecule of AcCoA, binding the second is enthalpically more favorable (ΔΔHA=−3.4 kcal mol−1 at 10°C), consistent with the formation of additional contacts, and entropically less favorable (ΔΔSA=−10 cal mol−1 K−1 at 10°C), consistent with the dampening of internal motions.
The unbound subunits undergo partial unfolding as the temperature is raised. The process is endothermic and entropically favored as would be expected, ΔHU = 71, 93 kcal mol−1 and ΔSU = 230, 300 cal mol−1 K−1 at 37°C in the 0-bound and 1-bound states, respectively. The model predicts that subunits are slightly more stable in the context of the 0-bound compared to the 1-bound state, with melting temperatures of 41.2 and 39.0 °C, respectively. At 37°C, KU0=[FU]/[FF]=0.20, while KU1=[BU′]/[BF′]=0.38. This difference in stability may be related to disruption of the symmetrical FF subunit interface when the first AcCoA molecule is bound. At higher temperatures, this destabilization leads to partial unfolding of the unbound subunit of the 1-bound enzyme (BF′→BU′), with a concomitant reduction in affinity for the second AcCoA molecule (KA2app) and a shift towards negative cooperativity. At lower temperatures, the unbound subunit is sufficiently stable to remain in the active (F′) state, and the intrinsic positive cooperativity of the native dimer dominates. This effect represents a modification of the HT (coupled folding and binding) model of allostery (Fig. 1c)10. In the HT model, ligand-induced folding of one subunit alters the folding equilibrium of the adjacent subunit. In AAC(6′)-Ii, each subunit can adopt at least three distinct conformational states, and it is largely the F to B transition that modulates partial unfolding of the adjacent subunit.
The modulation of folding/unfolding equilibria is emerging as a sensitive and versatile mechanism for connecting distant sites in proteins11,32,45–46. For example, in SecA, the motor protein of the bacterial Sec translocase machinery, local folding/unfolding transitions play a key role in communicating the signal produced by ATP hydrolysis to the rest of the multi-domain protein32. Using a combination of NMR and variable-temperature ITC, it was shown that loss of the γ-phosphate triggers an order-to-disorder transition in the nucleotide binding cleft. Mutations that abrogate this local folding/unfolding transition also disrupt the ability of SecA to distinguish between ATP and ADP32. A comparison of SecA and AAC(6′)-Ii highlights the ways in which folding-mediated allostery can be adapted to suit different situations. In SecA, ligand-controlled folding in one domain conveys a heterotropic allosteric signal to the rest of the protein via domain/domain interactions, which ultimately governs the activity of the translocation machinery. In AAC(6′), ligand binding in one subunit triggers a change in the subunit interface that promotes partial unfolding of adjacent subunit, conveying a homotropic allosteric signal and modulating ligand binding.
An important consequence of the HT model, and folding-mediated allostery in general, is that control of cooperativity can be shared by many or most residues in a protein, even those located far from subunit interfaces or the active sites themselves, provided that these residues influence subunit stability10. This view of allostery as a decentralized process contrasts sharply with other studies in which it has been explained in terms of specific networks of relatively small numbers of interacting residues15–16. In AAC(6′)-Ii, a negatively cooperative HT mechanism opposes the intrinsic positive (KNF) cooperativity of the native dimer. To our knowledge, this is the first reported observation of such an intertwined phenomenon. Interestingly, the presence of these competing allosteric mechanisms leads to additional properties beyond those of either the KNF or HT models alone. In the original HT model, the strength of subunit/subunit coupling is modulated by the stabilities of the domains, but the sign of the cooperativity is specified entirely by whether the interaction between the folded domains is favorable (positive) or unfavorable (negative)10. In the hybrid KNF-HT mechanism exhibited by AAC(6′)-Ii, both the sign and the magnitude of cooperativity can be modulated simply by changing the stability of the subunits. Allostery in such systems can be defined by three parameters: the intrinsic cooperativity coefficient of the native dimer47, αint=KA2/KA1, the equilibrium constant for melting in the 0-bound state, KU0, and the ratio of melting equilibrium constants in the 1-bound and 0-bound forms, ϕ=KU1/KU0. The apparent cooperativity is then given by the expression:
| [1] |
Even if both αint and ϕ remain constant, the apparent cooperativity can vary from positive (αapp>1) to negative (αapp<1) depending only on the intrinsic tendency of the subunits to partially unfold, KU0. At 37°C, global fits of AAC(6′)-Ii data give an intrinsic cooperativity coefficient, αint=1.3, and a ratio of thermal melting constants, φ=1.9. Cooperativity can therefore vary between weakly positive (αapp 1.3) to weakly negative (αapp 0.36) for KU0≪1 and KU0≫1, respectively (Fig. 6a). Interestingly, a dynamic range of up to six orders of magnitude in αapp can be achieved if KU0 varies between 10−4 to 102 with αint=φ=1,024 (Fig. 6b).
Figure 6.
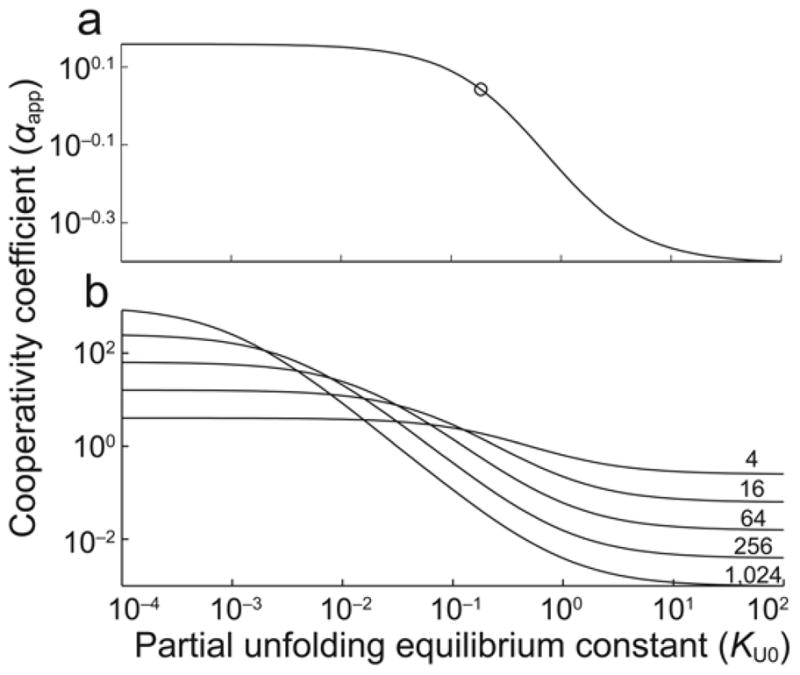
Dependence of the apparent cooperativity coefficient (αapp) on subunit instability (KU0=[UF]/[FF]) calculated using Eq. [1] and (a) the intrinsic cooperativity coefficient (αint=1.3) and ratio of melting equilibrium constants constants (φ=1.9) determined for AAC(6′)-Ii at 37°C and (b) hypothetical proteins in which αint=φ=4,16,64,256,1024. The circle in (a) corresponds to the KU0 value obtained for AAC(6′)-Ii at 37°C (0.2).
Several important lessons can be drawn from AAC(6′)-Ii as a model system. It represents one of clearest examples to date of a system following the HT coupled folding/binding allosteric model. It provides proof-of-principle for competition between simultaneous positive and negative cooperative mechanisms, and suggests a scenario in which the sign of cooperativity can be modulated simply by altering subunit stability. Finally, aspects of the approach we took to characterize this enzyme have the potential to be quite useful in future studies of allostery. The generalized global fitting scheme we employed for the variable-temperature ITC data greatly reduces the scatter in the extracted ΔHAapp and KAapp values, and permits definitive characterization of coupled folding and binding (fits using non-global methods are shown in Supplementary Fig. 6 online). Simultaneous analyses of variable-temperature ITC and CD data have been performed previously31, but to our knowledge this the first application of this method to study homotropic allostery. In addition, the combined analysis of ITC and NMR titration data facilitates characterization of the spectral properties of the 1-bound protein, even though its signals are not directly distinguishable. We have identified a new form of allosteric regulation in AAC(6′)-Ii by applying calorimetric and high-resolution spectroscopic techniques in concert. It seems likely that similar superpositions of MWC, KNF, and HT allosteric mechanisms will be observed in additional systems as more studies are performed using this sort of approach.
Methods
Sample Preparation
AAC(6′)-Ii (182 residues per subunit) was expressed in E. coli and purified by anion exchange, gel filtration and affinity chromatography as previously described29. NMR samples were isotopically enriched with 13C and/or 15N according to the procedure of Bracken et al.48
ITC
Isothermal titration calorimetry measurements employed a MicroCal VP-ITC instrument (MicroCal, North Hampton, MA, USA). Samples contained enzyme (50 to 200 μM) dialyzed against a solution of 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) (25 mM, pH 7.5) and Ethylenediaminetetraacetic acid (EDTA) (2 mM). Experiments were performed at 10(3), 15(3), 20(6), 25(4), 30(3), 34(2), 37(3), and 40(4) °C, where values in parentheses indicate the number of replicates obtained at each temperature. Titrations employed an initial delay of 60 s, a 2 μL initial injection volume followed by a 150 s delay, 25 × 10 μL injections followed by 330 s delays and a final 10 μL injection followed by a 600 s delay.
CD
Circular dichroism measurements were performed using a JASCO J-810 spectrometer and a 0.2 cm path length cuvette. Samples contained protein (1.5–5 μM) in HEPES buffer (25 mM, pH 7.5) supplemented with EDTA (2 mM). Scans from 200 to 300 nm were collected in triplicate at temperatures from 0.1 to 71°C using a Pelletier temperature controller. Melts performed in increments of 1°C with four minute equilibration times and increments of 3–5°C with 10 minute equilibration times were superimposible over the full temperature range and were fully reversible. The melting temperature was about 7°C higher in NMR buffer containing 100 mM sodium phosphate.
NMR
NMR experiments were performed on Varian INOVA spectrometers equipped with high-sensitivity cold-probes operating at 500 and 800 MHz 1H Larmor frequencies. Spectra were collected for protein samples (0.6 to 1.5 mM) in sodium phosphate buffer(100 mM, pH 6.5) containing EDTA (2mM) and D2O (10% v/v) at 37°C. ITC experiments performed under these conditions yield KA1app=4.5×104 M−1, ΔHA1app=−21 kcal mol−1, KA2app=19.5×104 M−1, and ΔHA2app=−24 kcal mol−1. Backbone assignments were obtained for 166 of 172 non-proline residues in AcCoA-saturated AAC(6′)-Ii using standard triple-resonance experiments49. EXSY spectra36 were collected for a 50% AcCoA-saturated sample with mixing times of 500 and 1000 ms. The presence of faint exchange cross-peaks in these spectra implies that dissociation rate constants are on the order of about 1 s−1.
1H/15N heteronuclear single quantum coherence (HSQC spectra)50 were collected for AAC(6′)-Ii with 0, 0.05, 0.1, 0.2, 0.3, 0.4, 0.6, 0.8, 1.1, 1.4, 1.7, 2.0 mM AcCoA. In the titration analysis, only well-resolved signals from apo peaks that disappear at high AcCoA concentrations and holo peaks that are not present in the absence of AcCoA were considered. Peak intensities were quantified using the NMRPipe/NMRDraw51 suite of software and were corrected for dilution of the sample caused by addition of AcCoA by multiplying each intensity by a factor of (V0+ΔVi)/V0, where V0 is the initial sample volume (910 μL) ΔVi is the total volume of AcCoA added by step i (100 μL in total). The fractions of protein in the 0-bound, 1-bound and 2-bound states at each titration point (f0, f1, f2) were calculated as described in the Supplementary Methods, online. The intensities of apo and holo peaks were fitted using the series of f0, f1, and f2 values, as described in the text. The values of I1apo and I1holo were varied on a per-peak basis in order to maximize agreement between experimental and calculated intensities in a non-linear least-squares analysis using MATLAB (7.8.0.347 MathWorks). The enzyme concentration was adjusted as single global variable in order to simultaneously optimize agreement for all apo and holo peak intensity series, and was within 10 % of the initial concentration estimate based on A280 measurements.
Allosteric Model
The experimentally observable parameters: KA1app, ΔH1app, KA2app, ΔH2app, were re-cast in terms of microscopic model parameters, which describe 4 thermodynamic transitions: binding of the first and second molecules of AcCoA to the native enzyme and subunit melting in the 0-bound and 1-bound forms. Each of these transitions is associated with 3 parameters: an equilibrium constant (K′) and enthalpy change (ΔH′) at an arbitrary reference temperature (T′) and the change in heat capacity (ΔCp). The temperature dependences of microscopic equilibrium constants and enthalpies are given by
| [2] |
and
| [3] |
The apparent equilibrium association constants for the first and second molecules of AcCoA are given by the expressions
| [4] |
and
| [5] |
where KA1 and KA2 are the intrinsic association constants of the native enzyme for the first and second molecules of AcCoA and KU0 = [FU]/[FF] and KU1=[BU′]/[BF′] are equilibrium constants for partial unfolding in the 0-bound and 1-bound states, respectively. The apparent binding enthalpies for the first and second molecules of AcCoA are given by
| [6] |
and
| [7] |
where ΔHA1 and ΔHA2 are the intrinsic binding enthalpies of the native enzyme with the first and second molecules of AcCoA and ΔHU0 and ΔHU1 are the melting enthalpies in the 0-bound and 1-bound forms, respectively. Additional explanation and derivations of these expressions are given in the Supplementary Methods, online. We found that the affinity and enthalpy profiles were relatively insensitive to the choices of ΔCp,U0 and ΔCp,U1. We therefore fixed both parameters equal to the value we have previously determined for a monomeric mutant of AAC(6′)-Ii, 2.1 kcal mol−1 K−1. The molar ellipticity of the protein was fitted as the population-weighted average of those of the F and U states, which were assumed to be linear functions of temperature, according to the expression
| [8] |
where [⊝]′F and [⊝]′U are the molar ellipticities of the F and U states at T′ and mF and mU are the corresponding temperature dependences. Fourteen parameters (K′A1, ΔH′A1, ΔCp,A1, K′A2, ΔH′A2, ΔCp,A2, K′U0, ΔH′U0, K′U1, ΔH′U1, [⊝]′F, mF, [⊝]′U, mU) were adjusted to minimize the residual function
| [9] |
using in-house MATLAB scripts, where the sums run over all data points. Errors in the thermodynamic parameters were calculated using a Monte Carlo technique described in the Supplementary Methods online.
Supplementary Material
Acknowledgments
The authors would like to thank Prof. G. D. Wright (McMaster University, Canada) for providing the AAC(6′)-Ii expression construct, as well as Cheen Euong Ang and Kevin Shopsowitz for their assistance with data collection and analysis. This research was funded by operating grants from the Canadian Institutes of Health Research (CIHR) (KA, AM, and AB). LF and OB were supported through a CIHR training grant and CIHR scholarship, respectively. AB holds a Canada Research Chair in Structural Biology. NMR experiments were recorded at the Québec/Eastern Canada High Field NMR Facility, supported by the Natural Sciences and Engineering Research Council of Canada, the Canada Foundation for Innovation, the Ministère de la recherche, de la science et de la technologie du Québec, and McGill University.
Footnotes
Author Contributions
LF and OM collected the data. LF, OM, and TS analyzed the data. AM, KA, and AB wrote the paper.
References
- 1.Perutz MF. Mechansism of cooperativity and allosteric regulation in proteins. Q Rev Biophys. 1989;22:139–236. doi: 10.1017/s0033583500003826. [DOI] [PubMed] [Google Scholar]
- 2.Monod J, Wyman J, Changeux JP. On nature of allosteric transitions - a plausible model. J Mol Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 3.Fenton AW. Allostery: an illustrated definition for the ‘second secret of life’. Trends Biochem Sci. 2008;33:420–425. doi: 10.1016/j.tibs.2008.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.DeDecker BS. Allosteric drugs: thinking outside the active-site box. Chem Biol. 2000;7:R103–R107. doi: 10.1016/s1074-5521(00)00115-0. [DOI] [PubMed] [Google Scholar]
- 5.Koshland DE, Nemethy G, Filmer D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry. 1966;5:365–385. doi: 10.1021/bi00865a047. [DOI] [PubMed] [Google Scholar]
- 6.Perutz MF, Wilkinson AJ, Paoli M, Dodson GG. The stereochemical mechanism of the cooperative effects in hemoglobin revisited. Annu Rev Biophys Biomol Struct. 1998;27:1–34. doi: 10.1146/annurev.biophys.27.1.1. [DOI] [PubMed] [Google Scholar]
- 7.Helmstaedt K, Krappmann S, Braus GH. Allosteric regulation of catalytic activity: Escherichia coli aspartate transcarbamoylase versus yeast chorismate mutase. Microbiol Mol Biol Rev. 2001;65:404–421. doi: 10.1128/MMBR.65.3.404-421.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cui Q, Karplus M. Allostery and cooperativity revisited. Protein Sci. 2008;17:1295–1307. doi: 10.1110/ps.03259908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kern D, Zuiderweg ERP. The role of dynamics in allosteric regulation. Curr Opin Struct Biol. 2003;13:748–757. doi: 10.1016/j.sbi.2003.10.008. [DOI] [PubMed] [Google Scholar]
- 10.Hilser VJ, Thompson EB. Intrinsic disorder as a mechanism to optimize allosteric coupling in proteins. Proc Natl Acad Sci USA. 2007;104:8311–8315. doi: 10.1073/pnas.0700329104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Reichheld SE, Yu Z, Davidson AR. The induction of folding cooperativity by ligand binding drives the allosteric response of tetracycline repressor. Proc Natl Acad Sci USA. 2009;106:22263–22268. doi: 10.1073/pnas.0911566106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Popovych N, Sun SJ, Ebright RH, Kalodimos CG. Dynamically driven protein allostery. Nat Struct Mol Biol. 2006;13:831–838. doi: 10.1038/nsmb1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cooper A, Dryden DTF. Allostery without conformational change - a plausible model. Eur Biophys J. 1984;11:103–109. doi: 10.1007/BF00276625. [DOI] [PubMed] [Google Scholar]
- 14.Tzeng SR, Kalodimos CG. Dynamic activation of an allosteric regulatory protein. Nature. 2009;462:368–U139. doi: 10.1038/nature08560. [DOI] [PubMed] [Google Scholar]
- 15.Gandhi PS, Chen ZW, Mathews FS, Di Cera E. Structural identification of the pathway of long-range communication in an allosteric enzyme. Proc Natl Acad Sci USA. 2008;105:1832–1837. doi: 10.1073/pnas.0710894105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lockless SW, Ranganathan R. Evolutionarily conserved pathways of energetic connectivity in protein families. Science. 1999;286:295–299. doi: 10.1126/science.286.5438.295. [DOI] [PubMed] [Google Scholar]
- 17.Tsai CJ, Kumar S, Ma BY, Nussinov R. Folding funnels, binding funnels, and protein function. Protein Science. 1999;8:1181–1190. doi: 10.1110/ps.8.6.1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tsai CJ, Ma BY, Nussinov R. Folding and binding cascades: Shifts in energy landscapes. Proc Natl Acad Sci U S A. 1999;96:9970–9972. doi: 10.1073/pnas.96.18.9970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kumar S, Ma BY, Tsai CJ, Sinha N, Nussinov R. Folding and binding cascades: Dynamic landscapes and population shifts. Protein Science. 2000;9:10–19. doi: 10.1110/ps.9.1.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pan H, Lee JC, Hilser VJ. Binding sites in Escherichia coli dihydrofolate reductase communicate by modulating the conformational ensemble. Proc Natl Acad Sci USA. 2000;97:12020–12025. doi: 10.1073/pnas.220240297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Volkman BF, Lipson D, Wemmer DE, Kern D. Two-state allosteric behavior in a single-domain signaling protein. Science. 2001;291:2429–2433. doi: 10.1126/science.291.5512.2429. [DOI] [PubMed] [Google Scholar]
- 22.Gunasekaran K, Ma BY, Nussinov R. Is allostery an intrinsic property of all dynamic proteins? Proteins. 2004;57:433–443. doi: 10.1002/prot.20232. [DOI] [PubMed] [Google Scholar]
- 23.Clarkson MW, Gilmore SA, Edgell MH, Lee AL. Dynamic coupling and allosteric behavior in a nonallosteric protein. Biochemistry. 2006;45:7693–7699. doi: 10.1021/bi060652l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wright GD, Ladak P. Overexpression and characterization of the chromosomal aminoglycoside 6′-N-acetyltransferase from Enterococcus faecium. Antimicrob Agents Chemother. 1997;41:956–960. doi: 10.1128/aac.41.5.956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Burk DL, Xiong B, Breitbach C, Berghuis AM. Structures of aminoglycoside acetyltransferase AAC(6′)-Ii in a novel crystal form: structural and normal-mode analyses. Acta Crystallogr D Biol Crystallogr. 2005;61:1273–1279. doi: 10.1107/S0907444905021487. [DOI] [PubMed] [Google Scholar]
- 26.Wybenga-Groot LE, Draker K-a, Wright GD, Berghuis AM. Crystal structure of an aminoglycoside 6′-N-acetyltransferase: defining the GCN5-related N-acetyltransferase superfamily fold. Structure. 1999;7:497–507. doi: 10.1016/s0969-2126(99)80066-5. [DOI] [PubMed] [Google Scholar]
- 27.Burk DL, Ghuman N, Wybenga-Groot LE, Berghuis AM. X-ray structure of the AAC(6′)-Ii antibiotic resistance enzyme at 1.8 angstrom resolution; examination of oligomeric arrangements in GNAT superfamily members. Protein Sci. 2003;12:426–437. doi: 10.1110/ps.0233503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gao F, Yan XX, Baettig OM, Berghuis AM, Auclair K. Regio- and chemoselective 6′-N-derivatization of aminoglycosides: Bisubstrate inhibitors as probes to study aminoglycoside 6′N-acetyltransferases. Angew Chem Int Ed Engl. 2005;44:6859–6862. doi: 10.1002/anie.200501399. [DOI] [PubMed] [Google Scholar]
- 29.Freiburger LA, Auclair K, Mittermaier AK. Elucidating Protein Binding Mechanisms by Variable-c ITC. Chem Bio Chem. 2009;10:2871–2873. doi: 10.1002/cbic.200900614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fisher HF, Colen AH, Medary RT. Temperature-dependent ΔCp0 generated by a shift in equilibrium between macrostates of an enzyme. Nature. 1981;292:271–272. doi: 10.1038/292271a0. [DOI] [PubMed] [Google Scholar]
- 31.Cliff MJ, Williams MA, Brooke-Smith J, Barford D, Ladbury JE. Molecular Recognition via Coupled Folding and Binding in a TPR Domain. J Mol Biol. 2005;346:717–732. doi: 10.1016/j.jmb.2004.12.017. [DOI] [PubMed] [Google Scholar]
- 32.Keramisanou D, et al. Disorder-order folding transitions underlie catalysis in the helicase motor of SecA. Nat Struct Mol Biol. 2006;13:594–602. doi: 10.1038/nsmb1108. [DOI] [PubMed] [Google Scholar]
- 33.Adler AJ, Greenfield NJ, Fasman GD. Circular dichroism and optical rotatory dispersion of proteins and polypeptides. Methods Enzymol. 1973;27:675–735. doi: 10.1016/s0076-6879(73)27030-1. [DOI] [PubMed] [Google Scholar]
- 34.Saxena VP, DBW New Basis for Interpreting Circular Dichroic Spectrao of Proteins. Proc Natl Acad Sci USA. 1971;68:969–972. doi: 10.1073/pnas.68.5.969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Uversky VN. Natively unfolded proteins: A point where biology waits for physics. Protein Sci. 2002;11:739–756. doi: 10.1110/ps.4210102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Farrow NA, Zhang O, Forman-Kay JD, Kay LE. A heteronuclear correlation experiment for simultaneous determination of 15N longitudinal decay and chemical exchange rates of systems in slow equilibrium. J Biomol NMR. 1994;4:727–734. doi: 10.1007/BF00404280. [DOI] [PubMed] [Google Scholar]
- 37.Farmer BT. Localizing the NADP(+) binding site on the MurB enzyme by NMR. Nat Struct Biol. 1996;3:995–997. doi: 10.1038/nsb1296-995. [DOI] [PubMed] [Google Scholar]
- 38.Koshland DE. Application of a theory of enzyme specificity to protein synthesis. Proc Natl Acad Sci U S A. 1958;44:98–104. doi: 10.1073/pnas.44.2.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Foote J, Milstein C. Conformational isomerism and the diversity of antibodies. Proc Natl Acad Sci U S A. 1994;91:10370–10374. doi: 10.1073/pnas.91.22.10370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Boehr DD, Nussinov R, Wright PE. The role of dynamic conformational ensembles in biomolecular recognition. Nat Chem Biol. 2009;5:789–796. doi: 10.1038/nchembio.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Koshland DE, Hamadani K. Proteomics and models for enzyme cooperativity. J Biol Chem. 2002;277:46841–46844. doi: 10.1074/jbc.R200014200. [DOI] [PubMed] [Google Scholar]
- 42.Bosshard HR. Molecular recognition by induced fit: How fit is the concept? News Physiol Sci. 2001;16:171–173. doi: 10.1152/physiologyonline.2001.16.4.171. [DOI] [PubMed] [Google Scholar]
- 43.Hammes GG, Chang YC, Oas TG. Conformational selection or induced fit: A flux description of reaction mechanism. Proc Natl Acad Sci U S A. 2009;106:13737–13741. doi: 10.1073/pnas.0907195106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Weikl TR, von Deuster C. Selected-fit versus induced-fit protein binding: Kinetic differences and mutational analysis. Proteins Struct Funct Bioinformat. 2009;75:104–110. doi: 10.1002/prot.22223. [DOI] [PubMed] [Google Scholar]
- 45.Radley TL, Markowska AI, Bettinger BT, Ha JH, Loh SN. Allosteric switching by mutually exclusive folding of protein domains. J Mol Biol. 2003;332:529–536. doi: 10.1016/s0022-2836(03)00925-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Laine O, Streaker ED, Nabavi M, Fenselau CC, Beckett D. Allosteric signaling in the biotin repressor occurs via local folding coupled to global dampening of protein dynamics. J Mol Biol. 2008;381:89–101. doi: 10.1016/j.jmb.2008.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ehlert FJ. Estimation of the affinities of allosteric ligands using radioligand binding and pharmacological null methods. Mol Pharmacol. 1988;33:187–194. [PubMed] [Google Scholar]
- 48.Marley J, Lu M, Bracken C. A method for efficient isotopic labeling of recombinant proteins. J Biomol NMR. 2001;20:71–75. doi: 10.1023/a:1011254402785. [DOI] [PubMed] [Google Scholar]
- 49.Cavanagh J, Fairbrother W, Palmer A, Skelton N. Protein NMR spectroscopy principles and practice. Academic Press, Inc; 1996. [Google Scholar]
- 50.Kay LE, Keifer P, Saarinen T. Pure absorption gradient enhanced heteronuclear single quantum correlation spectroscopy with improved sensitivity. J Am Chem Soc. 1992;114:10663–10665. [Google Scholar]
- 51.Delaglio F, et al. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J Biomol NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


