Abstract
Principled techniques for incomplete-data problems are increasingly part of mainstream statistical practice. Among many proposed techniques so far, inference by multiple imputation (MI) has emerged as one of the most popular. While many strategies leading to inference by MI are available in cross-sectional settings, the same richness does not exist in multilevel applications. The limited methods available for multilevel applications rely on the multivariate adaptations of mixed-effects models. This approach preserves the mean structure across clusters and incorporates distinct variance components into the imputation process. In this paper, I add to these methods by considering a random covariance structure and develop computational algorithms. The attraction of this new imputation modeling strategy is to correctly reflect the mean and variance structure of the joint distribution of the data, and allow the covariances differ across the clusters. Using Markov Chain Monte Carlo techniques, a predictive distribution of missing data given observed data is simulated leading to creation of multiple imputations. To circumvent the large sample size requirement to support independent covariance estimates for the level-1 error term, I consider distributional impositions mimicking random-effects distributions assigned a priori. These techniques are illustrated in an example exploring relationships between victimization and individual and contextual level factors that raise the risk of violent crime.
Keywords: Missing data, multiple imputation, linear mixed-effects models, complex sample surveys, mixed effects, random covariances
1 Background
Multivariate data encountered in social, behavioral and medical sciences often have a hierarchical or multilevel structure due to observational units nested within naturally occurring groups (e.g. patients within doctors, individuals within neighborhoods). Higher levels of hierarchies are also common, such as those seen in longitudinal studies of patients nested within doctors. In these studies, obtaining estimates of the effects and associated standard errors in a manner that fully incorporates the study design (e.g. clustering) is generally the main goal of the statistical analysis. In this pursuit, mixed-effects models have been very useful as they allow explicit modeling of the corresponding cluster-specific random-effects and distinct variance components.
In practice, the existence of arbitrary missing value patterns in clustered data applications is arguably the most common analytical challenge. Failing to adopt principled solutions that ignore relationships, variations (e.g. between and within cluster) and missing-data uncertainty may lead to biased inferences. Here I consider model-based multiple imputation (Rubin 1987, Schafer 1997b) for drawing inferences for multivariate incomplete multilevel data. This approach consists of two distinct but often complimentary models: (1) a model used to produce multiple imputations, also known as imputer’s model, typically chosen to reflect key features of data as well as causes of missingness (Rubin 1987; Schafer 1997b; Schafer and Yucel 2002); and (2) a model known as an analyst’s model, chosen to investigate scientific hypotheses of the study with the incomplete data (Schafer and Graham 2002; Rubin 1987; Meng 1994).
What is the appropriate way to impute missing values in multilevel data? Two crucial criteria are to incorporate unique design features such as clustering and preserve important relationships among variables of the current and future analyses in the imputations (see detailed discussion by Little and Rubin 2002, Rubin 1987, Schafer 1997b). In this regard, multivariate generalizations of linear mixed-effects models are natural choices as they preserve correlation structures arising from multilevel structures. Similar models have been considered in several studies (e.g. Schafer and Yucel 2002 and Liu, Taylor, and Belin 2000) and also have been implemented in the software packages R and MLwiN (R Development Core Team 2007, Rasbash, Steel, Browne, and Prosser 2006). The main difference between the models developed in this paper and those in previous papers relates to the distributional assumption on the variance-covariance term of the level-1 error ε. Here I allow the variances and covariances of this term to randomly vary across the clusters, mimicking the idea underlying random-effects. Consider, for example, clustered data where the ultimate interest is to explain the variation in a certain trait among the respondents. In the example that follows, this trait is whether the individual has been burgled. A standard mixed-effects model puts a structure on the means (or probabilities) so that they are allowed to vary across the clusters. While this might be a reasonable approach in most applications, certain applications may require the preservation of higher order relationships. The idea of random-covariances allows clusters to have varying two-way relationships between being burgled and other key covariates such as income or ethnic heterogeneity of the cluster.
In multilevel data, models addressing the analyst’s substantive research goals underlie the incorporation of distinct variance sources into the estimation. Since the landmark paper of Laird and Ware (1982), an extensive literature has developed that discusses a range of model-fitting techniques and applications, including Diggle, Liang, and Zeger (1994), Vonesh and Chinchilli (1997), Pinheiro and Bates (2000), Verbeke and Molenberghs (2000), McCulloch and Searle (2001), Demidenko (2004), and Fitzmaurice, Laird, and Ware (2004). Together, these provide a clear and comprehensive discussion of state-of-the-art methods for estimation, testing, and prediction in the context of linear, generalized linear, and nonlinear mixed-effects modeling. In addition, a broad array of applications are presented with a complete discussion of available software tools for implementation of existing methods. Methods allowing distinct estimation of covariance matrices have been considered by Daniels (2006) and Pourahmadi, Daniels, and Park (2007).
Under MI inference, the imputer’s model is used as a basis for creating the multiple imputations of missing values to be used in the substantive analyses. This is the stage where the problem of missing responses or covariates to be used in the substantive analysis is solved. Once missing values are multiply imputed, say m times (in most problems m < 10), an analyst’s model is fitted with these imputed data, resulting a set of m coefficients and associated standard errors. These results are then combined using rules by Rubin (1987). Other combining rules that operate on other inferential quantities (e.g. p-values) are also available, see for example Li, Meng, Raghunathan, and Rubin (1991) and Rubin (1987).
1.1 Example
The methods developed here were motivated by a missing-data problem in the Seattle crime victimization survey (Rountree, Land, and Miethe 1994). The sample consists of 5,302 adults within 600 Seattle city blocks. The city blocks were paired within 300 clusters or neighborhoods. Data were collected by telephone interview. Details of the sample design and interview procedure are given by Miethe and MacDowall (1993).
One analysis from this study involved modeling individual risk of violent crime and burglary victimization as a function of both individual crime opportunity factors (individual’s socioeconomic characteristics, routine activities and lifestyle) and contextual or neighborhood factors (e.g. ethnic heterogeneity). Burglary victimization is treated as the response variable for the purposes of motivating and illustrating the methods. Specifically, the substantive model is a hierarchical logistic mixed-effects regression model for the probability of being burgled. In the original study, cases with incomplete observations were discarded because the modeling procedure could not handle missing covariates. Summaries of the data along with the proportion of missing data are given in Table 1.
Table 1.
Means, standard deviations (S.D.) of observed variables and percentages of missing values
| Mean | S.D. | % missingness | |
|---|---|---|---|
| Level-1 individual effects | |||
|
| |||
| Burglary victim (0=no, 1=yes) | 0.028 | 0.166 | 0.34 |
| Age (1=10–19, …,7=70+) | 4.367 | 1.717 | 0.12 |
| Gender (0=female, 1=male) | 0.503 | 0.500 | 0 |
| Race (0=white, 1=nonwhite) | 0.150 | 0.358 | 1.25 |
| Home unoccupied (nights per week) | 1.791 | 1.969 | 1.81 |
| Expensive goods (# items owned) | 2.533 | 1.408 | 0 |
| Safety precautions (# precautions) | 3.837 | 1.509 | 0 |
| Live alone (0=no, 1=yes) | 0.258 | 0.437 | 1.36 |
| Family income (1: < $10K, …,7:> $100K) | 3.371 | 1.370 | 11.11 |
|
| |||
| Level-2 contextual variables | |||
|
| |||
| Busy places (# of places nearby) | 3.441 | 1.340 | 0 |
| Ethnic heterogeneity (% nonwhite * % white) | 0.090 | 0.079 | 0 |
| Neighborhood incivilities (# of indicators) | 1.328 | 0.704 | 0 |
Missing-data patterns indicate that covariates and response variables are missing in a non-overlapping fashion. There are only 18 missing values in the response variable, however, the key covariates such as family income or race are missing for 589 (11.11%) and 66 cases (1.25%), respectively. Overall, a complete-case only model-fitting procedure would eliminate 13.22% of the sample, potentially biasing the inferences to those who are less likely to be burgled. If the only variable subject to missingness were the response variable, then the theory of mixed-effects model indicates that inferences are valid under the assumption of missing at random. As this is not the case, I proceed with the inference by MI leading to asymptotically valid inferences under MAR (Rubin 1987).
Inference by MI offers a more efficient and objective way to draw inferences in the case of missing covariates than complete-case-only analysis. An important consideration in this problem is how to preserve clustering and important substantive relationships in the imputation model. These points are discussed in the following sections. As the relationship between the response and other covariates vary by cluster or neighborhood, I extend the current joint imputation models for clustered data (Schafer and Yucel 2002; Yucel 2008) to allow random covariance matrices at level 1 in addition to the random-effects at higher levels which preserve the substantively important relationships in imputations.
The remainder of this paper is organized as follows. Section 2 briefly introduces fundamental concepts in MI inference such as the missing-data mechanism and EM-and-MI-based techniques. Sections 3 and 4 introduce key models of this paper and computational algorithms for fitting these models. Finally, Section 5 illustrates the MI inference under a random-covariance approach. A discussion of current and future research on these topics concludes the paper.
2 Key concepts and methods for missing data
2.1 Missing-data Mechanism
Regardless of the method of choice to draw inferences in the presence of missing values, a certain mechanism generating the missing values must be assumed. Below brief definitions of these missingness mechanisms are given, and for more details readers are referred to Rubin 1987 or Schafer 1997b.
Let R denote a matrix of indicator variables whose elements are 0 or 1, identifying whether elements of a data matrix Y are missing or observed, denoted as Ymis and Yobs, respectively. The missing values are said to be MAR if P(R | Yobs, Ymis, θ) = P (R = r | Yobs = yobs, θ), holds for all θ, where θ contains all unknowns of the assumed model. This assumption states that the the probability distribution of the missingness indicators may depend on the observed data, but given these, not on the missing values. In applications where MAR is a reasonable assumption, MI gives valid inferences. While it is impossible to formally test MAR, an important attraction of model-based MI is in its ability make the models richer to account for missingness (by relying on extra information on Yobs or auxiliary information).
A special case of MAR is missing completely at random (MCAR) in which P(R | Yobs = yobs, Ymis, θ) = P (R | θ), for all θ. In MCAR, the probability distribution of missingness is independent of both the observed and missing data. MCAR is often seen as a very restrictive assumption as it essentially regards incomplete cases as a random subsample, which can be formally tested. Thus, analyses ignoring incomplete cases are only valid under MCAR. Finally, if MAR is violated, the probability distribution depends on the missing values and the missingness mechanism is said to be missing not at random (MNAR). In the case of MNAR, a joint probability model must be assumed for the complete data as well as R, the missingness indicators.
Models presented here assume that the missingness mechanism is ignorable in the sense defined by Rubin (1977), i.e. the missing data are MAR and the parameters of the missingness distribution and complete-data distribution are distinct (see a more detailed discussion in Rubin (1987) or Schafer (1997b)). When carrying out a likelihood-based analyses, the “ignorability” assumption merely means that missingness mechanism can be ignored when performing statistical analyses.
2.2 Principled methods for handling missing values
Several criteria qualify a method as a principled method for dealing with missing values. First the method of choice should be capable of carrying important relationships among variables (both between and within clusters) or between completely-observed and incompletely-observed variables into the substantive analyses. Second, it should incorporate distinct variance sources such as those seen in clustered data. Third, uncertainty introduced by the missing values and the analytical method tackling missing values should be quantified and/or incorporated into the uncertainty measures. In most cases, failure to adopt principled methods in dealing with missing data may result in biased estimates (e.g. regression coefficients) and inaccurate statements on uncertainty measures of these estimates (Rubin 1987, Little and Rubin 2002, Schafer 1997b). Therefore, methods such as case deletion and most ad hoc methods of single imputation are not preferred for any missing data problem as the required assumptions (e.g. MCAR) are often implausible.
The current state of the principled methods centers around the model fitting techniques (e.g. EM-type algorithms) and MI inference. Model fitting techniques tend to be problem-specific and have been well-addressed in the literature (see Schafer 1997b, Little and Rubin 2002 or Schafer and Yucel 2002). Another increasingly popular method for analyzing incomplete datasets is multiple imputation. In multiple imputation, missing data are treated as an explicit source of random variability to be averaged over, with the averaging being carried out by simulation. In some problems the process of creating imputations usually involves Markov Chain Monte Carlo (MCMC) techniques such as the Gibbs sampler and the Metropolis-Hastings algorithm. To produce the imputations, some assumptions about the data (typically a parametric model) and the mechanism producing missing data need to be made. As briefly mentioned in the previous section, the imputation model should be plausible and should be somewhat related to an analyst’s investigation (Schafer 1997b, Meng 1994).
In any given problem, it may be possible to handle the missing values either by EM-type methods or by multiple imputation. Inference by multiple imputation may have some practical advantages. Multiple imputation provides complete datasets for subsequent analyses, allowing the analyst to use their favorite models and software. This point is important as imputation models can be made much richer than the models serving substantive goals. Thus, in practice, imputation models account for reasons for missingness (by including additional variables such as those on the causal path) and serve for multiple substantive purposes. Another possible reason for preferring multiple imputation is that it avoids the problem of there being no algorithm or procedure available to maximize the potentially complicated observed likelihood. Furthermore, because multiple imputation treats missing data as an explicit source of variation, it allows the analyst to quantify missing-data uncertainty in addition to that of ordinary sampling variability.
3 Imputation models
3.1 Multivariate fixed-covariance and mixed-effects (FCME) models
For the purposes of creating multiple imputations, variables subject to missingness are viewed as responses and a model is imposed on them to formulate the predictive distribution of the missing values, given the observed values. One such model was considered by Schafer and Yucel (2002), Liu, Taylor, and Belin (2000), and Yucel (2008) where multivariate adaptation of the well-known linear mixed-effects models were used to model multivariate responses with incomplete observations. Notationally, suppose yi is an ni × r (r > 1) matrix of multivariate responses for sample unit i, i = 1, 2, …, m, where each row of yi is a joint realization of the variables Y1, Y2, …, Yr. The Multivariate adaptation of (2) is
| (1) |
where Xi (ni × p) and Zi (ni × q) are known covariate matrices, β (p × r) is a matrix of regression covariates common to all units (the “fixed effects”), and bi (q × r) is a matrix of coefficients specific to unit i (the “random effects”). Random effects are assumed to be distributed as vec(bi) ~ Nq×r(0, Ψ) independently for i = 1, …, m (the “vec” operator vectorizes a matrix by stacking its columns). Depending on the application and number of variables modeled, these random-effects may be allowed to be a priori independent, leading to a block-diagonal Ψ. Traditional mixed-effects models assume that the ni rows of r− dimensional vectors of εi are independently distributed as Nr(0, Σ). Some versions of mixed-effects models put further structures on Σ such as an auto-regressive structure in longitudinal studies. For the purposes of creating multiple imputations, an unstructured version of Σ is preferable where possible to fit.
3.2 Multivariate random-covariances and mixed-effects (RCME) models
Recall the example given in Section 1, where the associations are believed to vary randomly across the neighborhoods, even after accounting for some of the observable characteristics at the contextual and individual levels. When using a model of the form (1), one explicitly assumes equal covariance matrices for the errors in εi across all the clusters, i = 1, 2, …, m. When data or subject-matter relevance indicate that a heterogeneous covariance matrix is more appropriate, one might assume
| (2) |
where r × r covariance matrices Σ1, Σ2, …, Σm vary. Here “vec” operator is used to stack the columns of a matrix.
Depending on the size of yi, it may be possible to estimate a separate Σi for each individual or cluster. When the data are too sparse to support independent estimates for Σ1, Σ2, …, Σm, it makes sense to specify a model in which they are randomly sampled from a population, mimicking the idea of including random-effects in a mixed-effects model. In the Seattle victimization survey, for example, an imputation model of the form (1) with error terms in (2) could be employed to jointly impute missing responses and covariates. In this example, the large number of subject-specific parameters would create problems if we tried to estimate Σ1, Σ2, …, Σm separately.
For simplicity, we assume that the heterogeneous covariance matrices are sampled from an inverted-Wishart population. The motivation for this is similar to the motivation regarding b1, b2, …, bm as a sample from N (0, Ψ). Assuming that random effects are drawn from a common distribution allows the pooling information across clusters. Thus poor estimation of subject-specific parameters often does not have a significant impact. This random covariance model preserves random variation in the variances and covariances across the clusters, which is analogous to allowing fixed by random interactions among the variables.
In this new model which I call the random-covariances and mixed-effects (RCME) model, the response matrix yi (ni × r) for an individual or cluster i is expressed as
| (3) |
where Xi and Zi are completely-observed covariate matrices. Further
| (4) |
| (5) |
and , independently for i = 1, 2, …, m, where a ≥ r, A > 0 are the degrees of freedom parameter and scale matrix of the Wishart distribution.
In the following section, I describe a MCMC algorithm for fitting the RCME model, and hence imputing the missing data.
4 MCMC algorithm under RCME model for creating multiple imputations
Following the conventional notation in the missing-data literature, let Yobs = (y1(obs), y2(obs), …, ym(obs)), Ymis = (y1(mis), y2(mis), …, ym(mis)). Further, let θ = (β, Ψ, a, A), B = (vec(b1), …, vec(bm))T, and Σ̃ = (Σ1, Σ2, …, Σm) denote the unknown parameters, random-effects and the set of random covariance matrices, respectively.
The RCME model (3) has unknown components Ymis, θ, B and Σ̃. For the purpose of imputation we only need draws of Ymis, but in order to simulate proper values of missing data, we need to take into account the uncertainty introduced by other unknowns.
Simulation of these unknowns is accomplished in a four-step Gibbs sampler. The steps of the Gibbs sampler are
| (6) |
| (7) |
| (8) |
| (9) |
Executing this cycle repeatedly creates sequences {θ (1), θ (2), …} and { } whose limiting distributions are P(θ|Yobs ) and P (Ymis |Yobs ), respectively.
A prior distribution for θ must be specified to derive the conditional distribution (6). We follow the same practice as before for the prior distributions for β and Ψ, which is to set Ψ−1 ~ W(ν, Λ), where ν ≥ qr and Λ > 0, and to assign a uniform prior ‘density’ over
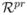 to β. For a and A, we adopt the new prior distributions
to β. For a and A, we adopt the new prior distributions
| (10) |
where γ, Γ and η are user-specified hyperparameters. Note that a, the degrees of freedom parameter of the Wishart distribution, must be greater or equal to r in order for A−1 to exist. I address this issue by working with a transformed version u = log(a + r) which may take values on the real line.
4.1 Simulation of θ
First, consider the problem of drawing Ψ and β from P(θ| Y, B, Σ̃). Since bi | Ψ ~ N(0, Ψ) independently for i = 1, 2, …, m and Ψ−1 ~ W(ν, Λ), Bayes’ theorem implies that Ψ−1 | B ~ W(ν + m, (Λ−1 + BTB)−1). As a result, the updated value of Ψ−1, at iteration t is drawn from W(ν +m, (Λ−1+(B(t))TB(t))−1). For drawing the fixed effects β, ordinary least-squares coefficients are calculated to initialize the Gibbs sampler:
and draw β (t+1) from a multivariate normal distribution centered at β̂ (t) with the covariance matrix
Drawing the scale matrix A(t+1) is similar to drawing Ψ,
where .
Simulating a(t+1) from its marginal posterior distribution completes the step (6). Unfortunately, this cannot be simulated directly. P(a | Σ̃) has the form
| (11) |
which is not a recognizable distribution. One can, however, approximate (11) to draw the value of a from a nearby distribution and correct for the approximation by a Metropolis-Hastings step. Using the parameterization u = log(a + r), we have
| (12) |
Given a current simulated value u(t), I sample a candidate value u† from a density function h(u†) that approximates the marginal posterior P(u | Σ̃). We then calculate the acceptance ratio
| (13) |
and set
where v ~ U(0, 1) is a uniform random variate. The algorithm defined above is a special type of Metropolis-Hastings algorithm which Tierney (1994) has called an independence sampler. It has the desired property of an MCMC method, i.e. as t → ∞, {u(t)} converges in distribution to P(u | Σ̃), provided that h(u) is nonzero over the support of P(u | Σ̃). The convergence is fast when h(u) is a good approximation to P(u | Σ̃). It is recommended to choose h(u) so that it has heavier tails than P(u | Σ̃) (Gelman, Carlin, Stern, and Rubin 2004). Doing so will improve the possibility that the candidate values fall into the region of posterior density and reduce the chance of “getting stuck” in the tails of P(u | Σ̃).
My approximation to P(u | Σ̃) is based on the t4 distribution, which is centered at the mode of P(u | Σ̃),
| (14) |
where um denotes the mode of P(u | Σ̃), , and
The use of t4, suggested by Gelman, Carlin, Stern, and Rubin (2004), offers a reasonable compromise between matching the shape of P(u | Σ̃) and keeping the tails of h(t) heavy. A Newton-Raphson algorithm is used to calculate um, the mode of P (u | Σ̃).
4.2 Simulation of random effects, random covariances and missing data
Using the new random values of θ, I proceed to draw new random values of the random effects b1, b2, …, bm from P (bi | Y, θ, Σ̃). Note that this step, (7), is almost identical to that of Gibbs operating under the FCME model as given in (1) (Schafer and Yucel 2002, Yucel 2008, Liu, Taylor, and Belin 2000); the only difference is that we now have different Σi’s for different clusters instead of the same Σ. After some algebra, we have the following conditional posterior distribution for the random-effects,
where and .
In step (8) of the Gibbs sampler, values of Σ1, Σ2, …, Σm are updated using the most recent values of θ (t+1), B(t+1), and . Note that under model (3) specifications, the pairs (yi, Σi) are distributed as
independently for i = 1, 2, …, m. It follows that the updated random value of is drawn from the distribution
The final step is to draw new values of εi from the conditional distribution given in (9), based on the updated values of the other unknown quantities. Note that, within cluster i, given the unknown values of θ, B and Σ̃, the rows of εi = yi − Xiβ − Zibi are independent and normally distributed with mean zero and covariance matrix Σi. Therefore, in any row of εi, the missing elements have an intercept-free multivariate normal regression on the observed elements; the slopes and residual covariances for this regression can be quickly calculated by inverting the square submatrix of Σi corresponding to the observed variables. Drawing the missing elements in εi from these regressions and adding them to the corresponding elements of Xiβ + Zibi completes the simulation of Yi(mis).
4.3 Implementation issues
In practice one needs to monitor the convergence behavior of the MCMC algorithm. The convergence of (6)–(9) is influenced by rates of missing information in y1, y2, …, ym and the degree to which the individual random effects b1, b2, …, bm and Σ1, Σ2, …, Σm can be estimated from the data. Gibbs samplers are slowest when the number of clusters (m) is large and the unknown random-effects and variance-covariance matrices are poorly estimated. As an example, poor estimation for random-effects occurs when the within unit precision matrices are small relative to the between-unit precision Ψ. Intuitively, as the number of subjects or clusters m grows, the random values of Ψ, a, and A produced at each cycle of the algorithm will be close to their previous values, inducing a high degree of dependence.
When modeling a large number of response variables at once, it may be advantageous to restrict Ψ to a block-diagonal structure—not only for the purpose of obtaining prior guesses, but also when running the Gibbs sampler itself. If Ψ is block-diagonal, then independent inverted Wishart prior distributions may be applied to the q × q nonzero blocks, for j = 1, 2, …, r. Weak priors are obtained by setting νj = q and where Ψj is an estimate or prior guess for Ψj. The distributions for these blocks in step (6) become where , and bij is the jth column of bi.
The choice between an unstructured or block-diagonal Ψ will depend on both theoretical and practical considerations. A block-diagonal structure indicates no a priori associations between the random effects for any two response variables Yj and Yj′. In a multivariate cluster sample with many variables, many units per cluster, but relatively few clusters, it may simply not be possible to estimate covariances among the random effects for all response variables. It is important to note that even if Ψ is block-diagonal, the columns of bi are not independent in an a posteriori sense because the posterior covariance matrix, Ui, is not block-diagonal.
5 Application: Seattle crime victimization survey
5.1 Preliminary analyses
This section illustrates the imputation procedures on data drawn from the Seattle crime victimization survey (Rountree, Land, and Miethe 1994). The sample consists of 5,302 adults within 300 clusters (each of cluster is defined as a paired city blocks). Data were collected by telephone interview. Preliminary analyses of these data indicate low percentages of missingness across the items making up the variables used in the substantive analyses (see Table 1 for descriptive statistics and % missingness). The seriousness of the missing-data problem is realized when investigating the missingness patterns: disproportionate distribution of burglary victimization across the key covariates raises a valid concern for subjective conclusions under an analysis ignoring incomplete cases.
In a previous set of analyses, Rountree, Land, and Miethe (1994) investigated victimization using individual and contextual factors. Hierarchical logistic regression models were used to predict the risk of individuals’ burglary victimization. Rountree, Land, and Miethe (1994) thoroughly analyzed the victimization survey data and found that certain individual crime opportunity factors in addition to contextual ones are important predictors of the risk of victimization. For the purposes of illustrating multiple imputation under the RCME model, I will assume that the model given below serves the investigators’ goals of modeling burglary victimization as a function of individual and contextual factors. Table 2 shows the estimates of the following random-intercept only hierarchical logistic regression model using the 4601 complete cases (R package lme4 by Pinheiro and Bates (2000) was used to compute these estimates).
Table 2.
Estimates from hierarchical logistic regression on burglary victimization using complete-cases only
| est. | SE | z value | p-value | |
|---|---|---|---|---|
| Individual effects | ||||
|
| ||||
| Intercept | −2.4830 | 0.279 | −8.889 | 0.00 |
| age | −0.0317 | 0.028 | −1.125 | 0.261 |
| gender | −0.0507 | 0.082 | −0.623 | 0.533 |
| race | −0.2446 | 0.127 | −1.931 | 0.053 |
| home unoccupied | 0.0429 | 0.021 | 2.004 | 0.045 |
| family income | 0.1032 | 0.033 | 3.137 | 0.002 |
| expensive goods | 0.1194 | 0.033 | 3.626 | 0.001 |
| safety precautions | −0.0793 | 0.029 | −2.688 | 0.007 |
| live alone | 0.1783 | 0.103 | 1.733 | 0.083 |
|
| ||||
| Contextual effects | ||||
|
| ||||
| busy places | −0.0433 | 0.039 | −1.120 | 0.263 |
| ethnic heterogeneity | 0.3495 | 0.647 | 0.540 | 0.589 |
| incivilities | 0.4991 | 0.079 | 6.337 | 0.000 |
| (15) |
where i, j denote data points (i = 1, 2, …, 300 indicating the neighborhoods and j = 1, 2, …, ni indexing individuals within neighborhoods) and ui denotes the cluster-specific intercept term (random intercept) assumed to be .
Consistent with the previous findings (Rountree, Land, and Miethe 1994; Miethe and MacDowall 1993), significant associations of burglary victimization with whether the home is left unoccupied, family income, amount of expensive goods at home, and whether the occupant lives alone are seen. A unit increase in the number of safety precautions results in about 8% decrease in the odds of burglary. Age, gender and race are also negatively associated but they are not statistically significant. Rountree, Land, and Miethe (1994) used models similar to (20) to investigate how the risk of violent and property victimization are affected by individual and contextual-level characteristics. From the estimates presented in Table II, we see that neighborhood incivilities play a major contextual role in predicting victimization. In contrast to this finding, ethnic heterogeneity and busy places, measured in number of places near the respondent’s residence are not statistically significant.
5.2 Inference by multiple imputation
5.2.1 Imputation models: FCMC and RCME
The model given by (20) and other substantive models of this form allow the effects of some variables on burglary victimization to vary by neighborhood. In this example, missing data pose critical threats to the validity of analyses, including biased regression coefficients and standard errors. How should one handle the missingness among variables which will be employed as both responses and covariates? As described in Section 1.1, because a significant portion of the missingness is due to incomplete covariates, inference via multiple imputation will be employed to prevent inefficient use of these data and potential biases.
This section explores two alternative joint modeling approaches for conducting MI inference: RCME (varying level-1 variance and covariance matrices) and FCME (fixed level-1 variance and covariance matrix). The main advantages of FCME is to preserve the varying mean structure across the clusters and RCME improves this by preserving the effects of the key covariates (of the substantive model) on the burglary victimization across the clusters in the imputed datasets. Below I explain the specification of the imputation model (6) with respect to both RCME and FCME which differ in the specification of the error term. The latter has the specification given by (9) with the inverted Wishart hyper-prior. The missing values in both the response and covariates of the model (20) are imputed using these models, and finally the model (20) or the analyst’s model is fitted with these imputed datasets. Then, the results are combined using rules by Rubin (1987) (MI estimates).
I will now illustrate the use of multiply-imputed datasets with an analysis of predictors of burglary victimization. I drew 50 independent imputed datasets from a converged MCMC chain (the computational details on convergence are given below), under both the FCME and RCME models. The response variables of the imputation models were burglary (whether or not individual has been burgled), age, race, number of evenings the home was unoccupied last week, whether the person lives alone and family income. Both imputation models included main effects for gender, number of safety precautions taken, an indicator of how “busy” the neighborhood is, neighborhood incivility and neighborhood ethnic heterogeneity. Note that all of the covariates in the imputation models are completely-observed. This model was chosen to impute all variables that are subject to missingness and had some degree of relevance in the substantive model as well as on the causes for missingness. The intercepts for all of the variables were allowed to randomly vary among neighborhoods as well as the slopes for the covariates gender, number of expensive goods owned, and number of safety precautions taken so that the imputation models are compatible with the substantive model.
5.2.2 Computational details
A practical question in creating MIs is how to monitor the convergence of the underlying Gibbs sampler. This question is crucial as it is the fundamental computational tool used to sample the missing values from their posterior predictive distribution of missing data. As noted by many, including Gelman, Carlin, Stern, and Rubin (2004) and Schafer (1997a), there are two general issues with the convergence: (1) whether the simulations are representative of the predictive distribution of missing data P(Ymis | Yobs ), and (2) whether the successive draws are significantly correlated. These two issues, individually or collectively, can seriously damage the overall quality of inferences in terms of accuracy and representativeness of the target distribution. Simple investigation of time series plots and autocorrelation function plots is often indicative of the interdependency of the successive draws. These plots can be used to assess the convergence behavior and to determine the number of iterations needed to achieve independent samples from the desired distributions P(Ymis |Yobs ) and P (θ| Yobs ). Running multiple independent chains from common starting values and checking if they converge to the same P(Ymis | Yobs ) are also powerful and practical tools to monitor the convergence.
To assess convergence under the RCME model (similar methodology applies to FCME), the algorithm was run for an initial 1,000 cycles under a very mild prior with νi = 4, , i = 1, …, 6, γ = 6, Γ−1 = 6I, η = 6, corresponding to a block diagonal Ψ. Time-series plots and sample autocorrelations for the components of θ were then examined. This initial analysis revealed that several hundred cycles might be sufficient to achieve approximate stationarity. The Gibbs sampler was then run for an additional 51,000 cycles, with the simulated value of Ymis stored at each 1000 cycles. Autocorrelations verified that the dependence in all components of θ had indeed died down by lag 200, so the fifty stored imputations could be reasonably regarded as independent draws from P(Ymis | Yobs ).
5.2.3 Results
After the imputation stage, a hierarchical logistic regression model given by (20) for the variable burglary victimization was fitted to each of the imputed datasets. Maximum likelihood estimates and standard errors were computed using R lme4 package by Pinheiro and Bates (2000). These estimates were then combined using the rules defined by Rubin (1987). The results of this procedure are summarized in Table 3. This table which contains estimates obtained under RCME and FCME as the imputation models indicates that the fixed-effects coefficients for the age, home unoccupied, family income, expensive goods, and safety precautions variables are statistically significant.
Table 3.
Estimated coefficients, standard errors, degrees of freedom and percent missing information from 50 multiply-imputed hierarchical logistic regression
| MI under RCME | MI under FCME | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| est. | SE | exp(est.) | p-value | % missing info. | est. | SE | exp(est.) | p-value | % missing info. | |
| Individual effects | ||||||||||
|
| ||||||||||
| intercept | −2.239 | 0.257 | 0.11 | <0.001 | 1 | −2.4831 | 0.266 | 0.08 | 0.000 | 1 |
| age | −0.042 | 0.028 | 0.96 | 0.148 | 1 | −0.0367 | 0.026 | 0.96 | 0.158 | 2 |
| gender | −0.054 | 0.081 | 0.95 | 0.505 | 0 | −0.0627 | 0.077 | 0.94 | 0.418 | 0 |
| race | −0.235 | 0.125 | 0.79 | 0.060 | 1 | −0.2316 | 0.118 | 0.79 | 0.052 | 1 |
| home unoccupied | 0.059 | 0.028 | 1.06 | 0.034 | 1 | 0.0491 | 0.023 | 1.05 | 0.038 | 2 |
| family income | 0.099 | 0.032 | 1.10 | 0.002 | 5 | 0.1181 | 0.052 | 1.13 | 0.001 | 5 |
| expensive goods | 0.112 | 0.033 | 1.12 | 0.001 | 1 | 0.1087 | 0.030 | 1.11 | <0.001 | 1 |
| safety precautions | −0.099 | 0.025 | 0.91 | 0.005 | 1 | −0.0865 | 0.027 | 0.92 | 0.002 | 1 |
| live alone | 0.152 | 0.097 | 1.16 | 0.117 | 2 | 0.1453 | 0.098 | 1.16 | 0.138 | 3 |
|
| ||||||||||
| Contextual effects | ||||||||||
|
| ||||||||||
| busy places | −0.042 | 0.038 | 0.96 | 0.269 | 1 | −0.038 | 0.038 | 0.96 | 0.319 | 1 |
| ethnic heterogeneity | 0.608 | 0.591 | 1.84 | 0.304 | 0 | 0.5715 | 0.633 | 1.77 | 0.367 | 0 |
| incivilities | 0.451 | 0.068 | 1.57 | <0.001 | 1 | 0.4857 | 0.077 | 1.63 | <0.001 | 1 |
While there are minor changes between MI estimates and the complete-case (CC) analysis, the two sets of analyses are generally consistent in terms of the estimates of regression coefficients. Important differences, however, occur in the estimation of the associated standard errors. Since all individuals with partial data are used in inferences, MI results in inferences that are more efficient than than CC analysis. The MI estimates combine between-imputation variance B due to missing data with sampling (within-imputation) variability U conditional on imputed data. The estimated rate of missing information, B/(B + U), is low for all coefficients due to the relatively small number of incomplete cases. While they are generally similar under two imputation models, RCME lead to slightly larger standard errors than their FCME counterparts. This is somewhat expected as, under RCME, there are more unknown parameters. However, under RCME, slightly lower estimates for the rate of missing information is observed (except family income which has the highest raw missingness) indicating RCME leads to slightly better-calibrated results. In applications where the quantity being estimated is influenced by the missing data, estimates of the fraction of missing information are expected to be non-zero and inform the users how much of the information (in the statistical sense) is lost due to missing data.
The MI estimates of the analyst’s model in Table 3 are fairly consistent with those reported by (Rountree, Land, and Miethe 1994) and also reported here in Table II. The most noticeable difference is observed in the standard errors (SEs). Though inefficient, CC analysis would give valid inferences under MCAR. However, MCAR is not plausible here as incomplete cases differ systematically from the complete cases with respect to the outcomes of interest (e.g. rate of reported burglary cases in the income groups). Another difference is observed in the varying degrees of significance in the effects. The effects of age, race, home unoccupied and ethnic heterogeneity became slightly more significant under MI inference even though the corresponding SEs incorporate the missing-data uncertainty. Overall, RCME and FCME lead to similar significant effects (only RCME-estimates given here): a unit increase in the race (white to non-white), home unoccupied, family income, expensive goods, safety precautions and live alone result a 23% decrease, a 6% increase, a 9% increase, an 11% increase, a 9% decrease, a 22% increase in the odds of burglary. Further, a unit increase in the contextual neighborhood incivility indicator result in a 67% increase in the odds of burglary. However, contextual effects of ethnic heterogeneity and busy places did not show significance in the MI inference.
6 Discussion
Models and algorithms developed here present important tools to researchers in the analysis of multivariate multilevel incomplete data where not only means but also covariances of the error term vary across the clusters. Multilevel models have been very popular because they allow researchers to pursue inferences that take into account clustering while presenting them the ability to estimate effects at the individual and cluster levels. Incorporating these key features into the missing-data methods carries a similar importance. The main goal of this paper was to develop an imputation model that will appropriately model not only the mean structure but also the covariance structure of the clusters. In applications where data have natural hierarchies as well as incompleteness among responses and covariates, the methods of this paper allows for a more flexible and appropriate joint model to be fitted to the observed data, which is also consistent with the substantive model of interest.
Most substantive analyses focus on an individual response variable as illustrated in Section 3. In the specific data-example used in Section 6, a binary variable was modeled under a logistic model. To overcome the missing-data problem in the response and covariates, I used a model based on the multivariate normal distribution with special structures imposed on means and variances. Should this raise a concern of compatibility? In other words, should the substantive model be compatible with the imputation model? General discussion on this subject is given by (Rubin 1987), (Meng 1994) and (Schafer 1997b). Several studies specifically investigate the use of continuous models as approximations to the imputation of binary variables (Schafer 1997b, Yucel, He, and Zaslavsky 2008, Horton, Lipsitz, and Parzen 2003, Demirtas, Freels, and Yucel 2008). These studies commonly indicate that the use of normality is a reasonable approach to imputing binary variables in most well-bahaved problems (e.g. moderate missingness and reasonable distributions of binary variable). Other studies offer imputation strategies (e.g. Demirtas and Hedeker 2008, Goldstein, Carpenter, Kenward, and Levin In press) for binary variables in longitudinal or multilevel settings under models with fixed-covariance terms. As a separate note on compatibility, the RCME model (3) implies a conditional univariate linear mixed-effects model with ε ~ N(0, Σi) for each response variable given the others, where the others are incorporated into the columns of Xi. Therefore, the procedures explained in this work can also be used in multilevel analyses with arbitrarily missing covariates which will be incorporated into subsequent analyses. However, the current methodology is not clear on how to formally test the varying variance-covariance structure at level-1, and I believe it is an area that is worthy of further research.
The methods developed in this paper can be extended in several directions. Here I focus on two levels of clustering, but extending this to higher levels of nesting is straightforward (see Yucel 2008). The second extension pertains to limitations of the current imputation model (3). Note that each column of yi is forced to have the same Xi. The most important role of this model is to incorporate all of the possible information into the imputation phase, and our current practice is to make the Xi as rich as possible disregarding the need for distinct Xis. When this is not the case, minor changes to the algorithms given in Section 5 can easily accomplish this task.
The third extension relates to incompletely-observed variables for level-2 units, or in multilevel applications with higher order clustering, level-3 units. These types of variables can also be found at level-1 in longitudinal studies among non-time varying covariates. If these covariates have no missing values, then they can be handled under the current model by simply moving them into the matrix Xi. When they are incompletely-observed, however, they have to be modeled. From a modeling perspective this is a simple task as it implies an imposed model marginal on such variables, and given these variables the model of this paper remains same. The Gibbs sampler described here can also be easily extended to reflect the introduced unknown parameters. One has to be cautious, however, if the model is over-specified especially when the categorical characteristics of the clusters are missing and modeled.
Another extension relates to other types of variables such as categorical or count variables. As discussed above, Gaussian-based models usually perform reasonably well for imputing binary or ordinal outcome variables. However, the normal approximation may not work well for other type of variables (e.g. nominal). Employing saturated loglinear models with appropriate random-effects to reflect cluster-specific effects offers a similar caliber of solutions to the methods introduced here. An important consideration should focus on the number of variables, as such models often suffer severe estimation problems in high dimensions. In such cases, one can adapt the methods of this paper into a variable-by-variable approach such as those by Van Buuren and Oudshoorn (2000) or Raghunathan, Lepkowski, and VanHoewyk (2001). However, the variable-by-variable approach is not immune to over-specified models for the categorical variables. Finally, imputation models that consider special structures such as multiple membership or non-nested clusters need to be developed not only to conduct traditional MI-based inferences (e.g. in surveys) but also to conduct inferences under missing-data-like problems (e.g. ambiguous genotype assignments in genetic studies).
References
- Bryk A, Raudenbush S, Congdon R. Hierarchical Linear and Nonlinear Modeling with HLM Programs. Chicago: Scientific Software International, Inc; 2007. [Google Scholar]
- Carpenter J, Kenward M. Instructions for MLwiN multiple imputation macros. Bristol, UK: Centre for Multilevel Modelling; 2008. [Google Scholar]
- Daniels M. Bayesian modeling of several covariance matrices and some results on propriety of the posterior for linear regression with correlated and/or heterogeneous errors. Journal of Multivariate Analysis. 2006;98:568–587. [Google Scholar]
- Demidenko E. Mixed Models: Theory and Applications. New York: J. Wiley & Sons, New York; 2004. [Google Scholar]
- Demirtas H, Freels S, Yucel R. Plausibility of multivariate normality assumption when multiply imputing non-Gaussian continuous outcomes: A simulation assessment. Journal of Statistical Computation and Simulation. 2008;78:69–84. [Google Scholar]
- Demirtas H, Hedeker D. An imputation strategy for incomplete longitudinal ordinal data. Statistics in Medicine. 2008;27:4086–4093. doi: 10.1002/sim.3239. [DOI] [PubMed] [Google Scholar]
- Diggle P, Liang K, Zeger S. Analysis of longitudinal data. Oxford: Oxford University Press; 1994. [Google Scholar]
- Fitzmaurice G, Laird N, Ware J. Applied Longitudinal Analysis. New York: John Wiley and Sons; 2004. [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian Data Analysis. 2. London: Chapman & Hall Ltd; 2004. [Google Scholar]
- Goldstein H, Carpenter J, Kenward M, Levin K. Multilevel models with multivariate mixed response types. Statistical Modelling In press. [Google Scholar]
- Hedeker D, Gibbons R. A random effects ordinal regression model for multilevel analysis. Biometrics. 1994;50:933–944. [PubMed] [Google Scholar]
- Horton NJ, Lipsitz SR, Parzen M. A Potential for Bias When Rounding in Multiple Imputation. The American Statistician. 2003;57:229–232. [Google Scholar]
- Laird N, Ware J. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. [PubMed] [Google Scholar]
- Li K, Meng X, Raghunathan T, Rubin D. Signicance levels from repeated p-values with multiply-imputed data. Statistica Sinica. 1991;1:65–92. [Google Scholar]
- Littell R, Miliken G, Stroup W, Russell D. SAS System for Mixed Models. Carey, NC: SAS Publishing; 1996. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. 2. New York: J. Wiley & Sons, New York; 2002. [Google Scholar]
- Liu M, Taylor J, Belin T. Multiple Imputation and Posterior Simulation for Multivariate Missing Data in Longitudinal Studies. Biometrics. 2000;56:1157–1163. doi: 10.1111/j.0006-341x.2000.01157.x. [DOI] [PubMed] [Google Scholar]
- McCulloch C, Searle S. Generalized, Linear and Mixed Models. New York: John Wiley and Sons; 2001. [Google Scholar]
- Meng XL. Multiple-Imputation Inferences with Uncongenial Sources of Input. Statistical Science. 1994;10:538–573. [Google Scholar]
- Miethe T, MacDowall D. Contextual effects in models of criminal victimization. Social Forces. 1993;71:741–759. [Google Scholar]
- Pinheiro J, Bates D. Mixed-Effects Models in S and S-PLUS. New York: Springer-Verlag Inc; 2000. [Google Scholar]
- Pourahmadi M, Daniels M, Park T. Simultaneous Modelling of the Cholesky Decomposition of Several Covariance Matrices. Journal of Multivariate Analysis. 2007;98:568–587. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2007. URL http://www.R-project.org. [Google Scholar]
- Raghunathan TE, Lepkowski JM, VanHoewyk J. A multivariate technique for multiply imputing missing values using a sequence of regression models. Survey Methodology. 2001;27:1–20. [Google Scholar]
- Rasbash J, Steel F, Browne W, Prosser B. MlWin User’s Manual. Bristol, UK: Centre for Multilevel Modelling; 2006. [Google Scholar]
- Rountree P, Land C, Miethe T. Macro-Micro integration in the study of victimization: A hierarchical logistic model analysis across Seattle neighborhoods. Criminology. 1994;32:287–313. [Google Scholar]
- Rubin DB. Formalizing subjective notions about the effect of non-respondents in sample surveys. Journal of the American Statistical Association. 1977;72:538–543. [Google Scholar]
- Rubin DB. Multiple Imputation for Nonresponse in Surveys. New York: John Wiley and Sons; 1987. [Google Scholar]
- SAS Institute. SAS/Stat User’s Guide, Version 8.2. Carey, NC: SAS Publishing; 2001. [Google Scholar]
- Schafer J. Analysis of Incomplete Multivariate Data. London: Chapman & Hall; 1997a. [Google Scholar]
- Schafer J. Multiple imputation of incomplete multivariate normal data. The Pennsylvania State University; PA, USA: 2000. [Google Scholar]
- Schafer J, Yucel R. Computational strategies for multivariate linear mixed-effects models with missing values. Journal of Computational and Graphical Statistics. 2002;11:421–442. [Google Scholar]
- Schafer JL. Analysis of Incomplete Multivariate Data. London: Chapman & Hall; 1997b. [Google Scholar]
- Schafer JL, Graham JW. Missing Data: Our View of the State of the Art. Psychological Methods. 2002;7:147–177. [PubMed] [Google Scholar]
- Stata. Stata Statistical Software: Release 10. StataCorp LP; College Station, TX: 2007. URL http://www.stat.com. [Google Scholar]
- Tierney L. Markov Chains for Exploring Posterior Distributions. Annals of Statistics. 1994;22:1701–1728. [Google Scholar]
- Van Buuren S, Oudshoorn C. TNO Preventie en Gezondheid: Report PG/VGZ/00.038. 2000. Multivariate imputation by chained equations: MICE V1.0 User’s Guide. [Google Scholar]
- Verbeke G, Molenberghs G. Linear Mixed Models for Longitudinal Data. New York: Springer-Verlag Inc; 2000. [Google Scholar]
- Vonesh EF, Chinchilli VM. Linear and nonlinear models for the analysis of repeated measurements. Marcel Dekker Inc; 1997. [Google Scholar]
- Yucel RM. Multiple imputation inference for multivariate multilevel continuous data with ignorable non-response. Phil Trans R Soc A. 2008;366:2389–2403. doi: 10.1098/rsta.2008.0038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yucel RM, He Y, Zaslavsky A. Using calibration to improve rounding in imputation. The American Statistician. 2008;62:125–129. [Google Scholar]


