Liquid crystal self-assembly of random-sequence DNA oligomers

Abstract

In biological systems and nanoscale assemblies, the self-association of DNA is typically studied and applied in the context of the evolved or directed design of base sequences that give complementary pairing, duplex formation, and specific structural motifs. Here we consider the collective behavior of DNA solutions in the distinctly different regime where DNA base sequences are chosen at random or with varying degrees of randomness. We show that in solutions of completely random sequences, corresponding to a remarkably large number of different molecules, e.g., approximately 10¹² for random 20-mers, complementary still emerges and, for a narrow range of oligomer lengths, produces a subtle hierarchical sequence of structured self-assembly and organization into liquid crystal (LC) phases. This ordering follows from the kinetic arrest of oligomer association into long-lived partially paired double helices, followed by reversible association of these pairs into linear aggregates that in turn condense into LC domains.

The selectivity and reversibility of DNA and RNA association enables crucial biological functions in which oligomers selectively pair to target sequences even within large amounts of nucleic acid chains. Selectivity is decisive, for example, in the microRNA-mRNA interactions, crucial in the regulation of gene expression. Similar high levels of selectivity are exploited in genomic PCR, relying on the capacity of primers to target their complementary sequence within a full genome. Selective interactions of DNA oligomers have been exploited in the past years in a variety of strategies for the construction of designed self-assembled nanostructures (1–4). Selectivity combines with self-assembly in the recent observation that short oligomers of nucleic acids having complementary sequences exhibit liquid crystal (LC) ordering (5–7). In this article, we report LC ordering in solutions of DNA oligomers with random sequences where the large body of different competing sequences effectively reduces the selectivity of the interactions. With these results, we show that the phenomenology of the self-assembly of nucleic acid oligomers is actually much richer than previously recognized, involving self-selection, linear aggregation, and ordering of fully random chains. Our results strengthen the notion that DNA and RNA have unequaled capacity of self-structuring and unavoidably suggests self-assembly as the possible key factor for the emergence of nucleic acids from the prebiotic molecular clutter as the coding molecules of life.

LC Ordering of Complementary DNA Sequences

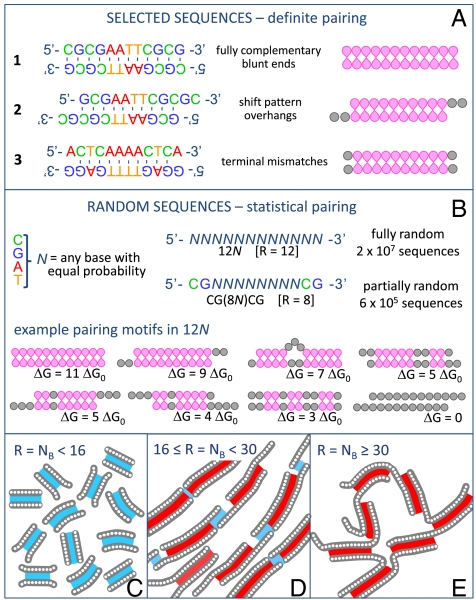
The first observations of LC ordering of oligonucleotides were performed in solutions of 6- to 20-base-pair DNA oligomers (6 bp ≤ N_B ≤ 20 bp) whose sequences promoted the formation of fully paired duplexes (example 1 in Fig. 1A). These were found to order into the chiral nematic (N^∗) LC phase in concentration (c_DNA) ranges depending on the oligomer length and sequence. At larger c_DNA, the solutions transform into the columnar (COL) phase and, at even higher c_DNA, into a columnar crystalline state (5, 7). The driving mechanism for this phase behavior is provided by the stacking interactions between the paired terminal bases of the blunt-ended duplexes. Later studies involved sequences with overhangs of length ℓ = 2, which exhibited N^∗ and COL phases when the terminal sequences are mutually complementary (as in example 2 in Fig. 1A), thus promoting—through stacking and pairing interaction—the linear aggregation of duplexes (8). Further investigations have revealed that the process of LC formation is selective, such that in an all-or-nothing mixture of complementary and noncomplementary oligomers the complementary oligomers tend to be incorporated into the LC domains and segregated from the surrounding isotropic phase of noncomplementary strands (9). Altogether, these findings, obtained with controlled sequences and involving at most mixtures of a few of them, reveal a remarkable and finely tuned combination of staged self-assembly: DNA hybridization, linear aggregation, liquid crystallization, phase separation, and condensation of sequences.

Fig. 1.

Duplex motifs of oligomeric DNA: pairing errors and random sequences. (A) Definite pairing achieved by selected sequences, e.g., LC-forming fully paired blunt-ended duplexes, and duplexes with mutually complementary overhangs (5, 8). Effects of errors introduced by design, such as terminal mismatches, are described in SI Text. (B) ranDNA sequences are synthesized by randomly choosing one of the four basic nucleobases at given positions along the chains and are thus mixtures of 4^R different sequences, where R is the number of randomly chosen bases. Because of the large number of sequences, ranDNA forms duplexes with a variety of distinct pairing motifs, the distribution of which is controlled by their binding energy ΔG, given in units of ΔG_o, the mean binding energy of a quartet of complementary bases, and by their lifetime τ ∼ exp(ΔG/ΔG_o). (C–E) Sketches of the behavior of ranDNA oligomers of different lengths in solution. Blue shading: ΔG < 15ΔG_o; τ short; equilibrium binding. Red shading: ΔG > 15ΔG_o, τ long compared to experimental time; kinetically arrested binding. Thus, short oligomers (C) form an equilibrated ensemble of duplexes; oligomers of intermediate length (D) form kinetically arrested duplex cores with weakly mutually attractive tails enabling linear aggregation and LC ordering; long oligomers (E) form multiple kinetically arrested cross-linking bonds leading to gelation.

The stacking of duplexes within the LC phases, in which the terminals of the oligonucleotides are held in continuous physical contact, appears as a templating environment that could favor the selective nonenzymatic ligation of short complementary oligomers into longer complementary ones, a crucial step in the appearance of early life (10). Random-sequence DNA is an important class of systems to understand in this regard, because pools of heterobase oligomers are likely prebiotic systems emerging from random ligation.

Random DNA Oligomers

In order to explore the scope of the self-assembly mechanisms of nucleic acids, we investigated aqueous solutions of DNA oligomers of length N_B ≤ 30 bp, into which various modes of random sequencing have been introduced, such that at selected positions in the sequence the four primary A, C, G, and T nucleobases are found with equal probability. Example of such “ranDNA” oligomers are indicated in Fig. 1B, where we denote a randomly chosen base with the character “N” in the sequence. For example, 8N indicates the set of 8-mers having eight randomly chosen bases and C(8N)G the set of 10-mers having complementary C-G terminal base pairs and eight internal randomly chosen bases. In both cases, the family of molecules corresponds to 4⁸ ≈ 65,000 different sequences mixed together in the same solution. The collective state of any such system crucially depends on the role of the polydispersity of interaction originating from the wide range of pairing strengths and pairing motifs. Well-matched oligomers may promote liquid crystal phases, contrasted by oligomers forming duplexes with low end-to-end interactions. On the other hand, there is a significant possibility of chains acting as cross-links (as sketched in Fig. 1E), the effect of which would be to take the system to a random isotropic gelated state similar to hydrogels formed by long DNA (11, 12). It was thus difficult to anticipate the solution behavior of ranDNA.

Sequence description, ranDNA synthesis, HPLC purification, and MALDI characterization can be found in SI Materials and Methods. In each case, solutions were prepared in pure water with c_DNA in the range 300 < c_DNA < 1,000 mg/mL, enclosed in cells made of glass slides spaced by 10 μm, and examined in depolarized transmitted light microscopy (DTLM). Concentrations were determined as described in ref. 5. LC ordering is heralded by the appearance of birefringent domains of characteristic color and texture that enable identification of the phases (5) (Fig. 2 A and B).

Fig. 2.

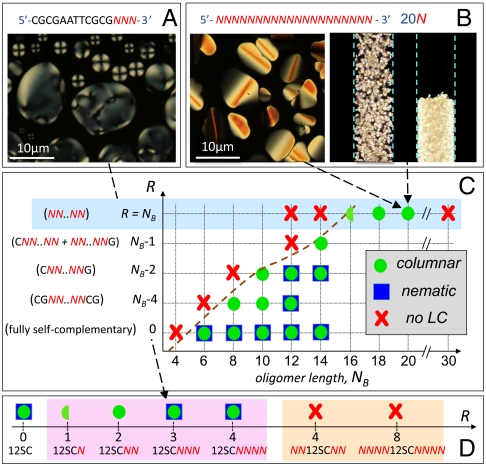
Phase diagram of ranDNA. (A and B) A variety of ranDNA solutions self-assemble into N^∗ (A) and COL (B) LC phases, recognized by the textures in thin cells observed in DTLM. (B) DTLM image of 0.5-mm-diameter capillary of 20N in solution, showing COL domains before and after centrifuging. (C and D) Maps of the LC phases observed in ranDNA of different total number of bases N_B and of random bases, R, either internally (C) or at the terminals (D). Symbols indicate the presence of the nematic (blue square) and of the columnar (green circle) phases in some range of concentrations and temperatures of the solution. The half green circle indicates that the columnar phase is present in a very narrow range of conditions (low T, large c_DNA). Shaded regions highlight specific phase behavior: light blue—fully random sequences; pink—double helices with a single overhanging random tail per duplex terminal; and orange—two random tails per duplex terminal.

We have first investigated the phase behavior of oligomers with designed sequence errors in the base pairing (as in example 3 in Fig. 1A). The systematic study of the effect of such errors on the LC phase formation, summarized in SI Text, indicates that even a single terminal mispairing reduces the self-association of the duplexes, as might be expected. Internal errors are less problematic, affecting the phase behavior only when there are more than two in a duplex. In general, the N^∗ phase is suppressed first, followed by the COL phase, as the number of pairing errors is increased. In solutions of sequences paired in a shifted mode with overhangs, LC ordering is stabilized if the overhangs are mutually complementary (8) but suppressed if the overhangs are noncomplementary.

LC Ordering of Random-Sequence DNA

Fig. 2C summarizes the phase behavior at room temperature of ranDNA as a function of the oligomer length N_B and of the number of random bases (R) when randomness is progressively increased from the center of the sequences. R = 0 corresponds to fully self-complementary (SC) sequences. We find that (i) the shortest sequence for which we find LC ordering increases with R, as indicated by the dashed line; (ii) the N^∗ phase is more easily suppressed by randomness than the COL phase; and (iii) quite remarkably, COL ordering can be found in fully random sequences (light blue shading), but only for N_B≥16, also confirming that the destabilizing effects of randomness are somehow mitigated by increase of length. (iv) This trend is limited, however, as LC ordering is not found for N_B≥30. The optical textures of the cells and local birefringence indicate that the N^∗ and COL LCs of ranDNA are the same phases as those observed in complementary duplexes aggregating by end-to-end stacking.

Fig. 2D summarizes the phase behavior observed when random bases are added to the terminals of a complementary core, in this case the “Dickerson dodecamer” self-complementary 12-mer (12SC), a very well characterized LC-forming (7) B-DNA-type structure (13). Random sequences added to the 3′ end only (pink shading) lead to 12SC duplexes with random overhangs (length ℓ). In this case, although short random overhangs (ℓ = 1[-N] or ℓ = 2[-NN]) cause the loss of the N^∗ phase (with the COL phase found in the case of ℓ = 1 in a very narrow range of c_DNA and T), we interestingly observe the full LC behavior (COL and N^∗) for larger ℓ = 3,4, a behavior closer to that of fully complementary overhangs than that of noncomplementary overhangs, e.g., -T and -TT, which always suppress LC ordering (5). We also explored the effect of random sequences of equal length added to both 12SC terminals (orange shading), a structure yielding duplexes with two random tails at each end. In this case, the LC ordering is disrupted for short and longer tails (-NN and -NNNN).

Phase Behavior of Random 20-mers (20N)

The most surprising finding of the lot is the observation of LC ordering in solutions of 20N, the 20-mers having all bases randomly chosen. A 20N sample corresponds to a molecular population of about 10¹² different sequences. Because we can assume that in 20N all sequences are equally represented, apart from statistical fluctuations (see SI Materials and Methods), in a typical solution used in the experiments (c_DNA ∼ 750 mg/mL), a given sequence has a molar concentration of the order of 0.1 pM, its fully complementary potential partners being at a mean mutual separation of about 10 μm.

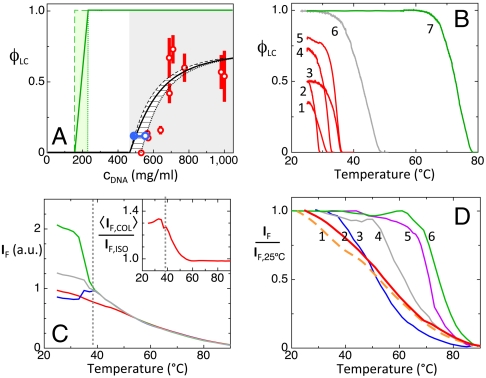
The LC phase behavior of the 20N was studied by measuring the fraction of the cell volume filled by LC domains, ϕ_LC, vs. c_DNA, following heating to the isotropic (ISO) phase and cooling back to T ∼ 25 °C. The ISO phase fills the cells for small c_DNA, whereas the COL domains appear and coexist with the ISO for c_DNA > 550 mg/mL. That is, the COL domains never grow to fill the whole area, with ϕ_LC increasing up to ϕ_LC ∼ 0.7 for c_DNA ∼ 1,000 mg/mL, as shown by the open red circles in Fig. 3A. This phase coexistence was further explored by using centrifugation to force macroscopic ISO/COL phase separation of 20N in capillaries (see Fig. 2B). COL domains are in this way compacted in the bottom of the capillary, with the ISO phase floating on top, enabling measurement of ϕ_LC. Capillaries were then cut so as to extract a known volume of each phase, which was then diluted to enable measurement of c_DNA via UV absorption (see SI Materials and Methods). The values of the DNA concentrations for coexisting COL and ISO found near the threshold of phase coexistence (c_DNA = 520 mg/mL and ϕ_LC = 0.17) are plotted in Fig. 3A as open and full blue squares, respectively. Their concentration difference, δc_DNA ∼ 80 mg/mL, is much smaller than the phase coexistence range in c_DNA, a typical feature of the phase diagram of multicomponent or polydisperse systems. This observed behavior is in contrast with that of solutions of single-component oligomers, such as the complementary 20SC, where the coexistence range is the same as the concentration difference between the two phases and ϕ_LC approaches 1 (see green lines in Fig. 3A). The (red) vertical bars in Fig. 3A indicate the variation of ϕ_LC for different thermal histories and cooling rates, as discussed in SI Materials and Methods. This dependence is rather weak, with similar ϕ_LC found for both rapid and slow cooling of isotropic solutions. Because rapid cooling is too fast for complementary partners capable of perfect duplexing to find one another, imperfectly paired oligomers must be the basis of LC ordering in solutions of random 20-mers.

Fig. 3.

Experimental characterization of the self-assembly and LC formation of 20N. (A) Red dots—LC-ISO phase coexistence at T = 25 °C as determined by the cell area fraction filled by the LC phase, ϕ_LC, as a function of the 20N concentration c_DNA. Green line and shading—LC-ISO phase coexistence of a self-complementary 20-mer. Full and empty blue dots—respectively, the concentration of coexisting ISO and COL phases as measured by UV absorption on a capillary as in Fig. 2B, where macroscopic phase separation was forced through centrifugation. Gray shading—LC-ISO phase coexistence range of 20N; black dashed and dotted lines—concentration of the coexisting ISO and COL phases. (B) LC volume fraction ϕ_LC vs. temperature T. Red curves (1–5)—progressive melting of the 20N COL phase in cells of various ϕ_LC in A. Curves 2 and 3 are obtained with the same cell and curve 3 with longer thermalization time at room T. Gray curve (6)—COL-ISO ϕ_LC vs. T for 12SC at approximately 1,200 mg/mL. Green curve (7)—COL-ISO ϕ_LC vs. T for 20SC at approximately 600 mg/mL. (C) Fluorescent emission I_F of EtBr in a 20N solution (c_DNA ≈ 700 mg/mL) vs. T as a probe of duplex unbinding, measured in both the coexisting COL (blue and green lines) and ISO (red line) phases. Because of the polarized fluorescent emission of EtBr, I_F depends on the orientation of the COL ordering, parallel (blue line) and perpendicular (green line) to the cell plane. The mean, orientation-independent, fluorescent emission in the COL phase (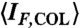, gray line) can be obtained from the weighted average of the parallel and perpendicular I_F. The Inset shows the excess of mean fluorescent emission of the COL phase with respect to the ISO phase. (D) Number of duplexes remaining at T relative to the number at T = 25 °C, extracted from I_F: orange dashed line (1)—12N. Red line (2)—20N. Blue line (3)—10SC. Gray line (4)—12SC. Purple line (5)—16SC. Green line (6)—20SC. For all the sequences, the curves were obtained in the concentration range 600–800 mg/mL.

The LC domains melt as T is raised. Examples of the melting curve ϕ_COL vs. T are shown in Fig. 3B, where they are compared to the melting of the COL phase of 12SC (gray line) and of a self-complementary 20SC (green line). Various melting curves for 20N are shown as red lines in the figure, corresponding to various concentrations and thermal histories of the samples. Quite evidently, the COL melting T (T_COL) of the 20N takes place at a much lower T than the 12SC, a clear indication that 20N interduplex interactions are weaker than those acting between well-paired blunt-ended duplexes.

The relatively low thermal melting temperature of the COL phase of 20N implies weaker duplexing and/or aggregation than in the fully complementary 20SC. The progressive disruption of duplexes can be monitored by measuring the intensity I_F of the fluorescent emission of ethidium bromide (EtBr) at low concentration in the 20N solution. In Fig. 3C, we plot I_F measured in COL and ISO phases in a cell where the two phases coexist. Above T_COL, marked by a dashed line, I_F decreases smoothly, indicating that the 20N helix unbinds at a temperature T_U ∼ 55 °C. At T < T_COL, because of the anisotropy of EtBr fluorescence, I_F measured in the COL phase depends on the LC orientation. However, by appropriately averaging, we can extract a value of 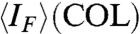(red line) that, in the absence of other factors, should equal I_F(ISO). We instead find 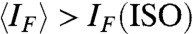(see Fig. 3C, Inset). Because data in Fig. 3C are taken with increasing T, the decrease of 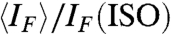as T grows above T = 40 °C reflects both the loss of the better quality of pairing promoted within the COL phase, which is lost as the LC melts, and the larger DNA concentration of the COL phase, slowly diffusing out.

Fig. 3D uses I_F to compare the duplex melting of 20N, measured in the ISO phase (red line 1), with that of 12N (orange dashed line) and of various SC sequences at similar concentration. Quite clearly, the melting of 20N and of 12N are very similar and distributed over a larger T interval than complementary sequences and take place in a T range between the 10SC and the 12SC, much lower than that of the 20SC, which indicates that the pairing of 20N is far from complete, involving a wide distribution of energies. It also suggests an average degree of pairing in the order of ten couples of adjacent base pairs for both 20N and 12N. As for the case of complementary blunt-end oligomers, the addition of salt weakly destabilizes the LC phases, with the addition of 150 mM NaCl depressing the I-LC transition temperatures by approximately 2 °C, a consequence of charge screening.

Discussion

Duplexes with Random Tails.

The observations reported here confirm that LC ordering of oligomeric DNA is mediated by linear aggregation. As errors and randomness are introduced at the duplex terminals, LC ordering is lost. The larger sensitivity of the N^∗ ordering to duplex mispairings agrees with the notion that upon reducing the interparticle bonding energy the N^∗ phase is disrupted before the COL phase, as recently found by investigating a model of linearly aggregating cylinders (14). The same behavior is also expected by theories describing the ordering of long rods as their flexibility increases (15, 16) and agrees with the intuition that the higher packing density of the COL phase leads to an increased stability of mismatched duplexes, thus reducing the disordering effects of randomness.

It is therefore not surprising that duplexes with a stable core and four random tails (one per sequence terminal, orange set in Fig. 2D) do not develop LC ordering, because in these cases the probability of attaining terminal pairing is small. More interesting is the behavior of duplexes with random overhangs (pink set in Fig. 2D). The addition of a ℓ = 1 random overhang strongly destabilizes the LC ordering. This behavior is expected because for a ℓ = 1 tail only 1/4 of the casual collisions with other duplex terminals leads to formation of paired bases and thus to interduplex attractive interaction. As ℓ increases, however, the probability that overhangs mutually bond because of random collision also increases. The average interduplex bond free energy 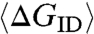can be estimated by computer generating collisions between random overhangs. ΔG_ID for each pair of colliding overhangs is evaluated on the basis of a simplified binary version of the standard nearest-neighbor model for DNA hybridization free energy (17) in which we attribute a free energy ΔG₀ to each group of two consecutive bases in a chain paired to their Watson-Crick (WC) complements (base quartet), whereas we give ΔG = 0 to quartets that involve mismatches (see SI Text). Here we assume ΔG₀ = 2.7k_BT, the room temperature DNA binding energy per base quartet averaged over all WC paired nucleobases (see SI Text). The resulting mean interduplex bonding free energy ranges from 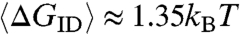for ℓ = 1 to 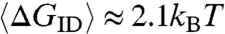for ℓ = 4 (Fig. 4D, right axis). These quantities should be compared with 5k_BT of blunt-end stacking and 6k_BT for interactions via mutually complementary overhangs of length 2 (8).

Fig. 4.

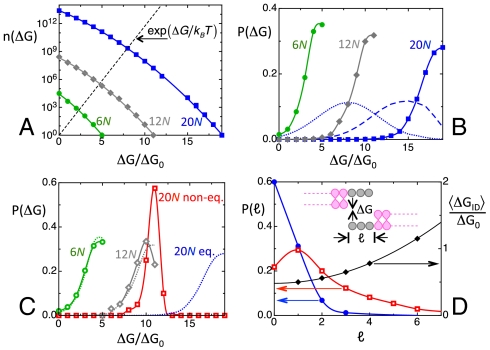
Calculated equilibrium and nonequilibrium distributions for ranDNA. (A) Number n(ΔG) of duplexes differing in sequences or in shift that can be formed within the ensemble of fully random sequences of a given length as a function of the pairing free energy ΔG. Blue squares—20N; gray diamonds—12N; green dots—6N. The n(ΔG) are normalized to n(ΔG) = 1 for the largest energy for each given oligomer length. Black dashed line—ΔG dependence of the Boltzmann factor, on the same scale. Free energy is expressed in units of ΔG₀. (B) Equilibrium distribution P(ΔG) of the intraduplex binding free energy in fully random ranDNA at T = 25 °C. Blue squares—20N. Gray diamonds—12N. Green dots—6N. Dashed and dotted blue lines—P(ΔG) for 20N at T = 45 °C and T = 60 °C, respectively. (C) Free energy distribution P(ΔG) calculated through kinetic evolution on the basis of duplex lifetime and random collisions. Red squares—20N. Gray diamonds—12N. Green dots—6N. Dotted lines repeat, for comparison, the equilibrium distributions in B. Whereas 6N and 12N are at equilibrium or nearly so, the distribution of 20N is kinetically arrested and far from equilibrium. (D) Left axis: Calculated overhang length distributions P(ℓ) for 20N. Blue dots—equilibrium distribution. Red open squares—kinetically arrested distribution, on the same scale. Right axis: black diamonds—mean interduplex interaction free energy, calculated as the average value of the binding free energy resulting from collisions of random overhangs.

Nonergodic Association.

With this background we can discuss the behavior of fully random sequences and of the 20N, in particular. When in solution, random sequences produce a variety of paired couples. An approximate calculation of the equilibrium distribution of all possible pair associations within the pools of ranDNA oligomers can be obtained as a Boltzmann distribution P(ΔG) = [n(ΔG)] exp(-ΔG/k_BT), where ΔG is the intraduplex binding energy, evaluated with the same crude approximation that ΔG = ΔG₀ for every WC paired quartet and ΔG = 0 for mismatched quartets. The number of possible oligomer combinations yielding a given value of ΔG is n(ΔG), which results from considering all possible pairs of sequences combined with all possible shifts ℓ. This enumeration encompasses various pairing motifs, some of which are sketched in Fig. 1B. The resulting n(ΔG) (see SI Text) is shown in Fig. 4A for 6N (green dots), 12N (gray diamonds), and 20N (blue squares). The spread in energy of the resulting equilibrium distributions (Fig. 4B) at T = 25 °C confirms the expected variety of pairing motifs in ranDNA. The 20N mean duplex binding free energy calculated from the equilibrium distribution is 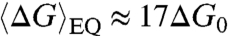, a value nearly as large as 19ΔG₀, the maximum binding energy for fully paired 20-mers. However, the 20N duplex melting behavior noted above (Fig. 3D) suggests instead a mean intraduplex binding energy to be of the order of ΔG ≈ 10ΔG₀. This discrepancy indicates that equilibrium distributions are generally not adequate to describe the association of ranDNA. In trying to understand this discrepancy, we realized that kinetics of pairing plays a crucial role that must be considered in modeling the pairing distribution. Indeed, the lifetime τ of well-paired DNA oligomers can easily exceed the typical times involved in experiments. At room temperature, complementary 8-mers have lifetimes τ ∼ 1 s (18), whereas complementary 20-mers have lifetimes τ > 10⁵ s (19, 20. If we assume an activated behavior to express these complementary duplex lifetimes as a function of free energy, τ[ΔG(N_B)] = τ₀ exp{ΔG(N_B)/k_BT}, where ΔG(N_B) ≈ (N_B - 1)ΔG₀ is the duplex binding free energy of well-paired duplex strands (see SI Text), we find a mean attempt time τ₀ ∼ 10 ns, which enables us to estimate the lifetimes of duplexes vs. their binding free energy ΔG.

The strong dependence of τ on ΔG is the critical factor in determining the thermodynamic status of ranDNA solutions. Oligomers collide and interact, the actual energy level attained in each interacting pair being determined by the number and location of well-paired bases. Collisions yielding weak binding originate short-lived pairs that rapidly separate and proceed to further collisions. Therefore, short sequences (N_B ≲ 12), whose binding and unbinding take place on time scales shorter than the experimental time, can reach equilibrium. As longer (N_B ≳ 12) sequences are considered, the situation changes because they can form duplexes having a lifetime comparable or larger than the experimental time, which are therefore effectively permanently stable. This fact prevents the system from exploring in time all the possible states, and thus the equilibrium distribution is never reached (nonergodic behavior). We modeled the kinetic behavior of ranDNA by computer generating successive encounters between one given N-mer sequence and randomly generated N-mers, evaluating ΔG and the lifetime τ(ΔG) for each event, and then summing these lifetimes until a given total time τ_TOT was reached (see SI Text). The energy distribution of the ensemble of duplexes found at a time τ_TOT = 10 h is shown in Fig. 4C. The precise choice of τ_TOT is not very critical because of the strong dependence of τ on ΔG: A choice of τ_TOT within the range 1 h < τ_TOT < 100 h displaces the distribution of at most ± 1ΔG₀.

Upon comparing the equilibrium and kinetically arrested distributions (see Fig. 4C), it appears that the 6N and the 12N are at equilibrium, or very close to it, whereas the 20N kinetic distribution is markedly different from equilibrium and it is characterized by a mean energy value . These results are in good agreement with duplex melting observations (Fig. 3D) and indicate that, in the case of 20N, the approach to equilibrium and to stronger binding is impaired by kinetic arrest.

The nonequilibrium behavior observed in the simulations opens a path to understanding the formation of LC phases of 20N. In Fig. 4D, we show the distribution in overhang length obtained from the equilibrium (blue dots) and nonequilibrium (red open squares) duplex distribution of 20N. As clearly visible in the figure, the equilibrium distribution favors well-paired duplexes and yields an average overhang length 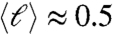, whereas the nonequilibrium ensemble of kinetically trapped duplexes is characterized by a broad distribution of overhang length with 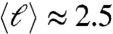bases. Therefore, successive random 20N collisions lead to a kinetic arrested population of duplexes having a central reasonably well-paired stretch with a terminating stretch of overhanging random bases, as sketched in Fig. 1D. Their condensation into LC domains is thus readily understood by the similarity of such a system to the 12SC with random overhangs (Fig. 2D, pink set) discussed above. Indeed, the low melting T for the COL phase of 20N further confirms this picture of duplexes interacting via the weak and, importantly, annealable end-to-end coupling provided by random tail interaction. From the evaluations above, we expect such coupling to be of the order of 1.6k_BT, thus significantly weaker than blunt-end interactions. Moreover, the strengthening of interduplex interactions observed upon aging the samples (see Fig. 3B) supports the notion that the interaction between adjacent duplexes can be improved by enhancing the matching of contacting overhangs, a process expected to take place by duplex flipping and hopping within the COL structure.

The same analysis performed on 12N reveals the importance of the oligomer length in the formation of LC phases. Equilibrium and kinetic distributions are in this case quite similar, both yielding 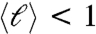, a picture confirmed by the fact that T_U for 12SC and for 12N are not very different (Fig. 3D). This observation, when combined with the significant probability of finding pairing errors at the duplex ends, justifies the fact that end-to-end interactions in 12N are too weak to support linear aggregation and LC phase formation.

The formation of duplexes in 20N can thus be regarded as a paradigmatic example of a system diffusing in a space populated by energy traps that are deep enough to produce nonergodic behavior (21, 22). This conceptual frame is intensively studied to account for nonergodicity and aging in condensed matter systems of various kinds, including disordered systems and polymers with multiple folded states. A remarkable consequence of the combination of factors at play, sketched in Fig. 1D, is that ranDNA develops LC long-range ordering only in a limited interval of lengths near N_B ∼ 20 (Fig. 2). In the 20N, kinetic arrest produces duplex pairs with interpair interactions that are sufficiently weak to enable annealing and equilibration into LC domains. Shorter ranDNA oligomers form a population of equilibrium duplexes that lack the interactions necessary for self-assembly and LC formation. At the opposite extreme, when the sequences are longer, the random overhanging tails can form additional kinetically arrested interduplex interactions, leading to oligomer networking and gelation (11) and suppressing LC formation. Observations show that ranDNA with N_B ≳ 30 yields viscous isotropic solutions without LC domains. Shearing between the cell plates with flow velocity at 45° to the DTLM polarizer gives transient optical transmission, indicative of transient birefringence, evidence for the formation of an isotropic gelated state.

It is of interest to question whether the nonergodic behavior of 20N can be avoided by thermal annealing at a temperature very close to the unbinding temperature T_U, as is the case in the known efficient annealing in PCR systems that enables N_B = 20 primers to find their complementary target sequence on very long DNA (a detailed comparison of ranDNA with genomic PCR is given in SI Text). As it turns out, in the ranDNA case, because of the enormously larger number of nonideal pairing motifs, annealing closer to equilibrium generates a broad distribution of weakly bound pairs that are nonideal for LC formation. Fig. 4B shows the equilibrium distribution at T = 45 °C (blue dashed line) and T = 60 °C (blue dotted line). Inspection of these curves clearly indicates that, upon lowering the pairing and stacking energy (i.e., upon increasing T), the behavior 20N system is even more strongly affected by its huge variety of conformations expressed in n(ΔG).

Polydispersity of Attraction.

The 20N COL-ISO phase coexistence range, in which the system never gets entirely into the COL phase at high c, is much broader than that found in complementary duplexes and also broader than the concentration difference δc_DNA of the coexisting phases, as shown in Fig. 3A. This finding is evidence that the polydispersity of 20N duplex structures affects the phase separation in a way comparable to that found in multicomponent lyotropics LCs, such as polydisperse mixtures of rods (23 24). In 20N, collisions and energy-dependent lifetimes give rise to a significant polydispersity of duplex structures, with larger and smaller overhangs (Fig. 4D), and a variable number of terminal mispairings. This polydispersity in structures yields a polydispersity of attraction that has the potential to induce phase separation, because the more strongly interacting duplexes give rise to longer and more stable aggregates, which in turn can more easily overcome the Onsager threshold (25). To test whether the variety of end-to-end duplex interactions can indeed yield phase separation, we studied a mixture of 12SC-CG (i.e., 12SC with a self-complementary 2-base overhang at the 3′ end), providing definite end-to-end attraction, and of two mutually complementary sequences, one of which terminated at the 5′ end by a FITC fluorescent group that prevents stacking and pairing interactions at one duplex end. This mixture promptly phase separates into coexisting birefringent COL domains with low fluorophore concentration and ISO fluid with high fluorophore concentration, with ISO-COL coexistence over nearly the complete range of relative concentration (see SI Text). This test highlights a route for the self-assembly of DNA oligomers, previously unnoticed. To the extent that this binary mixture of interacting and noninteracting duplexes can be considered a model for the polydispersity of attraction of 20N, the phase behavior described in Fig. 3A can be interpreted as a manifestation of the intrinsic polydispersity of random-sequence DNA duplexes. Through this phase separation, the system self-selects chains capable, through long-lived intraduplex binding and annealed interduplex pairing, to organize in long physically bound helices. This behavior unavoidably strengthens the notion that self-assembly of nucleic acids could have been instrumental in the formation of long double helices on the basis of shorter random sequences.

Conclusions

The study of ranDNA has revealed that LC ordering of DNA oligomers in solution is found even in the presence of a large amount of randomness. We find a range of lengths of random DNA sequences, between the isotropic fluid arrangement of short oligomers and the isotropic gel of long random DNA strands, where a rich combination of random pair formation, equilibrium annealing, kinetic arrest, phase demixing, and mesophase ordering yields a pathway toward long-range LC ordering. Evidence indicates that solutions of oligomers with 20 randomly chosen bases can evolve into a population of kinetically arrested self-assembled pairs characterized by a structural theme that enables the formation of linear aggregates and promotes condensation into LC domains. Given the extreme—but at the same time controllable—heterogeneity of these systems, and given the remarkable combination of self-assembly processes that guide their behavior, we envisage ranDNA as a paradigm for the study of the effects of random interaction disorder on the collective behavior of self-associating molecules in solution.