Classification of protein functional surfaces using structural characteristics

Abstract

Protein structure and function are closely related, especially in functional surfaces, which are local spatial regions that perform the biological functions. Also, protein structures tend to evolve more slowly than amino acid sequences. We have therefore developed a method to classify proteins using the structures of functional surfaces; we call it protein surface classification (PSC). PSC may reflect functional relationships among proteins and may detect evolutionary relationships among highly divergent sequences. We focused on the surfaces of ligand-bound regions because they represent well-defined structures. Specifically, we used structural attributes to measure similarities between binding surfaces and constructed a PSC library of ∼2,000 binding surface types from the bound forms. Using flavin mononucleotide-binding proteins and glycosidases as examples, we show how the evolutionary position of an uncharacterized protein can be defined and its function inferred from the characterized members of the same surface subtype. We found that proteins with the same enzyme nomenclature may be divided into subtypes and that two proteins in the same CATH (Class, Architecture, Topology, Homologous superfamily) fold may belong to two different surface types. In conclusion, our approach complements the sequence-based and fold–domain classifications and has the advantage of associating the shape of a protein with its biological function. As an expandable library, PSC provides a resource of spatial patterns for studying the evolution of protein structure and function.

A major goal of protein classification is to understand the structural, functional, and evolutionary relationships among proteins. Among the best-known protein classifications are Pfam (1) by a sequence-based method and CATH (class, architecture, topology, homologous superfamily) (2) and SCOP (Structural Classification of Proteins) (3), both of which are based on the fold–domain approach. From a sequence-based classification (1, 4), one gains knowledge of the expansion of protein families and their evolutionary relationships. From a fold–domain classification (2, 3), one obtains a global view of protein fold space (5).

An advantage of the sequence-based approach is that it requires only protein sequence data, but no structural data. However, it is difficult to relate amino acid changes to structural or functional changes (6, 7). Moreover, a sequence-based method may not be able to detect distant relationships among proteins because protein sequences may not be well-conserved in evolution (8, 9). In comparison, the fold–domain approach may be able to detect distant relationships, because most protein folds are well-conserved. However, protein folds may be too conservative to do a fine classification of proteins or to reveal functional divergence between two proteins. Indeed, examples exist where domain folds cannot guarantee the identification of biological functions (9). In addition, a classification may have other important missions such as the identification of functional sites involved in biochemical reactions and the evolutionary forces that affect functional divergence during protein evolution.

Our approach uses functional surfaces. Typically, the biochemical reactions of a protein occur on the surface region that mediates molecular interactions with either substrates or other proteins. Moreover, the structural information and biological function of a characterized protein can usually be transferred to another protein when the two proteins share a high similarity of surface structures (10, 11). In this study, we considered the local surface that interacts with cognate ligands and focused on ligand-binding surfaces for several reasons. First, a ligand-bound surface is well-defined because the conformation is fixed by its binding to the ligand and it contains abundant biological information. Second, ligand binding typically occurs in a protein pocket and usually can be identified from the 3D structure of the protein in the Protein Data Bank (PDB) (12). Third, including protein regions that interact with other proteins complicates the analysis because they are more difficult to predict than protein pockets. Fourth, including unbound forms will greatly increase the number of surface pairs to be compared, thus greatly increasing the computational cost. Our strategy is first to establish the classification of bound forms, which, as will be seen later, can serve as a library of surface types and subtypes for classifying unbound structures. Note that comparing binding surfaces has indeed proven powerful for identifying the binding site of an uncharacterized protein (10, 11, 13). In our definition, a binding surface includes all of the residues involved in ligand binding (i.e., the entire pocket where the binding occurs). In most cases, the binding surface includes binding sites and active sites (e.g., catalytic residues), although in some cases it does not include the active sites.

In this study, we develop an effective means of geometric matching to classify protein functional surfaces. The functional surfaces of proteins have attributes such as hydrophobic strength and charge concentration that can potentially reveal the relationships among proteins with different folds. This is because selective constraints on function restrict the spatial arrangement of functionally important residues of binding surfaces and may retain similar biochemical activities even when protein folds become distinct. Therefore, we use this technique to identify those residues involved in biochemical reactions and group proteins by their structural attributes. Its major advantage is to provide site-specific information pertaining to the binding sites, so that an association between the binding surface and molecular function(s) may be established.

Results and Discussion

Building a Basic Library of Functional Surface Types.

From a total of ∼68,000 PDB structures, we identified 28,986 bound forms for a functional surface classification. To assess the pairwise similarity between binding surfaces, we computed their local root-mean-square deviation (rmsd) by fPOP (14); if their P value was ≤10⁻⁴, they were classified into the same surface type. We computed the rmsd values of all binding surface pairs. Applying clustering analysis (Materials and Methods), we established a library of 1,974 surface types, which are used to build a basic set of binding surface shapes.

We use N_s to denote the number of members in a protein surface type. Among the 1,974 surface types only 502 have N_s ≥10, 95 surface types have N_s ≥50, and 31 surface types have N_s ≥100 (Fig. S1). This uneven distribution is partly due to biased selection of proteins in structural studies; most of the classified surface types are enzymes or soluble proteins.

Classifying Surface Subtypes.

The above coarse classification was based on the rmsd value of each surface pair. The discrimination power of rmsd starts decreasing when closely related surfaces are compared. For a finer classification, we selected a list of surface attributes (Table 1). Using shape analysis, we studied the selected surface attributes of each of the 28,986 identified binding surfaces (Fig. S2; SI Text, Selecting the Surface Attributes of a Protein). A detailed kernel-density plot of an attribute can reveal its high density area (Fig. S3). As an example of using the selected structural attributes to conduct a fine classification, let us consider oxidoreductases. Fig. S4 shows that the 41 structures of the oxidoreductase surface type lie scattered on the hyperplane when only three surface attributes [length (len), sphericity (sph), and anisotropic distance (d)] are used, but are clustered into three distinct subtypes when the 11 attributes in Table 1 are used (see more details below). This example shows the importance of using a sufficiently large number of attributes in classifying protein surfaces.

Table 1.

Structural attributes in a shape profile used to characterize protein surfaces

Selected attributes	Notation	Mean	Standard deviation
Number of residues in a pocket (aa)	len	30.74	25.93
Global polar solvent-accessible area (Å2)	Pams	5816.20	2981.12
Global apolar solvent-accessible area (Å2)	aPams	8731.59	4356.02
Local polar solvent-accessible area (Å2)	Polar	586.00	560.88
Local apolar solvent-accessible area (Å2)	aPolar	960.51	895.44
Global sphericity	Wsph	0.51	0.06
Local sphericity	sph	0.57	0.09
Anisotropic (Å)	d	10.28	5.15
Local surface density (g/mol Å2)	SD	0.76	5.63
Global skewness	WG1	−0.01	0.32
Global kurtosis	WG2	−0.18	0.56

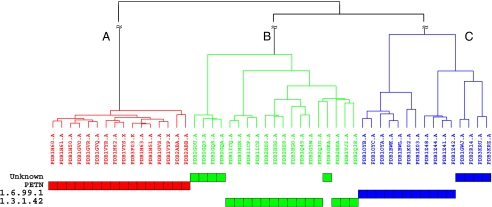
We now present more details about the classification of oxidoreductases. The oxidoreductase surface type consists of 41 members that have Enzyme Commission (EC)-annotated functions (Table S1). Their folds belong to the same CATH ID number of 3.20.20.70 (Aldolase class I). For each member, we computed their surface attributes (Table S1). For any two members, we calculated their functional similarity score Φ and then converted it into a dissimilarity score by a transformation (Materials and Methods). We then computed the dissimilarity matrix for the 41 members and represented all pairwise relationships in a heatmap (Fig. S5). The relationships of structural attributes suggested the partitions of a surface type (SI Text, Determining the Number of Subtypes in a Surface Type). Using a hierarchical clustering analysis (Fig. S6), we placed them into three distinct subtypes, A, B, and C, that exactly match their EC annotations. The binding surfaces of PDB1gvr.A, PDB2hs6.A, and PDB1z41.A are representatives of subtypes A, B, and C, respectively. Although the three subtypes belong to the same Aldolase class I fold (CATH 3.20.20.70), they have the following functions: PETN (pentaerythritol tetranitrate), EC 1.6.99.1, and EC 1.3.1.42 (Fig. S7). The residue compositions of their binding surfaces along with the geometrical measurements are available at http://pocket.uchicago.edu (15).

The residues on a binding surface, although noncontiguous in the primary sequence, provide surface characteristics of a protein: which type of residue occupies a specific position, how the residue is geometrically placed in space, and how its hydrophobic area and charge concentration are distributed. This is important because the spatial distribution of a set of binding residues usually determines the location and function of a binding region along the protein surface (Table S1). Our finding is that the residue composition of a binding surface gave rise to the surface attributes computed in Table S1. Thus, we directly applied these attributes to characterize subtypes (Table 2). For instance, the members within this surface type have similar binding pockets because the sph and surface density (SD) were highly similar. However, the d in subtype C was at least 1.5 Å longer than those in the other two subtypes. The hydrophobic occupation on a binding surface of subtype A was 6% lower than those of subtypes B and C. In terms of geometrical measurements, subtype C had the largest binding pocket involved in fatty acid biosynthesis [Gene Ontology (GO) 0008610 and 0000663].

Table 2.

Mean values of surface attributes of oxidoreductase subtypes

Subtype	len	Pams	aPams	Polar	aPolar	Wsph	sph	d	SD	WG1	WG2	EC
A	34.00	0.43	0.57	0.47	0.53	0.56	0.54	8.24	0.69	−0.40	−0.11	NA
B	30.64	0.41	0.59	0.41	0.59	0.54	0.57	7.53	0.63	−0.10	0.17	1.6.99.1
C	39.64	0.42	0.58	0.41	0.59	0.57	0.50	9.76	0.65	−0.36	−0.01	1.3.1.42

NA, not assigned.

The global shape of a protein is depicted by (WG1, WG2), where WG1 and WG2 are the skewness and kurtosis, respectively. When a value of WG1 is close to 0, it implies that the distribution of atoms of the protein is symmetrical. A large value of WG2 implies that the protein is segmented. The means of WG1 and WG2 were, respectively, −0.40 and −0.11 for subtype A, but (−0.10, 0.17) and (−0.36, −0.01) for subtypes B and C. The (negative, negative) values of (WG1, WG2) provided a signature for subtype A, whereas (negative, positive) and (negative, zero) provided a signature for subtypes B and C, respectively. Although the ratios of hydrophobic to hydrophilic areas on subtypes B and C are highly similar, the sizes of their pocket surfaces differed by a mean of nine residues. In terms of biological function, it had been experimentally shown that subtype C acts on the CH—CH group of a substrate with NADP⁺ (16), whereas subtype B acts on NADPH as a dehydrogenase (17).

Inferring the Molecular Function of an Uncharacterized Protein.

Clustering analysis of binding surfaces provides useful templates (11, 13) and also homogeneous subgroups, which can be analyzed separately for understanding molecular function (11, 18, 19). Indeed, the templates in our protein surface classification (PSC) database provide information for identifying the binding surface of an uncharacterized protein, from which one may formulate hypothetical molecular functions for enzymatic assays or for site-directed mutagenesis of binding residues (20).

We now give an example of inferring molecular function by analyzing the uncharacterized members of the oxidoreductase family. Of the 50 oxidoreductase ligand-bound forms, 25 have known EC annotations and 16 have PETN structures, whereas 9 have no EC annotation. PSC is applied to identify the surface subtypes of these 9 uncharacterized proteins. We first use the surface attributes to reconstruct a tree. Then, using the three surface subtypes as references, we classify the 9 structures into their corresponding subtypes (Fig. 1). For example, PDB3gka (with no EC label) is connected to PDB2q3o under the same branch of the surface subtype of EC 1.3.1.42, whereas PDB1gwj, 2r14, 3kru, and 3kr7 share the common ancestor with PDB1z41 (EC 1.6.99.1). From the 41 classified binding surfaces, we can identify the subtype of the binding surface of a related oxidoreductase and infer its function.

Fig. 1.

Oxidoreductase classification and functional inference of the oxidoreductases with no Enzyme Commission annotation. The evolutionary position of an uncharacterized protein is potentially identified when its functional surface matches a known surface subtype.

The same strategy may be applied to identify the surface type of an unbound structure, using the surface classification of bound forms. One benefit is: When the functional surface of a protein structure is identified, its related functional surfaces are automatically provided by PSC. For example, the common ancestor of subtypes EC 1.3.1.42 and EC 1.6.99.1 was duplicated and the two resultant genes evolved different enzymatic functions. The subset of binding surfaces of EC 1.3.1.42 and that of EC 1.6.99.1 can be potentially used to infer their ancestral binding surfaces. The comparison of the binding surfaces of the common ancestor and the subtypes may allow one to conduct experimental validation of a hypothetical evolutionary pathway and functional interchangeability (21, 22).

Classifying Highly Divergent Proteins.

Of the 1,974 surface types in PSC, 31 families, including kinases and glycosidases, have more than 100 members. In many cases, within the same surface type, members show no significant sequence similarity (≤30%). Glycosidase, for example, has members with a low sequence identity, but their binding surfaces are highly conserved. To cluster surface subtypes with divergent members into a fine classification scheme, it is important to use effective attributes to compute the distance matrix. Fig. S8 shows scatter plots of structural attributes. The distinct subtypes of EC numbers are shown in different colors. In an attempt to conduct a fine classification, we are interested in determining the boundary between two subtypes associated with molecular functions. Let us consider a subclassification for the surface type of glycosidase.

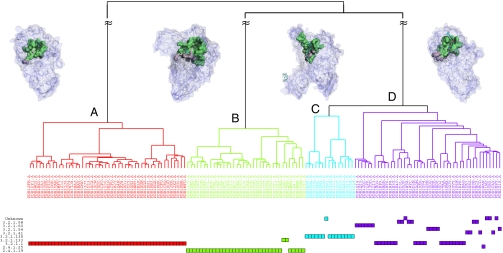
PSC includes 143 functional surfaces from the surface type of glycosidase. We compared their structural attributes and obtained a dendrogram by hierarchical clustering analysis (Fig. 2). The 143 members were divided into four subtypes, A, B, C, and D, containing, respectively, 48, 36, 15, and 44 members. Subtypes A, B, and C correspond to the following enzyme classes: EC 3.2.1.1, EC 2.4.1.19, and EC 3.2.1.135. Subtype D has multiple EC numbers: EC 3.2.1.98, EC 3.2.1.60, EC 3.2.1.54, EC 3.2.1.41, EC 3.2.1.135, EC 3.2.1.133, and partial EC 3.2.1.1. However, these EC numbers differ only by the last EC digit. Fig. 3 shows the representative subtypes of these binding surfaces.

Fig. 2.

Topology of the four major surface subtypes of glycosidase, containing 48, 36, 15, and 44 members, respectively. The representatives of subtypes A, B, C, and D are PDB1u33 (EC 3.2.1.1), PDB1ukt (EC 2.4.1.19), PDB2d2o (EC 3.2.1.135), and PDB1kxh (EC 3.2.1.1), respectively. Each member of a subtype is associated with an EC label, if available. Subtype D has a variety of members with mixed EC labels, whereas subtypes A, B, and C consist of members with EC annotations.

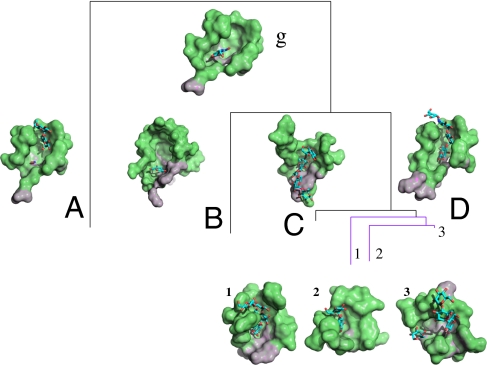
Fig. 3.

Structural conservation and divergence of binding surfaces of glycosidase. Binding surface g is the center of the surface type, which contains 143 members that are clustered by surface attributes into A, B, C, and D subtypes. Subtype A (18 aa) has a solvent-accessible area of 269.53 Ų and a molecular volume of 401.27 ų; subtypes B (26 aa), C (20 aa), and D (17 aa) have, respectively, solvent-accessible areas of 476.98, 261.61, and 270.00 Ų and molecular volumes of 867.84, 475.16, and 410.24 ų. Among them, subtype D can be further subclassified.

To better understand the functional divergence, we detected site-specific structural variation by comparing their residue compositions and geometrical measurements. Using shape profiles, we characterized each binding surface and found that these binding surfaces are physicochemically similar and evolutionarily conserved, so that they are clustered within the same surface type. That is, similar binding surfaces carry out related biological functions. However, their variation in residue composition on the binding surface causes dissimilarity in function. Notable differences are the size of a binding surface and the shape of a protein. For example, the binding surfaces of subtypes A, C, and D have 18, 22, and 18 residues, respectively, whereas subtype B has the largest binding surface with 24 residues. The shape of subtype B has mean (WG1, WG2) values of (−0.17, −0.40). The negative value of WG1 of subtype B (−0.17) is distinct from those of the other subtypes (0.01, 0.01, and 0.12). With respect to function, subtype B is associated with EC 2.4.1.19, whereas subtypes A, C, and D belong to EC 3.2.1.-. This shape analysis relies on the accuracy of geometrical computations. Their integrated surface attributes reveal subtle variations in residues and shapes, which explains the diversification of surface subtypes and their associated functions.

Identification of the Binding Surface of an Unbound Protein.

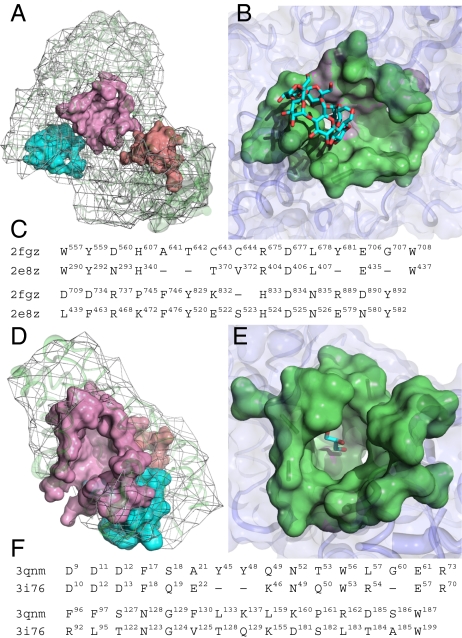
Our method may be used to identify the binding surface of an unbound protein. We first compute the putative surfaces of the unbound protein (23, 24) and then use each putative surface to search the PSC database by geometric matching (11). This footprinting approach is effective in identifying the bound or unbound binding surface of a structure (13–15). For example, we considered the unbound hydrolase of Klebsiella aerogenes (PDB2fgz chain A, 926 residues, unassigned CATH fold). We first partitioned the surface of this enzyme into 74 putative local surfaces. Each surface was then geometrically compared with those of the binding surfaces in the PSC database. In this example, the largest surface was found to have the most significant rmsd P value of 3.96 × 10⁻⁷ and matched PDB2e8z of Bacillus subtilis (Fig. 4 A–C). We found that the predicted binding surface of PDB2fgz (30 residues) likely has a function highly similar to the template (PDB2e8z) and is involved in the carbohydrate metabolic process of Pullulanase (EC 3.2.1.41). Thus, the binding surface of the unbound form of PDB2fgz was identified and classified with the same surface type as PDB2e8z.

Fig. 4.

Prediction of the binding surfaces of unbound structures using the binding surfaces in the PSC database. (A) The surface of PDB2fgz is partitioned into 74 putative local surfaces; only three putative pockets are shown. (B) The predicted surface (colored pink) is identified by an fPOP match to the binding surface of PDB2e8z with an rmsd of 1.95 Å. (C) The alignment of two pocket sequences has a sequence identity of 48.3%, much higher than the full-length sequence identity of 29.5%. Among the 29 aligned spatial pocket residues, there are 13 highly conserved residues. In particular, the six active sites of H³⁴⁰, R⁴⁰⁴, D⁴⁰⁶, E⁴³⁵, W⁴³⁷, and D⁵²⁵ on the template of PDB2e8z perfectly match those of the query of PDB2fgz. (D) Three of the 10 putative local surfaces are shown for PDB3qnm. As a query, the predicted binding surface (colored pink) with 36 spatial pocket residues of PDB3qnm is matched with the binding surface of PDB3i76 (P ≤ 10⁻⁷) (E). (F) Eleven of the 31 aligned pocket residues are highly conserved, with a Tanimoto coefficient of 0.93.

In some cases, the binding surface of a query may be predicted by a distantly related template. Fig. 4 D–F shows the identification of the binding surface of PDB3qnm of Bacteroides thetaiotaomicron of unknown function. With a significant rmsd P value of 3.38 × 10⁻⁷, the predicted binding surface of PDB3qnm matches that of PDB3i76, a Bacillus subtilis protein. We constructed an automated pipeline to carry out the site-specific computations of uncovering the binding surfaces of distant homologs. Note that the binding surface of a remote homolog may not be clustered with any existing surface type, so that a new surface type is created to expand the PSC database.

Collecting Related Binding Surfaces with Similar Ligands.

The PSC database can also be applied to find binding surfaces with the same or similar ligands in the PDB. In the PSC database, the binding surfaces and their cognate ligands were identified by the split pocket algorithm (13). Each surface with its binding ligand(s) and the corresponding surface subtype were already calculated beforehand. For example, let us consider searching for surfaces potentially bound to the cofactor FMN (flavin mononucleotide). Our search found a total of 1,114 FMN or FMN-like binding surfaces, which belong to 37 surface types in PSC. In Table S2, the representatives of these 37 surface types and their functions are summarized. It shows that these proteins of distinct surface types belong to different superfamilies. A subset of 494 surfaces is associated with EC 1 (oxidoreductases), indicating the preference of an FMN-binding surface for oxidoreductase activity. Some are in the classes of EC 2 (transferases), EC 4 (lyases), and EC 5 (isomerases) (Fig. 5).

Fig. 5.

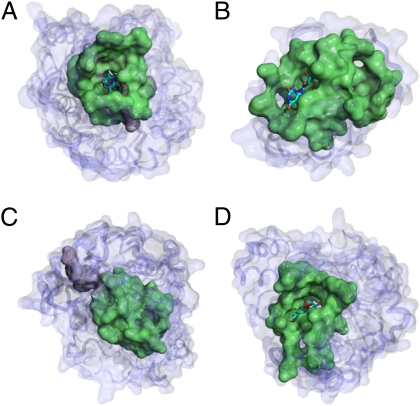
FMN-binding surfaces across protein superfamilies with different folds. (A) The binding surface of PDB1al7 (350 aa) of Spinacia oleracea has key residues (colored violet): Y²⁴, Y¹²⁹, D¹⁵⁷, H²⁵⁴, and R²⁵⁷. These are located on a typical oxidoreductase (EC 1.1.3.15) fold of Aldolase class I (CATH 3.20.20.70). (B) The identified transferase-binding surface on PDB2vbv (134 aa) of Methanococcus jannaschii is a riboflavin kinase (EC 2.7.1.161) with a CATH fold of 2.40.30.30. (C) Thermus DNA lyase (EC 4.1.99.3) has a complicated fold pattern: CATH 3.40.50.620, 1.25.40.80, and 1.10.579.10. These folds contain unique key residues (colored violet) on the local surface of PDB2j09 of Thermus thermophilus: W²⁵⁷, W³²⁸, and W³⁵¹. (D) The binding surface on PDB2zru (356 aa) of Sulfolobus shibatae has both isomerase (EC 5.3.3.2) and oxidoreductase activities with the same fold as in A.

In the PSC database there are 31 distinct surface types, each of which has >100 members. It seems that these surface types have important roles that led to duplication and divergence of these surfaces. Examples include glucose-, peptide-, NAD- (nicotinamide adenine dinucleotide), FAD- (flavin adenine dinucleotide), DNA/RNA-, and heme-binding proteins. Moreover, surface types such as kinases and NAD-binding proteins (10) require diverse surface types to fulfill complex cellular roles. Although the binding surfaces collected are only bound forms, their related unbound structures can be identified by the footprinting approach of fPOP (14), which is also useful for discovering the binding surfaces of distant homologs (Fig. 4).

Evaluation by EC Annotations and Comparison with CATH.

To assess the performance of our method, we evaluated the PSC database using the 1,145 EC annotation entries that were explicitly assigned to 15,783 bound structures (containing 16,560 chains in the PDB). All unbound forms were ignored. A positive result occurred when a classified protein matched its EC annotation. In each test entry, we matched members of PSC against EC to compute the Tanimoto coefficient, a good measure for the similarity of two classifications (SI Text, Performance Evaluation). As an example, we tested EC 3.4.22.56 (cysteine 3 endopeptidase), which has 33 annotation entries. PSC could find all of the cysteine 3 endopeptidases and correctly classified them into the same surface type (ST178), whereas CATH grouped 19 of the 33 entries into CATH ID 3.30.70.1470, 13 entries into CATH ID 3.40.50.1460, which involve 29 mixed members, and 1 entry with no CATH assignment (Table S3). For this comparison between the EC and PSC databases, we calculated a similarity of 0.589 [=33/(33 + 56 − 33) (i.e., 33 EC entries, 56 PSC entries in subtype ST178, and EC and PSC share 33 entries)]. For EC and CATH, we calculated a similarity of 0.576 [=19/(33 + 19 − 19)]. After evaluating the 1,145 test entries, we obtained a higher overall average similarity of 59.9% between PSC and EC than that obtained between CATH and EC (31.4%). Therefore, the PSC classification achieved a much higher correlation between function and structure (shape) than CATH.

Concluding Remarks

We have shown that using the structural attributes of ligand-binding surfaces is a powerful way to infer structural and functional relationships among proteins. Moreover, due to the conservative nature of protein structure, this approach is more powerful in detecting distant relationships than a sequence-based method. For the same reason, however, it may not be suitable for classifying closely related protein sequences, because there may not be enough structural variation among such proteins. On the other hand, we have demonstrated that considering structural attributes of ligand-binding surfaces can give a more refined classification of proteins than a classification based on protein folds such as CATH. Indeed, our classification agrees with the EC annotations much better than CATH. Thus, our approach has advantages over the fold-based and sequence-based approaches, especially in providing structural and functional insights into the molecular evolution of proteins.

Materials and Methods

Identifying the Binding Surface of a Protein.

The binding surface of a bound structure was analytically identified with the split pocket algorithm (13). We collected a total of 28,986 functional pockets of the 24,170 PDB bound structures in SplitPocket for surface classification (SI Materials and Methods). This was based upon a matching technique of pairwise surface alignments.

Clustering Analysis: A Coarse Surface Classification by an Agglomerative Approach.

We used a progressively agglomerative approach (SI Text, Clustering Algorithm of a Coarse Surface Classification) to cluster local surfaces. We grouped similar surfaces into a surface type at a threshold of structural similarity based on the local rmsd P value of ≤10⁻⁴. Each surface type was uniquely represented by a center as defined below. In principle, any member of a group can be the center of a surface type. However, there is one member with the highest degree of connections with the smallest mean rmsd that possesses the most generic (compatible) spatial pattern for the surface type. We selected it as the center of the surface type. The local surface classification is accomplished when each center is found.

Surface Characteristics of a Functional Pocket.

To characterize a protein functional surface, we assessed the global and local surface attributes in terms of geometrical, physicochemical, and evolutionary features. Collecting these attributes, we built an integrated framework for protein surface classification. The attributes collected in terms of geometrical, physicochemical, and evolutionary features are explained in SI Text, Surface Characteristics of a Functional Pocket.

Structural Similarity Between Two Surfaces.

To assess the structural similarity of two surfaces, we used the cosine transformation (SI Text, Cosine Similarity and Tanimoto Coefficient) to compare the two sets of the surface attributes selected in Table 1. Moreover, the cosine transformation was extended to the Tanimoto coefficient when the attributes were binary. We used the Tanimoto coefficient to assess the similarity of the residue compositions of two functional surfaces.

Assessment of the Functional Similarity of Two Proteins.

The functional similarity score between two surfaces is defined as 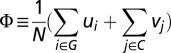, where N is the number of attributes, G is the set of geometrical attributes, and C is the set of physicochemical attributes, and the values of u_i and v_i are computed, respectively, based on the cosine similarity and the p-norm distance δ, which is converted to a similarity by the transformation of e^−δ. The value of Φ is computed to measure the functional similarity of two proteins based on shape and texture. Statistically, a cutoff P value of 5 × 10⁻⁴ is used to determine the significance of Φ, which is empirically measured in SI Text, Assessment of Statistical Significance for a Functional Surface Alignment.

Constructing a Structural Network of Surface Relationships.

A structural network of protein functional surfaces can be constructed by choosing a distance metric. Based on the integrated attributes, we converted the functional similarity Φ of two proteins to the distance by the transformation 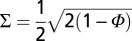. After defining the functional similarity of two surfaces, we compared all surfaces to produce a pairwise distance matrix. Using this matrix, we performed hierarchical clustering (25) to find the relationships among the surfaces.