Summary
A method is described based on high-performance immunoaffinity chromatography for examining the interactions of immobilized antibodies or related binding agents with their targets. It is shown how this method can be used to obtain information on the binding, elution and regeneration kinetics of immobilized binding agents, such as those used with immunoaffinity supports. The theory behind this approach is briefly described and it is demonstrated how both the kinetic and thermodynamic properties of a biointeraction can be determined experimentally through this method. Several applications are used to illustrate this technique, including antibody-antigen interactions and the binding of aptamers with their targets in the presence of silica-based supports. The same approach can be adapted for use with other types of targets, binding agents and support materials.
Keywords: Biointeraction analysis, Immunoaffinity chromatography, High-performance immunoaffinity chromatography, Antibody-antigen interactions, Aptamers
1. Introduction
Antibodies have been used for decades as agents for the selective binding of target analytes. One common application of antibodies has been their use in immunoaffinity chromatography (IAC) for the purification and isolation of biological compounds. Many IAC methods have been developed for the isolation of antibodies, hormones, peptides, enzymes, viruses and other biologically-relevant materials (1-8). The ability of an antibody to recognize a specific target and bind this target with high affinity has traditionally provided immunoaffinity methods with good selectivity and low limits of detection.
One important application of antibodies and IAC has been in a technique known as high-performance immunoaffinity chromatography (HPIAC) (9). HPIAC is a type of IAC that makes use of immobilized antibodies or antigens on a chromatographic support that can be used in a flow-based system at reasonably high pressures and flow rates. These properties make it possible to combine the strong and specific binding of antibodies with the precision, speed and wide range of detection formats that are possible when using a system designed for work with high-performance liquid chromatography (HPLC) (6,9-11).
To design methods such as IAC or HPIAC that utilize immobilized antibodies, it is valuable to have some information on the strength and rates of binding of an antibody to its target, as well as data on dissociation of the antibody-target complex. This information can also be valuable in the design of solid-phase immunoassays, biosensors, and related techniques. One approach for obtaining such data is to use surface plasmon resonance (SPR) (12-18). However, there are some limitations to this technique, especially when its results are to be used to develop IAC and HPIAC methods. For example, SPR is restricted to materials that have certain optical properties and this method makes use of a specific detection mode (i.e., surface plasmon resonance) which can have moderate detection limits (19). Additional methods that can be used to obtain information about antigen-antibody binding and other biointeractions include the enzyme-linked immunosorbent assay (ELISA), kinetic exclusion assay, or radioimmunoassay. These techniques tend to less expensive than SPR and can be employed to examine antibody-antigen interactions on either a solid phase or in solution; however, these approaches are usually manual methods with moderate precision and still require specific modes of detection (20,21).
An alternative approach, which will be discussed in this chapter, is to use HPIAC columns to examine the binding of targets to immobilized antibodies or related binding agents (9). One advantage of this method is that the same support material is used for the biointeraction analysis and in the final application of the immobilized antibodies or binding agents. Like SPR and other current methods, HPIAC and related affinity methods can be used to obtain both kinetic and thermodynamic data on a biointeraction (11,20-26). However, HPIAC is not limited to a particular detection mode but can be used with a wide variety of detection schemes, including absorbance, fluorescence, and mass spectrometry (11,25).
The theory of this chromatographic approach for biointeraction studies will be briefly discussed and the experimental use of this method will be described and illustrated through several examples. Some examples that will be presented will include the use of this method to examine the binding of immobilized antibodies against the herbicides 2,4-dichlorophenoxyacetic acid (2,4-D) or atrazine and against the hormone L-thyroxine (9,27-29). The extension of this method to other systems will also be considered, such as its use in studying the binding of L-thyroxine with anti-thyroxine aptamers (9,27-29). It will be shown how this approach can be used to obtain the association equilibrium constants and binding capacities for immobilized antibodies or aptamers against a given target, as well as the association and dissociation rate constants for these interactions under sample application conditions. The use of this method to examine the dissociation rates of bound targets under a given set of elution conditions will be demonstrated as well, along with the utilization of this approach to estimate the regeneration rate of an immobilized binding agent.
2. Materials
All aqueous solutions and running buffers should be prepared using deionized water, as was obtained in the following examples by using a NANOpure water purification system (Barnstead, Dubuque, IA, USA).
2.1. Binding Agents and Targets
The following methods can be used for a variety of antibodies, antigens, and related binding agents. The specific binding agents and targets that will be used as examples in this chapter are as follows.
The work with 2,4-D and the anti-2,4-D antibodies was carried out using E2/G2 monoclonal anti-2,4-D antibodies that were provided by the Vet Research Center in Brno (Czech Republic) (29). The 2,4-D; 2,4–chlorophenoxyacetate methyl ester (2,4-D-Me); 2,4,5-trichlorophenoxyacetic acid (2,4,5-T); 2-methyl-4-chlorophenoxy acetic acid (MCPA); and 4-chlorophenoxyacetic acid (4-CPA) were from Sigma-Aldrich (St. Louis, MO, USA).
The work with atrazine and its degradation products was carried out using anti-triazine monoclonal antibodies (cell line AM7B2) produced at the Monoclonal Antibody Production Facility at the University of California-Berkeley (Berkeley, CA, USA). The atrazine, deethylatrazine and deisopropylatrazine were supplied by Ciba-Geigy (Greensboro, NC, USA). Hydroxyatrazine was obtained from Dr. James D. Carr at the University of Nebraska (Lincoln, NE, USA) (31).
In the work using L-thyroxine and anti-thyroxine antibodies, the monoclonal L-thyroxine antibodies (clone 16A) and L-thyroxine were purchased from Sigma-Aldrich. The thyroxine aptamers (5′-CGG TCA GGC TTC CG-3′, 5′-/5amMC6/TCA GGC TTC CG-3′, and 5′-/5Bio/CGG TCA GGC TTC CG-3′) were purchased and synthesized from Integrated DNA Technologies (Coralville, IA, USA) (9,27-29).
2.2. Support Materials and Columns
A variety of supports and immobilization schemes can also be used with the described method. The examples given in this chapter were all conducted using Nucleosil Si-1000-7 silica (7 μm particle size, 1000 Å pore size) or Nucleosil Si-300-7 silica (7 μm particle size, 300 Å pore size) from P.J. Cobert (St. Louis, MO, USA).
In the examples that are provided in this chapter, the silica support was first converted into a diol-bonded form, according to a previously-reported method (see Note 1) (32). The antibodies, or desired binding agent with an amine terminal linker, were then immobilized onto the diol-bonded support by the Schiff base method (see Note 2) (33). Alternatively, the binding agent could be biotinylated and attached through biospecific adsorption to a support that contains immobilized streptavidin (e.g., as prepared by the Schiff base method) (9,27-29). In each case, a separate control support should be prepared from the same initial starting material but without the addition of any binding agent in the immobilization step.
Once packed, the support containing the immobilized antibodies or desired binding agent was typically packed into a 1 cm × 2.1 mm i.d. stainless steel column. This can be carried out by using a standard downward slurry-packing method. An alternative approach is to use a method for preparing sandwich microcolumns (see Note 3) (34). When working with silica, either approach would generally be carried out using a packing pressure of approximately 3000 psi and a neutral buffer as the packing solution (e.g., a pH 7.0-7.4 phosphate buffer). A column of equal length and diameter should also be packed by the same method but instead the column will contain a control support that is absent of any immobilized binding agent (see Note 3).
2.3. Apparatus
Many standard HPLC systems can be adapted for the types of measurements that are described in this chapter.
An example of an HPLC system that can be used with this method, and which was used for the work with the anti-thyroxine antibodies, was as follows. This system consisted of three Waters 590 pumps (Milford, MA, USA), two Rheodyne Labpro valves (Rohnert Park, CA, USA), and a Jasco UV-975 UV/Vis detector (Easton, MD, USA). Data acquisition was performed using an SCB-68 NI shielded interface and 16E series PCMCIA card from National Instruments (Austin, TX, USA). Data were collected using a Gateway Solo 2500 laptop computer (Poway, CA, USA) and analyzed with a spreadsheet prepared using Microsoft Excel (Microsoft, Redmond, WA, USA). A circulating water bath and column jacket can be added to this system for temperature control.
3. Methods
3.1. General Model
The scheme in Fig. 1 shows how interactions between an applied target and an immobilized binding agent such as an antibody are described in this chromatographic approach. This model is based on the on/off elution scheme that is typically used in IAC, HPIAC and other types of affinity chromatography (35,36). An example of a chromatogram that is obtained for this type of analysis is provided in Fig. 2.
The first step in Figs. 1 and 2 involves the application of the target analyte (A) to the immobilized binding agent or ligand (L). During this step, A is allowed to bind to L while other non-retained sample components are washed away in the presence of an appropriate application buffer.
The second step in this process involves the dissociation and elution of the bound target analyte by passing an elution buffer through the support. Antibody-antigen interactions typically have large association equilibrium constants under the application conditions that are used in IAC and HPIAC, so a change in the pH or mobile phase composition is often utilized during the elution step to disrupt this interaction and cause the target to dissociate from the support (35,36). This type of non-specific and general step gradient will be the elution mode emphasized in this report. Alternatively, a competing agent such as an analog of the antigen/target or a soluble binding agent for the antigen/target can be added to the mobile phase to produce biospecific elution through competitive binding or displacement of the antigen/target from the column (8,11,21,26).
The third step in this scheme is the regeneration step. During this step, the application buffer is re-applied to the support. This step allows the immobilized binding agent to return to its initial conformation before the next sample is applied to the system (35,36). The process is then repeated.
Figure 1.
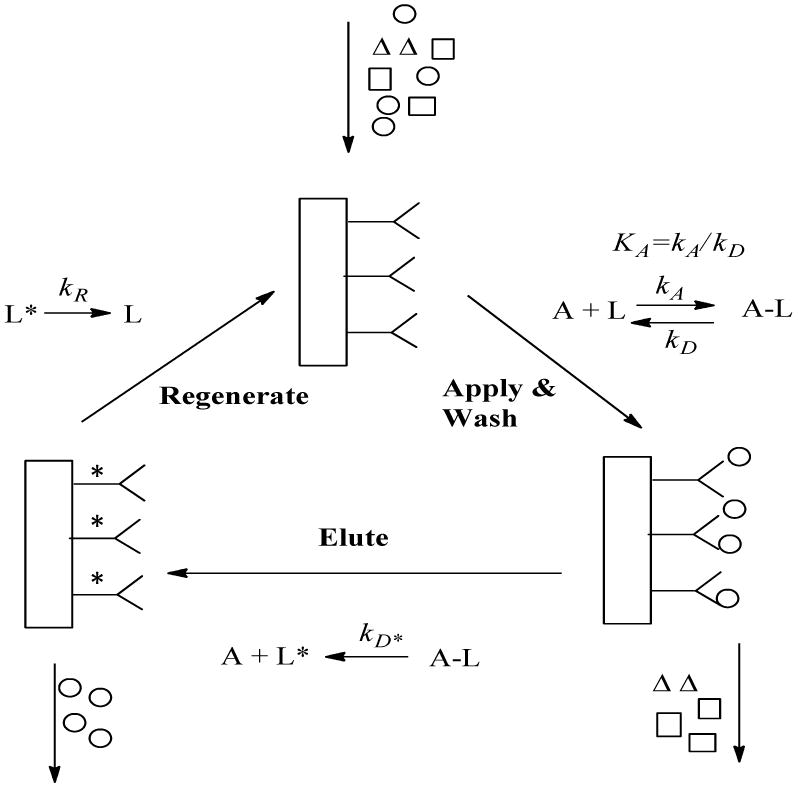
General scheme illustration the kinetic processes used in this experiment to model the binding and elution of an analyte in affinity chromatography. In this model kA and kD are the association and dissociation rate constants for the analyte–ligand interaction during sample application, kD* is the first-order dissociation rate constant which describes analyte elution. The term kR is the first-order rate constant that describes the regeneration of the immobilized ligand. The asterisk (*) that appears by the ligands during the elution step is used to indicate that these agents may be present in a denatured or altered state during this stage of the analysis.
Figure 2.
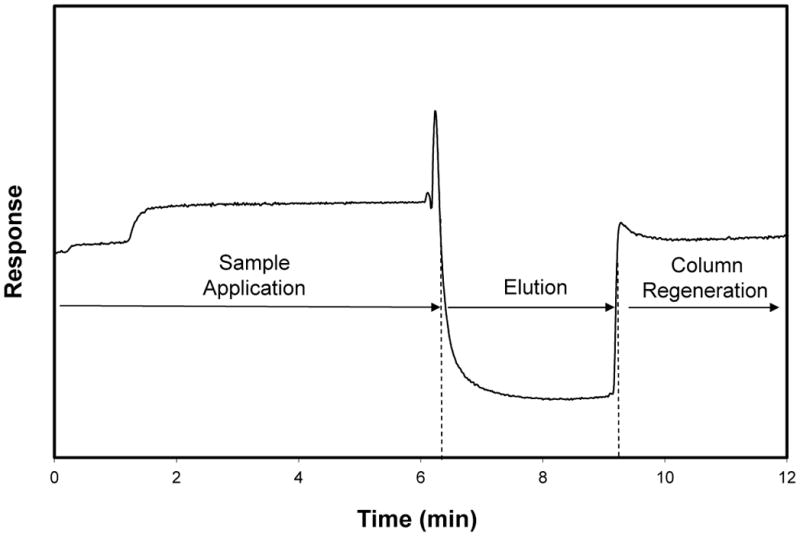
Typical chromatogram obtained during a biointeraction study using frontal analysis for sample application and the on/off elution mode for 2,4-D and a column that contained immobilized anti-2,4-D antibodies. Adapted with permission from Ref. (9).
3.2. Determination of the Extent of Target Retention during Sample Application
The first step in Figs. 1 and 2 (i.e., the sample application step) can be used with the method of frontal analysis, or frontal affinity chromatography (FAC), to obtain information on the interaction strength and number of binding sites for an immobilized binding agent with a target under the application conditions (see Note 4). In frontal analysis, a known concentration of the analyte [A] is applied to the column at a known flow rate while the amount of analyte that is leaving the column is monitored. As the binding sites within the column become saturated with the analyte, a breakthrough curve will form (see left section of Fig. 2). If a local equilibrium is present in the column during sample application, the mean position of this breakthrough curve can be related to the affinity and binding capacity of the column for the target.
-
If the analyte and ligand follow a model which has single-site binding between these agents, the frontal analysis data can be examined by utilizing one of the following the equivalent expressions in Eqns. (1) and (2), as discussed previously (see Refs. (11), (21) or (26) for details).
(1) (2) In these equations, KA is the association equilibrium constant for the binding of A to the immobilized ligand, mL,app is the apparent moles of analyte that are required to reach the mean point of the breakthrough curve at a given concentration of applied analyte [A], and mL represents the total moles of binding sites in the column. The value of mL,app is found by using the difference in breakthrough times for the analyte on the test column versus the control column and using this data along with the molar concentration of the applied analyte solution and flow rate at which this solution is passed through the columns (11). Similar expressions to Eqns. (1)-(2) can be written in terms of the effective concentrations of the immobilized binding agent in the column instead of the moles of this agent that are present (11,26). Expanded forms of these relationships can also be written for systems with multi-site interactions and analyzed through non-linear regression methods (11). In the case of a system with single-site interactions, Eqn. (1) predicts that a plot of 1/mLapp versus 1/[A] should give a linear response with a slope equal to 1/(KAmL) and an intercept that is equal to 1/mL for a system with single-site binding. Alternatively, a non-linear fit according to Eqn. (2) can be used. Either type of fit will make it possible to determine both the association equilibrium constant for the interaction between A and L and the total moles of binding sites in the column for A (11). Eqns. (1)-(2) are useful for ligands with weak to moderate affinities but they can also be utilized for higher affinity systems, such as many types of antibody-antigen interactions (9,11,21,26).
Fig. 3 shows a typical set of breakthrough curves and a double reciprocal plot that was prepared according to Eqn. (1) to analyze the interactions that occurred between the herbicide atrazine and various degradation products of atrazine with immobilized anti-atrazine antibodies in an HPIAC column (31). The moderate-to-weak affinities of some of the degradation products for the immobilized antibodies made it possible to use the data obtained from Fig. 3 to compare the association equilibrium constants and binding capacities for each agent on the HPIAC column (31). Other reports have used this method to examine the binding of L-thyroxine to anti-thyroxine aptamers and antibodies (28) and the binding of a 2,4-D and related herbicides to immobilized anti-2,4-D antibodies (9).
Figure 3.

Frontal analysis results, as plotted according to Eqn. (1), for the application of atrazine (●), hydroxyatrazine (○), deethylatrazine (□) or deisopropylatrazine (■) onto a column containing immobilized anti-triazine antibodies. Based on data from Ref. (30).
3.3. Kinetics of Analyte Retention
Another important application for this method is to study the association and dissociation kinetics of an analyte on an HPIAC column during the application step. For most supports used in HPIAC, the support is an efficient material with relatively fast mass transfer from the bulk of the mobile phase solution to the surface or interior of the support. Under these conditions the rate of capture of the analyte by an immobilized antibody during the sample application step can often be modeled by using an adsorption-limited process (11,25). This type of reaction is described in Fig. 1 through the use of a second-order adsorption rate constant (kA) and a first-order dissociation rate constant (kD).
-
One way to examine the association rate of the analyte with an HPIAC column during sample application is to measure the free fraction f for the analyte that is non-retained at various flow rates (see Note 5) (9). If adsorption-limited conditions are present and the rate of analyte dissociation is slow and negligible versus analyte adsorption (e.g., as occurs during the early stages of frontal analysis), Eqn. (3) can be used to relate this free fraction to the flow rate (F), association rate constant, total number of binding sites present in the column, and the amount of applied analyte (see Ref. (9) for details).
(3) The term So is equal to the ratio F/(kAmL), and Load A represents the ratio of the moles of the applied analyte versus the moles of binding sites in the column, where Load A= (mol A)/mL. The value of Load A can be found by dividing the moles of applied analyte at any given point in time by the total binding capacity of the column, such as determined according to frontal analysis (see Section 3.2). The free fraction f in Eqn. (3) represents the fraction or relative moles of applied analyte that are not bound to the immobilized ligand. The value of f at a given point in time and at any value of Load A can be determined through frontal analysis by comparing the elution profiles for the analyte on a column containing the immobilized ligand and on an inert control column over the same time period. During this comparison, the non-retained area and response for the analyte on the column containing the ligand is divided by the area over the same time period on the control column to give the free fraction of the analyte on the test column.
Fig. 4 shows a typical plot in which Eqn. (3) has been used to examine the association kinetics of an applied target with immobilized antibodies. This example is for the binding of 2,4-D to immobilized anti-2,4-D antibodies (9). The same approach has been used to study the binding of L-thyroxine to anti-thyroxine aptamers and antibodies (28). In Fig. 4, it was found that there was a good fit between Eqn. (3) and the early part of the frontal analysis curve during sample application (i.e., low Load A values, which represent conditions under which analyte dissociation should be essentially negligible) (9,25). From the value of So that was obtained from this fit, along with the known values of F and mL (the latter from the frontal analysis studies), it was possible to estimate the association rate constant kA for this interaction. By using the value of the KA that has been determined through frontal analysis (see Section 3.3), it was also possible to then obtain the dissociation rate constant kD during sample application, as based upon the relationship KA=kA/kD (9).
Figure 4.
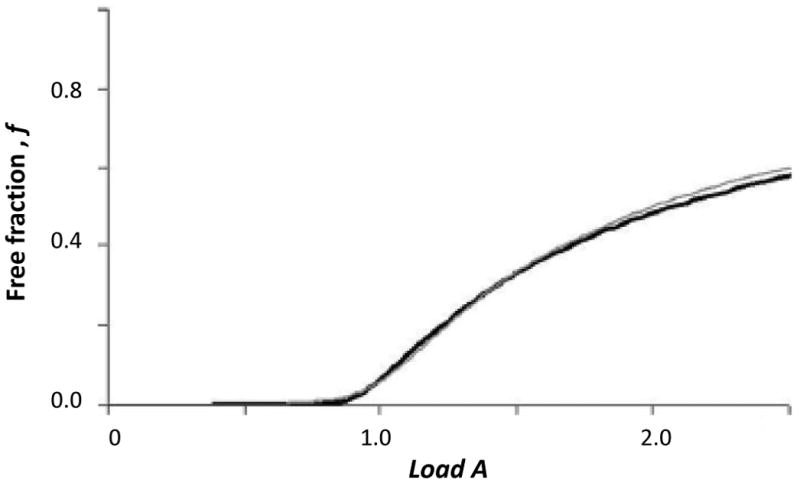
Comparison of experimental results and the best-fit results according to Eqn. (2) for the application of a 100 ppb solution of 2,4,5-T to an immobilized anti-2,4-D antibody column. The values of both Load A and f in this plot are unitless, as indicated by the definition of these terms. Adapted with permission from Ref. (9).
3.4. Characterizing Analyte Dissociation Kinetics During Elution
The HPIAC method can also be used to study the kinetics involved in the release of a retained analyte as an elution buffer is passed through the support (see Note 6). When using a step gradient for elution, this reaction can be described by a first-order process, as shown in step 2 in Fig. 1 (note: the addition of soluble ligand to the mobile phase could also again be used for analyte elution). In this reaction, L*, A*, A-L* represent the ligand, analyte, and analyte-ligand complex in the presence of the elution buffer. The term kD* is the dissociation rate constant for the complex A-L* under the elution conditions. During this process it can often be assumed that A* is removed rapidly enough from the column to prevent any significant rebinding with the immobilized ligand.
Based on this model, dissociation of the A-L* complex can be described by the following first-order rate law and integrated rate expression (see Refs. (10), (37) or (38) for details).
| (4) |
| (5) |
In these equations, t is the time allowed for the elution of A, [A*]o is the amount of A* that is initially present in the system, and [A*] is amount of analyte present at time t. According to Eqn. (5), a plot of ln[A*] versus t should be linear during the elution step, giving a slope equal to –kD* (9,10,37-39). If desired, the association equilibrium constant and association rate constant under the same elution conditions can be determined by frontal analysis, as described in Sections 3.2 and 3.3. Alternatively, any two of these parameters can be measured and used to calculate the third factor, as demonstrated in Section 3.3 (9). This set of information makes it possible to determine how both the affinity and kinetics of analyte-ligand binding may be altered as the elution conditions are varied (40).
Fig. 5 provides an example that utilized these equations and this approach for examining the dissociation rate constants for 2,4-D and related herbicides from anti-2,4-D antibodies. It was possible with this method to see how the use of different elution conditions affected the dissociation rate constant and the corresponding time needed for analyte elution from the column and to recover a given fraction of an applied analyte from an immunoaffinity column. In this particular case, the apparent rate of dissociation approached a constant value at flow rates above 0.4 ml/min and increased as a lower pH was used for antigen elution (9). The method has also been utilized to compare various approaches that can be used for the dissociation and elution of L-thyroxine from anti-thyroxine aptamers (28).
Figure 5.
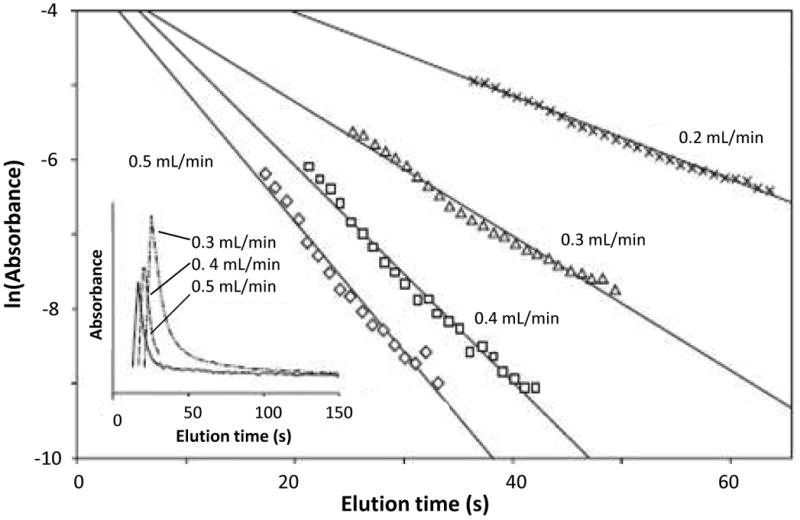
Analysis of the dissociation rate of 2,4-D from immobilized anti-2,4-D antibodies at various flow rates and at pH 2.5. Based on data from Ref. (9).
3.5. Determination of the kinetics of column regeneration
The rate of regeneration is another important factor to consider when an immobilized antibody support is used for multiple samples. This rate can also be examined by using HPIAC for biointeraction studies (9). Regeneration is described by the third step and reaction that are shown in Fig. 1. This reaction used a model for column regeneration that is based on a first-order reaction for the conversion of the form of the binding agent in its state during the elution step (L*) to the original fully active form under the application conditions (L). The term kR is the rate constant for the conversion of L* to L during column regeneration.
According to this first-order model, the rate of column regeneration rate can be described by using Eqns. (6) or (7).
| (6) |
| (7) |
It is assumed in both of these equations that the reverse reaction is negligible (i.e., that L does not have appreciable conversion to L* in the presence of the application buffer). Eqn. (6) can be integrated to give the equivalent expressions in Eqns. (8) and (9), in which t is the time allowed for column regeneration (see Ref. (9) for details).
| (8) |
| (9) |
It is possible to use frontal analysis (see Section 3.2) to acquire measurements of mol L* as a function of regeneration time. A plot can then be made of –ln(mol L*)o versus t, which should result in a straight line with a slope that is equal to -kR and an intercept that is equal to ln(mol L*)o.
Fig. 6 gives an example for this particular type of analysis, as was used to examine the regeneration of an immunoaffinity column containing immobilized anti-2,4-D antibodies. Good agreement with a linear relationship was seen in Fig. 5, as predicted by Eqn. (9). The slope of this plot made it possible to estimate the rate constant for column regeneration and to see how the time allowed for regeneration affected the apparent binding capacity of the column from one application and elution cycle to the next (9).
Figure 6.
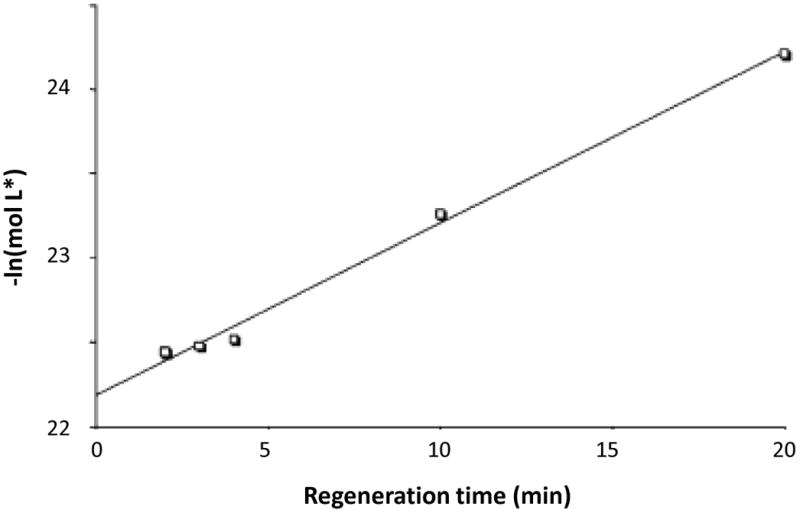
Examination of the regeneration rate for immobilized anti-2,4-D antibodies in going from pH 2.5, 0.1 M potassium phosphate buffer to pH 7.0, 0.1 M potassium phosphate buffer at a flow rate of 0.5 mL/min. Reproduced with permission from Ref. (9).
4. Notes
The typical coverage of diol groups on the Nucleosil Si-1000 supports for the examples used in this chapter were in the range of 35-55 μmol diol/g silica, as determined by an iodometric capillary electrophoresis assay (41). The coverage of diol groups on the Nucleosil Si-300 support was approximately 300 μmol diol/g silica. These values will vary from one type of support material to the next and are highly dependent on the nature of the support and its pore size.
In the case of the anti-2,4-D antibodies, the Schiff base method was carried out by using 1 mg antibodies/50 mg silica in a the total reaction volume was 5 mL, with the immobilization being completed at 4°C for three days. Slightly different amounts of antibody and support and alternative reaction times can also be used.
The following procedure has been used to prepare an anti-thyroxine sandwich microcolumn with total dimensions of 1 cm × 2.1 mm i.d. (27). First, a layer of diol-bonded silica with no immobilized antibodies present was packed into the column until a layer approximately 4 mm thick. This step was followed by the addition of enough immobilized antibody silica to create a 1 mm support layer through multiple injections of slurry that contained this support. A final layer of diol-bonded silica was then packed into the column at 3000 psi until the top of the column bed had been reached. This approach resulted in a 1 cm long column that contained a 1 mm layer of an immobilized anti-thyroxine antibody support between two layers of diol-bonded silica. A control column was prepared in the same manner using only diol-bonded silica throughout the column.
During the frontal analysis experiments, breakthrough curves should be generated over a wide range of analyte concentrations. The range of concentrations that can be used will depend on the solubility of the analyte and its lower limit of detection on the HPLC system, as described in detail in Ref. (11). Preliminary studies should also be carried out at using at least two different flow rates to ensure that moles of applied analyte that are needed to reach the breakthrough point are independent of flow rate. It is also recommended that each analyte concentration be applied in duplicate or triplicate. A correction for non-specific binding to the support and for the void volume of the system can be made by subtracting the results for the control column from the results for the column containing the immobilized binding agent. This correction should be made at each concentration of the applied analyte.
Measurements of the free fraction during the sample application step can be made by using the same chromatograms that are obtained during the frontal analysis experiments that are described in Section 3.2.
The analysis of analyte dissociation rates should be carried out at several flow rates to ensure that mobile phase mass transfer rates are negligible compared to the rate of analyte dissociation. A correction for the change in background response should be made by subtracting the results for the control column from the results for the column containing the immobilized binding agent.
Acknowledgments
This research was supported, in part, by the National Institutes of Health under grants R01 DK069629 and R01 GM044931 and by the NSF/EPSCoR program under grant EPS-1004094.
References
- 1.Bailon P, Roy SK, Swapan K. Recovery of recombinant proteins by immunoaffinity chromatography. ACS Symp Ser. 1990;427:150–167. [Google Scholar]
- 2.Calton GJ. Immunosorbent separations. Methods Enymol. 1984;104:381–387. doi: 10.1016/s0076-6879(84)04105-7. [DOI] [PubMed] [Google Scholar]
- 3.Ehle H, Horn A. Immunoaffinity chromatography of enzymes. Bioseparation. 1990;1:97–110. [PubMed] [Google Scholar]
- 4.Howell KE, Gruenberg J, Ito A, Palade GE. Immuno-isolation of subcellular components. Prog Clin Biol Res. 1988;270:77–90. [PubMed] [Google Scholar]
- 5.Nakajima M, Yamaguchi I. Purification of plant hormones by immunoaffinity chromatography. Kagaku Seibutsu. 1991;29:270–275. [Google Scholar]
- 6.Phillips TM. High Performance immunoaffinity chromatography: An introduction. LC Mag. 1985;3:962–972. [Google Scholar]
- 7.Phillips TM. Isolation and recovery of biologically active proteins by high performance immunoaffinity chromatography. Recpt Biochem Methodol. 1989;14:129–154. [Google Scholar]
- 8.Wilchek M, Miron T, Kohn J. Affinity chromatography. Methods Enzymol. 1984;104:3–55. doi: 10.1016/s0076-6879(84)04082-9. [DOI] [PubMed] [Google Scholar]
- 9.Nelson MA, Moser A, Hage DS. Biointeraction analysis by high- performance affinity chromatography: Kinetic studies of immobilized studies of immobilized antibodies. J Chromatogr B. 2010;878:165–171. doi: 10.1016/j.jchromb.2009.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bondeson K, Frostell-Karlsson A, Faegerstam L, Magnusson G. Lactose repressor-operator DNA interactions: Kinetic analysis by a surface plasmon resonance biosensor. Anal Biochem. 1993;214:245–251. doi: 10.1006/abio.1993.1484. [DOI] [PubMed] [Google Scholar]
- 11.Hage DS, Chen J. Quantitative affinity chromatography: practical aspects. In: Hage DS, editor. Handbook of Affinity Chromatography. CRC Press; Boca Raton: 2006. Chapter 22. [Google Scholar]
- 12.Andersson K, Haemaelaeinen M, Malmqvist M. Identification and Optimization of Regeneration Conditions for Affinity-Based Biosensor Assays. A Multivariate Cocktail Approach. Anal Chem. 1999;71:2475–2481. doi: 10.1021/ac981271j. [DOI] [PubMed] [Google Scholar]
- 13.Brigham-Burke M, Edwards JR, O'Shannessy DJ. Detection of receptor-ligand interactions using surface plasmon resonance: model studies employing the HIV-1 gp120/CD4 interaction. Anal Biochem. 1992;205:125–131. doi: 10.1016/0003-2697(92)90588-x. [DOI] [PubMed] [Google Scholar]
- 14.Hall DR, Cann JR, Winzor DJ. Demonstration of an upper limit to the range of association rate constants amenable to study by biosensor technology based on surface plasmon resonance. Anal Biochem. 1996;235:175–184. doi: 10.1006/abio.1996.0109. [DOI] [PubMed] [Google Scholar]
- 15.Karlsson R, Stahlberg R. Surface plasmon resonance detection and multispot sensing for direct monitoring of interactions involving low-molecular-weight analytes and for determination of low affinities. Anal Biochem. 1995;228:274–280. doi: 10.1006/abio.1995.1350. [DOI] [PubMed] [Google Scholar]
- 16.O'Shannessy DJ, Brigham-Burke M, Soneson KK, Hensley P, Brooks I. Determination of rate and equilibrium binding constants for macromolecular interactions by surface plasmon resonance. Meth Enzymol. 1994;240:323–349. doi: 10.1016/s0076-6879(94)40054-7. [DOI] [PubMed] [Google Scholar]
- 17.O'Shannessy DJ. Determination of kinetic rate and equilibrium binding constants for macromolecular interactions: a critique of the surface plasmon resonance literature. Curr Opin Biotechnol. 1994;5:65–71. doi: 10.1016/s0958-1669(05)80072-2. [DOI] [PubMed] [Google Scholar]
- 18.O'Shannessy DJ, Winzor DJ. Interpretation of deviations from pseudo-first-order kinetic behavior in the characterization of ligand binding by biosensor technology. Anal Biochem. 1996;236:275–283. doi: 10.1006/abio.1996.0167. [DOI] [PubMed] [Google Scholar]
- 19.Gaster RS, Xu L, Han S, Wilson RJ, Hall DA, Osterfeld SJ, Yu H, Wang SX. Quantification of protein interactions and solution transport using high-density GMR sensor arrays. Nature Nanotechnol. 2011;6:314–320. doi: 10.1038/nnano.2011.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Buter JE, editor. Immunochemistry of Solid-Phase Immunoassay. CRC Press; Boca Raton: 1991. [Google Scholar]
- 21.Hage DS, Tweed SA. Recent advances in chromatographic and electrophoretic methods for the study of drug-protein interactions. J Chromatogr B. 1997;699:499–528. doi: 10.1016/s0378-4347(97)00178-3. [DOI] [PubMed] [Google Scholar]
- 22.Hage DS, Walters RR. Non-linear elution effects in split-peak chromatography. I. Computer simulations for the cases of irreversible diffusion- and adsorption-limited kinetics. J Chromatogr. 1988;436:111–135. doi: 10.1016/s0021-9673(97)00975-8. [DOI] [PubMed] [Google Scholar]
- 23.Hage DS, Thomas DH, Beck MS. Theory of a sequential addition competitive binding immunoassay based on high-performance immunoaffinity chromatography. Anal Chem. 1993;65:1622–1630. doi: 10.1021/ac00059a023. [DOI] [PubMed] [Google Scholar]
- 24.Renard J, Vidal-Madjar C. Kinetic study of the adsorption of human serum albumin on immobilized antibody using the split-peak effect in immunochromatography. J Chromatogr A. 1994;661:35–42. doi: 10.1016/0021-9673(94)85174-3. [DOI] [PubMed] [Google Scholar]
- 25.Schiel JE, Hage DS. Kinetic studies of biological interactions by affinity chromatography. J Sep Sci. 2009;32:1507–1522. doi: 10.1002/jssc.200800685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Winzor DJ. Quantitative affinity chromatography: recent theoretical developments. In: Hage DS, editor. Handbook of Affinity Chromatography. CRC Press; Boca Raton: 2006. Chapter 23. [Google Scholar]
- 27.Clarke WSJE, Moser A, Hage DS. Analysis of free hormone fractions by an ultrafast immunoextraction/displacement immunoassay: studies using free thyroxine as a model system. Anal Chem. 2005;77:1859–1866. doi: 10.1021/ac040127x. [DOI] [PubMed] [Google Scholar]
- 28.Moser AC. Ph D Dissertation. University of Nebraska-Lincoln; Lincoln: 2005. [Google Scholar]
- 29.Oates MR, Clarke W, Zimlich A, II, Hage DS. Optimization and development of a high-performance liquid chromatography-based one-site immunometric assay with chemiluminescence detection. Anal Chim Acta. 2002;470:37–50. [Google Scholar]
- 30.Franek M, Kolar V, Granatova M, Nevorankova Z. Monoclonal elisa for 2,4-dichlorophenoxyacetic acid: characterization of antibodies and assay optimization. J Agric Food Chem. 1994;42:1369–1374. [Google Scholar]
- 31.Rollag J. Ph D Dissertation. University of Nebraska-Lincoln; Lincoln: 1996. [Google Scholar]
- 32.Walters RR. High-performance affinity chromatography: pore-size effects. J Chromatogr A. 1982;249:19–28. [Google Scholar]
- 33.Larsson PO. High-performance liquid affinity chromatography. Meth Enzymol. 1984;104:212–223. doi: 10.1016/s0076-6879(84)04091-x. [DOI] [PubMed] [Google Scholar]
- 34.Clarke W, Hage DS. Development of sandwich HPLC microcolumns for analyte adsorption on the millisecond time scale. Anal Chem. 2001;73:1366–1373. doi: 10.1021/ac000870z. [DOI] [PubMed] [Google Scholar]
- 35.Hage DS. Survey of recent advances in analytical applications of immunoaffinity chromatography. J Chromatogr B. 1998;715:3–28. doi: 10.1016/s0378-4347(97)00621-x. [DOI] [PubMed] [Google Scholar]
- 36.Hage DS, Phillips TM. Immunoaffinity chromatography. In: Hage DS, editor. Handbook of Affinity Chromatography. CRC Press; Boca Raton: 2006. Chapter 6. [Google Scholar]
- 37.Moore RM, Walters RR. Peak-decay method for the measurement of dissociation rate constants by high-performance affinity chromatography. J Chromatogr. 1987;384:91–103. [Google Scholar]
- 38.Chaiken IM, editor. Analytical Affinity Chromatography. CRC Press; Boca Raton: 1987. [Google Scholar]
- 39.Nelson MA. Ph D Dissertation. University of Nebraska-Lincoln; Lincoln: 2003. [Google Scholar]
- 40.Yang J, Hage DS. Effect of mobile phase composition on the binding kinetics of chiral solutes on a protein-based HPLC column: interactions of D- and L-tryptophan with immobilized human serum albumin. J Chromatogr A. 1997;766:15–25. doi: 10.1016/s0021-9673(96)01040-0. [DOI] [PubMed] [Google Scholar]
- 41.Chattopadhyay A, Hage DS. Determination of the diol content of chromatographic supports by capillary electrophoresis. J Chromatogr A. 1997;758:255–261. doi: 10.1016/s0021-9673(96)00742-x. [DOI] [PubMed] [Google Scholar]


