Selectivity for Spectral Motion as a Neural Computation for Encoding Natural Communication Signals in Bat Inferior Colliculus

Abstract

This study examines the neural computations performed by neurons in the auditory system to be selective for the direction and velocity of signals sweeping upward or downward in frequency, termed spectral motion. We show that neurons in the auditory midbrain of Mexican free-tailed bats encode multiple spectrotemporal features of natural communication sounds. These features to which each neuron is tuned are nonlinearly combined to produce selectivity for spectral motion cues present in their conspecific calls, such as direction and velocity. We find that the neural computations resulting in selectivity for spectral motion are analogous to models of motion selectivity studied in vision. Our analysis revealed that auditory neurons in the inferior colliculus (IC) are avoiding spectrotemporal modulations that are redundant across different bat communication signals and are specifically tuned for modulations that distinguish each call from another by their frequency-modulated direction and velocity, suggesting that spectral motion is the neural computation through which IC neurons are encoding specific features of conspecific vocalizations.

Introduction

Natural sounds, such as conspecific vocalizations and human speech, represent an important part of the sensory signals animals and humans encounter in their daily lives. Understanding the neural mechanisms involved in the processing of natural stimuli presents many challenges in all sensory modalities including vision and audition. While this has led to the development of novel computational methods that derive the relevant features of natural stimuli that sensory neurons encode in their spiking output (Theunissen et al., 2001; Machens et al., 2004; Sharpee et al., 2004; Touryan et al., 2005; David et al., 2007), little is known about the actual computation sensory neurons are using to create their selectivity for particular features of natural stimuli, and specifically stimuli used for social communication.

Previous studies have shown that response selectivity for natural communication signals can be observed as early as the inferior colliculus (IC) in the auditory midbrain (Klug et al., 2002; Portfors, 2004; Xie et al., 2005; Andoni et al., 2007; Holmstrom et al., 2007). Although it has been shown that blocking inhibition greatly reduced response selectivity to natural signals in the IC (Klug et al., 2002; Xie et al., 2005), it is still unclear which spectral and temporal features of conspecific vocalizations are encoded by an IC neuron and what computation IC cells are using to produce a feature selective output.

In most previous studies, the receptive field of an IC neuron was characterized as a single linear filter, which was derived as the spike-triggered average (STA). While this was effective in describing the stimulus–response relationship of a minority of neurons in the IC (Escabi and Schreiner, 2002; Andoni et al., 2007; Versnel et al., 2009), the majority of auditory neurons had significant nonlinear response properties and thus the predictions of the STA were relatively poor (Sahani and Linden, 2003; Machens et al., 2004; Andoni et al., 2007). In this study, we extracted the set of linear spectrotemporal filters that maximized the information between natural stimuli presented and their evoked response in the IC. We refer to each linear filter as a stimulus feature to which an IC neuron is tuned.

The most informative stimulus features of the majority of IC neurons in this study revealed their selectivity for the direction and velocity of frequency-modulated (FM) signals, sounds that contain a movement of sound energy across frequency. We refer to this movement as spectral motion, which is a prominent feature of animal vocalizations and the formant transitions that provide important cues for the perception of human speech (Liberman and Mattingly, 1989). Our analysis shows that, by having selectivity for spectral motion cues present in their conspecific vocalizations, IC neurons are able to encode specific features of these communication signals. This close agreement between neural tuning and features of natural conspecific signals shows that auditory neurons have evolved to specifically encode features of signals that are vital for the survival of the animal.

Materials and Methods

Surgical procedures

Experiments were conducted on Mexican free-tailed bats, Tadarida brasilensis mexicana, captured from local sources in Austin, Texas. Bats were of either sex. Surgical procedures were as described in a previous report (Xie et al., 2007). In brief, bats were sedated with isoflurane (inhalation) and then anesthetized with an intraperitoneal injection of ketamine/xylazine (75–100 mg/kg ketamine, 11–15 mg/kg xylazine; Henry Schein). Recordings began after recovery from the anesthetic, and thus all data were obtained from awake animals. Water was presented periodically with an eyedropper. Bats typically lay quietly during the experiments. If they showed signs of discomfort, data collection was stopped and doses of the neuroleptic ketamine hydrochloride (1:40 dilution; 0.01 ml injection) were administered. All experimental procedures were in accordance with a protocol approved by the University of Texas Institutional Animal Care Committee.

Electrophysiology

Single units were recorded with a single micropipette filled with buffered 1 m NaCl and 2% Fast Green, pH 7.4, to enhance the visibility of the electrode. The electrode was positioned over the IC and was subsequently advanced from outside of the experimental chamber with a hydraulic micropositioner (2650; Kopf). Recordings were made at depths ranging from ∼300 to 1600 μm, which covered most of the dorsoventral extent of the central nucleus of the IC. The electrode was connected via a silver wire to the headstage of a Dagan BVC 700A amplifier with its output digitized by a National Instruments DAQ board (PCI-6259), which was also used for stimulus generation. Data acquisition and stimulus generation were synchronously run using custom-built software written in Labview (National Instruments) and MATLAB (MathWorks). Sound was presented in free field from a 3 inch ribbon tweeter (Fountek JP3.0; Madisound Speakers) positioned 40–50° on the side contralateral to the IC from which recordings were made. The speaker was flat ±6 dB from 3 to 80 kHz. Speakers were calibrated with 0.25 inch Brüel and Kjær microphones.

Acoustic stimuli

Acoustic signals were pure tones, logarithmic FM sweeps, as well as species-specific social communication signals. All stimuli had a 0.5 ms rise and fall time constructed using a cosine-squared function.

FM sweeps.

FM sweeps were centered around the best frequency (BF) of each neuron and swept with different FM velocities either upward or downward on the logarithmic frequency axis. To construct a logarithmic sweep, we defined FM velocity as follows:

where f₀ and f₁ are expressed in hertz as the start and end frequencies, respectively, and Δt is sweep duration. Velocity, v, is expressed in octaves/second, where a positive value defines an upward moving sweep, whereas a negative value indicates a downward sweep. Thus, we can express the instantaneous frequency of the sweep as f(t) = f₀2^vt. To write the FM sweep as sin(ϕ(t)), we have to integrate over time for the instantaneous phase as follows:

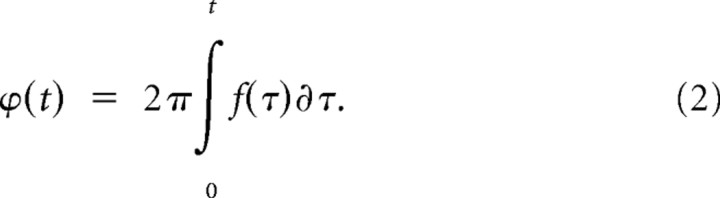Assuming an initial phase of 0°, the logarithmic FM sweep can be described as follows:

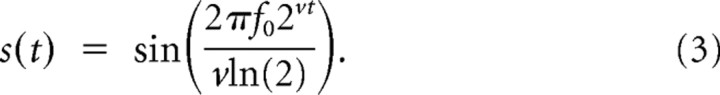Natural calls.

We used 25 bat social communication calls in this study. The calls were selected from a larger repertoire and were chosen because their acoustic features represent a range of spectrotemporal patterns that are used in a variety of important behavioral contexts (Bohn et al., 2008). Each call varied in length from 0.5 to 4 s with a sampling rate of 300 kHz. Most calls had their spectrum between 10 and 80 kHz, although some had energy as low as 6 kHz while others had harmonics that went up to 100 kHz. All calls were presented at a mean intensity of 50–70 dB SPL.

Dimensionality reduction

To derive the relevant features of natural communication signals that drive the response of an auditory neuron, we used dimensionality reduction methods that model the functional relationship between the auditory stimulus and neural response as a cascade of a set of linear filters and a static nonlinearity (Bialek and de Ruyter van Steveninck, 2005). This was done using the LNP (linear–nonlinear–Poisson) model (Simoncelli et al., 2004), modified to work with natural stimuli as described by Theunissen et al. (2001) and Touryan et al. (2005), and optimized using information theoretic methods (Pillow and Simoncelli, 2006). In this model, the spiking response of a neuron, r, to a given stimulus, s, is modeled as a set of linear filters, k₁, …, k_m, with their convolution output run through a static nonlinear function, g, as follows:

where m is the number of relevant dimensions that span the feature subspace needed to capture the stimulus–response relationship of the neuron. Here, the asterisk (*) denotes convolution over time such that the following:

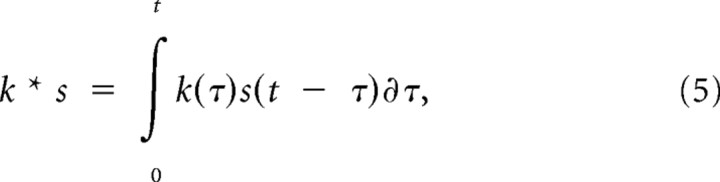and g is a static nonlinear function that maps m-dimensions onto a spiking rate output, r.

Natural stimulus correlations

Each natural sound was converted from a sound pressure waveform to a spectrogram form using a windowed discrete-time Fourier transform with zero mean and log amplitude. The resulting spectrogram for each stimulus segment had n bins in time with a bin size of ∼1 ms and m bins in log frequency with each bin spanning one-quarter of an octave. Each stimulus preceding a given time, t, was thus written as a single vector, s_t, with n × m dimensions. All natural stimuli presented can then be written as follows:

where N is the total number of time samples in the overall spectrogram, and T denotes the vector transpose. Writing each linear filter, k, from Equation 4 in vector form as well enables us to write the convolution operator as a projection across each filter such that k * S = k^TS.

To use spike-triggered averaging and covariance methods with natural stimuli, the stimulus had to be corrected for its second-order spectrotemporal correlations (Theunissen et al., 2001; Touryan et al., 2005). First, the stimulus autocorrelation matrix was computed as A = S^T S, which was then decomposed into its eigenvectors, U, and eigenvalues λ₁, λ₂,… , λ_n, using singular value decomposition. Then, the stimuli was “whitened” or “normalized” by correcting for the stimulus correlations as follows:

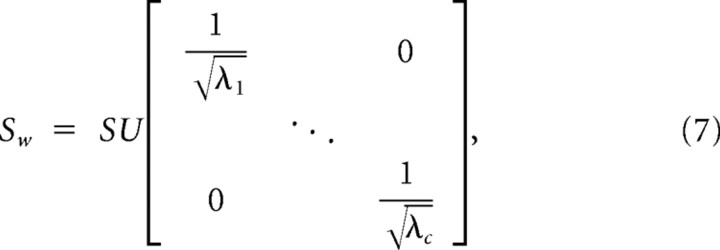where c < n such that only a subset of the eigenvectors are used for normalization since using very small eigenvalues will result in the amplification of high-frequency noise (Touryan et al., 2005; David et al., 2007; Lesica and Grothe, 2008). The percentage of eigenvectors used for whitening the stimulus, often referred to as the cutoff value, was treated as a free parameter and its value was chosen for each neuron such that it maximized the prediction accuracy of the test stimulus. For most neurons, the cutoff value was between 30 and 50%.

Most informative subspace

After correcting for stimulus correlations, the STA and spike-triggered covariance (STC) were computed for each neuron. The STA is simply the following:

where s_i is the stimulus vector preceding the ith spike and N is the total number of spikes evoked by all stimuli. The STC is then derived as follows:

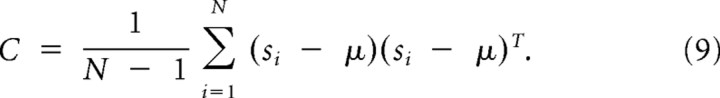While the STA and/or the significant eigenvectors of the STC could provide us with the relevant directions in stimulus space that span the feature subspace of the neuron, as described in Equation 4, they are restricted to orthogonal directions and it is difficult to know which axes of the subspace are most informative. Instead, we used an information-theoretic approach in which both the STA and STC are used to find the most informative subspace that maximizes the information between the raw stimuli and the stimuli that evoked a neural response. This was done using the iSTAC (“information-theoretic spike-triggered average and covariance”) analysis as described by Pillow and Simoncelli (2006). This method uses the Kullback–Leibler (KL) divergence, an information-theoretic measure of the difference between two probability distributions (Cover and Thomas, 2006), specifically, the difference between the probability distribution of the raw stimuli, P(s), and the stimuli that evoked a spiking response, P(s | spike), such that the following:

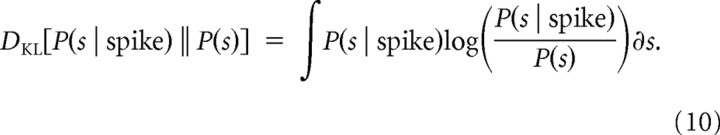Assuming both distributions are well approximated by a Gaussian, in which the raw stimulus distribution was whitened to have zero mean and unit covariance, as shown above, and the spike-triggered stimulus has a mean and covariance described in the STA and STC, respectively, then the KL divergence within a given subspace, B, can be reduced to the following (Pillow and Simoncelli, 2006):

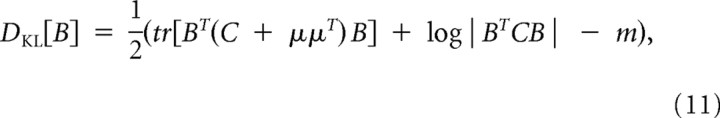where tr(.) and |.| indicate the matrix trace and determinant, respectively. The matrix B that maximizes the above equation gives us the most informative subspace, with its m-columns representing the set of linear filters that span this subspace. Therefore, the KL divergence is optimized as an objective function. First for a one-dimensional (1D) subspace, where m = 1, and then grown incrementally by adding columns to B such that KL divergence is maximized for each dimensionality. At each step, several initialization points are selected from the significant eigenvectors of the STC to ensure the optimization converges to a global maximum. To determine the number of significant subspace dimensions, a nested bootstrap test was used to examine whether the information gained by increasing the dimensionality is significantly above that expected from random sampling.

After finding the most informative subspace for the whitened stimulus, the columns of B, which represent the most informative dimensions (b₁, …, b_m), are projected back to the unwhitened space as follows:

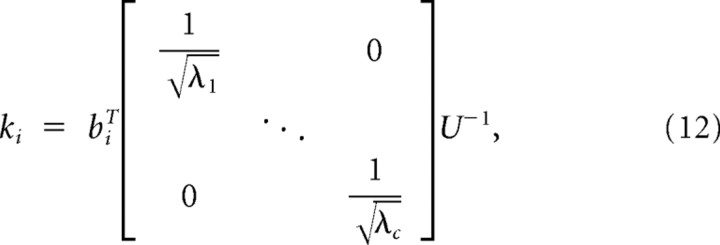Static nonlinearity

After finding the most informative set of linear filters that span the feature subspace of each neuron, as described above, an m-dimensional static nonlinearity has to be found that maps the stimulus projection across the most informative subspace onto an actual spiking rate response. When the maximally informative subspace is low dimensional, m ≤ 2, the nonlinearity can be easily estimated by first projecting the stimulus across the subspace, s* = B^Ts, then the nonlinearity can be estimated as follows:

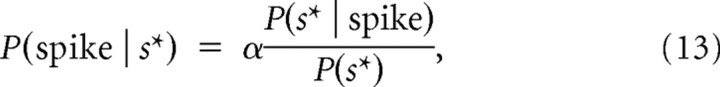where α is proportional to the mean spike rate, P(spike). This is often termed the histogram method, where the nonlinearity is derived by taking the ratio of the spike-triggered stimulus to the raw stimulus distributions, both projected across the most informative subspace. For higher dimensions, estimating the full nonlinearity is a lot more involved, but one can still use the histogram method across each informative dimension individually.

Predictions

To evaluate the performance of the most informative subspace and the static nonlinearity in predicting the neural response of each neuron, we first projected a test stimulus not used in deriving the most informative dimensions onto the subspace, s* = B_x^Ts, where x designates the dimension corresponding to the first, second, or both most informative dimensions. We then computed mutual information between the projection and the response of each neuron as follows:

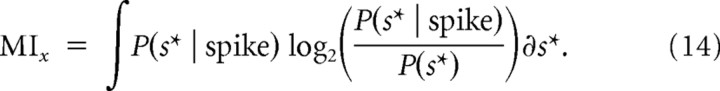We also evaluated the degree of synergy achieved by projecting the test stimulus onto both informative dimensions together compared with the sum of information calculated from each dimension separately, as follows:

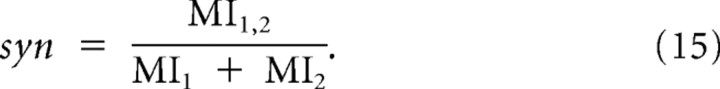Inseparability and directional selectivity

To assess the motion selective properties of each informative feature, we first calculated its inseparability by decomposing each feature into its singular values as follows:

The inseparability index (Ins) measured the dominance of the first singular value, λ₁, compared with the other singular values as follows:

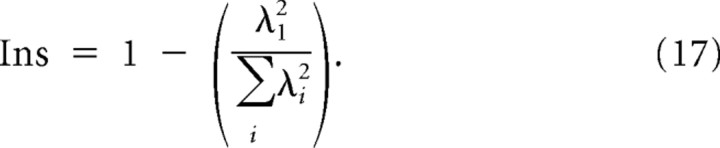The direction selectivity index (DSI) was computed by computing the Fourier transform of each feature and comparing the total power in the first quadrant, P₁, to the total power in the second quadrant, P₂, as follows:

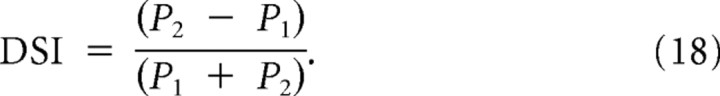The DSI for synthetic FM sweeps was calculated with the same equation, where P₁ refers to the total spike count to downward moving sweeps, whereas P₂ is the total spike count for upward sweeps.

Results

This study was based on 136 IC neurons recorded extracellularly from the IC of awake Mexican free-tailed bats in response to natural conspecific communication signals, FM sweeps, and tones. The communication calls were selected from a larger repertoire recorded from a local colony of Mexican free-tailed bats while the animals were engaged in a particular behavioral context (Bohn et al., 2008). The selected calls were chosen because their acoustic features represented most of the spectrotemporal patterns found in the larger set.

Neural selectivity to natural calls

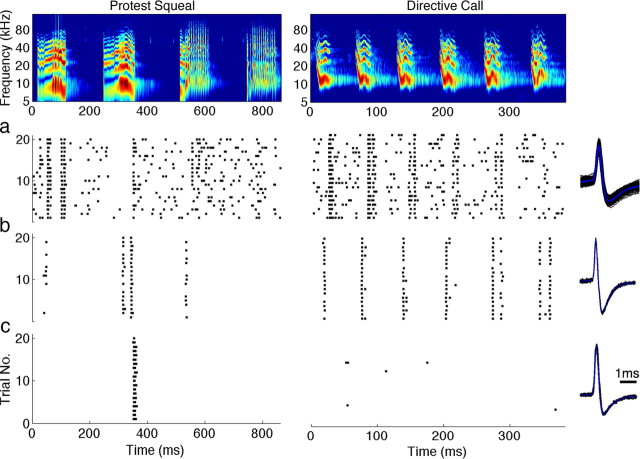
Spectrograms of two example calls and their responses recorded from three IC neurons are shown in Figure 1. As can be seen in the figure, IC neurons showed varying degrees of response selectivity to these natural signals. While some neurons responded vigorously to most vocalizations with very little selectivity (Fig. 1a), others were more selective as they showed strong responses to a particular subset of the syllables that compose each call with little or no response to the other syllables (Fig. 1b). A third group showed a higher level of selectivity and was only responsive to one or few syllables of these calls (Fig. 1c). In some neurons, their selectivity to a given syllable was similar since each neuron would respond to the same syllable of a call, as in the responses to the second syllable of the first call in Figure 1a–c. These neurons with similar selectivity could thus be tuned for the same stimulus feature that is similar to the syllable that evoked a shared response. Most neurons in the IC, however, rarely showed a homogeneous response to all vocalizations presented, and even though their responses could be similar to one syllable in a given call, they responded differently to other syllables and to other calls (Klug et al., 2002; Andoni et al., 2007; Portfors et al., 2009; Schneider and Woolley, 2010). For example, while the neurons in Figure 1, b and c, both responded strongly to the second syllable in the first call, the first and third syllables of the same call evoked responses in the neuron in Figure 1b but not in Figure 1c. Moreover, every syllable in the second call elicited strong responses in the neuron in Figure 1b, whereas the same call did not produce any responses in Figure 1c. This heterogeneity in selectivity shows that each IC neuron is tuned for different spectrotemporal features of natural calls. Therefore, deriving the relevant features each neuron is encoding by its spiking output could reveal the computation involved in creating neural selectivity to natural communication signals in the auditory midbrain.

Figure 1.

Different levels of neural selectivity in the IC. The top row shows the spectrogram of two example communication calls used by Mexican free-tailed bats. The bottom rows (a–c) display the raster plots of the extracellular response to each call from three IC neurons with their spike waveforms (black) and its average (blue) shown to the right of each row. Each IC neuron displayed a different level of neural selectivity to these calls. Whereas some neurons responded to most syllables in each call, as in a, others showed a higher degree of selectivity and only a subset of these syllables evoked a neural response (b). Other neurons were even more selective, responding strongly to only a single syllable from these two calls, as in c. This shows that each IC neuron is encoding a different set of spectrotemporal features present in these natural social communication signals.

Most informative features and their static nonlinearity

To characterize the spectrotemporal tuning of an auditory neuron, most previous studies relied on the STA, the average stimulus preceding each spike. It was usually assumed that an auditory neuron is tuned for a single spectrotemporal feature characterized by the STA such that the stimulus that is most similar to the STA would predict the largest response, and the more the stimulus differs from the STA, the weaker is the predicted response. Here, we assumed that the response of each IC neuron depended on multiple spectrotemporal features of the stimulus, including the STA, and that their nonlinear combination defines the overall receptive field of the neuron. To derive these features, we used the LN (linear–nonlinear) cascade model often used in describing the receptive fields of visual neurons (Simoncelli et al., 2004; Bialek and de Ruyter van Steveninck, 2005; Rust et al., 2005). These features together could then be treated as a set of linear filters with their outputs run through a multidimensional static nonlinearity. The nonlinearity describes the probability of spike generation as the similarity of the stimulus and each of the features varies (see Materials and Methods).

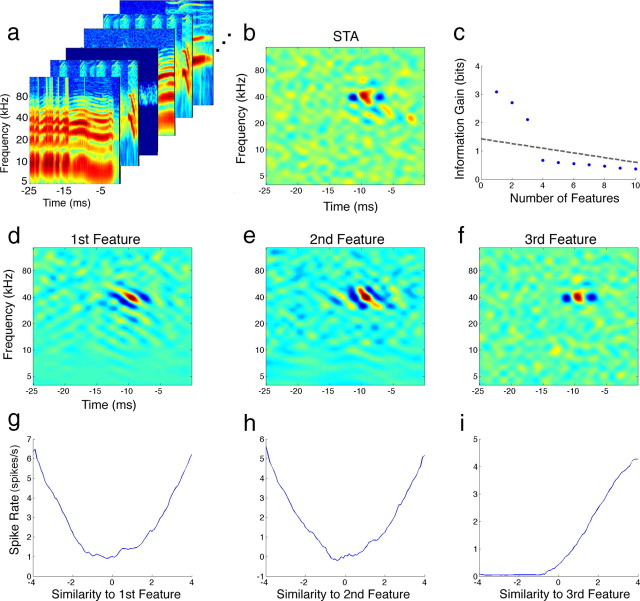
The process of deriving the relevant features of an IC neuron and their nonlinearity is illustrated in Figure 2. The set of stimuli that preceded each spike is referred to as the spike-triggered ensemble (STE). Only a subset of the STE for that IC neuron is shown in Figure 2a. Since natural communication signals typically contain strong spectrotemporal correlations that could bias our estimate, the stimuli were first normalized or “whitened” using their second-order correlations as described in Materials and Methods. Taking the corrected average of the STE resulted in the STA that is displayed in Figure 2b. While the STA could provide significant information regarding the feature selectivity of this neuron, there might be other features this IC cell is tuned for that were not revealed through averaging. To find the complete set of relevant features that resulted in the spiking response of this neuron, two separate methods could be used (Sharpee, 2007). The first method involves searching the stimulus space for additional features that, when combined together, would maximize a quantitative metric such as the predictability of the model (Theunissen et al., 2000; Machens et al., 2004) or the mutual information between the natural stimulus and the spiking response (Sharpee et al., 2004). An alternative to the latter approach is to use a method similar in some respect to principal components analysis in which the spectrotemporal correlations of the STE are computed by deriving the STC. The set of significant eigenvectors of the STC would then correspond to the relevant linear filters that span the feature subspace of the neuron (Simoncelli et al., 2004; Bialek and de Ruyter van Steveninck, 2005; Touryan et al., 2005). In this study, we used a hybrid of both methods in which we first computed both the STA and STC for each neuron and then used them to search for the set of features that maximized an information-theoretic measure, the KL divergence (Pillow and Simoncelli, 2006) (see Materials and Methods). This allowed us to derive the most informative stimulus features that each IC neuron is tuned to, in which each feature is ranked by the amount of information it preserves about the stimulus–response relationship of the neuron. The three most informative features for the neuron in Figure 2 are shown in the second row (Fig. 2d–f), and Figure 2c plots the amount of incremental information gain as the number of features considered is increased. In other words, it plots the increase in information (ΔKL) that resulted from projecting the stimulus across an additional feature. Note that using more than three features for this neuron does not increase the gain in information above the amount expected from noise or undersampling (dashed line). While the most informative features showed similar spectral and temporal tuning, they were uncorrelated and selective for spectrotemporal phases that were usually in quadrature as discussed below. It is important to note that the STA was not the most informative feature for this neuron but instead was very similar to the feature that was ranked as third. This shows that the STA does not always capture the most significant feature that defines the neural selectivity of an auditory neuron.

Figure 2.

Extracting the most informative features and their static nonlinearity. To extract the relevant features an IC neuron is encoding in its spiking output, each stimulus segment that preceded a spiking response is collected in the STE shown in a. Taking the average of the STE after correcting for spectrotemporal correlations, or “whitening” the stimuli, resulted in the STA displayed in b. Using both the STA and the STC, we searched for the set of spectrotemporal features that maximized the amount of information they preserved between the stimulus and the spiking response. The plot in c shows the amount of information gained as the number of features considered is increased. The dashed line in c indicates the level of significant information gain determined by nested bootstrap resampling (see Materials and Methods). The three most informative features are shown in the second row (d–f), in which the feature ranked as third resembled the STA. The static nonlinearity associated with each feature is displayed in the last row (g–i). Each nonlinearity shows how the spiking probability changes when the similarity between the stimulus and that feature varies.

The nonlinearity associated with each feature is displayed in the last row (Fig. 2g–i). Each nonlinearity maps the projection of the stimulus across a feature to the spiking rate of the neuron. A feature projection is generally equivalent to convolving the stimulus with that feature, where a high positive value indicates that the stimulus is very similar in its spectrotemporal shape to the given feature, and a low negative value indicates that the stimulus has spectrotemporal energy that is in opposite form from that of the feature. Therefore, each nonlinearity shows how the spiking rate of the neuron changes depending on the similarity of the stimulus to its associated feature. To compute the nonlinearity for each feature, both the raw stimuli as well as the STE were projected onto that feature and the ratio of the two distributions resulted in its static nonlinearity. Both symmetric (Fig. 2g,h), and nonsymmetric (Fig. 2i) nonlinearities were found in the IC. A nonsymmetric nonlinearity indicates that the spiking probability increases only when the stimulus becomes more similar to the feature. A symmetric nonlinearity, in contrast, indicates that the spiking probability of the neuron increases both when the stimulus is similar to the feature or when it is its complete opposite. Symmetric nonlinearities proved to be important in creating selectivity for spectral motion as discussed below. While each plot in the last row of Figure 2 shows how each feature affects the spiking response of the neuron individually, it does not show the effect of combining the features together. The full nonlinearity is derived separately and has as many dimensions as the number of relevant features. It defines the spiking probability as the similarity between the stimulus and each of the features changes.

Predicting neural response

Since the above method allowed us to derive the most informative features that an IC neuron is tuned to, here we investigated how many of these features each cell is encoding and whether using more than one feature could improve our predictability of the spiking response of the neuron. To verify the validity of the derived features, and their associated nonlinearity, they were used to predict the response of each neuron to natural stimuli not used in their derivation. We first used each informative feature alone and then studied how combining the features together would improve these predictions. In this study, we restricted our analysis to two features since most neurons in our sample were tuned for two significant features (see below), and deriving the full nonlinearity for more than two dimensions proved to be both computationally involved and sometimes not attainable for the amount of data we had collected.

To measure the performance of the derived features and their nonlinearity in predicting the neural responses evoked by novel natural stimuli not used in their derivation, we computed the amount of mutual information between the projection of the test stimulus onto the features and its evoked neural response (see Materials and Methods). Since the test stimuli were not used in estimating the features and their nonlinearity, mutual information provides an accurate measure of the predictive power of the model (Sharpee, 2007). We first calculated the information accounted for by each individual feature independently, and then compared it with the joint information captured by projecting the test stimulus across two features combined. The ratio of the joint information to the sum of information calculated separately from each feature defines the amount of synergy achieved by combining the features together (Atencio et al., 2008). A synergy value >1 indicates that the most accurate prediction can only be achieved by using the combination of the features and their nonlinearities.

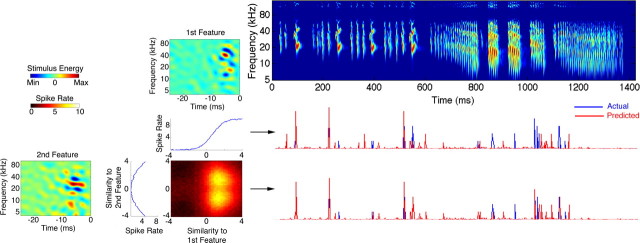
Figure 3 shows the effect of combining the two most informative features in predicting the neural response of an example IC neuron to a courtship vocalization not used in their derivation. The middle row shows the predicted response calculated by projecting the call onto the first feature alone. This projection was translated into a spiking rate using the 1D nonlinearity shown below the first feature. The bottom row plots the predictions when the call was projected across both features and mapped into a firing rate using the combined 2D nonlinearity. The amount of mutual information captured by the first and second features individually was 1.1 and 0.6 bits, respectively. When the test vocalization was projected across both features, the information increased to 2.2 bits. The resulting synergy index was 1.3, indicating superior predictions for the two-feature model. To further verify that using the combination of both features resulted in the most accurate prediction for this neuron, we computed a correlation coefficient (CC) between our predictions and the actual firing rate evoked by the bat call. Similarly, the CC increased from 0.4, when the first feature was used, to 0.6, when the response was predicted using both features and their 2D nonlinearity. It is evident that this neuron was tuned for multiple spectrotemporal features of the stimulus and using a single feature alone was not enough to produce the most accurate prediction.

Figure 3.

Predictions are improved when multiple stimulus features are considered. The two most informative features for an IC neuron are shown on the left, each with its 1D nonlinearity as well as their combined 2D nonlinearity. The 2D nonlinearity shows how the spiking probability varies when the similarity of the stimulus to both features changes. A spectrogram of a bat courtship song not used in deriving the features is displayed on the right with its evoked response (blue) and predicted response (red) shown in the bottom rows. Mutual information between the response of this neuron and projecting the vocalization through the first and second feature independently was 1.1 and 0.6 bits, respectively. The joint information using both features together increased to 2.2 bits. Therefore, information gain using both features together is greater than the sum of information calculated independently from each feature, resulting in a synergy index of 1.3. The middle row shows the predicted response using only the most informative feature, and its 1D nonlinearity, resulting in a CC of 0.4. Using both features and their combined 2D nonlinearity resulted in the most accurate prediction with a CC of 0.6. This shows that this IC neuron is tuned for multiple spectrotemporal features of natural signals.

The enhancement of predictability by using multiple features was generally the case for the population of 136 neurons sampled in the IC. In a subset of these neurons (49; ∼36%), the natural vocalizations presented did not evoke enough spiking responses to derive a meaningful set of features that had significant information gain, and their predictions were relatively poor (CC < 0.3). Therefore, these neurons were not used for further analysis. For the remaining 87 neurons, 81 cells were significantly tuned for multiple features as discussed below. In these neurons, the information captured by the first feature alone relative to the information in the two-feature model had a mean of ∼45%, whereas the second feature on average accounted for ∼31% of the joint information. The amount of synergy gained by using the two features together had a mean of 1.31 across these neurons, which was significantly greater than one (p < 0.01, Wilcoxon's rank sum test). Furthermore, the CC using the first feature alone compared with using the two-feature model increased significantly from a mean of 0.46 to 0.61 (p < 0.01, Fisher's r-to-z transformation). This suggests that neurons in the IC are tuned for multiple features of natural communication signals, which might explain the poor predictions observed for most neurons in our previous study that relied solely on the STA (Andoni et al., 2007).

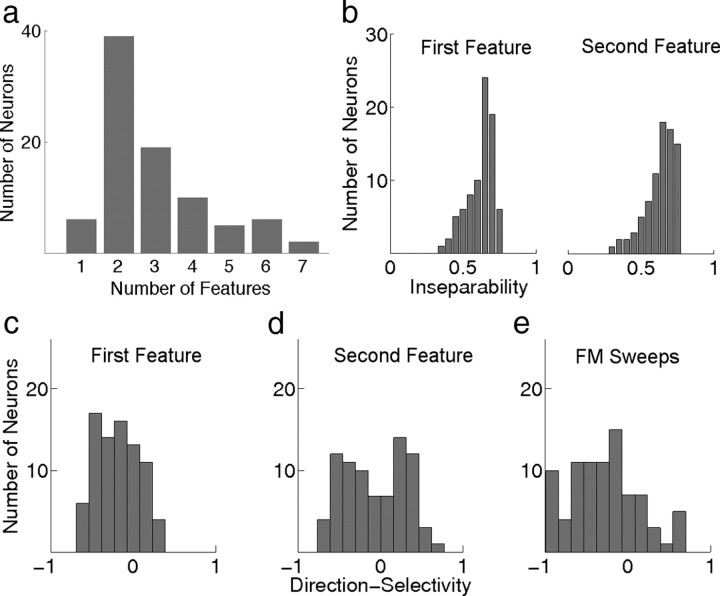
To evaluate the number of spectrotemporal features each neuron is encoding, we calculated the number of features that produced a significant information gain above that of noise or undersampling. As was shown in Figure 2c, that IC neuron had three features that carried a significant amount of information that were above noise level, and therefore, these three features and their nonlinearity should fully characterize the receptive field of that neuron and its spectrotemporal tuning. Figure 4a shows the number of significant features needed to characterize each neuron in our population of 87 cells with significantly derived features. It is evident that the majority of IC cells are tuned for multiple features and only ∼7% (6 of 87) could be fully described by a single spectrotemporal feature that was usually equivalent to the STA.

Figure 4.

Properties of feature selectivity in the IC. a, The number of significant features each neuron is encoding shows that the majority of IC neurons in our sample were tuned for two or more spectrotemporal features of the stimulus, and only a minority of them (7%; 6 of 87) were tuned for a single feature that was equivalent to the STA. The remaining 81 neurons were significantly tuned for multiple features and their first feature was compared with the second in the subsequent panels. b, Most of these features showed strong inseparability since they were usually tilted either upward or downward indicating a preference for the direction of FM sweeps. The mean inseparability index for the first and second most informative features were both ∼0.6 (n = 81). c, d, Direction selectivity index for the first and second feature shows that they have different directional tuning. While the first feature is biased toward downward (negative) motion with a mean of −0.2, the second feature showed a bimodal distribution with a mean around zero. e, Comparing direction selectivity extracted from features of communication signals to selectivity for the direction of synthetic FM sweeps showed similarity to the selectivity observed in the first feature but not the second. Yet selectivity to sweeps had an even stronger bias for the downward direction with a mean of −0.3.

We qualitatively evaluated the shape of the static nonlinearity associated with each feature across the neural population sampled. In a minority of neurons (13%; 11 of 87), the nonlinearity associated with the most informative feature was asymmetric. In these neurons, the most informative feature was equivalent to the STA and the subsequent features had symmetric nonlinearities. The example neuron in Figure 3 belonged in that group. However, the majority of these cells (87%; 76 of 87) had symmetric nonlinearities at least for the two most informative features such as the neuron displayed in Figure 2. Additionally, this group of 76 neurons showed strong selectivity for the direction and velocity of spectral motion as discussed below.

Selectivity for spectral motion

At first glance, it could be noted that most of the features encoded by the spiking output of neurons in the bat IC are tilted in shape and are usually spectrotemporally inseparable. Figure 4b shows the distribution of inseparability we observed in both the first and second most informative features in the 81 neurons tuned for multiple features. Since inseparability is generally a prerequisite for direction selectivity in a linear system, we computed a DSI for each feature by taking its Fourier transform and comparing the overall power between the two quadrants (Depireux et al., 2001). A negative DSI indicates selectivity for downward motion, whereas a positive value indicates tuning for the upward direction. It was not surprising to see that both features across most neurons were also directionally selective as shown in Figure 4, c and d.

To compare the spectral motion selectivity observed in response to natural stimuli to that in response to synthetic stimuli, and to further verify the validity of the extracted features, electronically generated FM sweeps were presented, which varied in both direction and velocity. The FM sweeps were centered around the BF of each neuron, the frequency to which the neuron was most sensitive. All FM sweeps had equal duration but varied in spectral range resulting in different FM velocities in both the upward and downward directions, as illustrated in Figure 5a. The DSI computed from responses to FM sweeps across the population of neurons is shown in Figure 4e. Note that the distribution of DSI in response to sweeps is similar to the DSI computed from the first informative feature, as both distributions show a clear bias for the downward direction. Nevertheless, the DSI calculated from responses to sweeps had an even stronger bias to the downward direction than the first feature, suggesting that the second feature might be playing a role in shaping the spectral motion selectivity of IC neurons. However, the selectivity extracted from the second informative feature was completely different from that of sweeps and showed both downward and upward selectivity across different neurons.

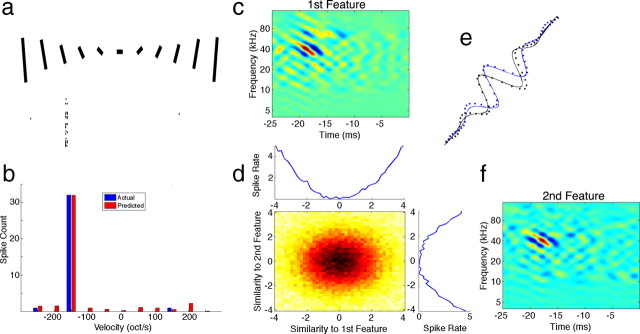
Figure 5.

Cooperative features for spectral motion selectivity. a, A set of downward and upward FM sweeps with varying velocities was presented to an IC neuron with its spiking response displayed below each sweep. b, Using the most informative features and their nonlinearity extracted from responses to natural stimuli we were able to predict the response of the neuron to only a single sweep velocity of around −150 octaves/s (oct/s) in the downward direction. c, f, Both features were tilted in the downward direction and had a BV of ∼150 oct/s. d, Both features also had a 1D symmetric nonlinearity and their combined 2D nonlinearity suggests their summation. e, Fitting a Gabor function to a smoothed cross-section perpendicular to the BV of the first (black) and second (blue) features revealed that they are offset in phase by 87°. This shows that spectral motion selectivity in this IC neuron could be described by a functional model similar to the energy model previously described in the processing of visual motion.

To look closer at motion selectivity for sweeping FM signals in individual neurons, Figure 5a shows a raster plot of the responses of an IC neuron to FM sweeps with varying velocities and direction. Note that the neuron only responded to a single FM velocity of −150 octaves/s, where the negative sign denotes the downward direction. The most informative features of this neuron that were extracted from its responses to natural communication signals are displayed in Figure 5, c and f. Both features were similar to oriented Gabor functions (i.e., a sinusoid with a Gaussian envelope) that were tilted to produce velocity selectivity for the same velocity that evoked the largest response to FM sweeps. The best velocity (BV) of each feature was computed by taking the ratio of the temporal to spectral modulation rates that had a peak magnitude in the Fourier domain (Andoni et al., 2007). The BV for both features was also around −150 octaves/s in agreement with the responses to synthetic FM sweeps. Taking a cross-section of each feature perpendicular to its BV shows that each feature is phase shifted from the other by 87°, suggesting that both features are forming a quadrature pair (Fig. 5e). Each feature also had a symmetric 1D nonlinearity with their combined 2D nonlinearity corresponding to their sum (Fig. 5d). A symmetric nonlinearity increases the spiking probability when the stimulus is either very similar in energy and shape to each feature or that it forms its complete opposite. In this manner, the spiking probability is increased only when the stimulus has the corresponding orientation in the spectrotemporal plane. Since both features in this neuron are tuned for the same direction and velocity, their cooperative nonlinear interaction produces strong selectivity for FM sweeping signals. Furthermore, the property of having a quadrature phase shift together with a symmetric nonlinearity suggests that selectivity for spectral motion in this IC neuron could be explained by a functional model analogous to the energy model previously described in vision (Adelson and Bergen, 1985). In this model, the output of two oriented filters, which are phase shifted to form a quadrature pair, is squared and summed to produce a motion-selective output. Figure 5b shows the prediction of the model to FM sweep responses and shows that it was able to accurately predict the high degree of selectivity of this neuron to a single FM velocity.

As mentioned previously, not all neurons had their two most informative features tuned for the same direction of motion. In fact, approximately one-half of the neurons sampled had the second feature tuned for the nonpreferred direction. An example neuron that is selective for features with opposing directions is shown in Figure 6, c and f. Although the second feature was tuned to the nonpreferred direction, its velocity tuning was very close to the BV of the first feature but in the opposite direction. The BV of both features was 93 octaves/s in opposing directions. When we examine the nonlinearity associated with each feature (Fig. 6d), we find that they are both symmetric but the nonlinearity of the second feature is actually suppressive since the spiking probability is decreased when the stimulus is either similar or opposite in shape to that feature. This indicates that the second feature suppressed the response to the nonpreferred direction at a velocity close to the BV to which the neuron is tuned in the preferred direction. Figure 6e plots the decomposition of both features into their spectral and temporal modulation rates (ripples), via a Fourier transform, which shows that each feature is similar to the mirror image of the other across quadrants, and both showing strong quadrant inseparability a necessary condition for velocity tuning. Using both features and their excitatory and suppressive nonlinearity, we were able to predict the response of the neuron to FM sweeps, indicating that our functional model captured the complex velocity tuning of this IC neuron. It is important to note that having an excitatory and suppressive filters tuned in opposite directions is similar to the Reichardt correlation model (Reichardt, 1961), in which two opponent directional subunits produce visual motion selectivity as described in the visual system of the fly (Borst, 2000; Bialek and de Ruyter van Steveninck, 2005).

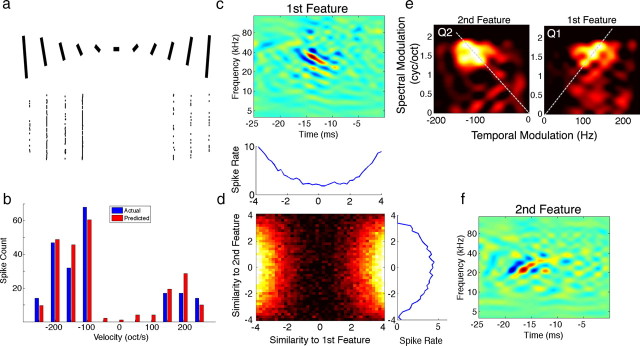
Figure 6.

Opponent features for spectral motion selectivity. a and b are as described in Figure 5. c, f, The most informative features extracted from responses to natural stimuli showed selectivity for opposing FM directions. d, While both features had a symmetric nonlinearity, the nonlinearity of the second feature was actually suppressive, reducing the response to the upward (nonpreferred) direction as shown in the full 2D nonlinearity. e, Decomposing each feature into its ripple components via a Fourier transform shows that each feature has power within a similar range of spectral and temporal modulations but in opposing quadrants. Furthermore, both features were tuned to the same velocity of 93 oct/s in opposing directions as indicated by the dashed lines.

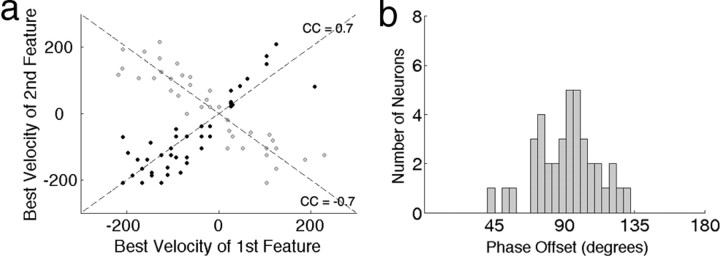
Examining the population of 76 IC neurons that had symmetric nonlinearities in our sample showed that approximately one-half of these cells had both of their most informative features tuned for the same direction and for the same velocity as illustrated by Figure 7a (black dots). These same features were also phase shifted by a mean of 92° (Fig. 7b), indicating a correspondence with the energy model for motion selectivity. The other one-half of the neurons had features that were tuned to opposing directions with the second feature providing suppression. While their features were tuned for opposite directions, their velocity tuning was very similar (Fig. 7a, gray dots). The significance of this similarity in velocity tuning in both excitatory and suppressive features suggests an important role for the spectrotemporal asymmetry in these features and is considered in Discussion.

Figure 7.

Spectral motion selectivity in the population of IC neurons. a, Two populations of IC neurons with symmetric nonlinearities were observed in this study. One with cooperative features tuned for the same direction (black dots; n = 39) and the other with opponent features tuned for opposite directions (gray dots; n = 37). The BV of the first feature is plotted against the BV of the second and shows that both the cooperative as well as the opponent features were tuned for velocities that were highly correlated. This indicates the importance of spectrotemporal asymmetry in two distinct computations of motion selectivity in the IC. b, Neurons that were tuned for cooperative features had a phase shift between them with a mean of 92° and a SD of 22°.

Motion in bat vocalizations

Our analysis of the spectrotemporal features that IC neurons are encoding has revealed a strong selectivity for the direction and velocity of spectral motion. To understand how this motion selectivity might be playing a role in creating selectivity for the natural communication calls themselves, we analyzed the motion cues present in these signals and compared their modulations over time and frequency to the modulation tuning of IC neurons.

It is apparent from simple visual inspection that most of the communication signals bats emit during different behaviors are mostly composed of frequency modulations that sweep downward or upward at various velocities (for example calls, see Figs. 1, 3). As described previously in the study by Andoni et al. (2007), each bat call could be decomposed into its Fourier (ripple) components showing the spectral and temporal modulation rates present in that call (Fig. 8a,b). This allowed us to measure both the FM direction of the call by comparing the power between the two quadrants, and its FM velocity by the alignment of energy around a line with a constant ratio of temporal to spectral modulation rates. Additionally, we could estimate the overall modulation spectrum across all the vocalizations recorded, which gives us an overall representation of the modulations in time and frequency that are present across all vocalizations (Singh and Theunissen, 2003). The same analysis could also be applied to the informative features we extracted from neural responses to compare neural tuning in the IC to the acoustic properties of conspecific vocalizations.

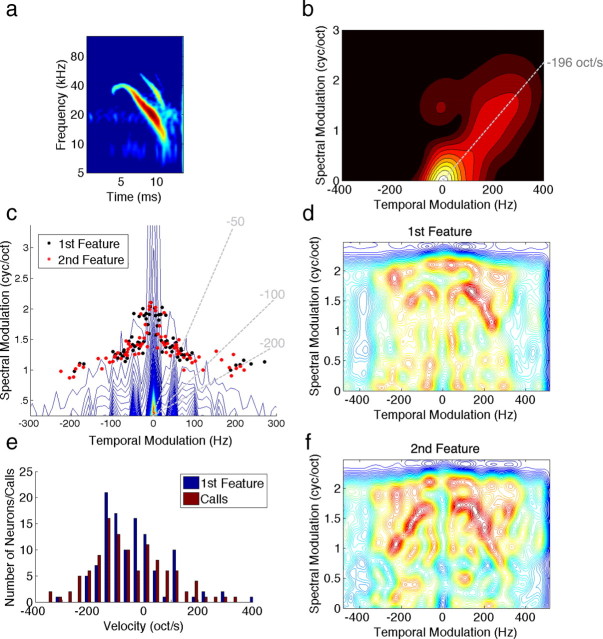
Figure 8.

Comparing spectrotemporal modulations of conspecific signals to neural tuning. a, A spectrogram of a single syllable taken from a courtship call. b, The Fourier transform of the syllable shows that most of the energy is concentrated around the origin with a tail that is oriented along a line that indicates the sweeping velocity of the syllable. c, The contour plot shows the modulation spectrum of all bat calls in our repertoire showing 1/f distribution that is typical of natural signals. The black and red dots designate the peak modulations present in the first and second most informative features of IC neurons, respectively. Note that peak tuning in the IC is organized to detect various FM velocities (dashed lines) while avoiding redundant energy found in most calls. d, f, Modulation spectrum of the most informative features shows that IC tuning is specifically aligned around the common modulations in the calls to be selective for modulations that represent motion cues found in their conspecific signals such as the extended tail in the modulation spectrum of the above syllable. e, Distribution of FM velocities found in the calls match the velocities of the most informative feature representing the velocity tuning of IC neurons. This suggests that IC neurons are tuned to detect spectral motion cues present in their conspecific social communication signals.

Figure 8c shows the modulation spectrum of all bat vocalizations. It plots the distribution of spectral and temporal modulations present in the complete repertoire of bat calls. Overlaid on top of the modulation spectrum are the peak modulations of the most informative features IC neurons are tuned to. One observation that could be made from this plot is that the peak modulation tuning of IC neurons is avoiding the dense areas of the contour plot, which indicates that they are avoiding modulations that are most common or redundant across the calls and are tuned instead to modulations that are present in some calls but not others. One can also note that the peak modulation tuning of IC neurons covers a wide range of FM velocities indicated by the dotted lines in the plot.

To further examine the modulation tuning of IC neurons, a contour plot of the average modulations found in the first and second most informative features are displayed in Figure 8, d and f, respectively. As was observed from their peak tuning, it is evident that tuning in the IC is aligned to detect modulations that deviate from the common modulations found across calls, allowing each neuron to be selective for the modulations that represent a given direction and velocity of spectral motion. In this manner, each IC neuron responds only to the calls that contain the FM sweeping direction and velocity the neuron is tuned for while failing to respond or only responding weakly to calls with modulations outside of its tuning.

Comparing the FM velocities present in the calls with the velocities IC neurons are tuned for, as represented by the best velocity in the most informative feature, shows a very close agreement (Fig. 8e). This correspondence between neural tuning and acoustic properties of conspecific communication signals shows that IC neurons are specifically encoding features of these signals through the neural computation of spectral motion selectivity.

Discussion

Synthetic versus natural stimuli

Our main motivation for this study was to understand the neural computation involved in creating selectivity for specific features of natural communication signals. This required us to derive receptive fields of IC neurons that we were not able to characterize previously with broadband synthetic stimuli such as noise and moving ripples (auditory gratings). In our previous study, we presented a large set of moving ripples with a range of spectral and temporal modulation rates to extract a linear estimate of the receptive field of each IC neuron (Andoni et al., 2007). In that study, approximately one-half of IC neurons sampled did not respond well to the broadband ripple stimuli, and we were able to extract a meaningful receptive field with accurate predictions in ∼25% of the total population. It is our general observation that neurons in the bat IC do not respond well to broadband stimuli such as noise and ripples, which could be a result of the broad sideband inhibition observed intracellularly (Xie et al., 2007), or simply an outcome of their high degree of selectivity discussed above. Nevertheless, most neurons in the IC respond well to natural stimuli, specifically the conspecific vocalizations these animals use for social communication. This allowed us to extract the relevant spectrotemporal features each neuron is encoding directly from the communication calls themselves without relying on synthetic stimuli. This strategy was in agreement with recent studies in birds (Woolley et al., 2006) and ferrets (David et al., 2009), in which it was shown that characterizing the receptive fields of auditory neurons had significant differences depending on whether synthetic or natural stimuli had been used. However, we presented synthetic FM sweeps in this study to verify the validity of the features extracted from natural calls and showed that the selectivity observed with natural stimuli is in agreement with responses to simpler synthetic stimuli.

Tuning for multiple spectrotemporal features of natural calls

One of our main findings in this study is that IC neurons are usually tuned for multiple spectrotemporal features of the stimulus. This was evident in our analysis of the number of features required to maximize the amount of information gained between the stimulus and response. It was further verified when the accuracy of the predictions increased when both informative features were combined, exhibiting a synergistic relationship. Since the IC receives a convergence of excitatory and inhibitory projections from various nuclei in the brainstem, it is not surprising to find that most neurons in the IC are actually tuned for multiple spectrotemporal features of sound. This property was studied previously in the processing of binaural cues, which showed that each IC neuron is encoding multiple cues regarding the level and timing differences between the two ears as well as notch detection (Chase and Young, 2006).

While tuning for multiple features was also present in the auditory cortex (Atencio et al., 2008), most cortical neurons showed an asymmetric nonlinearity for the most informative feature, which was also similar to the STA. This might suggest that the cortex and IC process the temporal envelope of an acoustic signal in a different manner. By having a symmetric nonlinearity for the most informative feature, the response of the majority of neurons in the bat IC were mostly affected by the direction and velocity of a spectrally moving sound, and were least sensitive to the phase of the temporal envelope of the signal. This might explain the difficulty in driving these neurons with moving ripple stimuli. In contrast, neurons in the auditory cortex were mostly sensitive to the phase of the envelope but were additionally tuned to phase-invariant features of the stimulus as indicated by the symmetric nonlinearity of their second informative feature (Atencio et al., 2008).

The result of having multiple features encoded in the spiking output of IC neurons might explain why previous studies had been unsuccessful in producing accurate predictions for a large population of auditory neurons (Sahani and Linden, 2003; Machens et al., 2004; Andoni et al., 2007). These studies solely relied on the STA to make these predictions, and as shown above the STA is not always the most informative feature auditory neurons are selective for. Furthermore, neurons in the IC in which a significant STA could not be derived have been reported in many previous studies (Escabi and Schreiner, 2002; Qiu et al., 2003; Andoni et al., 2007; Versnel et al., 2009).

Correspondence with visual motion

The majority of IC neurons in our population showed high degrees of selectivity to the direction and velocity of acoustic motion across the spectral axis. Our analysis of the most informative features extracted from these neurons revealed two distinct functional computations that enabled these cells to be selective for both the direction and velocity of spectral motion. The first motion-selective computation found in the IC was analogous to the energy model described in vision (Adelson and Bergen, 1985). In this model, motion selectivity is computed using two linear filters that are tilted in the spectrotemporal plane with a quadrature phase shift. Their output was then squared and summed to produce direction selectivity. By also having filters that were quadrant inseparable, as was shown in Figure 6e, they were also selective for the velocity of spectral motion. The energy model for FM selectivity described above agrees with recent intracellular studies in the bat IC, in which it was shown that, in some neurons, excitation and inhibition are balanced and exhibit similar tuning for the preferred direction (Gittelman et al., 2009).

While the energy model was consistent with approximately one-half of the neurons that showed strong selectivity for motion, the other one-half showed correspondence with a simplified opponent energy model (Adelson and Bergen, 1985) as well as the Reichardt correlation model (Reichardt, 1961). In these models, motion is computed by subunits that are tuned for opposing directions, in which one increases the neural response, whereas the other suppresses it. In IC neurons that corresponded with these models, motion selectivity was obtained by having two linear filters with opposite orientations and a spiking response equivalent to the difference between their squared output. While this could enhance responses to the preferred direction and suppress responses to sweeps moving in the nonpreferred direction, it was surprising to see that each filter in these neurons was tuned for the same velocity but in the opposite direction. This might indicate that excitatory and inhibitory inputs innervating these IC neurons have the opposite temporal asymmetry across the frequency axis. In other words, excitatory inputs from different frequency channels might have varying delays to produce coincidence for a particular velocity in the preferred direction, while inhibitory inputs have the opposite delays on the frequency axis, thereby suppressing the response for the same velocity but in the nonpreferred direction. This scenario would correspond with experimental evidence for the Reichardt model observed in the processing of visual motion in the fly (Borst, 2000).

The latter functional model of spectral motion selectivity through opponent filters could be the result of the interaction of excitatory projections from the cochlear nucleus with inhibitory innervations coming from the ventral nucleus of the lateral lemniscus and the superior paraolivary nucleus (Pollak et al., 2011). The model is also consistent with recent studies conducted in the auditory cortex of bats in which facilitatory excitation was observed for tones with different frequencies and a delay consistent with the best velocity of the neuron (Razak and Fuzessery, 2008), and it is also in agreement with intracellular recordings of FM-selective neurons in the cortex of rats in which excitation and inhibition were shown to have different temporal asymmetries (Ye et al., 2010).

Neural tuning and features of conspecific vocalizations

Comparing the general spectrotemporal features of conspecific communication sounds with those IC neurons are selective for revealed that IC cells are tuned to respond to spectral motion cues present in these signals. This was evident in the correspondence between FM velocities found in the calls and those IC neurons are tuned to. This agreed with our previous study in which we showed that the receptive fields of IC neurons mapped with moving ripples showed tuning for the FM direction and velocities that match those in the vocalizations (Andoni et al., 2007).

Furthermore, modulation tuning in the IC seemed to be avoiding redundant spectral and temporal modulations that are common among all vocalizations and neurons are instead tuned for modulations that differ from one call to another. This property of IC neurons was previously shown in the midbrain of birds (Woolley et al., 2005). Looking closer at the modulation tuning of IC neurons in the bat showed that they are aligned across various spectral and temporal modulations, allowing them to be tuned for the direction and velocity of spectral motion that distinguish each syllable of a call from another. Therefore, selectivity for spectral motion could be the neural computation through which IC neurons of the bat are encoding features of natural communication signals.