H-bonded N-heterocyclic base-pair phototautomerizational potential barrier and mechanism: The 7-azaindole dimer

Abstract

A theoretical analysis of the double proton transfer (PT) in a hydrogen-bonded N-heterocyclic base pair is presented. The calculated (time-dependent density functional theory) double PT barrier calculated for the concerted process of the 7-azaindole C_2h dimer in the first excited singlet electronic state S₁ conforms well to the kinetic data and the photophysical evidence reported in this article. The calculated PT energy barrier of 4.8 kcal/mol height, and the corresponding zero point energy value, yield for the S₁ state an activation energy barrier of 0.3 kcal/mol. This finding implies that the double PT concerted process is almost barrierless, confirming previous experiments. Upon N-H deuteration of the 7-azaindole dimer, the theoretical excited-state activation energy for the double deuterium transfer is determined to be 1.4 kcal/mol, in agreement with experiment, which in low-temperature spectroscopy is shown to negate excited-state double-deuteron transfer.

Multiple H-bonded base-pairing as a fundamental element of DNA structure was introduced by Watson and Crick (1), using the stable keto-tautomer base forms. They included consideration of the possibility of mutations by tautomeric proton transfer (PT) shifts. The example (2, 3) of an anomalous (imino tautomer) adenine-cytosine (A′C) pairing could arise from a biprotonic phototautomerism in a normal AT pair, in which the excited-state electronic redistribution would catalyze a simultaneous two-proton flip. A model base pair for such a biprotonic phototautomeric shift is 7-azaindole (7AI) H-bonded dimer (4), now a much-studied example (Scheme 1). This phenomenon has been demonstrated to represent a concerted process over a double-minimum potential energy (PE) curve (refs. 5–7; see also ref. 8 and references therein). Earlier quantum chemical calculations (9, 10) on DNA base-pair mutations concentrated on ground electronic-state proton tunneling. However, for a normal tautomer to be converted to an anomalous (more stable) form with a lower potential minimum as a driving force for tautomerization, electronic excitation is an essential step. In this article, we present the refinements in the quantum mechanical (QM) theory needed to yield a reliable and more accurate PE curve for the tautomeric conversion. The PE curve for the centro-symmetric dimer of 7AI biprotonic phototautomerism is given, and the resultant excitation energy was analyzed for N-H- and N-D-substituted species, explaining the blocking of the photo-tautomerization in the latter.

Scheme 1.

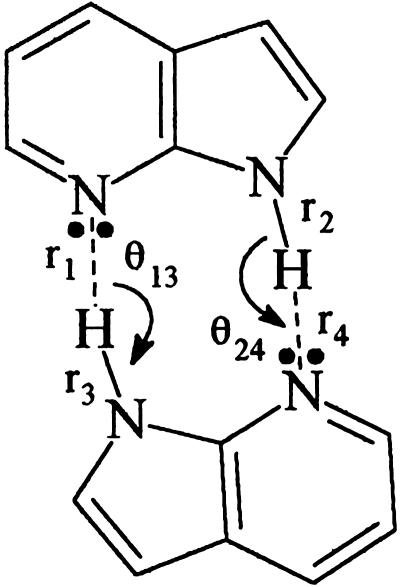
Coordinate labels for the C_2h coplanar 7AI dimer.

In recent years the subject of anomalous DNA base-pairings as a result of proton shifts within the H bonds has been the subject of accelerated study. The new interest has been stimulated by the application of ultra-fast laser excitation techniques and advances in QM molecular theories and calculations. Watson and Crick's initiating work (1–3) on DNA structure also focused attention on the possible production of anomalous base-pairing as a result of PT tautomeric shifts. Molecular spectroscopy has shown that tautomers unstable in the ground-electronic state may be the stable form in an electronically excited state.

The model base-pair 7AI dimer (7AI)₂ has been singled out for extensive research because of its dramatic excited-state biprotonic phototautomerism (4) (converting a violet-fluorescing normal base pair to a green-fluorescing PT tautomer base pair) and the facile adaptability of the molecule in gaseous or condensed phase to diverse spectroscopic techniques. A suggestion of an intermediate single PT step (11) aroused immediate attention as a possible “mutation caught in the act” (12), which would pose great interest for molecular genetics. The experimental evidence was taken to be the suggestive kinetic studies of (unidentified) photo-excited transient 7AI species. A QM calculation of the intermolecular PT PE function by an inadequate methodology (13, 14) was published; the QM results were shown to be misrepresented (compare figure 3 in ref. 15). Recent refined QM calculation (15, 16) has confirmed that the PT PE function for ground and first excited states of 7AI dimer are double-minimum potentials, and the biprotonic phototautomerism occurs via a concerted one-step simultaneous double PT with no intermediate single PT species for the 7AI dimer tautomerism. The complex kinetics observed in the ultra-fast laser dynamics studies could be attributed to any of the six or so dimeric species (5) emerging in the ultra-sonic molecular beam used in the preliminary kinetic studies (11).

Although knowledge of the height and shape of the PT energy barrier is indispensable for elucidation of the dynamics of the excited-state double PT (ESDPT) process in the 7AI dimer (Scheme 1), no accurate information has been reported on the PE curve for the S₁-S^′₁ excited state. Ingham and El-Bayoumi (17) interpreted the temperature effect on the F₁ (normal dimer fluorescence) and F₂ (PT tautomer-dimer fluorescence) emissions via a barrier in S₁-S^′₁ (4, 15) for the ESDPT process. A lower limit of 1.4 kcal/mol was estimated for the PT activation energy for 7AI dimer in 3-methylpentane. Hetherington et al. (18) showed that the excited electronic state (S₁) generates the PT tautomer within the 5-ps width of the excitation pulse. They estimated the barrier for ESDPT as the energy difference between the first peak, in the PT tautomer and the normal tautomer, dimer excitation spectra (77 K) of their respective fluorescences, yielding an upper limit barrier height of 2.0 kcal/mol.

Share et al. (19) observed the PT-tautomer species of excited 7AI dimer in the first 250 fs after S₁ photo-excitation, indicating a low or very narrow barrier.

Theoretical results on the barrier height for PT in analogue DNA base pairs have hitherto been quite exaggerated in comparison with the experimental evidence. Pecheneya and Danilov (20) reported an energy barrier of 32.5 kcal/mol for the excited-state PT reaction of the 7AI dimer by using the π-electronic model of DNA base pairs of Rein and Harris (9) and a distance of 3 Å between the two 7AI units of the dimer. Catalán and Pérez (21) calculated the PT curves for the first excited state of the 7AI dimer, obtained with configuration interaction (CI), for the first 50 single excitations in a CNDO/2 calculation (22). The result (21) indicated that the ESDPT barrier was base distance dependent, being 10 kcal/mol for a distance of 2.6 Å.

Calculations at the CIS/6–31G** level (compare below) without excited-state geometry optimization, but using optimized geometry for the concerted ground-state double PT at the B3LYP/6–31G** level of density functional theory (DFT), were reported in 1999 (15). The subsequent Franck–Condon calculations for the 7AI dimer (Scheme 1) indicated the first two excited electronic states 2A_g and 1B_u to be very close in energy, and that along the S₁-S^′₁ ESDPT coordinate they exchange in energy ordering, reflecting the Davydov molecular excitonic theory (23, 24), via the transition moment coupling geometry reorientation during tautomerization. The calculated excited-state PT-PE curve yielded (15) an energy barrier of ∼8 kcal/mol (∼8.5 kcal/mol for the 2A_g state and 7.8 kcal/mol for the 1B_u state). A presentation of CIS/6–31G* calculations (25) with geometry optimization gave a barrier of 28.6 kcal/mol for the ESDPT process of the 7AI dimer. This high PT barrier (25) is in strong conflict with the PE curve built by using DFT molecular geometries (15).

Our purpose is to assess the most accurate PE curve for the concerted ESDPT of the 7AI (C_2h) dimer (Scheme 1). From more accurate energetics we shall be able to interpret the excitation pathway.

Theoretical Methods

All calculations were performed with the split valence 6–31G(d,p) basis set, commonly named 6–31G**. A theoretical method is proposed, which permits assessment of a more accurate PT barrier of the doubly H-bonded 7AI dimer in the tautomerization S₁–S^′₁ state potential function (Fig. 1a). The essential requirements for an adequate method are inclusion of (i) polarization (via the polarized basis set that adds d functions on nitrogen and carbon atoms and p functions to hydrogen atoms), (ii) electron correlation (by DFT), and (iii) geometry optimization (for skeletal relaxation).

Fig. 1.

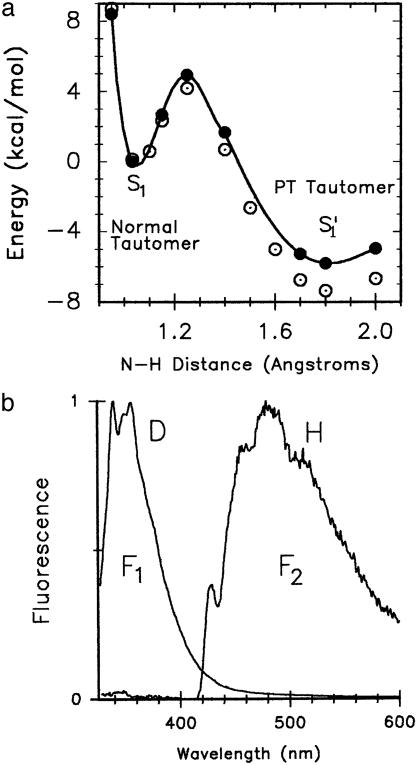
(a) PT PE curves obtained at the time-dependent B3LYP level, without excited-state geometry optimization (•) and with excited-state geometry optimization (compare text) (○) by using the 6–31G** basis set. (b) Fluorescence spectra of the 7AI dimers (Scheme 1) at 102 K. The spectra were obtained from independent anhydrous 2-methylbutane solutions. Spectrum F₁ (normal tautomer) was obtained from the deuterated 7AI dimer solution, and spectrum F₂ (PT tautomer) was recorded from the nondeuterated 7AI dimer solution. It is observed that deuteration hinders double-deuteron transfer.

The B3LYP-DFT (26, 27) calculation for the S_o state was carried out with full geometry optimization. For the S₁ excited state the hydrogen-bonding (H-bonding) coordinates (i.e., r₁, r₂, r₃, r₄, θ₁₃, and θ₂₄, Scheme 1) are frozen, and then the CI singles (28) with geometry optimization is used over the restricted geometry for calculating an optimized S₁ geometry. This method adds the contribution of the hetero-aromatic molecular ring relaxation of the two 7AI subunits of the C_2h dimer in the excited state. The demonstrated experimental results on the simultaneity of the excitonic excitation of the dimer components (ref. 8 and references therein), the demonstrated catalytic requirement for the ESDPT, and the concomitant symmetry of electronic simultaneity requirements (6) are the basis of the frozen H-bonding coordinate restriction. The restricted optimization geometry for the S₁ state is subsequently used for calculating the Franck–Condon ΔE value for the S₁-S_o transition at the time-dependent-DFT-B3LYP (29) level without further geometry optimization. All of the calculations described above were carried out by using the gaussian 98 (30) and spartan 4.1 programs (31).

Experimental Procedures

7AI was from Sigma in 99% purity and recrystallized twice in spectrograde cyclohexane. The solutions were freshly prepared in anhydrous 2-methylbutane (Aldrich). The cryostat was purged with dry nitrogen at 99.99% purity. The spectra were recorded at 102 K. The 2-methylbutane solvent melting point is at 113.1 K; experiments at 102 K thus were observed in a clear isotropic solid glass matrix. At the initial 10^–4 M concentration of 7AI monomer (298 K), it is totally converted to dimer <202 K (32). The N₁-deuterated 7AI was prepared by refluxing 7AI in alkaline D₂O for 1 h; NMR experiments revealed an isotopic purity of at least 90%.

Results and Discussion

The method used (Table 1) provides a significant improvement of the energy values in the PE curve of the ESDPT process (Fig. 1a). The barrier height was lowered from 8 to 4.8 kcal/mol. We emphasize that the excited-state PT reaction becomes more exothermic, so that the PT tautomer of 7AI is –5.3 kcal/mol more stable than the normal tautomer (S^′₁ state), compared with the –3 kcal/mol energy stabilization obtained previously (15).

Table 1. Electronic transition energies ΔE at the corresponding N—H distances calculated with the method described in Theoretical Methods, and the corresponding experimental values for absorption.

Transition energy	ΔE, nm	Experiment
S0 → S1	288 (1.032 Å)	λmax = 292*
		λ0-0 = 315*
S0′ → S1′	389 (1.8 Å)	λmax = 383†
	384 (1.7 Å)	λ0-0 = 463†
	377 (1.6 Å)

The S₀ → S₁ transition energy refers to the normal 7AI dimer, and the S₀′ → S₁′ transition energy refers to 7-methyl-7H-pyrrolo[2,3-b]pyridine.

^*In anhydrous 2-methylbutane (32).

^†In gas phase.

We use the N-H stretching vibrational frequency that corresponds to the normal mode frequency 3,200 cm^–1, which has been ascribed to the concerted double PT process of the normal 7AI dimer in its S_o state through visualization with the aid of the spartan 4.1 program (31). When this frequency value is assigned also to the S₁ state, it is found that the zero point energy (ZPE) value is 4.5 kcal/mol, which is very close to the top of the PT energy barrier previously calculated (4.8 kcal/mol). This reasoning leads to the surprisingly small value of 0.3 kcal/mol for the ESDPT activation energy. However, this theoretical result is in good concordance with the experimental observations reported in the literature (17–19).

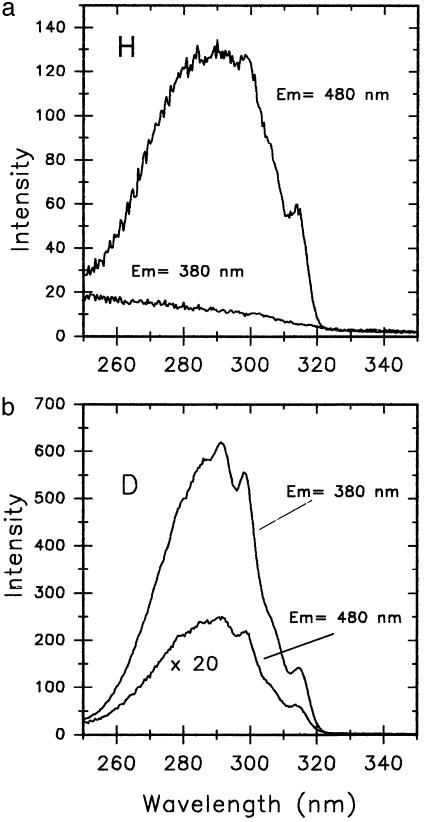
In sum, the calculated PT barrier for 7AI dimer in the S₁ state amounts to 4.8 kcal/mol for the concerted double PT process, yielding a corresponding ZPE value of ∼4.5 kcal/mol for the critical N-H vibrational normal mode ascribed to the double PT process. Thus, the ESDPT process should exhibit a negligible activation energy barrier. Deuteration of the N-H protons changes the situation markedly. For this latter case, the N-D vibrational frequency associated with the concerted double-deuteron transfer in the 7AI dimer becomes 2,368 cm^–1 (B3LYP-DFT with geometry optimization), which corresponds to a ZPE value of 3.39 kcal/mol. Thus, it is concluded that the activation energy for the double-deuteron transfer in the 7AI dimer will be 1.4 kcal/mol. This double-deuteron activation energy is two to five times that associated with the double PT. These results correspond well with the spectroscopic evidence on the 7AI dimer in 2-methylbutane (32) (Fig. 1b), in which by exciting at the 0–0 transition (315.2 nm) (compare Fig. 2) of the 7AI dimer only the double-PT 7AI dimer fluorescence (F₂) is observed. Conversely, with substitution of the two N-H hydrogens by N-D deuteriums (at least 90% in isotopic purity), only the normal deuterated 7AI dimer species emits fluorescence (F₁), and a long wavelength fluorescence tail is recorded that comes from the nondeuterated 7AI dimer (at 102 K). Fig. 2 depicts the excitation spectra observed by monitoring fluorescence light at 380 and 480 nm for both experiments, with or without deuterium substitution in 2-methylbutane. Fig. 2a shows that there is no fluorescence emission at 380 nm, thus with an excitation spectrum absent. However, the 480-nm (F₂) emission (102 K) exhibits an excitation spectrum that matches the absorption spectrum of the 7AI dimer. Furthermore, Fig. 2b shows two excitation spectra that match the absorption spectrum of the 7AI dimer in 2-methylbutane. However, the excitation spectrum monitored at 480 nm exhibits an intensity that is ∼70 times lower that that monitored at 380 nm, for the reason that the former comes from the nondeuterated dimer species double PT. The spectrum monitored at 380 nm is the fluorescence of the deuterated normal tautomer species. These measurements emphasize the remarkable isotopic effect, blocking the ESDPT at low temperature as suggested by theory.

Fig. 2.

(a) Excitation spectra of the nondeuterated 7AI dimer (Scheme 1) in anhydrous 2-methylbutane (102 K) by monitoring at 380 and 480 nm. The excitation and emission monochromator slits were 2 and 8 nm, respectively. (b) Excitation spectra of the deuterated 7AI dimer in anhydrous 2-methylbutane (102 K) by monitoring at 380 and 480 nm. The excitation and emission monochromator slits were 2 and 8 nm, respectively.

The results presented on the concerted mechanism for the excited-state phototautomerism of 7AI symmetrical (C_2h) dimer provide an element necessary for the Watson–Crick suggestion of an anomalous A′C pairing as a possible mutation source, i.e., the formation of the anomalous imino form of adenine.

However, AT normal pairing, even if it led to biprotonic tautomerism for the pair, e.g., A′T′ (imino A, enol T), would quickly revert to the AT normal tautomer (amino-A, keto-T) pair, within the nanosecond time range of the excited state, and no stabilized intermediate would be found. In pursuing this research we have found a method of stabilizing the polarized intermediate of the 7AI excited base pair, which may offer a long-sought pathway for a stabilized ionic and/or protonated base intermediate to be viable in the DNA replication time (12). These results will be reported elsewhere.

Conclusion

With base-pair ESDPT as a possible step in DNA mutations, inadequate quantum theoretical methods have led to exaggerated activation barriers and spurious features in PE curves. The essentials for reliability in QM calculations for such complex systems are (i) an adequate basis set of atomic orbitals for polarization effects, including p-orbitals for H atoms, and d-orbitals for heavier atoms; (ii) adequate electron correlation account by DFT; and (iii) full geometry optimization by available pathways.

The PE barrier for biprotonic photo-tautomerism, at N-H- and N-D-substituted H-bonding sites of the model base pair 7AI, is shown to conform closely to experimental observations. In particular, for protonated 7AI dimer it is shown that ESDPT is barrierless, as the 4.5 kcal/mol ZPE for the critical N-H vibration is comparable to the calculated PT barrier (4.0–4.8 kcal/mol). In contrast, for the N-D dimer the ZPE of 3.9 kcal/mol leads to an activation energy that in low-temperature spectroscopy largely negates excited-state double-deuteron transfer.