Abstract
Recent studies have provided insights into the modular structure of genetic regulatory networks and emphasized the interest of quantitative functional descriptions. Here, to provide a priori knowledge of the structure of functional modules, we describe an evolutionary procedure in silico that creates small gene networks performing basic tasks. We used it to create networks functioning as bistable switches or oscillators. The obtained circuits provide a variety of functional designs, demonstrate the crucial role of posttranscriptional interactions, and highlight design principles also found in known biological networks. The procedure should prove helpful as a way to understand and create small functional modules with diverse functions as well as to analyze large networks.
Large gene networks are increasingly thought of as being built from smaller subnetworks (1–3) or “modules.” It is thus important to understand the structure and dynamics of small functional building blocks. Recently, this has been pursued in new ways by using both experimental (4–9) and computer approaches (10). For instance, statistical analyses have been used to determine recurring motifs of interactions (11) in transcriptional networks. However, both the direct problem of finding the function associated with a given motif of interactions and the inverse problem of finding gene networks performing given functions are not straightforwardly solved for several reasons. In most cases, the knowledge of only a partial subset of the existing interactions renders the determination of a module and its function difficult. Even when fully known, the geometry of the interactions between proteins and genes constrains but does not determine network behavior. Whether a network possesses a single functioning state, can be induced to switch between different states, or oscillates in time depends on the quantitative interactions between its components (12, 13) as, for instance, recently shown for the biologically important case of the NF-κB module (14).
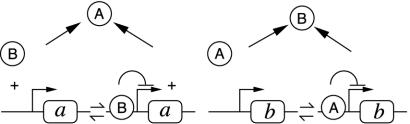
The inverse question can be illustrated by the design of a bistable switch, arguably one of the simplest functional elements. As classically conceived, this element is built out of reciprocal repression between two genes encoding transcription factors (15), as sketched in Fig. 1. In simple terms, when gene a is actively transcribed, the allied protein A is abundant and represses the transcription of gene b. B is thus expressed at a low level. A symmetric possibility is that gene b is active and B abundant, whereas a is repressed and A is present at a low concentration. A recently successful synthetic realization (5) demonstrates that indeed such a network of interactions can sustain two coexisting states. Mathematical analysis, however, shows that the laws of chemical interactions render it more complicated than naïvely thought (16): repression described by simple Michaelis–Menten kinetics is not sufficient to produce a working switch, and high-order Hill functions are required with, for instance, protein dimers or higher multimers interacting with DNA. When considering an existing gene network or the design of a new one, it would be useful to know whether a bistable switch can be made only out of two mutually repressing transcription factors or whether other interaction networks, less easily conceived, could serve the same purpose, perhaps even in a better and more robust way.
Fig. 1.
Sketch of a bistable switch with reciprocal transcriptional repression between genes a and b.
To provide theoretical insight into this question, we wondered whether it is feasible to determine a priori the possible designs of a small genetic network performing a given basic function. To sample the variety of working possible schemes, we have designed an evolutionary procedure in silico that we describe below. Computer-simulated evolution was previously used to optimize the kinetic parameters of a chemical circuit of fixed topology (17). The more general goal of the present procedure is to obtain a network of genes and proteins implementing a chosen function without imposing a priori any particular design. Here, we illustrate the general procedure by using it to create bistable switches and oscillating networks.
The Evolutionary Procedure in Silico
The algorithm proceeds in successive rounds of growth and selection of a collection of independent networks (typically ≈100 “cells”), a general strategy in evolutionary computation (18). Growth consists of the enlargement of the network collection by the addition of mutated copies of the existing networks. Selection takes place as follows: first, a score is attributed to each network in the enlarged collection depending on how well its dynamics approaches what is required. Second, a fraction of the networks is chosen based on the score attribution, and the remaining ones are deleted to reduce the collection to its original size before the next growing phase. This general algorithm requires a number of specific choices, and we precisely describe those that we have made.
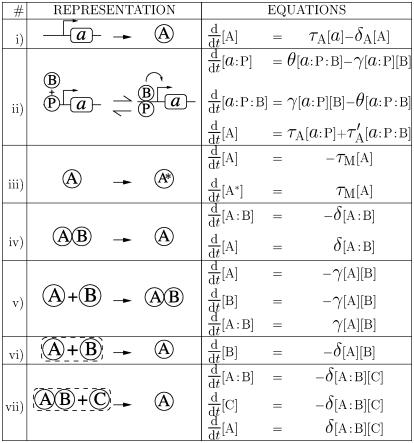
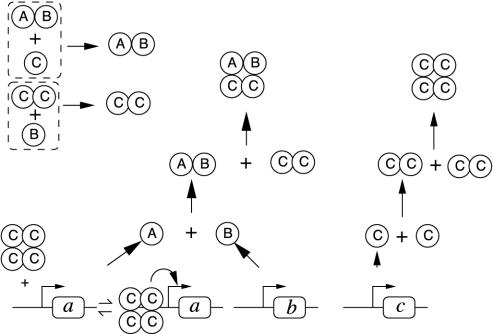
In our present implementation, a genetic network is defined by a number of genes and proteins† and chemical reactions described by deterministic rate equations. Possible chemical reactions are listed in Fig. 2 and consist of promotion or repression of gene transcription by proteins, along with posttranscriptional interactions. Posttranscriptional interactions have been included in two forms: two proteins can interact to produce another one (modeling formation of a complex catalytic degradation), or one protein can be modified (modeling phosphorylation or other posttranslational modifications).
Fig. 2.
List of possible reactions. The schematic representations are used to represent the reactions in Figs. 3, 4, 5. In the allied rate equations, Greek letters (τ, δ, γ, θ) denote kinetic constants; A:B denotes the bound complex of protein A and B; and a:P denotes gene a with protein P bound on its promoter. Reaction ii is illustrated here only for the case of an already existing bound complex between a protein P and the promoter of a gene a. The same reaction is also possible between a protein and a “naked” promoter (i.e., without P). Only the term corresponding to the displayed reaction has been written on the right side of the equations, giving the evolution of protein concentrations. In a given network of reactions, all such terms should be added to obtain the evolution of a particular species (e.g., the evolution of a protein A produced from gene a and only undergoing a posttranscriptional modification would be obtained by combining i and iii: d[A]/dt = τA[a] – δA[A] – τM[A]).
The algorithm starts with a collection of independent networks. These starting networks simply comprise two genes and their allied proteins, with randomly drawn production and degradation rates and no other reactions present. Then, alternate phases of growth and selection are performed to evolve the network collection and obtain networks achieving the specified function.
Growth Phase
The collection size is doubled by addition of a mutated copy of each network in the collection. The mutated copy differs by a fixed number of mutations from its parent network (two mutations gave satisfying results, and this is the choice made for the results presented below). The mutations are randomly drawn in succession from the five different following possibilities:
The degradation rate of a protein is modified.
-
A kinetic constant of one reaction is modified.
In these first two cases, the constant is chosen at random among the existing ones and is multiplied by a random number uniformly drawn between 0 and 2.
The three other possibilities of mutations involve adding a new reaction from among those listed in Fig. 2:
A new gene is created, and the reaction corresponding to the production and degradation of the allied protein (Fig. 2i) is added to the network.
A new interaction between a protein and a gene promoter is introduced (Fig. 2ii). We randomly choose a protein and a gene or an existing gene/protein complex (bound complexes of gene promoters with proteins may have been previously created) and create a new entity describing their bound complex. Three reactions are added to the network: the binding of the protein to the gene promoter (or to the existing complex), the reverse reaction, and the modified production rate of the protein allied to the gene in the new complex state.
-
Finally, a posttranscriptional reaction can be added. The choice of whether the reaction involves a single previously introduced protein or two proteins is made at random. In the single-protein case, a protein (or protein complex) is randomly drawn from among the existing ones. A new entity corresponding to a modified (e.g., phosphorylated) version of this protein is introduced (Fig. 2iii) together with the rate of the posttranscriptional modification and the degradation rate of the modified protein. When a protein complex is drawn, the reaction can alternatively be a partial degradation, with one protein of the complex chosen as the degradation product (Fig. 2iv). In the two-protein case, two proteins (or protein complexes) are drawn at random, and the reaction is chosen among possibilities v, vi, and vii of Fig. 2. It can be
- a dimerization (Fig. 2v). A new entity describing a bound complex of the two chosen proteins is introduced together with its rates of formation and degradation;
- catalytic degradation (Fig. 2vi) with the degraded species chosen between the two selected proteins with equal probability; or
- a partial catalytic degradation (Fig. 2vii) if one of the drawn entities is a protein complex. In this case, one of the proteins forming the complex is chosen as the reaction end product.
In cases iii–v, when a new reaction is added, its kinetic constants are randomly drawn. We assume the cellular volume to be unity so that concentrations and numbers of molecules are equivalent. The time unit is taken to be the minute. For simplicity, all kinetic constants are initially drawn randomly between 0 and 1 in these units, with uniform probability.‡ Kinetic constants obtained for the final selected circuits depend also on the imposed scoring function and are within the physiological range for the two cases investigated below. Further knowledge of physiological constraints in given cases could be incorporated by restricting the range of possible initial values and of mutation changes (cases i and ii).
The respective probabilities pa,..., pe of the five mutation possibilities are fixed in each set of simulations. Good results were obtained with comparable probabilities for the different possibilities.§
Selection Phase
Once the network collection has been enlarged by the addition of mutated copies of existing networks, each network is evaluated. This step consists of integrating the set of coupled differential equations corresponding to the network reactions [using a Runge–Kutta algorithm (20)]. This dynamical evolution serves to evaluate a scoring function and allows for the ranking of the networks. The choice of the scoring function depends on the function to be selected and is detailed below for the two cases investigated here. Based on the networks' ranking, the top-scoring half of the collection is kept and the other half deleted.¶ At the end of the selection phase, the network collection has regained its original size and is ready for the next round of growth and selection.
For the cases investigated below, this evolution procedure produces networks achieving the required function within <100 generations for switches and a few hundred generations for oscillators.
Results and Discussion
Bistable Switches. In this case, the in silico evolution was directed toward obtaining a network with two possible stable states differing in particular in the concentrations [A], [B] of proteins A and B. In the first stable state, the desired concentration [A]1 of protein A was high, and the concentration [B]1 of protein B was low, whereas in the second one, [A]2 was low and [B]2 high. Each network was started at time 0 with initial concentrations corresponding to one of the desired states, for instance with [A]1 and [B]1. The network dynamical evolution was then computed from time 0 to time T and the concentrations of proteins A and B monitored to assess how close they stayed to their desired values. A pulse of B was then added at time T to try to switch the network to the second desired state [A]2, [B]2. The network evolution was then followed from T to 2T and the concentrations of proteins A and B monitored again. A score was then assigned depending on how well the system under consideration had approached the two desired states in the two dynamical periods [that is, depending on the proximity to zero of the sum of the integral from time 0 to time T of ([A]–[A]1)2 +([B]–[B]1)2 in the first phase and of the integral from time T to 2T of ([A]–[A]2)2 +([B]–[B]2)2 in the second phase]. The time interval T was typically taken to be ≈100 min. The procedure was also run for different values of the imposed concentrations, with “high” concentrations ([A]1, [B]2) going from a few tens to several hundreds of molecules and “low” ([A]2, [B]1) concentrations from one to a few tens of molecules. The magnitude of the switching pulse of B was taken to be of the same order as the desired stable high concentration of B ([B]2) to avoid selecting networks with only a weakly stable first fixed point. Implementation of this procedure resulted in the creation of a variety of networks showing the required dynamical behavior. The networks were usually endowed with a multiplicity of accessory reactions that served to optimize the chosen scoring function but that also simply reflected evolutionary “trials” [this feature is related to the phenomenon of “code bloat” in evolving programs (18)]. To mitigate this phenomenon, a term depending on the number of reactions was added to the score function to penalize reaction multiplication and to direct evolution toward network simplification once a satisfying set of reactions had been found. The final networks were systematically pruned by deleting reactions from the most recently added to the oldest to leave a core set of reactions giving rise to the bistable behavior.
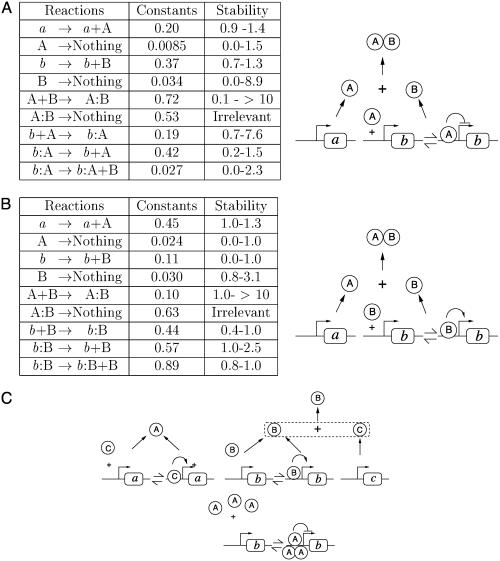
Three of these “core” networks are depicted in Fig. 3 together with the values of the kinetic constants. A sample of others is displayed in Figs. 6–12, which are published as supporting information on the PNAS web site. They show a number of noteworthy features. Most interesting, the obtained networks have various designs and are quite different from the “classical” one shown in Fig. 1. Fig. 3A displays a frequently found motif. Protein A represses gene b at the transcriptional level as in the classical case. However, protein B simply acts through complexation with A, the complex AB being unable to repress gene b. Thus if A is high, b is repressed, but if B is high, all of the As are titrated and complexed, and B remains high. In contrast to the case of Fig. 1, simple rate equations are now sufficient to make the design work. Fig. 3B provides an equally simple scheme but quite strikingly, without any transcriptional repression. Activation by B of its own gene naturally provides the high B state. In this state, complexation of A with B leads at the same time to a low level of free (uncomplexed) A. However, another state is also possible when the concentration of B is low, because it is transcribed at a low basal level without autoactivation, and an increase in B concentration is prevented by complexation with the abundant free A. Fig. 3C provides an example of a more complicated scheme with three genes that again crucially involves posttranscriptional interactions. Of note, our evolutionary algorithm produced several variations on the classical switch of Fig. 1 with reciprocal repression at the transcription level (Figs. 6 and 7) but less frequently than alternative designs. This probably results from the larger number of elementary reactions needed to really make the design work.
Fig. 3.
Three obtained bistable switches. Each diagram represents a network composed from individual reactions drawn from those listed in Fig. 2. In A and B, the values of the kinetic constants of all elementary reactions are provided together with the range of variation in which the network keeps its bistable character (a range of x–y means that the corresponding constant can be multiplied by any number between x and y, maintaining all others fixed). For instance, in A, the evolution of protein A concentration reads, d[A]/dt = 0.20–0.0085[A]–0.72 [A] [B]–0.19 [A]+0.42[b:A]. The different states of a gene (without or with proteins bound on its promoter) are assumed to sum to one (thus [b] + [b:A] = 1). The kinetic constants for the network shown in C are provided in Fig. 12.
Parameter values for the networks of Fig. 3 A and B are given in Fig. 3 (values for the network of Fig. 3C are given in Supporting Text, which is published as supporting information on the PNAS web site) for imposed high concentrations ([A]1, [B]2) of only a few tens of proteins. Parameter values are provided in Figs. 8 and 9 for the same networks with several hundred proteins in the high concentration species. This indicates that the networks are able to perform the required function for a wide range of parameters. We further checked that the bistable behavior of the obtained networks did not depend on the precise kinetic parameters produced by the algorithm. A quantitative and simple measure of network sensitivity to parameter variation is obtained by varying one parameter at a time, maintaining all of the others fixed; the results are shown in Fig. 3. Evolution using deterministic dynamics for network evolution as used here tends to give some kinetic constants close to one end of their permitted interval of variation (marginally satisfying the constraints), but the bistable behavior holds for a range of kinetic parameters. Admissible variations range from 30% to 50% for the few very sensitive parameters, to >10-fold.
The importance of noise in biological circuits has been emphasized (21) and has been the subject of several recent experimental studies (22–24). A detailed modeling of stochastic steps in transcription and translation is beyond the scope of the present investigation. Nonetheless, to further assess the robustness of the selected networks and to test their resistance to noise, we simulated the switch networks of Fig. 3 A and B with the stochastic dynamics corresponding to their rate equations, as detailed in Supporting Text. When the high-concentration species in the stable states have several hundred proteins, the finite particle number induces some fluctuations in the number of proteins but does not notably affect the networks' switch function (Fig. 13, which is published as supporting information on the PNAS web site). The networks still perform quite clearly as switches with only a few tens of particles in the high-concentration species despite much stronger fluctuations (Fig. 14, which is published as supporting information on the PNAS web site). So, the selected designs perform reassuringly well in the presence of noise. Under strong fluctuation conditions, the network of Fig. 3A switches spontaneously once every few hours between the two stable states (Fig. 14A). It can thus appear less robust to noise fluctuations than the design of Fig. 3B, which displays much rarer spontaneous switches (Fig. 14B). This is not an intrinsic weakness of the Fig. 3A scheme, however, because for other kinetic parameters, its stability is comparable to that of Fig. 3B (data not shown).
Oscillating Networks. To test the generality of the strategy beyond the creation of bistable switches, we set out to look for networks oscillating in time. The selection in this case was aimed at obtaining oscillations at the imposed period T in the concentration of protein A. This was simply achieved by choosing a priori two different arbitrary concentrations [A]1 and [A]2. The score of a particular network was then attributed based on how well it approached [A]1 at half-integer periods (T/2, 3T/2, 5T/2,...) and [A]2 at integer periods (T, 2T, 3T,...) over the course of 10 periods. This simple score assessment method was found to be more efficient at directing selection than alternative more sophisticated ways that were tried (based for instance on computing the amplitude of the desired Fourier mode of the time record of [A]).
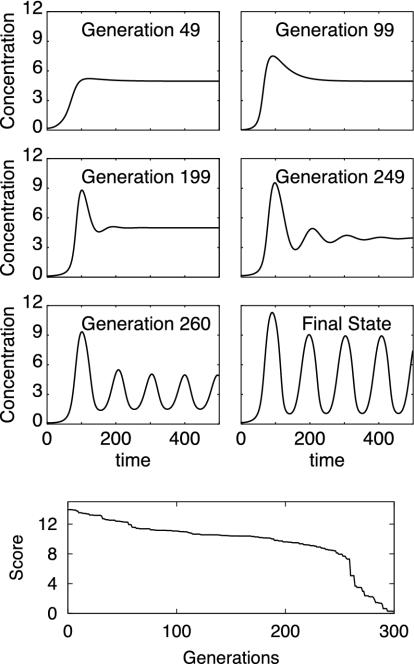
One evolution leading to the creation of an oscillatory network is shown in Fig. 4. The final network oscillatory dynamics and that of five of its ancestors are displayed, together with the score function evolution. Addition of interactions and modifications of kinetic constants led to the occurrence of oscillations and fast score improvement around generation 260. The “core” oscillating network is shown in Fig. 5 and is based on the interaction of three genes and allied proteins (the kinetic constants for this network are provided in Fig. 15, which is published as supporting information on the PNAS web site). Several other oscillating networks were obtained that crucially involved posttranscriptional interactions (see Fig. 16, which is published as supporting information on the PNAS web site), similarly to the previously described switch networks. Because our selection procedure was based on protein concentrations, oscillations at the transcription level were not required. Indeed, the procedure also created a network with constant transcription rates and biochemical oscillations occurring purely at the protein level (Fig. 17, which is published as supporting information on the PNAS web site).
Fig. 4.
Dynamics of six networks at different stages in the evolutionary process leading to the creation of an oscillatory network. The score evolution is shown (Bottom).
Fig. 5.
The “core” oscillating network extracted from the evolutionary process shown in Fig. 4. The kinetic constants for this network are provided in Fig. 15. In Fig. 4, the rapid score decrease and emergence of oscillations at generation 260 are associated with the creation of the complex ABCC.
Comparison with Known Biological Networks and Discussion. It is quite interesting to confront the created networks with some documented biological examples. The switch of Fig. 3A embodies a functioning principle that is, in a simplified way, quite analogous to that of the classic lac operon and was, in fact, also envisaged in ref. 15. The production of B by the gene b can be thought of as a shortcut version of the augmentation of allolactose (B) resulting from transcription of the lac operon (b) (via production of β-galactosidase and a membrane permease). Allolactose in turn binds to an operon repressor protein, a role played by A in Fig. 3A, and lifts the repression of the operon transcription, analogous to the effect of complexation of B and A.
The principle of Fig. 3B appears to be used in the switch underlying Xenopus oocyte maturation from a G2-arrested phase after exposure to progesterone. Conversion from the graded progesterone signal is thought to take place in the Mos/MEK1/p42 mitogen-activated protein (MAP) kinase (MAPK) cascade (25, 26). Mos can be thought of as playing the role of B in Fig. 3B, with positive feedback in the MAPK cascade arising via p42-induced Mos mRNA polyadenylation (27) and Mos stabilization (28), instead of the simple self promotion of b by protein B. The role of A appears to be played by the β-subunit of casein kinase II that binds to Mos and inhibits it (29).
The molecular switch controlling development of competence in B. subtilis under some starvation conditions seems to be even more directly related to the switch of Fig. 3B. Development of competence, that is, the ability to bind and internalize exogenous DNA, is under the control of a master competence gene comK that, like b in Fig. 3B, activates its own transcription. In noncompetent cells, MecA binds to ComK and inhibits its activity, an inhibition that is further induced by formation of a ternary complex with ClpC. Thus, MecA and CplC together play a role similar to that of A in Fig. 3B in the building of the competence switch (30).
The functioning principle of the oscillator of Fig. 5, where the complexation of the CC dimer with the heterodimer AB prevents activation of gene a by the C multimer, is quite reminiscent of that used by circadian oscillator gene networks. Using Drosophila network terminology as an example (31), this negative feedback loop acting on transcriptional activation via complexation can be compared to the transcriptional deactivation of period (per) and timeless (tim) genes after PER/TIM complexation with the Clock/Cycle (dCLK/CYC) transcriptional activating dimer. The circuit differs from that of any documented circadian network, but the analogy is close enough to suggest alternative models of circadian networks (P.F., unpublished data) which, contrary to some existing ones, do not make crucial use of high Hill coefficients (32) or delays coming from chains of phosphorylation (33).
The evolutionary algorithm described here is able to create a variety of small networks with prescribed behaviors that display both known and original designs. The selected networks make crucial use of posttranscriptional interactions and kinetics of interactions. Their functions could not be understood at all by focusing only on transcriptional interactions, a lesson of general value and a warning for future bioinformatics analyses.
Experimental procedures have recently been developed to reach goals related to that of the present work. In ref. 6, combinatorial synthesis was used to generate small networks of transcription encoding genes with various topologies. Subsequent screening allowed the extraction of networks performing a variety of simple tasks. As in the present study, no a priori design was imposed, and the same task was found to be realized by networks with different topologies. Ref. 7 used successive rounds of directed evolution to adjust kinetic rates in a rationally designed network and obtain a functional circuit. The evolved mutants present changes both in protein–DNA and protein–protein interactions. These studies appear quite complementary to the present one. On the one hand, the in silico route is certainly more flexible and less labor-intensive than the experimental ones. In the present investigation, we have, for instance, included without difficulty a much greater variety of interactions than in ref. 6 and evolutionary steps well beyond those accessible to ref. 7. In silico results are also easier to analyze than experimental ones, because a complete description of the created networks is available (in contrast, for instance, to some of those obtained in ref. 6). On the other hand, at present, computer descriptions of biological mechanisms are, by necessity, very simplified. In silico designs may not perform in vivo as anticipated. A combination of computer and experimental approaches may then be the most efficient, with for instance the approach of ref. 7 serving to tune kinetic rates of a network designed in silico. Another interesting next step would be to use the present procedure with appropriate constraints on the allowed mutations to select testable candidates for missing interactions in partially known existing networks.
The described algorithm is simple to implement and can be refined by including, for instance, more detailed protein–promoter interactions, regulation of mRNA stabilities and translation, noise in elementary chemical steps, and cellular compartments. It should therefore prove quite useful in designing gene networks and in helping to make sense of experimentally described interactions.
Supplementary Material
Acknowledgments
We thank F. Devaux for very useful discussions; F. Képes for kindly providing the database of ref. 3; and A. Moores, R. Reid, and S. Vaulont for useful comments on the manuscript. V.H. also thanks the Kavli Institute of Theoretical Physics for hospitality during the Bio-Molecular Networks Program and the National Science Foundation for supporting in part this research under Grant PHY99-07949.
This paper was submitted directly (Track II) to the PNAS office.
Footnotes
For simplicity, in the present first implementation, mRNAs are not explicitly described because regulation of translation or of mRNA stability is known to exist (19) but is less widely documented than transcriptional control.
This corresponds, for instance, to drawing initial protein degradation rates between 0 and 1 min–1 and initial forward rates of second-order reactions between 0 and ≈1nm/min for a typical bacterial volume.
Switches like those of Fig. 3 A and B were obtained for a large set of different mutation rates. However, to obtain in the same set of simulations switches as those of Fig. 3 and switches based on reciprocal inhibition (Figs. 6 and 7), the probability pe should be taken ≈20 times smaller than pd.
It might be thought that a milder selection procedure that would keep a proportion of bad-scoring circuits would be more efficient in some cases. This was tried by selecting the networks stochastically, based on the score attribution (high-scoring networks being retained with higher probability than low-scoring ones). For the particular examples studied here, this did not significantly change the convergence rate: the innovation rate is slow enough that significant improvements spread to all cells in a few generations.
References
- 1.Hartwell, L. H., Hopfield, J. J., Leibler, S. & Murray, A. W. (1999) Nature 402, C47–C51. [DOI] [PubMed] [Google Scholar]
- 2.Maslov, S. & Sneppen, K. (2002) Science 296, 910–913. [DOI] [PubMed] [Google Scholar]
- 3.Guelzim, N., Bottani, S., Bourgine, P. & Képes, F. (2002) Nat. Genet. 31, 60–63. [DOI] [PubMed] [Google Scholar]
- 4.Elowitz, M. B. & Leibler, S. (2002) Nature 403, 597–607. [DOI] [PubMed] [Google Scholar]
- 5.Gardner, T. S., Cantor, C. R. & Collins, J. J. (2000) Nature 403, 339–342. [DOI] [PubMed] [Google Scholar]
- 6.Guet, C. C., Elowitz, M. B., Hsing, W. & Leibler, S. (2002) Science 296, 1466–1470. [DOI] [PubMed] [Google Scholar]
- 7.Yokobayashi, Y., Weiss, R. & Arnold, F. H. (2002) Proc. Natl. Acad. Sci. USA 99, 16587–16591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Atkinson, M. R., Savageau, M. A., Myers, J. T. & Ninfa, A. J. (2003) Cell 113, 597–607. [DOI] [PubMed] [Google Scholar]
- 9.Isaacs, F. J., Hasty, J., Cantor, C. R. & Collins, J. J. (2003) Proc. Natl. Acad. Sci. USA 100, 7714–7719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kitano, H. (2002) Nature 420, 206–210. [DOI] [PubMed] [Google Scholar]
- 11.Shen-Orr, S. S., Milo, R., Mangan, S. & Alon, U. (2002) Nat. Genet. 31, 64–68. [DOI] [PubMed] [Google Scholar]
- 12.Smolen, P., Baxter, D. A. & Byrne, J. H. (2000) Bull. Math. Biol. 62, 247–292. [DOI] [PubMed] [Google Scholar]
- 13.Tyson, J. J., Chen, K. C. & Novak, B. (2003) Curr. Opin. Cell Biol. 15, 221–231. [DOI] [PubMed] [Google Scholar]
- 14.Hoffmann, A., Levchenko, A., Scott, M. L. & Baltimore, D. (2002) Science 298, 1241–1245. [DOI] [PubMed] [Google Scholar]
- 15.Monod, J. & Jacob, F. (1961) Cold Spring Harbor Symp. Quant. Biol. 26, 389–401. [DOI] [PubMed] [Google Scholar]
- 16.Cherry, J. L. & Adler, F. R. (2000) J. Theor. Biol. 203, 117–133. [DOI] [PubMed] [Google Scholar]
- 17.Bray, D. & Lay, S. (1994) Biophys. J. 66, 972–977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Foster, J. A. (2001) Nat. Rev. Genet. 2, 428–436. [DOI] [PubMed] [Google Scholar]
- 19.Kuersten, S. & Goodwin, E. B. (2003) Nat. Rev. Genet. 4, 626–637. [DOI] [PubMed] [Google Scholar]
- 20.Press, W. H., Flannery, B. R., Teukolsky, S. A. & Vetterling, W. T. (1986) Numerical Recipes (Cambridge Univ. Press, Cambridge, U.K.).
- 21.McAdams, H. H. & Arkin, A. (1997) Proc. Natl. Acad. Sci. USA 94, 814–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ozbudak, E. M., Thattai, M., Kurtser, I., Grossman, A. D. & van Oudenaarden, A. (2002) Nat. Genet. 422, 69–73. [DOI] [PubMed] [Google Scholar]
- 23.Elowitz, M. B., Levine, A. J., Siggia, E. D. & Swain, P. S. (2002) Science 297, 1183–1186. [DOI] [PubMed] [Google Scholar]
- 24.Blake, W. J., Kaern, M., Cantor, C. R. & Collins, J. J. (2003) Nature 422, 633–637. [DOI] [PubMed] [Google Scholar]
- 25.Ferrell, J. E., Jr., & Machleder, E. M. (1998) Science 280, 895–898. [DOI] [PubMed] [Google Scholar]
- 26.Ferrell, J. E., Jr. (1999) BioEssays 21, 866–870. [DOI] [PubMed] [Google Scholar]
- 27.Howard, E. L., Charlesworth, A., Weik, J. & MacNicol, A. M. (1999) Mol. Cell. Biol. 19, 1990–1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Matten, W. T., Copeland, T. D., Ahn, N. G. & Vande Woude, G. F. (1996) Dev. Biol. 179, 485–492. [DOI] [PubMed] [Google Scholar]
- 29.Chen, M. & Cooper, J. A. (1997) Proc. Natl. Acad. Sci. USA 94, 9136–9140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Turgay, K., Hamoen, L. W., Venema, G. & Dubnau, D. (1998) Genes Dev. 11, 119–128. [DOI] [PubMed] [Google Scholar]
- 31.Panda, S., Hogenesch, J. B. & Kay, S. A. (2002) Nature 417, 329–335. [DOI] [PubMed] [Google Scholar]
- 32.Ruoff, P., Vinsjevik, M., Monnerjahn, C. & Rensing, L. (2001) J. Theor. Biol. 209, 29–42. [DOI] [PubMed] [Google Scholar]
- 33.Leloup, J. C. & Goldbeter, A. (1998) J. Biol. Rhythms 13, 70–97. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.