Abstract
Detecting genetic variants that are highly divergent from a reference sequence remains a major challenge in genome sequencing. We introduce de novo assembly algorithms using colored de Bruijn graphs for detecting and genotyping simple and complex genetic variants in an individual or population. We provide an efficient software implementation, Cortex; the first de novo assembler capable of assembling multiple eukaryote genomes simultaneously. Four applications of Cortex are presented. First, we detect and validate both simple and complex structural variation in a high coverage human genome. Second, we identify over 3Mb of novel sequence in pooled low-coverage population sequence data from the 1000 Genomes Project. Third, we show how population information from 10 chimpanzees enables accurate variant calls without a reference sequence. Finally, we estimate classical HLA genotypes at HLA-B, the most variable gene in the human genome.
Introduction
Characterization of genetic variants present in an individual, population or ecological sample has been transformed by the development of high throughput sequencing (HTS) technologies. The standard approach to variant discovery and genotyping from HTS data is to map reads to a reference genome1-5, so identifying positions where the sample contains simple variant sequences. This approach has proved powerful in the study of single nucleotide polymorphisms6 (SNPs), short insertion-deletion (indel) polymorphisms3,5,7,8 and larger structural variation9-14 in well-characterised genomes, such as human15-17.
However, the mapping approach has limitations. First, the sample may contain sequence absent or divergent from the reference, for example through horizontal transfer events in microbial genomes18,19 or at highly diverse loci, such as the classical HLA genes20. In such cases, short reads either cannot or are unlikely to map correctly to the reference. Second, reference sequences, particularly of higher eukaryotes, are incomplete, notably in telomeric and pericentromeric regions. Reads from missing regions will often map, sometimes with apparently high certainty, to paralogous regions, potentially leading to false variant calls. Third, samples under study may either have no available reference sequence or it may not be possible to define a single suitable reference, as in ecological sequencing21. Fourth, methods for variant calling from mapped reads typically focus on a single variant type. However, where variants of different types cluster, focus on a single type can lead to errors, for example through incorrect alignment around indel polymorphisms6,7. Fifth, although there are methods for detecting large structural variants, using array CGH 22-25 and mapped reads11,12,14,26, these cannot determine the exact location, size or allelic sequence of variants. Finally, mapping approaches typically ignore prior information about genetic variation within the species.
Several of these limitations can potentially be solved through de novo assembly, which is agnostic with regards to variant type and divergence from any reference. However, while there are established algorithms for de novo assembly from HTS shotgun data, based on overlap27-29 or de Bruijn graphs30-32, current approaches have limitations. Notably, they focus on consensus assembly, treating the sequence as if derived from a monomorphic sample (e.g. haploid genome, inbred line or clonal population). Consequently, variation is ignored (processed in the same way as sequencing artefacts) and can lead to assembly errors. Some variation-aware de novo assembly algorithms have been developed31,33-36, but these do not represent a general solution to sequencing experiments where genetic variation is either the primary concern or unavoidable (outbred diploid samples, pooled data or ecological samples).
Current assembly methods also typically ignore pre-existing information, such as a reference sequence or known variants. Although variant discovery should not be biased by such information, nor should it be discarded. For example, in a single outbred diploid sample it is hard to distinguish paralogous from orthologous variation. However, if variation is also observed in the reference haploid genome it is most likely driven by paralogy. Finally, current implementations of de novo assembly algorithms for HTS data have very substantial computational requirements, which make them impractical for large-scale studies on eukaryote genomes.
Here, we introduce de novo assembly algorithms focused on detecting and characterising genetic variation in one or more individuals. These algorithms extend classical de Bruijn graphs37,38 by colouring the nodes and edges in the graph by the samples in which they are observed. This approach accommodates information from multiple samples, including one or more reference sequences and known variants. We show how the method can detect variation in species without a reference, combine information across multiple individuals to improve accuracy, and genotype known variants. Cortex has already contributed to public datasets as part of the 1000 Genomes Project17.
Colored de Bruijn graph algorithms for variant discovery and genotyping
De Bruijn graphs, which represent overlap information within a set of DNA sequences, are widely used in genome assembly and underlie many popular algorithms, including AllPaths-LG 31, SOAPdenovo 32, Abyss39 and Velvet 30,40. The graph consists of a set of nodes, representing words of length k (k-mers). Directed edges join k-mers seen consecutively in the input. Variation between genomes generates new nodes and edges. In the simplest case polymorphisms appear as bubbles within unique contigs. However, more complex structures also arise, for example where a variant generates a k-mer found in a paralogous location (Supplementary Figure 1).
A colored de Bruijn graph generalises the original formulation to multiple samples embedded in a union graph, where the identity of each sample is retained by colouring those nodes present in a sample. The samples may reflect HTS data from multiple samples, experiments, reference sequences, known variant sequences or any combination. Below we outline four algorithms for variant discovery and genotyping that make use of the colored de Bruijn graph structure (Methods Section 1-4).
Bubble-calling
The simplest use of colored de Bruijn graphs is to identify variant bubbles in a single diploid individual. This approach may have a high false positive rate because of the difficulty of separating repeat-induced and variant-induced bubbles. However, inclusion of a haploid reference genome improves the reliability of the algorithm because most repeat structures will be present in the reference and any bubble in the reference colour must be a repeat (Figure 1a). A reference genome also aids the detection of variants because only the variant allele contig need be assembled, and is essential for detecting homozygous variant sites. All types of variant can induce bubbles, hence the process of bubble detection is influenced by variant type only through the graph complexity of the variants and the probability of assembling both sides of the bubble given the sequence coverage, k-mer size and error rate (see Methods Section 1 for details of a model for predicting power). Haplotypes arising from variants within k bases of each other will naturally be assembled as single compound variants. Our implementation is referred to as the ‘bubble-calling’ (BC) algorithm (Methods Section 2).
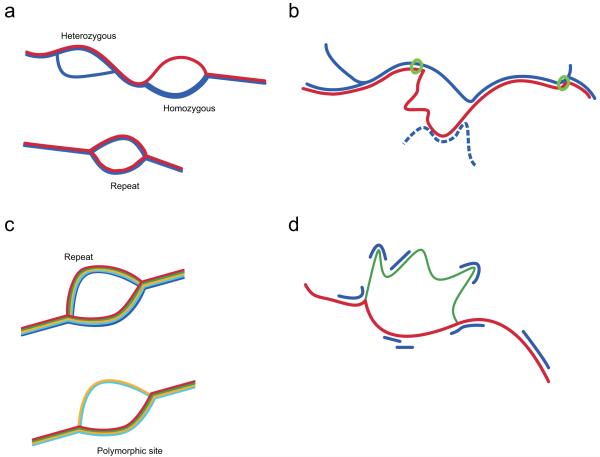
Figure 1.
Schematic representation of four methods of variation analysis using colored de Bruijn graphs; line width represents coverage. (a) Discovery of variants in a single outbred diploid individual (blue) with a reference sequence (red). True polymorphisms generate bubbles that diverge from the reference, while repeat structures lead to bubbles also observed in the reference. (b) Even when the reference allele (red) does not form a clean bubble, we can identify homozygous variant sites by tracking the divergence of the reference path from that of the sample. On finding a breakpoint, we take the longest contig in the sample (i.e. the path as far as the next junction) and ask whether the reference path returns before this point (green circle = anchoring sequence). The algorithm (path divergence) is not affected by repeat sequence within the reference allele present elsewhere in the genome of the sample (blue dotted). (c) When many samples (each in a different colour) are combined it is possible to distinguish repeat-induced bubbles (in which both sides of the bubble are present in all samples) from true variant sites (in which bubble coverage varies with genotypes and genotypes are in Hardy-Weinberg equilibrium). (d) The likelihood of any given genotype can be calculated from the coverage (blue) of each allele (green, red), accounting for contributions from other parts of the genome. In this example, the sample is heterozygous thus has coverage of both alleles, though not sufficient to enable full assembly.
Path divergence
The bubble-calling algorithm relies on the detection of clean bubbles. However, for complex variants (e.g. novel sequence insertions, large deletions and inversions), the path of at least one allele is unlikely to generate a clean contig. Nevertheless, in some cases, particularly deletions, path complexity is restricted to the reference allele. Such cases can be identified by following the (known) reference path through the joint graph and detecting where it diverges from the sample graph (Figure 1b; Methods Section 2 and Supplementary Figure 2). This ‘path-divergence’ (PD) algorithm typically only identifies homozygous variants and is biased towards identifying deletions. Nevertheless, the algorithm can substantially increase power to detect some variant types and potentially identifies events of arbitrary size, irrespective of read-length.
Multiple-sample analysis
The joint analysis of HTS data from multiple samples can improve the power and false discovery rate (FDR) of variant detection substantially. In the simplest case, samples are combined in a single colour (for example, in a pooling experiment) and the data can be analysed as above. However, by maintaining separate colours for each sample there is additional information about whether a bubble is likely to be induced by repeats (where many or all samples show coverage of both paths in the bubble; Figure 1c) or errors (where the error-carrying side of bubble will typically have low coverage). This observation leads to an approach to variant discovery even in species where there is no suitable reference. We have devised statistical methods that enable probabilistic classification of bubble structures into those arising from errors, repeat structures or variants (Methods Section 3). When a reference genome is available, this approach can still help distinguish true variants from errors and repeat structures absent from the reference.
Genotyping
Colored de Bruijn graphs can be used to genotype samples at known loci even when coverage is insufficient to enable variant assembly (Figure 1d). We construct a colored de Bruijn graph of the reference sequence, known allelic variants (which may include those discovered using the above methods) and data from the sample. The likelihood of each possible genotype is calculated accounting for the graph structure of both local and genome-wide sequence (Methods Section 4). The approach generalises to multiple allelic types and, because the algorithm does not require variants to form simple bubble structures, it is possible to genotype complex and compound variants such as those at classical HLA loci.
Graph building and cleaning
We have developed Cortex, a memory-efficient assembler for building and representing colored de Bruijn graphs and to perform variant calling and genotyping from HTS data (cortexassembler.sourceforge.net; Methods Section 5). The implementation uses an efficient hash table that implicitly encodes the graph; memory use is specified in advance according to a simple formula, and many standard operations have linear or better algorithmic complexity (Methods Sections 2, 5). Novel cleaning methods are used to increase sensitivity (Methods Section 6 and Supplementary Figure 3). Cortex is the only assembler able to handle multiple eukaryotes simultaneously, for example 1000 S. cerevisiae samples in under 64Gb of RAM, or 10 humans in under 256Gb of RAM.
Assessing the power and false discovery rate of Cortex through simulation
A single high coverage diploid genome
We simulated high coverage (10-50x) sequencing data from a diploid human sample that carries SNPs, indels and structural variants (Methods Section 7). Data was analysed by both the BC and PD methods.
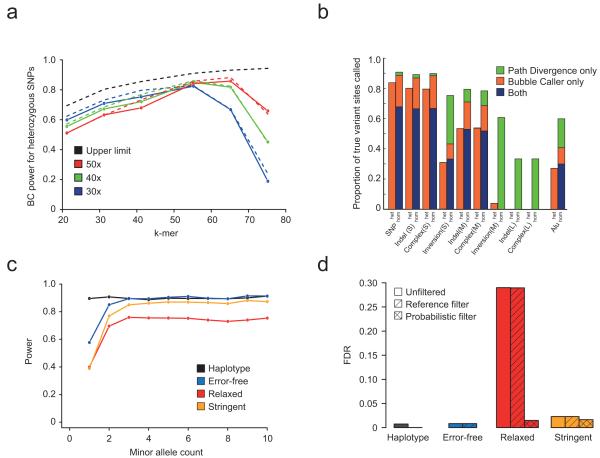
For a variant to be identified successfully, the bubble must both be assembled without gaps and be identifiable within the wider graph. Genome complexity, sequencing depth, read-length, k-mer size and error rate interact to influence both factors. As k-mer size increases, the fraction of SNP sites with unconfounded bubbles ranges from 51% with k=21 to 85% with k=75 in humans (Supplementary Figure 4). Increasing k-mer size reduces the risk of error-induced contigs confounding the graph, but also increases the probability of a k-mer containing an error. Furthermore, for a fixed per-base depth and read-length, as k-mer-size increases, the effective depth of each k-mer decreases leading to an increased probability of gaps in the assembly (Figure 2a, and Methods Section 1). Consequently, the k-mer size that maximises the sensitivity of the BC algorithm within the simulation varies with coverage and read-length; approximately 55 for 30x, 55 for 40x and 65 for 50x with 100bp reads. The loss in power relative to the theoretical maximum is, however, small. For example, with 50x coverage (k=65, 100bp reads) we identify 86% of heterozygous SNPs compared to the maximum possible of 92%. Simulation-based estimates of power closely track predictions (Figure 2a, Supplementary Figures 5, 6).
Figure 2.
Simulation-based evaluation of Cortex. (a) Power of the Bubble-calling (BC) algorithm to detect heterozygous SNPs in a single individual, as a function of k-mer size. Genome repeat content dictates an upper limit to power (black dashed line), while finite sequence coverage reduces power for large k-mer size (solid lines, circles) in a predictable manner (dashed lines). Increased coverage reduces power at lower k-mer sizes due to recurrent errors that evade error-cleaning. At high k (e.g. k=55, 50x) power is close to the upper limit. (b) Power to detect different variant types in homozygous and heterozygous states using the BC and Path divergence (PD) algorithms with 30x coverage (100bp reads, k=55). For simple variant types power is 80-85%. For medium-sized variants power remains high at homozygous sites, but is ≤50% at heterozygous sites. For large events, there is only power for homozygous sites and this only through PD. (c) Power to detect SNP variants using BC in population data (10 individuals, 10x coverage, 100bp reads, k=55). Fluctuations in coverage reduce power for low frequency variants. More stringent cleaning increases power because bubbles are less confounded by errors. (d) FDR for call sets in panel (c) before and after classifying bubbles as error-, repeat- or variant-induced. The probabilistic filter reduces FDR under relaxed cleaning from 29% to 1.5% with 1.7% loss in power and from 2.3% to 1.6% with 1% loss in power for the stringent cleaning.
To assess the power of Cortex to detect a range of variants of different types and sizes we applied the BC and PD algorithms at a single point (30x, read length 100, k=55; see Methods Section 7). For isolated SNPs, short indels (1-100bp) and small complex combinations of SNPs and indels (1-100bp) we have 80% power to detect heterozygous sites and 90% power to detect homozygous variant sites (Figure 2b). For moderate size (100-1000bp) indels and complex variants, power is 50% and 75-80% for heterozygous and homozygous sites respectively. For large variants (1-50kb) we only have power to detect homozygous variant sites (c. 35%), entirely through PD. These sensitivity estimates are attained with an FDR of 2%.
Population-based variant calling and bubble classification
We simulated sequence data from ten diploid individuals based on human chromosome 22 (100bp reads, 10x per individual; Methods Section 8). Data were analysed at the level of individual haplotypes, error-free reads and error-containing reads (k=55) under two cleaning thresholds (relaxed and stringent). Two filtering approaches were compared. First, we remove bubbles that are present in the reference. Second, we use a probabilistic model to classify bubbles as arising through errors, repeats or true variants (Methods Section 3).
At k=55, 10% of SNPs fail to make clean bubble structures (Supplementary Figure 4), however, coverage is sufficient that only for rare variants (count < 3) is there substantial loss of power (Figure 2c). With realistic levels of sequence error, power drops by an additional 10% under the relaxed cleaning threshold, but recovers under the more stringent cleaning threshold because confounding error contigs are removed. FDR with relaxed cleaning is 29%, but probabilistic classification reduces this to 1.5% with only a 1.7% loss in power (Figure 2d). The more stringent cleaning approach has an FDR of 2.3% before classification and 1.6% after, with a 1.0% loss in power. In contrast, removal of bubbles present in the reference has only a marginal effect on FDR (29.0% and 2.3% for the two cleaning thresholds respectively), as the majority of false calls are read-error driven.
Case 1: Variant calling in a high coverage human genome
We analysed high coverage data (26x with 100bp reads analysed at k=55; Methods Section 9) from a single individual of European ancestry (NA12878 from the CEU) for whom independent validation data are available through 3 Mb of fosmid sequence (median length 40kb), selected to contain structural variation41. This sample has been analysed using mapping-based strategies in the 1000 Genomes Project17 (63x of mostly 36bp paired-end reads), thus enabling comparison of Cortex with alternative strategies. The fosmid data enables us to estimate an upper-bound for FDR for variants of different types from the fraction of sites called as homozygous variant where the fosmid sequence contains only the reference allele. A detailed discussion of the validation results can be found in the Supplementary Methods.
After cleaning, the de Bruijn graph for NA12878 has 2,777,352,792 nodes (unique k-mers) compared to 2,691,115,653 in the reference sequence (cleaning reduces the initial number of nodes by 23%). The bubble-calling (BC) algorithm identifies 2,686,963 bubbles, of which 5.6% are removed because both sides of the bubble are also present in the reference. The path-divergence (PD) algorithm identifies 528,651 deviations from the reference, of which 39.8% were not identified by BC. The union of the BC and PD call-sets includes 2,245,279 SNPs, 361,531 short indels (insertion to deletion ratio in the 5-30bp range of 1:1.3 for BC and 1:1.7 for PD, compared with 1:3.7 for the 1000 Genomes calls) and 1,100 larger or more complex variants.
The Cortex and 1000 Genomes call sets have different properties arising from differences in experimental design and analysis approach. Only 80% of the genome is accessible to the 1000 Genomes SNP calls17, but power within these regions is high. In contrast, at k=55, over 85% of the genome is accessible to Cortex, but power is reduced (by approximately 40% at heterozygous, and <5% at homozygous, sites) due to fluctuations in coverage. Thus while the call set sizes for homozygous SNPs and short indels within the fosmid footprint are similar, Cortex calls only half the number of heterozygous sites (Table 1). Across the genome, Cortex detects variation at 87% of sites called as homozygous alternative by the 1000 Genomes Project and 67% of sites called as heterozygous (comparison to HapMap 2 sites gives equivalent figures, Supplementary Table 7).
Table 1. Comparison of 1000 Genomes and Cortex calls to fosmid data.
| Variant type | 1000 Genomes a |
Cortex | Bubble Caller | Path Divergence | |||
|---|---|---|---|---|---|---|---|
| All |
High confidenceb |
All |
High confidence |
All |
High confidence |
||
| SNP (Hom) | 1085 (0) | 1071 (4.0) | 605 (0.5) | 1057 (3.9) | 591 (0.5) | 340(8.5) | 144 (1.4) |
| SNP (Het) | 2350 (28) | 1155 (32) | 1029 (32) | 1155 (32) | 1029 (32) | 0 (−) | 0 (−) |
| Indel (Hom) | 64 (0) | 96 (6.3) | 20 (0) | 79 (6.3) | 16 (0) | 37 (5.4) | 5 (0) |
| Indel (Het) | 127 (29) | 67 (40) | 43 (30) | 67 (40) | 43 (30) | 0 (−) | 0 (−) |
| Complex (Hom) |
- | 258 (1.9) | 202 (1.5) | 112 (2.7) | 77 (1.3) | 174 (1.7) | 139 (2.2) |
| Complex (Het) | - | 161 (26) | 137 (25) | 161 (26) | 137 (25) | 0 (−) | 0 (−) |
Values reported are the number of each variant/genotype combination called and in parentheses the percentage of cases where only the reference allele was observed in the fosmid sequence data.
High confidence call set requires log10(Bayes factor) for the reported genotype to be at least 4.
SNP variants identified by Cortex have diagnostic properties such as transition-transversion ratio (Cortex = 2.02 (BC) / 2.1 (PD), 1000 Genomes = 2.07) and dbSNP rate (Cortex = 92.7% (BC) / 95.6% (PD), 1000 Genomes = 92.1%, dbSNP 129) that are comparable to the 1000 Genomes calls17.
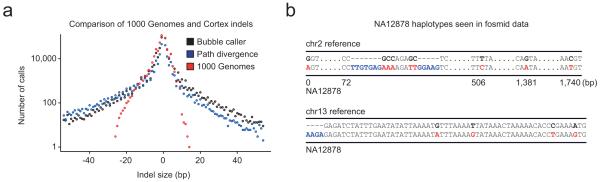
Overall FDR for Cortex SNP calls is 4%, reduced to 1.5% by applying a homopolymer filter and selecting high confidence calls (25% reduction in call set; Table 1 and Methods Section 9). None of the 1000 Genomes homozygous SNP calls invalidates (Table 1). Of the 43 invalidated homozygous SNP calls from Cortex, 35 were called as heterozygous sites by the 1000 Genomes Project, hence the FDR for Cortex is probably <1%. Short indels (1-100 bp) have similar FDR (0% for high confidence set), but whereas the 1000 Genomes calls are restricted to variants under 30bp in length, both the BC and PD approaches identify indels over 100bp (Figure 3a).
Figure 3.
Structural and complex variants identified in a single high coverage genome. (a) Size distribution of short indels discovered in NA12878 from 26x coverage of 100bp reads analysed using the BC (black) and PD (blue) algorithms. Also shown is the number of indels of different sizes called by mapping-based approaches from 63x coverage on the same sample within the 1000 Genomes Project17 (red). While the 1000 Genomes Project calls more small variants, only the two Cortex algorithms can detect longer variants, which are typically too short to be detected by larger structural variation discovery methods. The PD caller exhibits bias towards calling deletions for larger variant sizes. (b) Two examples of complex variants identified in NA12878 using Cortex and validated in the independent fosmid data. In the top example, the PD algorithm assembles a haplotype over 1.7kb containing a number of phased SNPs (red) and a complex insertion/deletion event (inserted material is blue). In the bottom example, the BC algorithm assembles two haplotypes containing four phased SNPs and an insertion.
Across the genome, Cortex identifies 138,262 complex variants, consisting of phased SNPs (74%), closely-sited SNPs and indels (25%) and complexes of insertions, deletions and local rearrangements (1%). FDR for complex variants is low (2.7% for BC and 1.7% for PD; Supplementary Table 1). While mapping-based approaches can call closely-sited variants of different types, these are often filtered out. However, our results indicate that Cortex can identify complex variants with FDR comparable to simple variants. Figure 3b shows examples of complex variants validated in the fosmid data.
Case 2. Detection of novel sequence from population graphs of low-coverage samples
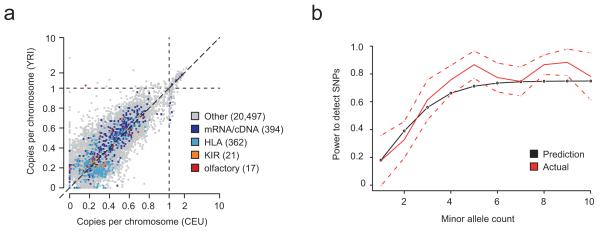
We constructed three pooled population graphs for 164 humans (CEU, YRI and CHB/JPT) sequenced at low coverage (2-4x) in the 1000 Genomes Project17 (Methods). By including the reference sequence as a fourth colour, we identified 21,281 novel contigs of ≥100bp (<90% homology to any reference sequence), totalling 3.2Mb. The novel unique sequence load carried by a typical individual is 1.4Mb for CEU, 1.5Mb for YRI and 1.5Mb for CHB/JPT respectively. Of this, 93% is estimated to be allelic, and copy-number estimates for other sequences range up to 6.3 (Figure 4a). On average, 45kb per individual is homologous to a known gene and we see strong over-representation for matches to variants at classical HLA and KIR loci, both known to be highly variable in sequence, structure and copy-number. Some sequences show very strong differentiation between populations. For example, we find three contigs in YRI, homologous to olfactory receptor genes, that are absent from other populations (Figure 4a).
Figure 4.
Population analysis with Cortex. (a) Estimates of mean copy number per genome in CEU and YRI for novel sequence contigs identified from analysis of pooled population graphs for 164 humans sequenced to low depth (2-4x) with the 1000 Genomes Project. Contigs are all at least 100bp long and have <90% homology to the reference genome (determined by BLAST). Allelic variation lies in the interval (0,1), while copy-number variable sequence can be present up to 6.3 times. Variants are annotated by whether they show significant homology to known transcripts, including HLA, KIR and olfactory receptor (OR) genes as specific categories, which are clearly enriched. We note the presence of several OR matches that are approximately 20% frequency in YRI but apparently absent from CEU. (b) Power to detect SNP variants previously analysed through SNP genotyping in HTS data from 10 chimpanzees (6x coverage, 50bp reads analysed at k=31). Empirical estimates (red, with normal approximation to binomial confidence intervals shown dotted) closely track predictions (black) from the theoretical model.
There are practical implications of these results. First, the novel sequences, particularly those matching genes or strongly differentiated between populations are candidates for functionally-relevant polymorphism. Second, the combined population graphs provide a summary of human genome diversity against which it is possible to map sequence data from future studies. We have released the novel sequence contigs, population estimates of the per-genome copy number, the combined population graph and tools for aligning reads to the graph (Methods Sections 10, 14).
Case 3: Using population information to classify bubble structures
We applied Cortex to data from 10 Western Chimpanzees (50 bp reads, average coverage 6x; Methods Section 11). Bubbles were identified after using the relaxed cleaning threshold and classified probabilistically. Power was estimated by comparison to previous SNP genotype data on the same samples42.
Across the genome we identify 3.5 million variants, of which 2.7 million are single nucleotide variants. The probabilistic filter classified 153,921 of these as repeats, of which 69% were bubbles in the reference. For bubbles classified as SNPs we estimate FDR from the fraction of sites that are also bubbles in the reference, here 3.5% (compared to 6.5% before classification). This estimate is substantially greater than that predicted from simulations. However, manual inspection revealed that many of these sites are segregating in the sample and therefore are either polymorphic segmental duplications (not currently considered in the classification process) or allelic variants mis-assembled as paralogous in the reference. Power compared to the SNP genotype data is 55% before classification and 54% after. Thus probabilistic classification results in a data set with low FDR at a small cost to power and can be applied to any species, regardless of reference availability. The relationship between allele count and detection rate closely follows the theoretical predictions (Figure 4b).
Case 4: Genotyping simple and complex variants
We applied the genotyping algorithm to both simple variants, here HapMap2 SNPs43, and complex variants, specifically HLA-B genotype, using the sequencing data from NA12878 described above and high coverage sequence data from an individual of African origin (NA19240). Both individuals have classical HLA alleles typed from a previous project44. At HapMap2 sites, we find discordance of less than 1% at high confidence sites (Methods Sections 9.4 and 12, Supplementary Tables 4, 5). Discrepancies are driven by sites called as homozygous variant by the BC algorithm and heterozygous by HapMap2; a result of stochastic loss of coverage of k-mers spanning the reference allele.
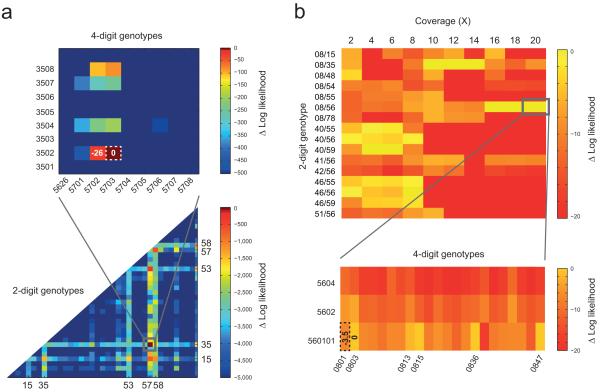
Classical HLA allele genotyping, of importance in many areas of medical genetics, is laborious and expensive. Although DNA-sequencing represents the gold-standard quality, most genotyping is performed through a mix of PCR amplification and oligo hybridisation. HTS genome-wide data has the potential to provide classical HLA sequence information, but sequence diversity, structural variation and extensive paralogy within the region currently restricts mapping-based approaches. To evaluate the performance of Cortex for genotyping HLA-B we constructed a graph containing the reference genome, all 1429 known HLA-B alleles and data from each high coverage sample as separate colours (Methods Section 12). We calculated the likelihood of all 1,021,735 possible genotypes. For NA19240, the most likely genotype (B*57:03:01, B*35:01:01) agrees at 4-digit resolution with previous data obtained using classical typing methods44 and is very strongly supported (likelihood ratio ~1023; Figure 5a). For NA12878 the most likely genotype contains B*56:01 and cannot distinguish between B*08:03, B*08:15, B*08:36, B*08:47 and B*08:13 for the second allele (Figure 5b). The lab-based genotype is B*56:01/B*08:01 which differs from the maximum likelihood estimate by 3.2 units of log-likelihood and agrees at the 2-digit level with the graph-based estimate. We note that lab-typing was based on primer amplication and oligo hybridisation, which can often lead to minor ambiguities at the 4-digit level. By sub-sampling NA12878 to generate graphs at between 2x and 20x we find that 16x coverage was required to attain 2-digit agreement with lab-based typing (Figure 5b).
Figure 5.
HLA-B genotyping from HTS data using Cortex. (a) Heat-plot showing the likelihood surface for HLA-B genotypes for NA19240 (the child of the Yoruban trio from the 1000 Genomes Project17). The lower part shows the likelihood surface at 2-digit resolution (represented by the most likely genotype among all compatible alleles) and the top shows a blow-up for the most-likely 2-digit genotype (B*57/B*35). The maximum likelihood genotype is B*57:03:01/B*35:01:01 which agrees with the 4-digit resolution data generated previously using standard experimental methods44 (MLE shown by dotted line; difference in log-likelihood from MLE shown for selected genotypes). Other alleles identified as possible at the 2-digit level (HLA-B*15, B*53 and B*58) are closely related to those present in the sample. B*53 is known to be a product of gene conversion from B*3552, and B*58 is a split antigen from B*15 with sister serotype B*57. (b) Heat plot showing the likelihood surface at 2-digit resolution for selected HLA-B genotypes for NA12878 (top) as a function of sequence depth. The blow-up shows 4-digit level resolution at 20x. At low coverage there is no consistent most likely genotype; from 10-14x the most likely is B*08/B*35, which switches to B*56:01/B*08:xx (where xx = 03, 13, 15, 36 and 47; all have log likelihood within 0.03 units) at 16x. Lab-based typing gives B*56:01/B*08:01, which is 3.2 units in log-likelihood less than the MLE.
Discussion
We have introduced a new approach to combining de novo assembly with variant detection and genotyping from HTS data. We use colored de Bruijn graphs to represent information from multiple sources and a mixture of graph-analytic and statistical approaches to detect variants of different types and subsequently genotype. Our method is the first de novo assembly-based variant caller, although previous work has made steps towards reference-free variant calling45,46. Technically, the key advance is the development of a highly efficient de Bruijn graph implementation. This efficiency enables data from multiple samples, as well as reference sequences and known variants to be included within a single graph structure that preserves sample identity through the use of colours. For single high coverage genomes the algorithms provide power to detect and genotype simple and complex variants. However, the major strength of the approach lies in the simultaneous analysis of multiple genomes, which enables powerful and accurate approaches to variant detection without any need of a reference genome. This makes possible HTS analysis of genetic variation in any species. It could also provide an approach for detecting changes between highly related genomes, as in tumour-normal pairs in cancer genomics47 or bacteria in within transmission chains48.
We have also developed a simple mathematical model to describe de Bruijn graph assembly from HTS data, which has two practical benefits. First, the model has predictive power both in simulated and empirical data, hence can guide experimental design. Second, the model can be used to calculate the likelihood of any particular genome sequence given HTS data and an estimate of error rates; one application of which is genotyping complex variants, such as the classical HLA loci.
Finally, the Cortex algorithms have several limitations. Most notably, we do not use read-pair information to improve local assembly, which can be of substantial value around repeat sequence. However, there are established algorithms for using read-pair information to disambiguate de Bruijn graphs30,31,39,40,49,50. There is also the potential for error correction51, which can compensate for the loss of coverage caused by errors. There are, however, more fundamental challenges in using de Bruijn graphs, including the greater need for error-correction as the k-mer size increases, the lack of any natural way of encoding read-pair information and the potential for graph explosion as more individuals are included in the graph. Nevertheless, multi-colored graphs provide one solution to the obvious inadequacy of representing the genetic composition of a species by a single haploid reference.
Supplementary Material
Acknowledgements
We would like to thank the members of the 1000 Genomes Project Consortium for discussion, suggestions and sequencing data. We thank Bartu Ahiska, Adam Auton, Ewan Birney, Richard Durbin, Gerton Lunter, Jon Woolf, Daniel Zerbino for discussion, two anonymous reviewers for their comments, and members of the PanMap Project and the Genomics Core at the Wellcome Trust Centre for Human Genetics for access to sequence data. ZI is funded by a grant from the Wellcome Trust (WT086084/Z/08/Z) to GM. The sequencing of NA12878 was done by the Wellcome Trust Sequencing Core at Oxford, under a grant from the Wellcome Trust (090532/Z/09/Z).
Appendix
Methods
Full details of the methods used in this paper can be found in the Supplementary Methods. These include definitions of terminology, followed by the sections: (1) Mathematical model for power to detect variants. (2)Variant calling algorithms (Bubble Caller and Path Divergence Caller). (3) Probabilistic Classification of graph structures as repeat-, error- or variant-induced. (4) Genotyping of simple and complex variants in a de Bruijn graph. (5) Description of Cortex software implementation. (6) Error-cleaning algorithms for high coverage samples and low coverage populations. (7) Single genome simulations. (8) Population simulations. (9) Case 1 - Analysis of high coverage human sample NA12878. (10) Case 2 – Pooled assembly of 164 samples from 1000 Genomes Pilot. (11) Case 3 – using probabilistic classification of bubbles on 10 chimpanzees. (12) Case 4 – Genotyping of simple and complex variants. (13) Making appropriate choice of parameters for experimental design. (14) Release of source code and 1000 Genomes population graph. Cortex is available from http://cortexassembler.sourceforge.net/.
References
- 1.Langmead B, Trapnell C, Pop M, Salzberg SL. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol. 2009;10:R25. doi: 10.1186/gb-2009-10-3-r25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Li H, Durbin R. Fast and accurate long-read alignment with Burrows-Wheeler transform. Bioinformatics. 2010;26:589–95. doi: 10.1093/bioinformatics/btp698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Li H, Ruan J, Durbin R. Mapping short DNA sequencing reads and calling variants using mapping quality scores. Genome Res. 2008;18:1851–8. doi: 10.1101/gr.078212.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li R, Li Y, Kristiansen K, Wang J. SOAP: short oligonucleotide alignment program. Bioinformatics. 2008;24:713–4. doi: 10.1093/bioinformatics/btn025. [DOI] [PubMed] [Google Scholar]
- 5.Lunter G, Goodson M. Stampy: A statistical algorithm for sensitive and fast mapping of Illumina sequence reads. Genome Res. 2010 doi: 10.1101/gr.111120.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.McKenna A, et al. The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res. 2010;20:1297–303. doi: 10.1101/gr.107524.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Albers CA, et al. Dindel: Accurate indel calls from short-read data. Genome Res. 2010 doi: 10.1101/gr.112326.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lee S, Hormozdiari F, Alkan C, Brudno M. MoDIL: detecting small indels from clone-end sequencing with mixtures of distributions. Nat Methods. 2009;6:473–4. doi: 10.1038/nmeth.f.256. [DOI] [PubMed] [Google Scholar]
- 9.Hajirasouliha I, et al. Detection and characterization of novel sequence insertions using paired-end next-generation sequencing. Bioinformatics. 2010;26:1277–83. doi: 10.1093/bioinformatics/btq152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Handsaker RE, Korn JM, Nemesh J, McCarroll SA. Discovery and genotyping of genome structural polymorphism by sequencing on a population scale. Nat Genet. 2011;43:269–76. doi: 10.1038/ng.768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Korbel JO, et al. PEMer: a computational framework with simulation-based error models for inferring genomic structural variants from massive paired-end sequencing data. Genome Biol. 2009;10:R23. doi: 10.1186/gb-2009-10-2-r23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Korbel JO, et al. Paired-end mapping reveals extensive structural variation in the human genome. Science. 2007;318:420–6. doi: 10.1126/science.1149504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mills RE, et al. Mapping copy number variation by population-scale genome sequencing. Nature. 2011;470:59–65. doi: 10.1038/nature09708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tuzun E, et al. Fine-scale structural variation of the human genome. Nat Genet. 2005;37:727–32. doi: 10.1038/ng1562. [DOI] [PubMed] [Google Scholar]
- 15.Bentley DR, et al. Accurate whole human genome sequencing using reversible terminator chemistry. Nature. 2008;456:53–9. doi: 10.1038/nature07517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang J, et al. The diploid genome sequence of an Asian individual. Nature. 2008;456:60–5. doi: 10.1038/nature07484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.The 1000 Genomes Project Consortium A map of human genome variation from population-scale sequencing. Nature. 2010;467:1061–73. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ge F, Wang LS, Kim J. The cobweb of life revealed by genome-scale estimates of horizontal gene transfer. PLoS Biol. 2005;3:e316. doi: 10.1371/journal.pbio.0030316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Beiko RG, Harlow TJ, Ragan MA. Highways of gene sharing in prokaryotes. Proc Natl Acad Sci U S A. 2005;102:14332–7. doi: 10.1073/pnas.0504068102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Holcomb CL, et al. A multi-site study using high-resolution HLA genotyping by next generation sequencing. Tissue Antigens. 2011;77:206–217. doi: 10.1111/j.1399-0039.2010.01606.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fonseca VG, et al. Second-generation environmental sequencing unmasks marine metazoan biodiversity. Nat Commun. 2010;1:98. doi: 10.1038/ncomms1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Iafrate AJ, et al. Detection of large-scale variation in the human genome. Nat Genet. 2004;36:949–51. doi: 10.1038/ng1416. [DOI] [PubMed] [Google Scholar]
- 23.Redon R, et al. Global variation in copy number in the human genome. Nature. 2006;444:444–54. doi: 10.1038/nature05329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sebat J, et al. Large-scale copy number polymorphism in the human genome. Science. 2004;305:525–8. doi: 10.1126/science.1098918. [DOI] [PubMed] [Google Scholar]
- 25.Sharp AJ, et al. Segmental duplications and copy-number variation in the human genome. Am J Hum Genet. 2005;77:78–88. doi: 10.1086/431652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kidd JM, et al. Mapping and sequencing of structural variation from eight human genomes. Nature. 2008;453:56–64. doi: 10.1038/nature06862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Myers EW. Toward simplifying and accurately formulating fragment assembly. J Comput Biol. 1995;2:275–90. doi: 10.1089/cmb.1995.2.275. [DOI] [PubMed] [Google Scholar]
- 28.Myers EW. The fragment assembly string graph. Bioinformatics. 2005;21(Suppl 2):ii79–85. doi: 10.1093/bioinformatics/bti1114. [DOI] [PubMed] [Google Scholar]
- 29.Simpson JT, Durbin R. Efficient construction of an assembly string graph using the FM-index. Bioinformatics. 2010;26:i367–73. doi: 10.1093/bioinformatics/btq217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zerbino DR, Birney E. Velvet: algorithms for de novo short read assembly using de Bruijn graphs. Genome Res. 2008;18:821–9. doi: 10.1101/gr.074492.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gnerre S, et al. High-quality draft assemblies of mammalian genomes from massively parallel sequence data. Proc Natl Acad Sci U S A. 2011;108:1513–8. doi: 10.1073/pnas.1017351108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Li R, et al. De novo assembly of human genomes with massively parallel short read sequencing. Genome Res. 2010;20:265–72. doi: 10.1101/gr.097261.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jones T, et al. The diploid genome sequence of Candida albicans. Proc Natl Acad Sci USA. 2004;101:7329–34. doi: 10.1073/pnas.0401648101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vinson JP, et al. Assembly of polymorphic genomes: algorithms and application to Ciona savignyi. Genome Res. 2005;15:1127–35. doi: 10.1101/gr.3722605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kim JH, Waterman MS, Li LM. Diploid genome reconstruction of Ciona intestinalis and comparative analysis with Ciona savignyi. Genome Res. 2007;17:1101–10. doi: 10.1101/gr.5894107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Donmez N, Brudno M. Research in Computational Molecular Biology, Lecture Notes in Computer Science. Vol. 6577. Springer; Berlin: 2011. Hapsembler: An assembler for highly polymorphic genomes; p. 38. [Google Scholar]
- 37.Pevzner PA, Tang H, Waterman MS. An Eulerian path approach to DNA fragment assembly. Proc Natl Acad Sci U S A. 2001;98:9748–53. doi: 10.1073/pnas.171285098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Idury RM, Waterman MS. A new algorithm for DNA sequence assembly. J Comput Biol. 1995;2:291–306. doi: 10.1089/cmb.1995.2.291. [DOI] [PubMed] [Google Scholar]
- 39.Simpson JT, et al. ABySS: a parallel assembler for short read sequence data. Genome Res. 2009;19:1117–23. doi: 10.1101/gr.089532.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zerbino DR, McEwen GK, Margulies EH, Birney E. Pebble and rock band: heuristic resolution of repeats and scaffolding in the velvet short-read de novo assembler. PLoS ONE. 2009;4:e8407. doi: 10.1371/journal.pone.0008407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kidd JM, et al. A human genome structural variation sequencing resource reveals insights into mutational mechanisms. Cell. 2010;143:837–47. doi: 10.1016/j.cell.2010.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Myers S, et al. Drive against hotspot motifs in primates implicates the PRDM9 gene in meiotic recombination. Science. 2010;327:876–9. doi: 10.1126/science.1182363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.The International HapMap Consortium A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449:851–61. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.de Bakker PI, et al. A high-resolution HLA and SNP haplotype map for disease association studies in the extended human MHC. Nat Genet. 2006;38:1166–72. doi: 10.1038/ng1885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ratan A, Yu Z, Hayes VM, Schuster SC, Miller W. Calling SNPs without a reference sequence. BMC Bioinformatics. 2010;11 doi: 10.1186/1471-2105-11-130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Peterlongo P, Schnel N, Pisanti N, Sagot M-F, Lacroix V. Identifying SNPs without a reference genome by comparing raw reads. In: Chavez E, Lonardi S, editors. String Processing and Information Retrieval - 17th International Symposium; Los Cabos, Mexico. 2010.pp. 147–158. [Google Scholar]
- 47.Ding L, Wendl MC, Koboldt DC, Mardis ER. Analysis of next-generation genomic data in cancer: accomplishments and challenges. Hum Mol Genet. 2010;19:R188–96. doi: 10.1093/hmg/ddq391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Harris SR, et al. Evolution of MRSA during hospital transmission and intercontinental spread. Science. 2010;327:469–74. doi: 10.1126/science.1182395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Butler J, et al. ALLPATHS: de novo assembly of whole-genome shotgun microreads. Genome Res. 2008;18:810–20. doi: 10.1101/gr.7337908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Chaisson MJ, Brinza D, Pevzner PA. De novo fragment assembly with short mate-paired reads: Does the read length matter? Genome Res. 2009;19:336–46. doi: 10.1101/gr.079053.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kelley DR, Schatz MC, Salzberg SL. Quake: quality-aware detection and correction of sequencing errors. Genome Biol. 2010;11:R116. doi: 10.1186/gb-2010-11-11-r116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Allsopp CE, et al. Sequence analysis of HLA-Bw53, a common West African allele, suggests an origin by gene conversion of HLA-B35. Hum Immunol. 1991;30:105–9. doi: 10.1016/0198-8859(91)90078-n. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.