Coupled Folding-Binding in a Hydrophobic/Polar Protein Model: Impact of Synergistic Folding and Disordered Flanks

Abstract

Coupled folding-binding is central to the function of many intrinsically disordered proteins, yet not fully understood. With a continuous three-letter protein model, we explore the free-energy landscape of pairs of interacting sequences and how it is impacted by 1), variations in the binding mechanism; and 2), the addition of disordered flanks to the binding region. In particular, we focus on two sequences, one with 16 and one with 35 amino acids, which make a stable dimeric three-helix bundle at low temperatures. Three distinct binding mechanisms are realized by altering the stabilities of the individual monomers: docking, coupled folding-binding of a single α-helix, and synergistic folding and binding. Compared to docking, the free-energy barrier for binding is reduced when the single α-helix is allowed to fold upon binding, but only marginally. A greater reduction is found for synergistic folding, which in addition results in a binding transition state characterized by very few interchain contacts. Disordered flanking chain segments attached to the α-helix sequence can, despite a negligible impact on the dimer stability, lead to a downhill free-energy surface in which the barrier for binding is eliminated.

Introduction

Intrinsically disordered (ID) proteins are functional proteins that partly or wholly lack a single, stable structure under native conditions. It has become clear that intrinsic disorder plays a crucial role in a wide range of cellular processes, with particularly high occurrence in proteins involved in the regulation of transcription and translation (1,2), cell signaling (3,4), and disease (5,6). ID regions often undergo a disorder-order transition upon binding to their target molecule. Such coupled folding-binding of ID proteins typically occurs upon contact with a partner molecule that is stable, but at least one example of interacting ID regions has been characterized (7). In this case, a stable complex is formed through a mutually induced folding-binding transition (also called synergistic folding and binding). The interfaces of protein complexes formed by ID proteins have some special characteristics. For example, they exhibit a greater number of intermolecular contacts than ordered complexes, indicating especially tight fits with their partner proteins, and they rely heavily on hydrophobic-hydrophobic attraction for stability (8). Because of their peculiar properties, several functional advantages of ID proteins over globular proteins have been proposed, including the ability to bind multiple targets (9), optimize allosteric interactions (10), and decouple binding affinity and specificity (11).

It has also been suggested that the coupled folding-binding process may provide a kinetic advantage by accelerating molecular associations owing to the larger capture radius of disordered protein chains. Specifically, it was imagined that ID proteins may bind their target molecules using a fly-casting mechanism (12), where after the formation of a few initial intermolecular contacts the target is reeled in during folding. In a critical assessment of this mechanism, increased association rates were indeed seen in a native-centric C_α model for a coupled folding-binding process (13). It is interesting to note that the increased rates were due to a stabilization of the encounter complex, whereas the effect of a greater capture radius was mainly offset by a slower chain diffusion. Binding through fly-casting can be classified as a mechanism of the induced-folding type, one of the two extreme mechanistic possibilities for coupled folding-binding in which folding is initiated only after binding occurs. In the other extreme case, conformational selection, binding occurs only to the correct preformed structural element selected from the dynamic ensemble of an ID chain, meaning that folding occurs before binding. Real ID complexes are expected to form by a combination of the two mechanisms, which has also been seen in recent simulations (14,15). However, it can be mentioned that several coarse-grained and all-atom models have seen a dominant role for an induced-folding mechanism (16–20). Our group has been involved in the development of an all-atom model to capture the detailed dynamics of domain-peptide interactions (21,22), showing that coupled folding-binding can occur even for short peptide segments.

Here, we investigate and compare the fundamental features of the free-energy landscape exhibited by coupled folding-binding processes. To this end, we develop a simplified continuous sequence-based model that we initially test on the folding of a set of ideally designed sequences. This test allows us to tune the relative strengths of the effective forces of the model, primarily hydrogen bonding and hydrophobic attractions. We then apply the model to the interaction of two different sequences, making a stable dimeric α-helix bundle structure at low temperatures, and we use this interaction to address two issues in particular: the role of the intrinsic stabilities of individual protein monomers in the interaction dynamics, and the impact of disordered flanking-chain segments on the coupled folding-binding process. We find that in the limit of low monomer stabilities the two sequences associate through a mutually induced coupled folding-binding mechanism. This mode of association leads to a binding transition state characterized by very few intermolecular contacts, and it should be ideally suited for fast molecular association. Disordered chain segments flanking the primary binding region are found to be able to strongly impact the basic features of the interaction. Despite a large impact on the activation barrier, the attractive forces involving the flanks are weak enough that they do not affect the stability of the complex. This suggests that care should be taken to consider disordered flanking regions in kinetic experiments of protein interactions involving ID proteins.

Methods

Model description

The model developed is a reduced-representation, continuous protein model with three amino acid types: polar (p), hydrophobic (h), and glycine (G). All backbone atoms, N, C_α, C′, H, O, H_α1, and H_α2, are included explicitly, whereas side chains are represented by a single atom, an enlarged C_β. Hence, h and p are geometrically related to alanine, whereas G is a normal glycine. Any N-amino-acid model conformation C is specified by the 2N dihedral angles ${\varphi }_{\text{i}}$ and ${\psi }_{\text{i}}$, in addition to the chain's overall translational and rotational orientation. All other minor degrees of freedom, such as bond lengths and angles, are fixed at standard values (see Table S1 in the Supporting Material).

The energy function can be written as $E\left(C\right)=E_{\text{exvol}}+E_{\text{local}}+E_{\text{hbond}}+E_{\text{hp}}$, where the four terms represent excluded volume, local partial charge interaction, hydrogen bonding, and hydrophobic attraction, respectively. In the following discussion, we describe the terms in turn. The excluded-volume energy is expressed as

$$E_{\text{exvol}}=k_{\text{exvol}}\sum _{\text{i}<\text{j}}{\left(\frac{{\lambda }_{\text{ij}}{\sigma }_{\text{ij}}}{r_{\text{ij}}}\right)}^{12},$$ (1)

where the sum is over all atom pairs ij, r_ij is the ij distance, ${\sigma }_{\text{ij}}={\sigma }_{\text{i}}+{\sigma }_{\text{j}}$ is the sum of the i and j atom radii with σ_i = 1.75 Å, 1.55 Å, 1.42 Å, and 1.00 Å, for C, N, O, and H atoms, respectively, and λ_ij is a scale factor. An exception to this choice of σ_ij is for C_β-C_β pairs where σ_ij = 5.0 Å, thereby mimicking side-chain bulkiness. The scale factor λ_ij is chosen in the following way: 1.00 for ij pairs connected by three covalent bonds, 1.25 and 1.00 for amide HH and carboxyl OO pairs, respectively, and 0.75 for all other pairs. The excluded-volume reduction (λ_ij < 1) for global ij pairs partially alleviates the reduced flexibility of a chain with only torsional angles as degrees of freedom. The overall excluded-volume weight factor is k_exvol = 0.1.

The next term takes into account locally the interactions between partial charges on the backbone,

$$E_{\text{local}}=k_{\text{local}}\sum _{\text{I}}\sum _{\text{i}<\text{j}}\frac{q_{\text{i}}{q}_{\text{j}}}{r_{\text{ij}}/\AA },$$ (2)

where the ij sum is over all pairs of N, H, C′, and O atoms in the amino acid I with partial charges q_i = –0.2, +0.2, +0.42, and –0.42, respectively, and the I sum is over all amino acids. The strength is k_local = 50.

The hydrogen-bond term can be written as

$$E_{\text{hbond}}=k_{\text{hbond}}\sum _{\text{ij}}{\gamma }_{\text{ij}}\left[5{\left(\frac{{\sigma }_{\text{hb}}}{r_{\text{ij}}}\right)}^{12}-6{\left(\frac{{\sigma }_{\text{hb}}}{r_{\text{ij}}}\right)}^{10}\right]{\left(\cos {\alpha }_{\text{ij}}\cos {\beta }_{\text{ij}}\right)}^{1/2},$$ (3)

where i and j sum over all NH and CO groups, respectively, but ij pairs must be separated by at least two NH (or CO) groups to be included. The quantities α_ij and β_ij are the N-H-O and H-O-C′ angles, respectively (the contribution of any ij with either α_ij < 90° or β_ij < 90° is set to zero), and the parameter σ_hb = 2.0 Å. The hydrogen-bonding strength is k_hbond = 3.1, but it can be reduced through the sequence-dependent scale factor γ_ij. For hh, hp, and pp hydrogen bonds, γ_ij = 1, and for GG, Gh, and Gp pairs, γ_ij = 0.75. We added the factor γ_ij < 1 for G mainly to enhance its propensity to break secondary structure in the model. This reduction may not be physically unreasonable, however, given glycine's lack of side chain, which may allow it to more easily interact with surrounding water molecules and therefore lead to effectively weaker intra chain hydrogen bonds compared to other amino acids (23).

The hydrophobicity energy, E_hp, is given by

$$E_{\text{hp}}=-k_{\text{hp}}\sum _{\text{ij}}{e}^{-{\left(r_{\text{ij}}-{\sigma }_{\text{hp}}\right)}^2/2},$$ (4)

where the sum runs over all hydrophobic C_β atoms, excluding nearest and next-nearest amino acid neighbors. The optimal C_β-C_β distance for a hydrophobic contact is σ_hp = 5.0 Å, which is set to coincide with the excluded-volume parameter σ_ij = 5.0 Å for C_β-C_β pairs. In this way, the excluded-volume repulsion (Eq. 1) and hydrophobic attraction (Eq. 4) combine into a smooth Lennard-Jones-like interaction (24,25). The hydrophobicity strength is k_hp = 0.805.

Monte Carlo simulation

In all simulations, the protein chains are kept in a (100 Å)³ box with periodic boundary conditions. To find the thermodynamic behavior, as determined by the amino acid sequence and the energy function E(C), we use simulated tempering (ST) (26–28), which is an expanded-ensemble Monte Carlo (MC) method. We perform three independent ST simulations for each system studied, and these are used to estimate statistical errors. Each run is at least 10⁹ elementary MC updates. For the single-chain simulations, two different MC update types are used: a pivot move, where a single ${\varphi }_{\text{i}}$ or ${\psi }_{\text{i}}$ angle is selected and assigned a new, random value, and a biased gaussian step (BGS) (29), where eight consecutive ${\varphi }_{\text{i}}$, ${\psi }_{\text{i}}$ angles are turned in a coordinated way to yield approximately local chain deformations. The pivot and BGS moves are efficient at evolving chains at high and low temperatures, respectively. For the two-chain systems, we use, in addition, single-chain rigid body translation and rotation updates. The fixed A1(S) and A2(S) conformations were picked from an A1+A2 test simulation at low E, i.e., where the three-helix bundle dimer was fully formed. In simulations with A1(S) or A2(S), only rigid-body updates are used for the (S)-chains, such that their internal conformations remain entirely fixed. The Monte Carlo kinetics runs differ from the thermodynamics runs in two ways. First, the unphysical, global pivot move is turned off. Second, simulations are performed at a single, fixed temperature. The A1_Lh5 and A1_Lp5 chains are initiated from random, high-T conformations and 500 independent runs are performed for each system.

Order parameters for folding and binding

As measures of binding progress we use two different order parameters, R_CM, the distance between the centers of mass (CM) of the 2 chains, and N_hh, the number of interchain hh contacts. Two h amino acids kl are considered in contact if $e_{\text{hp}}^{\text{kl}}<-0.25k_{\text{hp}}$, where $e_{\text{hp}}^{\text{kl}}$ is the kl contribution to the total hydrophobicity energy, E_hp. The CM is calculated over all C_α atoms in the A1 or A2 chains. All flanking chain segments are ignored in the CM calculation. Progress in folding is measured using the root mean-square deviation (RMSD), calculated over all C_α atoms, and the fractions of amino acids in an α or a β state. An amino acid i is considered to be in an α-helical state if $-90<{\varphi }_{\text{i}}<-30$ and $-77<{\psi }_{\text{i}}<-17$, and in a β-sheet state if $-160<{\varphi }_{\text{i}}<-100$ and $100<{\psi }_{\text{i}}<160$.

Results

Continuous hydrophobic/polar model for protein folding and binding

To investigate and compare the basic features of various protein-protein association modes, we developed a simplified protein model with three amino acid types, h, p, and G. The model is described in detail in Methods. The two main molecular driving forces in the model are pairwise hh attraction and hydrogen bonding. To determine optimal model parameters, we applied the model to the six sequences A1, A2, A3, B1, B2, and B3, which can be found in Table 1. The A sequences were designed according to the strategy of Regan and DeGrado (30). In A1, the 16 h and p amino acids are distributed along the sequence such that when the chain makes an α-helix, all the h amino acids appear on the same side. In A2 and A3, two and three A1 sequences, respectively, are joined by flexible GGG segments, allowing the formation of α-helical bundles stabilized in part by hydrophobic forces. The B1 sequence was inspired by the de novo design of the three-stranded antiparallel β-sheet Betanova (31). Its six h amino acids are distributed such that they can cluster on the same side of the β-sheet. B2 and B3 are similar to B1 but have slightly longer strands.

Table 1.

Three-letter amino acid sequences studied

Protein	N	Sequence
A1	16	pphpphhpphpphhpp
A2	35	A1-GGG-A1
A3	54	A1-GGG-A1-GGG-A1
B1	18	phphpGGphphGGhphph
B2	21	phphphGGhphphGGhphphp
B3	24	phphphpGGphphphGGhphphph
A1_Lhk	18 + 6k	(GhG)kG-A1-G(GhG)k
A1_Lpk	18 + 6k	(GpG)kG-A1-G(GpG)k

The three amino acids types are p (polar), h (hydrophobic), and G (glycine); N is the number of amino acids; and k = 1, 2, 3, 4, and 5.

The thermodynamic behavior of the six sequences is shown in Fig. 1. At high temperatures, T, all sequences exhibit a similarly low propensity for ordered structures. As T is lowered, however, the A and B sequences behave differently and form predominantly α- and β-structure, respectively. In fact, all sequences fold into distinct stable native states that are well represented by the minimum-energy conformations, shown in Fig. 2. This can be seen from the E-RMSD free-energy surfaces in Fig. 3, where E is the total energy and the RMSD is with respect to the corresponding min-E structures, which show global minima at low-E/low-RMSD values. The temperature dependence of the specific heat capacity, C_v, exhibits single-peak behavior for all sequences, indicating that folding is a cooperative transition from the unfolded to the native state (see Fig. 1, C and D). We identify the C_v peaks as the folding temperature, T_f, where the folded and unfolded ensembles are roughly equally populated. We note that the C_v peaks generally become more pronounced with chain length N and that the T_f values for the helical A sequences are generally higher than those for the B sequences, indicating lower thermal stabilities for the β-sheets compared to the α-helix bundles. Although we cannot directly compare the results for our model sequences with experimental thermodynamics data, we note that Betanova (31) and its variants (32) are relatively unstable, whereas three-helix bundle proteins can be quite thermostable (33,34).

Figure 1.

Folding thermodynamics of the A1–A3 and B1–B3 sequences. (A and B) The α-helix (blue lines) and β-sheet (red lines) contents, denoted $\langle \alpha \rangle$ and $\langle \beta \rangle$, where angled brackets indicate the thermodynamic average, as a function of the temperature (T). (C and D) The specific heat capacity, C_v, calculated using $C_{\text{v}}=\left(\langle E^2\rangle -{\langle E\rangle }^2\right)/N{k}_{\text{B}}{T}^2$, where E is the total energy, N the number of amino acids, and k_B the Boltzmann constant, as a function of T. For reference, we note that α = 0.83 – 0.88 for the structures in Fig. 2, A–C, and β = 0.67 – 0.71 for the structures in Fig. 2, D–F.

Figure 2.

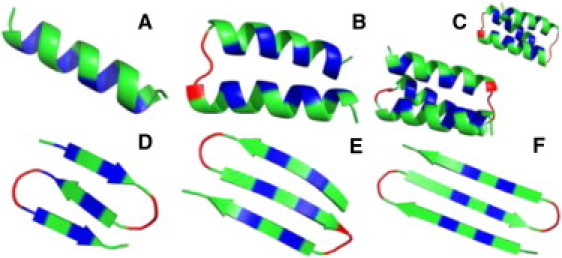
Minimum-energy conformations found across all MC simulations for the sequences A1, A2, A3, B1, B2, and B3 (A–F, respectively). A compact three-helix bundle has two distinct topological states corresponding to the two different ways of wrapping the α-helices, either clockwise or counterclockwise. Coarse-grained models of the type used in this study do not distinguish these two possibilities (54), and as a result, the native state of A3 exhibits a twofold topological degeneracy. For A3, we show the min-E conformations obtained within each topological state. Colors indicate h (blue), p (green), and G (red) amino acid types.

Figure 3.

Free-energy surfaces F(E, RMSD) taken at the folding temperature, T_f, for the sequences A1, A2, A3, B1, B2, and B3 (A–F, respectively), where E is the total energy and RMSD the root mean-square deviation measured with respect to the corresponding conformations in Fig. 2. For A3, we use, for each generated conformation, the smallest RMSD value obtained when comparing to both the clockwise and counterclockwise structures (see Fig. 2C). Free energies are calculated using F(E, RMSD) = –k_BT ln P(E, RMSD), where P is the equilibrium probability distribution at T = T_f.

Models with a similar level of coarse-graining have been developed previously, and applied to both protein folding (35–38) and misfolding and aggregation (39,40). An advantage of our approach is that by initially applying the model to the folding of a set of sequences, the relative strengths of the molecular driving forces can be adjusted to reasonable values (see Fig. S1 and Text S1 in the Supporting Material). Because this test is performed on sequences making both α- and β-structure, an unphysical bias toward one type of secondary structure is avoided. Moreover, nonnative interactions, which are likely particularly important for ID proteins, are naturally included in our model. In Gō-type or native-centric modeling approaches, by contrast, nonnative forces must be added separately, and calibrating their strength is not straightforward (14,24,41). All results presented in this work are obtained for the single set of model parameters, given in Methods.

Comparing binding mechanisms: docking, coupled folding-binding, and mutually induced folding-binding

Having seen that our model is able to capture the folding of the ideal A and B sequences in Table 1, we turn now to the interaction of two of the sequences, A1 and A2. Our aim is to investigate how various features of the free-energy landscape of binding depend on the binding mechanism. To this end, we enclose A1 and A2 in a periodic box and find the thermodynamic behavior using MC simulations, as before, but with additional single-chain rigid-body updates (see Methods). We denote this system by A1 + A2. The A1 and A2 chains are at low temperatures found predominantly in a stable bound state in which the two chains are folded into a heterodimeric three-helix bundle (see Fig. 4 A, inset). To understand the formation of this complex, we use two order parameters, N_hh and R_CM, which measure the number of interchain hh contacts and the CM distance between the two chains, respectively. N_hh and R_CM are thus independent of the folding process, allowing progress in the two processes to be delineated.

Figure 4.

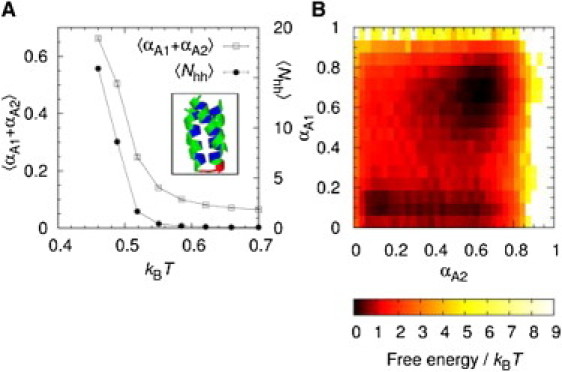
Mutually induced folding upon binding exhibited by A1 + A2, i.e., the interaction of the A1 and A2 sequences. (A) The total α-helix content, $\langle {\alpha }_{\text{A}1}+{\alpha }_{\text{A}2}\rangle$, and the number of interchain hh contacts, $\langle N_{\text{hh}}\rangle$, as a function of T. (Inset) The A1 + A2 min-E conformation. (B) The free-energy surface, F(α_A1, α_A2) = –k_BT ln P(α_A1, α_A2), where P is the probability distribution taken at the binding temperature, T_b.

Fig. 4 A shows N_hh and the total α-helix content, α_A1 + α_A2, as functions of the temperature. The two quantities are closely linked, meaning that for A1 + A2, folding of the two chains is concurrent with binding. An important factor controlling how a protein chain interacts with its partner is the stability of the complex as quantified by, e.g., the binding temperature, T_b, relative to the stabilities of the individual monomer native states. In analogy with the definition of T_f, we determine T_b using the maximum in the C_v curve for A1 + A2 (data not shown). We find that $k_{\text{B}}{T}_{\text{b}}^{\text{A}1+\text{A}2}=0.521$, which is higher than $k_{\text{B}}{T}_{\text{f}}^{\text{A}1}$ but lower than $k_{\text{B}}{T}_{\text{f}}^{\text{A}2}$. Hence, at T_b, both chains have some residual structure on their own, a situation common for many real ID segments (42). The impact of this residual structure can be seen from the α_A1, α_A2 free-energy surface in Fig. 4 B, which displays two major free-energy minima corresponding to low-α_A1 and high-α_A1/high-α_A2 states, respectively. This indicates a slight preference for A2 folding before A1. However, the free-energy landscape is rather flat, such that many different pathways are possible between the unbound, unfolded and the bound, folded states.

How is the A1 + A2 binding process influenced by an increase or decrease in the stability of the individual monomers? To address this question, we study two additional systems, A1 + A2(S) and A1(S) + A2(S). Here, (S) indicates that the chain's native state has been made artificially entirely stable, i.e., A1(S) is fixed in a single α-helix conformation and A2(S) in a two-helix bundle conformation (see Methods for details). By construction, association in A1(S) + A2(S) will occur via a docking mechanism. For A1 + A2(S), we find that k_BT_b = 0.579, i.e., the binding temperature is significantly higher than the folding temperature for A1, and binding can therefore occur under conditions where A1 is disordered. As it turns out, binding of A1 to A2(S) triggers the folding of A1. This is clear from the increase in the average A1 α-helix content, $\langle {\alpha }_{\text{A}1}\rangle$, from 0.10 for an isolated A1 to 0.68 for A1 + A2(S), at T = T_b. The coupled folding-binding process of A1 is also evident from the rather dramatically different free-energy profiles, F(α_A1), taken separately when the molecules are spatially separate (N_hh = 0) and in contact (N_hh ≥ 1), as shown in Fig. 5. We conclude that the presence of A2(S) induces the folding of A1, starting from a highly unstructured chain. It is interesting to note that a small activation barrier in the folding of A1 persists even in the presence of A2(S).

Figure 5.

Coupled folding-binding of the A1 sequence upon interaction with A2(S), a stable two-helix-bundle A2 conformation. (A) The free-energy surface F(α_A1, N_hh), where α_A1 is the α-helix content of A1 and N_hh is the number of interchain hh contacts, taken at T = T_b. (B) Free-energy profile, F (α_A1), taken separately for N_hh ≥ 1 (A1 and A2(S) in contact) and N_hh = 0 (no A1-A2(S) contact formed), at T_b.

Fig. 6 shows the free-energy profiles in the binding order parameters, N_hh and R_CM. All three systems exhibit a single local maximum (the transition state (TS)) between the unbound (U) and bound (B) states. The activation energy for binding (ΔF^TS–U) is highest for A1(S) + A2(S), i.e., when A1 and A2 associate via a pure docking mechanism. By comparison, for A1 + A2(S), where binding involves the coupled folding-binding of A1, the barrier height as measured by both order parameters is decreased. In N_hh, we find $\Delta F_{\text{hh}}^{\text{TS}-\text{U}}=\left(6.3\pm 0.3\right)k_{\text{B}}T$ and (5.9 ± 0.2)k_BT for A1(S) + A2(S) and A1 + A2(S), respectively. Another difference is a small shift in the TS toward larger R_CM values, such that $R_{\text{CM}}^{\text{TS}}\approx 16\AA$ for A1(S) + A2(S) and $R_{\text{CM}}^{\text{TS}}\approx 18\AA$ for A1 + A2(S). This signals a greater capture radius for a disordered A1 chain compared to the folded A1(S), as predicted by the fly-casting mechanism and seen in previous simulations (13,43,44).

Figure 6.

Comparing the binding-free-energy profiles for different association mechanisms: A1(S) + A2(S) (docking), A1 + A2(S) (coupled folding-binding of A1), and A1 + A2 (mutually induced folding upon binding). Shown is the free energy, F, as a function of (A) the number of interchain hh contacts, N_hh, and (B) the center-of-mass distance, R_CM, taken at the systems' respective binding temperatures, T_b.

The increase in $R_{\text{CM}}^{\text{TS}}$ and decrease in ΔF^TS–U in response to the coupled folding-binding of A1 are rather modest changes, however. A greater impact is obtained when both A1 and A2 are mutually induced to fold upon binding, as in the A1 + A2 system. For this case, we obtain $\Delta F_{\text{hh}}^{\text{TS}-\text{U}}=\left(4.9\pm 0.1\right)k_{\text{B}}T$. The A1 + A2 binding-free-energy landscape also exhibits a different shape such that a bias toward the bound state can be accessed after only one to two initial interchain hh contacts are formed (see Fig. 6 A). By contrast, both A1(S) + A2(S) and A1 + A2(S) require the formation of additional hh contacts before the TS is reached, involving a further climb in free energy. Hence, in the mutual folding-upon-binding scenario, as seen in A1 + A2, the binding TS is reached extremely easily upon chain-chain contact, a situation that should be highly suitable for fast binding kinetics.

Impact of flanking chain segments on coupled folding-binding

Many protein regions undergoing coupled folding-binding are found within longer regions of intrinsic disorder (45,46). To fully understand the properties of these interactions in vivo, it is therefore important to investigate the role played by flanking chain segments. Previously, it has been suggested that disordered flanks adjacent to short linear binding motifs may be important to suppress aggregation of ID proteins (47). Here, we investigate the impact of flanks on the coupled folding-binding process. To this end, we use our coarse-grained approach and model disordered flanking chain segments as repetitions of the sequence triplets, GhG or GpG, and attach them to both ends of A1 to give the long A1 sequences A1_Lhk and A1_Lpk, respectively, where k indicates the number of triplets attached at each end (see Table 1). For the A1_Lhk and A1_Lpk sequences with k = 1, 2, 3, 4, and 5, the flanking regions remain entirely disordered even under conditions where the A1 α-helix is fully formed (see Fig. S2). We study the interaction of A1_Lhk and A1_Lpk with A2(S) for various k and ask in particular how the attached p- and h-flanks impact 1), the stability of the complex and 2), the binding-free-energy landscape.

Fig. 7 A shows that the activation free energy of binding, $\Delta F_{\text{hh}}^{\text{TS}-\text{U}}$, decreases sharply with the flank length for A1_Lhk + A2(S), whereas for A1_Lpk + A2(S), there is an almost constant trend in k. This suggests that hh interactions between the h-flanks and the binding target A2(S) act to lower the free-energy barrier between the unbound and bound states. As it turns out, the impact of h-flanks is especially large in the R_CM order parameter where the shape of the free-energy curves changes, as can be seen from Fig. 8. For A1_Lh5 + A2(S), the free-energy profile in R_CM exhibits a plateaulike behavior over a relatively large R_CM range, ≈ 17 – 37Å, rather than a pronounced single peak. This indicates that long disordered h-flanks attached to A1 might be effective at increasing the A1 capture radius, reminiscent of the fly-casting mechanism (12,44), although our flanks remain disordered in both the bound and unbound states.

Figure 7.

Impact of disordered flanking chain segments on the coupled folding-binding process. (A) The activation free energy of binding, ΔF^TS–U, as a function of flank length, k, for A1_Lhk + A2(S) and A1_Lpk + A2(S), where k is the number of GhG (A1_Lhk) or GpG (A1_Lpk) triplets attached to both ends of A1 (see Table 1). ΔF^TS–Udecreases with k for the h-flanks while remaining more or less constant for the p-flanks. (B) The binding temperature, T_b, as a function of k.

Figure 8.

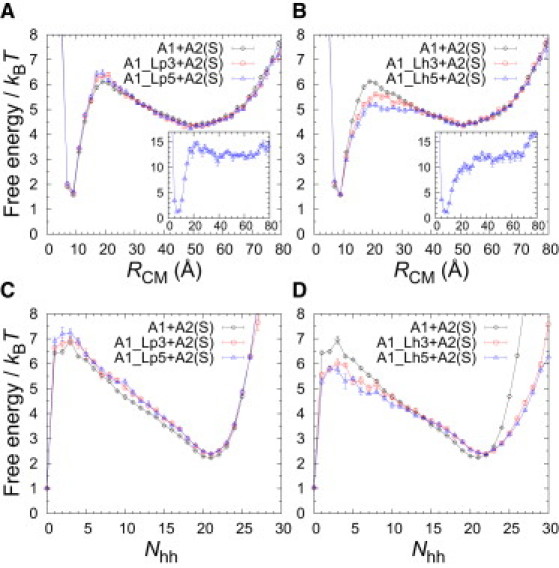
Impact of disordered flanks on the shape of binding-free-energy profiles. Free energy, F, as a function of R_CM (A and B) and N_hh (C and D) for different sequences interacting with A2(S): A1 with long flanks (A1_Lh5 and A1_Lp5), A1 with intermediate flanks (A1_Lh3 and A1_Lp3), and, for comparison, A1 with no flanks attached. The free energies are calculated at the A1 + A2(S) binding temperature, T_b. (Insets) F(R_CM) for A1_Lh5 and A1_Lp5, respectively, at k_BT = 0.48, corresponding to T = 0.83T_b.

To test this effect more directly, we perform a large number of small-step Monte Carlo kinetic runs for A1_Lh5 + A2(S) and A1_Lp5 + A2(S). All these runs are initiated with the two chains at the largest possible separation within our periodic box ($R_{\text{CM}}=50\sqrt{3}\AA =86.6$ Å), and relaxation toward equilibrium is thereafter observed, as shown in Fig. 9. Overall, the folding of the long A1 sequences, as measured by ${\langle {\alpha }_{\text{A}1}\rangle }_t$, where t is the number of MC steps, and their binding with A2(S), as measured by ${\langle R_{\text{CM}}\rangle }_t$, follow a similar trend. This is a direct observation of coupled folding-binding in our model. Despite the general similarity between the two systems, there are interesting differences in the details, especially at small t, where ${\langle R_{\text{CM}}\rangle }_t$ decreases significantly more rapidly for A1_Lh5 than for A1_Lp5 (see Fig. 9 A). This difference can be quantified by the mean time of formation of the first interchain hh contact. We find this capture time to be t_cap ≈ 6.3 × 10⁵ and ≈ 8.6 × 10⁵ MC steps for A1_Lh5 and A1_Lp5, respectively. Hence, on average, A1 with h-flanks captures its target faster than A1 with p-flanks, reflecting the different shapes of their free-energy profiles (see Fig. 8, A and B). However, in total, the relaxation process is not faster for A1_Lh5. In fact, after t $\gtrsim 5\times {10}^6$ MC steps, helix formation is slightly slower for A1_Lh5 than for A1_Lp5 (see Fig. 9 B). A possibility is therefore that although attractive flanks may aid in capturing the target, they may also result in kinetic traps, leading to slower subsequent folding.

Figure 9.

Impact of disordered flanks on coupled folding-binding kinetics. A large number of independent small-step MC relaxation runs are performed in which A2(S) binds either the A1_Lh5 sequence (A1 with attached h-flanks) or the A1_Lp5 sequence (A1 with attached p-flanks). Shown are (A) ${\langle R_{\text{CM}}\rangle }_t$ and (B) ${\langle {\alpha }_{\text{A}1}\rangle }_t$, where ${\langle \cdot \rangle }_t$ indicates the average over all runs at different MC time steps t. The runs are performed at k_BT = 0.579, corresponding to the A1 + A2(S) binding temperature.

Another interesting difference between the p- and h-flank systems emerges at lower temperatures. At T = 0.83T_b, e.g., a small but clear free-energy barrier in R_CM remains for A1_Lp5, whereas the barrier is absent for A1_Lh5 (see Fig. 8, A and B, insets), suggesting a different type of process. A fairly large free-energy barrier remains in N_hh for both systems, even at low T (data not shown), but this measure takes into account only a subset of formed hh contacts. A more revealing parameter by which to follow the combined folding-binding process would be $N_{\text{hh}}^{\text{tot}}$, counting both inter- and intrachain hh contacts. For $N_{\text{hh}}^{\text{tot}}$, the situation is analogous to R_CM, i.e., A1_Lp5 displays a distinct free-energy barrier, whereas the free-energy profile for A1_Lh5 is barrierless at low T (see Fig. S3). The observed differences thus indicate that flanking chain segments, if attracted to the target molecule, may lead to a binding scenario that is downhill in free energy. Finally, let us stress that while the h-flanks can be highly significant for the folding-binding process, as we have seen, their effect on the overall thermal stability of the bound state is negligible (see Fig. 7 B). In our model, therefore, attractive flanks transiently stabilize the binding TS during folding-binding thereby speeding up target capture while at the same time being weak enough that they do not affect the overall stability of the final complex.

Discussion

ID regions undergoing coupled folding-binding are common in protein-interaction networks and involve the formation of all types of secondary and irregular structures (48). One of the suggested biological advantages of coupled folding-binding is that it may result in fast associating/dissociating, weak-affinity complexes and therefore make ID proteins especially well suited for regulatory and cell-signaling processes. Although some ID regions fold into entire globular domains upon binding, most coupled folding-binding events involve short amphiphilic segments within longer regions of intrinsic disorder (11).

In our coarse-grained model, the amphiphilic A1 sequence undergoes a near-complete binding-induced folding transition upon interaction with the stable two-helix bundle structure A2(S) (see Fig. 5). By comparing the binding free-energy landscape of this interaction with the docking case of the same sequences, we find that the coupled folding-binding process both increases the capture radius of the A1 chain and reduces the height of the free-energy barrier for binding. This suggests an accelerated molecular association rate. Previous simulation studies (13,43) have shown qualitatively similar trends. In particular, Huang and Liu (13) showed that a key factor in controlling the binding kinetics is the height of the free-energy barrier for binding and that a greater capture radius does not automatically produce faster association kinetics, because it also leads to a slower chain diffusion (13). It is interesting, therefore, that the coupled folding-binding of our A1 sequence, with a length typical of many coupled folding-binding segments (11), reduces the binding barrier with only ≈ 0.5k_BT (see Fig. 6, A and B), a rather marginal effect compared to the overall barrier height, which is ≈10-fold larger.

This raises the possibility that other mechanisms may be used to further speed up the association/dissociation of short binding segments. Our simple model suggests two possibilities. The first is an association mode in which both chains bind and fold simultaneously, as exhibited by our A1 + A2 system (see Fig. 4). We find that such a mutually induced folding-binding mechanism reduces the binding barrier more substantially, with ≈ 1.5k_BT. In addition, A1 + A2 displays a binding TS characterized by the formation of only one or two attractive interchain contacts, which should further facilitate molecular association. Second, our results indicate that the shape of the binding free-energy surface can be strongly impacted by disordered flanking segments adjacent to the primary binding region. Evidence for the concerted evolution between short linear protein motifs and their flanks has been found (49), suggesting that they are often functional, and the conformational ensemble of a small α-helical peptide was found to be affected by its flanking residues (50).

The addition of flanks to our A1 sequence reveals that attractive intermolecular forces involving the flanks can be highly efficient at stabilizing the TS in a coupled folding-binding scenario. This stabilization occurs in our model despite the fact that the attached h-flanks have little impact on the bound-state stability, meaning that these nonnative intermolecular forces are relatively weak. Let us stress that nonattractive disordered flanks by themselves are not expected to impact the stability of a complex if they remain fully disordered in the bound state, as we see in the case of p-flanks attached to the A1 sequence.

In two recent restrained molecular dynamics simulations of the barnase-barstar complex (51,52), a downhill binding-free-energy surface was found, despite the fact that both proteins are stable on their own. This apparent disagreement with our results points to the potentially large role that can be played by electrostatic interactions in steering molecular associations. The stability of the barnase-barstar complex is, however, particularly strongly dependent on electrostatic interactions (53), with an association driven in part by a large net charge difference between the two molecules.

Conclusion

A simple, sequence-based protein model was developed and tested on the folding of a set of ideal sequences, allowing the relative strength of the molecular driving forces to be carefully tuned. It was thereafter used to investigate the general features of the binding-free-energy landscape of coupled folding-binding processes. Within the context of a helical system, our results indicate that coupled folding-binding, as compared to a docking scenario, provides a mechanism to lower the binding activation barrier, in line with previous investigations, and suggests that increased molecular association rates can be obtained. This reduction is, however, relatively small for a single α-helix with 16 amino acids which is a typical length for many functional coupled folding-binding events. We find that an association in which both chains are mutually induced to fold and bind concurrently provides a greater reduction of the activation free energy. Such synergistic folding-binding also leads to a binding TS that is characterized by the formation of very few intermolecular contacts, which could further accelerate binding. Disordered chain segments flanking a coupled folding-binding region are found to have a profound impact on the binding characteristics. In particular, attractive nonspecific interactions involving flanking chain segments may lead to an elimination of the activation barrier and a downhill free-energy surface. This can occur even when the addition of flanking sequences does not affect the overall stability of the complex. The model developed captures key elements of protein folding and binding, including secondary-structure formation and hydrophobic attraction, yet it is computationally manageable. It would therefore be interesting to apply it to coupled folding-binding processes of longer chains or those leading to the formation of β-sheet structure.