Evaluating prognostic accuracy of biomarkers in nested case–control studies

Abstract

Nested case–control (NCC) design is used frequently in epidemiological studies as a cost-effective subcohort sampling strategy to conduct biomarker research. Sampling strategy, on the other hoand, creates challenges for data analysis because of outcome-dependent missingness in biomarker measurements. In this paper, we propose inverse probability weighted (IPW) methods for making inference about the prognostic accuracy of a novel biomarker for predicting future events with data from NCC studies. The consistency and asymptotic normality of these estimators are derived using the empirical process theory and convergence theorems for sequences of weakly dependent random variables. Simulation and analysis using Framingham Offspring Study data suggest that the proposed methods perform well in finite samples.

1. INTRODUCTION

Novel markers promise to dramatically change the decision-making process in disease monitoring and treatment selection. Prospective cohort studies are crucial to establishing the value of a biomarker for predicting future events such as disease onset and recurrence, or patient survival. To enable future biomarker research, the biospecimens of the full cohort are often collected at baseline and stored for future studies. Many well-known cohort studies adopted such strategies. Examples include the Women's Health Initiative Study Johnson and others, 1999, the Nurses' Health Initiative Study, and the Framingham Offspring Study Kannel and others, 1979. However, since the assessment of biomarkers can be expensive and labor intensive, a standard full cohort design may be infeasible or inefficient for subsequent biomarker studies. To overcome such difficulties, the nested case–control (NCC) study design Thomas, 1977, Prentice and Breslow, 1978 is often adopted as a cost-effective cohort sampling strategy. Under such a study design, the biospecimen is assayed for all study cases but only for a fraction of controls selected randomly from the risk set of the matched cases.

To analyze data from NCC studies, conditional logistic regression is typically used to estimate relative risk parameters, which are equivalently hazard ratio parameters under the proportional hazards (PH) model. Stratified sampling of controls in NCC designs has been considered Langholz and Borgan, 1995 in order to improve efficiency of a simple NCC design. For the class of estimators based on the partial likelihood under NCC designs, asymptotic properties have been formally derived for estimators of both hazard ratios Goldstein and Langholz, 1992 and absolute risks Langholz and Borgan, 1997, using counting process and martingale theory Andersen and Gill, 1982.

An alternative approach is to consider the class of inverse probability weighted (IPW) estimators, where contributions of individuals are weighted inversely proportional to their sampling fractions. Compared with the partial likelihood–based method, IPW estimators can be more efficient as more individuals are included in risk sets. They are also more flexible in estimating functions beyond hazard ratios. Samuelsen 1997 proposed IPW partial likelihood estimators with weights accounting for NCC sampling; however, theoretical justification has not been formally developed. Recently, much progress has been made in the development of asymptotic theory for IPW estimator when fitting the Cox regression model using survey data obtained using two-phase sampling (Lin, 2000; Breslow and Wellner, 2007). In particular, Breslow and Wellner 2007 developed a modern theory on the conditions required for weak convergence of IPW empirical process under Cox regression with stratified case–cohort sampling. While it could be conjectured that the general theory developed there may be extended to other more complex sampling designs such as the stratified NCC sampling designs considered in this manuscript, to our knowledge, there does not exist a general theory that can be directly applied to IPW process under NCC settings.

Furthermore, most of the current developments in NCC study literature focus primarily on estimating relative risk parameters, with little attention given to other summaries of the data. Prognostic biomarker studies have recognized that the relative risk from risk modeling does not fully assess biomarker performance Pepe and others, 2004. Two classes of time-dependent accuracy measures, retrospective and prospective accuracies, are commonly calculated in these settings. Specifically, for a putative marker Y measured at baseline, its retrospective accuracies, such as the true-positive fraction (TPF) and false-positive fraction (FPF), evaluated at a future predicting time t and a cutpoint c, are defined as

A time-dependent receiver operating characteristic (ROC) curve, ROC_t(u) = TPF_t{FPF_t ^{− 1}(u)} for u∈(0,1), is a plot of TPF_t(c) versus FPF_t(c) for all c. The prospective accuracy summaries, positive predictive value (PPV) and negative predictive value (NPV), are time-dependent functions of the form

(1.1)

The prospective accuracy summaries are of more interest to the end users of the test since they quantify the subject's risk of an outcome by time t, given a positive or a negative test result. Statistical models for estimating these quantities using time-to-event data from full cohorts have been proposed Heagerty and others, 2000, Heagerty and Zheng, 2005, Moskowitz and Pepe, 2004, Zheng and others, 2008. However, those current methods do not consider subcohort sampling schemes and have only been developed for standard settings with biomarker values fully observed for individuals in the cohort. To efficiently evaluate novel biomarkers for risk prediction, there is an urgent need to expand the research to accommodate various subcohort sampling schemes.

The primary aim of this paper is to formulate and lay foundations for biomarker accuracy estimation with data from NCC studies. We develop estimators for time-dependent prediction accuracy measures based on the idea of inverse probability weighting Robins and others, 1994, Samuelsen, 1997. The asymptotic properties of these estimators are formally derived using convergence theorems for sequences of negatively associated (NegA) dependent random variables Liang and others, 2004, Liang and Baek, 2006. The remainder of the paper is organized as follows: we present the estimation procedures under both a simple NCC design and a stratified NCC design in Section 2; asymptotic theory is given in Section 3; Section contains numerical studies; an application to the Framingham Offspring Study is given in Section 5, and we conclude with some remarks in Section 6.

2. THE MODEL AND ESTIMATION

2.1. General notation

Suppose we have a cohort of N individuals followed prospectively for a clinical event of interest. Due to censoring, the observed event time data consist of N i.i.d. bivariate vector {(X_i,δ_i),i = 1,…,N}, where X_i = min(T_i,C_i), δ_i = I(T_i ≤ C_i), and T_i and C_i denote the event time and censoring time, respectively. Under a standard NCC design, all individuals observed to have an event are selected as “cases” for further evaluation of marker Y with their event times denoted as {t₁,…,t_n}. In addition, at each selected case's failure time t_j, a random sample of size m is selected without replacement from the risk set R(t_j) = {i:X_i ≥ t_j} as potential controls for marker measurement. The number of individuals at risk at the selected event time t_j is denoted n(t_j), with n(t_j) = ∑_i^NI(X_i ≥ t_j). Furthermore, let V_i be a binary random variable with V_i = 1 if subject i is ever sampled into the NCC subcohort either as a case or as a control.

2.2. Estimation with a cohort study

Using Bayes' theorem, we can rewrite the aforementioned retrospective prognostic accuracy summaries as

and the prospective accuracy summaries as

where 𝒮(t,c) = P(T > t,Y > c) is the bivariate survival function of T and Y, ℱ(c) = P(Y ≤ c) is the marginal cumulative distributional function of marker Y, and 𝒮(t) = P(T > t)≡𝒮(t, − ∞) is the marginal survival function of T. Therefore, the key components for calculating all 4 accuracy summaries involve ℱ(c), as well as the bivariate survival function 𝒮(t,c) for specific values of c and t.

When Y was measured for all individuals in the cohort, plug-in estimators of the accuracy measures had been proposed using either nonparametric or semiparametric estimators of these functionals Heagerty and others, 2000, Zheng and others, 2008, Zheng and others, 2010. Specifically, one can estimate the marginal distribution of Y empirically as

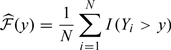(2.2)

and the bivariate survival function 𝒮(t,c) as

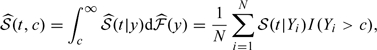(2.3)

where $\widehat{𝒮}\left(t\right|y)$ is an estimator for the conditional survival function 𝒮(t|y) = P(T > t|Y = y), relating to the absolute risk by time t given y. Under a PH model for survival time T and marker Y: λ(t) = λ₀(t)exp(βY), 𝒮(t|y) can be estimated as 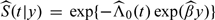, where $\hat{\beta }$ is estimated from the partial likelihood and

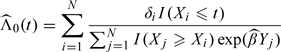is the Breslow estimator of Λ₀(t). Plug-in estimators 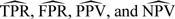can be obtained based on (2.2) and (2.3).

2.3. Estimation under an NCC design

Under an NCC design, since Y is selectively measured depending on outcome and other covariates, rather than completely at random, it is crucial to adjust for the sampling scheme of NCC in order to provide unbiased estimates of the aforementioned accuracy summaries. We will achieve this by casting the problem into the general framework of a failure-time regression model with missing covariates and develop IPW estimators for 𝒮(t,c) and ℱ(c). Our IPW-based procedures will provide consistent estimators of 𝒮(t,c) and ℱ(c) and consequently valid estimators for time-dependent accuracy summaries.

Sampling probability of an NCC design.

As a simple case of the IPW procedure, we consider weighing the contributions from the selected observations with weight 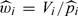, where ${\widehat{p}}_i$ is the probability of the ith subject being selected to the NCC cohort based on the sampling scheme. When all individuals in the cohort with δ = 1 are included in NCC samples, the selection probability is 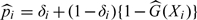as given by Samuelsen 1997, where

It is easy to show that 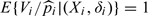. Note that this is the “true” weights dictated by the NCC design. Other weights can be considered. For example, Chen 2001 suggested using local averaging weights within intervals of censoring times. Such “estimated” weight has been shown to improve efficiency with simulations especially in situations when censoring is dependent on covariates.

Estimating 𝒮(t|y).

The log hazard ratio, β, under the PH model can be obtained by maximizing a weighted partial likelihood with weights accounting for outcome-dependent sampling as described above. Specifically, one may estimate β as 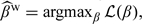, where

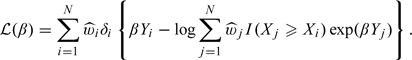(2.4)

Based on ${\widehat{\beta }}^{\text{w}}$, 𝒮(t|y) can be estimated as 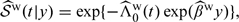, where

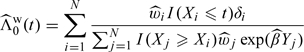can be viewed as a weighted Breslow estimator of Λ₀(t).

Note that ${\widehat{𝒮}}^{\text{w}}\left(t\right|y)$ is different from an existing absolute risk estimator for NCC design defined as 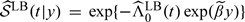, proposed by Langholz and Borgan 1997, where $\stackrel{\sim }{\beta }$ is the conditional logistic regression estimator of β,

and $\stackrel{\sim }{R}(t_j)$ indexes the case who failed at time t_j and the corresponding m matched controls. Intuitively, $\stackrel{\sim }{\beta }$ and ${\widehat{𝒮}}^{\text{LB}}\left(t\right|y)$ obtained from the above procedures might be less efficient since only the case and m selected controls, rather than all the samples at risk, are used in the partial likelihood and for calculating ${\widehat{\lambda }}_0^{\text{LB}}\left(t\right)$.

Estimating F_Y(y) and 𝒮(t,c).

With NCC sampling, we again construct IPW estimators for the distribution function of marker Y and the bivariate survival function of Y and T. Specifically, we consider the following empirical estimator:

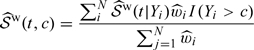for 𝒮(t,c), similar to the representation considered in Akritas 1994. Subsequently, we may estimate ℱ_Y(c) as 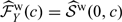and the marginal survival distribution of T, 𝒮(t), as .

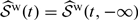Estimating accuracy summaries.

Let ${\widehat{𝒮}}^{\text{w}}(c,t)$, ${\widehat{𝒮}}^{\text{w}}\left(0t\right)$, and ${\widehat{F}}^{\text{w}}\left(c\right)$ denote the respective estimators of 𝒮(c,t), 𝒮(t), and F(c), plug-in accuracy estimators under an NCC study for retrospective accuracy summaries can be calculated as

and 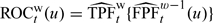. The estimators for prospective accuracy summaries are

Note that an alternative strategy to estimate the accuracy summaries is to replace 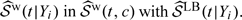IPW is still needed here in order to retrieve information on the marginal distribution of Y.

2.4. Stratified NCC sampling

Often in practice some covariate information is available for all cohort members. A stratified sampling of controls based on surrogate variables that are correlated with the marker may enhance the power of a simple NCC design. In a stratified NCC sampling, at each selected case's failure time, controls are selected for marker measurement randomly without replacement among those who are in the risk set and matched to the case based on some covariate Z. Without loss of generality, we assume that Z consists of discrete random variables. To incorporate additional matching in the proposed IPW approach, we replace ${\widehat{w}}_i$ in the weighted likelihood (2.4) with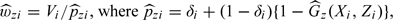

and n_z(X_j,Z_j) = ∑_{k = 1}^NI(X_k ≥ X_j,Z_k = Z_j) is the size of the covariate matched risk set for failure time X_j. It is easy to show that 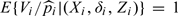. Note that under a stratified NCC sampling design, estimation procedures for obtaining $\stackrel{\sim }{\beta }$ and ${\widehat{𝒮}}^{\text{LB}}\left(t\right|y)$ remain the same, which is clear from equation (4.2) in Borgan and others 1995.

3. INFERENCE PROCEDURES

Deriving inference procedures for the proposed IPW-based estimators for accuracy summaries can be challenging due to the complex data structure induced by NCC sampling. In particular, under the finite-population sampling scheme, indicators of being sampled, V_i, are weakly dependent conditional on 𝒟 = {(X_i,δ_i,Y_i,Z_i),i = 1,…,N}. The standard convergence theorems, such as the law of large numbers or central limit theorems for i.i.d. cases, are not directly applicable here. In the supplementary material available at Biostatistics online, we provide more detailed justifications for the consistency and asymptotic normality of proposed IPW estimators for accuracy summaries for NCC design with finite-population sampling, using results on the strong and weak convergence of weighted sums of NegA dependent variables Liang and others, 2004, Liang and Baek, 2006. The key is to show that 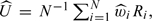where R_i = R(X_i,δ_i,Y_i) for some deterministic function R, can be viewed as weighted sums of NegA dependent variables, and it satisfies the conditions required for tightness and weak convergence of the NegA process (see Appendix B of the supplementary material available at Biostatistics online).

To obtain interval estimates of specific components of our proposed IPW estimators for TPF_t(c), FPF_t(c), ROC_t(u), PPV_t(c), and NPV_t(c), we show in Appendix A of the supplementary material (available at Biostatistics online) that for any of these accuracy measures, denoted by a generic term 𝒜, 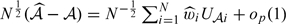which is asymptotically normal with mean 0 and variance

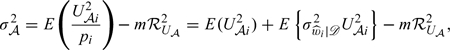where p_i is the limiting value of ${\widehat{p}}_i$, ${\sigma }_{{\widehat{w}}_i|𝒟}^2$ is the conditional variance of ${\widehat{w}}_i$ given 𝒟, and ℛ_U𝒜² as a functional of U_𝒜 is defined in Appendix A of the supplementary material (available at Biostatistics online). The term E(U_𝒜i²) in σ_𝒜² represents the variance of $\widehat{𝒜}$ if Y is observed for the full cohort, 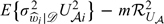represents the inflated variance due to the missing information on Y for the weighted estimator, and − mℛ_U𝒜² represents the variance adjustment due to the weak negative correlation among the V_i's. Omitting the last term from σ_𝒜² would lead to the robust variance estimator of $\widehat{𝒜}$ by treating ${\widehat{w}}_i$ as known independent weights. Thus, using the robust variance alone would always overestimate the true variance of $\widehat{𝒜}$.

In Appendix C of the supplementary material (available at Biostatistics online), we derive 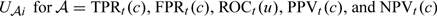, respectively. The asymptotic variance of these accuracy summary estimators can be estimated empirically, and the confidence intervals (CIs) can be constructed based on normal approximations. For example, we show in Appendix C of the supplementary material (available at Biostatistics online) that 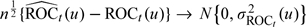in distribution, where 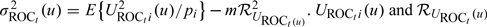are defined in Appendix C of the supplementary material (available at Biostatistics online). A 95% CI for ROC_t(u) may be obtained as 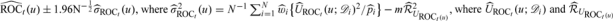are obtained by replacing all theoretical quantities in 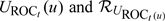by their empirical counterparts, respectively.

4. SIMULATIONS

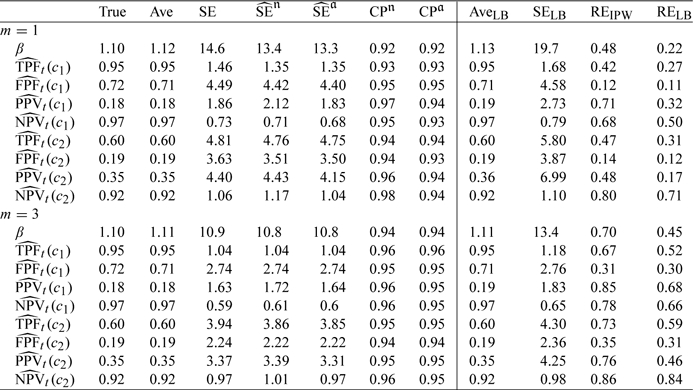
We conduct simulation studies to examine the performance of our proposed methods with practical sample sizes. All results are based on 2000 simulated data sets. We first consider a simple situation with a cohort of N = 1000. We simulate Y from a standard normal distribution and generate T from a PH model: λ(t) = 0.1exp(βY), where β = log(3). Censoring time C is taken to be the minimum of 2 and W, where W follows a gamma distribution, with a shape parameter of 2.5 and a rate parameter of 2. This yields approximately 87% censoring and an average of 133 observed cases. For each cohort, we assemble an NCC subcohort by selecting all cases and m controls per case, with m = 1 or 3. We consider estimating TPF_t(c), FPF_t(c), PPV_t(c), and NPV_t(c) for c equal to the 25th and 75th percentiles of the standard normal distribution and t = 1 under such an NCC sampling. We calculate the plug-in estimators for the accuracy measures by estimating 𝒮(t|y) based on either ${\widehat{𝒮}}^{\text{LB}}\left(t\right|y)$ (referred to as LB estimators) or ${\widehat{𝒮}}^{\text{w}}\left(t\right|y)$ (referred to as IPW estimators). In addition, analytical naive standard errors, ignoring correlations among V_i, and standard errors adjusted for correlations are calculated for the IPW estimators. The results are presented in Table 1 It appears that both sets of estimators are unbiased. However, the IPW estimators in general are more efficient than the LB estimators, as evidenced by their higher relative efficiencies, defined as the ratio of empirical variance estimated from full cohort data to the specific estimated variance from NCC samples. Our adjusted standard errors performed well, with coverage percentage close to 95%. The naive standard errors in most of the cases are quite close to their adjusted counterparts, indicating that correlations are quite weak among observations. However, they do appear to be more conservative when m = 1.

Table 1.

Averages of parameter estimates (Ave), empirical standard error of estimates (SE), the averages of the standard error estimates from naive (${\widehat{\text{SE}}}^n$) and adjusted (${\widehat{\text{SE}}}^a$) estimators, their corresponding coverage probabilities (CPⁿ and CP^a) using the “IPW” approach, average and empirical standard error using the “LB” approach (Ave_LB and SE_LB) based on NCC samplings with cohort size of N = 1000 and m = 1 or 3 controls. Relative efficiencies of both approaches (RE_ipw and RE_LB) are relative to the cohort. Accuracy summaries of marker Y are evaluated at t = 1 and c₁ = F_Y⁻¹(0.25), c₂ = F_Y⁻¹(0.75), respectively. Censoring times are independent of Y

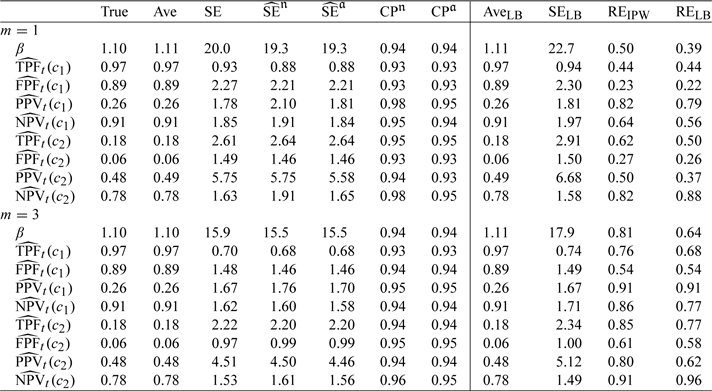
In the second scenario (Table 2, T is generated using the same model but Y and C are constructed with a more complicated scheme. Specifically, Y is generated from a mixture of normal distributions: Y = ℬW₁ + (1 − ℬ)W₂, where ℬ∼Bernoulli(0.9), W₁∼N(0,0.5), and W₂∼N(0.3,0.1). To introduce marker-dependent censoring, we let C∼Uniform(0.5,1.5) if ℬ = 1 and C = exp(𝒵/5 − 3Y) with 𝒵∼N(0,1) if ℬ = 0. The average number of cases in this setting is around 200. We would expect our IPW estimators to be robust in this situation. Indeed, all estimators are unbiased. The adjusted variance estimators also work well; however, the naive variance estimators for PPV_t(c) and NPV_t(c) again could have inflated values with one matched control.

Table 2.

Summary statistics (same as in Table 1.) from simulation studies based on NCC samplings with cohort size of N = 1000 and m = 1 or 3 controls and with censoring times dependent on Y

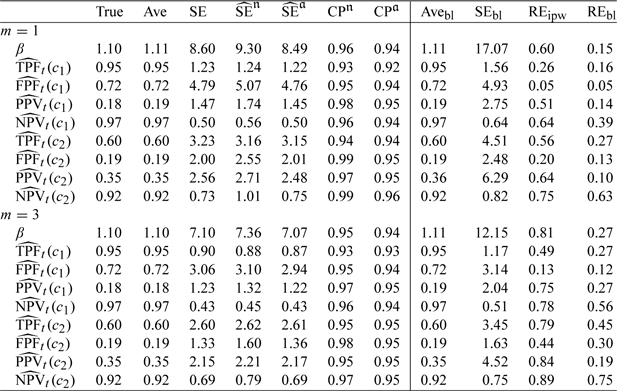
We also consider a scenario where controls are also matched with cases on a binary covariate Z. With a cohort of size 2000, we first generate Y from a standard normal distribution, we then generate a binary Z such that Z = 1 if Y > 0. The same models for T and C are used as in the first scenario, which yield on average 266 cases among 2000 simulated data sets. Results in Table 3 again indicate that our proposed estimators under stratified NCC design perform well. The naive variance, without considering the correlation due to finite sampling, often lead to overestimated variances.

Table 3.

Summary statistics (same as in Table 1) from simulation studies based on NCC samplings with cohort size of N = 2000 and matched on a binary covariate Z

5. EXAMPLE

We illustrate our proposal by evaluating the accuracy of an inflammation marker, C-reactive protein (CRP), for predicting the risk of cardiovascular disease (CVD) using the Framingham Offspring Study. Conventional risk factors have been identified for assessing CVD risk in the general population, but these characteristics explain only a fraction of CVD risk. Contemporary biomarkers such as CRP have been sought for use in risk stratification and preventive decision making Ridker and others, 2000. However, its clinical usefulness has not been established.

The Framingham Offspring Study was initiated in 1971 with a cohort of 5124 participants. The Framingham Study samples were monitored prospectively, providing a valuable resource for studying epidemiological and genetic risk factors of CVD. We consider here 3289 Offspring Study participants with CRP measurements at the second examination and who were free of CVD at the examination (mean age 44 years and 53% women). We consider outcome as time from examination date to first major CVD event or CVD-related death as defined previously Lloyd-Jones and others, 2004. Since we are interested in the short-term predictive capacity of CRP, individuals with follow-up time longer than 10 years were considered censored at 10 years. During the follow-up period, 251 participants were observed to encounter at least one CVD event. Since CRPs are complete in the cohort, the Framingham data allow us to illustrate our methods with a real data set and to compare the relative efficiency of a few sampling strategies with analysis using the full cohort. From the full cohort data, we further assemble NCC subcohorts with 1 or 3 controls who were selected either (i) without additional matching or (ii) matched to their corresponding cases based on gender and age groups (<30, 30–39, 40–49, >50).

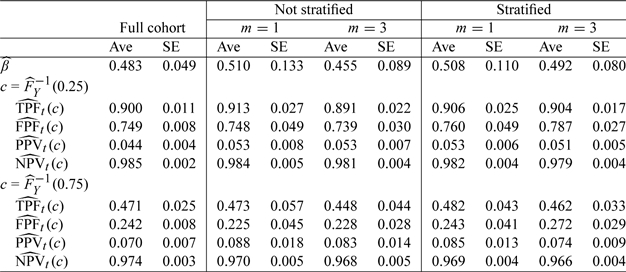
We use a PH model to specify the relation between the failure time and CRP concentration (in log scale). We then calculate the accuracy measures of CRP for predicting CVD by 5 years since the measurement of CRP (i.e., t = 5). We considered low and high thresholds, set as the 25th or 75th percentile of the CRP levels in the full cohort. That is, these thresholds would, respectively, classify approximately 75% or 25% of the population as testing positive based on CRP. The accuracy summaries at both values are presented in Table , where, in the first and second columns, parameter estimates and standard error estimates for the cohort data are given. The estimates from different NCC samples, presented in the rest of the columns, are quite close to the results using the full cohort data, suggesting that time-dependent accuracy summaries can be reliably estimated from the case–control data with our methods. Matching on age and gender improves the efficiency of most estimates slightly, and including more controls results in more precise inference. Compared to a full cohort analysis, the standard errors for TPF and FPF, although relatively larger using NCC samples, are still sufficiently precise for making decisions regarding the discriminatory capacity of CRP. For example, with a 24% FPF, we can detect about 47% of the subjects who experience a CVD event or death by 5 years, with a CI of (42%, 52%) estimated from the full cohort. The same detection rate with a CI of (36%, 58%) is observed from an NCC study selecting one matched control per case. Both suggest a significantly better performance than that of a noninformative marker, which is expected to have a TPF of only 24% at this threshold. Such information would be helpful for investigators to plan for more cost-effective future biomarker studies. Based on the results listed in Table 4, we conclude that the predictive accuracy of CRP is quite moderate and that using CRP for preventive decision making should be done with caution. Further assessment of the incremental value of CRP over conventional risk factors is warranted.

Table 4.

Estimated accuracy summaries (Ave) and standard errors (SE) of CRP at 2 thresholds for predicting 5-year CVD events from Framingham data with m = 1 and 3 controls and with/without stratified by age and gender

6. REMARKS

The NCC sampling has been recognized as a useful design option within cohort study in the field of biomarker research Rundle and others, 2005. Biomarker studies are often influenced by factors such as analytic batch, long-term storage, and freeze-thaw cycles. By matching individual controls to cases' failure times and other potential confounding factors, the accuracy of biomarkers can be evaluated more efficiently and rigorously with an NCC design. However, matching generates complex data that can be more difficult to analyze. We proposed estimators for 2 classes of accuracy measures under an NCC design based on the IPW approach. By reusing samples in each risk set, the approach yields more efficient estimators for those accuracy summaries compared to estimators derived from a partial likelihood, without requiring more information from the study. Furthermore, compared with a nonparametric MLE-based approach Scheike and Martinussen, 2004, this approach is very simple to implement and is robust to marker-dependent censoring. Extension of the proposed methods to models with multiple covariates and an estimation of covariate-specific accuracy is straightforward. Our theoretical development on the IPW estimators is useful for making inference on accuracy summary estimators in practice, given that justification for bootstrap-based variance estimators has not been developed under cohort sampling settings.

In our estimation procedure, we focused on weights with “true” selection probability according to the study design. The weights can be less optimal. Less expensive covariate information is often available for all subjects in a cohort. Incorporating such information may well yield estimators with improved efficiency. In particular, it is possible to derive semiparametric efficient estimators in this setting following the work of Robins and others 1994. Alternatively, parallel to recent work for case–cohort design Breslow and Wellner, 2007, Breslow and others, 2009, one may consider nonparametric procedures to obtain augmented weights using auxiliary information in order to gain efficiency. Our proposal here lays important groundwork for further investigation.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://www.biostatistics.oxfordjournals.org.

FUNDING

National Institutes of Health (RO1-GM085047, U01-CA86368, P01-CA053996, and R01-GM079330).