Checking semiparametric transformation models with censored data

Abstract

Semiparametric transformation models provide a very general framework for studying the effects of (possibly time-dependent) covariates on survival time and recurrent event times. Assessing the adequacy of these models is an important task because model misspecification affects the validity of inference and the accuracy of prediction. In this paper, we introduce appropriate time-dependent residuals for these models and consider the cumulative sums of the residuals. Under the assumed model, the cumulative sum processes converge weakly to zero-mean Gaussian processes whose distributions can be approximated through Monte Carlo simulation. These results enable one to assess, both graphically and numerically, how unusual the observed residual patterns are in reference to their null distributions. The residual patterns can also be used to determine the nature of model misspecification. Extensive simulation studies demonstrate that the proposed methods perform well in practical situations. Three medical studies are provided for illustrations.

1. INTRODUCTION

The proportional hazards model (Cox, 1972) is commonly used in the analysis of survival time and related data. The proportional hazards assumption may be violated in practice, and other models may provide more precise or more parsimonious summarization of data. The class of transformation models is a broad generalization of the proportional hazards model to allow various nonproportional hazards structures, such as proportional odds (Bennett, 1983; Pettitt, 1984). This generalization can substantially enhance the validity of inference and the accuracy of prediction. Transformation models have received tremendous recent attention (e.g. Cheng and others, 1995, 1997; Murphy and others, 1997; Scharfstein and others, 1998; Cai and others, 2002; Chen and others, 2002; Tsodikov, 2003; Kosorok and others, 2004; Lu and Ying, 2004; Lu and Tsiatis, 2006; Zeng and Lin, 2006, Zeng and Lin, 2007).

The class of linear transformation models relates an unknown transformation of the survival time T linearly to a p-vector of covariates X:

(1.1)

where H(·) is an unspecified increasing function, β is a set of unknown regression parameters, and ϵ is a random error with a parametric distribution (Dabrowska and Doksum, 1988; Kalbfleisch and Prentice, 2002, p. 241). Although it generalizes the proportional hazards model to nonproportional hazards models, this class of models can only handle survival time (i.e. single event) with time-independent covariates.

To accommodate time-dependent covariates and recurrent events, we use the counting process N^*(t) to denote the number of events the subject has experienced by time t and allow X to be a function of t. We then specify that the cumulative intensity function for N^*(t) conditional on {X(s);s ≤ t} takes the form

(1.2)

where G is a strictly increasing function, Y^*(·) is an indicator process, and Λ(·) is an unspecified increasing function (Zeng and Lin, 2006). For survival data, Y^*(t) = I(T ≥ t), where I(·) is the indicator function; for recurrent events, Y^*(·) = 1. We consider the class of Box–Cox transformations G(x) = {(1 + x)^ρ − 1}/ρ(ρ ≥ 0) with ρ = 0 corresponding to G(x) = log(1 + x) and the class of logarithmic transformations G(x) = log(1 + rx)/r(r ≥ 0) with r = 0 corresponding to G(x) = x. The choice of G(x) = x (ρ = 1; respectively r = 0) yields the proportional hazards model for survival data and the proportional intensity model (Andersen and Gill, 1982; Kalbfleisch and Prentice 2002, Section 9.3) for recurrent events data; the choice of G(x) = log(1 + x) (ρ = 0; respectively r = 1) yields the proportional odds model. Various choices of ρ and r are considered in this paper, but we are not trying to estimate the values of these parameters. If N^*(·) has a single jump at the survival time T and X is time independent, then (1.2) reduces to (1.1).

For recurrent events, (1.2) implies that the occurrence of an event is independent of the prior event history conditional on covariates. To remove this assumption, we consider the following class of transformation mean models

(1.3)

where μ_X(t) = E{N*(t)|X(s): s ≤ t} and μ(·) is an unspecified increasing function (Lin and others, 2001). This is a class of marginal models that formulates the effects of covariates on the mean function of the recurrent event process while leaving the dependence structure completely unspecified. The choice of G(x) = x yields the proportional means model (Lin and others, 2000). We also consider the class of random-effect transformation models Λ(t|X,ξ) = ξG{∫₀^te^βTX(s)dΛ(s)}, where Λ(t|X,ξ) is the cumulative intensity function for N^*(t) conditional on {X(s);s ≤ t} and ξ, and ξ is a random variable with mean 1 characterizing the dependence (Zeng and Lin, 2007). This model is a special case of model (1.3) in that the mean function of N^*(·) induced by it satisfies equation (1.3).

The classes of semiparametric transformation models as shown in (1.2) and (1.3) require specification of the following components: (i) the functional forms of individual covariates; (ii) the link function, that is, the exponential regression function; (iii) the proportionality structure, that is, the multiplicative effect of the regression function within the transformation; and (iv) the transformation function G. Misspecifying any of these components can result in erroneous inference and inaccurate prediction. Recent theoretical and methodological advances in transformation models have heightened the importance of model assessment and model selection.

In this paper, we introduce time-dependent residuals for semiparametric transformation models in the form of (1.2) or (1.3) and use the cumulative sums of the residuals to construct graphical and numerical procedures for model assessment. These methods can be used to assess specific model components as well as the overall fit of the model. A similar approach was taken by Lin and others (1993) for the proportional hazards model with survival data and time-independent covariates. It is substantially more challenging, both theoretically and numerically, to deal with nonproportional hazards models because of the nonlinearity of G(·) and the lack of an explicit expression for the estimator of Λ(·) or μ(·). To aid the selection of appropriate models, we explore the use of residual patterns in determining the nature of model misspecification.

2. METHODS

Let C denote the censoring time, which is assumed to be independent of N^*(·) conditional on X(·). The at-risk process is Y(t)≡Y^*(t)I(C ≥ t), and the observed counting process is N(t)≡N^*(t∧C), where a∧b = min(a,b). The data consist of n independent replicates of {N(t),Y(t),X(t);t∈[0,τ]}, where τ denotes the end point of the study.

We first focus on the class of models given in (1.2), under which the intensity function for N_i(t) is Y_i(t)e^βTX_i(t)λ(t)G^′{∫₀^tY_i(s)e ^βTX_i(s)d Λ(s)}, where λ(t) = Λ^′(t). Here and in the sequel, g^′(x) = dg(x)/d x, and g^′′(x) = d²g(x)/d x². The log-likelihood concerning parameters β and Λ(·) is given by

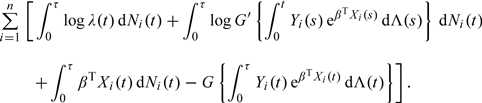(2.1)

Let 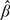and 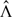denote the nonparametric maximum likelihood estimators (NPMLEs) of β and Λ based on (2.1). The existence and asymptotic properties of the NPMLEs were established in Zeng and Lin (2006). For the special case of the proportional hazards model, 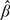and 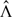correspond to the maximum partial likelihood estimator for β and the Breslow (1972) estimator for Λ.

Define

(2.2)

When the assumed model holds and β and Λ are evaluated at their true values, the M_i's are zero-mean martingales. Replacing β and Λ with their NPMLEs 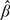and 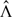yields the martingale residuals 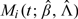. Since they characterize the differences between the observed and model-predicted numbers of events, the martingale residuals are informative about model misspecification. One can plot these residuals against certain coordinates (e.g. covariates or time) to check various model components (e.g. Fleming and Harrington, 1991, pp. 163–178).

To develop more objective and more informative model-checking techniques, we study the cumulative sums of martingale residuals over the covariate or time domain. To check the functional form of the effect of X^(j), the jth component of the covariate vector X, we consider the cumulative sum of residuals over that covariate, that is,

where X_ji is the jth component of X_i. To check the link function and the transformation function, we consider the cumulative sums of residuals over the linear predictor and the argument of the transformation function

and

respectively. To check the proportionality assumption for X^(j), we consider the score process

where 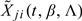is the jth component of

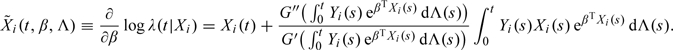To assess the overall fit of the model, we consider the process

Note that x is a p-vector in W_o(x,t) and a scalar in all other processes. For vectors x and y, x ≤ y means that every component of x is smaller than or equal to the corresponding component of y. Because 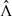changes its values at observed event times only, all above processes involve the values of time-dependent covariates at observed event times only. For processes W_c^(j) and W_p^(j), we may suppress the superscript (j) when we are interested in a specific covariate or when we wish to refer to the collection of the processes over all j. We refer to W_p(·) as the score process because it pertains to the score function for β (Andersen and others, 1993, p. 103). In the special case of the proportional hazards model with time-independent covariates, W_c(x,∞), W_l(x,∞), W_p(t), and W_o(x,t) reduce to the processes studied by Lin and others (1993), who provided intuitions for the use of such processes in model checking. Under (1.2), the relationship between the counting process and the argument of G determines the functional form of G; therefore, W_tr(x,t) is informative about the adequacy of the transformation function.

All the aforementioned processes are special cases of the multiparameter process

where f₁ and f₂ are known smooth functions, and 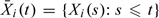. We assume Conditions 1–4 of Zeng and Lin (2006) and impose a slightly stronger version of the first part of their Condition 2 by assuming that, with probability 1, X(·) is left-continuous with right limits, and there exist constants K₁ and K₂ such that X(·) is bounded by K₁ and its total variation is bounded by K₂. We also assume that there is at least one continuous covariate in W_l(x,t) and W_tr(x,t); otherwise, W_l(x,t) and W_tr(x,t) may not be centered at zero asymptotically at the discontinuous points of x. Under these conditions and model (1.2), we show in Section S.1 of the supplementary material (available at Biostatistics online) that W_n(x,t) converges weakly to a zero-mean Gaussian process in the metric space 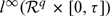and is asymptotically equivalent to the following process

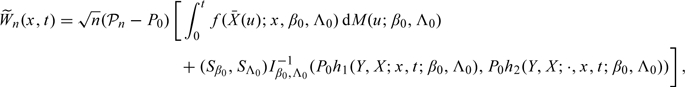where q is the dimension of f₂, 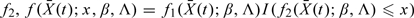, S_β0 and S_Λ0 are, respectively, the score operators for β and Λ at the true parameter values (β₀,Λ₀), I_β0,Λ0 is the information operator at (β₀,Λ₀), 𝒫_n and P₀ are, respectively, the empirical measure and the distribution under the true model,

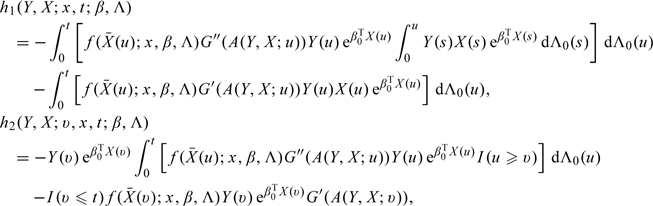and 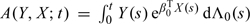. Here, we use Qf to denote ∫fdQ for a given measurable function f and measure Q.

We use Monte Carlo simulation to evaluate the null distribution of W_n(x,t). Define

where the Q_i's (i = 1,…,n) are independent standard normal random variables, and the S_i's are calculated in the following way. Let t₁,…,t_k be the distinct observed event times. We treat β and the jump sizes of Λ(·) at (t₁,…,t_k) as the parameters. We calculate the score vector for these parameters for the ith subject, denoted by l_i, and the observed information matrix for these parameters, denoted by I_n. Let 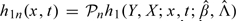and let h_2n(x,t) be a k-dimensional vector with the ith component being 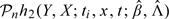. Then, 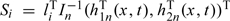. We show in Section S.2 of the supplementary material (available at Biostatistics online) that the conditional distribution of 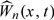given the observed data {N_i(t),Y_i(t),X_i(t);t∈[0,τ],i = 1,…,n} has the same limiting distribution as 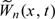. To approximate the null distribution of W_n(x,t), we simulate a number of realizations from 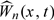by repeatedly generating the normal random sample (Q₁,…,Q_n) while fixing the data {N_i(t),Y_i(t),X_i(t);t∈[0,τ],i = 1,…,n} at their observed values.

The above results enable us to construct goodness-of-fit tests. For example, we can use the omnibus test statistic sup_x,t|W_o(x,t)| to assess the overall fit of the model and use sup_x|W_c^(j)(x,∞)| or sup_x,t|W_c^(j)(x,t)| to evaluate the adequacy of the functional form of X^(j). Likewise, we can use sup_x|W_l(x,∞)| or sup_x,t|W_l(x,t)| to check the link function and use sup_x|W_tr(x,∞)| or sup_x,t|W_tr(x,t)| to check the transformation function. In addition, we can use sup_t|W_p^(j)(t)| to test the proportionality assumption for X^(j). To calculate the p value of a supremum test, we generate a large number, say 1000, of realizations of the test statistic from its null distribution through the aforementioned Monte Carlo procedure. We can also visually assess how unusual an observed residual process is by plotting it against a few, say 20, realizations from the simulated process. The consistency of the supremum tests is stated in the Appendix.

REMARK 2.1

If there is only a single covariate in the model, then the functional form of the covariate is the same assumption as the link function. If the true model is proportional odds and the assumed model is proportional hazards, then we may say that the proportional hazards assumption fails or that the transformation function is misspecified. Thus, testing functional forms of covariates is related to testing the link function, and testing the proportionality assumption is related to testing the transformation function.

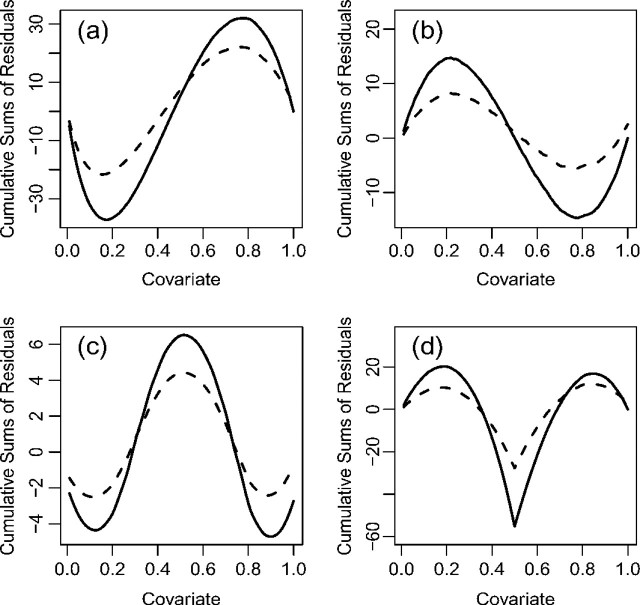
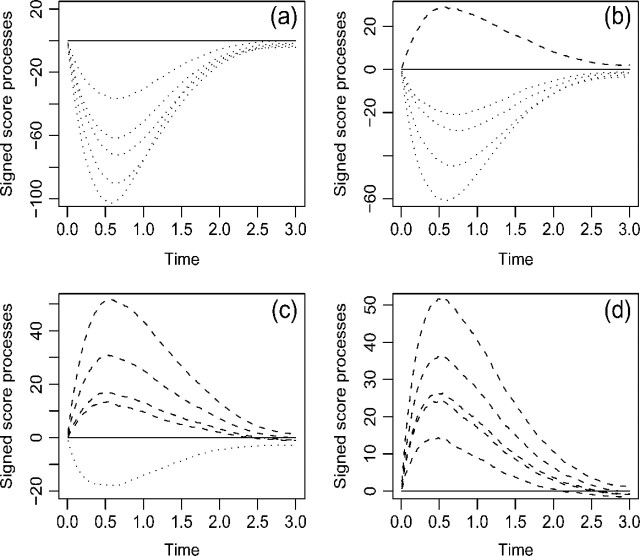
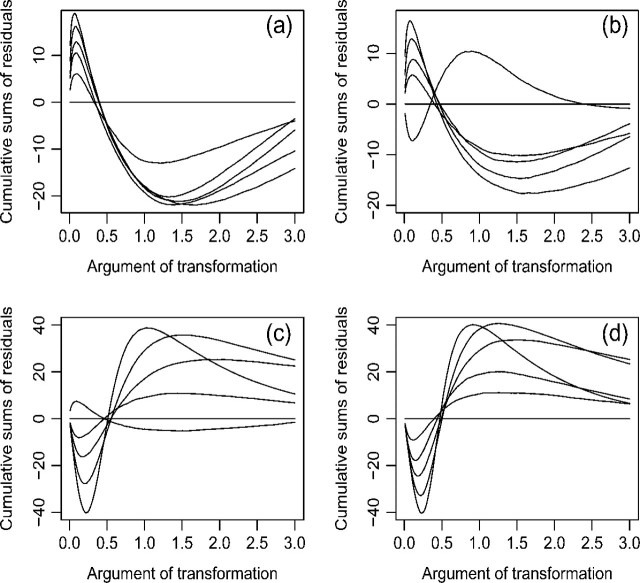
If a goodness-of-fit procedure reveals model misspecification, then the next step is to identify the nature of the misspecification and to correct the misspecification. To this end, it is helpful to ascertain the residual patterns under various forms of model misspecification. Figure 1 displays the mean functions for the cumulative sums of residuals W_c(·,∞) when the functional form of the covariate is misspecified in a few hypothetical situations. The trends are the same for all transformation models. By comparing the observed residual pattern with those of Figure 1, one may find a more appropriate functional form for a covariate. Figure 2 shows the mean functions of the signed score processes (i.e. W_p^(j)(·) times the sign of 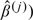) under the Box–Cox and logarithmic transformations. When the observed curve is concave and above zero, we should use a smaller ρ, respectively, a larger r; when the observed curve is convex and below zero, we should use a larger ρ, respectively, a smaller r. Figure 3 shows the mean functions of W_tr(·,∞) under the Box–Cox and logarithmic transformations. When the observed curve is convex at the beginning and then becomes concave, we should use a smaller ρ, respectively, a larger r; when the observed curve is concave at the beginning and then becomes convex, we should use a larger ρ, respectively, a smaller r. Figure 2 applies to a specific component of X, whereas Figure 3 applies to the whole vector of X in the argument of G.

Fig. 1.

The mean functions of the cumulative sums of residuals W_c(·,∞) when the function form of the covariate X is misspecified: (a) the true linear predictor γlogX is misspecified as β₁X; (b) the true linear predictor β₁X + γX² is misspecified as β₁X; (c) the true linear predictor β₁X + β₂X² + γX³ is misspecified as β₁X + β₂X²; and (d) the true linear predictor γI(X > 0.5) is misspecified as β₁X. We set X to be uniform(0,1) and γ = 1. The solid and dashed curves correspond to the proportional hazards and proportional odds models, respectively. The trends remain the same for other transformation models. The curves will look upside down under γ = − 1.

Fig. 2.

The mean functions of the signed score processes, that is, W_p(·) times the sign of 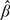, under Λ(t|X) = G(Λ(t)exp(βX)): (a) Box–Cox transformation with ρ = 2; (b) proportional hazards (ρ = 1; respectively r = 0); (c) proportional odds (ρ = 0; respectively r = 1); and (d) logarithmic transformation with r = 2. In each panel, the curves, as shown from top to bottom, pertain to the fitted models with ρ = 2, 1, and 0.5 and r = 0.5, 1, and 2 in that order. We set X to be uniform (0,9) and β = − 0.2.

Fig. 3.

The mean functions of the cumulative sums of residuals W_tr(·,∞) under Λ(t|X) = G(Λ(t)exp(β^TX)): (a) Box–Cox transformation with ρ = 2; (b) proportional hazards (ρ = 1; respectively r = 0); (c) proportional odds (ρ = 0; respectively r = 1); and (d) logarithmic transformation with r = 2. In each panel, the curves, as shown from bottom to top before crossing, pertain to the fitted models with ρ = 2, 1, and 0.5 and r = 0.5, 1, and 2 in that order. We set X to be uniform (0,9) and β = 1.0.

REMARK 2.2

A faulty functional form of a covariate may manifest itself in the residual plot for a correlated covariate or the link function. Thus, all the proposed methods are checking the fit of the entire model. However, W_c^(j) and W_p^(j) are most informative about the functional form and proportionality of X_j, respectively, while W_l and W_tr are most sensitive to misspecification of the link function and transformation function, respectively. We suggest the following strategy: for a given transformation model, apply the proposed tests in the order of W_c, W_l, W_p, W_tr, and W_o; if one of the tests is significant, determine the nature of model misspecification by examining the residual patterns and make appropriate correction; repeat this process until all p values are greater than a threshold, say 0.05 or 0.10.

We now consider the class of transformation mean models given in (1.3). We obtain a pseudo log-likelihood function for β and μ(·) from (2.1) by replacing Λ(·) with μ(·). The resulting maximum pseudo-likelihood estimators are denoted by 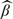and 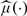. Define the residuals as 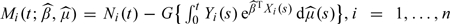. Then, all the methods developed in this section can be applied; see Section S.4 of the supplementary material (available at Biostatistics online) for theoretical justifications.

3. SIMULATION STUDIES

Our first set of studies was aimed at assessing the type I error of the supremum tests. We generated survival times from a special case of model (1.2): Λ(t|X) = G(texp( − X₁ + 0.2X₂)), where X₁ is Bernoulli with 0.5 success rate, and X₂ is a continuous variable that may be time independent or time dependent. For the time-independent case, X₂ is the sum of X₁ and a standard normal variable. For the time-dependent case, X₂(t) = a + (b + 2)logt + 0.5ϵ(t), where a and b are standard normal and ϵ(t) is an independent Gaussian process with mean 0 and variance 1. We also generated recurrent event times from the random-effect transformation model: Λ(t|X,ξ) = ξG(texp( − X₁ + 0.2X₂)), where ξ is a gamma random variable with mean 1 and standard deviation 0.5. We generated censoring times from the uniform (1.5,5) distribution and set τ = 3. As shown in Supplementary Tables 1 and 2 of the supplementary material (available at Biostatistics online), the supremum tests have adequate control of type I error when there are more than 70 events for the case of time-independent covariates and more than 140 events for the case of time-dependent covariates but tend to have inflated type I errors when there are fewer events.

Because there are no other goodness-of-fit tests for transformation models, we compared the power of the supremum tests against Wald tests in situations where the latter might be used. Wald tests are asymptotically efficient against nested alternatives but are inappropriate for nonnested alternatives. To illustrate this point, we compared the supremum tests to Wald tests in 2 simulation settings. In the first setting, we generated survival times and recurrent event times from models Λ(t|X) = G(texp(0.4X − 0.1X²)) and Λ(t|X,ξ) = ξG(texp(0.4X − 0.1X²)), respectively, where X takes values 0–9 with the same probability, and ξ is the same as before. We generated censoring times from the uniform (0,τ) distribution. In the second setting, the true functional form of X is exp{3(X − 5)}/[1 + exp{3(X − 5)}] and β = 3.5. In both settings, we performed the Wald test of the null hypothesis of β₂ = 0 under the model Λ(t|X) = G(Λ₀(t)exp(β₁X + β₂X²)). As shown in Supplementary Tables 3 and 4 of the supplementary material (available at Biostatistics online), the proposed supremum tests have reasonable power (relative to the Wald test) in the first setting and is much more powerful than the Wald test in the second setting. For the proportional odds model in the second setting, the power of the Wald test is 0.174, while the powers of sup_x|W_c(x,∞)| and sup_x,t|W_c(x,t)| are 0.825 and 0.841, respectively.

One can use the Wald statistic to detect nonproportionality in the form of an interaction between covariate and time. Such a Wald test will be asymptotically efficient if the form of the interaction is correctly specified but may have poor power if the form is incorrectly specified. To illustrate this point, we considered 2 simulation settings. In the first setting, we generated survival times from the model Λ(t|X) = G(∫₀^texp(0.2X + 0.2X×log(s))ds), where X takes values 0–9 with the same probability, and we generated censoring times from the uniform (0,3) distribution. The second setting was the same as the first except that Λ(t|X = x) = G(∫₀^texp( − 0.1x − 0.5x×sin(2×s))ds). In both settings, we used the Wald statistic to test the hypothesis of β₂ = 0 under Λ(t|X) = G(∫₀^texp(β₁X + β₂X×log(s))ds). As shown in Supplementary Table 5 of the supplementary material (available at Biostatistics online), the supremum test has reasonable power (relative to the Wald test) in the first setting and is much more powerful than the Wald test in the second setting. For the proportional odds model in the second setting, the power of the Wald test is 0.345 while that of the supremum test is 0.957.

4. EXAMPLES

In this section, we illustrate the proposed methods with 2 examples, one on survival data and one on recurrent events. A third example, which deals with time-dependent covariates, is provided in Section S.5 of the supplementary material (available at Biostatistics online).

4.1. Colon cancer data

Lin (1994) described a colon cancer study conducted to assess the efficacy of adjuvant therapy on cancer relapse and death for patients with resected colon cancer. For this illustration, we consider the time to cancer relapse and focus on the comparison between the observation and levamisole combined with 5-fluorouracil (Lev+5-FU) groups. By the end of the study, 155 of the 315 observation patients and 103 of the 310 Lev+5-FU patients had cancer relapse. We consider 4 covariates: treatment (1 = Lev+5-FU; 0 = observation), number of days from surgery to randomization, depth of invasion, and number of nodes. Treatment and depth of invasion are binary, whereas number of days and number of nodes are treated as continuous.

We start with the proportional hazards model. The supremum tests sup_x|W_c(x,∞)| for checking the functional forms of number of days and number of nodes have p values of 0.16 and 0.004, indicating that number of nodes on its original scale is inappropriate. After comparing the observed cumulative residual pattern with those of Figure 1, we take the transformation log(1 + number of nodes). Then, the p value of the supremum test is increased to 0.94. The supremum tests for checking the proportionality of treatment, number of days, depth, and log(1 + number of nodes) have p values of 0.75, 0.40, 0.72, and 0.012, respectively, indicating nonproportional hazards for log(1 + number of nodes). Figure 4 displays the score process W_p(·) for log(1 + number of nodes). The observed curve is concave and above zero, and the estimated regression parameter for log(1 + number of nodes) is positive. According to Figure 2, it is more appropriate to use a Box–Cox transformation with ρ < 1 or a logarithmic transformation with r > 0. Supplementary Figure 1 of the supplementary material (available at Biostatistics online) shows the plot of the cumulative sum of residuals W_tr(·,∞). The observed curve is convex at the beginning and then becomes concave, which (in comparison with Figure 3) also suggests a Box–Cox transformation with ρ < 1 or a logarithmic transformation with r > 0. The omnibus test sup_x,t|W_o(x,t)| has a p value of 0.19.

Fig. 4.

Plot of the score process W_p(·) for log(1 + number of nodes) in the colon cancer data: the observed pattern is shown by the solid curve while 20 simulated realizations from the null distribution are shown in dotted curves.

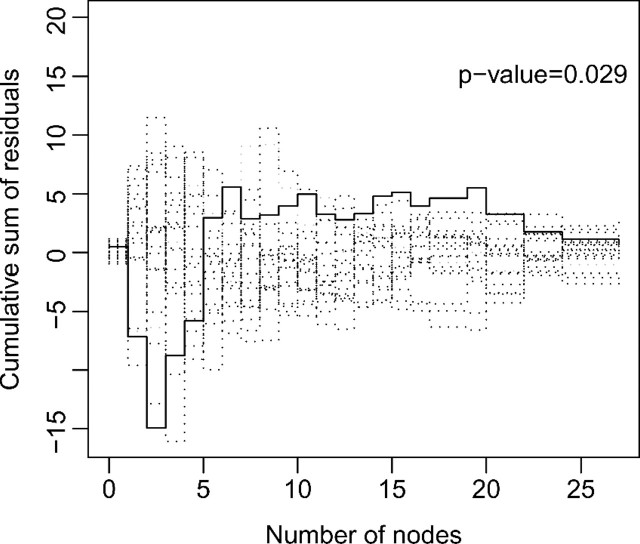
We consider the Box–Cox transformations with ρ = 2, 1, .5 and the logarithmic transformations with r = 0.5, 1, 2. The Akaike information criterion selects the logarithmic transformation with r = 1, that is, the proportional odds model. We then assess the adequacy of this model using the proposed goodness-of-fit methods. The supremum tests sup_x|W_c(x,∞)| and sup_x,t|W_c(x,t)| yield p values of 0.25 and 0.92 for the functional form of number of days and p values of 0.029 and 0.034 for number of nodes. Thus, the functional form for number of nodes is problematic. The p values for the link function tests sup_x|W_l(x,∞)| and sup_x,t|W_l(x,t)| have p values of 0.28 and 0.41. Figure 5 plots the cumulative sum of residuals W_c(·,∞) for number of nodes. The observed pattern resembles the dashed curve of Figure 1(a), suggesting the log transformation. After the log transformation, the 2 supremum tests for the functional form of number of nodes have p values of 0.84 and 0.52, and the 2 tests for the link function have p values of 0.58 and 0.81. The supremum tests for the proportionality assumption have p values of 0.80, 0.43, 0.39, and 0.25 for treatment, number of days, depth of invasion, and log(1 + number of nodes), respectively. Thus, the proportionality assumption is reasonable. The transformation function is also reasonable, the p values of sup_x|W_tr(x,∞)| and sup_x,t|W_tr(x,t)| being 0.35 and 0.44, respectively. The omnibus test has a p value of 0.71.

Fig. 5.

Plot of the cumulative sum of residuals W_c(·,∞) for the functional form of number of nodes in the colon cancer data: the observed pattern is shown by the solid curve while 20 simulated realizations from the null distribution are shown in dotted curves.

Table 1 contrasts the estimation results under the proportional hazards model and the selected proportional odds model. Although the levels of statistical significance for the 4 regression parameters are similar between the 2 models, the interpretations of the regression effects are very different under the proportional odds model versus the proportional hazards model. Also, the logarithmic transformation entails a different interpretation for the effect of number of nodes than the original scale.

Table 1.

Analysis of the colon cancer data under the proportional hazards and proportional odds models

	Proportional hazards model				Proportional odds model
Parameter	Est	SE	Est/SE	p value	Est	SE	Est/SE	p value
Treatment	– 0.510	0.128	– 3.977	< 0.001	– 0.638	0.165	– 3.863	< 0.001
Number of days	– 0.014	0.010	– 1.456	0.145	– 0.017	0.013	– 1.325	0.185
Depth	– 0.720	0.229	– 3.148	0.002	– 0.980	0.269	– 3.639	< 0.001
Log(number of nodes + 1)	0.734	0.097	7.539	< 0.001	1.009	0.133	7.582	< 0.001

4.2. Chronic granulomatous disease data

We consider the recurrent infection data from a placebo-controlled clinical trial on chronic granulomatous disease (CGD) (Fleming and Harrington, 1991). The study was conducted to evaluate the ability of gamma interferon in reducing the rate of CGD infection. A total of 128 patients were enrolled in the study. By the end of the study, 14 of the 63 patients on gamma interferon and 30 of the 65 placebo patients had experienced at least one infection.

We fit the proportional means model with treatment and age as covariates. As shown in Supplementary Figure 2 of the supplementary material (available at Biostatistics online), there is no evidence of lack-of-fit for any of the model components. The omnibus test has a p value of 0.224.

For further illustration, we consider the transformation mean model with r = 1. The supremum test sup_x,t|W_tr(x,t)| for checking the transformation function has a p value of 0.044, indicating that the choice of the transformation parameter r = 1 is not appropriate. The observed cumulative sum of residuals W_tr(·,∞) shows a pattern of being concave at the beginning and then becoming convex, which (in comparison with Figure 3) suggests that a transformation function in the direction of ρ = 1 is more appropriate.

5. DISCUSSION

Although goodness-of-fit methods for the proportional hazards model have been developed extensively over the last 3 decades, there are major limitations with the existing work. For example, there does not exist any method for checking the functional forms of time-dependent covariates. Also, the use of the observed cumulative sums of martingale residuals in determining the nature of model misspecification has never been investigated before. Our work fills those important gaps in the existing literature.

Due to the potential nonlinearity of G and the lack of an explicit form f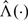or or 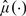, it is much more difficult to establish the weak convergence of the cumulative sum processes and the consistency of the supremum tests for general transformation models than for the proportional hazards model. In the special case of the proportional hazards model, it is straightforward to show that the supremum tests sup_x|W_c(x,∞)| and sup_x|W_l(x,∞)| are consistent against misspecification of the functional forms of covariates and misspecification of the link function, respectively. For other members of the transformation models, the consistency can only be established for sup_x,t|W_c(x,t)| and sup_x,t|W_l(x,t)|. Simulation results, such as those shown in Supplementary Table 4 of the supplementary material (available at Biostatistics online), reveal that sup_x|W_c(x,∞)| is more powerful than sup_x,t|W_c(x,t)| for the proportional hazards model and its neighbors but is less powerful than the latter for the proportional odds model and logarithmic transformations with r > 1.

To capture the dependence of recurrent event times, one may include the event history as covariates in model (1.3). The proposed methods remain valid as such covariates still satisfy our conditions. In the presence of such internal time-dependent covariates, μ_X no longer has the mean function interpretation. It is difficult to correctly formulate the dependence structure through time-dependent covariates even when recurrent event times follow a simple frailty model, and the inclusion of the event history in the model attenuates the estimates of treatment effects. Thus, we recommend not to use the event history as covariates. Indeed, an advantage of model (1.3) is that the dependence structure needs not be specified.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

National Institutes of Health (R37 GM047845 and R01 CA82659); University of North Carolina Cancer Research Fund.

APPENDIX

A.1 Consistency of Supremum Tests

We state below the results on the consistency of the supremum tests while relegating the proofs to Section S.3 of the supplementary material (available at Biostatistics online).

1. Omnibus test. The supremum test sup_x,t|W_o(x,t)| is consistent against the general alternative hypothesis that there do not exist a transformation function G, a vector β₀ and a function Λ₀(·) such that Λ(t;x)≡Λ(t|X = x) = G(Λ₀(t)exp(β₀^Tx)) for all t > 0 and all x in the support of X.

2. Functional forms of covariates. Assume that X has independent components and G^′(0)≠0. Then, the supremum test sup_x,t|W_c^(j)(x,t)| is consistent for testing the null hypothesis that Λ(t;x) = G(Λ(t)exp(β^Tx^{( − j)} + γx^(j))) for some β, γ, and Λ(·), against the alternative hypothesis that Λ(t;x) = G(Λ₀(t)e^{β₀Tx( − j)}g(x^(j))) for some β₀, Λ₀(·), and function g(·), where x^(j) is the jth component of x, x^{( − j)} consists of the other components of x, and logg(x^(j)) is not a linear function of x^(j).

3. Link function. Assume that, for any β₁ and β₂, if E[g(e^β₁TX)|e^β₂TX = x] = c₀x for some c₀ and all x > 0, then g(x) = cx^α for some constants c and α. Then, the supremum test sup_x,t|W_l(x,t)| is consistent against the alternative that Λ(t;x) = G(Λ₀(t)g(exp(β₀^Tx))) for some β₀, Λ₀(·), and function g, where there do not exist constants c and α such that g(x) = cx^α.

4. Proportionality. Suppose that X is binary and xG^′′(x)/G^′(x)≠ − 1. Then, the supremum test sup_t|W_p(t)| is consistent against the alternative that Λ(t;x) = G(∫₀^te^θ(s)xd Λ₀(s)), where θ(·) is not constant.

5. Transformation function. Assume that if E[e^β₁TX|e ^β₂TX = y] = y for all y > 0, then β₁ = β₂. Also, assume that G^′(0) = 1 and λ(0) = 1. Then, the supremum test sup_x,t|W_tr(x,t)| is consistent against the alternative that Λ(t;x) = G₀(Λ₀(t)exp(β₀^Tx)) for some β₀, Λ₀ and G₀, where G₀(·) is different from the assumed transformation function G.

REMARK A.1

It is easy to show that the conditions on X in results 3 and 5 hold when X follows a multivariate normal distribution.