Rates and Fitness Consequences of New Mutations in Humans

Abstract

The human mutation rate per nucleotide site per generation (μ) can be estimated from data on mutation rates at loci causing Mendelian genetic disease, by comparing putatively neutrally evolving nucleotide sequences between humans and chimpanzees and by comparing the genome sequences of relatives. Direct estimates from genome sequencing of relatives suggest that μ is about 1.1 × 10⁻⁸, which is about twofold lower than estimates based on the human–chimp divergence. This implies that an average of ∼70 new mutations arise in the human diploid genome per generation. Most of these mutations are paternal in origin, but the male:female mutation rate ratio is currently uncertain and might vary even among individuals within a population. On the basis of a method proposed by Kondrashov and Crow, the genome-wide deleterious mutation rate (U) can be estimated from the product of the number of nucleotide sites in the genome, μ, and the mean selective constraint per site. Although the presence of many weakly selected mutations in human noncoding DNA makes this approach somewhat problematic, estimates are U ≈ 2.2 for the whole diploid genome per generation and ∼0.35 for mutations that change an amino acid of a protein-coding gene. A genome-wide deleterious mutation rate of 2.2 seems higher than humans could tolerate if natural selection is “hard,” but could be tolerated if selection acts on relative fitness differences between individuals or if there is synergistic epistasis. I argue that in the foreseeable future, an accumulation of new deleterious mutations is unlikely to lead to a detectable decline in fitness of human populations.

FOR some time, it has been thought that each newborn human has many tens of new mutations that appeared in its mother’s or father’s germline. This extraordinarily high genomic rate of mutation includes a small fraction of advantageous mutations that have fueled the evolution of our species and that are the basis of ongoing adaptive evolution. The input of new variation brings along with it mutations that cause Mendelian genetic disease, kept at low frequencies by natural selection, and a burden of less harmful mutations that presumably maintain genetic variation in susceptibility to complex diseases. Timofeeff-Ressovsky (1940) and Muller (1950) argued that the rate for mutations with mildly deleterious effects exceeds that for mutations causing visible or lethal phenotypes, and Muller (1950) argued that these mutations cause a substantial load of genetic deaths. Haldane (1937) had shown that the reduction in mean fitness caused by a new deleterious mutation in a large population is largely independent of its selective value, because strongly deleterious mutations reduce fitness more than mildly deleterious mutations, but have shorter persistence times. These insights have fueled a great deal of interest in the total mutation rate in humans, particularly the genomic deleterious mutation rate. For example, a high genomic rate of deleterious mutations can make it difficult to explain how humans, a species with a relatively low reproductive potential, are able to persist (Crow 1970).

For anthropocentric reasons, we are fundamentally interested in the mutation rate in our own species, and a number of questions are unresolved or still only partially answered. A central parameter is the average number of new genetic variants each of us has that our parents did not possess. How many of these mutations came from our father and our mother, how much does the mutation rate change with parental age, and is there significant variation in the mutation rate in the population as a consequence of other environmental or genetic factors? A more difficult question to answer concerns the frequency of mildly deleterious mutations and the distribution of their fitness effects. Along with the nature of selection on fitness in human populations, these parameters hold the key to understanding how a high genomic rate of deleterious mutation can be tolerated without causing an implausibly high rate of genetic death. Finally, if natural selection has been relaxed in current populations, what are the plausible consequences of mutation accumulation in our species?

In this article, I review evidence on all of these issues. Technological developments in molecular genetics have opened up many previously inaccessible questions, especially via DNA sequencing of samples of genes from humans and our nearest relatives, and more recently by whole-genome sequencing. We are now starting to see the results of sequencing of relatives, including parents and their offspring.

The Mutation Rate in Humans

Three methods have been used for estimating the germline spontaneous mutation rate per nucleotide site (μ) in the nuclear genome of humans (Kondrashov and Kondrashov 2010) and have produced remarkably consistent results.

Human genetic disease phenotype frequencies

The incidence rate for a genetic disease can be used to estimate the gene mutation rate, under the assumption of mutation–selection balance, if the mean relative fitnesses of the mutant (or heterozygote) and wild type can be estimated (Haldane 1935). For example, the equilibrium frequency of an autosomal partially recessive mutation in an infinite population is approximately u/hs (Crow and Kimura 1970), where hs is the fitness disadvantage of the heterozygote and u is the mutation rate to the mutant allele. An estimate of μ can then be obtained by dividing u by the number of sites in the gene that produce the mutant phenotype, if mutated, which can be estimated from the nucleotide sequence, under certain assumptions. The two most detailed studies have analyzed frequencies of loss-of-function mutations at loci causing human dominant autosomal or X-linked Mendelian disease (Kondrashov 2002; Lynch 2010). Kondrashov (2002) focused on loss-of-function generated by nonsense and indel mutations, arguing that this gives the best estimate of the number of sensitive sites. Lynch (2010) analyzed missense mutations, arguing that focusing on nonsense mutations will overestimate the mutation rate, since termination codons are A + T rich, and there is a mutational bias toward A + T. A number of other factors, however, will cause the mutation rate to be underestimated. These include underdiagnosis of the mutant phenotype caused by incomplete penetrance, the tendency for some truncated proteins to retain residual activity, and failure to detect the causal molecular event. On the other hand, the mutation rate might be overestimated if the most intensively studied loci have atypically high mutation rates and because coding sequences have a higher frequency of hypermutable CpG dinucleotides than the genome as a whole.

Kondrashov (2002) and Lynch (2010) obtained mean estimates for μ of 1.8 × 10⁻⁸ and 1.3 × 10⁻⁸, respectively, both agreeing fairly well with estimates based on the nucleotide divergence between humans and chimps and with recent estimates based on direct genome sequencing of parent–offspring trios (see below). Kondrashov’s (2002) study suggests that small insertion–deletion events (indels) are comparatively uncommon among human spontaneous mutations, comprising only ∼4% of all mutation events, and deletions are about three times more common than insertions. Sequence divergence of processed pseudogenes between humans and chimpanzees suggests that the rate of indel mutation is about one-tenth that of single nucleotide events (Nachman and Crowell 2000). Humans, therefore, seem to be markedly less susceptible to small indels than the invertebrates Caenorhabditis elegans (Denver et al. 2004) and Drosophila (Petrov 2002; Haag-Liautard et al. 2007) and the flowering plant Arabidopsis thaliana (Ossowski et al. 2010).

Between-species nucleotide divergence at putatively neutral sites

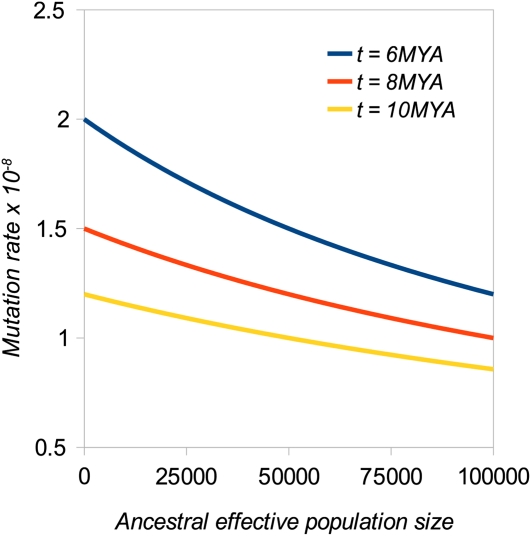
In a sequence evolving free from natural selection, the rate of accumulation of nucleotide substitutions is proportional to μ (Wright 1938), and the expected divergence is k = 2μt/g, where t is the time since speciation and g is the generation time. Additionally, if the time since the speciation event is relatively short, polymorphism in the ancestral population contributes significantly to divergence; the frequency of observing a difference at an autosomal locus if one allele is randomly sampled from each species is the nucleotide diversity θ = 4N_eμ, where N_e is the ancestral effective population size. Uncertainty about four parameters, k, t, g, and N_e, therefore contributes to uncertainty affecting estimates of the mutation rate. By sequencing human- and chimp-processed pseudogene orthologs, which are among the best candidates for loci that evolve strictly neutrally, Nachman and Crowell (2000) carried out the most rigorous analysis to estimate the mutation rate by these means. They observed a mean autosomal single nucleotide divergence per site (i.e., excluding indels) of 1.2%. If we assume values for g and t of 20 years and 5 MYA, respectively, and N_e = 10⁴, on the basis of current nucleotide diversity in humans (Li and Sadler 1991), the autosomal single nucleotide mutation rate in hominids is therefore 2.2 × 10⁻⁸. Two factors suggest, however, that this might be an overestimate. First, although controversial, new fossil finds have pushed back the human–chimp divergence date (Wood 2002; Benton and Donoghue 2007). For example, Benton and Donoghue (2007) suggest lower and upper limits of 6.5 and 10 MYA, respectively. However, speciation may not be an instantaneous event, and the time at which gene flow ceases may vary across the genome, leading to variation in lineage sorting among sites (Patterson et al. 2006). The importance of this effect concerning speciation in hominids has been debated (Barton 2006; Wakeley 2008; Presgraves and Yi 2009). Second, evidence from the pattern of substitutions among hominid lineages suggests that the effective population size of the human–chimp common ancestor (HCCA) could have been much larger than the recent effective sizes for humans or individual chimpanzee subspecies (Takahata et al. 1997; Chen and Li 2001; Burgess and Yang 2008). Information comes mainly from the variance of neutral allele coalescence times, which is proportional to the ancestral effective population size. This leads to variation in divergence among loci, leading in turn to incongruence between the species tree and gene tree. Takahata et al. (1997) compared the frequency distribution of the number of substitutions in human, chimp, and gorilla sequences with its theoretical expectation and concluded that the HCCA N_e was ∼10 times higher than recent human N_e. Chen and Li (2001) examined incongruence between the species and gene trees in 53 hominid orthologous genomic segments, and observed that 22 segments showed evidence of incomplete lineage sorting. On the basis of Hudson’s (1983) formula for the probability of incongruence between the gene and species trees, they obtained an estimate of the HCCA N_e of 52,000–96,000, depending on the generation time assumed. Burgess and Yang (2008) attempted to include the effects of variation in the mutation rate across the genome and sequencing errors (which have been a serious problem for the initial release of the chimp genome) and also concluded that HCCA N_e is 5- to 10-fold higher than recent human N_e. The effect of changing the ancestral population size on the estimate of μ is shown in Figure 1. Assuming N_e = 10,000 has little effect compared to ignoring ancestral polymorphism, whereas assuming N_e = 100,000 reduces the estimated mutation rate by about one-third, yielding an estimate of 1 × 10⁻⁸, if a divergence date of 8 × 10⁶ MYA is assumed. It is difficult to provide a confidence interval for this estimate, because the uncertainty affecting the divergence date and generation time cannot easily be quantified.

Figure 1 .

Human mutation rate estimate plotted against HCCA effective population size, assuming that the neutral site divergence k = 0.012, the speciation date (t) is varied between 6 × 10⁶ and 10 × 10⁶ MYA, and the generation interval g = 20 years.

Genome sequencing of relatives

High-throughput sequencing of related individuals, particularly one or more offspring and their two parents, offers the opportunity to directly estimate the mutation rate in current human populations, thereby avoiding most of the assumptions associated with approaches 1 and 2. This method has so far been attempted four times (Table 1). Xue et al. (2009) employed Illumina sequencing of flow-sorted Y chromosomes of two individuals separated by 13 generations and detected four mutations, which were then verified by Sanger sequencing. This gives an estimate of μ = 3.0 × 10⁻⁸ per generation for males, which has wide confidence limits and is expected to be higher than the sex-averaged rate for autosomes (see below). Roach et al. (2010) employed sequencing array methodology to sequence two offspring and their parents at a mean depth of coverage of >50×. Even at this high sequencing depth, there were many false positives (outnumbering confirmed mutations by more than 1000 to 1), which had to be excluded by further sequencing. There were also many false negatives, whose rate had to be estimated separately and a correction applied. The 28 confirmed mutations led to a mutation rate estimate of 1.1 × 10⁻⁸. Awadalla et al. (2010) sequenced 294 Mb of putatively nonfunctional DNA as a control in a study of new mutations producing human genetic disease and found four new mutations, giving an estimate for μ of 1.4 × 10⁻⁸. The 1000 Genomes Project Consortium (2010) employed Illumina technology to sequence one offspring and two parents each from two trios (one European and one Yoruba from West Africa) at a mean depth of coverage of 42×. They employed a coarse filter to identify candidate de novo mutations, resequenced these, and in the case of the European trio, checked for transmission of confirmed mutations in grand offspring. There were 49 and 35 confirmed mutations in the European and Yoruba trios, respectively. After correcting for false negatives (which were relatively infrequent; Conrad et al. 2011), these numbers yielded estimates for μ of 1.2 × 10⁻⁸ and 1.0 × 10⁻⁸ in the European and Yoruba trios, respectively. Although these estimates are very close to one another, further analysis of the parental origin of the mutations (Conrad et al. 2011) suggests that there could be substantial mutation rate variation among individuals. Excluding the Y chromosome study, the weighted average mutation rate is μ = 1.1 × 10⁻⁸ (Table 1), which is close to an estimate from the chimp–human nucleotide divergence, under the assumption of a larger ancestral population size (10⁵) and a more ancient speciation date than have typically been assumed (Figure 1). The findings in Table 1 should be viewed as work in progress, however, since current high-throughput sequencing is relatively error prone, produces many false positives, and potentially fails to detect some mutations; but this should improve in the future.

Table 1. Estimates of the human single nucleotide mutation rate (μ) obtained by large-scale sequencing of relatives.

Reference	Sequencing method	No. mutations detected	Mutation rate, μ (× 10−8)
Xue et al. (2009)	Illumina	4	3.0 (Chr Y)
Roach et al. (2010)	Array based	28	1.1
Awadalla et al. (2010)	Sanger	4	1.4
1000 Genomes Project Consortium (2010)	Illumina	49 (European)	1.2
1000 Genomes Project Consortium (2010)	Illumina	35 (Yoruba)	1.0
Weighted average			1.1 (excluding Xue et al. 2009)

One implication of a lower estimate of the mutation rate is that the recent human effective population size may have been about twice as high as previous estimates (e.g., Li and Sadler 1991). Silent site variation varies among human populations, but taking a figure of 0.1% (Cargill et al. 1999), and equating autosomal silent nucleotide diversity to 4N_eμ, yields an estimate for N_e of 23,000.

Sex Differences in the Human Mutation Rate

At loci causing human genetic disease, mutations originating in males greatly outnumber mutations originating in females (Crow 1997, 2000). This is believed to be a consequence of a higher number of cell divisions in male gametogenesis. The ratio of the male to female mutation rate, α, can be estimated by comparing evolutionary divergence between the sex chromosomes and between the sex chromosomes and the autosomes (Miyata et al. 1987). In mammals, autosomes spend equal amounts of time in males and females, the X chromosome spends two-thirds of its time in females, and the Y chromosome spends all of its time in males. Comparisons of sex chromosome and autsomal sequences of primates typically suggest values for α in the range 3–6 (e.g., Huang et al. 1997; Ebersberger et al. 2002; Makova and Li 2002; Chimpanzee Sequencing and Analysis Consortium 2005; Rhesus Macaque Genome Sequencing and Analysis Consortium 2007). Estimates of α from closely related species such as humans and chimps could be sensitive to ancestral polymorphism (Ebersberger et al. 2002; Makova and Li 2002; Chimpanzee Sequencing and Analysis Consortium 2005; Taylor et al. 2006). Consider a comparison of autosomal (k_A) and X chromosome (k_X) nucleotide divergences. For neutrally evolving sequences, these are expected to be

$$k_{\text{A}}\hspace{0.17em}=\hspace{0.17em}2\hspace{0.17em}t{\mu }_{\text{A}}/g+4\hspace{0.17em}{N}_{\hspace{0.17em}\text{e}}{\mu }_{\text{A}},$$ (1)

$$k_{\text{X}}\hspace{0.17em}=\hspace{0.17em}2\hspace{0.17em}t{\mu }_{\text{X}}/g+4\text{γ} N_{\text{e}}{\mu }_{\text{X}},$$ (2)

where t is the time since speciation, g is the generation interval, μ_A and μ_X are sex-averaged mutation rates for the autosomes and the X chromosome, respectively, N_e is the ancestral effective population size for the autosomes, and γ is the ratio of X chromosome to autosomal effective population sizes in the ancestral population. The terms in N_e in (1) and (2) represent the contributions to nucleotide divergence from nucleotide diversity in the ancestral population, which might have been substantially higher than predicted by present-day diversity in humans (e.g., Burgess and Yang 2008). Assuming that ${\mu }_{\text{A}}=\left({\mu }_{\text{M}}+{\mu }_{\text{F}}\right)/2,$ where μ_M and μ_F are male and female mutation rates, respectively, and that ${\mu }_{\text{x}}\hspace{0.17em}=\hspace{0.17em}\left({\mu }_{\text{M}}+2\hspace{0.17em}{\mu }_{\text{F}}\right)/3,$ we obtain the following estimator for α,

$$\alpha =\frac{{\mu }_{\text{M}}}{{\mu }_{\text{F}}}=\frac{4\left(\text{ζ}+\text{γ}\right)-3\left(K_{\text{X}}/K_{\text{A}}\right)\left(\zeta +1\right)}{3\left(K_{\text{X}}/K_{\text{A}}\right)\left(\zeta +1\right)-2\left(\text{ζ}+\text{γ}\right)},$$ (3)

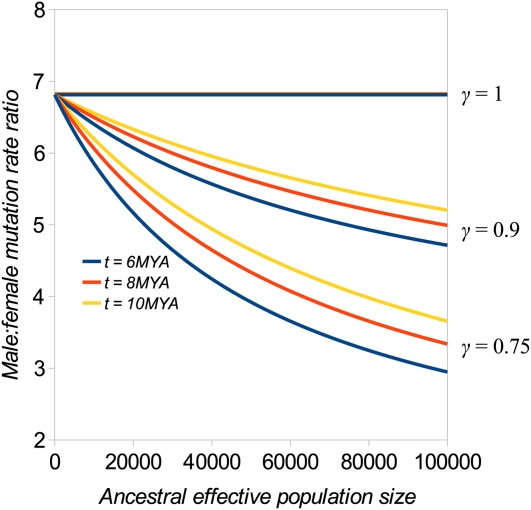
where ζ = t/(2N_eg). Figure 2 plots α calculated from Equation 3 against ancestral N_e for three values of γ, assuming autosomal and X chromosome divergences of 1.25% and 0.94%, respectively, which are genome-wide average estimates from the human–chimp genome comparison (Chimpanzee Sequencing and Analysis Consortium 2005). Estimates are therefore quite sensitive to the values assumed for ancestral N_e and γ. Under a neutral equilibrium model, γ = 3/4, but several factors, including a difference in reproductive success between males and females and differential effects of selective sweeps and background selection, are expected to cause departure from this expectation (Vicoso and Charlesworth 2009). In present-day human populations of European descent, for example, the genome-wide average for γ = 0.71, but γ exceeds 1 in regions distant from protein-coding genes, suggesting an influence of some or all of these processes (Hammer et al. 2010). Differences between assumed values of ancestral N_e and ancestral γ and variation in the contribution to divergence from ancestral polymorphism among sites in the genome could partly explain variation among estimates of α based on comparing humans with chimps (Ebersberger et al. 2002; Chimpanzee Sequencing and Analysis Consortium 2005). The mutation rate for hypermutable CpG dinucleotides seems to depend on absolute time rather than the number of cell divisions, leading to CpGs showing substantially weaker male mutation bias than non-CpG sites (Taylor et al. 2006). This may explain the higher relative rate of mutation at CpG sites compared to non-CpG sites in primates than murids and carnivores (Keightley et al. 2011).

Figure 2 .

The male:female mutation rate ratio (α) calculated by Equation 3 plotted against ancestral effective population size, assuming autosomal and X chromosome nucleotide divergences mentioned in the text, a generation interval (g) of 20 years, for three speciation dates (t), and three values of the ratio of X:autosomal effective population sizes in the ancestral population (γ).

A more direct estimate of α = 6.5 was obtained by Lynch (2010), on the basis of frequencies of human genetic disease originating from new parental and maternal mutations. This estimate is therefore at the upper end of the range obtained from nucleotide divergence between human and other apes (Huang et al. 1997; Ebersberger et al. 2002; Makova and Li 2002; Chimpanzee Sequencing and Analysis Consortium 2005). However, it is higher than an estimate obtained from a comparison of the human and macaque genomes (α = 2.9; Rhesus Macaque Genome Sequencing and Analysis Consortium 2007), which should not be substantially affected by ancestral polymorphism.

The advent of accurate, whole-genome sequencing of trios of offspring and their parents promises to resolve outstanding questions concerning the mutation rate sex bias, at least with reference to current human populations. It also promises to shed light on the causes of nonlinearity of the male mutation rate with age at some loci (Crow 2000, 2006; Goriely et al. 2003; Choi et al. 2008). Recently, the first direct information on the male:female mutation rate ratio has been published (Conrad et al. 2011). The results are surprising, since in one trio of European ancestry, 92% of mutations were paternal (α = 12), whereas in a second trio (Yoruba), only 36% of mutations were paternal (α = 0.6). There was significant heterogeneity in the maternal and paternal mutation rates between these trios, which could be caused by differences in paternal and/or maternal ages at conception (which are unknown for the individuals in question). The mutation rate differences may also reflect environmental and/or genetic variation in the mutation rate that is not associated with age of reproduction.

The Human Genomic Deleterious Mutation Rate

The mean number of single-nucleotide mutation events per diploid human genome per generation (M) is the product of the mutation rate per site and twice the number of base pairs in the genome, i.e., M ≈ 1.1 × 10⁻⁸ × 6 × 10⁹ ≈ 70. How many of these mutations are subject to sufficiently strong natural selection as to overcome genetic drift (i.e., |2N_es| > 1)? The number of nonneutral mutations, and the distribution of their fitness effects, particularly those that are deleterious, is important for knowing the burden of “genetic deaths” sustained by the human population. Kondrashov and Crow (1993) proposed a method for estimating the genome-wide deleterious mutation rate (U) for a model in which mutations are assumed to be either strongly deleterious (|2N_es| >> 1) or selectively neutral. The between-species nucleotide divergence for sites at which new mutations are assumed to be exclusively neutral, k_S (for example, pseudogenes or transposable element remnants), is compared with the divergence for the genome as a whole, k_G. The genomic deleterious mutation rate is estimated from the number of “missing” substitutions in the genome as a whole, i.e.,

$$U=M(1-k_{\text{G}}\text{/}{k}_{\text{S}}\text{)}.$$ (4)

Consider the rate for deleterious mutations caused by amino acid change in protein-coding genes (U_P). The human gene count is believed to be 20,000–25,000 (International Human Genome Sequencing Consortium 2004), the average length of concatenated coding exons per gene is ∼1340 bases (International Human Genome Sequencing Consortium 2001), about three-quarters of exonic mutations lead to an amino acid change, and ∼70% of these are strongly selected against (Eőry et al. 2010). The rate of deleterious amino acid mutation per diploid genome is therefore U_P ≈ 2 × 1.1 × 10⁻⁸ × 22,500 × 1,340 × 0.75 × 0.7 ≈ 0.35 (assuming the median of the range for gene number and disregarding a contribution of indels). This is 2–10 times lower than previous estimates (Eyre-Walker and Keightley 1999; Nachman and Crowell 2000; Eőry et al. 2010), because the per-nucleotide mutation rate seems to be about twofold lower (see above), and gene number is severalfold lower than estimates made prior to the sequencing of the human genome.

Estimating U for the complete human genome is more problematic, because the assumption that new mutations in noncoding DNA are either neutral or strongly deleterious is almost certainly seriously violated. For example, many new mutations in regions of the mammalian genome regulating gene expression seem to be weakly selected (Eyre-Walker and Keightley 2009; Torgerson et al. 2009; Kousathanas et al. 2011) and can therefore drift to higher frequencies. Applying Kondrashov and Crow’s (1993) method will therefore underestimate the number of such mutations. By comparing the human and mouse genomes, the Mouse Genome Sequencing Consortium (2002) estimated that ∼5% of the mammalian genome is under selection, but this is subject to some uncertainty because mouse and human noncoding sequences are difficult to align accurately. Undeterred by the difficulty of inferring U in the presence of weakly selected mutations in noncoding DNA, we have attempted to apply Kondrashov and Crow’s (1993) approach to the human–chimp genome comparison, using transposable element remnants as a neutral reference to estimate k_S (Eöry et al. 2010). We estimated that the nucleotide divergence for the fraction of the genome that excludes transposable elements, $k_{\text{G}}^{*}\approx 0.95ks.$ Assuming that the single nucleotide mutation rate is 1.1 × 10⁻⁸, and allowing for indel mutations occurring at 5% the rate of single nucleotide events (Kondrashov 2002), this leads to an estimate for U of ∼2.2. Let us now evaluate the potential consequences of this mutation rate for human fitness.

The Mutation Load in Human Populations

Haldane (1937) noted that in an equilibrium population, new deleterious mutations are wiped out at the same rate as they appear. Furthermore, he showed that a deleterious mutation reduces population mean fitness by an amount that is independent of its fitness effect. The term mutation “load,” first used by Muller (1950), is defined as the overall reduction in mean fitness relative to the mutation-free genotype brought about by recurrent deleterious mutation (Crow 1958). Muller also introduced the idea that the selective removal of each deleterious mutation is accompanied by one genetic death in an infinite population (see, e.g., Crow 1970, 1997; Kimura 1983; Kondrashov 1988; Eyre-Walker and Keightley 1999; Nachman and Crowell 2000; Reed and Aquadro 2006; Barton et al. 2007). However, the fitness consequences of deleterious mutations, and the mutation rate that the human population could tolerate (Kondrashov and Crow 1993; Crow 1999), depend on whether selection operates on absolute or relative fitness differences between individuals (Wallace 1970, 1975). Sved et al. (1967) had made a similar point in the context of the number of balanced polymorphisms that can be maintained. “One deleterious mutation one genetic death” applies to a model of “hard” selection (Wallace 1975), implying that selection is density independent and/or frequency independent. This would apply, for example, if a lethal mutation killed its carrier under all conditions, independent of the genotype of any other individual in the population. Consider a multiplicative model in which individuals survive to reproductive age with probability W = (1 – s)ⁿ, where s is the selective disadvantage of the heterozygote and n is the number of deleterious mutations carried. If mutations are eliminated deterministically, the proportion of surviving individuals, equivalent to the population mean fitness relative to a population free from deleterious mutations, is approximately $\stackrel{-}{W}$ = e^−U (Kimura and Maruyama 1966). We can now evaluate $\stackrel{-}{W}$ assuming the values previously calculated for U in humans. Considering only mutations that change an amino acid of a protein-coding gene (U_P = 0.35) predicted $\stackrel{-}{W}$= 0.7. For deleterious mutations occurring anywhere in the genome (U = 2.2), $\stackrel{-}{W}$= 0.11. This latter figure seems implausibly low. For example, if each female were capable of producing 20 offspring, 18 of these progeny, on average, would need to undergo genetic death. With the caveat that some selection may occur prior to fertilization (Otto and Hastings 1998) or early in development (Edmonds et al. 1982), this level of selective mortality seems too high, given that there are presumably many nongenetic causes of death. High genomic deleterious mutation rates in humans and Drosophila (Mukai 1964; Mukai et al. 1972), predicting high mutation loads, led to the hypothesis that a load-reducing mechanism, such as quasi-truncation selection, speeds up the elimination of deleterious mutations and maintains higher mean fitness (Crow and Kimura 1979). Truncation selection generates synergistic epistasis, which is also an important component of the “mutational deterministic” hypothesis for the maintenance of obligate sexual reproduction (Kondrashov 1982, 1988): if U is sufficiently high, sexuals can outcompete asexuals in the presence of a twofold cost, because asexuals do not benefit from synergistic epistasis (Kimura and Maruyama 1966). However, there is little empirical evidence that net synergistic epistasis for fitness is common (Kouyos et al. 2007; Halligan and Keightley 2009), although Peck and Waxman (2000) show that such epistasis can emerge in models involving competition in small groups.

So far, we have considered the load generated by strongly deleterious mutations eliminated deterministically. If mutations are slightly deleterious (i.e., have fitness effects close to the reciprocal of the effective population size), the mutation load can be higher, because mutant alleles can drift to higher frequencies (Kimura and Crow 1963; Crow 1970). Furthermore, slightly deleterious mutations may fix, and, in a population close to equilibrium, their fixations would presumably be balanced by fixations of advantageous mutations. Even a modest proportion of fixating deleterious mutations can lead to implausibly low mean fitness (Kondrashov 1995), at least under a model in which fitness is expressed relative to a mutation-free genotype.

It is unrealistic to compare the fitnesses of mutationally loaded individuals to that of a mutation-free genotype, which has a vanishingly small probability of existing (Wallace 1970; Ewens 1979). If selection acts on relative fitness differences between extant individuals in the population, as under density- or frequency-dependent selection, the mutation load paradox can disappear entirely, and instead, load is manifest as genetic variance for fitness (Ewens 1979; Y. Lecesque, P. Keightley, and A. Eyre-Walker, unpublished data). Relative rather than absolute fitness differences are important under a range of scenarios, including competition between individuals and sexual selection. Analysis of a multiplicative model in which individuals mate with probability $w=W/\stackrel{-}{W}$ suggests that 10s or even 100s of deleterious mutations can be eliminated from a population each generation if there is a plausible input of new mutational variation for fitness. In reality, pure hard and soft selection is unlikely, and fitness effects of new mutations may be manifest via both relative and absolute fitness differences. However, a high genomic deleterious mutation rate, together with the absence of evidence for widespread synergistic epistasis, suggests that much natural selection in humans occurs via relative fitness differences between individuals.

Consequences of Deleterious Mutation Accumulation for Human Population Fitness

Timofeeff-Ressovsky (1940) and Muller (1950) hypothesized that mutations with inconspicuous effects are more frequent than lethal mutations. Muller (1950) warned that mildly deleterious mutations may be accumulating in modern human populations, because natural selection has been relaxed by better environmental conditions. He also warned that mutation accumulation will be paid for by genetic deaths in future generations, unless improved environmental conditions can be sustained. This argument has been reiterated, with attempts to predict the rate of mutational degradation, assuming that natural selection in current human populations is substantially reduced (Crow 1997, 2000; Lynch et al. 1999; Eyre-Walker et al. 2006; Lynch 2010). The maximal rate of loss of fitness, if selection is completely removed, is the “mutation pressure” $U\stackrel{-}{\mathrm{hs}}$ (Shabalina et al. 1997), where U is the deleterious mutation rate per diploid genome, and $\stackrel{-}{\mathrm{hs}}$ is the mean heterozygous fitness effect of a new mutation. The mutation pressure can be estimated by fitting models of the distribution of fitness effects (DFE) of new mutations to human polymorphism data, or by estimating the rate of decline of fitness in mutation accumulation experiments in model organisms and extrapolating to humans.

Unfortunately, parameter estimates based on the DFE inferred from polymorphism data are highly model dependent, making prediction of the rate of change of mean fitness under relaxed selection problematic. Most information currently comes from the analysis of polymorphism data for protein-coding genes. Boyko et al. (2008) fitted several models of the DFE to data for over 11,000 genes from individuals of African and European ancestry. The best-fitting DFE was a mixture distribution containing a normally distributed class of mutational effects and a point mass of strongly deleterious mutational effects. Estimates of the mean fitness effect of an amino acid mutation drawn from the normally distributed class were 10⁻⁴ and 10⁻³ for Africans and Europeans, respectively. Assuming that U_P = 0.35 (see above), maximum rates of fitness loss per generation if selection were completely relaxed on these mutations are only 0.0015% and 0.02% for Africans and Europeans, respectively. The class of strongly deleterious mutations represents mutations (including some lethals) with effects N_ehs > ∼10 that are kept so rare by purifying selection as to be essentially absent from polymorphism data. A meaningful estimate of their mean effect cannot be obtained, at least based on numbers of alleles sequenced in currently available data sets (Keightley and Eyre-Walker 2010). This difficulty in interpreting estimates of the mean of the DFE is a general problem of similar models fitted to polymorphism data (Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007; Boyko et al. 2008; Yampolsky et al. 2005).

Inferences from Mutation Accumulation in Invertebrates

In a mutation accumulation (MA) experiment, new spontaneous mutations accumulate almost free from effective natural selection in inbred sublines or on replicated chromosomes protected by a balancer chromosome. There are currently no MA experiments in model mammals, such as mice or rats, and data on the fitness consequences of spontaneous mutation accumulation in animals principally come from experiments in Drosophila and nematodes. Prediction of the rate of loss of fitness in humans under relaxed selection (Δ_R) can be made, albeit speculatively, by calculating the product of the rate of change of fitness, Δ_MA, in D. melanogaster or nematodes under MA and the ratio of estimates of the genomic deleterious mutation rate for humans (U_h) to Drosophila or nematodes (U_x), i.e.,

$${\Delta }_{\text{R}}{=\Delta }_{\text{MA}}{U}_{\text{h}}/U_{\text{x}},$$ (5)

implicitly assuming that the mean selection coefficient is the same in the different species. We also assume, conservatively, that h = 0.5 for all loci, and Δ_MA can therefore be equated to the predicted rate of fitness loss in an outbred population evolving free from selection. Taking estimates of Δ_MA from a recent review (Halligan and Keightley 2009), results of this calculation are shown in Table 2. In nematodes, there are no direct estimates of U, but an estimate of the total mutation rate per diploid genome in MA lines of C. elegans of M = 4.2 (Denver et al. 2004) yields an estimate of U = 2.5, under the assumption that the fraction of selectively constrained sites in the Caenorhabditis and Drosophila genomes are similar (i.e., ∼60%; Halligan and Keightley 2006). For Drosophila, a direct estimate of U is obtained from the average mutation rate in D. melanogaster MA lines of three genotypes (Haag-Liautard et al. 2007; Keightley et al. 2009) multiplied by genome-wide selective constraint between closely related Drosophila species (Halligan and Keightley 2006).

Table 2. Estimates of the rate of change of fitness per generation in nematodes and Drosophila under whole-genome mutation accumulation (Δ_MA) and predicted rates of fitness loss per generation for humans (Δ_R), if selection is completely relaxed, calculated using Equation 5.

Species	No. MA experiments	Mean ΔMA under MA	U	Predicted ΔR in humans
Nematodes	7	0.15%	2.5	0.13%
Drosophila	6	1.2%	1.4	1.8%

At an arbitrary time point 200 years in the future (about eight human generations), the nematode and Drosophila parameters predict maximum fitness losses of 1 and 14%, respectively. However, several factors suggest that the reduction in fitness could be considerably smaller. First, calculations have assumed additive gene action, but theory suggests that large-effect mutations tend to be partially recessive (Wright 1934; Kacser and Burns 1981). Fitness reduction caused by an accumulation of recessive deleterious mutations is delayed, and predicted Δ_R values could be 50% or more lower (García-Dorado and Caballero 2000; Vassilieva et al. 2000). Second, doubts have been raised about D. melanogaster MA experiments, particularly the validity of controls, and the possibility of nonmutational changes in fitness or unusual transposable element activity, and these doubts have been debated (Keightley 1996; García-Dorado 1997; Crow 1997; Keightley and Eyre-Walker 1999; Lynch et al. 1999; Fry 2004; Halligan and Keightley 2009). Third, although modern medicine and lifestyle changes have undoubtedly reduced natural selection in some human populations, natural selection still occurs in all human populations. There is scope for selection in the germline cell lineages (Reed and Aquadro 2006), and many pregnancies spontaneously abort (Edmonds et al. 1982). Sexual selection still operates in human societies (Perrett et al. 1999), and this and other factors generate family size variation, allowing opportunities for natural selection. For example, selection associated with variation in male wealth in contemporary populations is at least as strong as selection measured in field studies of natural populations of other species (Nettle and Pollet 2008). Finally, a change in mean fitness could be inconsequential if selection is soft (for example, it might not matter if everyone becomes 5% less sexually attractive). The above considerations lead to doubts about whether deleterious mutation accumulation will produce a detectable fitness loss in humans in the foreseeable future. Less speculative, perhaps, is the existence of finite global energy, food, and water resources. Coupled with expanding human populations, these factors may intensify competition and lead to stronger natural selection in years to come.