Dissociable neural representations of reinforcement and belief prediction errors underlie strategic learning

Abstract

Decision-making in the presence of other competitive intelligent agents is fundamental for social and economic behavior. Such decisions require agents to behave strategically, where in addition to learning about the rewards and punishments available in the environment, they also need to anticipate and respond to actions of others competing for the same rewards. However, whereas we know much about strategic learning at both theoretical and behavioral levels, we know relatively little about the underlying neural mechanisms. Here, we show using a multi-strategy competitive learning paradigm that strategic choices can be characterized by extending the reinforcement learning (RL) framework to incorporate agents’ beliefs about the actions of their opponents. Furthermore, using this characterization to generate putative internal values, we used model-based functional magnetic resonance imaging to investigate neural computations underlying strategic learning. We found that the distinct notions of prediction errors derived from our computational model are processed in a partially overlapping but distinct set of brain regions. Specifically, we found that the RL prediction error was correlated with activity in the ventral striatum. In contrast, activity in the ventral striatum, as well as the rostral anterior cingulate (rACC), was correlated with a previously uncharacterized belief-based prediction error. Furthermore, activity in rACC reflected individual differences in degree of engagement in belief learning. These results suggest a model of strategic behavior where learning arises from interaction of dissociable reinforcement and belief-based inputs.

Decision-making in the presence of competitive intelligent agents is fundamental for social and economic behavior (1, 2). Here, in addition to learning about rewards and punishments available in the environment, agents also need to anticipate and respond to actions of others competing for the same rewards. This ability to behave strategically has been the subject of intense study in theoretical biology and game theory (1, 2). However, whereas we know much about strategic learning at both theoretical and behavioral levels, we know relatively little about the underlying neural mechanisms. We studied neural computations underlying learning in a stylized but well-characterized setting of a population with many anonymously interacting agents and low probability of reencounter. This setting provides a natural model for situations such as commuters in traffic or bargaining in bazaars (1). Importantly, in minimizing the role of reputation and higher-order belief considerations, the population setting using a random matching protocol is perhaps the most widely studied experimental setting and has served as a basic building block for a number of models in evolutionary biology and game theory (1, 2).

Behaviorally, there is substantial evidence that strategic learning can be parsimoniously characterized by using two learning rules across a wide range of strategic contexts and experimental conditions: (i) reinforcement-based learning (RL) through trial and error, and (ii) belief-based learning through anticipating and responding to the actions of others (3, 4). The goal of this study is to provide a model-based account of the neural computations related to these two learning rules and their respective contributions to behavior. First, RL models have been central to understanding the neural systems underlying how reward learning (5). In the temporal-difference (TD) form, RL models posit that learning is driven by a prediction error defined as the difference between expected and received rewards and have been highly successful in connecting behavior to the underlying neurobiology (5, 6). Moreover, recent experiments in social and strategic domains have shown that RL models explain a number of important features of the data at both behavioral (3, 7) and neural levels (8, 9).

Despite their success, standard RL models provide an incomplete account of strategic learning even in the simple population setting. Organisms blindly exhibiting RL behavior in social and strategic settings are essentially ignoring that their behavior can be exploited by others (3, 10). In contrast, belief-based learning posits that players make use of knowledge of the structure of the game to update value estimates of available actions and comes in two computationally equivalent interpretations. One interpretation assumes the existence of latent beliefs and requires players to form and update first-order beliefs regarding the likelihood of future actions of opponents. Specifically, these models posit that players select actions strategically by best responding to their beliefs about future strategies of opponents and update these beliefs by using some weighted history of opponents' choices (1, 3). Mathematically, players engaging in belief learning correspond to Bayesian learners who believe opponent's play is drawn from a fixed but unknown distribution and whose prior beliefs take the form of a Dirichlet distribution (1). Under the alternative interpretation, beliefs and mental models are not assumed and action values are updated directly by reinforcing all actions proportional to their foregone (or fictive) rewards (11). The equivalence of these two mathematical interpretations thus makes it clear that belief-based learning does not necessarily imply the learning of mental, verbalizable beliefs commonly referred to in the cognitive and social sciences, because specific beliefs about likely strategies of opponents are sufficient but not necessary for this type of learning.

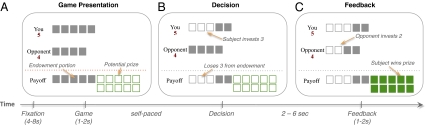
In this study, we used a multi-strategy competitive game, the so-called Patent Race (12), in conjunction with functional magnetic resonance imaging (fMRI). In the game, players of two types, Strong and Weak, are randomly matched at the beginning of each round and compete for a prize by choosing an investment (in integer amounts) from their respective endowments. The player who invests more wins the prize, and the other loses. In the event of a tie, both lose the prize. Regardless of the outcome, players lose the amount that they invested. In the particular payoff structure we use, the prize is worth 10 units, and the Strong (Weak) player is endowed with 5 (4) units (Fig. 1).

Fig. 1.

Patent Race game. (A) After a fixation screen of a random duration between 4–8 s, subjects were presented with the Patent Race game for between 1–2 s, with information regarding their endowment, the endowment of the opponent, and the potential prize. (B) Subjects inputted the decision (self-paced) by pressing a button mapped to the desired investment amount from the initial endowment. (C) After 2–6 s, the opponent's choice was revealed. If the subject's investment is strictly more than those of the opponent, the subject won the prize; otherwise, the subject lost the prize. In either case, the subject kept the portion of the endowment not invested.

To illustrate how players can anticipate and respond to the actions of others in this game, suppose the Weak player observes the Strong players frequently investing five units. He may subsequently respond by playing zero to keep his initial endowment. Upon observing this play, Strong players can exploit the Weak player's behavior by investing only one unit to obtain both the prize while keeping four units from the endowment. This behavior may, in turn, entice the Weak player to move away from investing zero to win the prize. In contrast, pure RL players will respond to these changes in behavior of the opponents in a much slower manner, because they behave by comparing received payoffs from past investments without consideration for the strategic behavior of others (SI Results and Fig. S1).

This paradigm has three key features that build on insights from previous experimental and theoretical studies on learning models that together help to computationally characterize behavior and, statistically, minimize collinearity in the model outputs (13, 14). First, by using a random matching protocol, we minimize reputation concerns and, thus, the role of higher-order belief considerations (1). This paradigm allowed us to focus on first-order belief inferences, which are highly tractable and a key reason for its popularity in theoretical and experimental studies. Second, the large strategy space of the 6 × 5 game combined with the presence of secure strategies (i.e., investing zero or five), due to asymmetry in endowments between Strong and Weak players, allowed us to separate the relative contributions of belief and reinforcement inputs. The intuition is that secure strategies yield the same received payoffs regardless of actions by the opponents, giving us a control for the received payoff but still allowing the beliefs about the actions of the other players to change. In contrast, previous studies have typically used simple games that are well-suited to an experimental setting but statistically suboptimal in separating the relative behavioral contribution of two learning rules (13). Moreover, games with small strategy space often result in high negative correlation between foregone and received payoffs, making it problematic to dissociate the associated neural signals. Finally, to speed up game play, we replaced the standard matrix form display, which can be unintuitive even to highly educated subjects, with an interface that directly reflected the logic of the game (Fig. 1). In contrast, previous behavioral experiments yielding comparable behavior lasted over 2 h (SI Results and Table S1).

Results

Model Fits to Behavior.

To characterize and disaggregate neural signatures of these two learning rules and their relationship to behavior, we adopted a hybrid model—experience weighted attraction—that combines and nests both reinforcement and belief learning (11, 15). The crucial insight connecting reinforcement and belief learning is to weight beliefs by using payoffs to obtain action values. That is, whereas action values are reinforced directly by the obtained outcomes in RL, in belief learning, they are weighted by beliefs that players hold about future actions of other players (SI Methods). This hybrid approach has been highly successful in explaining behavior across a wide range of games, thus offering a model-based framework to characterize the relative contributions of the two learning rules (3, 11).

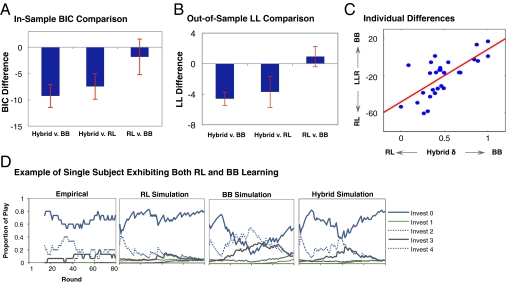
Consistent with previous behavioral studies (3), the hybrid model outperformed both RL and belief learning models alone in explaining choices of subjects, as measured by the Bayesian Information Criterion penalizing for number of free parameters (Fig. 2A). In contrast, there was no significant difference between the base reinforcement and belief learning models. To account for overfitting, we conducted out-of-sample predictions by using holdback samples and found that the results were consistent with in-sample fits (Fig. 2B).

Fig. 2.

Computational model estimates and single subject exhibiting both RL and belief learning. (A) In-sample model fit comparisons using the Bayesian Information Criterion showed that the hybrid model fits behavioral choices significantly better than RL and belief learning (paired Student's t test, P ≤ 0.01, two-tailed), whereas RL and belief learning did not differ significantly among themselves. Error bars indicate SEM. (B) Out-of-sample predictive power was also superior for hybrid model compared with RL and belief learning (paired Student's t test P ≤ 0.01, two-tailed). Error bars indicate SEM of log-likelihood differences. (C) Individual variation in the relative weights placed on RL and belief learning can be captured by using parameter δ_i of the hybrid model. As δ_i increases, behavioral fit of belief learning improves relative to that of the RL (Pearson ρ = 0.70, P < 0.01, two-tailed). (D) Illustration of behavior and model predictions using a single subject in the Weak role exhibiting both RL and BB learning. Empirical time series of choice is plotted by using a 15-round bin average. Choice probabilities were generated from calibrated models by using RL, belief, and hybrid learning models, respectively.

Separable Contribution of RL and Belief Inputs.

Critically for our goal of disaggregating the neural signatures of the two learning rules, we next investigated whether behavior in the Patent Race was driven by subjects engaging in both reinforcement and belief inputs at the individual level, rather than a mixture of distinct types of pure reinforcement and belief learners. Using the hybrid model parameter ∂_i that governs the weighting between the two learning rules, we found that the individual estimates were distributed along the unit interval, rather than clustered at the boundaries as would be expected if the population consisted of distinct types (Fig. 2C and Table S2). This variation further allowed us to use these estimates as a between-subject measure in subsequent neuroimaging analysis. To test the robustness of our estimates to assumptions of the hybrid model, we used the log-likelihood ratio between RL and belief learning models and found that this measure was significantly correlated with ∂_i (Pearson ρ = 0.70, P < 0.01, two-tailed; Fig. 2C). This analysis can be interpreted as a model-free check that our individual difference measure was not unduly driven by assumptions underlying the hybrid model.

To illustrate the separable contributions of the respective learning rules to behavior, we compared the empirical choice frequencies of a single subject in the Weak role exhibiting both types of learning (∂_i = 0.47) to simulations using the respective models (Fig. 2D). RL missed the increased probability of investing 4 in rounds 30–50. This corresponded to periods when Strong players invested one to three units with a high probability. In contrast, belief learning captured this change but overestimated its magnitude. By combining the two learning rules, the hybrid model was able to capture both the direction and magnitude of changes in investments reasonably well.

Ventral Striatum Activity Correlated with Both RL and Belief-Based Prediction Errors.

Having characterized behavior of subjects computationally, we next sought to identify the brain regions where neural activity was significant correlated with the internal signals of each model. At the time of outcome, according to the TD form of the hybrid model, players update their action values by using a combination of the RL and belief components (SI Methods). Critically, the correlation between the two types of prediction errors is sufficiently low (Pearson ρ ≃ 0.28; Table S3) for us to characterize the unique contribution of the underlying neural signals.

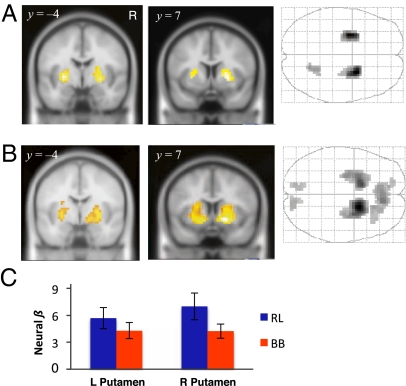
First, we found that the RL prediction error was significantly correlated with activity in bilateral putamen and a small region in the cerebellum (Fig. 3A and Table 1). The RL prediction error is defined as the difference between expected and received rewards, and the striatum has been consistently implicated in encoding this quantity in fMRI studies of reward learning (16, 17). In contrast, we know much less about the neural underpinnings of belief learning. Studies of mentalization in social neuroscience have suggested that medial prefrontal cortices (mPFC) and temporo-parietal junction (TPJ) mediate social cognitive processes such as belief inference (18). However, studies on reward-guided behavior in social settings have suggested that these computations build on the same brain structures associated with reward, including the striatum, rostral anterior cingulate (rACC), and orbitofrontal cortex (19). Thus, using our model-based framework, we next sought to localize neural signatures associated with belief learning.

Fig. 3.

Ventral striatal responses to RL and belief prediction errors. (A) Coronal sections and glass brain of putamen activation to the RL prediction error (P < 0.001 uncorrected, cluster size k ≥ 20). (B) Significant activation of bilateral putamen and ventral caudate to the belief prediction error for the chosen action (P < 0.001 uncorrected, k ≥ 20). (C) Region of interest analyses show that activities in bilateral ventral striatum (Table 1) were significantly correlated with both RL and belief prediction errors; error bars indicate SEM.

Table 1.

List of brain activations responding to RL, belief, and hybrid prediction errors

		Cluster level		Voxel level*
Model	Region	pcor	Voxels	pfdr	T-val	X	Y	Z
Reinforcement	R ventral striatum	0	120	0.004	6.01	24	4	0
	L ventral striatum	0.001	91	0.004	5.87	−28	−4	0
	R cerebellum	0.093	30	0.025	4.19	18	−60	−28
Belief-based	R ventral striatum	0	334	0	7.22	18	7	−7
	L ventral striatum	0	294	0	5.9	−14	10	−10
	rACC/mPFC	0	224	0.001	4.96	7	38	7
	R superior frontal gyrus	0.023	51	0.005	4.2	18	28	49
	R occipital cortex	0.057	39	0.009	3.9	14	−88	14
	L occipital cortex	0.107	31	0.013	3.72	−14	−84	7
Hybrid	R putamen	0	234	0	8.51	14	7	−7
	L putamen	0	148	0.004	6.91	−14	7	−10
	rACC/mPFC	0	150	0.18	5.3	7	38	35
	Occipital cortex	0	347	0.172	5.32	7	−84	4
	Cerebellum	0.111	28	0.006	4.64	−4	−56	−38

Regions significantly correlated with the different notions of prediction errors derived from the three models considered in this study. All activations survived a threshold of P < 0.001, uncorrected, and cluster size k ≥ 20. L, left; R, right.

*Voxel locations given in MNI Coordinates.

Surprisingly, we found that the belief prediction error for the chosen action was also correlated with activity in the putamen, but also extending to parts of the ventral caudate (Fig. 3B). To assess the robustness of this result to the correlation between the regressors, we searched for brain regions correlated with the unique share of variance attributed to RL and belief prediction errors, respectively. That is, we simultaneously included both the RL prediction error and the orthogonalized belief prediction error, and we verified that the striatal activation remained significant using this procedure (Fig. S2). The same procedure was used in reverse as a robustness check on the striatal activation to the RL prediction error.

Rostral ACC Activity Uniquely Correlated with Belief-Based Prediction Error.

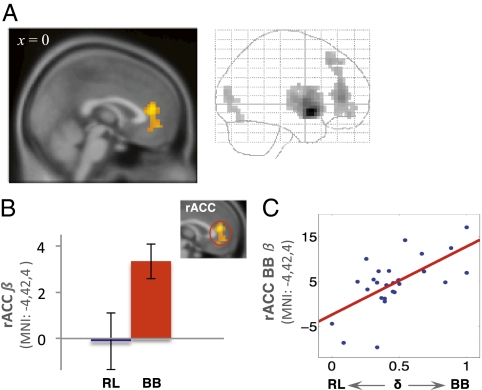
In contrast, we found that activity in the rACC extending to the mPFC was correlated with only the belief prediction error (P < 0.001, uncorrected, cluster size k ≥ 20; Fig. 4A and Table 1), and not with RL prediction error even at a liberal threshold of P > 0.5. To verify the functional selectivity of the belief prediction error in the rACC, we conducted a paired Student's t test on the average beta values of the rACC activation and found that betas associated with belief prediction error were significantly greater than those for the RL prediction error (P < 0.05, two-tailed, Fig. 4B).

Fig. 4.

Rostral ACC responds uniquely to belief prediction error. (A) Sagittal section and glass brain of rACC activation to the belief prediction error associated with the chosen action (P < 0.001 uncorrected, cluster size k ≥ 20). (B) Neural activity in the rACC is correlated only with belief and not with RL prediction error, error bars indicate SEM. (C) Between-subject neural response to the belief prediction error in rACC is correlated with individual differences in behavioral engagement of belief learning as measured using ∂_i estimates (Pearson P = 0.66, P < 0.01, two-tailed).

To investigate modulation of the two learning rules, we examined between-subject variability in the weighting placed on belief learning inputs by correlating the estimated behavioral parameter ∂_i to the neural response to the belief prediction error. Using brain regions that were found significantly correlated with the belief prediction error as regions of interest, we found that ∂_i was correlated with individual differences in activation of rACC (Pearson P = 0.66, P < 0.01, two-tailed; Fig. 4C), but not in the striatum (P > 0.5). That is, we found subject who assigned higher weights to belief learning behaviorally exhibited greater neural sensitivity in the rACC to the belief prediction error.

fMRI Correlates of Hybrid Model.

Finally, to test our hypothesis that the neural correlates of hybrid prediction error can be disaggregated into RL and belief-based components, we searched for brain regions significantly correlated with the hybrid prediction error. We found that the activations to the hybrid prediction error were contained by the union of activations associated with the RL and belief prediction errors, in particular the ventral striatum and the mPFC, and also parts of the occipital cortex and cerebellum (Table 1 and Fig. 5). In contrast, we found that reward predictions during the response period for all three models were represented in overlapping areas of the ventromedial PFC (Fig. S3). This finding thus suggests that inputs converge at the time of choice and is consistent with findings in animal literature of hybrid-type signals in sensory-motor regions (20).

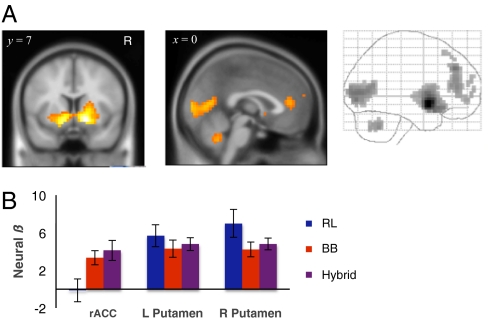
Fig. 5.

Hybrid model prediction error activations. (A) Glass brain and section of bilateral putamen rACC activation in response to hybrid model prediction error (P < 0.001 uncorrected, cluster size k ≥ 20). (B) Neural betas with respect to RL, belief, and hybrid prediction errors at three ROIs defined by 8-mm sphere at the peak of hybrid model activation clusters (Table 1).

Discussion

Notions of equilibrium, such as the well-known Nash equilibrium and related notions such as quantal-response equilibrium (21), are central to theories of strategic behavior. It has long been recognized, however, that equilibria do not emerge spontaneously, but rather through some adaptive process whereby organisms evolve or learn over time, which cannot be accounted for by purely static equilibrium models (3). Here, we studied the neural correlates of the adaptive process by using a unique multi-strategy competitive game. Our results show how the brain responds to multiple notions of prediction errors derived from well-established behavioral models of strategic learning in a partially overlapping but distinct set of brain regions known to be involved in reward and social behavior.

First, we found that activity in the ventral striatum was correlated with both the RL and belief prediction errors. Unlike the RL prediction error, which has been extensively studied (16, 17), the belief prediction error corresponds to the discrepancy between the observed and expected frequency of actions of an opponent weighted by the associated payoffs. Thus, unlike RL models, belief learning predicts that players will be sensitive to foregone (or fictive) payoffs in addition to the received payoffs. Various notions of foregone payoffs have been studied in neuroimaging experiments of decision-making and reward learning, including fictive error, regret, and counterfactuals (22–24). Unlike these measures, our belief learning prediction error does not involve direct comparison of the possible payoffs, but rather requires subjects to incorporate their knowledge of the structure of the game to track payoffs associated with all actions to update their value estimates.

The overlapping set of activations in ventral striatum can potentially shed light on previous neuroimaging studies of social exchange games. These studies have consistently found neural signals that qualitatively resemble prediction errors in the striatum (25, 26). Our results raise several interesting possibilities regarding contents of the neural encoding. First, these regions may, in fact, contain, or receive information from, neurons whose activity represents multiple notions of prediction errors, including those related to belief-based considerations we study here. Alternatively, information processing in these regions may be sensitive to, or correlated with, beliefs and/or foregone payoffs, without necessarily encoding a literal belief prediction error. Future research will be needed to unravel the precise nature of the information processing in these regions.

In contrast to the ventral striatum, we found that activity in the rACC responded to the belief, but not the RL, prediction error. This finding is consistent with known roles of rostral and caudal ACC for error (27, 28) and conflict processing (29, 30), and in the social domain, mentalization and belief inference (18). When activation involves more anterior and rostral portions of the ACC, as in our case, it is usually in tasks with an emotional component (31, 32). Therefore, it seems a good candidate to modulate error processing and learning when it has a higher level, social, or regret based flavor (33). Furthermore, and unlike the putamen involvement in belief prediction error, rACC activity reflected individual differences in the sensitivity to belief inputs (Fig. 5B). Thus, although it is an open question precisely how these prediction errors interact at the trial level, these results suggest the role of rACC as a control region that mediates the degree of influence played by belief learning.

This distributed representation of different forms of prediction errors is consistent with other recent computational accounts of social behavior distinguishing between reward and social learning inputs. In a reward learning task where participants received social advice, activity in dorsomedial PFC was correlated with prediction errors associated with confederate's fidelity, whereas activity in the ventral striatum was correlated with the standard reward prediction error (34). A similar dissociation was found in an observational learning setting between the dorsolateral PFC and ventral striatum in encoding of observational and reward prediction errors, respectively (35). Unlike these studies, however, we found that activity in the ventral striatum contained both RL and belief updating signals. Although speculative, we conjecture that these differences may in part reflect differences in the cognitive demands for behaving in strategic settings versus more passive types of social learning, where subject's payoffs are not directly affected by the action of the other agents. Such a hypothesis can be tested by using studies that manipulate dependence of payoffs in strategic interactions.

Moreover, our results complement and extend current understandings of the role of the rACC and mPFC in mentalization in economic games. The rACC, but not the mPFC, was shown to be activated in subjects exhibiting first-level reasoning in an iterative reasoning game, whereas the reverse was true for subjects exhibiting second-level reasoning (36). Similarly, mPFC but not the rACC was implicated in higher-order mentalization in a competitive game (10). Together with our findings, these results raise the interesting possibility that more ventral mPFC regions, including rACC, are involved in first-order belief inference, and more dorsal regions in higher-order inferences. Such a functional division is consistent with previous proposals in the mentalization literature (18) and may reflect differences in the type of information being learned. That is, in addition to responding to history of actions of opponents, players engaging in higher-order mentalization may also respond to beliefs about the learning parameters of opponents (10). Future studies combining computational models of higher-order mentalization with games that directly manipulate the level of strategic reasoning of the players will be necessary to test this hypothesis.

Strategic learning is ubiquitous in social and economic interactions, where outcomes are determined by joint actions of the players involved, and is in sharp distinction to more passive social learning environments where social information could be manipulated independently of outcomes. The inherent correlation between actions and payoffs in strategic environments, however, introduces important methodological hurdles in disentangling the contributions of the underlying learning rules at both behavioral and neural levels. We were able to characterize them only through a tight integration of experiment design, computational modeling, and functional neuroimaging. More broadly, our results add to the growing literature suggesting that neural systems underlying social and strategic interactions can be studied in a unified computational framework with those of reward learning (19, 37). Although the current study is restricted to a specific competitive game, there is a wealth of theoretical and behavioral studies that suggest these learning rules generalize to other strategic settings, including not only competitive games but also those involving cooperation, iterative reasoning, or randomization (3). Such a general framework opens the door to understanding the striking array of social and behavioral deficits that appear to have their basis in damage and dysfunction related to the same dopaminergic and frontal-subcortical circuits implicated in our study (38).

Methods

Participants.

Thirty-five healthy volunteers (19 female) were recruited from Neuroeconomics Lab subject pool at the University of Illinois at Urbana–Champaign (UIUC). Subjects had a mean age of 23.3 ± 4.6 y, ranging 19–47. Of these subjects, five were excluded from the study because of excessive motion and three because of repeating the same strategy for >95% of the trials during the experiment.

Procedure.

Subjects undergoing neuroimaging completed 160 rounds of the Patent Race game (Fig. 1) in two scanning sessions lasting 15–20 min each, alternating between Strong and Weak roles over 80 rounds, counterbalanced (SI Methods). Informed consent was obtained as approved by the Internal Review Board at UIUC. They were informed that they would be paid the average payoff from a randomly chosen 40 rounds from each session plus a $10 participation fee.

Behavioral Data Analysis.

Details of the computational models used in the analysis are provided in SI Methods. All models learned the value of actions in a temporal-difference algorithm by tracking expected value of each action. The values differed only in the type of information that was used to form and update these expected values. For each model, we estimated by maximizing, for each subject, the log-likelihood of predicted decision probabilities generated by the models against the actual choices of subjects (SI Methods).

fMRI Data Analysis.

Details of the fMRI acquisition and analysis are provided in SI Methods. Event-related analyses of fMRI time series were performed, with reward prediction and prediction errors values generated from the respective computational models. The decision event was associated with choice probabilities, and the feedback event was associated with prediction errors for chosen actions. All analyses were performed on the feedback event data, except the expected reward region analysis (Fig. S3). Regressors were convolved with the canonical hemodynamic response function and entered into a regression analysis against each subject's BOLD response data. The regression fits of each computational signal from each individual subject were then summed across their roles and then taken into random-effects group analysis (SI Methods).