GeoFold: Topology-based protein unfolding pathways capture the effects of engineered disulfides on kinetic stability

Abstract

Protein unfolding is modeled as an ensemble of pathways, where each step in each pathway is the addition of one topologically possible conformational degree of freedom. Starting with a known protein structure, GeoFold hierarchically partitions (cuts) the native structure into substructures using revolute joints and translations. The energy of each cut and its activation barrier are calculated using buried solvent accessible surface area, side chain entropy, hydrogen bonding, buried cavities, and backbone degrees of freedom. A directed acyclic graph is constructed from the cuts, representing a network of simultaneous equilibria. Finite difference simulations on this graph simulate native unfolding pathways. Experimentally observed changes in the unfolding rates for disulfide mutants of barnase, T4 lysozyme, dihydrofolate reductase, and factor for inversion stimulation were qualitatively reproduced in these simulations. Detailed unfolding pathways for each case explain the effects of changes in the chain topology on the folding energy landscape. GeoFold is a useful tool for the inference of the effects of disulfide engineering on the energy landscape of protein unfolding.

INTRODUCTION

The configurational space of a polypeptide chain is astronomically large, yet the folding of most proteins is completed within a fraction of a second. This paradoxical observation strongly suggests that well-defined folding pathways exist, dictated by energetic interactions and topological constraints. Since the folding pathway is the inverse of the unfolding pathway, a mechanistic model for the unfolding pathway would be a helpful step towards understanding folding pathways and developing a predictive model for folding.

The folding and unfolding sides of the same energy landscape present distinct modeling issues. Easily computed structural bioinformatic models can predict the folding rate, and with it the height of the energetic barrier. The relative contact order¹, a simple calculation based on the native structure, is highly anti-correlated to and predictive of the folding rate. However, the unfolding rate depends on topology of the backbone, the oligomerization state, the presence of bound ligands, local sequence-structure propensities and the protein environment. Models of unfolding based on the native state statistics alone have had only modest success².

The other extreme of the modeling continuum are all-atom, explicit molecular dynamics simulations. These models are manageable for the unfolding process but not the folding process, because of the enormous search space of folding. For example, molecular dynamics simulations starting from the native state have produced realistic intermediate states of unfolding ^3-5 and approximate unfolding rates⁶ for small proteins. While a few small proteins have been successfully folded by explicit molecular dynamics^{4, 7-8}, deriving folding rates would require numerous runs and is still too computationally challenging. It is possible to speed up the folding process by reducing the energy function to a simple Go model^9-10 and thereby get folding rates, but this oversimplification of the energy landscape creates its own inaccuracies⁹. In short, folding lends itself to statistical models but not to all-atom simulations, while unfolding lends itself to all-atom simulations but not to easily computed statistical models.

The challenge is to distill a simplified model of unfolding based on what we know about the mechanism. Along these lines, Xia et al have identified some of the structural characteristics that appear to correlate with high kinetic stability (very slow unfolding) in proteins¹¹. They find that kinetically stable proteins tend to be of mixed secondary structure content (alpha/beta), rather than pure beta sheet or pure alpha helix. They often have a dimeric or high order assembly with the N and C termini buried in the multimer interface. In kinetically stable monomers, the termini are often tucked into the middle of a beta sheet. When not buried, chain termini are often observed wrapped around the protein like a belt or latch. The impression from structure gazing is that the situation of the chain termini somehow speaks to the unfolding rate. Therefore a simplified model must account for steric hindrance to unfolding in the native state and along the pathway.

The mechanistic model described here encodes a strictly tree-like unfolding pathway consistent with the “parsing perspective” of Dill¹², the “block folding” model of Nussinov¹³, and Finkelstein’s “folding nuclei”^14-15. Viewed in the folding direction, all steps are on-pathway, and each condensation step involves previously condensed substructures. We further restrict the pathway such that no intermediate can be formed if it requires the chain to pass through itself or if it forces an unlikely concerted motion of three or more parts, like the act of tying of a knot. Similar arguments may be found in Maity and Englander’s work on cytochrome c, describing folding events as the stepwise assembly of foldon units¹⁶. These basic principles are well established in the literature of folding theory and even taken for granted in some of the most successful algorithms for de novo structure prediction^17-18.

Our program, GeoFold (Geometric unFolding) follows on the conceptual framework of our previous model, UNFOLD¹⁹. We model all steps in a pathway as two-body condensations. An ordered set of two-body condensations is a tree, and a given protein may have many such trees, comprising an ensemble of pathways. In UNFOLD, protein structures were reduced to weighted secondary structure element graphs. Contact energies were assigned to pairs of secondary structure elements using solvent accessible surface area and other terms. The graph was then hierarchically partitioned at each step, without regard for chain crossing. In nine case-studies, the simple UNFOLD pathways were found to be predictive of phi-values and other experimental data on folding pathways. The new program GeoFold now accounts for chain crossing and contains energy terms that account for most of the known energetic components of protein stability. It carries out unfolding on a graph using a finite difference approach, producing simulated experimental data, whereas the previous method only produced a heirarchy of intermediate states.

Because of the absence of any off-pathway intermediates in our model, and because off-pathway states dominate the unfolded side of the energy landscape, the current model cannot predict folding rates, only unfolding rates.

In this paper, we demonstrate that a mechanistic model which accounts for steric interactions is sufficient to explain previously unexplained differences in stability and unfolding rate for four proteins with engineered disulfide linkages.

The new program and server will be useful to explore and anticipate the energetic consequences of protein engineering, and for deciphering the genetic roots of protein aggregation and amyloid formation²⁰. As we will show, mutations affect the kinetic stability of a protein and the accumulation of intermediate states depending on how they perturb the protein folding pathway. A better understanding of the structural determinants of kinetic stability may lead to ways to improve the shelf life of proteins by design.

RESULTS

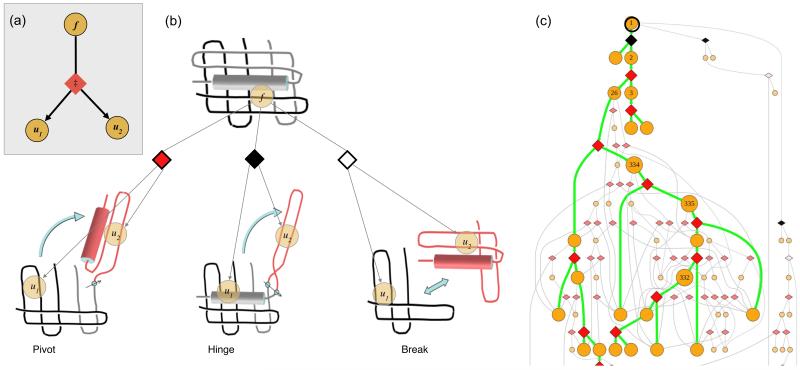
Geofold first determines all geometrically possible pivot, hinge and break points (Figure 1) in a protein structure, splits that structure into non-overlapping substructures, then proceeds recursively, until the substructures are fully unfolded. The series of splits comprise unfolding pathways. Unfolding pathways are structured as directed acyclic graphs (DAGs) with bifurcating edges (one node connecting to two nodes) as shown in Figure 1(c). Each bifurcating edge represents an elemental unfolding step, or “cut”, that splits one substructure into two, using a pivot, hinge or break move as shown in Figure 1a-b. Each node in the graph represents a native substructure, which is a spatially contiguous subset of the native protein structure. The forward and reverse rates of reaction of each elemental subsystem are calculated using the energy function defined in Methods. The combined set of all cuts, along with the associated energy functions, represent a system of simultaneous equilibria whose solution is a set of equilibrium concentrations. The equilibrium state can be found numerically using finite difference methods. The equilibrium state and the rate at which it is obtained are the values we compare to equilibrium stability and unfolding rate in this study.

Figure 1.

(a) Elemental subsystem for the kinetic model, a cut. f is any spatially contiguous substructure of a protein, and is partitioned into spatially contiguous substructures u₁ and u₂. (b) Diamond shapes represent the cuts, each having a type (color) and an associated energy barrier ‡. A pivot motion is single point revolute joint. A hinge rotates around two points. A break is a pure translational motion. Rotations and translations must not cross chains. (c) Top portion of an unfolding pathway DAG for DHFR. Node 1 is the fully folded state. Green lines indicate the pathway of maximum unfolding traffic; grey lines are other significant pathways. Unfolding simulations start with all of the protein in node 1, and end when node concentrations reach equilibrium.

To carry out a virtual unfolding experiment, the energy landscape is tilted from the folded state to the unfolded state by changing either the temperature (T) or the desolvation energy (ω). Finite difference calculations produce a time course of all substructure concentrations. For the purposes of easy analysis, we have grouped substructures together into three classes -- folded, unfolded and intermediate -- based on buried surface area. The time course of folded state concentrations from the finite difference simulations were fit to a simple exponential decay to give empirical unfolding rates (k_u). It should be noted that complex, multi-phasic unfolding has been observed in these simulations, and this is noted where appropriate, but for most purposes we used a simple half-life analysis.

GeoFold unfolding pathways can be broadly characterized as follows. At high solvation energy (ω) the folded state is always the dominant state at equilibrium, while at low ω the unfolded state always dominates. The transition in ω from folded to unfolded is generally sigmoidal, characteristic of a cooperative process, but the degree of cooperativity varies. Both two-state and three state unfolding behaviors have been observed. In three-state systems, there are values of ω where intermediate states exist at equilibrium. The unfolding rate is estimated from the half-life of unfolding and is often roughly log-linear with ω, but sometimes shows a “roll-over” at very low ω as the kinetics approaches diffusion control. We observe curvature throughout the range of ω when more than two states predominate at equilibrium. The energy landscape of the unfolding pathway generally has a maximum in the middle, characteristic of a two-state system.

Initial studies of small monomeric proteins

Ideally, GeoFold should be able to mimic the unfolding mechanism well enough to reproduce kinetics experiments and predict experimentally determined unfolding rates. To test this, simulated unfolding rates (k_u) were determined for a set of well-studied, small, monomeric proteins²¹. Kinetic simulations were carried out over a range of desolvation free energy values ω. Rates were determined by finding the half-life t_1/2 at each ω, converting it to an unfolding rate k_u = ln(2)/t_1/2, and then finding the rate in “pure water” by log-linear extrapolation of the ln(k_u) versus ω plot. Unfortunately, the simulated unfolding rates were found to be insignificantly correlated with experimentally determined k_u values (data not shown).

This meant that one or more of the assumptions built into the model were wrong. Since the failure could not be attributed to inaccuracies in the folding pathways versus inaccuracies in the energy calculations, we turned to case studies intended to isolate the effects of topology on the folding pathway. As you will see, the results suggest that the folding pathways are accurate and serve to explain the experimental results, leaving as the cause of failure the inaccuracies in the energy function, although precisely where remains to be determined.

Studies of topological perturbations versus unfolding rate

We asked whether the changes in topology created by disulfide linkages could explain experimentally determined changes in stability or unfolding rate. Four case studies are presented here: three mutants of barnase^22-24 five mutants of T4 lysozyme²⁵, two of factor for inversion stimulation (FIS)²⁶, and one of E.coli dihydrofolate reductase (DHFR)²⁷. In each case, biophysical studies were done to determine the stability or unfolding rate.

Because the task of optimizing the energy parameters to fit the kinetics of unfolding proved to be an impossibly difficult one, the energy function was necessarily left in an unrefined state, with each component set to a physically reasonable value as described in Methods. No attempt has been made with the current case studies to identify parts of the energy function that are responsible for higher or lower rates. Fortunately, the topological effects of disulfides on the unfolding pathway dominate other energetic components, affecting the order of events rather than the energy of each event. For the most part in these case studies, the addition of a disulfide linkage does not change the non-covalent terms of the energy function. For that reason, we can proceed to validate the mechanistic aspect of the program and its prediction of the order of events, without further empirical proof of the validity of the energy function.

Disulfide mutants of barnase

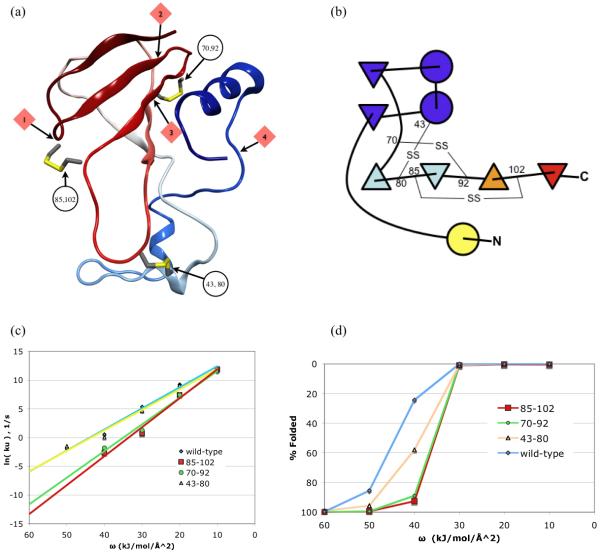
In work by Clark et al, barnase has been mutated to add disulfide linkages at three positions, 43-80, 70-92, and 85-102^22-24. The crystal structures of each have been solved, and the equilibrium stabilities were determined for each mutant, both in the oxidized and reduced forms. The 85-102 mutant (PDB ID: 1bng) was stabilized against urea denaturation due to disulfide formation, unfolding at >7.5M urea as compared to 4.5M for the reduced form. The oxidized 43-80 mutant (PDB ID: 1bne) was somewhat more resistant to urea denaturation, unfolding at 5.8M versus 4.0M for the dithiol form. The 70-92 mutant (PDB ID: 1bnf) was destabilized by the disulfide bond, unfolding at 3.0M urea versus 3.4M for the dithiol form. The loss of stability was attributed to disulfide-induced distortion of local structure and disruption of a salt-bridge near the site of mutation. Further inspection on our part finds that 1bnf in the oxidized state contains local structure that is less favorable than the wild type local structure. Specifically, the Type II beta turn at high propensity sequence KSGR is replaced with a Type I turn at low turn propensity sequence SGRC in the oxidized double mutant. Turn propensity was measured using HMMSTR²⁸.

Clarke et al attempted to explain the disulfide stabilization on the basis of decreased entropy of the denatured state, using Flory’s formula ΔS = −2.1 – 3/2(ln n); where n is the number of residues encompassed by the disulfide²⁹. But this theory could not explain how a shorter encompassed loop, 85-102, was more stabilizing than a longer one, 43-80. The differences can be explained by the unfolding pathway predicted by GeoFold, which finds the wild type 85-102 contact to be broken early in unfolding, followed by the 70-92 contact, followed by 43-80. The C-terminal region 50-110 is a 4-stranded beta-meander with an exposed C-terminus, which provides a series of pivot points starting from the C-terminus and working inward (Figure 2(a)). The predicted pathway shows the C-terminal strand unfolding first, exposing the neighboring strand (strand 3), which unfolds, leaving residues 1-90. At this point, the rate limiting step is the pivoting of the N-terminal helix away from the (now partially unfolded) beta sheet. In 1bng, the 85-102 disulfide prevents the unfolding of strand 3, forcing the N-terminal helix to expose a greater surface area when it separates from the beta sheet. The higher solvation energy cost of this step explains the greater stability of the 85-102 mutant.

Figure 2.

(a) Barnase ribbon showing locations of first four pivot locations and the disulfide positions. (b) Secondary structure element diagram of barnase showing locations of disulfide linkages. Online color version shows the predominant pathway of unfolding from red (early unfolding) to blue (late unfolding). (c) Simulated unfolding kinetics, showing a slowing effect for mutants 85-102 and 70-92, a result of blocking early unfolding steps. Note that slow unfolding rates with ln(k_u) < −5 cannot be measured. (d) Equilbrium unfolding simulation, varying desolvation energy ω.

GeoFold predicts no difference in the unfolding rate of 43-80 as compared to wild type. It also predicts only a minor difference between the 85-102 mutant and the 70-92 mutant, and both are predicted to unfold much slower than wild type. The 70-92 mutant is predicted to be much more stable than it actually is, but this is believed to be the result of loop distortions observed in the 70-92 mutant. Distortion and local structure propensity are not part of the current GeoFold model.

Figure 2(b) shows the locations of the engineered disulfides relative to the unfolding order of the secondary structure elements. Figure 2(c-d) shows a plots of equilibrium unfolding, using desolvation energy ω, and unfolding rate k_u with respect to ω. The log-linear relationship is steeper for the oxidized 85-102 mutant than for the wild type and 43-80 mutant, consistent with a greater amount of surface area exposed in the transition state of the former.

Disulfide mutants of lysozyme

Matsumura²⁵ used a rational design algorithm to insert disulfide bonds into phage T4 lysozyme in places where they were predicted to minimally disturb the backbone conformation. Five double mutants were created and then subjected to thermal denaturation under reduced and oxidizing conditions. A cysteine-free mutant (C54T-C97A) served as the wild type (called WT*) and as the base from which the five disulfide mutants were made. All of the reduced mutants were slightly less stable than WT*, while three of the five mutants were significantly more stable when oxidized (Figure 3(a)).

Figure 3.

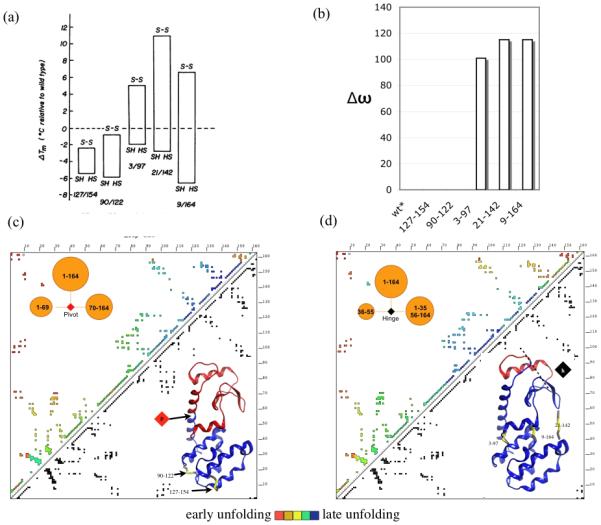
(a) Figure 2 from Matsumura et al, used by permission, showing the changes in melting temperature for reduced versus oxidized disulfide mutants of T4 lysozyme. (b) Changes in equilibrium unfolding point, as ω value, in GeoFold simulations. Mutants 127-154 and 90-122 unfold at the same w at WT*. (c-d) Age plot for unfolding pathway of (c) wild type T4 lysozyme, or reduced, or 127-154 or 90-122 mutants, and (d) oxidized 21-142 or 9-164 mutants, with contacts colored red to blue according to unfolding order. Upper inset in (c-d): first unfolding step, a pivot move in (c), a hinge move in (d). Lower inset: ribbon drawing showing how the structure is divided in the first unfolding step by (c) the pivot move p, and (d) the hinge move h.

Models for the five disulfide mutants were made using the molecular modeling software MOE (Chemical Computing Group, Montreal), using its Rotamer Explorer function plus energy minimization. All models have good disulfide bond geometry and no significant changes in the backbone coordinates.

The wild type unfolding pathway starts with the separation of the N and C-terminal domains with a pivot position located in the middle of a long, domain-crossing helix, at residue 69 (Figure 3(c), insets). According to the program, cleavage at this particular location exposes a minimum amount of buried surface area, allows a maximum number of pivoting directions as compared to all other positions in the chain, and maximally exposes new flexible pivot and hinge locations along the pathway of unfolding, as compared with all other cleavage locations. In two of the mutants, 127-154 and 90-122, the initial step of the unfolding pathway was the same as that of WT*, and the equilibrium melting point in ω was also the same, while in the other three mutants the melting point in the oxidized state was increased (Figure 3(b)), similar to the experimental results.

In the three stabilized mutants, 3-97, 21-142, and 9-164, a pivot at any position between the two cysteines was disallowed by the algorithm, and the unfolding pathway began instead with small N and C-terminal segments. But these small pivot moves did not unlock domain opening steps. Hinge motions, revolute joints with two fixed points, were required for unfolding to proceed. Figure 3(d) (insets) shows the first significant unfolding step in the stabilized mutants. Unfolding in the simulation is slower because the program awards hinges a lower configurational entropy gain than pivots, given that a single-axis revolute joint adds only one rotational degree of freedom, while a pivot motion adds two or three rotational degrees of freedom. Exposing the same amount of buried surface area while gaining less configurational entropy leads to a higher transition state energy and therefore a lower unfolding rate.

Figure 3(c-d) also show a summary of the two pathways as “age plots” where contacts are colored in the order they are lost, illustrating the inside-out unfolding order of the stabilized mutants, versus the outside-in unfolding pathway of the WT*. Flory’s equation and our mechanistic approach predict the same overall result in this case, although for barnase they do not.

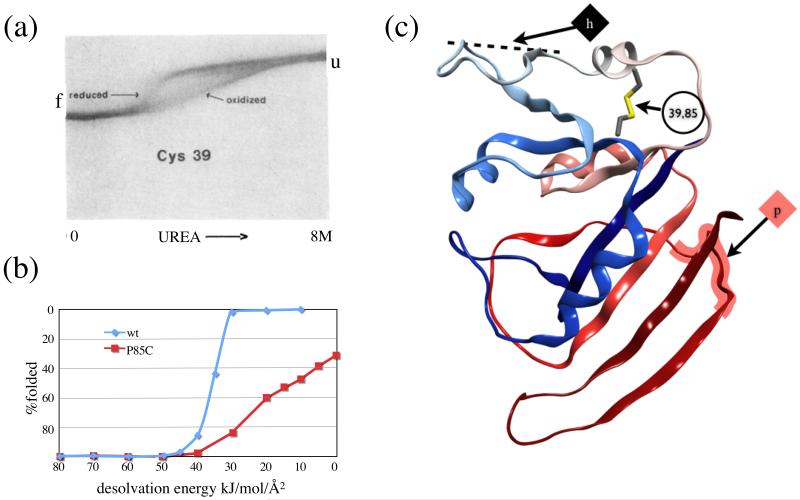
A disulfide mutant of dihydrofolate reductase

A single mutation in E. coli dihydrofolate reductase (DHFR), P39C, allows a disulfide to form with wild type cysteine 85²⁷. The wild type and the mutant in both the oxidized and reduced state were characterized by GndHCl and urea equilibrium unfolding experiments, showing that the reduced form was identical in stability to the wild type, and that the oxidized form unfolded at higher urea (or GndHCl) concentrations. Furthermore, the wild type enzyme has a sharp, two-state equilibrium unfolding curve while the oxidized mutant has an extended transition region, suggestive of one or more intermediate states (Figure 4(a)).

Figure 4.

DHFR. (a) Figure 4 from Villafranca et al, used by permission, showing urea gradient gel electrophoresis equilibrium denaturation of reduced and oxidized P39C DHFR. (b) Simulated equilibrium denaturation curve from GeoFold. The axes have been reversed to match the image. (c) DHFR ribbon showing location of engineered disulfide and first unfolding steps in the inside-out pathway, hinge h, and the outside-in pathway, pivot p.

In remarkable agreement, the simulated equilibrium unfolding curve also shows the extended transition for the oxidized state, and the initial unfolding begins at the same urea concentration (desolvation energy ω in the simulations) for both oxidized and reduced states (Figure 4(b)).

At high ω (low urea) the predicted pathway of DHFR unfolding begins with a series of hinge motions within the loosely-packed “adenosine binding domain”, residues 37 to 91 (ABD), unfolding generally from the middle of the chain outward to the termini (Figure 4(c)). This “inside-out” pathway makes sense energetically, given that the terminal segments have extensive contacts and are more topologically tangled than the ABD, and experimentally, given that the ABD is somewhat flexible, rotating between crystal structures³⁰. The 39-85 disulfide blocks the inside-out pathway, forcing the unfolding of the remaining protein to proceed from the termini, or “outside-in”, which requires a much lower desolvation energy ω. At low ω (high urea), the pathway is outside-in, unfolding from the C-terminus and without the use of hinge motions. Two distinct unfolding pathways lead to the broad transition seen in Figure 4(a-b).

The existence of multiple pathways in DHFR folding (two or four channels) was proposed by Matthews^31-32. Their descriptions of mutually exclusive channels without equilibrium intermediate states is perfectly consistent with the mutually exclusive inside-out and outside-in pathways observed here. A similar outside-in unfolding scenario was developed based on the kinetics of methotrexate binding and tryptophan flourescence^31,33, and was later supported by Gō simulations³⁴ which showed the C-terminus folding last and the adenosine binding domain folding first. On the other hand, hydrogen/deuterium exchange NMR experiments supporting a pathway in which the termini fold first, and unfold last³⁵; specifically, a burst phase intermediate of folding contained protected backbone H-bonds in the C-terminal strand. Iwakura³⁶, using circular permutants, has suggested that DHFR folding depends only on the presence of early folding units and not on their order along the chain. The NMR experiments and the indifference of DHFR to circular permutation agrees with the inside-out pathway. In retrospect, it makes perfect sense that the outside-in pathway that exposes more surface area early would be favored at high denaturant versus the inside-out pathway, which is more sterically hindered, because steric hindrance does not depend on denaturant. Note that the NMR experiments and the inside-out unfolding pathway were carried out at low denaturant, whereas the Trp fluorescence and the outside-in pathways were done at high denaturant.

Symmetric disulfides in the fragment for inversion stimulation dimer

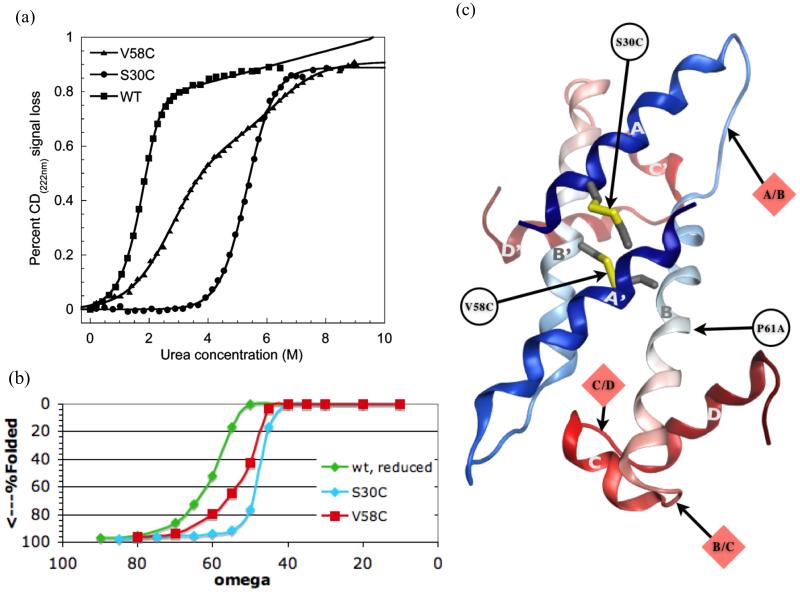
Factor for inversion stimulation (FIS, PDB ID:3jrh) is an intertwined, homodimeric DNA-binding protein. Two single site cysteine mutations were engineered into the dimer, and both mutants formed a disulfide at the two-fold symmetry interface²⁶. This created proteins with branched, non-cyclic topology, in contrast to the other disulfide linkage mutants presented here, all of which produced a cyclic topology. For this reason, the increased stability of the these mutants cannot be explained by Flory’s formula, which models the loss of entropy in the unfolded state due to cycle formation²⁹.

The rate limiting step in wild type FIS unfolding has been shown to occur before dissociation of the monomers³⁷, so that any increase in stability must be due to slower unfolding, not to a faster association of monomers or decreased entropy of the unfolded state. Both disulfide bridges were shown to stabilize FIS, but the S30C mutant was more stabilized and denatured more cooperatively than the V58C mutant (Figure 5(a)). Equilibrium unfolding curves for wild type and S30C both fit a dimeric two-state model, whereas V58C best fits a 3-state model. In previous studies, a mutation of proline 61 in helix B to alanine increased stability by 4 kcal/mol and changed the folding pathway from 2-state to three-state³⁸, and the C-terminal helices C and D were shown by limited trypsin proteolysis to unfold first in this mutant. The equilibrium intermediate was determined to be a trypsin-resistant dimeric fragment consisting of intertwined helices A and B.

Figure 5.

FIS. (a) Figure 4 from Meinhold et al, used by permission, showing equilibrium unfolding circular dichroism data for FIS disulfide variants. (b) Simulated equilibrium unfolding curves from GeoFold for the same variants. Note that axes are reversed to conform with (a). (c) Ribbon diagram for alpha helical part of FIS dimer, showing principle cleavage points and locations of mutations.

In the simulations, the transition state of the wild type protein was dimeric. The slow step in wild type unfolding was the initial pivoting of helix A (either one) away from the rest of the dimer (Figure 5(a)). Both mutants were more stable than the wild type, and S30C was more stable and more cooperative than V58C, agreeing with the experimental results (Figure 5(b)). The kinetics of wild type and S30C unfolding show a log-linear relationship with ω but V58C has a distinctly curved relationship, suggesting different pathways at high and low denaturant, again similar to the experimental results.

Ignoring the floppy N-terminal hairpin which is disordered in most crystal structures, FIS is an all alpha helical dimeric protein, and unfolding can proceed only at the three junctures between the four helices, A/B, B/C, and C/D (Figure 5(a)). The intertwined dimer cannot dissociate before the A/B pivot. We observed an A/B pivot in the wild type versus a B/C pivot in the S38C mutant, where the A helices are linked and not free to pivot. In the V58C mutant, ambiguous pathways, both A/B and B/C, were observed in the simulation.

The simulated pathways agree with experimental data wherever possible. Inasmuch as the P61A and V58C mutations both serve to strengthen the dimeric interaction between helices B, the similarity between the experimental pathway of P61A and the simulated pathway of V58C is supportive of the accuracy of the program. Both mutations serve to block the propagation of the wild type unfolding pathway, forcing B/C in lieu of dissociation.

DISCUSSION

A recent study has found that it is possible to predict the unfolding rates of single-domain proteins using only information about the structural class of the protein and its size³⁹. Indeed, kinetically stable proteins have structural class preferences¹¹.

A model for protein flexibility has been previously described as a network glass⁴⁰, where unfolding is done by a stochastic simulation using multi-jointed tethers for hydrophobic interactions and a template-based hydrogen bond potential. This method has been used to identify a transition state cluster in barnase unfolding, and consistently identified the regions most protected from H/D exchange. But H/D exchange only identifies broken hydrogen bonds, not necessarily capturing non-local side chain contacts, and in principle, hydrogen bonds in late folding helical regions could be protected from exchange early in folding. The pathway proposed by Rader⁴⁰ has the helical domain unfolding first, which disagrees with our prediction (Figure 2). But predictions of phi-values in barnase by Garbuzynskiy¹⁵ using dynamic programming agree with our results, finding the high phi-values in the N-terminal helix. GeoFold differs in many ways from Rader’s method. It is deterministic and exhaustively samples alternative pathway, like Garbuzynskiy’s method, and it treats pivot and hinge energies differently. This last feature accounts for our barnase pathway, which agrees more with the experimental data. Admittedly, we placed more weight on entropic terms than on hydrogen bonds, but that is because these terms, not hydrogen bonds, explain the kinetic effects of topological changes in the chain. In barnase, unfolding internal helices requires hinge motions whose barrier heights depend on chain stiffness and the orientation of the hinge axis, and this may be more energetically unfavorable step than would be expected from the breaking of hydrogen bonds alone.

Our model uses rigid body motions to unfold proteins. This is clearly a convenient simplification of a more detailed process. An actual pivot most likely involves micro-steps in which single hydrogen bonds or hydrophobic contacts are broken, much like the model of Rader. Our simplification is justified because it models that way a set of contacts is often broken in a concerted and cooperative way with one large-scale motion, effectively separating relatively rigid sub-structures. The relative simplicity of the model and the fact that it is deterministic, not stochastic, has the advantage of allowing the pathways to be explored essentially exhaustively.

The effects of disulfide linkages on folding and unfolding have been previously explored using lattice simulations and theory. Shakhnovich⁴¹ showed that even in a very simple model, the kinetic effect of tying together two sequence positions is a function of the topology of the native state and can either speed up or slow folding, depending on whether the linkage occurs in the folding nucleus or not. Although not discussed in that paper, the implication is that the unfolding rate would be slowed if the linkage occurs outside the folding nucleus, not inside. This would place the energy perturbation on the unfolding side of the energy landscape, increasing the height of the barrier to unfolding. Indeed this is what we find.

Compared to the subtle energetic perturbations of a point mutation, the basis of phi-value analysis of folding pathways⁴², the addition of a disulfide bond is a relatively blunt instrument, probing the pathway by changing its course. We do not expect the current method to be able to reproduce the results of phi-value experiments unless the finer points of the energy function are extensively refined and trained first. Nonetheless, a clearer understanding of the effects of topology on kinetic stability is immensely valuable. In combination with simulations such as those presented here, disulfide mutations can experimentally elucidate the first steps in the unfolding pathway., and conversely, predictions of the first steps in unfolding could help us to engineer stability by inserting disulfide linkages.

CONCLUSIONS

The mechanism of protein unfolding has been hypothesized in this work to be a directed acyclic graph of native substructures, is accordance with theoretical studies and views¹². An element of this tree is a revolute joint or a translation, splitting a substructure into two. We show that experimentally determined energetic and kinetic effects of engineered disulfides in four different proteins are captured in the energy landscapes produced for these proteins by GeoFold, based on their respective crystal structures. The unfolding pathways explain variable stabilization in barnase, lysozyme, DHFR and FIS that could not be explained by Flory’s equation for entropy loss in the unfolded state²⁹. Disulfide links stabilize the protein relative to wild type if the linked positions dissociate early in the pathway of the wild type molecule.

Simulated disulfide mutations in DHFR and FIS both reproduced the experimentally observed increases in stability and the decreases in the cooperativity of folding. Simulated disulfide mutations in barnase and lysozyme reproduced the relative changes in the unfolding rate and in stability.

METHODS

A kinetic model

A kinetic simulation for a system of chemical equations simulates the changes in concentration of each chemical species with time. For example, given a system of two coupled equilibria, A⇆B⇆C, and starting concentrations [A], [B], and [C], the change in [B] over time is given as

$$\frac{d\left[B\right]}{dt}=k_{AB}\left[A\right]+k_{CB}\left[C\right]-(k_{BA}+k_{BC})\left[B\right]$$ (1)

where the subscripts indicate the directions of the reactions. Eq. 1 is multiplied by a time-step to get new concentrations and the process is repeated. The simulation eventually reaches equilibrium, in this example, when k_AB[A]+k_CB[C] = (k_BA+k_BC)[B]. An accurate time-course of concentrations is obtained if the rates are correct and the time-step is sufficiently small. Protein unfolding can be viewed as a system of coupled elemental unfolding steps (Figure 1(a)).

Unfolding operators

Protein topology defines the allowable unfolding motions. Three geometric operators can be defined to describe all two part structural partitions on a chain (Figure 1(b)). As a rule, covalent linkages cannot be broken or stretched in an unfolding operation, and atoms cannot penetrate each other. If the chain crosses only once from u₁ and u₂, then the allowable motion is a pivot, or a single point revolute joint. Pivot rotations can be in any direction, regardless of the direction of the backbone. If the chain crosses twice, rotation around the two crossing points defines a hinge, or two-point revolute joint. If the chain crosses more than twice, then a simple non-distorting motion is impossible unless all of the points lie in a line, in which case it is still a hinge. If the chain does not cross from u₁ and u₂, then the model consists of multiple chains or disjoint segments of one chain. The motion in this case is a simple translation, called a break in this study. A break is assigned the highest entropy change, followed by pivots, followed by hinges.

The elemental unfolding subsystem (cut)

The directed graph consists of linked cuts. Starting from the native structure as the root of the graph, each folded species, f, is partitioned using pivots, hinges, and breaks into two smaller species, u₁ and u₂, at all possible locations as defined by the following conditions.

Pivots

(Figure 6, GetPivot) Residue i of f is the location of a pivot if the substructure N-terminal to i (u₁=f[:i]) can rotate around i at least pivotcut=30° in any direction without colliding with the substructure C-terminal to i (u₂= f[i+1:]). If f is composed of multiple chains, then the coordinates of the additional chains are grouped with u₁ or u₂, in all combinations. If several adjacent positions qualify as pivots, a central representative position is chosen.

Figure 6.

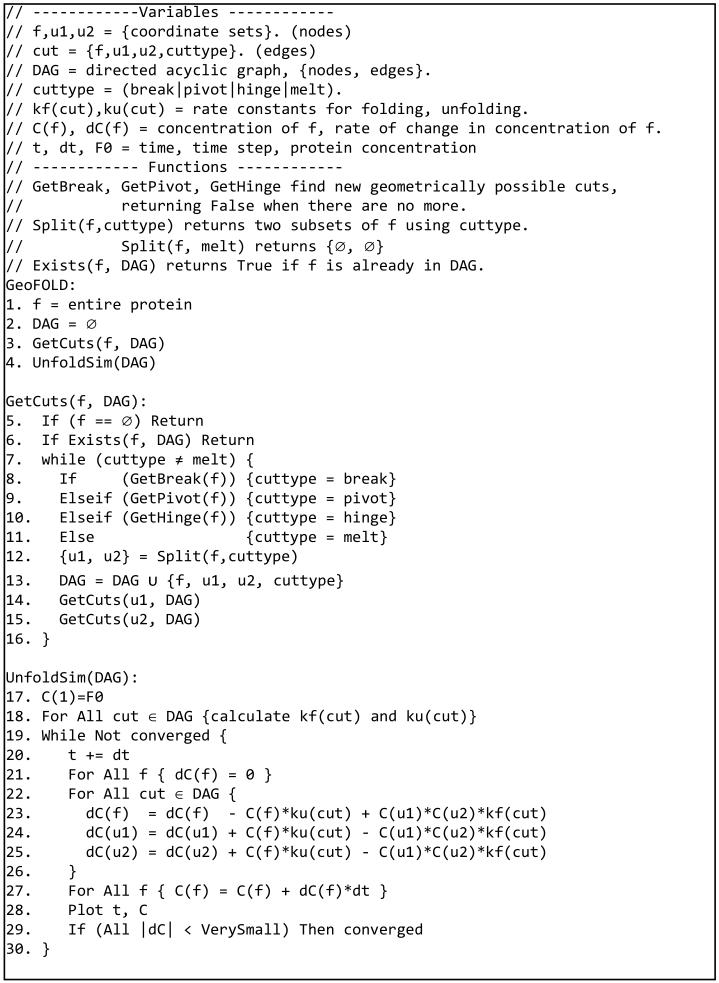
GeoFOLD algorithm.

Hinges

(Figure 6, GetHinge) A single-axis rotation exists around an axis defined by residues i and j if the substructure represented by u₁=f[i:j] can rotate at least hingecut=30° degrees in either direction about the axis i->j without colliding with the subset u₂=f[:i-1] * f[j+1:]. If multiple chains are involved, then they are grouped with u₁ or u₂ in all possible combinations. If several consecutive hinge positions are possible, a central representative ij pair is chosen. The two parts of u₂ are labeled as different chain segments, allowing break moves.

Breaks

(Figure 6, GetBreak) If a substructure contains two chain segments, either because the protein is oligomeric or because a hinge operation has created two chain segments, and these segments can be separated by a simple translation without collisions in at least breakcut=0.05 of all possible directions, then a break exists and the two chain segments are labeled u₁ and u_2. If more than two segments are present in f, then all combinations of segments are tried.

The unfolding graph

(Figure 6, GetCuts) Starting with the native structure as the substructure f of the first cut, we find all geometrically possible cuts, giving preference to breaks, then pivots, then hinges. Each cut generates two substructures, u₁ and u₂. We then apply the same method to each of the substructures u₁ and u₂, recursively until the substructures are unfolded (defined below). The result is a directed acyclic graph (DAG), where the nodes are substructures and the bifurcating edges represent transition states of binary partitionings. Figure 1(c) shows a partial DAG for DHFR, showing geometrically possible unfolding steps with the energetically favored unfolding pathway highlighted in green.

Kinetic simulations

(Figure 6, UnfoldSim) A simulation of concentration changes over time can be produced by considering a single cut containing a folding intermediate f and the products u₁ and u₂ of a cut type, a pivot, hinge or break. The amount of f lost is proportional to its concentration [f] and the unfolding rate, which can be calculated using transition state theory⁴³:

$${\kappa }_u=\frac{d\left[f\right]}{dt}=\gamma \left[f\right]e^{(-\Delta G_u^{‡}∕RT)}$$ (2)

κ_u may be called the elemental unfolding rate. The barrier to unfolding for one cut, ΔG^‡_u, is a function of the energies of the f, u₁ and u₂, and of the cut type. The subscript ‘u’ indicates that the barrier height is measured in the unfolding direction. The transmission coefficient γ is equal to the rate of decomposition of the transition state. For a normal chemical reaction, this is γ =k_BT/h, or about 10¹³ s⁻¹_. But a diffusion-controlled folding reaction is much slower, estimated by Fersht⁴³ to be about 10⁶ s⁻¹, since compared to a chemical reaction, the protein folding reaction has a longer and flatter energy landscape with respect to a bond vibration.

The amount of f gained is proportional to the [u₁] and [u₂] and the folding rate term

$${\kappa }_f=\frac{d\left[f\right]}{dt}=\gamma \left[u_1\right]\left[u_2\right]e^{(-\Delta G_f^{‡}∕RT)}$$ (3)

κ_f may be called the elemental folding rate. The finite element simulations as described in Figure 6, UnfoldSim, are carried out on the set of all κ_f and κ_u to produce a set of all concentrations for each timestep dt. By summing over all cuts, q that involve f, and then multiplying by the timestep, we obtain the concentration change.

$$d\left[f\right]=\sum _{q\ni f\in q}\frac{d{\left[f\right]}_q}{dt}dt$$ (4)

To simulate unfolding, we initialize the concentration of the native state to F₀. Concentrations of all nodes are recalculated until equilibrium is established. To simulate folding, the leaf nodes are initialized to F₀. Equilibrium is assumed if there was no net change in concentration of the whole system. Note that the sum of the concentrations of all intermediates f that contain a given residue i, is equal to a constant, F₀, throughout the simulation. That is, the total concentration of residue i is conserved.

$${\left[i\right]}_{total}=\sum _{f\ni i\subset f}\left[f\right]=F_0$$ (5)

In other words, mass is conserved.

Components of the energy function

The folding and unfolding rates for a cut, κ_u and κ_f, are calculated directly from the substructures f, u₁ and u₂. Free energies are composed of two parts: the dissociation energy ΔE_d, and the backbone configurational entropy ΔS_q. The dissociation energy is composed of four terms: solvation energy ΔE_ω, hydrogen bonds ΔH_h, side chain entropy ΔS_λ, and buried void entropy ΔS_v. Disulfide linkages are treated as constraints rather than energies.

Dissociation Energy, ΔE_d

The energy of dissociation of two substructures is modeled using the increased solvation, increased sidechain entropy, loss of hydrogen bonds, and loss of buried void spaces.

$$\Delta {\mathrm{E}}_{\mathrm{d}}=\Delta {\mathrm{E}}_{\omega }+\Delta {\mathrm{H}}_{\mathrm{h}}-\mathrm{T}(\Delta {\mathrm{S}}_{\mathrm{v}}+\Delta {\mathrm{S}}_{\lambda })$$ (6)

where each term is defined below. Throughout this discussion, ΔE is used for free energies with unspecified entropic and enthalpic components, ΔG for free energies with specified enthalpic and entropic parts, ΔH for purely enthalpic terms and ΔS for purely entropic terms.

Solvation free energy, ΔE_ω

For simplicity we assume that the hydrophobic effect, coulombic interactions and the van der Waals attractive force, are all roughly proportional to the change in solvent exposed surface area, and we therefore combine them in one term, called the solvation free energy. Note that the van der Waals repulsive term is assumed to play no part in unfolding since native structures are assumed to have no collisions. Changes in solvent accessible surface area are computed using MASKER⁴⁴. The buried solvent accessible surface (SAS) exposed upon splitting one substructure, f, into two, u₁ and u₂, is approximated as the sum of pairwise residue SAS terms, where each term SAS_jk is the burial of SAS upon contact of residues j and k. Thus for a given cut, summing over residues separated by the cut, we get

$$\Delta SAS=\sum _{j\in u_1}\sum _{k\in u_2}SA{S}_j+SA{S}_k-SA{S}_{j,k}$$ (7)

The buried surface is a good measure of the amount of water displaced by the folding step, and also is a rough estimate of the scale of the VDW attractive force. Desolvation of hydrophobic groups and hydrogen bonding groups is the primary force driving protein folding.

The solvation free energy in units of kJ mol⁻¹ is simply

$$\Delta {\mathrm{E}}_{\omega }=\omega \Delta \mathrm{SAS}$$ (8)

where ω is the surface tension in J mol⁻¹Å⁻², a value that may be thought of as a modeling the effect of urea at different concentrations. A negative or low value favors solvation and unfolding (high urea), while a high value favors desolvation and folding (low urea). The value of ω corresponding to pure water may be chosen empirically. Theoretical values for hydration of buried protein surfaces^45-46 range from 30 to 80 J mol⁻¹ Å⁻². In this study, we did not attempt to break down ΔE_ω into its component parts.

Side-chain entropy increase, ΔS_λ

Upon unfolding, buried sidechains are exposed to the solvent and gain flexibility, each to a different extent. To calculate the change in sidechain entropy ΔS_λ, we multiply the relative change in the sidechain exposure with published values^47-48 for intrinsic sidechain entropy, ω, summing over all residues in f.

$$\Delta S_{\lambda }=m_{\lambda }\sum _{i\in f}\frac{\Delta SA{S}_i}{SA{S}_i^0}{\lambda }_i$$ (9)

SAS⁰_i is the total surface area of residue i in the unfolded state, and ω_i is its intrinsic sidechain entropy.

Buried void entropy, ΔS_v

All internal spaces large enough to hold one spherical probe of radius 1.2A, but not large enough to hold a water molecule (radius 1.4A), were found using MASKER⁴⁴. A typical high resolution crystal structure contains dozens of such cavities, which are entropically unfavorable⁴⁹. Surrounding each void are neighbor residues with atoms less than 7Å from the void center. The void v is said to exist in substructure f if f contains all of v’s neighbors. ΔS_v

$$\Delta S_{\nu }=U_{\nu }(N_{\nu }\left(f\right)-N_{\nu }\left(u_1\right)-N_{\nu }\left(u_2\right))$$ (10)

is the difference in the number of voids N_v, times the void cost U_v, an entropic term.

Hydrogen bonds, ΔH_h

Backbone hydrogen bonds were identified by adding hydrogens onto backbone amide nitrogens and finding backbone oxygens within a distance of 2.5Å. An H-bond exists within f if both donor nitrogen and acceptor oxygen are present in f. Each H-bond was assigned an enthalpic value H_h, yielding,

$$\Delta H_h=H_h(N_h\left(f\right)-N_h\left(u_1\right)-N_h\left(u_2\right))$$ (11)

where N_h(f) is the number of H-bonds present in substructure f. For simplicity, all H-bonds were assigned the same energy. Sidechain H-bonds were ignored.

Disulfide linkages

Disulfide bonds are treated as inseparable residues, but otherwise contribute nothing to the interaction energy. Any unfolding motion that would separate two disulfide-linked cysteines is disallowed.

Configurational entropy, ΔS_q

Our model assumes that configurational entropy depends only on the number of degrees of conformational freedom gained, and is independent of the size of the substructure. For example, partitioning a large subset of the protein was rewarded with the same entropy gain as partitioning a small piece. Rough entropic values were assigned to each of the three cut types, break, pivot and hinge, reflecting the approximate number of added degrees of freedom. A hinge adds a single angular degree of freedom, a pivot adds two, and a break adds all three plus some degree of translational freedom. For the two entropies,

$$\Delta {\mathrm{S}}_{\mathrm{hinge}},<<\Delta {\mathrm{S}}_{\mathrm{break}}$$ (12)

is enforced, and specific values were set empirically. ΔS_pivot was necessarily set to the average of the two so that alternative pathways to the same state would always have the same entropy change, a requirement of any state function.

Transition state free energy

Interactions must be broken before full configurational entropy increase is possible during an unfolding step, therefore we spread the configurational entropy, ΔS_q, unevenly along the reaction coordinate, apportioning more than half of the entropy to the products side, after the transition state of unfolding. A term, 0.5 ≥ σ^‡ ≥ 0.0, is used to set the fraction of ΔS_q expressed before the transition state. σ ^‡ was set to 0.25 for this work.

Another term, 0.2 ≤ θ ^‡≤ 0.8, sets the fraction of ΔE_d expressed before the transition state. θ ^‡ is calculated using the Hammond postulate, which states that the transition state most resembles the higher energy ground state. To quantify the Hammond behavior we adopted a reasonable simplifying assumption, that the slope of the energy with respect to the reaction coordinate is the same on both sides of the transition state. Using only the ground state energies and this assumption, the solution for the position of the transition state θ ^‡ is found using similar triangles.

$${\theta }^{‡}=\frac{(2\Delta E_d-\Delta S_q)}{2\Delta E_d}$$ (13)

Note that θ^‡ goes to zero as ΔS_q approaches twice the value ΔE_d, which means that there would be no barrier (diffusion controlled) for weakly connected substructures. To maintain physical realism, θ^‡ is constrained to be in the range 0.2 ≤ θ^‡≤ 0.8.

Cavitation, ΔG_c^‡

Theoretical studies done independently by Scheraga⁵⁰ and Baker ⁵¹ have shown a barrier to hydrophobic collapse (or its inverse) due to the atomic size of solvent. The free energy of cavitation, ΔG_c^‡, is expressed only in the transition state of the cut, reflecting the cavity formation that must precede the inward diffusion of water. Based on the cavitation studies of Hummer et al⁴⁹ we assume a quadratic relationship between ΔSAS and ΔG_c^‡.

$$\Delta {G_c}^{‡}={{\mathrm{m}}_c}^{‡}\Delta {\mathrm{SAS}}^2$$ (14)

Configurational entropy barriers, ΔG_q^‡

A hinge motion may require the concerted motion of several backbone torsion angles, a pivot motion only one or two angles, and a break motion requires no angular shifts. Strain due to steric interactions may be greater in a hinge motion, than in a pivot motion. ΔG_q^‡ serves to model the barriers to rotation that occur only in the transition state and are dependent on the type of motion. Allowed empirical settings are

$$\Delta {G_{hinge}}^{‡}\ge \Delta {G_{pivot}}^{‡}\ge \Delta {G_{break}}^{‡}=0.$$ (15)

Equilibrium and transition state free energies, ΔG_u-f, ΔG^‡_f, ΔG^‡_u

Using the transition state placement variables σ^‡ and θ^‡, the free energy barriers for folding and unfolding are,

$$\Delta {\mathrm{G}}_{u-f}=\Delta {\mathrm{E}}_{\omega }+\Delta {\mathrm{H}}_h-T(\Delta {\mathrm{S}}_{\nu }+\Delta {\mathrm{S}}_{\lambda })$$ (16)

$$\Delta {{\mathrm{G}}^{‡}}_u={\theta }^{‡}[\Delta {\mathrm{E}}_{\omega }+\Delta {\mathrm{H}}_h-T(\Delta {\mathrm{S}}_{\nu }+\Delta {\mathrm{S}}_{\lambda })]-{\sigma }^{‡}T\Delta {\mathrm{S}}_q+\Delta {G_c}^{‡}+\Delta {G_q}^{‡}$$ (17)

$$\Delta {{\mathrm{G}}^{‡}}_f=(1-{\theta }^{‡})[-\Delta {\mathrm{E}}_{\omega }-\Delta {\mathrm{H}}_h+T(\Delta {\mathrm{S}}_{\nu }+\Delta {\mathrm{S}}_{\lambda })]+(1-{\sigma }^{‡})T\Delta {\mathrm{S}}_q+\Delta {G_c}^{‡}+\Delta {G_q}^{‡}$$ (18)

Note that ΔG_u-f, = ΔG^‡_u - ΔG^‡_f, as required. Values from Eqs 17 and 18 for each elemental subsystem are used in Eqs 2 and 3 to define the elemental rates, and the whole system is simulated using the finite difference method (Figure 6, UnfoldSim).

Folded/Unfolded states

For purposes of calculating the unfolding rate from a simulated unfolding trajectory, the folded state is defined as the set of all intermediate substructures in the folding pathway that retain 90% or more of the buried SAS of the native state. In unfolding trajectories, the concentration of the folded state [F] is the sum over all folded states.

The unfolded state is defined as all intermediates substructures that have less than 1000Ų of buried SAS. This corresponds to an extended 10-residue fragment or smaller. The concentration of the unfolded state [U] is the average, over all sequence positions i, of the sum of the concentrations of all unfolded states that contain residue i.

Simulated unfolding kinetics

The empirical unfolding rate k_u was defined as ln(2)/t_1/2, where t_1/2 is the time at which [F] first reaches 1/2 of its initial value.

Table1.

Term	Value	Equation
R	8.314472 J °K−1 mol−1	2, 3
dt	10−7 - 0.01 s	4
F0	1.0 M	5
Uv	0 J mol−1 °K−1	8
ω	0 - 100 J mol−1Å−2	8
mλ	1.0	9
Hh	100 J mol−1	11
δ S break	90 J mol−1 °K−1	12
ΔShinge	30 J mol−1 °K−1	12
ΔSpivot	60 J mol−1 °K−1	12
mc‡	10−6 J mol−1	14
Δ Ghinge‡	50 J mol−1	15, 17, 18
Δ Gpivot‡	10 J mol−1	15, 17, 18
Δ Gbreak‡	0 J mol−1	15, 17, 18
σ*	0.5	17, 18
T	300°K	17, 18