Computational Protein Design with Explicit Consideration of Surface Hydrophobic Patches

Abstract

De novo protein design requires the identification of amino-acid sequences that favor the target folded conformation and are soluble in water. One strategy for promoting solubility is to disallow hydrophobic residues on the protein surface during design. However, naturally occurring proteins often have hydrophobic amino acids on their surface that contribute to protein stability via the partial burial of hydrophobic surface area or play a key role in the formation of protein-protein interactions. A less restrictive approach for surface design that is used by the modeling program Rosetta is to parameterize the energy function so that the number of hydrophobic amino acids designed on the protein surface is similar to what is observed in naturally occurring monomeric proteins. Previous studies with Rosetta have shown that this limits surface hydrophobics to the naturally occurring frequency (~28%) but that it does not prevent the formation of hydrophobic patches that are considerably larger than those observed in naturally occurring proteins. Here, we describe a new score term that explicitly detects and penalizes the formation of hydrophobic patches during computational protein design. With the new term we are able to design protein surfaces that include hydrophobic amino acids at naturally occurring frequencies, but do not have large hydrophobic patches. By adjusting the strength of the new score term the emphasis of surface redesigns can be switched between maintaining solubility and maximizing folding free energy.

Introduction

In addition to adopting a stable folded conformation, many proteins must be soluble in water in order to perform their biological function. This requirement constrains protein evolution, as sequences that are optimized only for folding free energy may not be optimized for solubility, and vice a versa.¹ Folding free energy is equal to the difference in free energy of the folded and unfolded states. In the unfolded state proteins adopt an ensemble of conformations that are less compact and more solvated than folded protein. In the folded state proteins adopt a unique set of structures with desolvated cores. The desolvation of hydrophobic amino acids is a primary driving force for protein folding, and increasing the difference in buried hydrophobic surface area between the folded and unfolded state will often stabilize proteins.^2,3 Even partially buried hydrophobic amino acids on the surface of a protein can dramatically boost protein stability. For example, introducing a cluster of four hydrophobic amino acids on to the surface of procarboxypeptidase A2 stabilizes the protein by more than 5 kcal/mol.⁴

Protein solubility is determined by many factors, including net electrostatic charge⁵, folding free energy, and the amount of exposed hydrophobic surface area in the folded state. A comparison of the surfaces of proteins that are monomeric and water-soluble with the surfaces of proteins that form obligate oligomers provides an indication of what surface features prevent association. The most striking difference between the two sets of proteins is the amount of exposed hydrophobic surface area. Jones and Thornton⁶ found that the interfaces of oligomeric proteins are more hydrophobic than the interfaces of other protein-protein complexes and of non-interface surfaces. In the set of oligomeric proteins examined by Janin et al⁷, the average amount of non-polar surface area at oligomer interfaces is 8% greater than the amount seen in monomeric protein surfaces. In agreement with these findings, Chiti et al⁸ found that the rate of aggregation of proteins and peptides increases as the amount of exposed hydrophobic surface area increases. Because exposed hydrophobic surface area can be so detrimental to protein fitness, computer-based methods for protein design must take this in to account when designing sequences for the surfaces of proteins.

Protein design programs contain two key components, a scoring function for evaluating the fitness of an amino-acid sequence for a given target structure and an optimization procedure for identifying low scoring sequences. Several studies have shown that if the scoring function is constructed to model only folding free energy then the surfaces of the designed proteins do not resemble the surfaces of naturally occurring proteins^9,10. In these cases, structural models of the unfolded and folded state are used to calculate the free energy difference between the folded and unfolded state. Pokala and Handel observed protein surfaces dominated by hydrophobic amino acids because their model emphasizes the importance of the hydrophobic effect in driving protein folding and surface residues were predicted to bury more hydrophobic surface area in the folded state than in the unfolded state. This problem can be alleviated by explicitly disallowing hydrophobic amino acids at all surface positions^11,12, but this solution is not ideal because partially exposed hydrophobics can contribute significantly to protein stability and surface hydrophobic amino acids are often important for protein function. A more permissive approach is to allow surface hydrophobics, but modify the scoring function so that it disfavors surfaces that are likely to promote aggregation.

A variety of scoring schemes have previously been used to control the placement of surface hydrophobic amino acids in design simulations^10,12–15. In many cases, the end result is that the scoring function represents more than folding free energy. This outcome can be achieved by including separate scoring terms for aggregation propensity and folding energy, or by creating a single score that implicitly reflects both criteria. Explicit scoring terms that have been used include penalties for exposed hydrophobic surface area^13,14 and negative design against sequences with favorable energy in a low dielectric environment¹⁶. More implicit strategies include constraining amino-acid composition to match naturally occurring proteins^17–19 and up weighting the strength of hydrogen bonds and electrostatic interactions on protein surfaces¹⁵.

The computer program we use for protein design studies, Rosetta, produces a single score that depends on both protein stability and aggregation propensity. Instead of parameterizing the Rosetta scoring function to predict folding free energies, Rosetta was trained to recapitulate naturally occurring sequences when performing design simulations with naturally occurring protein backbones. Critical to this recapitulation is the inclusion of reference energies for each amino-acid type. These energies are subtracted from the total energy of the protein, and their main function is to control amino-acid composition during design simulations. By setting the reference values to favor the correct ratio of polar and hydrophobic amino acids in protein sequences, the design of polar protein surfaces is implicitly favored. However, we have observed that in many cases the Rosetta scoring function fails to prevent large hydrophobic clusters on the surface of proteins, even though the overall amino-acid composition of the protein surface is not significantly different from other soluble proteins. This result reflects the favorable energetics of placing similar types of amino acids near each other. Pokala and Handel¹⁰ used an alternative strategy for setting amino-acid reference values. They used their force field to calculate the average energy of each amino-acid type on the surface for a large set of proteins and used these values as reference values. This strategy reduced the formation of hydrophobic clusters, but it also resulted in an underrepresentation of leucine, isoleucine, valine, phenylalanine and tyrosine on protein surfaces.

Here we describe the implementation of a new, non-pairwise-decomposable scoring term (called hpatch) that penalizes the formation of hydrophobic patches on the surfaces of designed proteins. Unlike previously described scoring terms that disfavor aggregation, the new term explicitly disfavors large patches, rather than the total amount of exposed hydrophobic surface area. We find that redesigning proteins with the hpatch score term reduces the size of hydrophobic patches to levels seen in native proteins, but preserves a natural ratio of hydrophobic and polar amino acids on the surface. We parameterize a new Rosetta scoring function using the hpatch score and assess its performance on native sequence recovery and ability to predict changes in free energy for characterized protein mutants. We find that we are able to create a single scoring function that performs well in sequence recovery tests when the hpatch score is included, and additionally performs well in predicting changes in protein stability if the weight on the hpatch score is set to zero.

Methods

Rosetta energy function

Rosetta uses a Monte Carlo search algorithm with simulated annealing to find low scoring sequences for a target backbone.^19–21 The energy function uses the 12-6 Lennard-Jones potential, the Lazardis-Karplus implicit solvation model²², a statistics-based electrostatics term²³, an explicit hydrogen-bond potential²⁴, a side-chain rotamer preference term, a knowledge-based backbone torsional term, and reference energies that are assigned to each amino-acid type. Side chain conformations are restricted to those found in the Dunbrack backbone-dependent rotamer library.²⁵

Monomer protein set

A monomer protein set was assembled from structures available in the PDB using metadata from the EBI macromolecule database PISA²⁶ and the PDB header. First, all structures listed as ‘monomers’ in PISA with the keyword ‘Protein’ were downloaded. This query resulted in 2489 structures. All PDB files which contained the words ‘dimer’ or any higher-order oligomer were removed, leaving ~2300 structures. ~570 of these were definite monomers with a line indicating the biological unit to be monomeric in the PDB header. The remaining structures had nothing to indicate oligomerization, and were assumed to be monomeric. Additional monomeric structures were downloaded from the RCSB²⁷ using the Advanced Search page. The PDB files for all single-chain, protein-containing structures determined using X-ray crystallography, having <1.8Å resolution and <50% sequence identity were downloaded and those containing ‘monomer’ as the biological unit were saved. This query resulted in 285 structures, approximately 50 of which were also contained in the previous set. The two sets of ~2500 structures were then clustered with CD-HIT²⁸, using a sequence identity threshold of 40%. CD-HIT performs sequence-based clustering using a greedy incremental algorithm, making it much faster than doing all-by-all comparisons using BLAST. The algorithm generated 1300 clusters, of which the representative PDB from each cluster was used for statistics.

A second set of proteins was used for energy function weight optimization. From the 285 structures returned by the RCSB search query, 64 of these structures, ranging in size from 61 to 240 residues, were randomly assigned into training and testing sets of equal size. The PDB codes for these structures are listed in the supplementary material (Table SI).

Development of a score term that disfavors hydrophobic patches

Our goal was to create a score term that favors protein surfaces with distributions of hydrophobic amino acids similar to the distributions observed in naturally occurring soluble proteins. Two different implementations of the hpatch score, hpatch-fast and hpatch-SASA, were developed and tested. Both versions are knowledge-based and are derived from the typical amounts of hydrophobic surface area exposed on protein surfaces. Statistics on hydrophobic accessible surface area were calculated from the set of monomeric structures described above.

The hpatch-fast score assigns all surface residues a score that depends on the amount of exposed hydrophobic surface area (hSASA) in their vicinity. Precalculated average hSASA values that depend on amino-acid type and degree of burial (as measured by number of neighbors) are used to rapidly estimate the hSASA for each residue. To derive these average values, the exact amount of hSASA exposed by every residue with 24 or fewer neighbors (Cβ within 10 Å) in the monomer protein set was calculated using Rosetta. The areas were grouped by residue type and number of neighbors and averaged (Table SII). Five different levels of burial were considered: residues with 10 or fewer neighbors, 11 to 13 neighbors, 14 to 16 neighbors, 17 to 20 neighbors, and 21 to 24 neighbors. Using these precalculated values avoids the slow calculation of exact SASA, making optimization of the score during a design run fast.

The hpatch-fast score for a given position depends on two things: the total amount of hSASA surrounding that position and the number of neighbors it has (Cβ distance), both within 10 Å. To parameterize the score, the hSASA around every surface residue in the set of naturally occurring monomeric structures was calculated using Rosetta. Residues were considered surface residues if they had 20 neighbors or less. Using the precalculated average values for the hydrophobic area exposed by each residue type, the sum of the amount of hydrophobic area exposed by a given surface residue and all of its neighbors within 10 Å, along with that residues’ number of neighbors, was saved. Neighboring residues with greater than 24 neighbors were assumed to have zero exposed hydrophobic surface area. All of the hSASA values were then grouped by number of neighbors. The distribution of areas was binned into increments of 25 Ų and the inverse log of the probabilities was taken to create a score that favors native-like amounts of hydrophobic area surrounding residues on protein surfaces (Figure S1). The score values are reported in the supplementary material (Table SIII). The score is defined out to a maximum area size of 1100 Ų. Areas of size 1100 Ų and greater are given a score of 25. A maximum value of 25 was chosen so that it would impose a great penalty on residues with very large amounts of surrounding hSASA, but not so great that it overwhelms the contribution of all other residues to the score.

The hpatch-SASA score uses the exact SASA for each atom in the protein and, instead of assigning a score to each surface residue; explicit patches that can span many residues are detected and given a score. During rotamer optimization, the SASA of the protein is kept up-to-date in the same manner as in Leaver-Fay et al²⁹. Briefly, a set of dots is distributed evenly on a sphere centered on an atom, where the radius of the sphere is the radius of the atom plus the probe radius. Each dot keeps track of the number of other residues that "cover" it, determined by using distance and angle calculations and precalculated masks that specify which dots are covered given two spheres.³⁰ When a rotamer substitution is considered, only the dot coverage counts for atoms which have overlapping SASA radii with either the previous rotamer or the new rotamer are updated. The SASA of each atom is determined by counting the number of dots not covered by any other atoms.

The hpatch-SASA score also uses a more rigorous method for finding hydrophobic patches, similar to that of the program QUILT³¹. After the SASA computation has completed, all hydrophobic atoms with nonzero SASA are assigned as nodes in a graph. An edge is placed between two nodes in this graph if their corresponding atoms have exposed overlap. The requirements for being considered exposed overlap are given in the following section. The union-find algorithm³² is run on the graph to find all of its connected components. Each connected component represents a hydrophobic patch on the surface of the protein.

Statistics on the patches found in native proteins were calculated to derive the function used for the hpatch-SASA score. A distribution of patch size for all patches with four or more atoms in the set of monomeric structures is shown in Figure S2. Using the inverse log of the probabilities does not provide a score bonus for splitting a large patch into two smaller sized patches as the score is mostly linear with a slope close to 0.5. Therefore, various exponential curves were plotted with the inverse log probabilities and y=0.4*((x/50-1)^2) was selected for the score because it greatly penalizes large patches without overpenalizing smaller, native-sized patches. The score values were adjusted so that patches with an area of 50 Ų or less receive a score of 0.0 (Table SIV). During scoring, patch areas are binned to the nearest 50 Ų. Patches of size 900 Ų or greater are assigned a score of 100. This maximum score ensures that very large patches are heavily penalized and quickly broken up during sequence optimization. It is important to note that the score being attached to a patch in hpatch-SASA cannot be directly compared to the score given to a single residue in the hpatch-fast approach. With the hpatch-fast method each surface residue gets a score, while with the hpatch-SASA method a score is explicitly assigned to a patch, which contains several residues.

Hydrogen atoms are excluded from both SASA calculations and patch identification. The van der Waals radii used here were taken from Chothia et al³³ (Table SV). For comparison, hydrophobic patch areas were also calculated using QUILT³¹. All QUILT runs used the maximum number of dots per atom, 252, the recover option -R, and a polar expansion radius of 1.4.

Implementation of the hpatch scores as non-pairwise decomposable terms in Rosetta

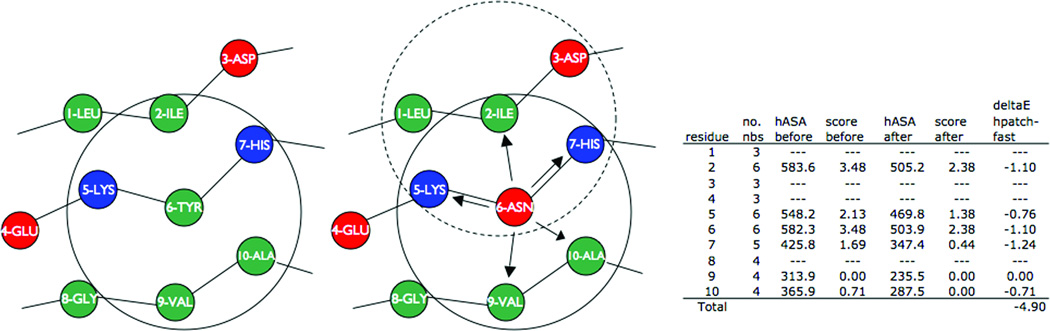
As patch identification is not pairwise decomposable, the hpatch scores were implemented differently than the other score terms in the Rosetta energy function. Their implementation closely follows that of the SASApack score described in Leaver-Fay et al²⁹. During a design simulation using the hpatch-fast score, each surface-exposed residue keeps track of the sum of exposed hydrophobic area within 10 Å. An amino-acid substitution at an exposed residue causes that residue and all its neighboring residues to update their hSASA sums (Fig. 1). The updated hSASA is used to get the new hpatch-fast score for that residue. The hpatch-fast score of the protein is the sum of the hpatch-fast score of all residues. For the hpatch-SASA score, two sets of calculations are performed after every amino-acid or rotamer substitution (Fig. 2). First, the SASA values of the residues near the changing residue are updated. Then, all of the hydrophobic patches for the current rotamer assignment are found using the union-find algorithm. The sum of the scores of all patches with 4 or more atoms becomes the hpatch-SASA energy for that state assignment.

Figure 1. Overview of how the hpatch-fast score updates in response to a sequence substitution.

Consider a substitution from tyrosine to asparagine at position (node) 6. Each of the neighbors within 10 Å (solid circle) of node 6 - nodes 2, 5, 7, 9 and 10 (indicated by arrows) - updates its record of the total amount of hydrophobic accessible surface area (hASA) within 10 Å assuming the substitution is accepted. The sum of the change in the hpatch-fast score at node 6 and all of the neighboring nodes becomes the hpatch-fast score change for the substitution. The table shows how the hASA and hpatch-fast score change at all of the nodes. Dashed circle, neighbors within 10 Å of node 2.

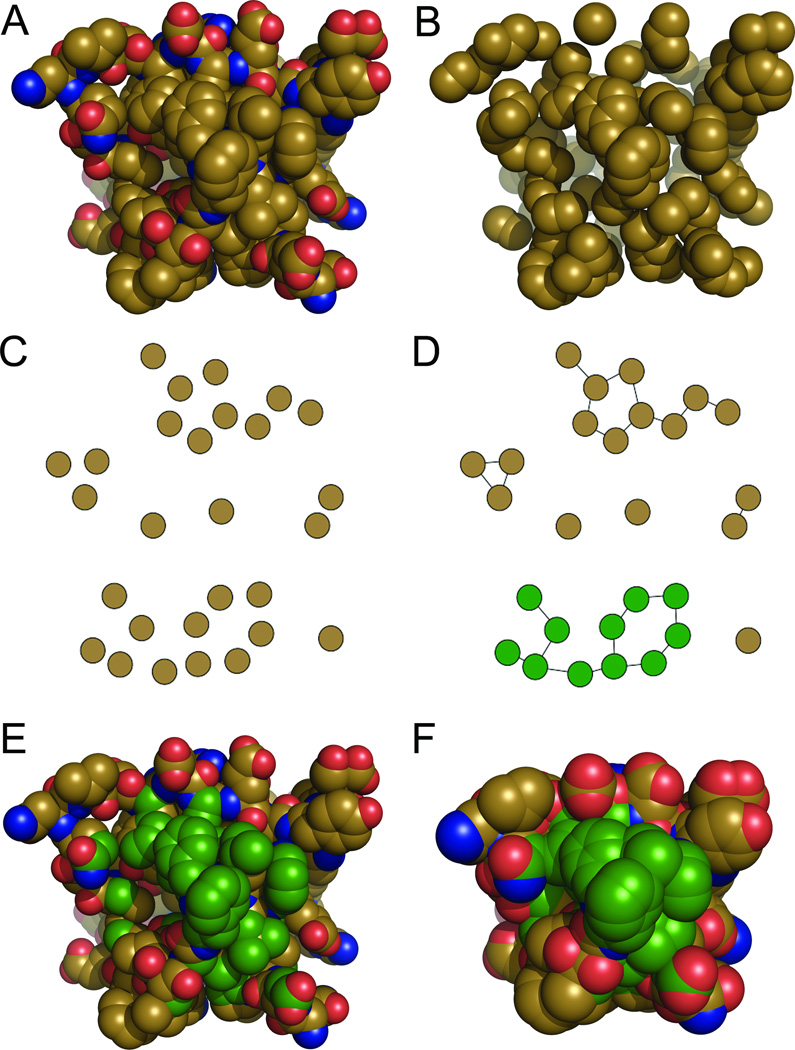
Figure 2. Overview of how the hpatch-SASA score finds and scores hydrophobic patches.

Consider a protein being designed (A). During simulated annealing, after each substitution all nonpolar atoms with nonzero SASA (B) are assigned to nodes in a graph (C). The union-find algorithm is run on this graph, which places edges between nodes whose atoms have exposed overlap. The output of the union-find algorithm is the set of all connected components in the input graph (D), which represents all of the hydrophobic patches on the protein. The largest hydrophobic patch on the input protein is shown in green in (E), with the atom radii expanded to their SASA radii in (F).

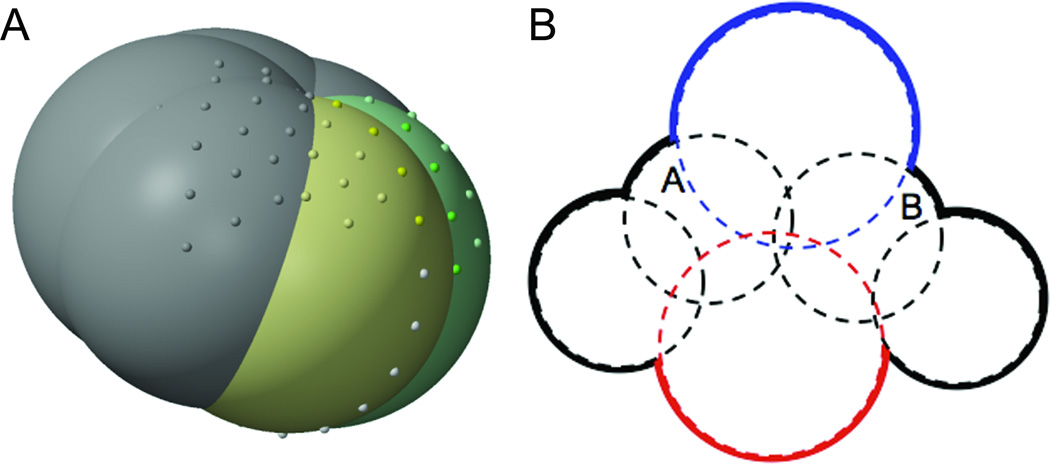
Two additional considerations are necessary with the hpatch-SASA score to prevent assigning all of the hydrophobic surface area to one large patch. One way an overly large patch can arise is if narrow strips of hydrophobic surface area connect large regions of hydrophobic surface area. As was done by Lijnzaad et al³¹ to avoid this situation, the polar atom SASA radii are expanded by 1.4 Å. Expanding the polar atom radii reduces the number of thin strips of hydrophobic area, delimiting the surface into separate hydrophobic patches. The other way in which an overly large patch can arise is if atom-pair adjacency is considered by sphere-overlap alone. Instead, the overlap region must be exposed for two atoms to be considered to contribute to the same patch. Two overlapping atoms, a and b, are defined to have exposed overlap if there exists an exposed dot on a adjacent to the plane of intersection with atom b, and if there exists an exposed dot on the surface of b adjacent to the plane of intersection with atom a (Figure 3a). Computing whether any dot on atom a is adjacent to the plane of intersection with atom b is logically a boolean AND of the bit-vector representing a's exposed dots and the pre-computed overlap mask³⁰ for b's overlap on a taken at distance max(0, r - τ), where r is the actual distance between a and b, and τ is the distance threshold limiting a dot's distance from the plane of intersection to be considered adjacent to the intersection. In this work, we use a cutoff distance τ = 0.8Å. Not checking for exposed overlap between two atoms can result in overlapping atoms with noncontiguous surface area being assigned to the same connected component (Figure 3b). With this approach, it is possible that two atoms are placed into the same patch even though their accessible hydrophobic surface area is not contiguous. This result would occur when the exposed dots in each ring are on opposite sides of the plane of intersection between the two atoms. We assume this case happens rarely and do not check for it during simulations.

Figure 3. Checking for exposed overlap.

A) Dots on the surface of PHE4 from ubiquitin (PDB id: 1UBQ). The white dots are buried, all other dots are exposed. The neighbors of this PHE, which bury most of its surface, are not shown. Atoms CZ (yellow) and CE1 (green) have exposed overlap according to the criteria used in this paper. The white dots and dark-yellow dots represent the set of dots on CZ adjacent to the plane of intersection with CE1. The dark green dots on the surface of CE1 are both exposed and adjacent to the intersection with CZ. Because both the dark-yellow set and the dark-green set are non-empty, atoms CZ and CE1 are said to have exposed overlap. B) If the adjacency condition for considering two atoms as part of the same patch were merely sphere overlap, instead of exposed overlap, then the two dimensional atoms A and B would be considered part of the same patch. Intuitively, this is mistaken, since the nitrogen (blue) and oxygen (red) atoms pictured here disrupt the patches from joining. A and B overlap, but the region where they overlap is not exposed to solvent.

As with the SASApack score, to speed up design simulations, hpatch score evaluations are procrastinated if the change in energy of the pairwise-decomposable terms for a rotamer substitution exceeds some threshold value. If the substitution is later accepted by the Metropolis criterion, the hpatch calculations are performed. This optimization is particularly helpful at the end of simulated annealing when most rotamer substitutions are rejected.

Explicit unfolded state energy term

An explicit unfolded state energy was used in place of the reference energies for some of the simulations. The unfolded state energy was calculated using a peptide-based model, which uses the energy of amino acids in fragments of structure to approximate the unfolded state energy. The average energy of each amino acid in the unfolded state was obtained by excising fragments from a set of PDB files and calculating the energy of the central residue. The set of PDB files used was the Dunbrack non-redundant subset of crystal structures with resolution ≤ 2.0 Å and R-factor ≤ 0.25 assembled in June 2005.³⁴ Fragments of size 13 were randomly selected from each structure and repacked. Additional rotamers were created by expanding all χ angles ±1 standard deviation around their preferred values. The number of residues in the protein multiplied by 0.1 determined the number of fragments taken from each structure. The unweighted energies of the central residue in every fragment were stored and then grouped by residue type. Unweighted, as opposed to weighted, energies were kept so that the same weights found during weight optimization and applied to the folded state could be used for the unfolded state. The mean values of the unweighted, unfolded energy by score type for each residue type are shown in the supplementary material (Table SVI).

Rosetta energy function and weight optimization

The various energy functions tested in this work were each optimized for native sequence recovery using a weight-fitting protocol implemented in Rosetta (Andrew Leaver-Fay, in preparation). The current Rosetta energy function was optimized using an approach similar to the one used here.²⁰ The protocol works by adjusting the weights of the energy terms and the reference energies so that the Boltzmann probability of the native amino acid is maximal over all positions in a set of proteins. More formally, the fitness is defined as Σ_proteins Σ_positions -ln [ exp(-E(aa_nat)) / Σ_aa,i exp(-E(aa_i))] where E(aa_nat) is the energy of the native amino acid at a position and the denominator is the partition function for all 20 amino acids at that position. To reduce floating-point errors from multiplying probabilities, the sum of inverse log of the probability was minimized. At each position in a representative set of proteins, the unweighted energy for all rotamers for every amino acid were obtained at that position, holding the other positions in the protein fixed at their native rotamers. Extra χ₁ and χ₂ torsion angles were used for all residue types at all positions. The best scoring rotamer for each residue type was used for evaluation of the fitness function. Candidate weight sets were created using particle swarm optimization followed by conjugate-gradient-based minimization of the best set of weights found using the swarm. The best, minimized weight set is then used to fully redesign all proteins in the set. Weight sets that improve both the overall sequence recovery and the designed amino-acid composition are accepted, and the weight optimization-redesign cycle is repeated until the weights converge. If the overall sequence recovery or amino-acid composition worsens, the reference energies are adjusted and redesign of the training set is repeated iteratively until both improve or until a predefined limit of 6 iterations is reached. If the limit is reached, the weight set is rejected and the next cycle of weight optimization begins from the previously accepted weight set. Natural amino-acid composition is obtained by minimizing the cross entropy between the distribution of designed amino acids and native amino acids. The cross entropy is minimized by raising the reference energy of amino acids overrepresented in the redesigned proteins and lowering those that are underrepresented. Typically, 6–8 rounds of reference energy adjustment are needed to obtain native-like amino-acid compositions.

The energy functions that were optimized include the standard Rosetta energy function and the standard energy function with both forms of the hpatch score and/or the unfolded state energy term. Not all of the terms in the energy function were allowed to vary. The omega, long-range and short-range backbone-backbone hydrogen bond weights were held fixed at 0.5, 1.17, and 0.585, respectively. In fixed-backbone design, these terms do not help in improving sequence recovery as all backbone coordinates are fixed. The fa_atr term, representing the attractive portion of the Lennard-Jones potential, was also held fixed at 0.8 so that the optimized weights could be compared to the current Rosetta weights. Because only one residue is being considered at a time during fitness function evaluation, the weight optimization procedure is also not appropriate for fitting the weights for the hpatch scores. Therefore, multiple weight optimization simulations were performed with varying fixed weights on the hpatch scores. The weight on the hpatch-fast score was left at 1.0. A weight of 0.3 on the hpatch-SASA score gave the best results without changing the sequence recoveries and amino-acid composition. The other energy functions optimized are as follows: the standard energy function with the hpatch-fast term (“standard + hpatch-fast”) and with the hpatch-SASA term ("standard + hpatch-SASA"); a standard one which replaces the reference energies with the unfolded state energy term (“standard, no refE + unfoldedE”), and the same with the hpatch-SASA score added ("standard, no refE + unfoldedE, hpatch-SASA") (Table SVII).

Predicting changes in free energy for protein mutants

Each of the optimized energy functions were also used to predict the change in free energy for a set of experimentally characterized mutants. Wild type and mutant structures were relaxed using the protocol described in Row 16 of Table 1 in Kellogg et al³⁵. Briefly, all of the side chains are first repacked using a soft repulsive energy function. Then the structure’s side-chain and backbone torsions are minimized using a hard-repulsive energy function. During minimization, harmonic restraints are placed on all pairs of C-alpha atoms within 9 Å keeping the backbone from moving too far from the crystal structure. Three rounds of minimization are performed, where the weight on the repulsive term is increased, starting at 1/10^th of its full weight, then at 1/3^rd of its full weight, and ending at the full weight. This protocol is applied 50 times to both the wild type and mutant species, and the average of the three-lowest energies for each species is taken as its energy. The predicted ΔΔG is the difference between the energies of the mutant and wild type species. A set of 1210 mutants assembled by Yin et al³⁶ and Guerois et al³⁷ were used for testing prediction accuracy. When weight sets that included the hpatch term were used in ΔΔG prediction, the weight on the hpatch term was set to 0. Prediction accuracy was measured by calculating the Pearson correlation coefficient.

Table I. Recoveries and energies of weight optimized standard and standard + hpatch energy functions.

This table reports the native sequence recoveries, largest hydrophobic patch area and total hydrophobic surface area averages for various energy functions. The energy functions tested include the current Rosetta energy function, the current energy function with the hpatch-SASA score (“current + hpatch-SASA”), a reweighted standard energy function, the standard energy function with the hpatch-fast term (“standard + hpatch-fast”) and with the hpatch-SASA term ("standard + hpatch-SASA"). Each of the reweighted energy functions were optimized for native sequence recovery and native amino-acid composition. Extra χ¹ and χ² rotamers were used for all residues (−ex1 −ex2 −extrachi_cutoff 0) except for training of the standard + hpatch-SASA energy function which used extra rotamers around χ¹ only.

	recovery			avg QUILT −ep 1.4	avg total hASA	% hp on surface	hpatch score weight
energy function	core	overall	surface
				462	1090	27.4
				448	1080	27.0
natives (all/train/test)	---	---	---	476	1100	27.8	---
current Rosetta weights	49.2	32.9	24.9	813	1270	29.5	---
current Rosetta, fit refEs only, training	56.5	38.0	24.9	775	1213	31.2	---
current + hpatch-SASA, fit refEs only, training	55.8	38.2	26.3	385	984	26.1	0.3
current Rosetta, fit refEs only, test	51.7	35.1	27.9	694	1206	31.8	---
current + hpatch-SASA, fit refEs only, test	52.5	35.5	27.3	446	1046	27.1	0.2
standard, training	56.7	38.1	25.9	697	1134	27.7	---
standard + hpatch-fast, training	56.9	37.9	24.1	590	1078	24.9	1.0
standard + hpatch-SASA, training	55.4	37.4	25.3	374	970	24.6	0.5
standard, test	51.6	35.2	27.3	735	1225	28.9	---
standard + hpatch-fast, test	51.6	35.2	26.6	723	1105	23.8	1.0
standard + hpatch-SASA, test	52.3	36.5	28.9	433	1089	27.7	0.3

Results

We first examined the performance of the current full atom energy function from Rosetta (version 3.1), which was originally parameterized to best reproduce native amino-acid sequences when performing whole protein redesigns of high-resolution crystal structures^4,19. Sequence redesigns were performed on a test set of 32 monomeric proteins. The results were similar to what we have observed previously¹⁹. In the core of the proteins, 49% of the wild type amino acids and 33% of all residues were recovered (Table I). The surfaces of the redesigns have 1270 Ų of hSASA, on average, similar to the wild type proteins which have 1100 Ų on average. However, in the redesigns the surface hydrophobics are more clustered than in the wild type proteins. The average size of the largest hydrophobic patch on the wild type proteins is 476 Ų, while for the redesigns it is 813 Ų. For three designs there were extremely large hydrophobic patches, with areas greater than 1200 Ų. Surface residue design is heavily influenced by the amino-acid reference energies. To see if the patches are a result of the current reference energies, we used a weight optimization protocol to refit the reference energies holding the weights on the other energy terms fixed. Designing with this energy function results in redesigns with sequence recoveries of 52% in the core and 35% overall. The amount of total hydrophobic surface area in the redesigns, 1206 Ų, is again similar to what is seen in natives, 1100 Ų. As with the current Rosetta energy function, though, large hydrophobic patches are found on the surfaces of the redesigns. The average size of the largest hydrophobic patch in the redesigns is 694 Ų, 1.5 fold larger than the patches seen on wild type proteins. As before, there are several proteins with very large patches. This set includes two all-β proteins, on which the largest hydrophobic patch in each protein spans the surface of a β-sheet. Refitting the reference energies is not sufficient for producing native-like surfaces.

The energy function currently used by Rosetta has been modified since the weights on the score terms were last parameterized. New smoothing functions have been applied to the Lennard-Jones and solvation potentials and hydrogen bond energies are scaled so that buried interactions score more favorably. To create a more appropriate point of reference, we also used the weight optimization protocol to refit the weights on the Rosetta score terms in addition to the amino-acid reference energies. With the reweighted energy function 52% of amino acids are recovered in the core of proteins and 35% are recovered for all residues. The surfaces of these redesigns have 1225 Ų of hydrophobic surface area, on average. Large hydrophobic patches are still present in these redesigns, with the average largest hydrophobic patch being 735 Ų. Refitting the weights on the energy terms and/or the reference energies improves native sequence recovery, but does not change how hydrophobic residues are clustered on the surface of designed proteins.

Redesigning proteins with the hpatch score

To counter the tendency of Rosetta to place hydrophobic residues near other hydrophobic residues on the surface, we developed and tested two score terms that explicitly penalize surface hydrophobic patches. Our first implementation was that of the hpatch-fast score, which gives all surface residues a score that depends on the amount of exposed hydrophobic surface area within 10 Å and the number of neighbors that residue has. Each surface residue calculates the sum of the amount of hydrophobic area exposed by all of its neighbors within 10 Å. Average precalculated SASA values based on residue type and number of neighbors are used instead of explicit SASA calculations to approximate how much exposed hydrophobic area a residue adds to the total. Residues with more exposed hydrophobic area surrounding them than what is seen in native proteins get a high score. From tests on individual structures, we found that the hpatch-fast score slightly reduced the size of hydrophobic patches in redesigned proteins. As part of a larger test, and to see what effect the score has on native sequence recovery, we optimized an energy function that included the hpatch-fast score. The weight on the hpatch-fast score was held fixed at 1.0. Sequence recoveries for the proteins created by this optimized energy function are given in Table I. Core and overall recovery are 52% and 35%, respectively, the same as recoveries obtained from the reweighted standard energy function. No significant change is seen in the sizes of the hydrophobic patches in the redesigns, however. The average largest patch size goes from 735 Ų in the standard redesigns to 723 Ų in the hpatch-fast redesigns. These designs have more native-like amounts of total hydrophobic surface area, 1105 Ų on average, but this improvement does not extend to the hydrophobic patches. Increasing the weight on the hpatch-fast score does result in smaller patches, but only because the surfaces become less hydrophobic overall compared to natives.

Since the hpatch-fast redesigns still had large hydrophobic patches, we implemented another version of the score that more rigorously identifies and penalizes patches. Our hypothesis was that the hpatch-fast score was not effective for two reasons. First, we noticed that using precomputed average values for the amount of hydrophobic area each residue adds to a patch introduces a considerable amount of error into the patch areas. Second, hydrophobic patches can easily extend beyond the 10 Å threshold the score considers. For these reasons, the hpatch-SASA score uses the exact SASA for patch areas and the union-find graph algorithm for patch detection (see Methods). By using a graph structure to find patches, the hpatch-SASA score is not limited to a distance threshold for finding patches and can identify patches of arbitrary shape and size.

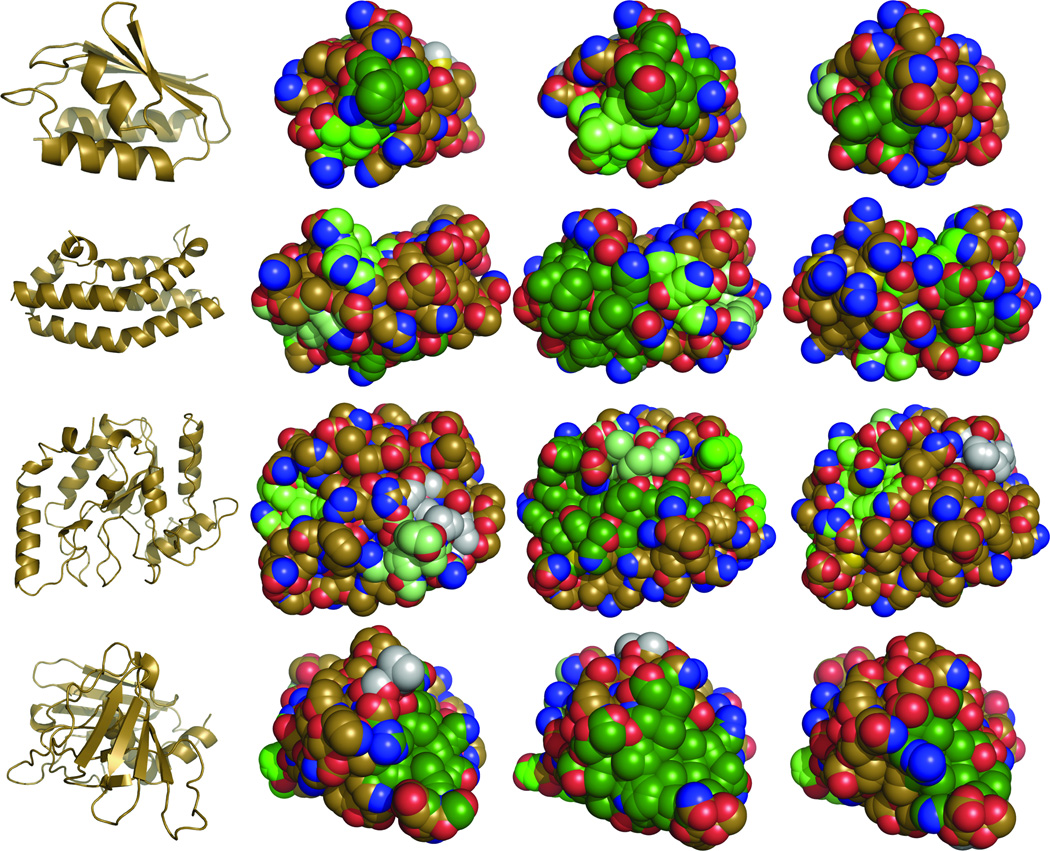
The hpatch-SASA score has a dramatic effect on the surfaces of designed proteins. Adding the score with a weight of 1.0 to the current Rosetta energy function caused a marked decrease in the size and number of hydrophobic patches in designed proteins but also decreased the number of designed hydrophobic residues (data not shown). Therefore, the weight fitting protocol was again used to optimize the weights of the other energy terms around the hpatch-SASA score. As was done for the standard Rosetta energy function, the protocol was used to refit the values of the reference energies alone and for all energy terms and reference energies together. The recoveries and surface metrics for proteins redesigned with the reweighted energy functions are given in Table I. For the hpatch-SASA energy function where only the reference energies were optimized, core and overall recovery stand at 53% and 36%, respectively. These recoveries are very close to the recoveries obtained with the reweighted standard Rosetta energy function. The average largest hydrophobic patch size in these redesigns is 446 Ų, much smaller than what is seen in the current and reweighted standard Rosetta redesigns and smaller also than what is seen in the native proteins. The total amount of hydrophobic surface area in these redesigns, 1046 Ų, is close to what is seen in natives, 1100 Ų. When allowing all weights and reference energies to be optimized, the hpatch-SASA energy function gets recoveries of 52% in the core and 37% overall. The average largest hydrophobic patch size in these redesigns is 433 Ų and the average total amount of hydrophobic surface area in these redesigns is 1089 Ų. For both optimized hpatch-SASA energy functions, the reduction in the average largest hydrophobic patch size is achieved without a change to the total amount of hydrophobic surface area. Examples of the difference in largest hydrophobic patch size between a native protein, a reweighted standard Rosetta redesign, and a redesign with the hpatch-SASA score are shown in Figure 4.

Figure 4. Surfaces of native and redesigned proteins.

From left to right, the native protein in cartoon representation, and spherical representations of the native protein, a current Rosetta redesign, and a reweighted Rosetta + hpatch-SASA redesign. Hydrophobic patches are colored according to size (largest to smallest: dark green, green, lime, pale green, gray). Oxygen and nitrogen atoms colored red and blue, respectively, and all other atoms are colored gold. Proteins shown are histidine-containing protein (1OPD), histidine-containing protein phosphotransfer domain (2A0B), uracil DNA glycosylase (3EUG), and toxic shock syndrome toxin-1 (3TSS). Figures created with PyMOL.

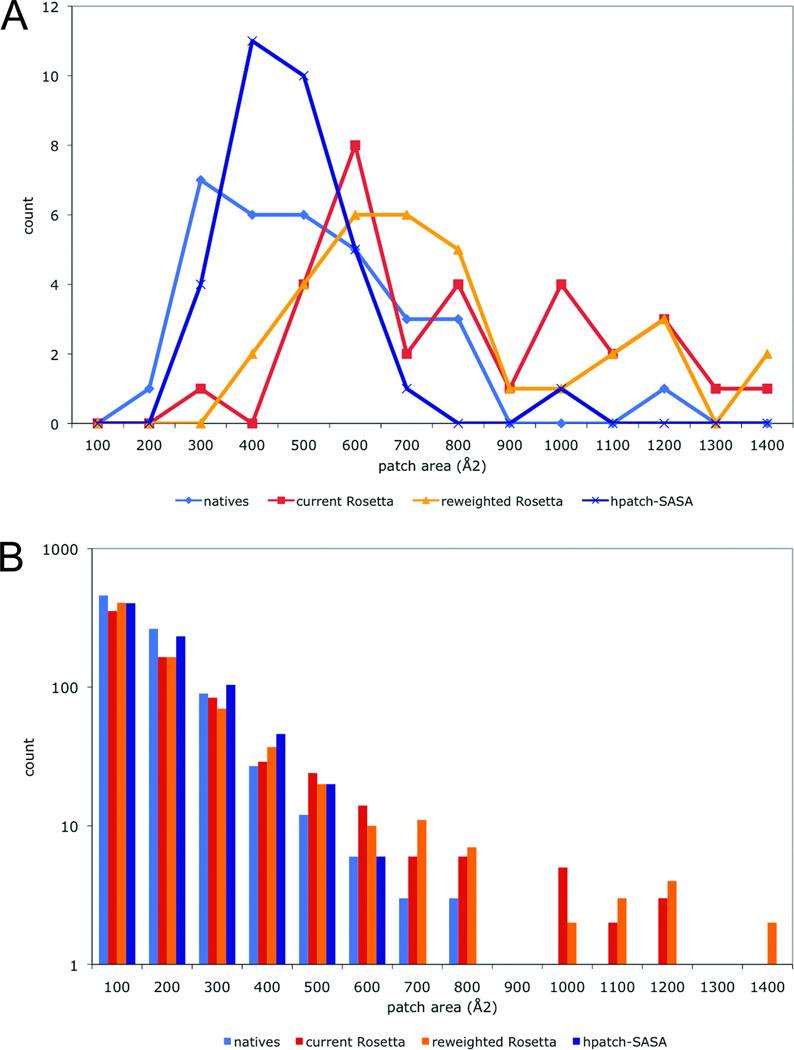
Designing with the hpatch-SASA score results in distributions of hydrophobic patch sizes more like that of native proteins. A histogram of largest hydrophobic patch size for the native and redesigned proteins is shown in Figure 5a. There is a noticeable shift toward larger patches in the proteins redesigned with the current and reweighted Rosetta energy functions that is shifted back to near-native levels with the addition of the hpatch-SASA score. The score also corrects the size distribution of all patches, not just the largest patch. Figure 5b shows the distribution of patch sizes for all patches in the native and redesigned proteins. The redesigns created with the hpatch-SASA score have patch sizes that track the sizes seen in native proteins better than the current and reweighted standard energy function redesigns. Using the hpatch-SASA score, it is possible to design surfaces with native-like amino-acid composition and smaller than native sized patches of hydrophobic area.

Figure 5. Hydrophobic patches in native and redesigned proteins.

The bar graphs show hydrophobic patch area distributions for the largest (A) and all (B) patches in native (blue), current Rosetta redesigns (red), reweighted Rosetta redesigns (orange) and reweighted Rosetta + hpatch-SASA redesigns (dark blue)

Design simulations using the hpatch-SASA score take longer to complete because patch energies cannot be precalculated and stored in memory, as can rotamer pair energies. To see what effect the hpatch-SASA score has on the final energies and run times of design simulations, we performed complete redesigns of seven proteins using the standard Rosetta energy function and the hpatch-SASA optimized energy function. Protein names, final energies, and running times are reported in Table II. The total time of simulations with the hpatch-SASA score increases by a factor of 21, on average. This increase appears to be independent of protein size as the fold increase in runtime for the 72 residue protein 1HZ5A is roughly the same as the increase for the 185 residue protein 1GBS.

Table II. Energies, hydrophobic patch areas and run times of proteins redesigned with the hpatch score.

Each protein was redesigned with the current Rosetta energy function and the optimized standard + hpatch-SASA energy function. All residue types were allowed at all positions, and extra χ₁ and χ₂ torsion angles were used for all residues. Hydrophobic patch areas were calculated using QUILT, with a polar expansion radius of 1.4Å. Sim. annealing time represents the time spent in the sequence optimization part of the simulation.

protein	no. residues	rotamers	scoring function	hpatch- SASA score	area largest QUILT patch	total time (s, app)	sim annealing time (s)
1HZ5A	72	---	native	6.88	258	---	---
		96520	standard redesign	26.3	548	344	327
		96551	standard + hpatch-SASA redesign	5.1	399	6691	6667
1LMBA	87	---	native	14.2	563	---	---
		114005	standard redesign	15.7	493	478	457
		114057	standard + hpatch-SASA redesign	2.2	463	8184	8152
1QYS	92	---	native	12.2	481	---	---
		127087	standard redesign	21.8	661	546	522
		127132	standard + hpatch-SASA redesign	5.9	588	12419	12390
1FKB	107	---	native	7.7	585	---	---
		134025	standard redesign	16.2	674	578	551
		134096	standard + hpatch-SASA redesign	7.4	525	11330	11297
1IFC	131	---	native	11.0	554	---	---
		183274	standard redesign	15.8	767	879	840
		183342	standard + hpatch-SASA redesign	8.0	558	21755	21715
1GBS	185	---	native	6.2	411	---	---
		195483	standard redesign	27.7	426	1161	1115
		195563	standard + hpatch-SASA redesign	2.6	309	22965	22905

Design using an energy function with an explicit unfolded state energy

Instead of explicitly modeling the unfolded state Rosetta uses amino acid-specific reference energies that are parameterized to favor a native-like distribution of amino acids in designed sequences. This implicitly favors proteins with hydrophobic cores and polar surfaces as the solvation model in Rosetta strongly penalizes the burial of polar chemical groups. Because the hpatch score provides an alternative mechanism for controlling amino composition on the protein surface we were curious if we could replace Rosetta’s reference energies with an explicit unfolded state energy term in combination with the hpatch score. The attractiveness of this approach is that it removes 19 adjustable parameters from the weight fitting process and creates a scoring function with an explicit protein stability term (energy of the folded state minus the unfolded state) and an explicit measure of protein solubility (hpatch score). A variety of approaches can be used to model the unfolded state. Creamer and Rose³⁸ found that using fragments excised from the structures of folded proteins serve as better models of the unfolded state than do tripeptides. Based on this conclusion, Pokala and Handel¹⁰ used the average energy of amino acids in short fragments as a per-residue unfolded state energy in their design algorithm. They found that the fragment-based unfolded state model outperforms the tripeptide model in predicting changes in stability for a large number of protein mutants. Here, we use 13-residue fragments excised from folded proteins to estimate the average energy of each amino-acid type in the unfolded state (see Methods).

Using the unfolded state energy term in place of the Rosetta reference energies lowers native sequence recovery and leads to very hydrophobic surfaces. We first optimized the weights of an energy function using the unfolded state term for native sequence recovery (Table III). Redesigning the testing set with this energy function gives core and overall recoveries of 48% and 31%, respectively. The average amount of hydrophobic SASA in the designs is 1844 Ų, nearly twice as large as the wild type proteins. The average largest hydrophobic patch size jumps to 1479 Ų compared to 735 Ų for the reweighted standard Rosetta energy function. We also optimized weights for the same energy function but with the hpatch-SASA score added. The core and overall recoveries with this energy function are 48% and 30%, respectively, similar to the recoveries of the energy function without the hpatch-SASA score. However, the surfaces of these redesigns have considerably smaller hydrophobic patches than when the hpatch-SASA score is not present. The average largest hydrophobic patch size drops from 1479 Ų to 464 Ų upon addition of the hpatch-SASA score and the total average hSASA, 1064 Ų, is close to the amount seen in the wild type proteins.

Table III. Recoveries and energies of weight optimized standard + unfolded state energy functions.

This table reports the native sequence recoveries, largest hydrophobic patch area and total hydrophobic surface area averages for various weight optimized energy functions. The energy functions tested include a reweighted standard energy function that replaces the reference energies with the unfolded state energy term (“standard, no refE + unfoldedE”) and the same energy function with the hpatch-SASA score (“standard, no refE + unfoldedE, hpatch-SASA”). Both of the reweighted energy functions were optimized for native sequence recovery alone. Extra χ1 and χ2 rotamers used for all residues (−ex1 −ex2 −extrachi_cutoff 0).

	recovery			avg QUILT patch −ep 1.4 -R	% hp on surface	avg total hASA −ep 1.4	hpatch weight
energy function	core	overall	surface
natives	---	---	---	476	27.8	1100	---
standard, no refE + unfoldedE, training	55.9	32.8	17.9	1403	48.1	1837	---
standard, no refE + unfoldedE, hpatch-SASA, training	50.6	31.8	18.9	424	29.3	1024	0.5
standard, no refE + unfoldedE, test	47.7	30.5	21.0	1479	46.4	1844	---
standard, no refE + unfoldedE, hpatch-SASA, test	48.4	29.8	19.9	464	30.3	1064	0.5

Despite having a more native-like distribution of hydrophobic surface area on the surface, the amino-acid composition on the surface of proteins designed with the hpatch-SASA score and the unfolded state term is still significantly different than the native sequences. While the native sequences have 37 histidines and 12 tryptophans on their surfaces in total, the designs have 308 histidines and 168 tryptophans (Table SVIII). Conversely, alanine and lysine are grossly underrepresented on the surfaces of the designs. These results can be interpreted in a variety of ways. The peptide model of the unfolded state may be missing important features that determine the favorability of each amino acid in the unfolded state. The over abundance of tryptophan in the design models indicates that tryptophan makes more favorable interactions on a protein surface (using the Rosetta energy function) than in the peptide fragments used here. This could indicate that true unfolded states allow for more contacts and burial than is present in the fragments. Alternatively, the additional tryptophans on the surface may be favorable for folding free energy, but may have other negative consequences, such as favoring misfolded conformations or non-specific interactions with other proteins. Amino-acid composition may also be partially determined by metabolic constraints that influence the overall fitness of an organism.

Predicting changes in stability for mutations

Rosetta can also be used to predict the change in free energy for protein mutants (ΔΔG). Given that we optimized the energy functions described above only for native sequence recovery, we wanted to see how they would perform at predicting ΔΔG. We follow the protocol described in Kellogg et al³⁵, which uses repacking and side-chain and backbone torsion minimization to create mutant structures. First, all residues in the mutant structure are repacked using the Rosetta energy function with a dampened Lennard Jones energy. Then the wild type and mutant structures are cycled through side-chain and backbone torsion minimization using either the standard Rosetta energy function or one of the weight-optimized energy functions described above. The average of the three lowest energy wild type and mutant structures is taken to obtain the wild type and mutant energy, and their difference is the predicted ΔΔG. We tested the performance of each of the optimized energy functions in predicting ΔΔG of stability for a set of 1210 mutants assembled by Yin et al³⁶ and Guerois et al³⁷ (Table SIX). The correlation coefficient and the root mean square error for each energy function are reported in Table IV and in the supplementary material (Figure S3). The current Rosetta energy function has a correlation coefficient of 0.69³⁵, and a root mean square error of 1.76 kcal/mol between the experimental and predicted ΔΔG values. When only the reference energies are reweighted, both the standard Rosetta energy function and the standard energy function with the hpatch-SASA score have correlation coefficients of 0.68 and root mean square errors of 1.66 and 1.71 kcal/mol, respectively. If all of the score terms and the reference energies are reweighted, the standard Rosetta energy function and the hpatch-SASA energy function get correlation coefficients of 0.61 and 0.63, respectively. These results show that despite being optimized for native sequence recovery with the hpatch-SASA score, the above energy functions still perform well in predicting mutant ΔΔG values.

Discussion

In previous de novo protein design projects with Rosetta it has been necessary to restrict the amino-acid alphabet available at specific surface residue positions in order to avoid the design of large hydrophobic patches on the protein surface^20,39,40. As seen in the tests performed here, the primary problem is not the overall amino-acid composition of the protein surface, but rather the clumping of similarly typed amino acids. Hydrophobic and polar amino acids probably segregate on the surfaces of the designs for the same reason that oil and water do not mix, the hydrophobic amino acids can not satisfy the hydrogen bonding potential of the polar amino acids. Most protein design algorithms, including Rosetta, use energy functions that are pairwise additive at the residue level. In this case, there is not a straightforward mechanism for explicitly disfavoring hydrophobic patches while maintaining a native-like distribution of amino acids on the surface. Here, we have shown that a non-pairwise additive score term that explicitly detects patches of exposed hydrophobic surface area can be combined with the standard Rosetta energy function to design surfaces that more closely resemble naturally occurring monomeric proteins.

Our use of the hpatch score to disfavor hydrophobic patches is an example of negative design. The purpose of the score term is not to increase the thermodynamic favorability of the folded state relative to the unfolded state, but rather to disfavor aggregation. This suggests that by changing the weight on the hpatch score it will be possible to shift the emphasis of surface redesigns between maintaining solubility and maximizing folding free energy. For example, in a previous study, Rosetta was used to redesign the sequence of the activation domain of human procarboxypeptidase A2⁴¹. The redesigned protein was 10 kcal / mol more stable than the wild type protein. In these simulations, all amino acids were allowed at each sequence position in the protein and a large hydrophobic patch, with an area of 730 Ų, was created on the surface of the protein’s β-sheet. Subsequent NMR analysis indicated that at concentrations >100 µM the redesigned protein self-associates and buries the hydrophobic residues on the surface of the β-sheet⁴. A similar interaction was seen in the crystal structure of the protein. If we redesign procarboxypeptidase (1VJQ) using the hpatch score, a large hydrophobic patch is no longer placed on the surface of the sheet. Instead, the largest patch in this redesign is created by one of the loops of A2 and has an area of 257 Ų.

Because patch identification is not pairwise-decomposable, simulations with either implementation of the hpatch score take longer to complete than standard Rosetta design runs. For comparison, designing with another non-pairwise-decomposable score term in Rosetta, the SASApack score, increased the runtimes of simulation by 26-fold. Design simulations with the hpatch-SASA score increase the runtime by a factor of 21. In addition to making the surface area calculations, time is also spent finding patches using the union-find algorithm with the hpatch-SASA score. As with the SASApack score, procrastination of hpatch score calculations helps to speed up the simulations. If a substitution causes an increase in the energy of the other energy terms over some threshold amount, the hpatch score is not calculated unless the substitution is later accepted. This optimization applies to both forms of the hpatch score. As simulations with the hpatch-SASA score take longer than current Rosetta, we recommend that the hpatch-SASA score only be used during the final design runs of a protocol. Alternatively, as the score is fast to compute for a single structure, it could be used as a filter at the end of a protocol. Chennamsetty et al⁴² recently used a spatial aggregation propensity score that gives positions with exposed hydrophobic neighbors a high score to increase the solubility of two antibodies.

As discussed above, one function of the 20 amino-acid reference values used in Rosetta is to implicitly disfavor the placement of large numbers of hydrophobic amino acids on the surfaces of redesigns. For this reason, we tested if the reference values could be replaced with the hpatch score and explicitly calculated unfolded state energies. The hpatch score was successful at preventing large hydrophobic patches on the surface; however, the amino-acid composition of the redesigned surfaces was considerably different than naturally occurring proteins. This discrepancy could indicate that our model for the unfolded state is poor, or it may also be a consequence of the fact that the amino-acid composition of proteins is probably determined by several factors including: protein stability, protein solubility, metabolic constraints and negative design against alternative structures and complexes. Without an empirical energy term that can be varied to titrate amino-acid composition, it is difficult to match the naturally occurring frequencies on protein surfaces. Pokala and Handel had some success using amino-acid reference energies that were derived from calculating the average energies of the various amino acids on a protein surface, but hydrophobic amino acids were underrepresented with this approach. In future surface redesigns with Rosetta, we plan to continue using the empirically determined reference values in combination with the hpatch score. However, as alternative models for the unfolded state are developed it will be important to revisit if the empirically determined reference values can be replaced with explicit unfolded state energies.

In this study we have focused on the surfaces of monomeric proteins. The hpatch-SASA score may also prove useful when designing transient protein-protein interactions. In this scenario, proteins must be soluble in the unbound state, and therefore, cannot rely on large hydrophobic surfaces to mediate the interaction with the target protein. When performing standard single-state computational protein design on a protein-protein complex there is no energetic penalty for designing an interface mediated by hydrophobics as the solubility of the unbound state is not being considered during the simulation. The solution to this problem is to perform a multi-state design simulation in which the sequence is simultaneously optimized for binding as well as solubility in the unbound state¹⁶. The hpatch-SASA score could be used to provide a measure of solubility in the unbound state for candidate sequences.

Code availability

Source code for the hpatch scores is available for free as part of the Rosetta molecular modeling program, version 3.3.

Table IV. Correlation coefficients for predicting changes in stability.

Correlation coefficients (R) and root mean square error (RMSE) between experimental and predicted ΔΔG for a set of 1210 protein mutants using the weight-optimized energy functions.

energy function	R	RMSE
current Rosetta weights	0.69	1.76
current Rosetta, fit refEs only	0.68	1.66
current + hpatch-SASA, fit refEs only	0.68	1.71
standard	0.61	2.18
standard + hpatch-SASA	0.63	2.27