Intrinsic disorder: signaling via highly specific but short-lived association

Abstract

The association between signaling proteins and their cellular targets is generally thought to be highly specific (implicating a high association constant, K_a) and, at the same time, transient or short-lived (corresponding to a high dissociation rate constant, k_d). However, a combination of high K_a and high k_d would lead to a high association rate constant (k_a = K_ak_d), which poses a problem because there is a limit to which k_a can be increased, set by the diffusional approach to form the complex. In this Opinion, I propose that having the signaling protein disordered before binding the target provides a way out of this quandary. The intrinsic disorder of the signaling protein would decrease K_a without sacrificing the specificity of the complex, and thereby would allow k_d to be increased to a range appropriate for signaling.

Signaling proteins: a kinetic argument

Intrinsically disordered proteins (IDPs), which do not have a specific stable structure under native conditions, are widespread [1–5], and their study is a thriving field [6–12]. Although some of these proteins function without binding, and others remain disordered upon binding their cellular targets, many of them gain structures, i.e. undergo a disorder-to-order transition, upon binding. The binding processes may serve regulatory roles [13, 14] or be a part of a signal-transduction cascade [15]. Suggested benefits of intrinsic disorder include the ability to interact with different target proteins, a high specificity with low affinity, extended interaction surfaces, and enhancement of association rates. In this Opinion, I appraise these prevailing views and argue for a yet unappreciated benefit – that intrinsic disorder inevitably leads to high dissociation rates, which are essential for regulatory and signaling proteins.

The basic premise of my argument is that the proper functioning of a regulatory or signaling protein that binds to a cellular target puts constraints on both the thermodynamics of the intermolecular interactions and the kinetics of the binding process. The interactions with the cognate target must be sufficiently favorable (for affinity) and much more so than those with potentially adverse non-cognate targets (for specificity) (Box 1). The affinity must be sufficiently high so that, at the cellular concentration of the protein, a significant fraction of the cognate target is bound by the protein; meanwhile, the specificity must be sufficiently high so that the bound fraction of any non-cognate target is strictly controlled. In addition, the association and dissociation rate constants must also be sufficiently high so that neither association nor dissociation creates a kinetic bottleneck in the overall biological process (Box 2).

Box 1. Binding thermodynamics.

The thermodynamics of the binding between a protein P and its target T,

$$\mathrm{P}+\mathrm{T}\rightleftharpoons \text{PT}$$ (I)

to form a noncovalent complex PT is characterized by the association constant, denoted as K_a. At equilibrium, the concentrations of the three species, [P], [T], and [PT], satisfy the condition

$$K_{\mathrm{a}}=\frac{[\text{PT}]}{[\mathrm{P}][\mathrm{T}]}$$ (II)

Experimentalists prefer to use the inverse of K_a, which is known as the dissociation constant and is denoted as K_d. Assuming that P is in excess over T, the bound fraction of the target is

$$\varphi =\frac{[\text{PT}]}{[\text{PT}]+[\mathrm{T}]}=\frac{1}{1+K_{\mathrm{d}}/[\mathrm{P}]}$$ (III)

At [P] = K_d, ϕ = 0.5. So K_d represents the protein concentration at which it saturates 50% of the target. A high affinity means that the 50% saturation requires a low protein concentration. Because maintaining a high concentration of any protein is a burden on cells, there is an evolutionary pressure to decrease protein cellular concentrations. To compensate, binding affinities have to be increased in order to achieve significant saturation of the cognate targets.

For a given protein, the cognate target may face competition from non-cognate targets. This problem is resolved if the protein is highly specific for the cognate target. That is, the binding affinity for the cognate target is much higher than those for the non-cognate targets.

The association constant is determined by the energy functions of the binding molecules and their interactions. The energy function, U(X), of a molecule represents the dependence of its potential energy on the coordinates, X, of its atoms (it is understood that the three degrees of freedom arising from the overall translation of the molecule are eliminated from X). At equilibrium, the probability of the molecule occupying any position in the configurational space is proportional to the Boltzmann factor, e^−U(X)/k_BT, where k_B is Boltzmann’s constant and T is the absolute temperature. The configurational integral,

$$Q={\displaystyle \int d\mathbf{X}{e}^{-U(\mathbf{X})/k_{\mathrm{B}}T}}$$ (IV)

is a measure of the statistical weight of the molecule. The binding process of Equation I involves three species, with configurational integrals Q_P, Q_T, and Q_PT. The association constant is given by [47] as

$$K_{\mathrm{a}}=\frac{Q_{\text{PT}}}{Q_{\mathrm{P}}{Q}_{\mathrm{T}}}$$ (V)

The energy function of the complex can be written as

$$U_{\text{PT}}=U_{\mathrm{P}}+U_{\mathrm{T}}+U_{\text{int}}$$ (VI)

where the third term, U_int, is due to the interactions between the protein and the target within the complex. The complex consists of configurations in which the intermolecular interactions are favorable; correspondingly, the integration of Equation IV for the complex is confined to these configurations. Strengthening the favorable interactions corresponds to an increased Q_PT and, hence, an increased K_a.

Box 2. Binding kinetics.

The rates of the forward and reverse steps in Equation I from Box 1 are characterized by the association rate constant k_a and the dissociation rate constant kd, respectively. Thermodynamic reversibility dictates that

$$K_{\mathrm{a}}=\frac{k_{\mathrm{a}}}{k_{\mathrm{d}}}$$ (I)

Assuming that the protein P is in excess over its target T, the lifetime τ_f of the free T species is 1/k_a[P]. An overly long τ_f may create a kinetic bottleneck in the overall biological process, so k_a[P] cannot be too small. In particular, k_a for an IDP has to be sufficiently high to compensate the low cellular concentration of the protein. Similarly, the lifetime τ_b of the bound T species is 1/k_d, and k_d has to be sufficiently high in order for the dissociation step not to be a kinetic bottleneck.

One can envision that the association (as well as the dissociation) step goes through an intermediate, P·T, referred to as the initial complex (or encounter complex), in which P and T form some contacts, while their translational and rotational motions become coupled:

$$\mathrm{P}+\mathrm{T}\underset{k_{1-}}{\overset{k_{1+}}{\rightleftharpoons }}\mathrm{P}·\mathrm{T}\underset{k_{2-}}{\overset{k_{2+}}{\rightleftharpoons }}\text{PT}$$ (II)

The sub-step leading to P·T is dominated by the translational and rotational diffusion of the binding molecules, whereas the subsequently sub-step is dominated by internal motions (i.e., conformational rearrangement). The second sub-step usually encounters a free energy barrier [37, 48]. The kinetic scheme of Equation II can be used to describe the dock-and-coalesce association mechanism [32] (Figure 2), where docking and coalescence corresponds to the first and second sub-steps, respectively. Making a steady-state approximation for P·T, one finds

$$k_{\mathrm{a}}=\frac{k_{1+}{k}_{2+}}{k_{1-}+k_{2+}}$$ (IIIa)

$$k_{\mathrm{d}}=\frac{k_{1-}{k}_{2-}}{k_{1-}+k_{2+}}$$ (IIIb)

If k₂₊ is much higher than k₁₋, then k_a ≈ k₁₊, and the overall association is rate-limited by diffusion. Conversely, if k₂₊ is much lower than k₁₋, then k_a ≈ k₂₊k₁₊/k₁₋, and the overall association is rate-limited by conformational rearrangement. In these two regimes, the dissociation rate constant is k_d ≈ k₁₋k₂₋/k₂₊ and k_d ≈ k₂₋, respectively.

For the association of ordered proteins, the initial complex is the so-called transient complex, which has near-native separation and relative orientation between the subunits but not the short-range specific intermolecular interactions of the native PT complex [49]. The association of ordered proteins tends to be rate-limited by diffusion. In cases where the transient complex is formed by unbiased translational and rotation diffusion, k_a is usually between 10⁴ to 10⁶ M⁻¹s⁻¹ [32]. When the diffusional approach of P and T is under the influence of long-range electrostatic attraction, k_a can be increased by three to four orders of magnitude.

Binding promiscuity

IDPs can bind multiple targets via different conformations (either presumed or observed). For example, the kinase inhibitory domain of the cyclin-dependent kinase (Cdk) inhibitor p21^Cip1 can bind to a diverse family of cyclin-Cdk complexes [15]. Similarly, the GTPase-binding domain of the Wiskott-Aldrich syndrome protein (WASP) can bind to its own C-terminal VCA domain, resulting in auto-inhibition, whereas, in a different conformation, can bind to the GTPase Cdc42, resulting in WASP activation for initiating actin polymerization [14]. However, it should be noted that many ordered proteins also have many binding partners, via the same binding site or separate binding sites on the protein surface [16, 17]. Some studies have suggested a correlation between the increase in the number of interaction partners and the increase in the propensity of disorder [18, 19], but this conclusion has been debated [17, 20].

In the cell, IDPs tend to be less abundant than structured proteins owing to an increased degradation and reduced translation rate [21]. As a high abundance of IDPs might result in undesirable interactions, a tight regulation of signaling and regulatory IDPs could minimize any potentially harmful effects of such interactions. Supporting this idea, intrinsic disorder has been identified as a determinant of genes that are harmful when overexpressed, and this dosage sensitivity has been attributed to vulnerability of IDPs to promiscuous binding at high concentrations [22].

In short, the ability to bind with multiple targets is not unique to IDPs, and the intermolecular interactions of both IDPs and ordered proteins have to be confined to intended cellular targets. If intrinsic disorder indeed increases the chance of promiscuous binding, the potentially harmful consequences must be minimized by controlling the availability of the IDPs.

High specificity with low affinity

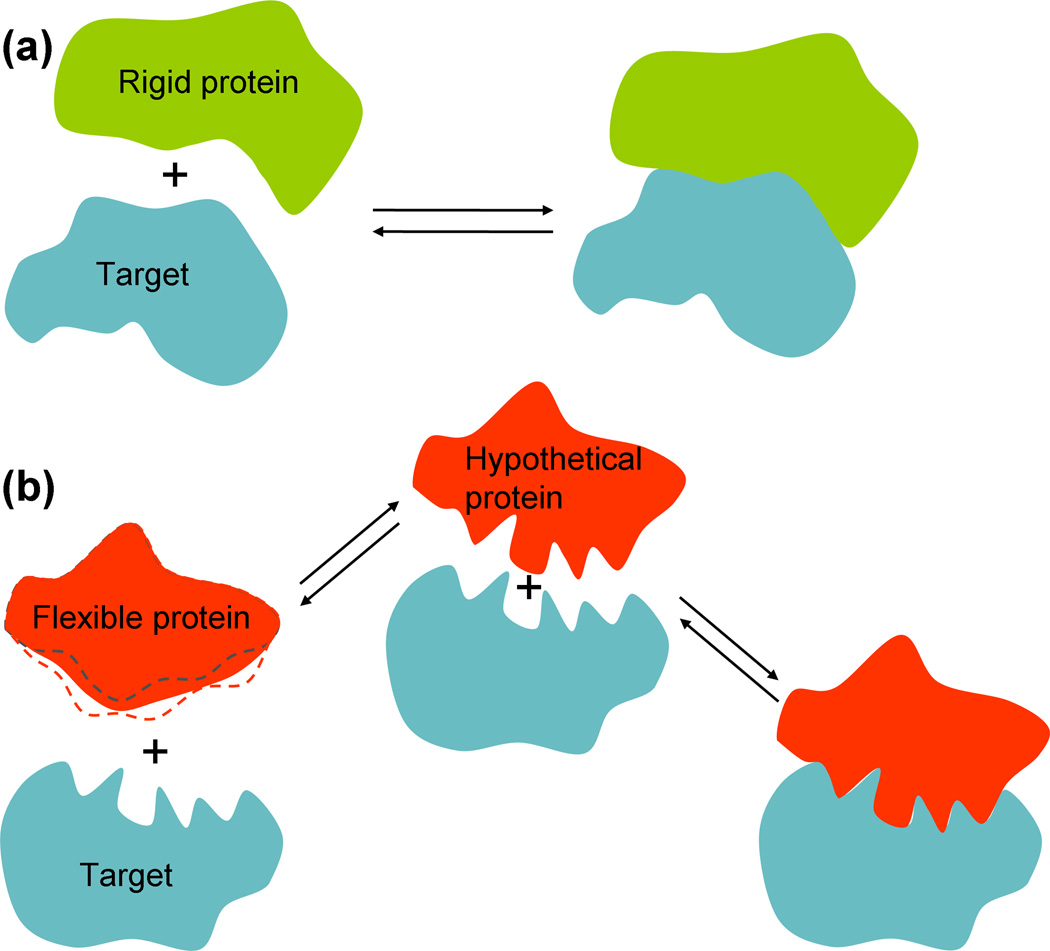
Schulz [23] observed that nucleic-acid binding proteins are often quite flexible, and proposed that flexibility leads to high specificity without an overly strong association constant. A flexible protein can potentially form a more intricate and extended interaction surface than a structured protein (Figure 1), allowing for a precise fit to the target and hence a high specificity (see below for further discussion). However, the rigidification (akin to a disorder-to-order transition) of the protein upon binding the nucleic acid costs free energy. Hence, the overall binding affinity is not excessive. Schulz’s concern was that an overly strong association constant would mean that the nucleic acid is always in the bound state, making the binding effectively irreversible. However, it should be noted that the bound fraction depends both on the association constant and on the protein concentration (Box 1). Regardless of the magnitude of the association constant, any desired bound fraction can be obtained by tuning the protein concentration.

Figure 1.

Binding affinity and specificity of a rigid (or ordered) protein and a flexible (or disordered) protein. (a) A rigid protein tends to form a simple, relatively smooth interaction surface with the target. (b) Left: a flexible protein, when unbound, can sample different conformations, especially around the binding site (as illustrated by dashed curves representing alternative conformations). Right: in the bound state, the flexibility allows the protein to wrap around protrusions and indents of the target, giving rise to an intricate interaction surface and high specificity. Middle: a hypothetical protein that adopts the bound conformation even when unbound would have a much higher free energy than the flexible protein. However, the hypothetical protein would have the same high specificity but a much higher binding affinity than the flexible protein.

Intrinsic disorder is similar to flexibility, and the resulting high specificity with low affinity was proposed as a benefit of IDPs [2–4]. However, does an IDP really have an advantage in this regard over a hypothetical ordered protein (Figure 1b), which would have both high specificity and high affinity? Potentially, the low affinity associated with intrinsic disorder could present a problem, since it would mean that the IDP has to be maintained at a high cellular concentration in order to achieve a significant bound fraction for its cognate target (Box 1). As seen above, cells work against such high concentrations of IDPs. It is worth noting that, whereas Schulz viewed the low affinity due to the free-energy cost of an disorder-to-order transition as an advantage, Spolar and Record [24] viewed it as a necessary expense for achieving high specificity.

Extended interaction surfaces

Following Schulz’s observation for flexible nucleic-acid binding proteins [23], others have recognized that IDPs often form extended interaction surfaces with their cellular targets [2–5, 25]. Gunasekaran et al. [25] compared the areas of binding interfaces involving IDPs and those involving ordered proteins, and concluded that, to achieve the same interface area, IDPs require much smaller protein sizes than ordered proteins do. They suggested that smaller protein sizes allow a decrease in cellular macromolecular crowding, which significantly affects thermodynamic and kinetic properties of biological processes [26].

What is the benefit of an extended interaction surface? Obviously, the resulting extensive, specific intermolecular interactions allow the IDP to overcome the free-energy cost of the disorder-to-order transition, such that the overall binding affinity is not excessively low [27]. And as already alluded to, the disorder-to-order transition allows a precise fit of the IDP to its target, leading to high specificity. However, it should be noted that, if the argument of binding promiscuity holds, the malleability of IDPs could also allow them to fit with non-cognate targets, thereby losing specificity. Nussinov [28] further suggested that extended interaction surfaces facilitate efficient signal propagation.

Enhanced association rates

Based on somewhat different lines of reasoning, several studies have argued or predicted that intrinsic disorder (or flexibility) can speed up protein association [29–32]. That disorder should lead to an increase in k_a is really not unexpected, as illustrated by the simple example where flexible loops of a protein close up the binding pocket after a ligand binds (a scenario referred to as gating binding-pocket [33]). In this case, the hypothetical ordered protein has the loops closing the binding pocket, and hence the ligand cannot enter the binding pocket at all. In contrast, the protein with the flexible loops allows the ligand to enter some of the time, and binding becomes possible. In cases where IDPs wrap around their targets, steric clashes can similarly make it impossible for the hypothetical ordered proteins to bind the targets [2].

Pontius [29] proposed that attaching weakly interacting, disordered polymers to ordered macromolecules would enhance the latter’s association rate. His argument was that the polymers would hold the macromolecules together, allowing them to explore different separations and relative orientations to find the stereospecific fit. In some sense this argument is similar to the idea of reduction in dimensionality proposed by Adam and Delbruck [34] many years ago to rationalize the possibility that nonspecific DNA sequences flanking a specific site facilitate the search of a protein for the specific site. This possibility was later confirmed by experiments [35, 36].

Shoemaker et al. [30] recognized that, compared to an ordered protein, an IDP can have a greater capture radius (see Glossary) for a specific site on the target. In their view, the IDP binds the target weakly at a relatively large distance, followed by folding as the protein approaches the binding site. Their calculation, using the separation as the reaction coordinate, found a modest 1.6-fold rate enhancement for the IDP over the ordered protein. Huang and Liu [31] used Langevin dynamics simulations to further assess this “fly-casting mechanism.” They found that, when the lower diffusion constant of the IDP is accounted for, the initial capture rate constant (k₁₊ in Box 2) is actually lower than that of the ordered protein. However, the free energy barrier in the subsequent sub-step, i.e. the conformational rearrangement to form the native complex, is lowered by the disorder. As a result, the overall association rate constant k_a is enhanced. Again, the rate enhancement obtained, ~2.5-fold, is modest.

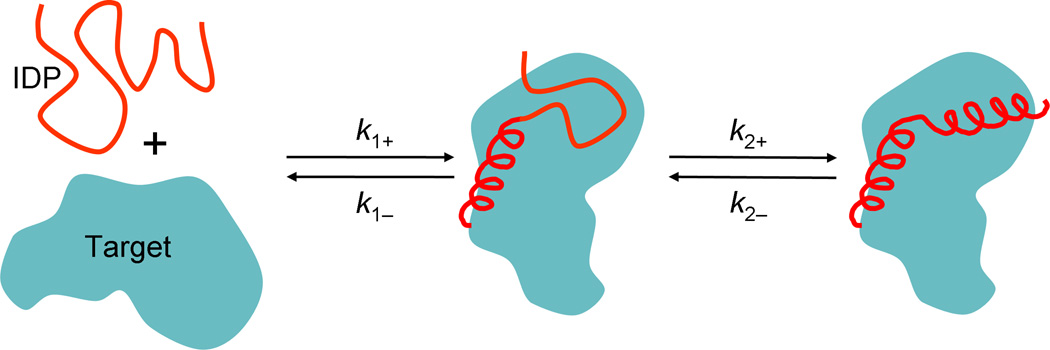
Qin et al. [32] proposed a dock-and-coalesce mechanism for the association of IDPs that form extended interaction surfaces (Figure 2), whereby a segment of the IDP first docks to its cognate sub-site on the target, allowing the remaining segments to explore conformational space and coalesce around their cognate sub-sites. In this mechanism, the disorder is essential for overcoming the severe orientational restraints that the hypothetical ordered protein would experience in forming the native complex. The severe orientational restraints were found to reduce k_a by at least 35-fold for the binding of hirudin (an IDP) to thrombin [32]. In addition, the free energy barrier in the coalescence sub-step seems to have a minimum as the flexibility of the IDP is varied, resulting in an optimal k_a (L. Cai & H. X. Zhou, unpublished).

Figure 2.

The dock-and-coalesce mechanism for the association of IDPs that form extended interaction surfaces with their targets. In the first sub-step (with rate constant k₁₊), a segment of the IDP makes the disorder-to-order transition and docks to its cognate sub-site. This docked segment can either dissociate (with rate constant k₁₋), or allows the remaining segment to coalesce around its sub-site (with rate constant k₂₊), resulting in the native complex.

Thus, theoretical calculations have found either modest enhancements of association rates for IDPs over their ordered counterparts, or significant enhancements over excessively low association rates of ordered proteins. The upper bound of k_a for ordered proteins is ~10⁹–10¹⁰ M⁻¹s⁻¹, which occurs when the diffusional approach to form the transient complex (Box 2) is accelerated by long-range electrostatic attraction by 1,000-fold or more [32, 37]. Rate constant calculations based on the dock-and-coalesce mechanism for hirudin-thrombin association [32] and for WASP-Cdc42 association (X. Pang & H. X. Zhou, unpublished) suggest that this upper bound also applies to the association of IDPs. Experimental k_a data for IDPs [38–42] are consistent with this prediction.

High dissociation rates: a beneficial consequence of intrinsic disorder

Given that k_a has an upper bound set by diffusion, proteins can increase their association constants, and hence affinity and specificity, by decreasing k_d (note that K_a = k_a/k_d). For example, the complex formed by the ribonuclease barnase and its inhibitor barstar has a very small k_d (8 × 10⁻⁶ s⁻¹) and a large k_a (6 × 10⁸ M⁻¹s⁻¹), which result in a very high affinity (K_a ~ 10¹⁴ M⁻¹) [43]. However, for proteins that play regulatory or signaling roles via binding with cellular targets, decreasing k_d is not an option, because the complex formed must dissociate rapidly for the protein to act as a switch. So, there is potentially a conflict between high specificity and rapid dissociation. In this Opinion, I propose that intrinsic disorder provides a perfect solution to this conflict. As noted, IDPs achieve high specificity with low affinity. The low affinity itself is not a benefit, but it does allow k_d to be high. This consequence is the real benefit: it means that the complex between an IDP and its target, formed with high specificity, can still rapidly dissociate.

To illustrate the idea, consider a typical ordered protein, with a binding affinity of 10⁹ M⁻¹, k_a at 10⁵ M⁻¹s⁻¹, and k_d at 10⁻⁴ s⁻¹. Now suppose that, by making the protein intrinsically disordered, the unbound state lowers its free energy and becomes more stable by 10³-fold (Figure 1b). As a result, the affinity is reduced to 10⁶ M⁻¹, without sacrificing the specificity, because the structure of the complex remains the same. If k_a of the IDP increases moderately, to 10⁶ M⁻¹s⁻¹, k_d will increase significantly, to 1 s⁻¹, within a range appropriate for signaling or regulation.

How is the significant increase in k_d achieved? Again, let us compare an IDP with its ordered counterpart. As noted above, in the association step the ordered protein suffers severe orientational restraints, which reduce k_a. In the dissociation step, the ordered protein must simultaneously break all the stereospecific interactions with the target; the resulting huge energy barrier would lead to an exceedingly small k_d. In contrast, as envisioned in the dock-and-coalesce mechanism [32], in the association step a segment of the IDP first docks to a sub-site and then additional intermolecular contacts accumulate. In the dissociation step, only a subset of all the stereospecific interactions with the target is broken at a time; the resulting energy barriers are all moderate, leading to much greater k_d than that of the ordered protein. In addition, in a case where an IDP wraps around its target such that dissociation of the protein with the bound conformation is prevented by steric clashes, a local order-to-disorder transition will allow dissociation to proceed [2].

Concluding remarks

IDPs perform important biological functions, but there are still ongoing debates on the unique benefits associated with intrinsic disorder. The ability of IDPs to structurally adapt to their targets has been argued both as the basis for their high specificity and as the basis for their binding promiscuity. Similarly, the low binding affinity associated with intrinsic disorder has been viewed both as a benefit and as a necessary expense for achieving specificity. I have argued here that regulatory and signaling proteins require both high specificity and dissociation, and that intrinsic disorder provides a perfect solution to these potentially conflicting demands.

My argument is centered on fundamental thermodynamic (K_a) and kinetic (k_a and k_d) properties. Although both types of properties are essential for understanding molecular recognition, it is important to distinguish between them: thermodynamic properties concern the stability of end states, whereas kinetic properties concern transition rates between end states. When Schulz [23] suggested low binding affinity as a benefit of intrinsic disorder, his reasoning was based on thermodynamics. Specifically, his concern was that an overly stable complex would have exceedingly low probability of being back in the unbound state (even though, as I have emphasized, that probability can be arbitrarily tuned by protein concentration). In contrast, my focus is the dissociation rate constant (which is independent of protein concentration). A requirement for regulatory and signaling proteins is that the complexes formed with cellular targets must rapidly dissociate, so k_d is the heart of the matter.

Intrinsic disorder complicates the mechanisms of association and dissociation. Many recent experimental [38–42] and computational [30–32, 44–46] studies have been devoted to these mechanisms as well as the rate constants. These issues will likely be a fertile ground for further studies.

Glossary

Capture radius

the largest distance at which a protein still experiences significant interactions with its target. An intrinsically disordered protein (IDP) can sample extended conformations, which allows the IDP to contact the target at a much greater distance than an ordered protein

Langevin dynamics

a type of motion assumed for a molecule in a viscous solvent. In addition to forces arising from interatomic interactions within the molecule, each atom is assumed to experience two other forces arising from interactions with the solvent. One is a frictional force, mimicking the viscous drag of the solvent and proportional to the atomic velocity. The other is a random force, accounting for the constant collision of the molecule by the solvent

Statistical weight

in a microscopic description of thermodynamics, each observed state, or macro-state, is a statistical average over many invisible micro-states. Each micro-state is accorded a statistical weight, proportional to its Boltzmann factor. The sum of the statistical weights of all the constituent micro-states is the statistical weight of the macro-state