Abstract
Owing to the rapid development of biomarkers in clinical trials, joint modeling of longitudinal and survival data has gained its popularity in the recent years because it reduces bias and provides improvements of efficiency in the assessment of treatment effects and other prognostic factors. Although much effort has been put into inferential methods in joint modeling, such as estimation and hypothesis testing, design aspects have not been formally considered. Statistical design, such as sample size and power calculations, is a crucial first step in clinical trials. In this paper, we derive a closed-form sample size formula for estimating the effect of the longitudinal process in joint modeling, and extend Schoenfeld’s sample size formula to the joint modeling setting for estimating the overall treatment effect. The sample size formula we develop is quite general, allowing for p-degree polynomial trajectories. The robustness of our model is demonstrated in simulation studies with linear and quadratic trajectories. We discuss the impact of the within-subject variability on power and data collection strategies, such as spacing and frequency of repeated measurements, in order to maximize the power. When the within-subject variability is large, different data collection strategies can influence the power of the study in a significant way. Optimal frequency of repeated measurements also depends on the nature of the trajectory with higher polynomial trajectories and larger measurement error requiring more frequent measurements.
Keywords: sample size, power determination, joint modeling, survival analysis, longitudinal data, repeated measurements
1. Introduction
Censored time-to-event data, such as the time to failure or time to death, is a common primary endpoint in many clinical trials. Many studies also collect longitudinal data with repeated measurements at a number of time points prior to the event, along with other baseline covariates. One of the most original examples was an HIV trial that compared time to virologic failure or time to progression to AIDS [1, 2]. CD4 cell counts were considered as a strong indicator of a treatment effect and are usually measured at each visit as secondary efficacy endpoints. Although CD4 cell counts are no longer considered a valid surrogate for time to progression to AIDS in the current literature, the joint modeling strategies originally developed for these trials led to research on joint modeling in other research areas. As discoveries of biomarkers advance, more oncology studies collect repeated measurements of biomarker data, such as prostate-specific antigen (PSA) in prostate cancer trials, as secondary efficacy measurements [3]. Many studies also measure quality of life (QOL) or depression measures together with survival data, where joint models can also be applied [4–9]. Most clinical trials are designed to address the treatment effect on a time-to-event endpoint. Recently, there has been an increasing interest in focusing on two primary endpoints such as time-to-event and a longitudinal marker, and also to characterize the relationship between them. For example, if treatment has an effect on the longitudinal marker and the longitudinal marker has a strong association with the time-to-event, the longitudinal marker can potentially be used as a surrogate endpoint or as a marker for the time-to-event, which is usually lengthy to ascertain in practice. The issue of surrogacy of a disease marker for the survival endpoint by joint modeling was discussed by Taylor and Wang [10].
Characterizing the association between time-to-event and the longitudinal process is usually complicated due to incomplete or mis-measured longitudinal data [1, 2, 11]. Another issue is that the occurrence of the time-to-event may induce informative censoring of the longitudinal process [11, 12]. The recently developed joint modeling approaches are frameworks which acknowledge the intrinsic relationships between the event time and the longitudinal process by incorporating a trajectory for the longitudinal process into the hazard function of the event, or in a more general sense, introducing shared random effects in both the longitudinal model and the survival model [2, 7, 13–16]. Bayesian approaches that address joint modeling of longitudinal and survival data was introduced by Ibrahim et al. [4], Chen et al. [17], Brown and Ibrahim [18], Ibrahim et al. [19], and Chi and Ibrahim [8, 9]. It has been demonstrated through simulation studies that the use of joint modeling leads to correction of biases and improvement of efficiency when estimating the association between the event time and the longitudinal process [20]. A thorough review on joint modeling is given by Tsiatis and Davidian [11]. Further generalizations to multiple time-dependent covariates was introduced by Song et al. [21], and a full likelihood approach for joint modeling of a bivariate growth curve from two longitudinal measures and event time was introduced by Dang et al. [22].
Design is a crucial first step in clinical trials. Well-designed studies are essential for a successful research and drug development. Although much effort has been put into inferential and estimation methods in joint modeling of longitudinal and survival data, design issues have not been formally considered. Hence, developing statistical methods to address design issues in joint modeling is much needed. One of the fundamental issues is power and sample size calculations for joint models. In this paper, we will describe some basics of joint modeling in Section 2, and then provide a sample size formula associating the longitudinal process and the event time for study design based on a joint modeling in Section 3. In Section 4, we provide a detailed methodology to determine the sample size and power with an unknown variance–covariance matrix, discuss longitudinal data collection strategies, such as spacing and frequency of repeated measurements, to maximize the power. In Sections 5 and 6, we provide a sample size formula to investigate treatment effects in joint models, and discuss how ignoring the longitudinal process would lead to biased estimates of the treatment effect and a potential loss of power. In Section 7, we briefly compare the two-step inferential approach and the full joint modeling approach for the ECOG trial E1193, and show that the sample size formulas we develop are quite robust. We end this paper with some discussions in Section 8.
2. Preliminaries
For subject i, (i = 1, …, N), let Ti and Ci denote the event and censoring times, respectively; Si = min(Ti, Ci ) and Δi = I (Ti ≤ Ci ). Let Zi be a treatment indicator, and let Xi (u) be the longitudinal process (also referred to as the trajectory) at time u ≥ 0. In a more general sense, Zi can be a q-dimensional vector of baseline covariates including treatment. To simplify the notation, Zi denotes the treatment indicator in this paper. Values of Xi (u) are measured intermittently at times u ≤ Si, j = 1, …, mi, for subject i. Let Y (ti j ) denote the observed value of Xi (ti j ) at time ti j, which may be prone to measurement error.
The joint modeling approach links two sub-models, one for the longitudinal process Xi (u) and one for the event time Ti, by including the trajectory in the hazard function of Ti. Thus,
| (1) |
Although other models for Xi (u) have been proposed [7, 13, 14], we focus on a general polynomial model [17, 19]
| (2) |
where θi = {θ0i, θ1i, …, θpi }T is distributed as a multivariate normal distribution with mean μθ and variance–covariance matrix Σθ. The parameter γ is a fixed treatment effect. The observed longitudinal measures are modeled as Yi (ti j ) = Xi (ti j )+ ei j, where , the θi’s are independent and Cov(ei j, ei j′)= 0, for j ≠ j′. The observed data likelihood for subject i is given by:
| (3) |
In expression (3), is a univariate normal density function with mean and variance , and f (γi |μθ, Σθ) is the multivariate normal density with mean μθ and covariance matrix Σθ. The density function for the time-to-event, f (Si, Δi |θi, β, γ, α), can be based on any model. In this paper, we focus on the exponential model, where .
The primary objectives here are:
To test the effect of the longitudinal process (H0: β = 0) by the score statistic.
To test the overall treatment effect (H0: βγ+ α= 0) by the score statistic.
When the trajectory, Xi (t) is known, the score statistic can be derived directly based on the partial likelihood given by Cox [23], namely
| (4) |
When the trajectory is unknown, the observed hazard is λ(t|Ȳ(t)) instead of λ (t|X̄(t)), where Ȳ (t) denotes the observed history up to time t, and X̄ (t) denotes the hypothetical true history up to time t. By the law of conditional probability, and assuming that neither the measurement error nor the timing of the visits prior to time t are prognostic, λ (t|Ȳ(t)) = λ0(t)E[f (X (t), β|Ȳ(t), S ≥ t)] [1]. Then, an unbiased estimate of β can be obtained by maximizing the partial likelihood
instead of modeling the observed history directly. The analytic expression of E[f (X(t), β|Ȳ(t), S ≥ t)] is difficult to obtain. Tsiatis et al. [1] developed a two-step inferential approach based on a first-order approximation, E[f (X(t), β|Ȳ(t), S ≥ t)] ≈ f [E(X(t)|Ȳ, S ≥ t, β)]. Under this approximation, we can replace {θ0i, θ1i, …, θpi }T in the Cox model with the empirical estimates {θ̂0i, θ̂1i, …, θ̂pi }T described by Laird and Ware [24], so that Xi (Si ) in (4) will be replaced by X̂i (u) = θ̂0i + θ̂1i u + θ̂2i u2 +· · ·+ θ̂pi up + γZi. The partial likelihood (4) can then be used for inferences in obtaining parameter estimates without using the full joint likelihood (3).
3. Sample size determination for studying the relationship between event time and the longitudinal process
The sample size formula presented in this section is based on the assumption that the hazard function follows equation (1) and the trajectory follows a general polynomial model as specified in equation (2). No time-by-treatment interaction is assumed with the longitudinal process. Furthermore, we assume that if any Yi j ’s are missing, they are missing at random.
3.1. Known Σθ
We start by assuming a known trajectory, Xi (t), so that the score statistic can be derived directly based on the partial likelihood. We show in the supplement that the score statistic converges to a function of Var{Xi (t)}, and thus a function of Σθ. When Σθ is known, and assuming that the trajectory follows a general polynomial function of time as in equation (2), we derive a formula for the number of events required for a one-sided significance level α̃ test with power β̃ (see detailed derivation in the supplement‡). This formula is given by
| (5) |
where
| (6) |
p is the degree of polynomial in the trajectory, τ = D/N is the event rate, and t̄f is the mean follow-up time for all subjects. E{(I ≤ t̄f)Tq} is a truncated moment of Tq, whose calculation is provided in Appendix A. It can be estimated by assuming a particular distribution of the event time T, and a mean follow-up time. Therefore, the power for estimating β depends on: (a) the expected log-hazard ratio associated with a unit change in the trajectory, or the size of β. As β increases, the required sample size decreases; (b) Σθ. A larger variance and positive covariances lead to smaller sample sizes, while larger negative covariances imply less heterogeneity and require larger sample sizes; and (c) the truncated moments of the event time T, which depends on both the median survival and length of follow-up. Larger E{(I ≤ t̄f)Tq}implies larger , and thus requires smaller sample size. Details for estimating E{(I ≤ t̄f)Tq}are provided in Appendix A. Because τ, the event rate, also affects , censored observations do in fact contribute to the power when estimating the trajectory effect.
Specific assumptions regarding Σθ are required in order to estimate , regardless of whether Σθ is assumed known or unknown (see Sections 3.2 and 4). It is usually difficult to find relevant information concerning each variance and covariance for the θ’s, especially when the dimension of Σθ, or the degree of the polynomial in the trajectory is high. A structured covariance matrix, such as an autoregressive or compound symmetry, can be used. One can simplify formula (6) with a structured covariance matrix. This also facilitates the selection of a covariance structure in the final analysis.
3.2. Unknown Σθ
When Σθ is unknown, sample size determination can be based on the two-step inferential approach suggested by Tsiatis et al. [1]. Despite several drawbacks in this two-stage modeling approach [2], it has two major advantages: (a) the likelihood is simpler and standard statistical software for the Cox model can be used directly for inferences and estimation; (b) it can correct bias caused by missing data or mis-measured time-dependent covariates. Therefore, when Σθ is unknown, the trajectory is characterized by the empirical Bayes estimates of θ̂i. Σθ in equation (6) can then be replaced with an overall estimate of Σθ̂i, where Σθ̂i is the covariance matrix of {θ̂0i, θ̂1i, …, θ̂pi }T.
Σθ̂i is clearly associated with the frequency and spacing of repeated measurements on the subjects, duration of the follow-up period, and the within-subject variability, [25]. Since Σθ is never known in practice, sample size determination using Σθ in equation (6) will likely over-estimate the power. Therefore, we need to understand how the longitudinal data (i.e. frequency of measurements, spacing of measurements, etc.) affect Σθ̂i, and design a data collection strategy to maximize the power for the study. We defer the discussion of this issue to Section 4.
3.3. Simulation results
We first verified in simulation studies that when Σθ is known, formula (5) provides an accurate estimate of the power for estimating β. Table I shows a comparison of the calculated power based on equations (5) and (6), and empirical power in a linear trajectory with known Σθ. In this simulation study, the event time was simulated from an exponential model with exponential parameter η and λi (t) = λ0(t)exp{βXi (t)+ αZi }, where Xi (t) = θ0i + θ1i t + γZi. To ensure a minimum follow-up time of 0.75 y (9 months), censoring was generated from a uniform [0.75, 2] distribution. (θ0i θ1i ) was assumed to follow a bivariate normal distribution. We simulated 1000 trials and each trial has 200 subjects. Empirical power was defined as the % of trials with a p-value from the score test ≤0.05 for testing H0: β= 0. The quantities D, η, and t̄f were obtained based on the simulated data, η was obtained from the median survival of the simulated data, and t̄f was the mean follow-up time of the simulated data using the product limit method. Thus, Table I shows that if the input parameters are correct, formula (5) returns an accurate estimate of power in various Σθ.
Table I.
Validation of formula (5) for testing the trajectory effect β when Σθ is known.
| β | Var(θ0i ) | Var(θ1i ) | Cov(θ0i, θ1i ) | Power for estimating β* |
|
|---|---|---|---|---|---|
| Empirical | Calculated | ||||
| 0.15 | 0.5 | 0.9 | 0 | 41.6 | 39.8 |
| 0.15 | 0.8 | 1 | 0 | 52.9 | 52.4 |
| 0.15 | 0.8 | 1 | 0.5 | 66.1 | 67.0 |
| 0.2 | 1.2 | 0.7 | 0 | 87.1 | 86.0 |
| 0.2 | 0.7 | 1.2 | 0 | 75.9 | 76.4 |
| 0.2 | 0.7 | 1.2 | 0.2 | 82.7 | 82.7 |
| 0.2 | 0.7 | 1.2 | −0.2 | 69.8 | 68.4 |
Covariance matrix of (θ0i, θ1i ) is assumed known. Empirical power is based on 1000 simulations, each with 100 subjects per arm. Minimum follow-up time is 0.75 y (9 months), and maximum follow-up time is 2 y. The event time is simulated from an exponential distribution with λ0 = 0.85, α= 0.3, and γ = 0.1. The θ’s are simulated from a normal distribution with E(θ0i ) = 0, E(θ1i ) = 3, and Σθ as specified in columns 2–4.
4. Estimating Σθ̂i and maximization of power
4.1. Estimating Σθ̂i
Following the notation in Section 2, Let
be an mi × (1+ p) matrix, and Zi = 1miZi, and . Then θ̂i and Σθ̂i can be expressed as [24]
and
| (7) |
4.2. Determinants of power
Based on equation (7), Σθ̂i is associated with the following: (a) the degree of the polynomial in (2); (b) Σθ, that is, the between-subject variability; (c) , the within-subject variability; (d) tij, the time of the repeated measurements of the longitudinal data. Larger ti j imply a longer follow-up period, or more data collection points toward the end of the trial, and (e) mi, the frequency of the repeated measurements. (a)–(c) above are likely to be determined by the intrinsic nature of the longitudinal data, and have little to do with the data collection strategy during the trial design. Based on (7), Σθ̂i is associated with the inverse of , meaning larger will lead to smaller Σθ̂i, and thus a decrease in the power for estimating β. This is confirmed in the simulation studies (Table II).
Table II.
Power for estimating β by maximum number of data collection points (mx ) and size of —linear trajectory.
| mx | β̂ | Power for estimating β† |
||||
|---|---|---|---|---|---|---|
| Empirical | Calculated with maximum Σθ̂i | Calculated with weighted average Σθ̂i‡ | ||||
| True trajectory | 0.2098 | 87.1 | 86.0* | |||
| 0.09 | 6 | 0.2080 | 86.6 | 85.4 | 82.7 | |
| 0.09 | 5 | 0.2075 | 85.8 | 85.3 | 82.6 | |
| 0.09 | 4 | 0.2071 | 86.3 | 85.1 | 82.7 | |
| 0.09 | 3 | 0.2076 | 86.4 | 84.9 | 82.9 | |
| 0.09 | 2 | 0.2065 | 85.3 | 84.6 | 83.3 | |
| 0.64 | 6 | 0.1960 | 76.3 | 82.2 | 75.9 | |
| 0.64 | 5 | 0.1978 | 76.9 | 81.6 | 75.5 | |
| 0.64 | 4 | 0.1939 | 74.8 | 80.8 | 74.9 | |
| 0.64 | 3 | 0.1972 | 75.0 | 79.6 | 74.4 | |
| 0.64 | 2 | 0.1967 | 74.0 | 77.4 | 74.4 | |
| 1 | 6 | 0.1919 | 71.9 | 80.5 | 72.2 | |
| 1 | 5 | 0.1918 | 71.8 | 79.7 | 71.5 | |
| 1 | 4 | 0.1917 | 69.7 | 78.5 | 70.7 | |
| 1 | 3 | 0.1940 | 70.1 | 76.8 | 69.9 | |
Calculated with Σθi.
β was estimated using the two-step inferential approach [1]. Empirical power was based on 1000 simulations, each with 100 subjects per arm. Minimum follow-up time is 0.75 y (9 months), and maximum follow-up time is 2 y. The event time is simulated from an exponential distribution with λ0 = 0.85, α = 0.3, γ = 0.1, β = 0.2, E(θ0i ) = 0, E(θ1i ) = 3, Var(θ0i ) = 1.2, Var(θ1i ) = 0.7, and Cov(θ0i, θ1i ) = 0 (the same simulated data used in Row 4 of Table I).
Power based on the weighted average of Σθ̂i.
Although , the within-subject variability, can be reduced by using a more reliable measurement instrument, this is not always possible. We therefore focus on investigating the impact of (d) and (e). Note that the hazard function can be written as λi (t) = λ0(t)exp{β (θ0i + θ1i t + ···+ θpi tp)+ θ* Zi }, where β* = βγ+ α. In the design stage, instead of considering a trajectory with γ ≠ 0 and a direct treatment effect of α, we can consider a trajectory with γ= 0 and a direct treatment effect of α+ βγ. This will simplify the calculations for Σθ̂i. Since formula (7) represents Σθ̂i when Zi = 0, it should provide good approximation when Σθ̂i is similar between the two treatment groups. To see the relationship between mi, ti j and Σθ̂i, let us consider the alternative trajectory with γ= 0. Equation (7) then simplifies to
| (8) |
and
| (9) |
When the trajectory is linear. Wi jk is the element in the jth row and kth column of Wi. Now we decompose Vi as , where Pi is an mi × mi matrix with orthonormal columns, and Dgi is a diagonal matrix with non-negative eigenvalues. Let Pi jk denote the element of the jth row and kth column of Pi, and Dgij denotes the element in the jth row and jth column of Dgi. Then the diagonal elements of Q in (9) can be expressed as
| (10) |
and
| (11) |
We can see that both equations (10) and (11) are sums of mi non-negative elements, and thus are non-decreasing functions of mi. Equation (11) is also positively associated with ti j, implying a larger variance with longer follow-up period or with longitudinal data collected at a later stage of the trial. However, we should keep in mind that some subjects may have failed or are censored due to early termination. If we schedule most data collection time point toward the end of the study, mi could be reduced significantly in many subjects. An ideal data collection strategy should take into account drop-out and failure rates and balance ti j and mi for a fixed maximum follow-up period.
The maximum follow-up period is usually prefixed due to timeline or budget constraints. We can observe more events with a longer follow-up and the increase in power is likely to be more significant due to an increased number of events. With a prefixed follow-up period, the most important decision is perhaps to describe an optimal number of data collection points. Here, we speculate that the power would reach a plateau as mi increases. The number of data collection points required to reach the plateau is likely to be related to the degree of the polynomial in the trajectory function. A lower order polynomial may require smaller mi.
4.3. Simulation studies and illustrations of using Σθ̂i in sample size calculation
We investigated the power assuming an unknown Σθ for different mi ’s in simulation studies. The results are summarized in Table II for a linear trajectory, and in Table III for a quadratic trajectory. We note that the longitudinal data, Yi j, are missing after the event occurs or after the subject is censored and is assumed to be missing at random. Therefore, mi varies among subjects. Let mx denote the scheduled, or maximum number of data collection points if the subject has not had an event and is not censored at the end of the follow-up period. In the simulation studies described in Tables II and III, mx was assumed to be the same for all subjects, and ti j was equally spaced. In the linear trajectory simulation studies, we further assumed that the longitudinal data was also collected when the subject exits the study due to an event or censoring, so that each subject would have at least two measurements (baseline and the end of the study). In the quadratic trajectory simulation studies, the longitudinal data was also collected when the subject exited the study before their first post-baseline scheduled measurement. Therefore, Ri in equation (8) was not the same for all subjects. Some had different numbers of measurements; and some had measurements at different ti j ’s. This results in a different Σθ̂i for each subject.
Table III.
Power for estimating β by the maximum number of data collection points (mx ) and size of —quadratic trajectory.
| mx | β̂ | Power for estimating β† |
||||
|---|---|---|---|---|---|---|
| Empirical | Calculated with maximum Σθ̂i | Calculated with weighted average Σθ̂i‡ | ||||
| True trajectory | 0.2212 | 91.6 | 90.6* | |||
| 0.09 | 10 | 0.2117 | 90.0 | 90.2 | 88.0 | |
| 0.09 | 7 | 0.2102 | 89.5 | 90.0 | 88.0 | |
| 0.09 | 5 | 0.2098 | 89.0 | 89.9 | 88.2 | |
| 0.09 | 4 | 0.2014 | 89.3 | 89.8 | 88.4 | |
| 0.09 | 3 | 0.1720 | 89.1 | 89.6 | 88.4 | |
| 0.25 | 10 | 0.2135 | 89.7 | 89.5 | 86.1 | |
| 0.25 | 7 | 0.2104 | 88.2 | 89.2 | 85.8 | |
| 0.25 | 5 | 0.2089 | 86.7 | 88.8 | 85.8 | |
| 0.25 | 4 | 0.2038 | 86.9 | 88.5 | 85.9 | |
| 0.25 | 3 | 0.1621 | 86.6 | 88.0 | 85.8 | |
| 0.81 | 10 | 0.2041 | 84.7 | 87.6 | 81.0 | |
| 0.81 | 7 | 0.1984 | 81.5 | 86.6 | 79.7 | |
| 0.81 | 5 | 0.2021 | 80.3 | 85.4 | 79.0 | |
| 0.81 | 4 | 0.1818 | 79.1 | 84.7 | 78.8 | |
| 0.81 | 3 | 0.1402 | 74.9 | 83.3 | 78.3 | |
Calculated with Σθi
βwas estimated with the two-step inferential approach [1]. Empirical power was based on 1000 simulations, each with 100 subjects per arm. Minimum follow-up time is 0.75 y (9 months), and maximum follow-up time is 2 y. The event time is simulated from an exponential distribution with λ0 = 0.85, α= 0.3, γ= 0.1, β= 0.22, θi = (0, 2.5, 3)T, and Σθ = diag(1.2, 0.7, 0.8).
Power based on the weighted average of Σθ̂i.
Note that Σθ̂i converges to Σθ when . However, Σθ̂i does not converge to Σθ when . It is not an estimator for Σθ as it is influenced by the magnitude of the residual (measurement error), . During the design stage, we need to find a single quantity that can represent an average effect of Σθ̂i, which will take into account the impact of , to replace Σθ in the sample size calculation. One choice of such a quantity is to assume that all subjects will have the same number of measurements at the same time points, and thus Σθ̂i will be the same for all subjects. As the measurement error will have a greater impact on the ‘bias’ when the number of measurements are small, assuming a maximum number of measurements for all subjects will result in an over-estimation of the power, while assuming a minimum number of measurements for all subjects will result in an under-estimation of the power. Assuming a median number of measurements may be adequate in assessing the average effect of Σθ̂i. We recommend using the weighted average of Σθ̂i’s because it takes into account the impact of from the smallest to the largest number of measurements. For a fixed mx, the weighted average can be calculated as
| (12) |
where ξm is the % of non-censored subjects who have m measurements of the longitudinal data, Im is the m × m identity matrix, and R·m is the R matrix with m measurements,
t·k in the R·m matrix represents the mean measurement time of the kth measurement in the subjects who had m measurements if not all measurements are taken at a fixed time point.
In the second to the last column of Tables II and III, we present the calculated power based on the maximum Σθ̂i instead of a weighted average of Σθ̂i’s. The maximum . The simulation setup in Tables II and III is the same as in Section 3.3. The longitudinal data Yi j was simulated via a normal distribution with mean θ0i + θ1i ti j + γZi (linear), or (quadratic), and variance . Yi j was set to be missing after an event or censoring occurred.
When the measurement error is relatively small and non-systematic, the two-step inferential approach yields nearly unbiased estimates of the longitudinal effect. The number of data collection points did not seem to be critical when the trajectory is linear as long as each subject had at least two measurements of the longitudinal data. There is a slight decrease in the power when mx < 5 and is large. When the trajectory is quadratic, mx plays a more important role. The power for estimating β decreases as mx decreases. Smaller numbers of measurements (mx < 4) can also lead to a biased estimate of the longitudinal effect and result in a significant loss of power. The effect of mx on estimates and power is more significant when is large. Note that when , Σθ̂i reduces to Σθ, and is unrelated to mx. The effect of mx comes from the magnitude of reducing the contribution of the within-subject variability, . If we have a very accurate and reliable measurement instrument, we can reduce the number of repeated measurements and can still obtain unbiased estimates and maximum power.
The power calculation under the assumption of known Σθ or perfect data collection (maximum Σθ̂i) can result in a significant over-estimation of the power especially when is large. We next demonstrate that if we use the weighted average of Σθ̂i’s, we can obtain a good estimate of power based on formula (5).
Example 1 from Table II: For the scenario with and mx = 2, we observed that the mean measurement time for the subjects who had an event in the simulated data is about 0.5 y. We used to calculate Σθ̂i instead of setting which assumes that the second measurement was taken at 2 y. As a result, the power based on formula (5) changed from 77.4 to 74.4 per cent, which is more closer to the empirical power of 74.0 per cent. We used the mean measurement time in the non-censored subjects, because the power calculation is mainly based on the number of events. In practice, we need to make certain assumptions about t·k based on the median survival and length of the follow-up period.
Example 2 from Table III: For demonstration, we chose the scenario with and mx = 4. In this example, the second measurement was taken at 0.45 y (on average) in subjects who had only two measurements. For subjects who had more than two measurements, longitudinal data was collected at scheduled time points of 0, 0.5, 1, and 1.5. Therefore,
A weighted average of the Σθ̂i’s was calculated based on formula (12). The resulting power is 78.8 percent instead of 84.7 per cent, which is close to the empirical power of 79.1 per cent.
For trajectories that are quadratic or higher, it is important to schedule data collection to ensure mi is large enough for a reasonable proportion of subjects. For example, when the trajectory is quadratic and only a small proportion of subjects had three measurements of the longitudinal data (mx = 3 in Table III), we obtain a very biased estimate of β.
5. Sample size determination for the treatment effect
Using the same model as specified in Section 3, the overall treatment effect is βγ + α. Thus, the null hypothesis is H0: βγ + α = 0. Following the framework of Schoenfeld [26], we show that Schoenfeld’s formula can be extended to a joint modeling study design by taking into account the additional parameters β and γ. The number of events required for a one-sided level α̃ test with power β̃, assuming the hazard and trajectory follow (1) and (2) in Section 2, is given by
| (13) |
where p1 is the % of patients assigned to treatment 1 (Zi = 1). The properties of the random effects in the trajectory do not play a significant role in the sample size and power determination for the overall treatment effect at the design stage. However, correct assumptions must be made with regard to the overall treatment effect (βγ + α). If the longitudinal effect is a biomarker, αand βγ should have the same sign (aggregated treatment effect). We acknowledge that under the proposed longitudinal and survival model, the ratio of the hazard functions of the two treatment groups will be non-proportional, as the trajectory is time dependent. However, the method of using the partial likelihood can readily be generalized to allow for non-proportional hazards. It is unlikely that the proportional hazards assumption is ever exactly satisfied in practice. When the assumption is violated, the coefficient estimated from the model will be the ‘average effect’ over the range of time observed in the data [27]. Thus, the sample size formula developed using the partial likelihood method should provide good approximation of the power for estimating the overall treatment effect in a joint modeling setting.
The simulation studies presented in Table IV show that formula (13) works approximately well in the two-step inferential approach when the primary objective is to investigate the overall treatment effect. The power is not sensitive to Σθ, and works well with different sizes of β and γ. We show in Sections 6 and the supplemental material that the two-step inferential approach and the full joint likelihood approach yield similar unbiased estimates of the overall treatment effect and have similar efficiency.
Table IV.
Validation of formula (13) for testing the overall treatment effect α + βγ.
| β | γ | Var(θ0i ) | Var(θ1i ) | Cov(θ0i, θ1i ) | Power for estimating overall treatment effect βγ + α |
|
|---|---|---|---|---|---|---|
| Empirical* | Calculated† | |||||
| 0.3 | −0.1 | 1.2 | 0.7 | 0.2 | 69.2 | 67.2 |
| 0.3 | −0.4 | 1.2 | 0.7 | 0.2 | 85.8 | 85.9 |
| 0.3 | −0.8 | 1.2 | 0.7 | 0.2 | 96.7 | 97.1 |
| 0.3 | −1.2 | 1.2 | 0.7 | 0.2 | 99.4 | 99.6 |
| 0.1 | −0.4 | 1.2 | 0.7 | 0.2 | 65.8 | 62.7 |
| 0.4 | −0.4 | 1.2 | 0.7 | 0.2 | 92.3 | 92.6 |
| 0.8 | −0.4 | 1.2 | 0.7 | 0.2 | 98.7 | 99.8 |
| 0.3 | −0.4 | 1.2 | 1 | 0.2 | 86.2 | 85.9 |
| 0.3 | −0.4 | 1.2 | 1.5 | 0.2 | 86.4 | 85.9 |
| 0.3 | −0.4 | 1.2 | 2 | 0.2 | 86.5 | 85.9 |
| 0.3 | −0.4 | 1.2 | 4 | 0.2 | 85.5 | 85.9 |
| 0.4 | −0.4 | 1.2 | 0.7 | −0.8 | 92.7 | 92.6 |
| 0.4 | −0.4 | 1.2 | 0.7 | −0.4 | 92.2 | 92.6 |
| 0.4 | −0.4 | 1.2 | 0.7 | 0.4 | 91.4 | 92.6 |
| 0.4 | −0.4 | 1.2 | 0.7 | 0.8 | 92.0 | 92.6 |
Empirical power was based on the two-step inferential approach in 1000 simulations, each with 150 subjects per arm. Minimum follow-up time is 0.75 y (9 months), and maximum follow-up time is 2 y. The event time is simulated from an exponential distribution with λ0 = 0.85, α= −0.3, E(θ0i ) = 0, and E(θ1i ) = 3. The longitudinal data are measured at years 0, 0.5, 1, 1.5 and at exit with a linear trajectory and .
6. Biased estimates of the treatment effect when ignoring the longitudinal trajectory
When a treatment has an effect on the longitudinal process (i.e. γ ≠ 0 in equation (2)) and the longitudinal process is associated with survival (i.e. β ≠ 0 in equation (1)), the overall treatment effect on the time-to-event is βγ + α. Thus, it is obvious that ignoring the longitudinal process in the proportional hazards model can result in a biased estimate of the treatment effect on survival. When the longitudinal process is not associated with the treatment (i.e. γ = 0 in equation (2)), it is not obvious that ignoring the longitudinal trajectory in the proportional hazards model would result in an attenuated estimate of the hazard ratio for the treatment effect on survival (i.e. bias toward the null). This attenuation is known in the econometrics literature as the attenuation due to unobserved heterogeneity [28, 29], and has been discussed in the work by Gail et al. [30].
We demonstrated in simulation studies (Table V) that the bias associated with ignoring the longitudinal effect is related to the size of β in the joint modeling setting.
Table V.
Effect of β on the estimation of direct treatment effect on survival (α) based on different models.
| β | λi (t) = λ0(t)exp(αZi ) |
λi (t) = λ0(t)exp{β (θ0i + θ1i )t + αZi }
|
||
|---|---|---|---|---|
| exp(α̂) * based on Cox partial likelihood | exp(α̂) based on known trajectory | exp(α̂) based on two-step approach (partial likelihood)† | exp(α̂) based on full joint likelihood as specified in (3) | |
| 0 | 0.668 (0.062) | 0.667 (0.062) | 0.667 (0.062) | 0.667 (0.062) |
| 0.4 | 0.697 (0.057) | 0.668 (0.053) | 0.667 (0.053) | 0.667 (0.053) |
| 0.8 | 0.755 (0.063) | 0.670 (0.050) | 0.673 (0.050) | 0.668 (0.051) |
| 1.2 | 0.800 (0.068) | 0.670 (0.049) | 0.684 (0.051) | 0.668 (0.051) |
exp(α̂) is the average value based on 1000 simulations, each with 200 subjects per arm. Minimum follow-up time is set to be 0.75 y (9 months), and maximum follow-up time is set to be 2 y. The baseline hazard is assumed constant with λ0 = 0.85, and the true direct treatment effect on survival α= −0.4 (i.e. HR = 0.670).
Longitudinal data is measured at years 0, 0.5, 1, 1.5 and at exit with a linear trajectory and .
7. Retrospective power analysis for the ECOG trial E1193
To illustrate parameter selection and the impact of incorporating Σθ̂i in the power calculation, we apply the sample size calculation formula retrospectively based on the parameters obtained from the Eastern Cooperative Oncology Group (ECOG) E1193 trial [31, 32]. E1193 is a phase III cancer clinical trial of doxorubicin, paclitaxel, and the combination of doxorubicin and paclitaxel as front-line chemotherapy for metastatic breast cancer. Patients receiving single-agent doxorubicin or paclitaxel crossed over to the other agent at the time of progression. QOL was assessed using the FACT-B scale at two time points during induction therapy. The FACT-B includes five general subscales (physical, social, relationship with physician, emotional, and functional), as well as a breast cancer-specific subscale. The maximum possible score is 148 points. A higher score is indicative of a better QOL. In this subset analysis, we analyzed the overall survival after entry to the crossover phase (survival after disease progression), and its association with treatment and QOL. A total of 252 patients entered the crossover phase and have at least one QOL measurement, 124 patients crossed over from paclitaxel to doxorubicin (median survival is 13.0 months in this subgroup), 128 patients crossed over from doxorubicin to paclitaxel (median survival is 14.9 months in this subgroup). The data we used are quite mature, with only two subjects who crossed over to doxorubicin and six subjects who crossed over to paclitaxel being censored. We applied the Cox model with treatment effect only, the two step model incorporating the two QOL measurements, and the proposed joint model as specified in Section 2 of the paper, to analyze the treatment effect and effect of QOL. Since there are only two QOL measurements, we fit a linear mixed model. To satisfy the normality assumption for the longitudinal QOL, we transformed the observed QOL into . The results are report in Table VI. Similar results are also reported by the same authors [32].
Table VI.
Parameter estimates with standard errors for the E1193 data.
| Parameters | Cox model with treatment only | Two-step model | Joint model |
|---|---|---|---|
| Overall treatment (α̂ + β̂γ̂) | 0.251 (0.1302) | 0.261(0.1304) | 0.271 (0.1413) |
| α̂ | 0.245 (0.1362) | ||
| γ̂ | −0.073 (0.1291) | ||
| β̂ | −0.277 (0.0708) | −0.445 (0.1184) |
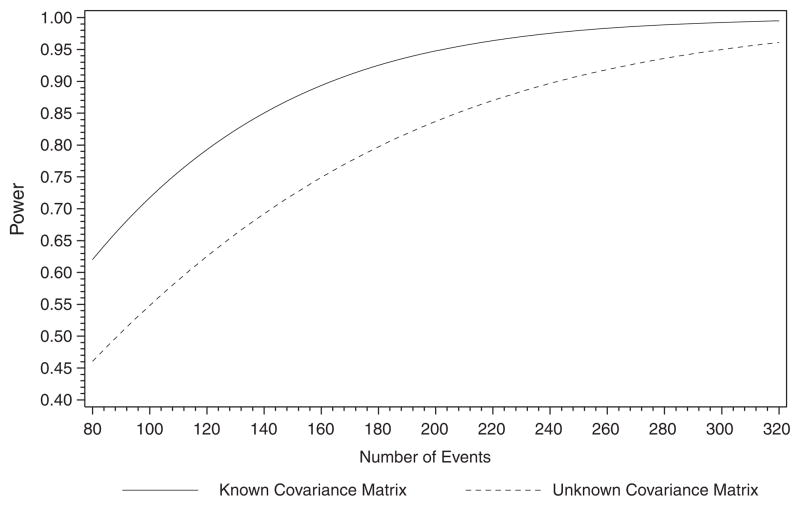
Treatment effects are similar between the two-step model and the joint model. The difference in the QOL effect, β̂, is similar to that of Wulfsohn and Tsiatis [2]. They reported a slightly larger β̂ and standard error in the joint model as compared with the two-step model. In Section 6 of this paper, we used simulation studies to demonstrate that β̂ is sensitive to whether the constant hazard assumption is satisfied in the joint model we used. We obtained the following parameter estimates for the retrospective power calculation: The median overall survival is 13.56 months , σe = 0.7188, the mean measurement time for the first QOL is 0.052 months, the mean measurement time for the second QOL is 2.255 months, and 35 per cent of the subjects had only one QOL measurement. If we assume a known Σθ, the power with 243 events and β = 0.3 is 98 per cent. When we assume an unknown Σθ and use a weighted average of Σθ̂i, the power is reduced to 90 per cent. The relationship between sample size and power for both known and unknown Σθ cases is illustrated in Figure 1.
Figure 1.
Retrospective power analysis for the E1193 trial with known and unknown Σθ.
8. Discussion
In this paper, we have provided a closed-form sample size formula for estimating the effect of the longitudinal data on time-to-event and discussed optimal data collection strategies. The number of events required to study the association between event time and the longitudinal process for a given follow-up period is related to the covariance matrix of the random effects (coefficients for the p-polynomial), within-subject variability, frequency of repeated measurements, and timing of the repeated measurements. Only a few parameters are required in the sample size formula. The median event time and mean follow-up time are needed to calculate the truncated moments. The mean follow-up time can be approximated by the average of the minimum and maximum follow-up times under the assumption of uniform censoring. A structured covariance matrix can be used when we do not have prior data to determine each element of Σθ. More robust estimates can be achieved by assuming an unknown Σθ. An unknown Σθ requires further assumptions about the number and timing of repeated measurements, and the percentage of subjects who are still on-study at each scheduled measurement time. This is exactly what researchers should consider during the design stage. It is useful to consider a few scenarios and compare the calculated power. When the measurement error is small, estimates with known Σθ also provide good approximation of power.
We have also extended Schoenfeld’s [26] sample size estimation formula to the joint modeling setting for estimating an overall treatment effect. When the longitudinal data was associated with treatment, the overall treatment effect is an aggregated effect on time-to-event directly and on the longitudinal process. When the longitudinal data is not associated with treatment, ignoring the longitudinal data will still lead to attenuated estimates of the treatment effect due to unobserved heterogeneity. The degree of attenuation depends on the degree of the association between the longitudinal data and time-to-event data. Use of a joint modeling analysis strategy leads to reduction of bias and increase in power in estimating the treatment effect. However, joint modeling is not yet commonly used in designing clinical trials. Most applications of joint modeling in the literature focus on estimating the effect of the longitudinal outcome on time-to-event.
The sample size formula we derived was based on a score test. Under the assumption that the fixed covariates are independent of the probability that the patient receives treatment assignment, the fixed covariates cancel from the final score statistic. Therefore, the number of patients required for a study does not depend on the effects of other fixed covariates. However, this does not mean that we should exclude all covariates from the analysis model, as they may be required to build an appropriate model.
The sample size formula we considered in this paper is based on the two-step inferential approach proposed by Tsiatis et al. [1], which is known to have several drawbacks [2]. In the supplementary material of this paper, we examined two joint modeling approaches: the two-step model and a model that is based on the full likelihood as specified in (3). The purpose of the supplemental section is to compare robustness and efficiency of the two joint models and evaluate whether the current sample size determination method can still provide an approximate estimate for the parametric joint model. We show that: (1) the two-step model may be more robust than the parametric joint model, especially when the parametric model is miss-specified; (2) if the parametric model is correctly specified, it is more efficient than the two-step model. Thus, a sample size based on the proposed method in this paper will be conservative for the parametric joint model for testing β; and (3) when testing the overall treatment effect, the two modeling approaches have similar efficiency and thus the method proposed can provide good estimate of sample size for both joint models.
Missing longitudinal data in practice is typically non-ignorably missing in the sense that the probability of missingness depends on the longitudinal variable that would have been observed. In order to examine the robustness of our sample size formulas to non-ignorable missingness, we conducted several simulation studies in which the empirical power was computed under a non-ignorable missing data mechanism using a selection model. Under several scenarios, our calculated powers based on the proposed sample size formulas were quite close to the empirical powers, therefore illustrating that our sample size formulas are quite robust to non-ignorable missing data. Developing closed-form sample size formulas in the presence of non-ignorable missing data is a very challenging problem that requires much further research.
One known drawback of the two-step method is that the random effects are assumed to be normally distributed in those at risk at every event time. This is unrealistic under informative dropout. It is also known that the empirical Bayes estimate of the random effect, θ̂i, from the Laird and Ware method [24] is biased under informative dropout. Therefore, non-informative censoring of the longitudinal process is an important assumption for the proposed method. Another limitation of this method is that we did not consider the treatment-by-time interaction in the model, which precludes the random slopes model. An extension of the classical Cox model introduces interaction between time and covariates, with the purpose of testing or estimating the interaction via a smoothing method. When testing a treatment effect alone, we are interested in showing that the treatment effect is constant over time (no interaction). Therefore, in the sample size calculation, we should not assume both a treatment effect and a treatment-by-time interaction. When the purpose is to test the effect of the longitudinal data on survival, if we need to assume a treatment-by-time interaction, we should fit a separate two-step model for each treatment.
Finally, we mention here that although simulations and distributional assumptions of the random effects in this paper were based on a Gaussian distribution, such distributional assumptions are not required for the formula. It may be applied to more general joint modeling design settings. To the best of our knowledge, this is the first paper that addresses trial design aspects using joint modeling.
†Calculated based on the mean number of deaths from simulations and fixed value of p1 = 0.5, β, γ, and α.
Supplementary Material
Appendix A: Truncated moments of T
To obtain the truncated moments of Tq, E{(I ≤ t̄f)Tq}, in equation (6), we must assume a distribution for T. In practice, the exact distribution for T is unknown. However, the median event time or event rate at a fixed time point for the study population can usually be obtained from the literature. It is a common practice to assume that T follows an exponential distribution with exponential parameter η in the study design stage. Thus, the truncated moment of Tq only depends on η and t̄f, and has the following form:
where Γ(q + 1, t̄f) is a lower incomplete gamma function with q = {1, 2, 3, ……}. η can be estimated based on the median event time or event rate at a fixed time point. e.g. if the median event time, TM, is known for the study population, η = −log(0.5)/TM. When the trajectory is a linear function of time,
Both E{I (T ≤ t̄f)T2} and E{I (T ≤ t̄f)T } have closed-form expressions, given by
and
There are certain limitations of this distributional assumption for T. It does not take into account covariates that are usually considered in the exponential or Cox model for S. A more complex distributional assumption can be used to estimate E{(I ≤ t̄f)Tq} if more information is available. However, simple distributional assumptions for T, without the inclusion of covariates or using an average effect of all covariates, are easy to implement and it is usually adequate for sample size or power determination.
E{(I ≤ t̄f)Tq} also depends on t̄f, the mean follow-up time for all subjects. It is truncated because we typically cannot observe all events in a study. Therefore, it is heavily driven by the censoring mechanism, and can be approximated by the mean follow-up time in censored subjects. One way to estimate t̄f is to take the average of the minimum and maximum follow-up times if censoring is uniform between the minimum and maximum follow-up times. It can also be estimated based on more complex methods. If data from a similar study are available, t̄f can be estimated with the product-limit method by switching the censoring indicator so that censored cases would be considered as events and events would be considered as censored.
Footnotes
Supporting information may be found in the online version of this article.
References
- 1.Tsiatis AA, DeGruttola V, Wulfsohn MS. Modeling the relationship of survival to longitudinal data measured with error. Applications to survival and CD4 counts in patients with AIDS. Journal of American Statistical Association. 1995;90:27–37. [Google Scholar]
- 2.Wulfsohn MS, Tsiatis AA. A joint model for survival and longitudinal data measured with error. Biometrics. 1997;53:330–339. [PubMed] [Google Scholar]
- 3.Renard D, Geys H, Molenberghs G, Burzykowski T, Buyse M, Vangeneugden T, Bijnens L. Validation of a longitudinally measured surrogate marker for a time-to-event endpoint. Journal of Applied Statistics. 2003;30:235–247. [Google Scholar]
- 4.Ibrahim JG, Chen MH, Sinha D. Bayesian Survival Analysis. Chapter 7. Springer; New York: 2001. Joint models for longitudinal and survival data. [Google Scholar]
- 5.Billingham LJ, Abrams KR. Simultaneous analysis of quality of life and survival data. Statistical Methods in Medical Research. 2002;11:25–48. doi: 10.1191/0962280202sm269ra. [DOI] [PubMed] [Google Scholar]
- 6.Bowman FD, Manatunga AK. A joint model for longitudinal data profiles and associated event risks with application to a depression study. Applied Statistics. 2005;54:301–316. [Google Scholar]
- 7.Zeng D, Cai J. Simultaneous modeling of survival and longitudinal data with an application to repeated quality of life measures. Lifetime Data Analysis. 2005;11:151–174. doi: 10.1007/s10985-004-0381-0. [DOI] [PubMed] [Google Scholar]
- 8.Chi Y-Y, Ibrahim JG. Joint models for multivariate longitudinal and multivariate survival data. Biometrics. 2006;62:432–445. doi: 10.1111/j.1541-0420.2005.00448.x. [DOI] [PubMed] [Google Scholar]
- 9.Chi Y-Y, Ibrahim JG. A new class of joint models for longitudinal and survival data accommodating zero and non-zero cure fractions: a case study of an international breast cancer study group trial. Statistica Sinica. 2007;17:445–462. [Google Scholar]
- 10.Taylor JMG, Wang Y. Surrogate markers and joint models for longitudinal and survival data. Controlled Clinical Trials. 2002;23:626–634. doi: 10.1016/s0197-2456(02)00234-9. [DOI] [PubMed] [Google Scholar]
- 11.Tsiatis AA, Davidian M. Joint modeling of longitudinal and time-to-event data: and overview. Statistica Sinica. 2004;14:809–834. [Google Scholar]
- 12.Hogan JW, Laird NW. Model-based approaches to analyzing incomplete longitudinal and failure time data. Statistics in Medicine. 1997;16:239–257. doi: 10.1002/(sici)1097-0258(19970215)16:3<259::aid-sim484>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 13.Henderson R, Diggle P, Dobson A. Joint modeling of longitudinal measurements and event time data. Biostatistics. 2000;1:465–480. doi: 10.1093/biostatistics/1.4.465. [DOI] [PubMed] [Google Scholar]
- 14.Wang Y, Taylor JMG. Jointly modeling longitudinal and event time data with application to acquired immunodefinicency syndrome. Journal of American Statistical Association. 2001;96:895–905. [Google Scholar]
- 15.Lin H, Turnbull BW, McCulloch EE, Slate EH. Latent class models for joint analysis of longitudinal biomarker and event process data: application to longitudinal prostate-specific antigen readings and prostate cancer. Journal of American Statistical Association. 2002;97:53–65. [Google Scholar]
- 16.Song X, Davidian M, Tsiatis AA. A semiparametric likelihood approach to joint modeling of longitudinal and time-to-event data. Biometrics. 2002;58:742–753. doi: 10.1111/j.0006-341x.2002.00742.x. [DOI] [PubMed] [Google Scholar]
- 17.Chen M-H, Ibrahim JG, Sinha D. A new joint model for longitudinal and survival data with a cure fraction. Journal of Multivariate Analysis. 2004;91:18–34. [Google Scholar]
- 18.Brown ER, Ibrahim JG. A Bayesian semiparametric joint hierarchical model for longitudinal and survival data. Biometrics. 2003;59:221–228. doi: 10.1111/1541-0420.00028. [DOI] [PubMed] [Google Scholar]
- 19.Ibrahim JG, Chen M-H, Sinha D. Bayesian methods for joint modeling of longitudinal and survival data with applications to cancer vaccine trials. Statistica Sinica. 2004;14:863–883. [Google Scholar]
- 20.Hsieh F, Tseng YK, Wand J-L. Joint modeling of survival and longitudinal data: likelihood approach revisited. Biometrics. 2006;62:1037–1043. doi: 10.1111/j.1541-0420.2006.00570.x. [DOI] [PubMed] [Google Scholar]
- 21.Song X, Davidian M, Tsiatis AA. An estimator for the proportional hazards model with multiple longitudinal covariates measured with error. Biostatistics. 2002;3:511–528. doi: 10.1093/biostatistics/3.4.511. [DOI] [PubMed] [Google Scholar]
- 22.Dang Q, Mazumdar S, Anderson SJ, Houck PR, Reynolds CF. Using trajectories from a bivariate growth curve as predictors in a Cox regression model. Statistics in Medicine. 2007;26:800–811. doi: 10.1002/sim.2558. [DOI] [PubMed] [Google Scholar]
- 23.Cox DR. Partial likelihood. Biometrika. 1972;62:269–276. [Google Scholar]
- 24.Laird NM, Ware JH. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. [PubMed] [Google Scholar]
- 25.Fitzmaurice GM, Laird NM, Ware JH. Applied Longitudinal Analysis. Chapter 15. Wiley; New York: 2004. Some aspects of the design of longitudinal studies. [Google Scholar]
- 26.Schoenfeld DA. Sample-size formula for the proportional-hazards regression model. Biometrics. 1983;39:499–503. [PubMed] [Google Scholar]
- 27.Allison PD. Survival Analysis Using SAS—A Practical Guide. Chapter 5. SAS Institute Inc; Cary. NC, U.S.A: 1995. Estimating Cox Regression Models with PROCPHREG. [Google Scholar]
- 28.Horowitz JL. Semiparametric estimation of a proportional hazard model with unobserved heterogeneity. Econometrica. 1999;67:1001–1028. [Google Scholar]
- 29.Abbring JH, Van den Berg GJ. The unobserved heterogeneity distribution in duration analysis. Biometrika. 2007;94:87–99. [Google Scholar]
- 30.Gail MH, Wieand S, Piantadosi S. Biased estimates of treatment effect in randomized experiments with nonlinear regressions and omitted covariates. Biometrika. 1984;71:431–444. [Google Scholar]
- 31.Sledge GW, Neuberg D, Bernardo P, Ingle JN, Martino S, Rowinsky EK, Wood WC. Phase III trial of doxorubicin, paclitaxel, and the combination of doxorubicin and paclitaxel as front-line chemotherapy for metastatic breast cancer: an intergroup trial (E1193) Journal of Clinical Oncology. 2003;21:588–592. doi: 10.1200/JCO.2003.08.013. [DOI] [PubMed] [Google Scholar]
- 32.Ibrahim JG, Chu H, Chen LM. Basic concepts and methods for joint models of longitudinal and survival data. Journal of Clinical Oncology. 2010;28:2796–2801. doi: 10.1200/JCO.2009.25.0654. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.