Stochastic differential equation models for ion channel noise in Hodgkin-Huxley neurons

Abstract

The random transitions of ion channels between conducting and nonconducting states generate a source of internal fluctuations in a neuron, known as channel noise. The standard method for modeling the states of ion channels nonlinearly couples continuous-time Markov chains to a differential equation for voltage. Beginning with the work of R. F. Fox and Y.-N. Lu [Phys. Rev. E 49, 3421 (1994)], there have been attempts to generate simpler models that use stochastic differential equation (SDEs) to approximate the stochastic spiking activity produced by Markov chain models. Recent numerical investigations, however, have raised doubts that SDE models can capture the stochastic dynamics of Markov chain models.

We analyze three SDE models that have been proposed as approximations to the Markov chain model: one that describes the states of the ion channels and two that describe the states of the ion channel subunits. We show that the former channel-based approach can capture the distribution of channel noise and its effects on spiking in a Hodgkin-Huxley neuron model to a degree not previously demonstrated, but the latter two subunit-based approaches cannot. Our analysis provides intuitive and mathematical explanations for why this is the case. The temporal correlation in the channel noise is determined by the combinatorics of bundling subunits into channels, but the subunit-based approaches do not correctly account for this structure. Our study confirms and elucidates the findings of previous numerical investigations of subunit-based SDE models. Moreover, it presents evidence that Markov chain models of the nonlinear, stochastic dynamics of neural membranes can be accurately approximated by SDEs. This finding opens a door to future modeling work using SDE techniques to further illuminate the effects of ion channel fluctuations on electrically active cells.

I. INTRODUCTION

Hodgkin and Huxley’s mathematical model of action potential dynamics [1] is a cornerstone of computational neuroscience. This system of equations provides a conductance-based framework for describing the dynamics of the membrane potential of a neuron. The essential features of the Hodgkin-Huxley (HH) model are quantitative descriptions of the permeability of a neuronal membrane to ion-specific currents (conductances) coupled to a current-balance equation that characterizes the voltage across a neural membrane. The physical basis for this empirical model is that conductances are determined by the proportion of ion channels in a conducting (i.e., an open) state, and that the states of the ion channels are determined by the configuration of components of the ion channels, referred to as subunits, particles, or gates (see [[2], e.g.]). The HH equations produce a deterministic description of neuronal dynamics and can be interpreted as a model of the mean behavior of the ion channels and their subunits.

Advances in single-channel recording techniques [3] demonstrated that individual ion channels can transition between open and closed states in an apparently random manner. This can generate an internal source of noise, known as channel noise, which adds fluctuations to ionic conductances [4]. Channel noise, which is distinguished from external sources such as synaptic events [[5], e.g.] and stimulus noise, can have important effects on neuronal dynamics and coding. It can alter the firing threshold [6–8], spike timing [9,10], interspike interval statistics [11], the amount of stochastic resonance [12,13], and influence synaptic integration [14]. Channel noise can also contribute to the overall variability in the nervous system, which in turn may pose constraints on the fidelity of the motor and sensory systems of an animal [7,15–18] and limit neuron miniaturization [19].

The classical HH formalism is deterministic, so alternative models have been proposed to account for channel noise. These models assume that the activity of ion channels is governed by random transitions among a number of possible channel conformations, which leads to intrinsically stochastic models of neuronal dynamics. Although a variety of models of this type have been proposed, including those that capture fractal properties of patch-clamp data [20] and history dependence in the activity of ion channels [21], the most widely used channel noise model is the Markov chain (MC) model. MC models assume that the state of an ion channel is described by a discrete-state, continuous-time Markov chain, where each state in the chain represents a particular configuration of the ion channel. The Markov property requires that a channel’s transition from one state to the next depends on its current state alone, thus the transition rates are determined solely by the state of the channel and the voltage potential of the membrane. As a consequence, all channels are coupled due to their common dependence on the membrane potential. For a recent review of MC models in computational neuroscience, see [22].

MC models are valuable tools for investigating the effects of channel noise on neural dynamics and coding, but these models are computationally expensive to simulate and are difficult to analyze mathematically. As a result, there has been widespread interest in formulating stochastic differential equation (SDE) models of channel noise. This line of research was initiated by Fox and Lu [23,24] and has been applied extensively to HH-type neuron models as well as models of calcium release from IP₃ receptors [25] (see [26] for a review of past applications of this approach). The SDE model that is most commonly used extends the original HH equations by including noise terms in the differential equations that describe the gating variables. Computationally, this model can be orders of magnitude faster than the MC model [24,27], so it has often been used in place of, or as an approximation to, the MC model. Simulation studies have shown, however, that the SDE approach does not accurately replicate the stochastic response properties of the MC models [26–30] and it has been suggested that SDE models are inadequate for simulations of channel noise [31] or must be modified to correctly reflect the stochastic properties of the MC models [26].

Despite recent numerical indications that the commonly used SDE model does not approximate the behavior of the MC model, there has been no definitive study detailing the root cause of discrepancies between the MC and SDE approaches. Moreover, other SDE models that have been proposed [23,25] have never been tested to gauge whether there may be alternative, and more accurate, reduced models of channel noise. There are several possible reasons as to why an SDE model may not closely approximate a MC model. The system size expansion that produces an SDE model is an asymptotic method that is formally valid in the limit of a large number of channels; it is possible that there are too few ion channels in a realistic model neuron for these approximate methods to be accurate. Another possible discrepancy between the two approaches could be numerical error in the simulation algorithms [29]. Finally, it could be that the widely used SDE models are formulated in a manner that neglects, or distorts, important dynamical and stochastic structure in the MC model.

In this paper, we will demonstrate that the formulation of the SDE is critical for preserving the stochastic characteristics of MC models. In Sec. II, we describe three SDE models that have been proposed in the literature. Among these, we distinguish between channel-based and subunit-based SDE models and provide an intuitive explanation for why the channel-based approach is the more appropriate framework. We use a combination of mathematical analysis (Sec. III) and simulation results (Sec. IV) to show that the MC model can be well approximated by a channel-based SDE model that was first introduced by Fox and Lu [23]. To our knowledge, ours is the first numerical implementation of the channel-based Fox and Lu model [32]. Prior studies have provided numerical evidence that a widely used subunit-based model does not accurately approximate the MC model [26–30], and our analysis confirms and elucidates these findings. We conclude that properly defining the structure and dynamics of ion channels is critical to formulating SDE models in a way that is consistent with MC models. We provide additional evidence for this conclusion by formulating reduced, quasistationary models based on our analytical results. Simulations of these models show that temporal correlation in the noise, which is shaped by the structure of ion channels, is critical for accurately approximating responses of the MC model.

II. CONDUCTANCE MODELS BASED ON ION CHANNELS AND THEIR SUBUNITS

We consider the HH model throughout this study. Our analysis, however, is applicable to any conductance-based model with ion channels governed by linear, voltage-dependent kinetics. The membrane potential of an HH neuron is modeled as

$$C\frac{dV}{dt}=-g_{\text{Na}}(V-E_{\text{Na}})-g_{\text{K}}(V-E_{\text{K}})-g_{\text{L}}(V-E_{\text{L}})+I,$$ (1)

where C is the membrane capacitance, E_Na, E_K, and E_L are reversal potentials for Na⁺, K⁺, and leakage currents, respectively, and I is the applied current. Our central question is how to appropriately define the ion channel conductances (g_Na for sodium and g_K for potassium) when one wants to include channel noise. Generally, one defines the conductance based on the fraction of open channels. For instance, the K⁺ conductance is g_K = ḡ_Kf, where f is the fraction of K⁺ channels that are open, and ḡ_K is the maximal conductance per ion channel. The problem of appropriately reproducing K⁺ channel behavior reduces to computing the evolution of f. In the following, we will describe a number of methods for computing f. We outline the standard MC model of ion channel kinetics [6,33] and highlight how this approach relates to the classical (deterministic) HH model. We will then consider three distinct approaches for defining SDE models: two that were proposed by Fox and Lu [23] and a variant suggested by Shuai and Jung [25].

Capturing the kinetics of a single subunit is the starting point for all of the models considered here. In the standard HH model, the K⁺ channel has four independent identical subunits, traditionally given the symbol n, that must all be in an open state for the channel to be in the conducting state [2,23]. The kinetics of an individual subunit is described by a two-state process:

$$\text{Closed}\underset{{\beta }_n}{\overset{{\alpha }_n}{\rightleftarrows }}\text{Open},$$ (2)

where the voltage-dependent transition rates are [1]

$$\begin{array}{l}{\alpha }_n(V)=\frac{0.01(10-V)}{exp[(10-V)/10]-1},\\ {\beta }_n(V)=0.125exp(-V/80).\end{array}$$

To simplify the notation, we will often omit the explicit dependence on V and write only α_n and β_n.

The Na⁺ channels are modeled using two different subunit types, traditionally labeled m and h, where each is described by an open-closed kinetic scheme. The analysis of the two channel types is fundamentally the same, but entails significantly more notational complexity for the Na⁺ channel. For conciseness, we will present a detailed analysis of the K⁺ channel, and display analytical and simulation results for both channel types in the relevant figures. In the remainder of this section, we review how the two-state subunit has been used as a building block to construct models of the K⁺ conductance.

A. Markov chain ion channel model

The kinetic scheme in Eq. (2) can be used to define a Markov chain that describes the behavior of a single subunit that randomly transitions between two states [[2], e.g.]. If we let p_sub be the probability that the subunit is in the open state, then the evolution of this probability satisfies

$$\frac{{dp}_{\text{sub}}}{dt}={\alpha }_n(1-p_{\text{sub}})-{\beta }_n{p}_{\text{sub}}.$$ (3)

This equation follows from Eq. (2) and the fact that the probability of a subunit being closed is 1 − p_sub. Since the K⁺ channel is assumed to consist of four statistically identical and independent subunits, its configuration can be modeled as a five-state Markov chain, where each state indicates the number of open subunits at a given instant in time:

$$0\underset{{\beta }_n}{\overset{4{\alpha }_n}{\rightleftarrows }}1\underset{2{\beta }_n}{\overset{3{\alpha }_n}{\rightleftarrows }}2\underset{3{\beta }_n}{\overset{2{\alpha }_n}{\rightleftarrows }}3\underset{4{\beta }_n}{\overset{{\alpha }_n}{\rightleftarrows }}4.$$ (4)

The channel is said to be in the open or conducting state if all four subunits are open simultaneously. Let p be a column vector where the ith element represents the probability at time t that a channel has i open subunits, then this probability distribution evolves in time according to the master equation

$$\frac{d\mathbf{p}}{dt}=A\mathbf{p},$$ (5)

where the matrix A is

$$\left[\begin{array}{ccccc}-4{\alpha }_n& {\beta }_n& 0& 0& 0\\ 4{\alpha }_n& -(3{\alpha }_n+{\beta }_n)& 2{\beta }_n& 0& 0\\ 0& 3{\alpha }_n& -2({\alpha }_n+{\beta }_n)& 3{\beta }_n& 0\\ 0& 0& 2{\alpha }_n& -({\alpha }_n+3{\beta }_n)& 4{\beta }_n\\ 0& 0& 0& {\alpha }_n& -4{\beta }_n\end{array}\right].$$

The conductance for a population of K⁺ channels is determined by the proportion of the channels in the open state, g_K = ḡ_Kf, where ḡ_K is the conductance per K⁺ channel and f is the fraction of open K⁺ channels.

B. Deterministic conductance models

If we consider an idealized neuron with an infinite number of statistically identical and independent channels, we can obtain a deterministic description of the fraction of open channels f. In this limit, the fraction of open channels is equivalent to the probability that any one channel will be open. In other words, Eq. (5) also defines a deterministic model of conductance where g_K = ḡ_Kp₄ and p₄ is given by the solution of the system of ordinary differential equations in Eq. (5).

At first glance, the deterministic definition of g_K appears to differ from that in the classical HH model, in which g_K = ḡ_Kn⁴. As discussed in [2], however, these two models are equivalent: first, note that p_sub in our notation can be identified with the gating variable n in the HH model because both satisfy the differential equation (3) and both represent the proportion of subunits that are open. Next, observe that the entire system of differential equations in Eq. (5) can be derived from the single HH gating variable by making the following substitutions:

$$p_i=\left(\begin{array}{c}4\\ i\end{array}\right){(1-n)}^{4-i}{n}^i,\text{where}i=0,1,2,3,\text{or}4.$$

For instance, setting p₄ = n⁴, we find

$$\begin{array}{l}\frac{{dp}_4}{dt}=\frac{d}{dt}[n^4]\\ =4n^3\frac{dn}{dt}\\ =4n^3[{\alpha }_n(1-n)-{\beta }_{n}n]\\ ={\alpha }_n{p}_3-4{\beta }_n{p}_4.\end{array}$$

This equation is identical to the final row of Eq. (5). The remaining equations in that system, as well as those for Na⁺, can be derived in a similar manner.

C. SDE conductance models

1. Channel SDE model

In the previous section we arrived at a deterministic model for K⁺ conductance because we considered the case of infinitely many channels. If we define the number of K⁺ channels to be finite, however, we can derive stochastic models using a system-size expansion [34]. Fox and Lu first applied this method to the HH model by [23]. Following their notation, we define x_i to be the proportion of K⁺ channels that have i open subunits. Since we are dealing with a finite population, the proportion of channels in a particular state x_i is no longer a measure of probability p_i. Rather, the number of open subunits fluctuates from one realization to the next, which inevitably leads to a stochastic description of the channel. The system-size expansion provides a formal method for deriving a SDE model based on the master equation (5). Fox and Lu showed that the SDE for the K⁺ channel is

$$\frac{d\mathbf{x}}{dt}=A\mathbf{x}+S\xi ,$$ (6)

where x is a vector of the x_i, A is the matrix in Eq. (5), ξ is a vector of five independent Gaussian white noise processes with zero mean and unit variance, and S is the matrix square root of the diffusion matrix D,

$$D=\frac{1}{N}\left[\begin{array}{ccccc}4{\alpha }_n{x}_0+{\beta }_n{x}_1& -(4{\alpha }_n{x}_0+{\beta }_n{x}_1)& 0& 0& 0\\ -(4{\alpha }_n{x}_0+{\beta }_n{x}_1)& 4{\alpha }_n{x}_0+(3{\alpha }_n+{\beta }_n)x_1+2{\beta }_n{x}_2& -(3{\alpha }_n{x}_1+2{\beta }_n{x}_2)& 0& 0\\ 0& -(3{\alpha }_n{x}_1+2{\beta }_n{x}_2)& 3{\alpha }_n{x}_1+2({\alpha }_n+{\beta }_n)x_2+3{\beta }_n{x}_3& -(2{\alpha }_n{x}_2+3{\beta }_n{x}_3)& 0\\ 0& 0& -(2{\alpha }_n{x}_2+3{\beta }_n{x}_3)& 2{\alpha }_n{x}_2+({\alpha }_n+3{\beta }_n)x_3+4{\beta }_n{x}_4& -({\alpha }_n{x}_3+4{\beta }_n{x}_4)\\ 0& 0& 0& -({\alpha }_n{x}_3+4{\beta }_n{x}_4)& {\alpha }_n{x}_3+4{\beta }_n{x}_4\end{array}\right],$$ (7)

in which N is the number of channels. To our knowledge, neither Fox and Lu nor other researchers have implemented this channel-based SDE model [32]. We will mathematically analyze it under voltage clamp conditions and perform numerical simulations to show that it accurately replicates the stochastic properties of the MC model. We refer to this model as the channel SDE model because the variable x is defined based on the states of the ion channels.

2. Subunit SDE models

Unfortunately, the channel SDE model above does not preserve the dynamical structure of the classical HH equations: closed states are distinguishable and are modeled with distinct random processes. This expands the dimensionality of the system beyond the four dimensions of the deterministic HH model. In an attempt to avoid this increase in complexity, one can apply the system-size expansion procedure to the subunits rather than to the states of the channels. This leads to stochastic models that resemble the classical HH model, but includes noise in the equations governing the subunit variables m, n, and h. We refer to such approaches as subunit SDE models. The subunit approach leads to the following SDE for the proportion of open subunits n [23,25]:

$$\frac{dn}{dt}={\alpha }_n(1-n)-{\beta }_{n}n+{\sigma }_n(V)\xi (t),$$ (8)

where the stochastic term ξ(t) is a Gaussian white noise process with zero mean and unit variance that is scaled in a voltage-dependent manner by σ_n(V):

$${\sigma }_n^2(V)=\frac{{\alpha }_n(1-n)+{\beta }_{n}n}{N}.$$ (9)

The model for the channel population is then built from the subunit populations. Since each K⁺ channel is composed of four statistically identical and independent subunits, Shuai and Jung proposed a model in which the proportion of open K⁺ channels is defined as the product of four independent realizations (denoted n_i) of solutions to the SDE in Eq. (8) [25]. This defines the K⁺ conductance to be g_K = ḡ_Kn₁n₂n₃n₄. We refer to this as the independent subunit model, InS. Shuai and Jung did not implement this method. Instead, they followed a method introduced by Fox and Lu [23] in which only one realization of a solution to Eq. (8) is computed (denoted n), and this realization is raised to the fourth power. This defines the K⁺ conductance to be g_K = ḡ_Kn⁴, built out of four identical subunit populations. We refer to this as the identical subunit model, IdS. In the limit of an infinite number of K⁺ channels, both of the subunit models converge to the deterministic HH model.

D. Distinction between subunit and channel models

The fundamental difference between the channel SDE model in Sec. II C 1 and the subunit SDE models in Sec. II C 2 is that in the former, one first groups subunits together to construct a channel and then defines the dynamics of the proportion of channels in each state. In the latter, one defines the dynamics of subunits first, before grouping the subunits together to compute the conductance of the channel. We note that the deterministic model in Sec. II B derived from the master equation is a channel-based approach while the classical HH model is a subunit-based approach. Nonetheless, as discussed above, the two models are equivalent. It is tempting therefore to conclude that both the channel and subunit SDEs will also produce identical stochastic models. As we will show in the remainder of this study, these two approaches generate distinct stochastic processes: the channel-based SDE model can approximate the channel noise and spiking statistics of the MC model, but the subunit-based SDEs cannot.

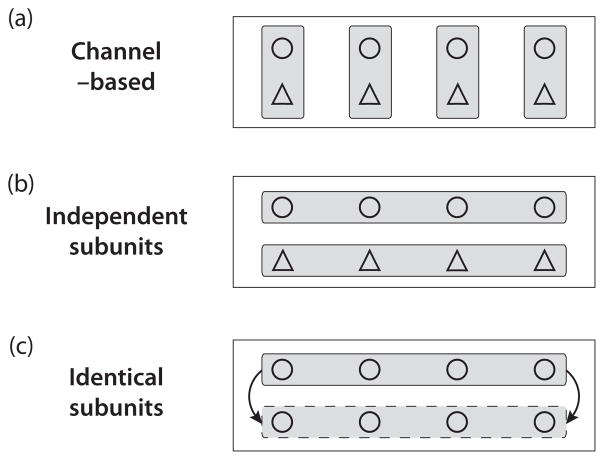
To gain some intuition for how the subunit and channel SDE approaches differ, consider the following example of a neuron with N channels, where each channel consists of two statistically identical and independent subunits. This configuration is illustrated in Fig. 1(a). The analysis can be extended to the four subunit K⁺ channel, but for illustrative purposes we consider the simpler case of two subunits. At a given instant in time, define the state of the ith subunit in each class by the binary random variables z_i1 and z_i2. These variables take the value of 1 with probability p_sub and are 0 otherwise. The probability that the ith channel is open is determined by the probability that both subunits are open, $p_{\text{sub}}^2$. A channel-based approach defines the conductance from the proportion of open channels, so we average over all channels to obtain the proportion of open channels:

$$f_{\text{chan}}=\frac{1}{N}\sum _{i=1}^N{z}_{i,1}{z}_{i,2}.$$ (10)

FIG. 1.

Illustration of conceptual differences between channel-based and subunit-based models. In this example, each channel consists of two subunits, “△” and “○.” (a) In the channel-based model, subunits are first grouped together to form channels (vertical rectangles) and the ionic conductance is determined by the fraction of channels in the conducting state. (b) In the independent subunits (IdS) approach, the subunits are divided into two classes (horizontal rectangles) and the fraction of open subunits is computed by averaging over all subunits in each class. The proportions of open subunits in each class are then used to approximate the fraction of channels in the conducting state. (c) Identical subunit (InS) models also average across all subunits in a class, but assume that both subunit classes are identical.

The products z_i,1z_i,2 define identical and independent binary random variables that take the value 1 with probability $p_{\text{sub}}^2$, thus their sum is binomially distributed with the following mean and variance:

$$\begin{array}{l}E[f_{\text{chan}}]=p_{\text{sub}}^2,\\ \text{Var}[f_{\text{chan}}]=\frac{1}{N}{p}_{\text{sub}}^2(1-p_{\text{sub}}^2).\end{array}$$

Instead of grouping subunits into predefined channels, the subunit approach first computes the fraction of open subunits by averaging over each class of subunits, as shown in Fig. 1(b). The proportions of open subunits in the two subunit classes are

$$f_{\text{sub},j}=\frac{1}{N}\sum _{i=1}^N{z}_{i,j},\text{where}j=1\text{or}2.$$

If we assume that each subunit class is independent and define the proportion of open channels f̃_chan to be the product of the f_sub,1 and f_sub,2, then we can write the proportion of open channels as

$${\stackrel{\sim }{f}}_{\text{chan}}=\frac{1}{N^2}\sum _{i,j=1}^N{z}_{i,1}{z}_{j,2}.$$

The proportion of open channels under the subunit approach is an average of N² binary random variables, as opposed to N random variables as in Eq. (10) for the channel approach. The probability that the product z_i,1z_j,2 is equal to 1 is $p_{\text{sub}}^2$, so the expected value of $E[{\stackrel{\sim }{f}}_{\text{chan}}]=p_{\text{sub}}^2$, identical to E[f_chan]. The variance in the two models, however, is different. To see this, write the variance of f̃_chan as the sum of covariances:

$$\text{Var}[{\stackrel{\sim }{f}}_{\text{chan}}]=\frac{1}{N^4}\sum _{i,j,k,l=1}^N\text{Cov}(z_{i,1}{z}_{j,2},z_{k,1}{z}_{l,2}).$$

This sum is over all of the N⁴ possible pairings of z_i,1,z_j,2,z_k,1, and z_l,2. To leading order in N, the dominant contribution to this sum is among pairings that have one index in common. There are N² possible pairs of z_i,1 and z_j,2, and for any given pair there are 2(N − 1) ways to choose the indices of z_k,1 and z_l,2 such that i = k or j = l. To leading order in N therefore there are 2N³ of these terms, and the variance of f̃_chan can thus be written as

$$\text{Var}[{\stackrel{\sim }{f}}_{\text{chan}}]=\frac{2}{N}\rho \text{Var}[z_{i,1}{z}_{j,2}]+O(N^{-2}),$$

where ρ is the correlation coefficient between random variables of the form z_i,1z_j,2 and z_k,1z_l,2 for either i = k or j = l. The product of two independent z variables is a Bernoulli random variable. It follows that $\text{Var}[z_{i,1}{z}_{j,2}]=p_{\text{sub}}^2(1-p_{\text{sub}}^2)$ and the above equation can be rewritten as

$$\text{Var}[{\stackrel{\sim }{f}}_{\text{chan}}]=2\rho \text{Var}[f_{\text{chan}}]+O(N^{-2}).$$ (11)

In Appendix A, we show that $\rho =\frac{p_{\text{sub}}}{1+p_{\text{sub}}}$. Since p_sub takes values in [0,1], ρ is bounded between 0 and 1/2. Equation (11) implies therefore that the variance of the fraction of open channels using the subunit-based averaging is not larger than the variance in the channel-based approach. Moreover, the variance decreases as p_sub decreases. This implies that the subunit method underestimates the variance when p_sub is small.

An assumption in the above analysis is that there are two independent classes of subunits. This can be thought of as the analog of the InS SDE model. Another variation of the subunit approach, used in the IdS SDE, is to assume that the two subunit classes are identical. This approach is illustrated in Fig. 1(c). Since both subunit classes are identical, we drop the second subscript and define a random variable z_i that represents the state of the ith subunit in both classes. The proportion of open channels, after averaging across all subunits, is

$${\stackrel{\sim }{f}}_{\text{chan}}=\frac{1}{N^2}\sum _{i,j=1}^N{z}_i{z}_j.$$

The expected value of f̃_chan in this case is composed of N (N − 1) terms of the form E[z_i z_j ] for i ≠ j and N terms of the form $E[z_i^2]$. To leading order, $E[f_{\text{chan}}]=p_{\text{sub}}^2$, but there is an O(N⁻¹) difference between the expected value of open channels for this approach and the channel-based averaging method.

The variance is

$$\text{Var}[{\stackrel{\sim }{f}}_{\text{chan}}]=\frac{1}{N^4}\sum _{i,j,k,l=1}^N\text{Cov}(z_i{z}_j,z_k{z}_l).$$

To leading order in N it suffices to consider the covariance of pairings that share one index in common. There is no distinction between the two subunit classes, so Cov(z_i z_j,z_i z_k) = Cov(z_i z_j,z_k z_i). There are therefore twice as many such terms as in the previous subunit approach, and we find

$$\text{Var}[{\stackrel{\sim }{f}}_{\text{chan}}]=4\rho \text{Var}[f_{\text{chan}}]+O(N^{-2})$$ (12)

with the same correlation coefficient $\rho =\frac{p_{\text{sub}}}{1+p_{\text{sub}}}$.

This analysis illustrates how averaging across channels and averaging across subunits leads to fundamentally different probabilistic descriptions of the proportion of open channels. In particular, since $\frac{p_{\text{sub}}}{1+p_{\text{sub}}}\le \frac{1}{2}$, Eq. (11) guarantees that the variance of the proportion of open channels given by the subunit model with two independent classes of subunits will never exceed the variance given by the MC model. Equation (12) shows that the variance in the subunit model with identical subunit classes will always be twice as large as the variance in the independent subunit model. Depending on whether $\frac{p_{\text{sub}}}{1+p_{\text{sub}}}$ is smaller or larger than 1/4 therefore the variance in the subunit model with identical subunit classes can be either smaller or larger than the variance of the MC model. These differences are a direct consequence of how each approach aggregates the channels’ subunits. Importantly, we observe that the differences between these approaches will persist for any finite number of channels. In the limit of infinitely many channels, the variance goes to zero, so all of the modeling approaches discussed here become equivalent. It is a straightforward exercise to extend this analysis to the case of four subunits (i.e., the K⁺ channel), and a similar discrepancy between the channel and subunit approaches holds in that case.

The three methods for grouping subunits that we have considered represent the three different approaches to performing a system-size expansion that have been proposed by Fox and Lu [23,24] and Shuai and Jung [25]. These combinatorial arguments provide an intuitive understanding for why the three SDE approaches that we are studying will lead to channel noise models with different statistical properties. We now confirm this by directly analyzing the SDE and MC models.

III. VOLTAGE CLAMP ANALYSIS OF STOCHASTIC MODELS

A. Stationary distribution

We seek to characterize the probability distribution of the fraction of open channels f. To simplify the analysis, we will mimic the experimental technique of voltage clamp and perform our analysis while holding the membrane potential constant.

1. Markov chain model

In the MC model, each K⁺ channel consists of four subunits that transition between open and closed states. Under voltage clamp, the stationary distribution for the number of open channels can be completely determined because this process is homogeneous in time [34]. We are primarily interested in the stationary probability that all four subunits are open because this is equivalent to the probability that the channel itself is open. From Eq. (3), the equilibrium value of p_sub is $\frac{{\alpha }_n}{{\alpha }_n+{\beta }_n}$. The probability that the K⁺ channel is open is therefore

$$p_{\text{chan}}=\frac{{\alpha }_n^4}{{({\alpha }_n+{\beta }_n)}^4}.$$

All K⁺ channels are assumed to be statistically identical and independent, so the distribution of the total number of open K⁺ channels at a given time is a binomial distribution with population parameter N (the total number of K⁺ channels) and bias parameter p_chan. To define the distribution of the fraction of open channels f, we rescale the binomial distribution by 1/N. The mean and the variance of this stationary distribution are

$$E_{\text{MC}}[f]=p_{\text{chan}}\triangleq {\mu }_{\text{chan}}$$ (13)

$${\text{Var}}_{\text{MC}}[f]=\frac{p_{\text{chan}}(1-p_{\text{chan}})}{N}\triangleq {\sigma }_{\text{chan}}^2,$$ (14)

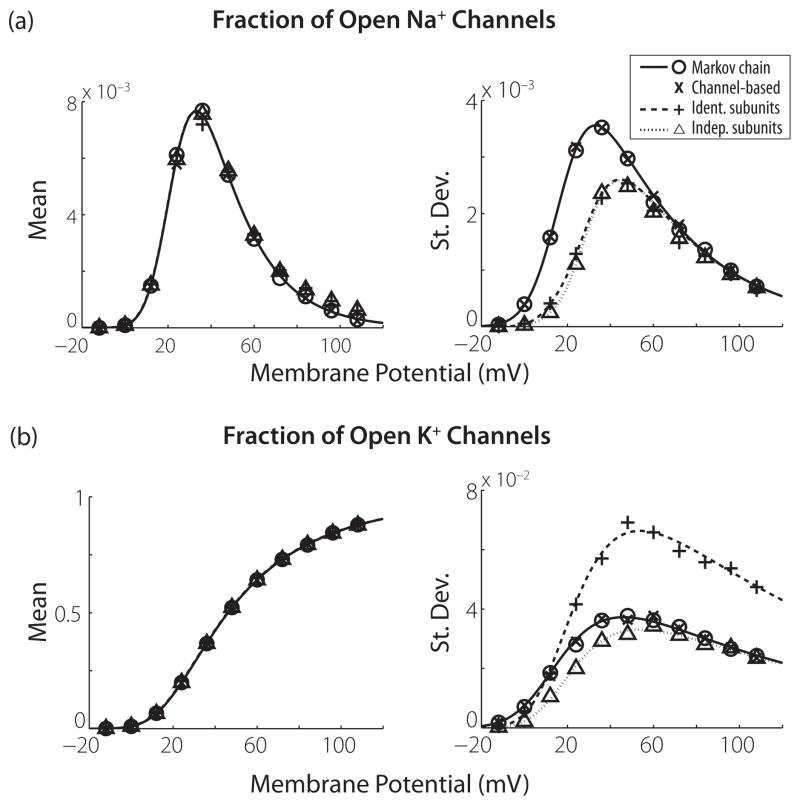
which we define as μ_chan and ${\sigma }_{\text{chan}}^2$, respectively, as a shorthand. Note that these quantities are functions of V, even though we do not explicitly include this dependence in our notation. Equation (13) shows that the mean does not depend on the number of channels and Eq. (14) shows that the variance scales with 1/N. The mean and standard deviation of the fraction of open channels are shown by the solid black lines in Fig. 2. The mean and variance for the Na⁺ channel can be computed in a similar fashion and Fig. 2 includes those results. The results shown are for a membrane area of 10 μm², which corresponds to 180 K⁺and 600 Na⁺ channels.

FIG. 2.

Analytical (lines) and numerical (symbols) results for means and standard deviations of the fractions of open channels in voltage clamp. The membrane area is 10 μm² (600 Na⁺channels and 180 K⁺channels). The abscissa gives the voltage clamp value. (a) Results for Na⁺channels. (b) Results for K⁺channels. Analytical results for the channel SDE model are not shown because they are identical to those of the MC model.

2. Channel SDE model

To analyze the channel SDE model for the K⁺ channels [Eq. (6)], we apply the simplification suggested by Fox and Lu: we set values of the state variables in the diffusion matrix [Eq. (7)] to their mean equilibrium values. We refer to this approximation as the equilibrium noise approximation and show in Appendix C that, for the voltage clamp case, it holds to O(N⁻²). In principle, the values of each x_i should be confined to [0,1] since they represent proportions of open channels, but to simplify the mathematical analysis we do not impose this condition. Under these simplifications, the SDE model is a multivariate Ornstein-Uhlenbeck (OU) process that, by definition, has a Gaussian stationary distribution. The fraction of open channels f is defined as the fraction of channels that have all subunits open. In the notation of Eq. (6), f is given by x₄ for K⁺. The mean and variance of f, which can be calculated directly using standard methods [34], are identical to the values found for the MC model in Eqs. (13) and (14). The stationary distribution of the fraction of open K⁺ channels therefore is given by

$$p(f)=\frac{1}{\sqrt{2\pi {\sigma }_{\text{chan}}^2}}{e}^{-{(f-{\mu }_{\text{chan}})}^2/2{\sigma }_{\text{chan}}^2}.$$ (15)

This is the expected result for a system-size expansion since, in the limit of a large number of channels, the binomial distribution for the MC model can be approximated by a Gaussian distribution with mean μ_chan and variance ${\sigma }_{\text{chan}}^2$. Any description of channel noise that aims to reproduce the behavior of the Markov state model should have this as its limiting distribution, so this result is our first confirmation that the channel SDE model provides an accurate approximation to the MC model.

3. Subunit SDE models

To analyze the subunit-based SDE models for the K⁺ channels, we apply similar approximations as before: we replace n in the equation for ${\sigma }_n^2$ [Eq. (9)] with its mean value at equilibrium and do not restrict the values of n to the interval [0,1]. As was the case for the channel SDE, this allows us to rewrite the SDE for n [Eq. (8)] as an OU process:

$$\frac{dn}{dt}=\frac{1}{{\tau }_n}({\mu }_{\text{sub}}-n)+{\overline{\sigma }}_n\xi (t),$$ (16)

where ${\tau }_n=\frac{1}{{\alpha }_n+{\beta }_n},{\mu }_{\text{sub}}=\frac{{\alpha }_n}{{\alpha }_n+{\beta }_n}$, and ${\overline{\sigma }}_n^2=\frac{2{\alpha }_n{\beta }_n}{N({\alpha }_n+{\beta }_n)}$. The stationary distribution of the fraction of open subunits n is therefore Gaussian with mean μ_sub and variance ${\sigma }_{\text{sub}}^2=\frac{{\alpha }_n{\beta }_n}{N{({\alpha }_n+{\beta }_n)}^2}$. Note that ${\sigma }_{\text{sub}}^2$ is scaled by 1/N; for simplicity we report analytical results to O(N⁻¹).

In Sec. II C 2 we discussed two methods for defining the proportion of open K⁺ channels based on the stochastic dynamics of the subunits. If we follow the approach of Shuai and Jung and combine four statistically identical and independent solutions to Eq. (16), the stationary distribution for the proportion of open channels is defined by the product of four independent and identically distributed Gaussian random variables:

$$p_{\text{InS}}(f)=\int {dn}_1\cdots {dn}_4\left[\prod _{j=1}^4\frac{e^{-{(n_j-{\mu }_{\text{sub}})}^2/2{\sigma }_{\text{sub}}^2}}{\sqrt{2\pi {\sigma }_{\text{sub}}^2}}\right]\delta \left(f-\prod _{j=1}^4{n}_j\right).$$

Unlike the channel SDE distribution in Eq. (15), in the limit of a large number of channels, this distribution does not approach a Gaussian. The InS model therefore is fundamentally incompatible with the MC model. Furthermore, it is straightforward to compute the mean and variance of this distribution directly from the first two moments of the subunit distribution. We find

$$\begin{array}{l}{E}_{\text{InS}}[f]={\mu }_{\text{sub}}^4\\ ={\mu }_{\text{chan}},\end{array}$$ (17)

$$\begin{array}{l}{\text{Var}}_{\text{Ins}}[f]=4{\mu }_{\text{sub}}^6{\sigma }_{\text{sub}}^2+O(N^{-2})\\ \ne {\sigma }_{\text{chan}}^2.\end{array}$$ (18)

This leading order result for the moments can also be obtained following the combinatorial approach outlined in Sec. II D.

If we go further and assume that all four populations of subunits are identical and perfectly correlated (i.e., following the approximation proposed by Fox and Lu), then the stationary distribution for the fraction of open K⁺ channels is the distribution of a Gaussian random variable raised to the fourth power, which has the closed form

$$p_{\text{IdS}}(f)=\frac{1}{4\sqrt{2\pi {\sigma }_{\text{sub}}^2}}{f}^{-3/4}{e}^{-{(\sqrt[4]{f}-{\mu }_{\text{sub}})}^2/2{\sigma }_{\text{sub}}^2}.$$

This distribution also does not limit to a Gaussian and is fundamentally incompatible with the MC model. As above, we can compute the mean and variance of n⁴:

$$\begin{array}{l}{E}_{\text{IdS}}[f]={\mu }_{\text{sub}}^4+6{\mu }_{\text{sub}}^2{\sigma }_{\text{sub}}^2+O(N^{-2})\\ ={\mu }_{\text{chan}}+O(N^{-1}),\end{array}$$ (19)

$$\begin{array}{l}{\text{Var}}_{\text{IdS}}[f]=16{\mu }_{\text{sub}}^6{\sigma }_{\text{sub}}^2+O(N^{-2})\\ \ne {\sigma }_{\text{chan}}^2.\end{array}$$ (20)

Equations (17) and (19) show that the mean fraction of open channels computed with the subunit approaches agrees with the MC model in the limit of a large number of channels. The variance, however, is poorly described. For instance, the ratio of the open channel variance of the MC model [Eq. (14)] to that of the IdS model [Eq. (20)] is

$$\frac{{\sigma }_{\text{chan}}^2}{{\text{Var}}_{\text{IdS}}(f)}=\frac{1+{\mu }_{\text{sub}}+{\mu }_{\text{sub}}^2+{\mu }_{\text{sub}}^3}{16{\mu }_{\text{sub}}^3+O(N^{-1})},$$

where we have used the facts that ${\sigma }_{\text{chan}}^2=\frac{{\mu }_{\text{sub}}^4(1-{\mu }_{\text{sub}}^4)}{N}$ and ${\sigma }_{\text{sub}}^2=\frac{{\mu }_{\text{sub}}(1-{\mu }_{\text{sub}})}{N}$. For subthreshold values of V, μ_sub is small and therefore the IdS model drastically underestimates the magnitude of the channel noise.

These analytical results for the two subunit SDE models are plotted in Fig. 2 with dotted (independent subunit populations; InS) and dashed (identical subunit populations; IdS) lines. We observe that standard deviations in the open channel distributions are underestimated by both subunit models for V near the resting potential of 0 mV.

B. Autocorrelation in voltage clamp

We now analyze temporal correlations in the proportion of open K⁺ channels for a given voltage clamp level. As in prior sections, equations presented here depend on voltage potential V, but to simplify notation we do not explicitly indicate this. If we denote the time series of the proportion of open channels as f(t), then the autocorrelation function for f(t) is

$$R(t)=\frac{\text{E}[f(t)f(0)]-\text{E}{[f(0)]}^2}{\text{Var}[f(0)]}.$$

We assume that R(t) does not depend on the initial time since our analysis is restricted to the stationary distribution of open channels in voltage clamp.

1. Markov chain model

Let c_i(t) denote the state of the ith channel at time t, where c_i(t) = 1 indicates an open channel and c_i(t) = 0 indicates that the channel is closed. The autocorrelation for the fraction of open channels then becomes

$$\begin{array}{l}{R}_{\text{MC}}(t)=\frac{E\left[\frac{1}{N^2}{\sum }_{i,j=1}^N{c}_i(t)c_j(0)\right]-{\mu }_{\text{chan}}^2}{{\sigma }_{\text{chan}}^2}\\ =\frac{E[c_i(t)c_i(0)]-{\mu }_{\text{chan}}^2}{{\mu }_{\text{chan}}(1-{\mu }_{\text{chan}})}.\end{array}$$ (21)

This simplification is possible because the MC model assumes that all channels are statistically identical and independent. The only unknown term in Eq. (21) is E [c_i (t)c_i (0)]. Since c_i is a binary random variable, the expected value of c_i (t)c_i (0) is equal to the probability that the channel is open at the initial time and is also open at the later time t. This probability can be determined by solving the master equation (5), which is possible in voltage clamp because this system of ordinary differential equations is a linear equation with constant coefficients. The probability that the channel is open is given by p₄ in Eq. (5), so E [c_i (t)c_i (0)] is equal to the entry in the last row and the last column of the matrix exponential of the matrix in Eq. (5). We find

$$R_{\text{MC}}(t)=\frac{4{\alpha }_n^3{e}^{-t/{\tau }_n}+6{\alpha }_n^2{\beta }_n{e}^{-2t/{\tau }_n}+4{\alpha }_n{\beta }_n^2{e}^{-3t/{\tau }_n}+{\beta }_n^3{e}^{-4t/{\tau }_n}}{(2{\alpha }_n+{\beta }_n)(2{\alpha }_n^2+2{\alpha }_n{\beta }_n+{\beta }_n^2)},$$ (22)

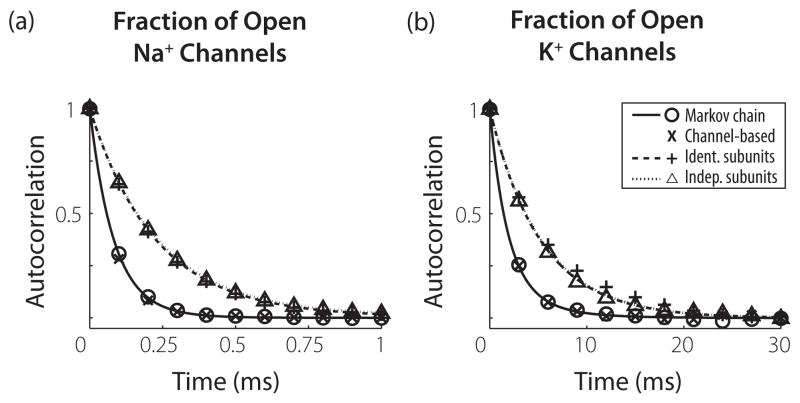
where ${\tau }_n=\frac{1}{{\alpha }_n+{\beta }_n}$. The solid black line in Fig. 3(b) shows this function for a voltage clamp value of V = 0 mV. The same analysis was applied to the Na⁺ channel, the result of which is also shown in Fig. 3(a). Temporal correlations in the fraction of open Na⁺ channels decay rapidly within the first millisecond, whereas the temporal correlation in the fraction of open K⁺ channels persists for nearly 10 ms.

FIG. 3.

Analytical (lines) and numerical (symbols) results for autocorrelations R(t) of the fractions of open channels in voltage clamp. The voltage clamp is set to 0 mV and the membrane area is 10 μm² (600 Na⁺channels and 180 K⁺channels). (a) Results for Na⁺channels. (b) Results for K⁺channels. Analytical results for the channel SDE model are not shown because they are identical to those of the MC model.

Equation (22) reveals an important feature of the MC models—the structure of the channel defines the temporal profile of the channel noise statistics. In the case of the K⁺ channel, the transitions between the five possible channel configurations induce correlations on four time scales, the first four multiples of 1/τ_n. The Na⁺ channel has eight possible channel configurations because it has three m subunits and one h subunit, so the autocorrelation function for the fraction of open Na⁺ channels has seven time scales.

2. Channel SDE model

Using the same approximations that allow the channel models to be described as a multivariable OU process, we can compute the autocorrelation function for the proportion of open channels using known analytical results for OU processes [34]. We find that the autocorrelation function is identical to Eq. (22) and thus do not include it in Fig. 3.

3. Subunit SDE models

We compute the autocorrelation for the InS and IdS models using the OU approximation of n in voltage clamp. Using the Ito calculus, the known solution for long time behavior of the OU process in Eq. (16) is [34]

$$n(t)={\mu }_{\text{sub}}+{\int }_0^t{\overline{\sigma }}_n{e}^{-t-u/{\tau }_n}dW(u).$$ (23)

To calculate the autocorrelation in the InS model, we take the expectation of the product of four independent solutions of the form of Eq. (23) and normalize by the voltage clamp mean and variance shown in Eqs. (17) and (18):

$$\begin{array}{l}{R}_{\text{InS}}(t)\frac{E[{\mathrm{\Pi }}_{i=1}^4{n}_i(t)n_i(0)]-E_{\text{InS}}{(f)}^2}{{\text{Var}}_{\text{InS}}(f)}\\ =\frac{4{\mu }_{\text{sub}}^6{e}^{-t/{\tau }_n}+6{\mu }_{\text{sub}}^4{\sigma }_{\text{sub}}^2{e}^{-2t/{\tau }_n}}{4{\mu }_{\text{sub}}^6+6{\mu }_{\text{sub}}^4{\sigma }_{\text{sub}}^2}+O(N^{-2}).\end{array}$$ (24)

For the IdS model, we instead take a single solution of the form of Eq. (23) and raise it to the fourth power and normalize it by the voltage clamp mean and variance from Eqs. (19) and (20). The autocorrelation is

$$\begin{array}{l}{R}_{\text{IdS}}(t)=\frac{E[n{(t)}^{4}n{(0)}^4]-E_{\text{IdS}}{(f)}^2}{{\text{Var}}_{\text{IdS}}(f)}\\ =\frac{(2{\mu }_{\text{sub}}^6+12{\mu }_{\text{sub}}^4{\sigma }_{\text{sub}}^2)e^{-t/{\tau }_n}+9{\mu }_{\text{sub}}^4{\sigma }_{\text{sub}}^2{e}^{-2t/{\tau }_n}}{2{\mu }_{\text{sub}}^6+21{\mu }_{\text{sub}}{\sigma }_{\text{sub}}^2}+O(N^{-2}).\end{array}$$ (25)

Calculation of the higher-order terms shows that the same exponential time scales (the first four multiples of 1/τ_n) are present in R(t) for all of the models, but the coefficients are different. In particular, Eqs. (24) and (25) show that, to leading order in 1/N, the subunit models lack the faster time scales of the K⁺ channel. As a result, temporal correlations in the subunit-based channel noise models persist longer than in either the MC model or the channel-based SDE model. Figure 3 displays these differences in the autocorrelation functions of the subunit models for voltage clamped at V = 0 mV. The dotted line shows the result for the InS model (independent subunit populations) and the dashed line shows the result for the IdS model (identical subunit populations), with autocorrelation in the Na⁺ channel displayed in panel in (a) and the K⁺ channel in panel (b).

IV. NUMERICAL SIMULATIONS

In this section we report results from numerical simulations of the MC model as well as the three SDE models analyzed above. We first verify the results of our analysis of voltage clamp statistics and then measure the statistics of interspike intervals in order to test how well the SDE models replicate the stochastic features of the MC model when voltage is allowed to evolve freely according to Eq. (1). In all simulations we use the parameter values listed in Table I. We perform simulations for three different membrane areas: 1, 10, and 100 μm². The corresponding channel counts are shown in Table II.

TABLE I.

Parameter values from [1]. Note that resting potential has been shifted to 0 mV.

Symbol	Definition	Value (units)
C	membrane capacitance	1 (μF/cm2)
ḡNa	maximal sodium conductance	120 (mS/cm2)
ḡK	maximal potassium conductance	36 (mS/cm2)
gL	leak conductance	0.3 (mS/cm2)
ENa	sodium reversal potential	115 (mV)
EK	potassium reversal potential	−12 (mV)
EL	leak reversal potential	10.6 (mV)
ρNa	sodium channel density	60 (μm−2)
ρK	potassium channel density	18 (μm−2)

TABLE II.

Membrane areas and corresponding channel counts used in numerical simulations

Membrane area (μm2)	No. of channels
	Na+	K+
1	60	18
10	600	180
100	6000	1800

A. Methods

Sample FORTRAN code used to simulate the four stochastic models is available online in the ModelDB repository (accession number 128502) [35]. All simulations used a time step of size 0.01 ms. We define a spike using two conditions: the membrane potential must exceed 60 mV and it must have remained below 60 mV for the previous 2 ms (approximately the width of a spike). To generate Gaussian random numbers, we first produced uniform random numbers using the Mersenne Twister algorithm [36] and then transformed these to Gaussian random numbers using the Box-Muller method [37].

In Sec. IV C, we characterize the spiking response of the different models in response to stimuli of the form

$$I(t)=I_{\text{DC}}+I_{\text{noise}}\xi (t),$$ (26)

where ξ(t) is a Gaussian white noise process with zero mean and unit variance. This type of input is commonly used to characterize the response of stochastic Hodgkin-Huxley models [ [11,30], e.g.]. The additive white noise term can be interpreted as a simplified method for representing the combined effect of numerous synaptic inputs that neurons in cortex and other networks receive in vivo; see, for instance, [38]. We simulate spike trains for varying membrane area, DC input I_DC, and input noise I_noise. We report the mean and coefficient of variation (CV) for the first 2000 interspike intervals (ISI) for each spike train, where the CV is defined as the standard deviation of the ISIs divided by the mean value.

1. Markov chain model

The Markov chain describing each K⁺ channel is shown in Eq. (4). The Markov chain that governs the state of each Na⁺channel includes three m subunits and one h subunit and is therefore described by an eight-state Markov chain:

$$\begin{array}{ccccccc}0,0& \underset{{\beta }_m}{\overset{3{\alpha }_m}{\rightleftarrows }}& 1,0& \underset{2{\beta }_m}{\overset{2{\alpha }_m}{\rightleftarrows }}& 2,0& \underset{3{\beta }_m}{\overset{{\alpha }_m}{\rightleftarrows }}& 3,0\\ {\alpha }_h\downarrow \uparrow {\beta }_h& & {\alpha }_h\downarrow \uparrow {\beta }_h& & {\alpha }_h\downarrow \uparrow {\beta }_h& & {\alpha }_h\downarrow \uparrow {\beta }_h\\ 0,1& \underset{{\beta }_m}{\overset{3{\alpha }_m}{\rightleftarrows }}& 1,1& \underset{2{\beta }_m}{\overset{2{\alpha }_m}{\rightleftarrows }}& 2,1& \underset{3{\beta }_m}{\overset{{\alpha }_m}{\rightleftarrows }}& 3,1.\end{array}$$ (27)

The channel is in the conducting state when all three m subunits and the h subunit are open. The voltage-dependent transition rates for the m and h subunits are [1]

$$\begin{array}{l}{\alpha }_m(V)=0.1\frac{25-V}{exp(\frac{25-V}{10})-1},\\ {\beta }_m(V)=4exp\left(-\frac{V}{18}\right),\\ {\alpha }_h(V)=0.07exp\left(-\frac{V}{20}\right),\\ {\beta }_h(V)=\frac{1}{exp(\frac{30-V}{10}+1)}.\end{array}$$

The Markov chains in Eqs. (4) and (27) define the possible states of each individual channel. Rather than simulating individual channels in the membrane patch, however, it is more efficient to track the number of channels in each state using the Gillespie algorithm [39,40]. At each time step, the fraction of open Na⁺channels f_Na and K⁺channels f_K is computed and the voltage is updated using the forward Euler algorithm applied to Eq. (1).

2. Channel SDE model (IdS)

The channel SDE model is a system of 12 differential equations derived by Fox and Lu [23]. In matrix form, it can be written as

$$\begin{array}{l}C\frac{dV}{dt}=-{\overline{g}}_{\text{Na}}{y}_{31}(V-E_{\text{Na}})-{\overline{g}}_{\text{K}}{x}_4(V-E_{\text{K}})-{\overline{g}}_{\text{L}}(V-E_{\text{L}})+I,\\ \frac{d\mathbf{x}}{dt}=A_{\text{K}}\mathbf{x}+4{\alpha }_n{x}_0{\mathbf{e}}_{\mathbf{1}}+S_{\text{K}}{\xi }_{\text{K}},\\ \frac{d\mathbf{y}}{dt}=A_{\text{Na}}\mathbf{y}+3{\alpha }_m{y}_{00}{\mathbf{e}}_{\mathbf{1}}+{\alpha }_h{y}_{00}{\mathbf{e}}_{\mathbf{4}}+S_{\text{Na}}{\xi }_{\text{Na}}.\end{array}$$ (28)

The vector x is made up of entries x_i (i = 1,2,3,4) that represent the proportion of K⁺channels with i open n subunits. The entries of y are denoted y_ij (i = 0,1,2,3 and j = 0,1) and represent the proportion of Na⁺channels with i open m subunits and j open h subunits. The vectors e_i are column vectors with a 1 in the ith entry and 0 elsewhere. Following Fox and Lu, we use the fact that ${\sum }_{i=0}^4{x}_i=1$ and ${\sum }_{i=0}^3{\sum }_{j=0}^1{y}_{ij}=1$ to define x₀ and y₀₀. This allows us to reduce the dimension of the system of SDEs from 14 to 12. We note that this reduction of dimension is exact, following from properties of the A and S matrices. The matrices A_Na, A_K, S_Na, and S_K are defined in Appendix B.

The elements of x and y represent proportions of channels in a particular configuration so they should lie within five-dimensional and eight-dimensional hypercubes bounded by the intervals [0,1]. Moreover, since the x_i and y_ij each sum to 1, the values of these variables should in fact lie on hyperplanes within these hypercubes. If, in the course of numerical simulations, there are excursions of x and y off of these high-dimensional bounded surfaces, then the solution will lack biological meaning because a value that represents the proportions of channels should not be negative or exceed 1. Another numerical difficulty arises if these variables do not lie on the proper bounded hyperplanes. To define S_K and S_Na, one needs to take matrix square roots of diffusion matrices in every time step. If the x and y do not lie on the bounded surfaces, then the diffusion matrices, which depend on the values of x and y, will no longer be guaranteed to be positive semidefinite, which may make it impossible to compute real valued matrix square roots.

In principle, it may be possible to incorporate a projection or a reflection into the numerical method to ensure that x and y remain on these bounded, high-dimensional surfaces of admissible values. We demonstrate that a simpler approach in which the individual values of the x_i and y_ij are not confined within [0,1], but rather are free to evolve without boundary conditions, gives an adequate numerical approximation to the interspike interval statistics of the MC model. With this simplification, there is no longer a guarantee that real matrix square roots of the diffusion matrices will exist, so we replace the values of x_i and y_ij in the diffusion matrices with their equilibrium values. The validity of this approximation is discussed in Appendix C. After implementing the above simplifications, we solved the resulting system of SDEs using the Euler-Maruyama method [41]. Comparing our results with implementations that bound the SDE solutions would be an interesting subject for future work, but is beyond the aims of this paper.

3. Subunit SDE models

The two subunit SDE models that we study are the independent subunit (InS) model:

$$\begin{array}{l}C\frac{dV}{dt}=-{\overline{g}}_{\text{Na}}{m}_1{m}_2{m}_{3}h(V-E_{\text{Na}})-{\overline{g}}_{\text{K}}{n}_1{n}_2{n}_3{n}_4(V-E_{\text{K}})-g_{\text{L}}(V-E_{\text{L}})+I,\\ \frac{{dm}_i}{dt}={\alpha }_m(1-m_i)-{\beta }_m{m}_i+{\sigma }_m(V){\xi }_{m_i}(t),\text{where}i=1,2,3,\\ \frac{dh}{dt}={\alpha }_h(1-h)-{\beta }_{h}h+{\sigma }_h(V){\xi }_h(t),\\ \frac{{dn}_i}{dt}={\alpha }_n(1-n_i)-{\beta }_n{n}_i+{\sigma }_n(V){\xi }_{n_i}(t),\text{where}i=1,2,3,4\end{array}$$ (29)

and the identical subunit (IdS) model

$$\begin{array}{l}C\frac{dV}{dt}=-{\overline{g}}_{\text{Na}}{m}^{3}h(V-E_{\text{Na}})-{\overline{g}}_{\text{K}}{n}^4(V-E_{\text{K}})-g_{\text{L}}(V-E_{\text{L}})+I,\\ \frac{dm}{dt}={\alpha }_m(1-m)-{\beta }_{m}m+{\sigma }_m(V){\xi }_m(t),\\ \frac{dh}{dt}={\alpha }_h(1-h)-{\beta }_{h}h+{\sigma }_h(V){\xi }_h(t),\\ \frac{dn}{dt}={\alpha }_n(1-n)-{\beta }_{n}n+{\sigma }_n(V){\xi }_n(t).\end{array}$$

The difference between these two models is that, in the former, we compute multiple independent realizations of the n and m type subunits and the product of these terms enter into the equation for V whereas in the latter, all subunit classes are assumed to be perfectly correlated so only one SDE is solved for each subunit type and the solution is raised to the appropriate power (4 for n and 3 for m). The gating variables represent proportions of open subunits so we enforce boundary conditions that prevent the values of the gating variables from exceeding 1 or becoming negative.

We note that the form of ${\sigma }_x^2(x=m,h,\text{or}n)$ that we use is given in Eq. (9). In particular, the noise terms depend on voltage as well as the subunit variables themselves. We do not apply the equilibrium noise approximation in our simulations of the subunit SDEs, although this approximation has been used in past simulation studies [23,26,30]. We solve these systems of SDEs using the Euler-Maruyama method [41].

B. Simulation results: Voltage clamp

In Figs. 2 and 3, we compare results from numerical simulations for a membrane patch size of 10 μm² against the analytical calculations presented in Sec. III. To simulate the voltage clamp condition, we fix V at a particular value and keep it constant throughout the simulation. Figure 2 shows the mean and standard deviation of the proportion of open Na⁺ and K⁺ channels as a function of the voltage clamp value. In most cases, the values computed from numerical simulations (symbols) match the analytical results (lines). Of particular note is the fact that the computed values for the MC model (circle) and the channel model (x) are virtually indistinguishable.

The only deviation between the numerical results and the analytical solutions occurs in the subunit models for the mean values of the Na⁺ channels at high voltage values. The cause of this discrepancy is that the analytical treatment assumes that the proportions of subunits are Gaussian-distributed whereas in the numerical methods the values of m and h are bounded between 0 and 1. For high voltage values of V, the proportion of open m-type subunits is very small and the variance is nonzero, so approximating the distributions of m as a Gaussian will allow m to take negative values. This cannot occur in the numerical simulations, thus the theoretical value for the mean fraction of open Na⁺ channels will be less than the simulated value. As the number of channels increase, the variance of the fraction of open m subunits decreases, which decreases the probability that a Gaussian-distributed m will take negative values. The discrepancy between the analytically and numerically calculated values for the mean fraction of open Na⁺ channels decreases therefore as the number of Na⁺ channels increases.

C. Simulation results: Interspike intervals

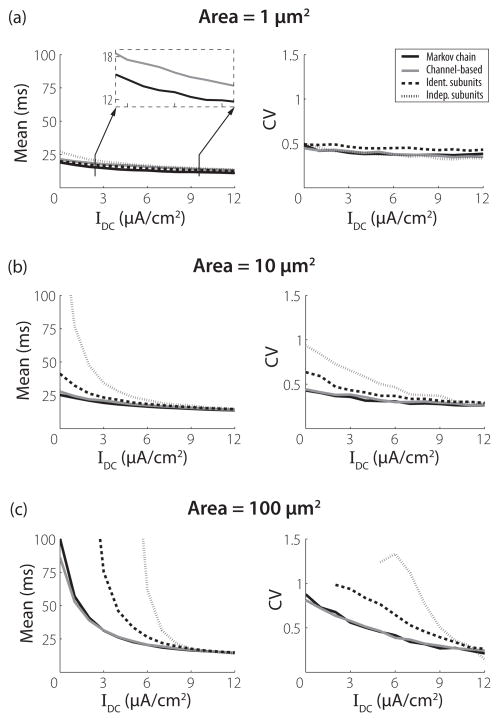
Figure 4 shows mean and CV (left and right columns, respectively) of ISIs for three membrane areas that increase from top to bottom in each column. The input to the model is a constant DC input [I_noise = 0 in Eq. (26)]. The value of I_DC is shown on the x axis. In general, these simulations show that the rate and regularity of spiking activity produced by the MC (black line) and channel (gray line) models are in close quantitative agreement whereas the IdS (dashed line) and InS (dotted line) models produce, on average, dramatically longer ISIs. The behaviors of the models are most disparate for low stimulus levels and larger membrane areas. In these cases, the stimulus is not sufficiently strong to drive regular firing, so spike events are predominantly determined by stochastic fluctuations in the conductances due to channel noise. As the DC level is increased, the models respond to the external stimulus and there is a smaller effect of channel noise on spike timing. This leads all models to exhibit similar mean ISI and CV values at high current levels. As the membrane area increases, spiking events become increasingly rare at low current levels. This is consistent with the fact that, for large channel numbers, the behavior of all models will approach that of the deterministic Hodgkin-Huxley equations, which are known to transition from quiescence to repetitive firing when DC input is increased beyond approximately 6.2 μA/cm² [42].

FIG. 4.

Means and coefficients of variation (CV) of first 2000 interspike intervals as a function of the DC level (abscissa) for a constant current input. (a) Results for a membrane area of 1 μm². The inset magnifies the ordinate to illustrate the difference in mean ISIs between the MC and channel SDE models. (b) Results for a membrane area of 10 μm². (c) Results for a membrane area of 100 μm².

The mean ISIs for the subunit SDE models exceed those of the MC model for all stimulus conditions and membrane areas. This has been previously observed for the IdS model [30]. In the voltage clamp analysis we found that the variance in the proportion of open K⁺ and Na⁺ channels for V near the resting potential of 0 mV is smaller for both of these models than for the MC model. This lack of conductance fluctuations leads to reduced spike rates at low stimulus levels, relative to the MC model.

Overall, the results for the channel model show that it is possible to approximate the MC model with SDE and still obtain quantitatively accurate results, even for small numbers of channels. This is an important and a nontrivial result—the system-size expansion is formally valid only in the limit of infinitely many channels, but we show here that it can be applied to a small number of channels, where membrane fluctuations have a major impact on spiking statistics. Moreover, the equilibrium noise approximation and treatment of boundary conditions do not appear to substantially degrade solution accuracy over a wide range of stimuli.

Nevertheless, there are some discrepancies between the channel and MC models. At the smaller membrane areas (1 μm² and 10 μm²), the mean ISIs for the channel model tend to be longer than the MC model ISIs. This point is highlighted in the inset of Fig. 4(a). At the largest membrane area tested, for the case of weak or no input current, this trend is reversed and the channel model has shorter mean ISIs than the MC model. A possible source for these differences between the channel and MC models is our treatment of the boundary conditions in the channel model and the equilibrium noise approximation. Further investigation of this approximation is needed, but the similar ISI statistics obtained with the channel and MC models suggest that this approximation may be suitable in many cases.

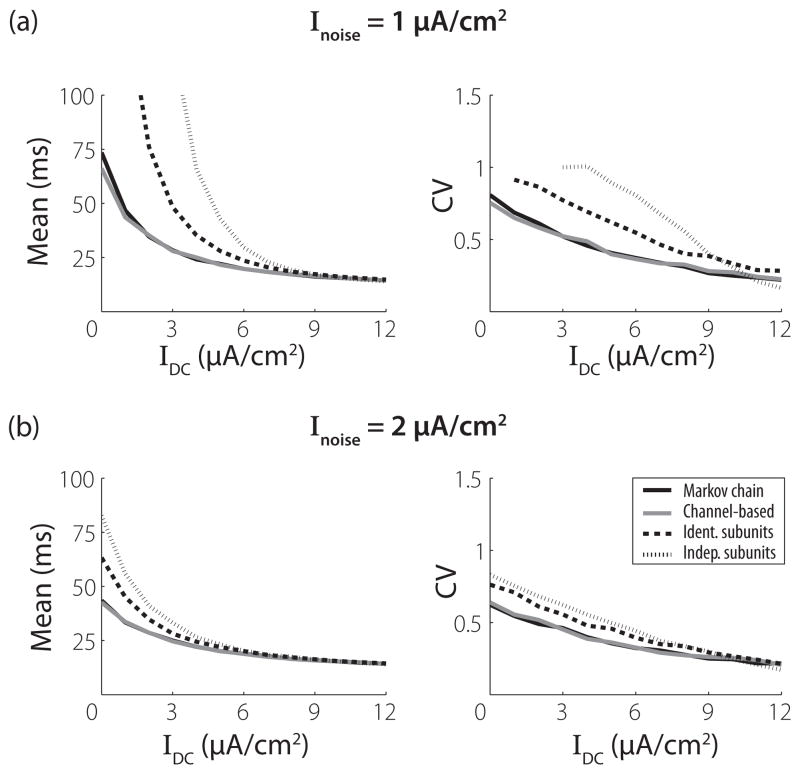
Figure 5 shows results obtained for two different levels of input noise added to the DC stimulus with current level shown on the x axis. We only present ISI statistics for the membrane size of 100 μm² because the smaller membrane areas produce the same qualitative differences among the models. Overall, the effect of the stimulus noise is to reduce the mean ISIs. Importantly, the ISI statistics of the responses of the MC and channel SDE models to these noisy stimuli remain quantitatively similar. In fact, the stimulus fluctuations elicit spikes even at low or no DC levels, so the differences in the mean ISIs between the MC and channel SDE models become less apparent. This result indicates that the equilibrium noise approximation does not break down in the presence of a rapidly fluctuating external stimulus. Finally, the results for the subunit SDEs show, once again, that the stochastic dynamics and spiking activity of these approximate models do not accurately replicate the statistics of the MC model.

FIG. 5.

Means and coefficients of variation (CV) of first 2000 interspike intervals as a function of the DC level (abscissa) for a current input of the form I_DC + I_noise ξ (t) where ξ (t) is a Gaussian white noise process with mean zero and unit variance. Membrane area is 100 μm². (a) and (b) show results for I_noise = 1 and 2 μm², respectively.

V. DISCUSSION

Beginning with the work of Fox and Lu [23,24], the question of whether SDE models of channel noise can accurately approximate MC models has been explored. SDE models of membrane voltage fluctuations in HH models have several attractive features, including possible improvements in the speed of numerical simulations and the opportunity to analyze these models using nonlinear SDE theory [[43], e.g.]. In recent years, however, the SDE approach has come under increasing scrutiny. Numerical simulations of the most commonly used SDE model, which we have called the identical subunit model, have shown that this approach produces weaker conductance and voltage fluctuations than the corresponding MC model [26,31]. As a consequence, the firing rates of this SDE model are substantially lower [30] (and, equivalently, the mean ISIs are longer [28]), there is less variability in the occurrences and timing of spikes in response to a brief pulse of current [27], and information is transmitted at a higher rate [30]. Furthermore, these discrepancies persist even as the number of channels increases [26,28,30]. In short, there is an emerging consensus in the literature that the MC model cannot be approximated accurately using a subunit system of SDEs.

We have demonstrated in this paper that an alternative SDE approach that is based on the multistate structure of each ion channel can approximate the channel noise effects that are present in the MC model, even for relatively small numbers of channels, as long as the system-size expansion that is used to derive the SDE model is carried out properly. If one first defines the structure of a channel and then defines the dynamics of the proportions of channels in each configuration, one arrives at the channel-based SDE model (see discussion in Sec. II D and equations in Sec. IV A 2). If, instead, one approximates the proportion of subunits in the open or closed states with an SDE, then one obtains a subunit-based SDE model (see discussion in Sec. II D and equations in Sec. IV A 3). Through our analysis of the stationary statistics of the proportion of open channels in voltage clamp, we have shown that the former approach, which we call channel based, can provide a quantitatively accurate approximation to the MC model. We have also confirmed that the latter, subunit based, approach should not be considered an approximation of the MC model because its stochastic properties are fundamentally different from those of the MC model. We conclude that the SDE approach is a valid approximation of the MC channel noise model, but that it is necessary to properly define the system of SDEs based on the structure of each channel. In particular, one cannot include noise in the subunit equations in the manner suggested by Fox and Lu and expect results that are consistent with the MC ion channel model.

We present numerical results for the channel SDE model at three membrane areas (1, 10, and 100 μm², as in [30]), where the number of Na⁺ channels range from 60 to 6000 and the number of K⁺ channels range from 18 to 1800. Our simulation results show that, in most cases, the ISI statistics for this model in response to constant and noisy current inputs are in close quantitative agreement with the MC model (see Figs. 4 and 5). This finding is encouraging because the channel SDE model was derived by Fox and Lu using a system-size expansion [23,24] that is formally valid only in the limit of a large number of channels. Although we found some evidence that the approximation is imperfect for the smallest populations of ion channels tested, we note that in many applications, the channel counts are in fact much higher. For instance, Rowat suggested that typical channel numbers in spike initiation zones may be on the order of 10⁴–10⁶ [11]. The channel counts used in the present study may be relevant to applications in which small patches of neural membrane can drive spiking activity. For example, a node of Ranvier of the auditory nerve fiber can produce a spike in response to cochlear implant stimulation. Typically, the nodes have surface areas of a few square micrometers [44] and are usually modeled with 1000 or fewer Na⁺ channels [44–46].

As first pointed out by Fox and Lu [23] and as discussed in Sec. IV A 2, numerical simulations of the channel SDE model can be computationally expensive. One particularly computationally intensive part of the algorithm is calculating matrix square roots to determine stochastic terms in the SDE at every time step of the simulation. We have performed this operation using the optimized CBLAS library, yet the channel SDE model still required approximately 25 times as much computational time as the IdS model. Fortunately, as is the case with all three SDE approaches, the channel model has one considerable advantage over MC—its computation time does not depend on the number of channels. For example, in our implementation of the Gillespie method, the computational time increased 12-fold as we increased the number of channels from 600 Na⁺ and 180 K⁺ to 6000 Na⁺ and 1800 K⁺. We found that even the channel model, the slowest of the SDE approaches discussed in this paper, is faster than the MC model once the number of channels is greater than approximately 1200 Na⁺ and 360 K⁺. Furthermore, the computational burden of solving the channel SDE model may be reduced by considering other methods for computing matrix square roots [[47], e.g.]. Higher-order SDE solvers than the Euler-Maruyama method could also speed up SDE simulations [[48], e.g.].

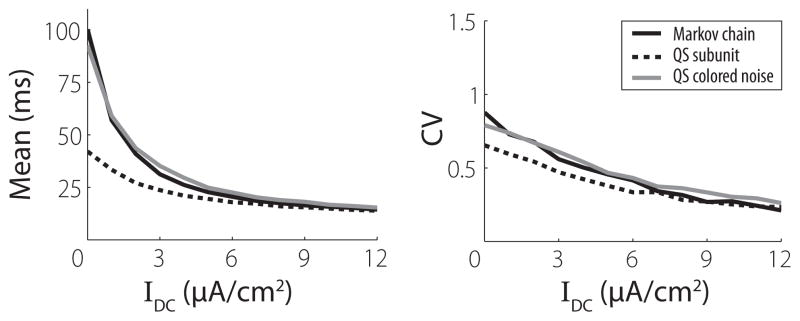
Even with increasingly efficient numerical methods for the channel SDE, a stochastic model that more closely resembles the classical HH equations, as opposed to the 12-dimensional system of SDEs that defines the channel model, is still desirable, as it would connect more directly with a wealth of studies of the original four-dimensional HH equations. In a simulation study of the Fox and Lu model, Bruce [26] sought to derive noise terms numerically for the subunit equations that would “correct” the Fox and Lu model so that the fluctuations in the proportions of open channels would match the MC model. We have performed a similar analysis using the analytical voltage clamp results (see Appendix D for details). We can redefine the magnitude of the noise in the subunit equations [i.e., σ_n in Eq. (8)] to produce a modified subunit SDE model with the same means and variances for the proportion of open channels in voltage clamp, to O(N⁻¹). This model is constructed based on our analytical results for the stationary distributions of the proportions of open channels, so we call it a quasistationary model. The ISI statistics for this modified subunit SDE model are shown by the dashed line in Fig. 6. This demonstrates that adjusting the noise terms in a subunit SDE model in order to fit the variances of the open channels in voltage clamp is not sufficient to provide an improved fit to the spiking dynamics of the MC model.

FIG. 6.

Means and coefficients of variation (CV) of first 2000 interspike intervals for the MC model (black line) and two quasistationary models (see text and Appendix D for details) in response to constant current input. DC level is given by the abscissa. Membrane area is 100 μm².

The reason for this can be seen in the multiple time scales of the autocorrelation functions for the MC model [Eq. (22)] and subunit models [Eqs. (24) and (25)]. We can alter the noise terms in the subunit model so that it produces the correct stationary variances of the fractions of open channels, but we cannot modify the autocorrelation functions in a way that makes them consistent with the MC model. We therefore formulated a second quasistationary model by adding colored Gaussian noise to the conductances in the HH equations (details of this model are in Appendix D). This second quasistationary model reproduces the Gaussian stationary distribution of the channel SDE in voltage clamp, so the proportion of open channels in voltage clamp has the same mean, variance, and autocorrelation as the MC and channel SDE models.

ISI statistics for this model are shown by the gray line in Fig. 6. We found that this model reproduced the statistics of the MC model much better than any of the subunit SDE models, so we conclude that temporal correlations in the channel noise play a critical role in influencing spike timing. Moreover, since the structure of the ion channel determines the history dependence of the channel noise, a valid channel noise model must properly describe the dynamics of the entire channel and not only the kinetics of individual subunits. Using numerical simulations, Bruce has pointed out that the subunit model does accurately approximate the MC model for the case of channels with a single subunit [26]. Our analysis explains this observation because, for channels with one subunit, the channel-based and subunit-based SDE models are mathematically identical.

We close by emphasizing that the models described in this paper do not represent complete descriptions of channel noise. As is always the case, when one attempts to formulate a mathematical description of complex biological processes, numerous assumptions and simplifications are at play. As our understanding of the structure and dynamics of these membranes improves, it may be necessary to update and improve our mathematical models of channel noise. Nonetheless, the central theme of this work will remain relevant: the statistics of channel noise are shaped by the activity of individual ion channels, and therefore the approximation methods must also include information about the states of the channels in order to correctly describe the effects of channel noise.

Note added in proof

Findings similar to those in our work have recently appeared in [50].

APPENDIX A: DERIVATION OF CORRELATION COEFFICIENT IN EQ. (11)

Here we detail the derivation of ρ in Eq. (11). We seek the correlation coefficient for random variables of the form z_i,1z_j,2 and z_k,1z_l,2 where either i = k or j = l. Without loss of generality, assume i = k, then

$$\begin{array}{l}\rho =\frac{\text{Cov}(z_{i,1}{z}_{j,2},z_{i,1}{z}_{l,2})}{\text{Var}[z_{i,1}{z}_{j,2}]}.\\ \end{array}$$

The variables z_i,1,z_j,2,z_k,1, and z_l,2 are identical, independently distributed Bernoulli random variables that have the value 1 with probability p_sub. The expected values of z_x and $z_x^2(x=i,j,k,l)$ therefore are p_sub. Thus the covariance and variance can be expressed as

$$\text{Cov}(z_{i,1}{z}_{j,2},z_{i,1}{z}_{l,2})=p_{\text{sub}}^3-p_{\text{sub}}^4$$

and

$$\text{Var}[z_{i,1}{z}_{j,2}]=p_{\text{sub}}^2(1-p_{\text{sub}}^2).$$

After some algebraic manipulations, we obtain a simple expression for ρ in terms of the probability that a subunit is open:

$$\rho =\frac{p_{\text{sub}}}{1+p_{\text{sub}}}.$$

APPENDIX B: MATRICES USED IN NUMERICAL SIMULATIONS OF THE CHANNEL SDE MODEL

The state vectors are defined as x = [x₁,x₂,x₃,x₄]^T and y = [y₁₀,y₂₀,y₃₀,y₀₁,y₁₁,y₂₁,y₃₁]^T. The number of K⁺ and Na⁺ channels are denoted by N_K and N_Na, respectively. The matrices A_K and A_Na in Eq. (28) are

$$\begin{array}{c}{A}_{\text{K}}=\left[\begin{array}{cccc}-(3{\alpha }_n+{\beta }_n)& 2{\beta }_n& 0& 0\\ 3{\alpha }_n& -2({\alpha }_n+{\beta }_n)& 3{\beta }_n& 0\\ 0& 2{\alpha }_n& -({\alpha }_n+3{\beta }_n)& 4{\beta }_n\\ 0& 0& {\alpha }_n& -4{\beta }_n\end{array}\right],\\ A_{\text{Na}}=\left[\begin{array}{ccccccc}-(2{\alpha }_m+{\beta }_m+{\alpha }_h)& 2{\beta }_m& 0& 0& {\beta }_h& 0& 0\\ 2{\alpha }_m& -({\alpha }_m+2{\beta }_m+{\alpha }_h)& 3{\beta }_m& 0& 0& {\beta }_h& 0\\ 0& {\alpha }_m& -(3{\beta }_m+{\alpha }_h)& 0& 0& 0& {\beta }_h\\ 0& 0& 0& -(3{\alpha }_m+{\beta }_h)& {\beta }_m& 0& 0\\ {\alpha }_h& 0& 0& 3{\alpha }_m& -(2{\alpha }_m+{\beta }_m+{\beta }_h)& 2{\beta }_m& 0\\ 0& {\alpha }_h& 0& 0& 2{\alpha }_m& -({\alpha }_m+2{\beta }_m+{\beta }_h)& 3{\beta }_m\\ 0& 0& {\alpha }_h& 0& 0& {\alpha }_m& -(3{\beta }_m+{\beta }_h)\end{array}\right].\end{array}$$

The matrix S_K and S_Na are the square root matrices of the following diffusion matrices:

$$\begin{array}{c}{D}_{\text{K}}=\frac{1}{N_{\text{K}}}\left[\begin{array}{cccc}4{\alpha }_n{\overline{x}}_0+(3{\alpha }_n+{\beta }_n){\overline{x}}_1+2{\beta }_n{\overline{x}}_2& -(3{\alpha }_n{\overline{x}}_1+2{\beta }_n{\overline{x}}_2)& 0& 0\\ -(3{\alpha }_n{\overline{x}}_1+2{\beta }_n{\overline{x}}_2)& 3{\alpha }_n{\overline{x}}_1+2({\alpha }_n+{\beta }_n){\overline{x}}_2+3{\beta }_n{\overline{x}}_3& -(2{\alpha }_n{\overline{x}}_2+3{\beta }_n{\overline{x}}_3)& 0\\ 0& -(2{\alpha }_n{\overline{x}}_2+3{\beta }_n{\overline{x}}_3)& 2{\alpha }_n{\overline{x}}_2+({\alpha }_n+3{\beta }_n){\overline{x}}_3+4{\beta }_n{\overline{x}}_4& -({\alpha }_n{\overline{x}}_3+4{\beta }_n{\overline{x}}_4)\\ 0& 0& -({\alpha }_n{\overline{x}}_3+4{\beta }_n{\overline{x}}_4)& {\alpha }_n{\overline{x}}_3+4{\beta }_n{\overline{x}}_4\end{array}\right],\\ D_{\text{Na}}=\frac{1}{N_{\text{Na}}}\left[\begin{array}{ccccccc}{d}_1& -2({\alpha }_m{\overline{y}}_{10}+{\beta }_m{\overline{y}}_{20})& 0& 0& -({\alpha }_h{\overline{y}}_{10}+{\beta }_h{\overline{y}}_{11})& 0& 0\\ -2({\alpha }_m{\overline{y}}_{10}+{\beta }_m{\overline{y}}_{20})& d_2& -({\alpha }_m{\overline{y}}_{20}+3{\beta }_m{\overline{y}}_{30})& 0& 0& -({\alpha }_h{\overline{y}}_{20}+{\beta }_h{\overline{y}}_{21})& 0\\ 0& -({\alpha }_m{\overline{y}}_{20}+3{\beta }_m{\overline{y}}_{30})& d_3& 0& 0& 0& -({\alpha }_h{\overline{y}}_{30}+{\beta }_h{\overline{y}}_{31})\\ 0& 0& 0& d_4& -(3{\alpha }_m{\overline{y}}_{01}+{\beta }_m{\overline{y}}_{11})& 0& 0\\ -({\alpha }_h{\overline{y}}_{10}+{\beta }_h{\overline{y}}_{11})& 0& 0& -(3{\alpha }_m{\overline{y}}_{01}+{\beta }_m{\overline{y}}_{11})& d_5& -2({\alpha }_m{\overline{y}}_{11}+{\beta }_m{\overline{y}}_{21})& 0\\ 0& -({\alpha }_h{\overline{y}}_{20}+{\beta }_h{\overline{y}}_{21})& 0& 0& -2({\alpha }_m{\overline{y}}_{11}+{\beta }_m{\overline{y}}_{21})& d_6& -({\alpha }_m{\overline{y}}_{21}+3{\beta }_m{\overline{y}}_{31})\\ 0& 0& -({\alpha }_h{\overline{y}}_{30}+{\beta }_h{\overline{y}}_{31})& 0& 0& -({\alpha }_m{\overline{y}}_{21}+3{\beta }_m{\overline{y}}_{31})& d_7\end{array}\right],\end{array}$$

where the elements on the diagonal are

$$\begin{array}{l}{d}_1=3{\alpha }_m{\overline{y}}_{00}+(2{\alpha }_m+{\beta }_m+{\alpha }_h){\overline{y}}_{10}+2{\beta }_m{\overline{y}}_{20}+{\beta }_h{\overline{y}}_{11},\\ d_2=2{\alpha }_m{\overline{y}}_{10}+({\alpha }_m+2{\beta }_m+{\alpha }_h){\overline{y}}_{20}+3{\beta }_m{\overline{y}}_{30}+{\beta }_h{\overline{y}}_{21},\\ d_3={\alpha }_m{\overline{y}}_{20}+(3{\beta }_m+{\alpha }_h){\overline{y}}_{30}+{\beta }_h{\overline{y}}_{31},\\ d_4={\alpha }_h{\overline{y}}_{00}+(3{\alpha }_m+{\beta }_h){\overline{y}}_{01}+{\beta }_m{\overline{y}}_{11},\\ d_5={\alpha }_h{\overline{y}}_{10}+3{\alpha }_m{\overline{y}}_{01}+(2{\alpha }_m+{\beta }_m+{\beta }_h){\overline{y}}_{11}+2{\beta }_m{\overline{y}}_{21},\\ d_6={\alpha }_h{\overline{y}}_{20}+2{\alpha }_m{\overline{y}}_{11}+({\alpha }_m+2{\beta }_m+{\beta }_h){\overline{y}}_{21}+3{\beta }_m{\overline{y}}_{31},\\ d_7={\alpha }_h{\overline{y}}_{30}+{\alpha }_m{\overline{y}}_{21}+(3{\beta }_m+{\beta }_h){\overline{y}}_{31}.\end{array}$$

As discussed, we use the equilibrium mean values of x and y in the diffusion matrices. They are

$${\overline{x}}_i=\left(\begin{array}{c}4\\ i\end{array}\right)\frac{{\alpha }_n^i{\beta }_n^{4-i}}{{({\alpha }_n+{\beta }_n)}^4}$$

and

$${\overline{y}}_{ij}=\left(\begin{array}{c}3\\ i\end{array}\right)\frac{{\alpha }_m^i{\beta }_m^{3-i}{\alpha }_h^j{\beta }_h^{1-j}}{{({\alpha }_m+{\beta }_m)}^3({\alpha }_h+{\beta }_h)}.$$

APPENDIX C: EQUILIBRIUM NOISE APPROXIMATION

1. Voltage clamp

The equilibrium noise approximation in voltage clamp can be justified using a small noise expansion [34]. Let us define the small parameter ε = 1/N and fix the membrane potential at a voltage clamp value so that α_n and β_n can be treated as constants. Assume that n can be written as a series in the small noise parameter ε:

$$n(t)=n_0(t)+\epsilon n_1(t)+{\epsilon }^2{n}_2(t)\cdots .$$

If we plug the small noise expansion into the subunit SDE for n in Eq. (8) and collect terms of O(1), we find

$$\frac{{dn}_0}{dt}={\alpha }_n(1-n_0)-{\beta }_n{n}_0,$$ (C1)

and for terms of O(ε):

$$\frac{{dn}_1}{dt}=-{\alpha }_n{n}_1-{\beta }_n{n}_1+\sqrt{{\alpha }_n(1-n_0)+{\beta }_n{n}_0}\xi (t).$$ (C2)

Equation (C1) shows that n₀ satisfies a deterministic equation that does not depend on stochastic fluctuations in n. In the context of analyzing the stationary distribution of n therefore we are justified in replacing n₀ with its equilibrium value $\frac{{\alpha }_n}{{\alpha }_n+{\beta }_n}$. If we make this substitution for n₀ in the equation for n₁ [Eq. (C2)] and then form the sum n₀ + εn₁, it is straightforward to arrive at the OU process in Eq. (16). The equilibrium noise approximation is therefore the O(N⁻¹) approximation of the long-time behavior of n(t) in voltage clamp. The same argument applies for the m and h subunits as well as for the multivariate SDE that defines the channel SDE model.

2. Time-dependent voltage

Fox and Lu suggested applying this approximation in all cases, not just voltage clamp [23,24], and we have used the approximation to simplify the numerical methods for solving the channel SDE model. When V is not in voltage clamp, it evolves naturally and complicates the small noise expansion because it can introduce additional stochastic fluctuations into the gating variables and the voltage-dependent functions transition rate functions. Fox argued that the approximation would be accurate if the relaxation of V to its equilibrium value occurred on a much slower time scale than the relaxation of the gating variables (for the case of the subunit SDE model) [24]. Unfortunately, this separation of time scales does not appear to be a generic feature of HH models. Nevertheless, as shown in Figs. 4 and 5, the equilibrium noise approximation appears to be sufficiently accurate to reproduce spiking statistics to a high degree of accuracy.

APPENDIX D: QUASISTATIONARY MODELS

In the Discussion (Sec. V), we introduced two models that we discuss in greater detail here. We refer to both models as quasistationary approximations because they rely on results from our analysis of the stationary statistics of open channels in Sec. III. In the first model, we were motivated by [26] to attempt to improve the accuracy of the subunit SDE model by modifying the noise terms in the gating equations. We have shown that the stationary variances for the proportion of open channels in the subunit SDE models does not match those of the MC model. To correct for this discrepancy, we can redefine ${\sigma }_n^2(V)$ in Eq. (8) to guarantee that the stationary variance of n⁴ matches the stationary variance of the proportion of open K⁺channels under the MC models. The problem is simplified if we invoke the equilibrium noise approximation and use the facts that Var[n⁴] = E[n⁸] − E[n⁴]² and that these higher moments of the stationary distribution of n are known since in voltage clamp n is an OU (Gaussian) process with mean ${\mu }_{\text{sub}}=\frac{{\alpha }_n}{{\alpha }_n+{\beta }_n}$ and variance ${\sigma }_n^2(V){\tau }_n(V)/2$. The final step is to set Var[n⁴] = Var[f_chan] and solve for σ_n(V). The exact solution would require inverting a nonlinear equation, but if we neglect terms that are of higher order than O(N⁻²), we find σ_n(V) by finding the roots of $168{\mu }_n^4{\sigma }_n^4+16{\mu }_n^6{\sigma }_n^2-[{\mu }_n^4(1-{\mu }_n^4)]/N$, which is quadratic in ${\sigma }_n^2$. The same approach was also used to derive a new expression for σ_m so that this model also had the same stationary variance for the Na⁺channel. The formula for σ_h was left unchanged.

As explained in the Discussion, this first approach did not provide a satisfactory approximation to the MC model, so we formulated a second quasistationary approximation. We constructed this second model so that it and the MC model would have the same autocorrelation functions for the proportion of open channels and the same means and variances in voltage clamp. The mathematical structure of this model is somewhat unusual in that the conductance is defined as the sum of a deterministic part (given by the HH equations for m, h, and n) and a colored Gaussian processes that is defined by the autocovariance function for the proportion of open channels in the MC model. As usual, we illustrate our approach with the K⁺ channel. The conductance is defined to be

$$g_{\text{K}}={\overline{g}}_{\text{K}}(n^4+{\sigma }_{\text{chan}}\eta (t)),$$ (D1)

where n is the classical (deterministic) gating variable satisfying an ordinary differential equation of the form of Eq. (3) and η(t) is a stochastic process. To define η(t), first note that the channel SDE model provided a quantitatively accurate approximation of the MC model, so it is reasonable to describe the stationary conductance as a Gaussian process. Second, recall from Eq. (22) that the autocorrelation function for the proportion of open K⁺ channels has four distinct time scales (the first four multiples of 1/τ_n). Taken together, these facts lead us to model the K⁺ conductance as a non-Markovian Gaussian process. The representation theory of Gaussian processes furnishes a systematic method for constructing the stochastic process η(t) based on the autocorrelation function for the K⁺ channel [49]. In particular, this theory guarantees that η(t) can be written in terms of a stochastic (Wiener) integral of the form

$$\eta (t)={\int }_0^t\sum _{i=1}^4{a}_i(V)e^{-i(t-u)/{\tau }_n(V)}dW(u).$$

The coefficients a_i are voltage dependent and are computed by solving the system of nonlinear equations:

$$\begin{array}{l}{\tau }_n(V)a_1(V)\sum _{i=1}^4\frac{a_i(V)}{i+1}=4{\alpha }_n{(V)}^3\mathrm{\Gamma },\\ {\tau }_n(V)a_2(V)\sum _{i=1}^4\frac{a_i(V)}{i+2}=6{\alpha }_n{(V)}^2{\beta }_n(V)\mathrm{\Gamma },\\ {\tau }_n(V)a_3(V)\sum _{i=1}^4\frac{a_i(V)}{i+3}=4{\alpha }_n(V){\beta }_n{(V)}^2\mathrm{\Gamma },\\ {\tau }_n(V)a_4(V)\sum _{i=1}^4\frac{a_i(V)}{i+4}={\beta }_n{(V)}^3\mathrm{\Gamma },\end{array}$$

where $\mathrm{\Gamma }=\frac{{\beta }_n(V)}{{[{\alpha }_n(V)+{\beta }_n(V)]}^4-{\alpha }_n{(V)}^4}$. In practice, the system of non-linear equations defining a_i (V) must be solved numerically. We used the Minimize command in Maple (Waterloo Maple Inc., Version 13) to generate a data table of values of a_i (V) that solved these equations for voltage values ranging from −20 to 120 mV in increments of 0.01 mV. The procedure for constructing the non-Markovian Gaussian process for the Na⁺ conductance is similar but slightly more complicated because there are seven time scales in the autocorrelation function. We omit these details here and direct the interested reader to computer code available in the ModelDB repository [35].

To numerically integrate this quasistationary model, we used a forward Euler method to update the value of V and n in each time step, where the stochastic integral for η_t is integrated as follows:

1. Compute the voltage dependent terms τ_n, σ_n, α_n, β_n, and a_i using the value of V from the previous time step.

2. Update the terms associated with each time scale: $A_i(t+\mathrm{\Delta }t)=A_i(t)e^{-i\mathrm{\Delta }t/{\tau }_n}+a_i{\sigma }_{n}r\sqrt{\mathrm{\Delta }t}$, where i = 1,2,3,4, Δt is the time step, and r is a mean zero, unit variance Gaussian random generated on each time step.

3. Update the stochastic process: $\eta (t+\mathrm{\Delta }t)={\sum }_{i=1}^4{A}_i(t+\mathrm{\Delta }t)$.