Abstract
Joint linkage association mapping (JLAM) combines the advantages of linkage mapping and association mapping, and is a powerful tool to dissect the genetic architecture of complex traits. The main goal of this study was to use a cross-validation strategy, resample model averaging and empirical data analyses to compare seven different biometrical models for JLAM with regard to the correction for population structure and the quantitative trait loci (QTL) detection power. Three linear models and four linear mixed models with different approaches to control for population stratification were evaluated. Models A, B and C were linear models with either cofactors (Model-A), or cofactors and a population effect (Model-B), or a model in which the cofactors and the single-nucleotide polymorphism effect were modeled as nested within population (Model-C). The mixed models, D, E, F and G, included a random population effect (Model-D), or a random population effect with defined variance structure (Model-E), a kinship matrix defining the degree of relatedness among the genotypes (Model-F), or a kinship matrix and principal coordinates (Model-G). The tested models were conceptually different and were also found to differ in terms of power to detect QTL. Model-B with the cofactors and a population effect, effectively controlled population structure and possessed a high predictive power. The varying allele substitution effects in different populations suggest as a promising strategy for JLAM to use Model-B for the detection of QTL and then to estimate their effects by applying Model-C.
Keywords: joint linkage association mapping, model comparison, QTL detection
Introduction
Joint linkage association mapping (JLAM) holds great potential for the evaluation of quantitative traits, as it potentially combines the high power of linkage mapping with the good mapping resolution of association mapping (Yu et al., 2008; Lu et al., 2010). The combination of the advantages of both approaches in JLAM is especially promising in applied plant breeding, where many segregating bi-parental populations are routinely generated in the course of the breeding program. As the costs for genotyping are constantly decreasing, it is appealing to further exploit the collected phenotypic data for quantitative trait loci (QTL) detection by combining it with genotypic data. In addition, JLAM in these populations will identify QTL, which are of direct relevance for the improvement of crop species (Reif et al., 2010).
The mapping resolution of JLAM is determined by the extent of linkage disequilibrium (LD) in the population of the parents used to generate the segregating populations (Myles et al., 2009). LD is affected by different forces such as recombination, selection, migration and mutation (Flint-Garcia et al., 2003). It is, therefore, population-specific and must be examined empirically for the data set under consideration (Rafalski, 2002). In addition, LD in the JLAM population affects the QTL detection power and is influenced by the mating design (Verhoeven et al., 2006).
The bi-parental populations of a JLAM data set result in more balanced allele frequencies compared with association mapping populations, thus enhancing QTL detection power while reducing the potentially confounding effects of population structure (McMullen et al., 2009). Although the balanced experimental design should render the correction for population stratification in JLAM unnecessary, spurious associations may arise if the trait is associated with the population structure. In contrast to JLAM populations designed for a scientific purpose, however, JLAM populations from applied breeding are more unbalanced with regard to population size (Reif et al., 2010). This raises the question if and how correction for population stratification should be performed.
Several statistical approaches for JLAM have been suggested based on linear (Yu et al., 2008; Liu et al., 2011) or linear mixed models (Stich et al., 2008). In addition, the QIPDT approach has been suggested (Stich et al., 2006), but the relationship between parents can better be exploited by using linear mixed models including a kinship matrix. In analogy to composite interval mapping, Yu et al. (2008) used cofactors to correct for the genetic background, and compared this approach in a simulation study with a model including a general population effect. A lower QTL detection power was observed for the latter model, indicating that incorporating cofactors might be advantageous as they control both population structure and genetic background within populations. Another conceptually different approach is to model the marker effect as nested within population (Liu et al., 2011). These three approaches based on linear models have been compared in a recent analysis based on experimental data and were shown to result in different QTL being detected (Reif et al., 2010; Liu et al., 2011). Although linear mixed models have been used to analyze JLAM studies in elite breeding populations (for example, Stich et al., 2008), they have to our knowledge not yet been compared with other biometrical models for JLAM.
The availability of these different statistical methods for the analysis of JLAM data sets has stimulated us to conduct a comparison study and evaluate the advantages and limitations of the different approaches. To this end, we combined simulation studies, a cross-validation approach, resample model averaging (RMA) and empirical data analyses. In particular, the objectives of our study were to (1) analyze the population structure and the extent of LD in the population underlying this study; (2) assess the LD used by different models; (3) compare three linear and four linear mixed models empirically with regard to the number of detected QTL and the proportion of genotypic variance explained by these QTL, and to evaluate the number of overlapping and model-specific QTL; (4) implement a cross-validation approach to assess the predictive power of each of the models, and an RMA approach to evaluate their precision and (5) elaborate the advantages and limitations of the evaluated models and their applicability for JLAM.
Materials and methods
Plant materials and field experiments
This study was based on 441 diploid elite sugar beet (Beta vulgaris L.) inbred lines, which were randomly derived from 12 crosses between 16 parental inbred lines (Supplementary Table 1). Testcross progenies were produced by crossing the genotypes to a single-cross hybrid as tester. All material used in this study was provided by the breeding company Strube GmbH & Co. KG (Söllingen, Germany).
The 441 genotypes were evaluated in routine plant breeding trials, with two replicates at 7 or 8 locations per genotype in 2009. The evaluated traits were beet yield (BY, mg ha−1), sugar yield (SY, mg ha−1), sugar content (SC, %), potassium content-(K, decamol mg−1), sodium content (Na, hectamol mg−1) and α-amino nitrogen content (N, hectamol mg−1) (Supplementary Figure 1).
Phenotypic data analyses
Lattice analyses of variance (Cochran and Cox, 1957) were performed for all traits for each environment. Adjusted entry means and corresponding error mean squares were used in the combined analyses based on the linear mixed model: y∼Environment+Genotype+Genotype × Environment. Variance components were determined by the restricted maximum likelihood method by using PROC MIXED of the software package SAS by assuming random genotypic and environmental effects (SAS Institute, 2008). A Wald F-test (Wald, 1943) was used to test whether variances were significantly greater than 0. Heritability (h2) on an entry-mean basis was estimated as the ratio of genotypic to phenotypic variance according to Melchinger et al. (1998). Furthermore, genotypes were regarded as fixed effects and best linear unbiased estimates were determined for all genotypes and traits. Simple correlation coefficients (r) were calculated among all traits based on the best linear unbiased estimates of the 441 testcrosses.
Molecular data analyses
The 441 genotypes were fingerprinted by following standard protocols using 183 single-nucleotide polymorphism (SNP) markers. These markers were randomly distributed across the sugar beet genome, with an average marker distance of 3.1 cM and a maximum gap of 33.0 cM between adjacent markers (Supplementary Figure 2). Map positions of all markers were based on the linkage map of Strube GmbH & Co. KG with a total map length of 555 cM (unpublished data).
Associations among the 441 genotypes were analyzed by applying principal coordinate analysis (PCoA) (Gower, 1966) based on the modified Rogers' distances of the individuals (Wright, 1978). The extent of LD was assessed among the 16 genotyped parents by the LD measure r2 (Weir, 1996). Decay of LD with genetic distance was evaluated by non-linear regression by following Remington et al. (2001). The 95th percentile of r2 estimates between unlinked markers was taken as a population-specific critical value for r2 owing to genetic linkage. LD computations and PCoA were performed with the software package Plabsoft (Maurer et al., 2008).
Joint linkage association mapping
For the JLAM approaches, an additive genetic model was chosen for the testcross progenies as described by Utz et al. (2000). A two-step approach was applied in which the best linear unbiased estimates across locations were used for the JLAM analysis. We compared seven different statistical models for JLAM, three multiple-regression approaches and four mixed-model approaches (Supplementary Table 2). For the regression approaches, we applied a two-step procedure for QTL detection. In a first step, cofactors were selected by stepwise multiple linear regression based on the Schwarz Bayesian Criterion (Schwarz, 1978). In the second step, we calculated a P-value for the F-test by using a full model (including SNP effect) versus a reduced model (without SNP effect). Model-A contained the selected cofactors and the SNP under consideration. Model-B was identical to Model-A, but in addition included an effect for the segregating population. Model-C also included the selected cofactors and a population effect, but the cofactors and the SNP effect were modeled as nested within population. Cofactor selection was performed by using Proc GLMSELECT implemented in the statistical software SAS (SAS Institute, 2008).
Models D, E, F and G were based on linear mixed models. Model-D included a population effect as a random effect and the SNP effect. In Model-E this population effect was modeled as a random effect and the variance of this random population effect was assumed to be Pσ2Pop, where P was a 12 × 12 matrix with similarity coefficients that define the degree of genetic covariance between all 12 populations. Model-F was similar to the K-model applied in association mapping (Reif et al., 2011a, 2011b; Würschum et al., 2011) and models a random genotypic effect. The variance of this effect was assumed to be Var(g)=Kσ2g, where σ2g refers to the genetic variance estimated by restricted maximum likelihood and K was a 441 × 441 matrix of kinship coefficients that define the degree of genetic covariance between all pairs of entries. We followed the suggestion of Bernardo (1993) and calculated the kinship coefficient Kij between inbreds i and j on the basis of marker data as Kij=1+(Sij−1)/(1−Tij), where Sij is the proportion of marker loci with shared variants between inbreds i and j, and Tij is the average probability that a variant from one parent of inbred i and a variant from one parent of inbred j are alike in state, given that they are not identical by descent. The coefficient Tij was estimated separately for each trait by using a restricted maximum likelihood method (Supplementary Figure 3) (Reif et al., 2011a). In case negative kinship values between inbreds were obtained, these were set to 0. Model-G is comparable to the QK model (Yu et al., 2006) and included the first 10 principal coordinates (Price et al., 2006), and the K-matrix. All mixed-model calculations were performed by using the software ASReml 2.0 (Gilmour et al., 2006).
For the detection of main-effect QTL, a genome-wide scan for marker–trait associations was performed. We detected significant main effects with P<0.05 and controlled for multiple testing by applying the Bonferroni–Holm procedure (Holm, 1979). Matrix of pairwise percentage of common QTL among models was calculated. The resulting similarity matrix was used for PCoA for model comparison. The total proportion of genotypic variance (pG) explained by the detected QTL was calculated by fitting all QTL simultaneously in a linear model to obtain R2adj. The ratio pG=R2adj/h2 yielded the proportion of genotypic variance (Utz et al., 2000). For a fair comparison of the biometrical models, the same approach was applied for all seven models.
To estimate the explained genotypic variance among and within populations, the following strategy was adopted for all seven biometrical models. The model y∼Population+QTL(Population) was applied, where y represents the best linear unbiased estimates of the 441 individuals and the QTL detected with the different models were modeled as nested within population. The sum of the SSQTLs (Population) divided by SSTotal yielded the within-population variance explained by the detected QTL. SSPopulation divided by SSTotal represents the among-population variance. To assess how much of that among-population variance was explained by the detected QTL, each individual was assessed its population mean. The regression of these assessed population means of each of the 441 individuals on the detected QTL yielded the proportion of the among-population variance that could be explained by the detected QTL.
Cross-validation approach and RMA
To assess the predictive power of the seven models a cross-validation approach was established. We used a fivefold cross-validation in which 80% of the lines from each population were used as the estimation set (ES) in which QTL detection was performed. The remaining 20% of the lines represented the test set (TS), which was used for validation. For validation the QTL mapping results from the ES were used to predict the genotypic value of line j in TS QTS.ESj according to QTS.ESj=XTSj βES, where XTSj is the vector of marker informations of line j at the QTL positions, and βES is the vector of the genetic effects of these QTL estimated as partial regression coefficients from a simultaneous fit in the ES (Utz et al., 2000). The proportion of genotypic variance explained by the QTL in the TS (pG−TS) was calculated from the adjusted squared correlation coefficient, R2adj, between the phenotypic values observed for the lines in the TS and the predicted genotypic values QTS.ESj on the basis of the results derived from the ES, divided by the heritability of the trait. The presented results are the average values from 1000 cross-validation runs. The relative bias in the proportion of explained genotypic variance was calculated as the reduction in pG from the estimation set (pG−ES) to the test set (pG−TS) as 1−(pG−TS/pG−ES).
Our RMA approach was similar to the subagging (80%) described by Valdar et al. (2009). We used re-sampling without replacement as described for the cross-validation. In contrast to Valdar et al. (2009), we did not use forward selection to select the multiple-QTL model, but used QTL detection by the seven biometrical models described above.
Results
The genotypic variances estimated in the population of 441 sugar beet lines were significantly larger than 0 (P<0.01) for all six traits (Table 1). Heritability was high and ranged from 0.69 for sugar yield to 0.85 for potassium content. Absolute values of phenotypic correlations among the six traits were minimum between beet yield and potassium content (0.01), and maximum between beet yield and sugar yield (0.89) (Supplementary Figure 4).
Table 1. Mean, minimum and maximum testcross performance of 441 sugar beet genotypes from 12 populations; variances of the testcrosses for genotypes (σ2G), genotype × location (σ2G × L), residuals (σ2e) and heritabilities (h2) for the six traits.
| Parameter | BY | SY | SC | K | Na | n |
|---|---|---|---|---|---|---|
| Mean | 76.99 | 14.11 | 18.35 | 43.46 | 34.05 | 95.75 |
| Min | 63.13 | 10.97 | 17.26 | 38.95 | 25.16 | 72.86 |
| Max | 84.49 | 15.22 | 19.14 | 50.04 | 60.21 | 168.77 |
| σ2G | 5.57** | 0.12** | 0.07** | 1.80** | 11.45** | 72.30** |
| σ2GxL | 7.32** | 0.23** | 0.07** | 1.44** | 14.89** | 70.08** |
| σ2e | 11.03 | 0.41 | 0.14 | 2.42 | 25.68 | 105.34 |
| h2 | 0.78 | 0.69 | 0.80 | 0.85 | 0.77 | 0.83 |
Abbreviations: BY, beet yield; K, potassium content; N, α-amino-nitrogen content; Na, sodium content; SC, sugar content; SY, sugar yield.
**Indicates significance at P<0.01.
The 12 populations were of varying size, as is typical for populations from breeding programmes, and in the PCoA showed the expected pattern, in that progenies from one population clustered together (Supplementary Figure 5). None of the populations was clearly separated from the others, and the genetic similarity between the 12 populations was 0.69, whereas the average genetic similarity within the populations was 0.83 (Supplementary Table 1). The first two principal coordinates together explained 29.8% of the total variation.
LD decayed with genetic map distance and met the population-specific threshold for LD because of linkage within 10 cM (Supplementary Figure 6). The average r2 between adjacent markers was 0.12. Our simulation study revealed high LD stretching over longer distances within a bi-parental population and lower LD in the diallel (DIA) and single round robin (SRR) populations (Supplementary Figure 7). This was true for both simulation scenarios, the base population in linkage equilibrium or in LD. The extent of LD between unlinked markers was lower for the DIA design than for the SRR design.
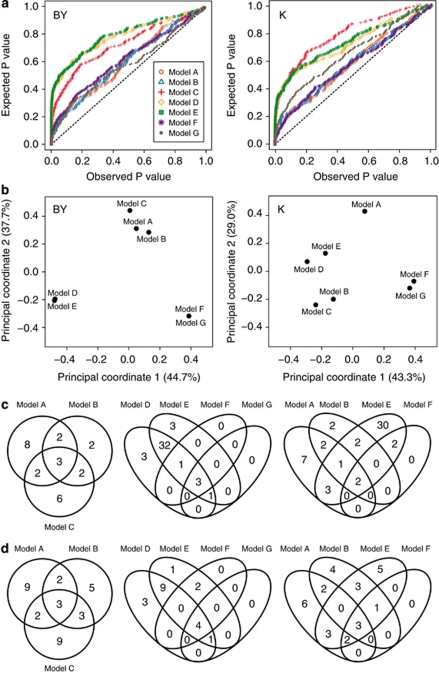
We performed a full-genome scan for main-effect QTL with all seven models. The plot of observed versus expected P-values of the seven models revealed that models A, B, F and G followed the diagonal line more closely than models C, D and E (Figure 1a). For all traits there was considerable variation between the models with regard to the number of detected QTL and the proportion of genotypic variance explained by these QTL (Table 2). Models D and E generally detected a much higher number of QTL than the other models, without substantially increasing the proportion of explained genotypic variance in the final fit. Models F and G detected the lowest number of QTL, but these still explained a rather high proportion of genotypic variance. The highest proportion of explained genotypic variance was always found for Model-A.
Figure 1.
(a) Cumulative density function plot of all seven models for beet yield (BY) and potassium content (K). (b–d) Comparison of the main-effect QTL detected for the six traits using the linear models A, B and C, and the mixed linear models D, E, F and G. (b) Principal coordinate plot based on pairwise comparisons between the models with regard to model-specific detected QTL. (c, d) Venn diagrams for (c) beet yield and (d) potassium content showing overlapping and model-specific QTL.
Table 2. Comparison of the number of detected main-effect QTL (n) and the explained genotypic variance (pG in %) of these QTL for the seven statistical models.
| BY | SY | SC | K | Na | n | |
|---|---|---|---|---|---|---|
| Model-A | ||||||
| n | 15 | 10 | 17 | 16 | 15 | 8 |
| pG | 69.9 | 81.0 | 89.3 | 75.3 | 77.9 | 88.4 |
| Model-B | ||||||
| n | 9 | 10 | 4 | 13 | 15 | 7 |
| pG | 46.5 | 69.9 | 37.4 | 50.6 | 74.0 | 83.6 |
| Model-C | ||||||
| n | 13 | 11 | 6 | 17 | 17 | 7 |
| pG | 50.5 | 63.3 | 46.8 | 59.0 | 52.6 | 78.4 |
| Model-D | ||||||
| n | 40 | 33 | 26 | 17 | 31 | 14 |
| pG | 65.2 | 76.2 | 75.0 | 60.8 | 65.8 | 86.8 |
| Model-E | ||||||
| n | 40 | 34 | 28 | 18 | 29 | 15 |
| pG | 67.5 | 78.3 | 79.3 | 63.4 | 68.2 | 87.2 |
| Model-F | ||||||
| n | 4 | 6 | 4 | 6 | 8 | 5 |
| pG | 37.2 | 58.8 | 36.0 | 49.8 | 48.4 | 73.8 |
| Model-G | ||||||
| n | 4 | 5 | 6 | 5 | 7 | 7 |
| pG | 34.4 | 49.0 | 34.4 | 48.9 | 30.9 | 73.3 |
Abbreviations: BY, beet yield; K, potassium content; N, α-amino-nitrogen content; Na, sodium content; QTL, quantitative trait locus; SC, sugar content; SY, sugar yield.
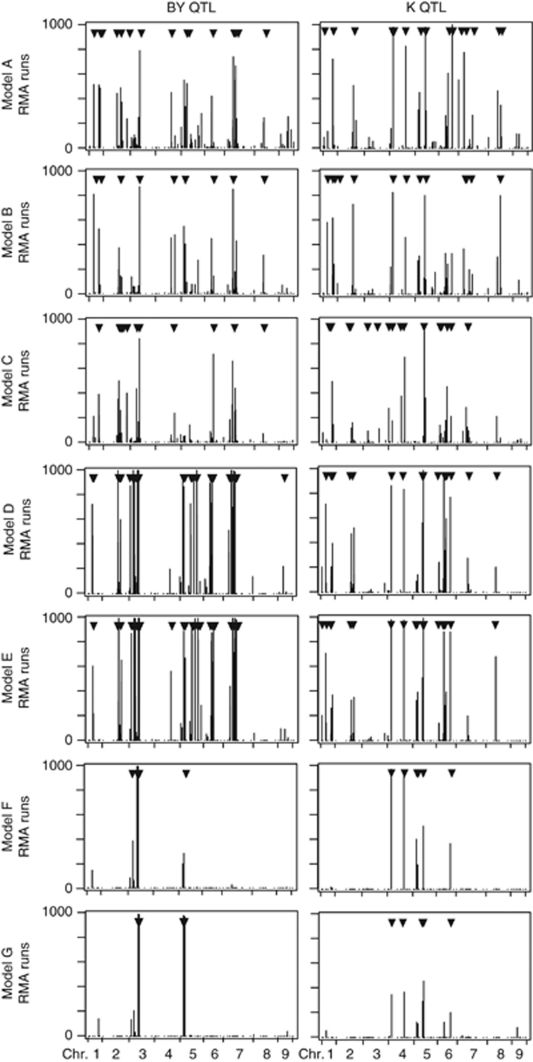
We assessed the predictive power of the seven models in a cross- validation approach (Table 3). The highest cross-validated proportion of genotypic variance was again observed for Model-A. The relative bias in the proportion of explained genotypic variance in the estimation set and in the test set ranged from 3.4 to 39.7% for beet yield and from 17.1 to 42.9% for potassium content. The only observable trend was that Model-C always showed the strongest bias. The RMA approach revealed that models D and E showed the broadest peaks, whereas the mixed models F and G had the narrowest and best defined peaks (Figure 2).
Table 3. Assessment of the predictive power of the seven biometrical models by fivefold cross-validation with 1000 runs.
| Model | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| BY | |||||||
| QTL | 13.7 | 9.8 | 9.4 | 31.9 | 31.5 | 3.3 | 4.6 |
| pG−ES | 73.1 | 52.1 | 59.0 | 64.9 | 66.1 | 35.5 | 35.0 |
| pG−TS | 49.9 | 39.6 | 35.6 | 51.9 | 50.8 | 31.8 | 33.8 |
| Bias | 31.7 | 24.0 | 39.7 | 20.0 | 23.1 | 10.4 | 3.4 |
| K | |||||||
| QTL | 12.4 | 10.6 | 7.2 | 11.1 | 11.3 | 3.3 | 2.2 |
| pG−ES | 70.8 | 52.6 | 26.6 | 52.6 | 58.0 | 36.3 | 24.2 |
| pG−TS | 57.5 | 41.3 | 15.2 | 43.1 | 48.1 | 29.4 | 15.8 |
| Bias | 18.8 | 21.5 | 42.9 | 18.1 | 17.1 | 19.0 | 34.7 |
QTL, average number of main-effect QTL detected in the estimation set; pG−ES, the proportion of explained genotypic variance (%) of these QTL in the estimation set and in the test set (pG−TS), and the relative bias in the proportion of explained genotypic variance for beet yield (BY) and potassium content (K).
Figure 2.
QTL frequency distributions for beet yield (BY) and potassium content (K) derived from 1000 RMA runs for all seven biometrical models. The positions of the QTL detected using the full data set are indicated by arrowheads.
The comparison of the detected QTL from the seven models revealed that there were both overlapping and model-specific QTL. For example, the beet yield (BY) QTL on chromosome-3 or the potassium content QTL on chromosome-5 were consistently detected with all seven models (Supplementary Figure 8). The Venn diagrams showed that for both the linear models A, B and C, and for the mixed models D, E, F and G, there were a few overlapping QTL, but the majority of the QTL were detected only by one or two models (Figures 1c and d). The same was found for the four-way Venn diagram comparing models A, B, E and F, which only have a small proportion of the totally detected QTL in common. The PCoA of the seven models based on pairwise comparisons between the models with regard to model-specific detected QTL confirmed this picture and showed that the examined models were different and have very distinct properties (Figure 1b). This was also supported by the correlation plot of the P-values from the seven models (Supplementary Figure 9).
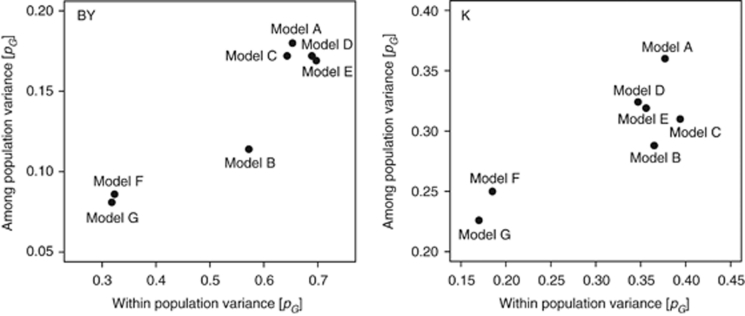
The QTL detected with the seven models explained different proportions of among-population and within-population variance (Figure 3). Model-B QTL explained a high proportion of within-population variance and only little among-population variance, and the ratio of within to among-population variance was highest for Model-B for both beet yield and potassium content.
Figure 3.
Proportion of genotypic variance explained by the detected QTL of the variance among populations and within populations for the seven models for beet yield (BY) and potassium content (K).
Discussion
Properties of the JLAM population
The power of QTL detection in JLAM is determined by different factors, including the population size, the population structure, the mating design, the extent of LD in the parental population, as well as the genetic architecture and the heritability of the trait under consideration (Yu et al., 2008). The present study was based on experimental data of 441 testcross progenies from 12 segregating populations, and a population structure typical for JLAM populations appeared to be present in this population. The good quality of the phenotypic data is reflected by the high heritabilities for all traits (Table 1). For the model comparison, we focused on beet yield (BY) and potassium content (K) as both have a high heritability, represent a yield and a quality trait, and are not correlated (Supplementary Figure 4).
Mapping resolution is determined by the LD structure in the parental population of 16 parents (Yu and Buckler, 2006). LD decayed with genetic map distance, and the non-linear regression of LD and map distance intersected the population-specific threshold for LD owing to linkage at approximately 10 cM (Supplementary Figure 6). This is comparable with a recent JLAM study in sugar beet using the opposite heterotic pool of the same breeding programme (Reif et al., 2010). The average map distance of 3 cM and the average r2 between adjacent markers of 0.1 likely enable the detection of QTL with large effects, whereas medium- and small-effect QTL may escape detection with the applied marker density. In summary, the population parameters, including the extent of LD, represent a good data set for the comparison of different biometrical models for JLAM in unbalanced data sets such as breeding populations.
LD used by different JLAM models and consequences on the power of QTL detection
QTL detection power and mapping resolution in JLAM are based on the LD exploited by the biometrical model. The fundamental difference between the applied biometrical models is that only the nested model, Model-C, exploits fully the LD within the segregating populations and is not affected by the historical LD present in the parental population (Supplementary Figures 7b and f). Historical LD in the parental population will in most instances lead to a lower extent of LD in the global JLAM population as compared with single segregating populations. Consequently, Model-C counterbalances the decrease in QTL detection power caused by the higher significance threshold owing to the higher number of parameters involved in the test as compared with the other models (Jansen et al., 2003) with full exploitation of LD within populations. This, however, is achieved at the expense of a reduction in the mapping resolution owing to the large linkage blocks within single segregating populations. It should be noted that the size of the linkage blocks within populations depends on the type of the population, that is, on the number of meioses the population went through. Furthermore, the exclusive exploitation of LD within segregating populations by Model-C can be regarded as an advantage as it allows avoiding LD generated by the mating design. This is especially of interest for highly unbalanced mating designs, which often occur in breeding programmes.
All tested biometrical models, except Model-C, use both the LD within populations but also the historical LD, and thus potentially enable a much higher mapping resolution (Supplementary Figure 7). It should be noted, however, that even in the case of linkage equilibrium in the base population, LD between the JLAM parents will be generated. This follows from population genetics theory and approximates 1/n, where n is the number of sampled parental lines (Weir and Hill, 1980). For a base population, which is already in LD, this is increased further depending on the LD in the base population (Supplementary Figure 7). It thus follows, that designs with a higher n, that is, more parental lines, allow a higher mapping resolution.
Apart from the LD generated by the sampling of the parents, LD will also inevitably arise in designs with multiple segregating populations owing to the mating design (Verhoeven et al., 2006). Within segregating populations alleles at unlinked loci will be in linkage equilibrium, but they will be in LD across populations. This can create a population structure and thus an inter-chromosomal LD that was lower in the balanced DIA design than in the SRR design (Supplementary Figure 7). Verhoeven et al. (2006), therefore, concluded that it is essential to account for population structure in the biometrical model.
Correction for population structure and false-positive QTL
We compared three linear and four linear mixed models, and plotted the observed versus the expected P-values (Figure 1a). Under the assumption that none of the markers are associated with the trait, the P-values are expected to show an equal distribution and to follow the diagonal in the plot of observed versus expected P-values. For real data sets, this distribution is expected to deviate from the diagonal, depending on the genetic architecture of the trait. True QTL will cause a bulge at the left side of the plot. As the true genetic architecture is not known, the true distribution of P-values also cannot be predicted. Strong bulges, however, may indicate an inflated false-positive rate and this plot may thus serve as a criterion for model selection.
The plot of observed versus expected P-values revealed that for models A, B, F and G, the distribution followed the diagonal more closely, which indicates that they might control the background better than the other three models, resulting in a reduced probability to detect false-positive QTL with these models. The population effect in models D and E apparently does not constitute a sufficient control for population structure. Model-B, which also includes a population effect, shows a more stringent control of the genetic background, indicating the power of cofactors as a mean to control for population structure. Importantly, cofactors not only correct for population stratification, but also for genetic background noise, thereby increasing QTL detection power (Jansen and Stam, 1994; Zeng, 1994). The mixed models including the kinship matrix (models F and G) also closely followed the diagonal in the plot, which indicates that the kinship matrix controlled the underlying population stratification. Surprisingly, the nested model, which is expected to be rather conservative, also showed a P-value distribution far off the expected diagonal. A possible explanation for this is the selection of cofactors, which was performed nested within populations, but the same set of selected cofactors was used in each of the populations. Thus, the background is controlled efficiently in some populations in which many of the selected cofactors are segregating and in which they have a strong effect, but in populations with only few segregating cofactors or in which the cofactors have only small effects owing to the genetic background in this population (Supplementary Table 4), the P-values tend to be lower owing to a reduced correction.
Comparison of the biometrical models
Previously, different biometrical models for JLAM were compared based on simulation data (Yu et al., 2008). Simulation studies, however, face the problem that the underlying assumptions do not necessarily reflect reality, such that the applicability of the results to experimental data is not always given. We therefore based our comparison study on experimental data and evaluated the models with regard to the number of detected QTL and the proportion of genotypic variance explained by these QTL. In addition, we implemented a cross-validation approach to assess the predictive power of the seven biometrical models.
The model with the nested marker effect, Model-C, is the only tested model, which assumes population-specific QTL effects. In terms of the number of detected QTL and the proportion of genotypic variance explained by these QTL, Model-C was most comparable to Model-B. This was further supported by the PCoA of the seven models (Figure 1b). For JLAM data sets with only small populations, the nested Model-C can probably only detect QTL with large or medium effect size, and is then expected to perform worse than Model-A or Model-B.
The second category of models assumes uniform QTL effects across all populations. We found that models D and E detected many QTL (Table 2), but the proportion of genotypic variance was not increased compared with the other models. This indicates an insufficient control for co-linearity with these two models (Supplementary Figure 8), and considering the distribution of observed versus expected P-values, may also reflect an enhanced false-positive rate.
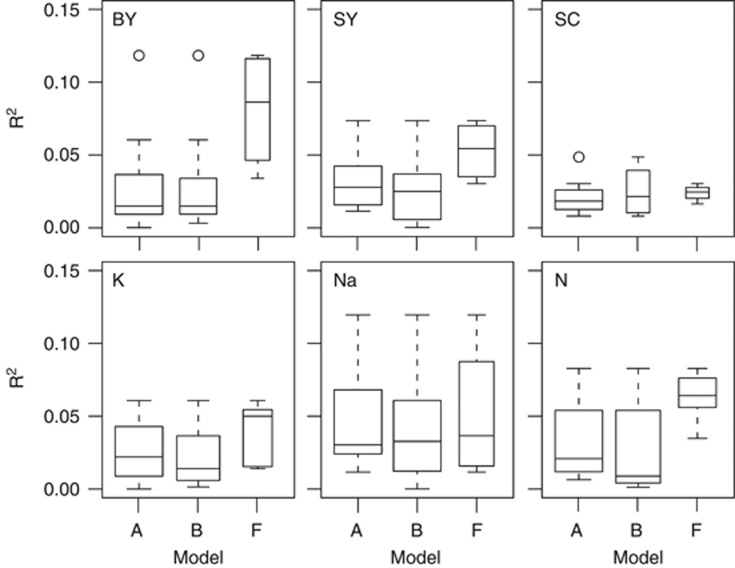
The mixed models including the kinship matrix, models F and G, were very similar and detected the lowest number of QTL for all traits, but these still explained a rather high proportion of genotypic variance. The low number of detected QTL with these models indicates that the kinship matrix sufficiently controlled for population stratification, but may not be an adequate tool to control the within-population background noise. This inappropriate control of background noise within populations may be the reason for the reduced QTL detection power compared with models incorporating cofactors. This is supported by the observation that Model-F appeared to detect more QTL with a strong effect, whereas some of the medium and small effect size QTL that were detected with models A and B escaped detection using Model-F (Figure 4).
Figure 4.
Proportion of phenotypic variance [R2] of the QTL detected using models A, B and F. The variable width of the box plots indicates the number of detected QTL for the respective model.
Model-A generally detected more QTL than Model-B, which are likely QTL due to exploitation of variance among populations (Figure 3; Liu et al., 2011). This corroborates findings of simulation studies (Yu et al., 2008) reporting that QTL detection power was higher for a model including only cofactors (Model-A) compared with a model, which in addition included a population effect (Model-B). The adjusted R2 values of the cofactors from Model-A and of the cofactors plus population effect for Model-B were very similar for all traits (Supplementary Table 3). The addition of the population effect to the cofactors from Model-A did not increase the adjusted R2 values, indicating that the cofactors selected for Model-A also cover the variance among populations. In accordance with published simulation studies (Yu et al., 2008), we observed that Model-A appeared to possess a higher power than Model-B for some traits, whereas for other traits, that is, sodium content and α-amino nitrogen content, models A and Model B were comparable (Table 2). The difference between Model-A and Model-B with regard to the explained genotypic variance was much more pronounced for beet yield, sugar content and potassium content than for the other three traits (Table 2). A recent publication indicated that this might be due to higher associations between the phenotype and the population structure for some traits, or by higher R2 values of the population effect (Liu et al., 2011). None of these parameters, however, explained the differences in this data set (Supplementary Table 3). In addition, we tested the variance among and within populations for the six traits, but observed no major trends that would explain the difference between Model-A and Model-B. The most obvious difference was in the number of detected QTL, which might have led to the observed differences in explained genotypic variance. The stronger reduction in the number of QTL and consequently in the proportion of explained genotypic variance by the inclusion of the population effect in the model for some traits could not be explained by any of the parameters estimated here. It may be due to certain QTL alleles being fixed in some populations with different population means. These QTL would mainly explain among-population variance that is absorbed by the population effect fitted in Model-B. In Model-A these loci may be selected as cofactors, which later become QTL. This is in agreement with the much higher among-population variance explained by the QTL detected with Model-A than with Model-B (Figure 3).
Some QTL were consistently detected with all seven models (Supplementary Figure 8). The comparison of overlapping QTL in Venn diagrams (Figures 1c and d) showed that for the linear models there were a few QTL detected with all three models, but many of the QTL were model-specific. This appeared less pronounced in the mixed models even though the much larger number of QTL detected with models D and E makes this comparison difficult. The PCoA of the seven models (Figure 1b) and the correlation plot of their P-values (Supplementary Figure 9) confirmed that each of the models has specific properties and, thus, the choice of the appropriate model for JLAM greatly determines the QTL detection results.
Cross-validation and RMA
The fivefold cross-validation approach applied to assess the predictive power of the seven biometrical models revealed that the average number of detected QTL in the estimation set as well as the explained proportion of genotypic variance closely followed those observed with the full data set (Table 3). The relative bias, that is, the reduction in the proportion of genotypic variance explained by the detected QTL, was around 20% for most models. This is comparable to results from QTL studies of maize for different complex traits (Schön et al., 2004) and shows the good predictive power of QTL detected in JLAM studies.
To provide a measure of precision and reliability of position estimates, we implemented a recently described frequentist measure (Valdar et al., 2009). This subagging approach resulted in QTL frequency distributions indicating the proportion of times an SNP was identified as QTL (Figure 2). Some QTL were identified in the majority of the runs and thus appear more reliable. By contrast, we also observed for most models that SNPs, which in the analysis of the full data set were identified as QTL, were only identified as QTL in a small number of runs and thus must be treated more carefully. In addition, these QTL frequency distributions may identify the most likely position of a QTL as the position with the highest peak in a region of co-linear markers. Broad peaks may point to a long-ranging LD in that region or to multiple QTL clustering in the respective chromosomal region.
Choice of a biometrical model for JLAM
The choice of the model greatly depends on the properties of the population and on basic quantitative genetic assumptions. The main conceptual decision is whether a model, which assumes a uniform SNP effect throughout all populations, should be applied or whether the model allows varying SNP effects between populations. Only the nested model, Model-C, fulfils the latter assumption. A recent study of maize has shown that the SNP allele substitution effects vary greatly among populations and even changed in sign (Buckler et al., 2009; Liu et al., 2011), which clearly suggests the need for a nested model. The nested Model-C should, however, only be applied when the populations of the data set have a certain minimum size, as otherwise the power for QTL detection with this model is expected to be low.
If a similar SNP effect can be assumed in all populations, the other six models can be applied. The conclusions derived from the analysis of this data set should also be valid for data sets with higher marker densities. Owing to the employment of LD by these models, they should even profit from a further increase in marker density as compared with Model-C. Disregarding models D and E, which appeared inappropriate to sufficiently control the genetic background, leaves four models to choose from. We observed no major difference between the models with regard to the number of populations in which the detected QTL were segregating (Supplementary Table 5). Models F and G appear to control the population stratification well but possessed a reduced QTL detection power. In addition, these two linear mixed models appeared to detect mainly large-effect QTL, which may be due to an inappropriate control of the background noise within populations. Model-A had a high predictive power across populations, but this can be mainly attributed to among-population variance, whereas the pG for within-population variance was comparable to Model-B (Figure 3). QTL with a strong component of among-population variance, however, are critical in JLAM owing to a potentially higher number of false positives. Thus, Model-B might be regarded as an option to reduce the detection of QTL based on variance among populations and mainly identify QTL of interest based on within-population variance.
Conclusions
JLAM is a powerful tool for plant genomics but the results greatly depend on the choice of the biometrical model. The main conceptual difference between the tested models is the assumption of a uniform or population-specific SNP effects. In addition, the nested Model-C uses exclusively the LD within populations and can be applied to data sets with large subpopulations. A promising strategy joining the two concepts might, therefore, be to use Model-B to detect QTL and then estimate their effects in each of the populations by applying Model-C (Supplementary Table 6). Generally, a cross-validation strategy should be applied irrespective of the biometrical model used for analysis, to obtain unbiased estimates of the QTL detection results in JLAM.
Data archiving
Data have been deposited at Dryad: doi:10.5061/dryad.tg763.
Acknowledgments
This research was conducted within the Biometric and Bioinformatic Tools for Genomics based Plant Breeding project supported by the German Federal Ministry of Education and Research (BMBF) within the framework of GABI–FUTURE initiative. We greatly appreciate the helpful comments and suggestions of three anonymous reviewers.
The authors declare no conflict of interest.
Footnotes
Supplementary Information accompanies the paper on Heredity website (http://www.nature.com/hdy)
Supplementary Material
References
- Bernardo R. Estimation of coefficient of coancestry using molecular markers in maize. Theor Appl Genet. 1993;85:1055–1062. doi: 10.1007/BF00215047. [DOI] [PubMed] [Google Scholar]
- Buckler ES, Holland JB, Bradbury PJ, Acharya CB, Brown PJ, Browne C, et al. The genetic architecture of maize flowering time. Science. 2009;325:714–718. doi: 10.1126/science.1174276. [DOI] [PubMed] [Google Scholar]
- Cochran WG, Cox GM.1957Experimental Designs2nd edn.John Wiley and Sons: New York [Google Scholar]
- Flint-Garcia SA, Thornsberry JM, Buckler ES. Structure of linkage disequilibrium in plants. Ann Rev Plant Biol. 2003;54:357–374. doi: 10.1146/annurev.arplant.54.031902.134907. [DOI] [PubMed] [Google Scholar]
- Gilmour AR, Gogel BJ, Cullis BR, Thompson R. ASReml User Guide Release 2.0. VSN International Ltd: Hemel Hempstead, UK; 2006. [Google Scholar]
- Gower JC. Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika. 1966;53:325–338. [Google Scholar]
- Holm S. A simple sequentially rejective Bonferroni test procedure. Scand J Stat. 1979;6:65–70. [Google Scholar]
- Jansen RC, Jannink JL, Beavis WD. Mapping quantitative trait loci in plant breeding populations: use of parental haplotype sharing. Crop Sci. 2003;43:829–834. [Google Scholar]
- Jansen RC, Stam P. High resolution of quantitative traits into multiple loci via interval mapping. Genetics. 1994;136:1447–1455. doi: 10.1093/genetics/136.4.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu W, Gowda M, Steinhoff J, Maurer HP, Würschum T, Longin CFH, et al. Association mapping in an elite maize breeding population. Theor Appl Genet. 2011;123:847–858. doi: 10.1007/s00122-011-1631-7. [DOI] [PubMed] [Google Scholar]
- Lu Y, Zhang S, Shah T, Xie C, Hao Z, Li X, et al. Joint linkage–linkage disequilibrium mapping is a powerful approach to detecting quantitative trait loci underlying drought tolerance in maize. Proc Natl Acad Sci USA. 2010;107:19585–19590. doi: 10.1073/pnas.1006105107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurer HP, Melchinger AE, Frisch M. Population genetic simulation and data analysis with Plabsoft. Euphytica. 2008;161:133–139. [Google Scholar]
- McMullen MD, Kresovich S, Villeda HS, Bradbury P, Li HH, Sun Q, et al. Genetic properties of the maize nested association mapping population. Science. 2009;325:737–740. doi: 10.1126/science.1174320. [DOI] [PubMed] [Google Scholar]
- Melchinger AE, Utz HF, Schön CC. Quantitative trait locus (QTL) mapping using different testers and independent population samples in maize reveals low power of QTL detection and large bias in estimates of QTL effects. Genetics. 1998;149:383–403. doi: 10.1093/genetics/149.1.383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myles S, Peiffer J, Brown PJ, Ersoz ES, Zhang Z, Costich DE, et al. Association mapping: critical considerations shift from genotyping to experimental design. Plant Cell. 2009;21:2194–2202. doi: 10.1105/tpc.109.068437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Rafalski JA. Novel genetic mapping tools in plants: SNPs and LD-based approaches. Plant Sci. 2002;162:329–333. [Google Scholar]
- Reif JC, Gowda M, Maurer HP, Korzun V, Longin CFH, Korzun V, et al. Association mapping for quality traits in soft winter wheat. Theor Appl Genet. 2011a;122:961–970. doi: 10.1007/s00122-010-1502-7. [DOI] [PubMed] [Google Scholar]
- Reif JC, Liu W, Gowda M, Maurer HP, Möhring J, Fischer S, et al. Genetic basis of agronomically important traits in sugar beet (Beta vulgaris L.) investigated with joint linkage association mapping. Theor Appl Genet. 2010;121:1489–1499. doi: 10.1007/s00122-010-1405-7. [DOI] [PubMed] [Google Scholar]
- Reif JC, Maurer HP, Korzun V, Ebmeyer E, Miedaner T, Würschum T.2011bMapping QTLs with main and epistatic effects underlying grain yield and heading time in soft winter wheat Theor Appl Genet 123283–292.doi 10.1007/s00122-011-1583-y [DOI] [PubMed] [Google Scholar]
- Remington DL, Thornsberry JM, Matsuoka Y, Wilson LM, Whitt SR, Doebley J, et al. Structure of linkage disequilibrium and phenotypic associations in the maize genome. Proc Natl Acad Sci USA. 2001;98:11479–11484. doi: 10.1073/pnas.201394398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SAS Institute Inc . SAS User's Guide, Version 9.2. SAS Institute: Cary, NC, USA; 2008. [Google Scholar]
- Schön CC, Utz HF, Groh S, Truberg B, Openshaw S, Melchinger AE. Quantitative trait locus mapping based on resampling in a vast maize testcross experiment and its relevance to quantitative genetics for complex traits. Genetics. 2004;167:485–498. doi: 10.1534/genetics.167.1.485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. [Google Scholar]
- Stich B, Melchinger AE, Piepho HP, Heckenberger M, Maurer HP, Reif JC. A new test for family-based association mapping with inbred lines from plant breeding programs. Theor Appl Genet. 2006;113:1121–1130. doi: 10.1007/s00122-006-0372-5. [DOI] [PubMed] [Google Scholar]
- Stich B, Möhring J, Piepho H-P, Heckenberger M, Buckler ES, Melchinger AE. Comparison of mixed-model approaches for association mapping. Genetics. 2008;178:1745–1754. doi: 10.1534/genetics.107.079707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Utz HF, Melchinger AE, Schön CC. Bias and sampling error of the estimated proportion of genotypic variance explained by quantitative trait loci determined from experimental data in maize using cross validation and validation with independent samples. Genetics. 2000;154:1839–1849. [PMC free article] [PubMed] [Google Scholar]
- Valdar W, Holmes CC, Mott R, Flint J. Mapping in structured populations by resample model averaging. Genetics. 2009;182:1263–1277. doi: 10.1534/genetics.109.100727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verhoeven KJF, Jannink JL, McIntyre LM. Using mating designs to uncover QTL and the genetic architecture of complex traits. Heredity. 2006;96:139–149. doi: 10.1038/sj.hdy.6800763. [DOI] [PubMed] [Google Scholar]
- Wald A. Tests of statistical hypotheses concerning several parameters when the number of observations is large. Trans Am Math Soc. 1943;54:426–482. [Google Scholar]
- Weir BS. Genetic Data Analysis. Sinauer: Sunderland, MA, USA; 1996. [Google Scholar]
- Weir BS, Hill WG. Effect of mating structure on variation in linkage disequilibrium. Genetics. 1980;95:477–488. doi: 10.1093/genetics/95.2.477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S.1978Evolution and Genetics of Populations, Variability within and Among Natural Populations4th edn.The University of Chicago Press: Chicago, USA [Google Scholar]
- Würschum T, Maurer HP, Schulz B, Möhring J, Reif JC. Genome-wide association mapping reveals epistasis and genetic interaction networks in sugar beet. Theor Appl Genet. 2011;123:109–118. doi: 10.1007/s00122-011-1570-3. [DOI] [PubMed] [Google Scholar]
- Yu J, Buckler ES. Genetic association mapping and genome organization of maize. Curr Opin Biotech. 2006;17:155–160. doi: 10.1016/j.copbio.2006.02.003. [DOI] [PubMed] [Google Scholar]
- Yu J, Holland JB, McMullen MD, Buckler ES. Genetic design and statistical power of nested association mapping in maize. Genetics. 2008;178:539–551. doi: 10.1534/genetics.107.074245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J, Pressoir G, Briggs WH, Vroh Bi I, Yamasaki M, Doebley JF, et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet. 2006;38:203–208. doi: 10.1038/ng1702. [DOI] [PubMed] [Google Scholar]
- Zeng ZB. Precision mapping of quantitative trait loci. Genetics. 1994;136:1457–1468. doi: 10.1093/genetics/136.4.1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.