RNA and Its Ionic Cloud: Solution Scattering Experiments and Atomically Detailed Simulations

Abstract

RNA molecules play critical roles in many cellular processes. Traditionally viewed as genetic messengers, RNA molecules were recently discovered to have diverse functions related to gene regulation and expression. RNA also has great potential as a therapeutic and a tool for further investigation of gene regulation. Metal ions are an integral part of RNA structure and should be considered in any experimental or theoretical study of RNA. Here, we report a multidisciplinary approach that combines anomalous small-angle x-ray scattering and molecular-dynamics (MD) simulations with explicit solvent and ions around RNA. From experiment and simulation results, we find excellent agreement in the number and distribution of excess monovalent and divalent ions around a short RNA duplex. Although similar agreement can be obtained from a continuum description of the solvent and mobile ions (by solving the Poisson-Boltzmann equation and accounting for finite ion size), the use of MD is easily extended to flexible RNA systems with thermal fluctuations. Therefore, we also model a short RNA pseudoknot and find good agreement between the MD results and the experimentally derived solution structures. Surprisingly, both deviate from crystal structure predictions. These favorable comparisons of experiment and simulations encourage work on RNA in all-atom dynamic models.

Introduction

Since the discovery of RNA enzymes, or ribozymes, in the 1980s, biological roles for RNA that transcend its function as a messenger have continued to emerge. Over the past 30 years, explorations of RNA's role in gene expression and its potential for treating disease have expanded. Most recently, attention has shifted to biological roles for noncoding RNAs in the cell (1,2). As the family of functional RNA groups increases, so will the need for quantitative characterization of ions around RNA. The study of these counterions remains a challenge because their spatial distribution is not readily accessible to investigations based on the most common experimental approaches. Mean-field and approximate theories (3–6) and indirect experimental techniques (7,8) provide a general overview of ion atmosphere properties; however, there is a need for a quantitative and atomically detailed description of ions around RNA that is benchmarked by experimental results (9,10). Such models are able to better link structure, thermodynamic, and kinetic information about RNA molecules. Ideally, a single theoretical framework should model tightly bound, diffusive, and fully and partially hydrated ions of the polyelectrolyte cloud, without free parameters. A comparison of fully atomistic models with experiments will greatly advance our understanding of RNA's roles and functions.

Metal ions are integral to RNA structure and enable a wide variety of biological functions, and hence should be considered in any theoretical or experimental treatment of RNA molecules (11). Ions stabilize all degrees of structure (12). Those in the major and minor grooves contribute to helical stability and binding propensity (13). Localized or bridging ions stabilize the compact RNA cores that are required for tertiary folding (14). Diffusely bound ions provide positive charges to neutralize RNA's negatively charged phosphate backbone and mediate the long-range interactions that are crucial for folding and assembly (15). Additionally, the exchange and displacement of ions contribute to a free-energy balance in binding interactions (16–18). Thus, ions are intricately linked to RNA stability, conformation, and interactions.

Here, we compare a recently developed experimental technique (19) for quantifying the ion cloud around a short RNA duplex with all-atom molecular-dynamics (MD) simulations that provide a comprehensive molecular picture of the RNA in ionic solution, using explicit water and ions in the simulation box. We find excellent agreement between predictions of ion number and spatial distribution around the (static) RNA duplex obtained from MD simulations and those obtained experimentally by anomalous small-angle x-ray scattering (ASAXS) (19,20). However, one must take care not to overinterpret this agreement; other theoretical approaches can reproduce these results as well (21).

Investigators have made significant progress in the field of bioelectrolytes using numerical solvers of Poisson-Boltzmann (PB) and nonlinear PB (NLPB) equations. Sharp and Honig (22,23) pioneered and popularized the use of numerical solvers of PB and NLPB equations for these systems. The Draper group (12,15,24–31) used these tools extensively in conjunction with thermodynamic experiments to probe ion distributions and their structural and thermodynamic properties. Good agreement between theory and experiment was obtained for many systems (e.g., tRNA (29), pseudoknot (26), and RNA helical folding (25)). Nevertheless, questions remain regarding the application of PB to polynucleotides. For example, it is less desirable to empirically determine ion radii to fit the experimental data than to determine them from physical principles. MD is essentially parameter-free, which is an advantage. Perhaps the most significant advantage of MD simulations is their ability to consider thermal fluctuations explicitly and consistently.

By exploiting the above advantages of MD, we were able to extend all-atom simulations to model a small RNA pseudoknot from beet western yellows virus (BWYV) (26,32), allowing full mobility of the RNA molecule, ions, and water in the neighborhood of the native state. Measured SAXS profiles of this small RNA are in excellent agreement with those computed from MD simulations. Surprisingly, both deviate from SAXS profiles derived from the crystal structure.

Our main goal in this work is to highlight our ability to benchmark scattering data to all-atom MD simulations. The favorable comparisons reported here increase our confidence in the simulations and enable detailed analyses that will lead to a better understanding of the roles played by ions in RNA conformation and function. They also encourage simulations of ion distributions, which are currently inaccessible to experiment.

Materials and Methods

All-atom simulations

We used the MOIL suite of programs (33) to study the ion distributions around the A-form of RNA and the dynamics of an RNA pseudoknot. The nonbonding terms were obtained from the OPLSAA force field (34), the bonding terms were obtained from AMBER99 (35), and the ions were as described previously (36,37). The parameters are available from MOIL distribution (http://clsb.ices.utexas.edu/prebuilt/). We used the RNA sequence (GCA UCU GGG CUA UAA AAG GGC GUC G) and its complementary strand that form an A-form duplex. The duplex was solvated with explicit (TIP3P (38)) water molecules and two different monovalents (Na⁺ and Rb⁺) or divalent (Sr²⁺) ions of ∼0.1 M in the bulk. Further details on the simulations and an image of the simulation box (Fig. S1) can be found in the Supporting Material, and in Kirmizialtin and Elber (39).

ASAXS experiments on the duplex RNA

We performed ASAXS experiments to characterize the ion atmosphere around RNA molecules (19,20). To that end, we measured SAXS signals at several x-ray energies (tabulated in the Supporting Material) close to but below the absorption edge of the ions of interest. The measured absorption edges for Rb⁺ and Sr²⁺ ions are 15.200 keV and 16.113 keV, respectively. Near an ion's absorption edge, the atomic scattering factor (in units of electrons) is denoted by:

$$f_{ion}\left(E\right)=f_0+f^{\prime }\left(E\right)+\mathrm{i}{f}^{″}\left(E\right)$$ (1)

where f_o is the energy-independent solvent-corrected scattering factor (atomic number Z in vacuum) of the resonant element, f′ and f″ are the energy-dependent anomalous scattering factors, and E is the x-ray energy. The scattering intensity from the nucleic acid and counterion cloud system is a function of both energy E and momentum transfer q (q = (4π/λ)·sinθ, where λ is the x-ray wavelength and 2θ is the scattering angle) and is given by:

$$I\left(q,E\right)={\left|f_{NA}{F}_{NA}\left(q\right)+f_{ion}\left(E\right)N_{ions}{F}_{ion}\left(q\right)\right|}^2.$$ (2)

The terms described by Fs reflect the spatial arrangement of the scattering particles (treated as unity at q = 0), and those represented by f_NA describe the effective number of electrons from a nucleic acid duplex. N_ions equals the number of excess cations around the nucleic acid (greater than the ion number in the bulk solution).

ASAXS measurements were performed on 0.2 mM dsRNA molecules (Dharmacon, Lafayette, CO) with the same sequence used in the simulations. The RNA molecules were annealed in 50 mM NaCl, 25 mM HEPES buffer (pH 7.0) for 2 min at 90°C, cooled slowly to room temperature, and then extensively dialyzed in 100 mM strontium acetate or 100 mM rubidium acetate in the presence of 1 mM Na⁺MOPS buffer (pH 7.0). The ASAXS setup and experimental conditions were described previously (19,20).

In a recent publication (19), we described an extension of the ASAXS technique that provides the number of ions in addition to their distribution around nucleic acids, enhancing previously published information (13). This improvement provides a second degree of comparison with simulation. To enable ion counting in this particular study, we measured the anomalous scattering factors using x-ray fluorescence for both Rb⁺ and Sr²⁺ (40) and calibrated the x-ray scattering intensity using water as a SAXS calibrant, as described previously (41). SAXS profiles were acquired at multiple x-ray energies at the C1 beamline at the Cornell High Energy Synchrotron Source (CHESS). The energy-dependent scattering intensities were decomposed into

$$I\left(q,E\right)=b\left(q\right)·f^{\prime }\left(E\right)+c\left(q\right).$$ (3)

The number of ions was calculated from

$$N_{ions}=\frac{b\left(0\right)}{\left(2\sqrt{c\left(0\right)}\right)}$$ (4)

as described previously (19) and detailed in the Supporting Material. The shape of the anomalous signal is given by b(q) and accounts for the spatial distribution of the ions with respect to the nucleic acid. This could also be derived by comparing scattering profiles from two x-ray energies (one far away, the other near the absorption edge) as described previously (13) and in the Supporting Material.

SAXS experiments on the RNA pseudoknot

The BWYV RNA pseudoknot with sequence GGC GCG GCA CCG UCC GCG GAA CAA ACG G was synthesized, and high-performance liquid chromatography–purified by Integrated DNA Technologies (Coralville, IA). The RNA was reconstituted in 10 mM Na-MOPS pH 7.0 buffer and dialyzed against the same buffer with 100 mM NaCl (Amicon Ultra 0.5 mM Y3K concentrator). We determined the concentration using UV absorption at 260 nm, assuming an extinction coefficient of 264,200 L/(mole cm). The sample was diluted to 0.44 mM (4.0 mg/mL), annealed at 92°C, and cooled slowly to room temperature. Samples were stored at 4°C before experiments were conducted.

We acquired SAXS data at the G1 beamline at CHESS using 10.4 keV x-rays. The RNA sample was held in a temperature-controlled cell at 25 ± 0.2°C, and the scattering pattern was recorded on a fiber-coupled CCD detector (FLICAM) ∼1 m away. The transmitted intensity was measured via a pin diode in the beamstop and used to normalize each image. The integrated intensities from multiple exposures were buffer-subtracted and inspected for time dependence, and then averaged together.

Results

Because short duplexes are fundamental units in numerous RNA folds, in our first coupled investigations we examined a 25-basepair (bp) A-form duplex. The RNA sequence was selected for comparison with experiments (13) and previous simulation studies (39) that reported the spatial distribution of Na⁺ and Mg²⁺ ions around this duplex. For compatibility with experimental methods, we extended the latter simulations to include RNA in 0.1 M Rb⁺ and Sr²⁺. The Rb and Sr K-edges at 15.2 keV and 16.1 keV are experimentally accessible to synchrotron x-rays, which enables the use of contrast variation methods to extract quantitative information about counterion number and spatial distribution. The relatively high ion concentration facilitates more rapid equilibration in the simulations and improves statistics. This combination uniquely enables direct comparison of experiment and simulation, and allows us to describe and compare two key parameters: the number of excess ions in the presence of RNA, and the spatial distribution of these ions around the duplex.

Number of excess ions

Results of all-atom MD of an RNA duplex with explicit ions and water

We performed all-atom replica-exchange MD simulations of duplex RNA in explicit solvent and ions using the MOIL suite of programs (33). The simulations were conducted with asymptotic concentration of 0.1 M (for details, see Materials and Methods and the Supporting Material). We kept the RNA molecule rigid to enable replica-exchange simulations and to focus on the properties of the ions and their distribution around the RNA. Fig. S1 shows a sampled equilibrium configuration of an A-form RNA double helix with water molecules (red sticks), Sr²⁺ ions (green spheres), and Cl⁻ ions (cyan spheres). The number of excess divalent ions (with respect to the bulk concentration) near the RNA is ∼20 in 0.1 M SrCl₂. We obtained this value by establishing an influence radius, i.e., the distance from the RNA line of center in which the probability density of cations approaches the bulk value (R_bulk ∼18 Å). Manning and Ray (42) suggested the use of an inflection point in the radial distribution function to determine the transition from the regime in which the ions are bound to the regime of bulk behavior. We used a related measure. The distance in which the derivative of the accumulated excess ion distribution is zero as a function of distance from the RNA center (in practice, the shortest distance in which dN/dr < 0.1) is defined as R_bulk. We counted the number of excess ions within the volume defined by this radius. This number of excess ions was averaged over 15,000 MD configurations.

Experimentally determined values obtained with anomalous SAXS

SAXS results from the electron density differences between the sample and background. Here, the sample consists of the 25-bp RNA duplex and excess counterions, and the background consists of the solution containing bulk ions. ASAXS exploits the energy dependence of ion scattering factors near atomic absorption edges to distinguish ion scattering from all other contributions (20). When scattering factors and scattering intensities are calibrated in units of electrons and electrons squared, respectively, ASAXS experiments provide the number of excess ions relative to the surrounding (bulk) salt solution (see Materials and Methods, Supporting Material, and Pabit et al. (19)).

Comparison of simulation and experiment

We applied ASAXS to measure the number of excess counterions present in samples containing 25-bp RNA duplexes. Fig. 1 shows our results for Rb⁺ and Sr²⁺ ions around RNA. In 0.1 M Sr²⁺, we count 19.2 ± 1.7 ions per duplex, whereas MD gives 20 ± 0.2 excess ions. The MD results provide additional insight, showing three distinct regimes for the ions, distinguished by their distance from the RNA central axis (Fig. 2). Distances between 0 and 8 Å from the RNA central axis correspond to major and minor groove binding, and reflect tightly bound ions (39). The region between 8 and 18 Å has a steeper slope and includes diffusively bound ions. Finally, for distances > 18 Å from the axis, the slope is nearly constant in Sr²⁺, reflecting the bulk density profile. From this plot we find that the condensed ions form an ion cloud with radius ∼18 Å. Experiments carried out on identical duplexes in solutions with bulk concentrations of 10 mM Sr²⁺ yield a spatial distribution and ion number (20.6 ± 1.8) that are indistinguishable from the results obtained at 0.1 M. Simulations on Na⁺ suggest that the extent of charge neutralization is independent of ionic strength or salt concentrations (Fig. S4). Both observations are consistent with ion condensation theory (5,43,44).

Figure 1.

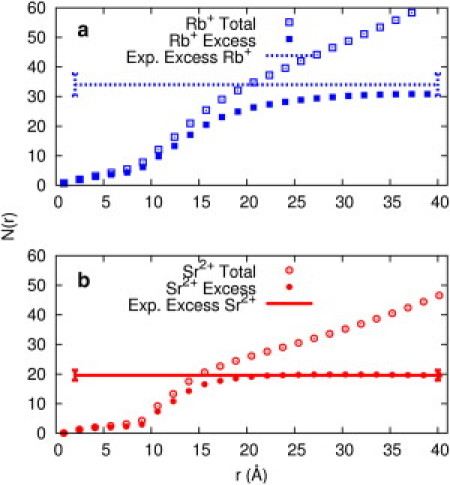
Number of cations in a cylindrical volume of radius r, where r is the distance from the center of the A-form RNA duplex's long axis, is shown for simulations of (a) 0.1 M RbCl (blue, top panel) and (b) 0.1 M SrCl₂ (red, bottom panel). Open points are the total number of cations in a cylindrical volume with radius r, and filled points are the number of cations when the bulk contribution is subtracted from the total number. The horizontal lines are the experimental results for the number of excess ions, with error bars shown at the ends of the lines. We obtained these values using ASAXS to count the number of excess cations around a 25-bp RNA duplex in 0.1 M RbCl (blue dashed) or 0.1 M SrCl₂ (red solid) aqueous solutions (see text for details).

Figure 2.

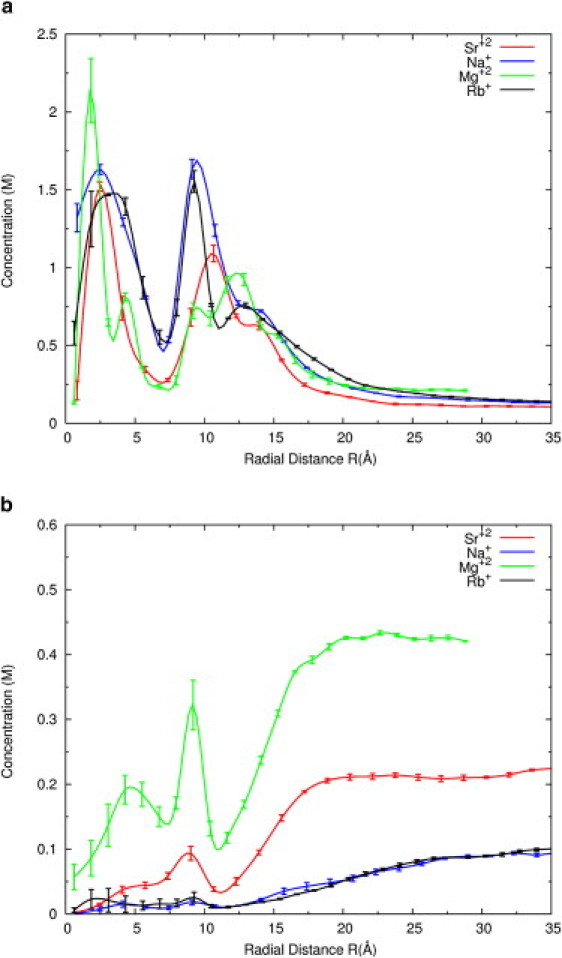
(a) Radial concentration profiles of cations as a function of r, the radial distance from the center of the RNA long axis, are computed from the simulations for four different aqueous solutions. The distance of the phosphates from the central axis is ∼11 Å. Shown here are 0.1 M Na⁺ (blue), 0.1 M Rb⁺ (black), 0.1 M Sr²⁺ (red), and 0.2 M Mg²⁺ (green) distributions. The lines are guides to the eye. Error bars are calculated by grouping the data into three sets and taking the average and standard deviation (see Supporting Material for details). (b) The radial distribution of chloride ions for cations shown in part a are displayed here, using the same color code.

Fig. 1 also shows results in solution containing 0.1 M Rb⁺ ions for comparison. ASAXS counts 35 ± 3 (Rb⁺) ions, whereas MD simulations report 31 ± 0.4 (Rb⁺) ions and an influence radius of ∼28 Å. The number of bound ions found in 0.1 M Na⁺ is 32 ± 0.3. The difference between the distributions of Na⁺ and Rb⁺ ions is small, suggesting that neutralization by monovalent ions is independent of the ion size. Indeed, the influence of ion type is not as critical for monovalent ions as it is for divalent ions (12,24). For monovalent ions, ion condensation theory (5,43,44) (G. S. Manning, Rutgers State University of New Jersey, personal communication, 2010) predicts that the effective charge of 25-bp dsRNA at distances larger than the condensation boundary (∼28 Å) is −12e. Because the charge of the bare RNA in our simulations is −48e, the 32 excess ions enclosed within the influence radius lead to an effective RNA charge of −16e in MD simulations, close to the value predicted by ion condensation theory. The experimental value is in even better agreement (−13e). This agreement with condensation theory was also observed in studies of short DNA helices (7). Given the finite size of the systems, the agreement is remarkable. Counterion condensation (CC) is an asymptotic theory, and its limits have been investigated extensively. In particular, the length of the polyelectrolyte is assumed to be infinite and the counterion bulk concentration approaches zero. For an excellent review of the implications of the theoretical limits and expected failures of CC, see Mohanty et al. (45). For example, the analysis indicates that the number of condensed ions in CC depends weakly on the bulk concentration of counterions for ion concentrations < 0.1 M (44). We quoted the results of CC to contrast the simplest successful model of a polyelectrolyte with more-complex and detailed simulations. The concentrations considered here are above the proposed limit, and we did not expect the CC results to be quantitative. It is remarkable that for the particular observable reported, the number of bound or excess ions, CC is in excellent agreement with both experiment and atomically detailed simulations. It is therefore possible that CC is applicable even beyond the limits posed by rigorous mathematical analysis. For example, Keyser et al. (46) estimated a constant number of bound ions in the concentration range of 0.01–1 M, although their measurement is less direct than the one reported here.

Spatial distribution of ions around duplex RNA

Results of all-atom MD of an RNA duplex with explicit ions and water

We extracted the spatial distribution of the ions from ∼15,000 configurations of the simulations that were recorded every 0.5 ps. The distance of each ion from the RNA line of center was computed and binned in cylindrical shells of width dr. The bins were normalized to the available volume, and results for 0.1 M Sr²⁺ from this simulation are presented in Fig. 2 a. For comparison, we also conducted a simulation of 0.1 M of Rb⁺ and Na⁺. Fig. 2 also displays previous data (39) showing the ion distribution around RNA with bulk concentrations of 0.2 M Mg²⁺. At these concentrations, the overall features of these distributions are only weakly dependent on bulk ionic strength for a given ionic species (39). For each ion type, they are nearly identical at short distances from the axis. The MD simulations also provide insight into anion distributions near RNA. Chloride ion concentrations show colocalizations with the peak positions of cation distributions, as shown in Fig. 2 b. Of interest, this type of association between cations and anions is missing in NLPB models. MD simulations also report that although the absolute number of co-ions near the RNA increases somewhat with the salt concentration, more co-ions are depleted from RNA proximity as the concentration increases (see Fig. S5). This trend was previously observed in the ion-counting experiments of Bai et al. (7).

The computed Rb⁺ and Sr²⁺ ion distributions can be converted into a scattering profile for comparison with experiment using the Debye formula (47) (Fig. 3). To mimic the contrast variation effect that provides the ASAXS signal, the scattering is computed using two different values for the energy-dependent electron density (contrast) for Rb⁺ and Sr²⁺ ions near the Rb and Sr K-edges, as described below. More details of this conversion are provided in the Supporting Material.

Figure 3.

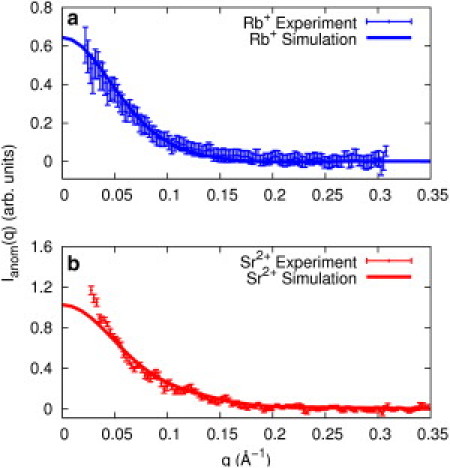
ASAXS signal of 0.1 M (a) Rb⁺ ions (blue points, top panel) and (b) Sr⁺² (red points, bottom panel) around an A-form RNA duplex is plotted as a function of momentum transfer (see text for more details). The spectrum is compared with ASAXS profiles computed from MD simulation data of 0.1 M RbCl (blue solid line, top panel) and 0.1 M SrCl₂ (red solid line, bottom panel). The discrepancy at low q (q < 0.05 Å⁻¹) seen in the lower panel is attributed to structure factor effects from duplex end-to-end stacking that does not manifest in the MD simulations.

Experimentally determined ion distributions obtained with anomalous SAXS

ASAXS is one of only a few experimental techniques that are sensitive to the spatial distribution of counterions around charged macromolecules. Using multiple x-ray energies near the absorption edge of an ion, one can decompose SAXS data into components that provide information about the spatial distribution of the counterion cloud. For example, in previous studies we used ASAXS to compare the spatial distribution of ions around short DNA and RNA helices (13). We reported ion-nucleic acid correlation vector lengths and used models based on the NLPB equation (3) to generate ion distributions for comparison. Because the choice of ion radius subtly modifies NLPB predictions of ASAXS scattering profiles, we obtained a best-fit value of ion size by comparing computed and measured curves. In a previous work (20), we described how the probe ion radius is optimized to achieve this agreement. Of particular relevance to this work is the more dramatic dependence on ion size of counterion number and distribution around RNA, relative to DNA (13). Other groups using NLPB also fit the radii of the mobile ions to the problem instead of determining them independently (48). Hence, PB approaches, with adjustment of parameters such as the ionic radii, succeed in reproducing the number of ions around the polyelectrolyte and the corresponding ASAXS spectra. In contrast, MD simulations are conducted with essentially no free parameters. However, they are significantly more expensive than the application of PB solvers. It is therefore not surprising that NLPB is more popular than MD for addressing these problems. Nevertheless, the results of MD and NLPB are not the same for magnesium (21). MD includes ionic correlation effects that are generally ignored in PB approaches, leading to significantly different shapes of ionic clouds (39). However, ion distributions similar to those computed by MD have been obtained by application of coarse-grained models (49,50). The computed number of ions is similar to measured values in solutions containing monovalent or divalent ions alone, which makes it difficult to differentiate between alternative theoretical approaches. At present, no available experimental techniques report the distribution of Mg²⁺ ions, which is required to distinguish between the theories.

Fig. 3 shows a comparison of experimental and MD-derived ASAXS profiles under identical bulk solutions of mono- and divalent ions. For ease of comparison, the data and MD simulations were scaled to match at momentum transfer (q) in the interval 0.08 < q < 0.13 Å⁻¹ to account for direct comparison of scattering profiles. For the Sr²⁺ data, the experimental curve deviates from the computed curve at low q, because these short duplexes stack end to end when the solution divalent ion concentration exceeds 5 mM (13). The effect of this interparticle association is corrected for in the calculation for the number of ions, as described in the Supporting Material. Structure-factor effects diminish at q > 0.05 Å⁻¹ (51), and indeed, agreement with MD predictions occurs at and above this momentum transfer.

Simulations predict the effect of changing ion valence and size

The detailed agreement between experiment and simulation for the ions presented above validates simulation predictions for the number and distribution of ions, and lends confidence to predictions for other, more biologically relevant counterions. Simulation predictions for distributions of Na⁺ and Mg²⁺ are also shown in Fig. 2 a. Of interest, all distributions are rather complex and involve multiple peaks that correspond to specific binding locations as detailed previously (39). The results shown in Fig. 2 a invite comparison between distributions of different ions. For example, the Mg²⁺ distribution has more structure and is tightly bound in the 0–5 Å region to the major groove G-C pairs. Na⁺ and Rb⁺ ions distributions are very similar and are distributed around RNA more diffusively, with two broad peaks. The first peak occurs at the grooves, and the second occurs near the oxygen atoms of the phosphate backbone. Both hydrated and dehydrated Na⁺ ions are found in the simulations. The properties of Sr²⁺ ions are intermediate between those of Na⁺ and Mg²⁺. These ions bind diffusively to RNA and are more likely to possess partial solvation shells in sites near the backbone phosphates. Twenty percent of the Sr²⁺ ions are without one of the expected water molecules in their first solvation shell when they are near RNA while Sr²⁺ is 5% dehydrated in the bulk. Throughout the simulation period, the magnesium ion was fully hydrated at room temperature. It is interesting to note that the number of excess ions of 0.1 M Sr²⁺ is slightly larger than that of 0.2 M Mg²⁺ (see Fig. S6). This result is a consequence of the concentration change and not of different atom type. Once the diffusively bound ions are taken into consideration, the total number of Mg²⁺ ions is larger.

Comparison of SAXS profiles of an RNA pseudoknot: experiment and MD

Simulations of the 25-bp duplex allowed full mobility of the ions and water molecules; however, the RNA structure itself was kept rigid in the simulations, which is a reasonable assumption for short duplexes. The favorable comparison of MD simulations with experimental results (discussed above) prompted us to extend these coupled studies to an RNA molecule with tertiary interactions. We chose the BWYV pseudoknot, a short 28-nucleotide RNA (32), and allowed full mobility of ions, water molecules, and the RNA molecule near the neighborhood of the native state.

Simulation parameters

The simulations were carried out for the sequence (GGCGCGGCACCGUCCGCGGAACAAACGG) that forms a pseudoknot. The study was conducted in solutions containing 0.17 M NaCl, at room temperature (300K). Further details of the simulations are provided in Materials and Methods and the Supporting Material.

Experimental parameters

SAXS profiles of the solution structure of this small RNA motif were recorded at 0.1 M NaCl concentration. Because these studies focused on the RNA conformation, not the ion distribution, we employed regular (as opposed to anomalous) SAXS with Na⁺ counterions. Excellent agreement is found between experiment and simulation. Fig. 4 shows these results as Kratky plots of I · q² versus q, emphasizing the higher-angle scattering, which reflects structural information on length scales smaller than the overall size of the macromolecule. The inset shows I(q) versus q. We also computed the SAXS profile of a structure determined by x-ray crystallography (PDB ID 437D (32)) using CRYSOL (52) (with default parameters). To facilitate a reliable comparison, we also generated the solution structure from the MD results using CRYSOL with the same default parameters. Of interest, the SAXS spectra from experiment and MD agree well with each other, but not with that computed from the crystal structure (Fig. 4, dashed line). To investigate these differences, we overlapped representative configurations from MD simulations with the crystal structure (Fig. 5). The MD structures were chosen by clustering with the k-means algorithm (53) (using the RMSD as a distance measure). The configurations shown are the cluster centers. All cluster centers are similar in the 3′-end region and deviate significantly in the 5′-end region with respect to the crystal structure. These alternative structures sampled at room temperature can explain the significant differences between SAXS spectra of solution and crystal structures (see Fig. 5).

Figure 4.

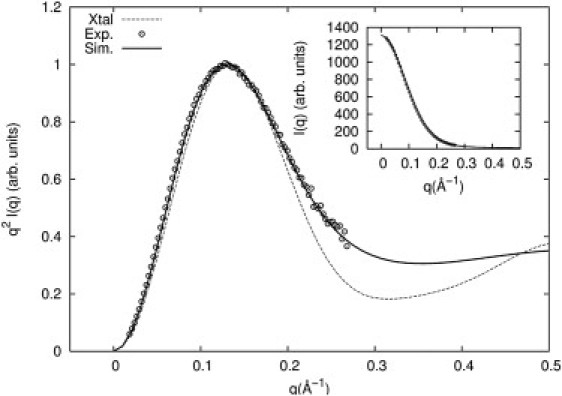
Measured scattering profiles of a 28-nt RNA pseudoknot from BWYV (PDB ID 437D) in 0.1 M NaCl solution at room temperature are shown as Kratky plots (open circles). The solid line is the computed spectrum from the MD simulations, sampling many configurations of the RNA and ion distributions in the vicinity of the folded state. A Kratky plot computed from the PDB structure is shown as a dashed line. All plots are normalized to their maximum value. The inset compares the SAXS profiles from the experiment (circles) and MD simulation (line).

Figure 5.

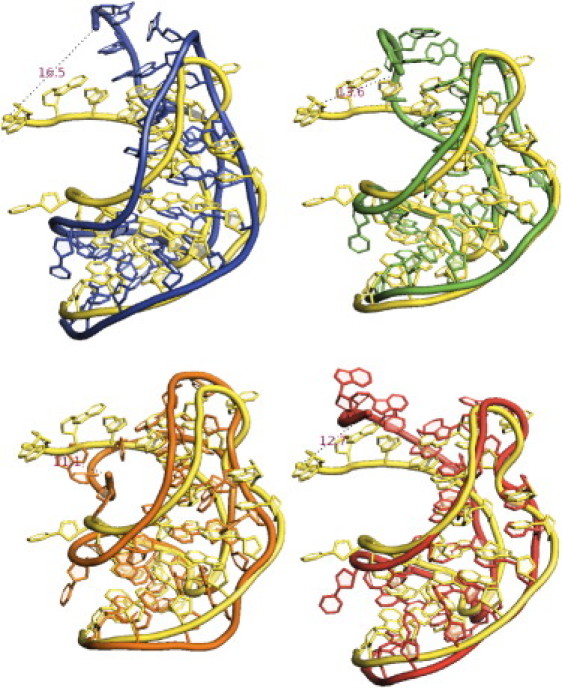
Representative configurations from the MD simulations of the BWYV pseudoknot are overlaid on the crystal structure 437D (yellow-lighter). We chose these representative configurations by clustering the simulation data to four clusters via a k-means algorithm. Each configuration shown represents one of the centers of these four clusters. The dashed lines are the distances between the 5′ end of the RNA in the crystal structure and the MD configuration.

The distribution of ions around the pseudoknot is of considerable interest. However, ASAXS data for Na⁺ are not available. Fig. S7 shows simulation results describing the ion distribution and the number of excess ions. Simulations predict 14.8 ± 0.3 excess ions with a condensation boundary of ∼30 Å. Because the charge of the bare pseudoknot is −27e, the excess ions enclosed within the influence radius lead to an effective RNA charge of −11e.

Discussion

RNA's negatively charged phosphate backbone attracts charge-compensating ions and molecules in solution. These counterions modulate the behavior of RNA molecules and affect RNA folding, stability, and binding to target partners. Therefore, it is important to fully understand the ion distributions and the number of ions around RNA molecules. Because the low electron binding energies of physiologically relevant counterions (such as Mg²⁺ or K⁺) preclude measurement by anomalous scattering, we made comparisons using heavier ions that are amenable to study. ASAXS provides unique, quantitative information about ion number and distribution that can be used to validate atomically detailed MD predictions. Agreement with simulations in the case of heavy ions supports the assumptions and methods used in the MD simulations. Thus, simulations can be readily extended to the ions with smaller atomic numbers than are experimentally accessible at the present time. We began with a rigid, short dsRNA and compared the experimental results with those obtained from the MD simulations with explicit ions and water. Excellent agreement is found when we compare the number and distribution of excess divalent cations. For RNA in 0.1 M divalent counterion solution, ASAXS counts 19.2 ± 1.7 ions per duplex, whereas MD gives 20 ± 0.2 ions. Similarly, we obtain 35 ± 3 ions from ASAXS, whereas MD simulations report 31 ± 0.4 for monovalent counterions (Rb⁺) in solution. The experimental number does not change at lower ionic strength (taken at 10 mM Sr²⁺). When internucleic acid association effects are taken into consideration (at q < 0.05 Å⁻¹), we find that the ion-nucleic acid distribution shown by the full anomalous scattering profile agrees well with predictions from MD simulations (q > 0.05 Å⁻¹). However, predicting the number of ions near the RNA is not a difficult test for a theory. In fact, NLPB and size-modified NLPB provide identical results (21). Judging from the number of ions as the sole indicator, PB theory is adequate.

Information about ions of different sizes and charges also provides insight into the physical parameters that determine ion-RNA interactions. For example, comparisons involving monovalent ions of different sizes, such as sodium and rubidium, suggest a high degree of similarity in interactions with RNA. For these diffusively bound counterions, ion size does not appear to be critical; the number of excess ions and distributions of ions around RNA changes little when Na⁺ is replaced with Rb⁺. It is also interesting that the number of excess ions is the same in different concentrations of the same monovalent ion type (see Fig. S4), which agrees with the prediction of ion condensation theory. Simulations show that monovalent ions form a diffuse cloud around RNA with a radius of ∼28 Å from the line of center of the RNA. In contrast to monovalent ions, divalent ions can bind tightly and specifically to well-defined sites at the RNA surface and form an ion cloud that is more compact, with a radius of ∼18 Å. The MD simulation results for Mg²⁺ and Sr²⁺ distributions differ in that Mg²⁺ binds more tightly to RNA, and its distance distribution function (Fig. 2 a) is dramatically different from those of other ions. Because of its small size (and very high charge density), the magnesium ion binds exceptionally well to RNA and has a significantly more structured distribution compared with strontium. Koculi et al. (49,54) argued that the charge density (i.e., the ion charge divided by its volume) of divalent ions is an important parameter in determining the stability of RNA and its interactions with the solution. Our results on the magnesium/strontium pair support this argument.

To further compare experiment with simulation, and to exploit the promise of MD for studying fluctuating systems (an option that is not available in PB methods), we modeled a short RNA pseudoknot. Thermodynamic studies have shown that this pseudoknot has a stable folded tertiary structure in purely monovalent solutions at room temperature (25,26). As an added feature of the MD simulation, we allowed full mobility of the RNA molecule so that we could study pseudoknot RNA tertiary structure interactions in the vicinity of the folded state. We find good agreement between the MD results and the experimental SAXS profiles, yet both deviate significantly from SAXS profiles derived from the published crystal structure. The solution structure of the pseudoknot (not including magnesium ions) appears to be less compact than the crystal structure. In fact, a number of SAXS-derived solution structures deviate from crystal structures (55,56). This is perhaps not surprising, considering that the ionic conditions and procedures that are necessary for crystallization can bias molecules toward a rigid configuration that restricts fluctuations. Here, we demonstrate that these partially relaxed structures, sampled at thermal equilibrium, can be accessed through MD simulations.

Conclusions

RNA studies that combine experiment and simulation allow for more-extensive investigations of ion-RNA interactions than can be achieved by either method alone. On the one hand, simulations provide atomically detailed information and insights that are difficult to obtain directly from experiment. On the other hand, experiments are essential to test the validity of the approximations that are used in the simulations. Here, we have illustrated two aspects of this collaboration. Our ability to reproduce experimental ASAXS and SAXS spectra by simulations confirms that the simulations accurately predict counterion properties as well as RNA fluctuations in the neighborhood of the native structure. The simulations also provide atomically detailed insights into the RNA-counterion systems. In the future, our combined approach of experiment and simulations may allow us to explore the equilibrium and nonequilibrium states of RNA that are required for folding and function.