Aggregation of α-synuclein is kinetically controlled by intramolecular diffusion

Abstract

We hypothesize that the first step of aggregation of disordered proteins, such as α-synuclein, is controlled by the rate of backbone reconfiguration. When reconfiguration is fast, bimolecular association is not stable, but as reconfiguration slows, association is more stable and subsequent aggregation is faster. To investigate this hypothesis, we have measured the rate of intramolecular diffusion in α-synuclein, a protein involved in Parkinson’s disease, under solvent conditions that accelerate or decelerate aggregation. Using the method of tryptophan-cysteine (Trp-Cys) quenching, the rate of intramolecular contact is measured in four different loops along the chain length. This intrinsically disordered protein is highly diffusive at low temperature at neutral pH, when aggregation is slow, and compacts and diffuses more slowly at high temperature or low pH, when aggregation is rapid. Diffusion also slows with the disease mutation A30P. This work provides unique insights into the earliest steps of α-synuclein aggregation pathway and should provide the basis for the development of drugs that can prevent aggregation at the initial stage.

The protein α-synuclein is the primary component of intracellular aggregants known as Lewy bodies, a hallmark of Parkinson’s disease, and likely plays a central role in neuronal cell death (1). When recombinantly expressed and purified it is intrinsically disordered in solution and highly prone to aggregation (2). Recent work has shown that the native structure in human cells is likely a helical tetramer that is resistant to aggregation, but when this tetramer is denatured the monomers cannot autonomously refold and aggregate very quickly (3, 4). Thus it is likely that the aggregation pathway passes through the monomer. In vitro, the aggregation propensity of α-synuclein is very sensitive to solution conditions such as temperature, pH, salt concentration, and solution cofactors. There has been significant work to discover the structures that form in association with lipids, structures of final aggregates, and structures that may be the aggregation precursor (5–15). However, the underlying reason for why monomeric α-synuclein is so prone to aggregation is still unknown. We propose that a physical influence on aggregation is the internal dynamics of the disordered chain, that is, the rate of intramolecular diffusion.

Over the past decade, a number of groups have measured intramolecular diffusion in a variety of sequences using measurements of intramolecular contact between two probes placed in the chain. All unstructured peptides, including fragments of α-synuclein, diffuse relatively rapidly, approximately 1–3 × 10^-6 cm² s^-1 (16–18). These rates are less than 10 times slower than free diffusion of individual amino acids and about the same as translational diffusion of the entire chain, suggesting that the chain does not exert significant drag on the movement of individual segments (19), although there are measurable tail effects when the probe positions are internal in the sequence (20). The slowest intrinsically disordered protein measured is apocytochrome c (D = 2.2 × 10^-7 cm² s^-1) a protein that folds upon binding to the heme (21). These results suggest that intrinsically disordered proteins require high rates of intramolecular diffusion to maintain solubility and conformational plasticity. Natively folded proteins in high denaturant also have high diffusion coefficients (22, 23). In contrast, protein L has been measured under folding conditions before folding to have a much slower diffusion coefficient, 5 × 10^-10 cm² s^-1, demonstrating that unfolded proteins are not necessarily rapidly diffusing random coils (24). A single point mutation in protein L, F22A, has been shown to increase the diffusion coefficient by two orders of magnitude and shows how sensitive diffusion is to the exact sequence (25). Finally, two sequences prone to aggregation have diffusion coefficients between these two extremes. Several short polyglutamine peptides were measured to have diffusion coefficients that decreased with length and an extrapolation of these rates to lengths that are prone to aggregation (> 30 residues) gives D ∼ 9 × 10^-8 cm² s^-1 (26). The N-terminal domain of hydrogenase maturation factor (HypF-N), a highly aggregation-prone protein, was reported to have D ∼ 1 × 10^-7 cm² s^-1 (22), but this rate is an extrapolation from measurements made at moderate concentrations of denaturant and likely represents the upper limit. Taken together these measurements suggest that there is a range of diffusion coefficients (10^-7 to 10^-8 cm² s^-1) that make unfolded sequences prone to aggregation.

In this paper we present a systematic investigation of intramolecular diffusion along the entire 140 residue chain of α-synuclein and show how dynamics vary with solvent conditions and mutation. We find that diffusion of this intrinsically disordered protein is almost as fast as any unstructured peptide under conditions that prohibit aggregation, but diffusion slows by more than an order of magnitude under conditions that promote aggregation, specifically low pH and high temperature at neutral pH. These results are consistent with a model of aggregation in which intramolecular reconfiguration of the monomer determines the rate of bimolecular association and subsequent aggregation steps.

Results

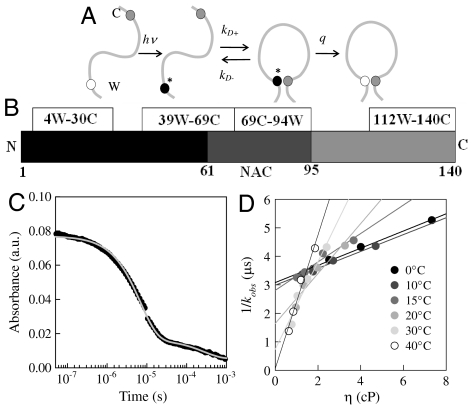
Measurement of intramolecular diffusion requires a long-lived probe that is quenched on contact with an efficient quencher within the same sequence. We use the triplet state of tryptophan (Trp) which lives for approximately 40 μs in water (27) as the probe and cysteine (Cys) to efficiently quench the triplet state only upon close contact. The observed kinetics can be modeled as a two-step process as shown in Fig. 1A (28). The observed decay rate of the tryptophan triplet is given as

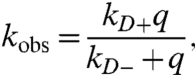[1]

where k_D+ is the rate of diffusion of the Trp and Cys toward each other, k_D- is the rate away, and q is the rate of quenching upon contact. Eq. 1 can be rewritten as

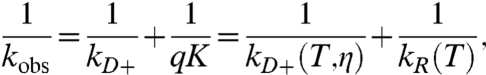[2]

where K ≡ k_D+/k_D- is the equilibrium constant for forming the Trp-Cys encounter complex and the reaction-limited rate, k_R ≡ qK. Lapidus et al. have shown the quenching is short-range and determined the distance dependence (28). We assume the k_R depends only on temperature (T) but k_D+ depends on both temperature and viscosity of the solvent (η) (19). Therefore, by making measurements at different viscosities (with the addition of sucrose) for a constant temperature we can extract both k_R and k_D+ by fitting a plot of 1/k_obs versus η at a given temperature to a line. Cheng et al. have derived the general viscosity dependence for loop closure and conclude that the linear approximation is reasonable when the average size of the loop is large compared to the length scale of the quenching reaction (29). This approximation holds for all sequences investigated here. Furthermore, it is possible that k_R will be affected by changing sucrose concentration due to collapse of the chain. Sucrose is well-known to stabilize folded states, but Fig. S1 shows that the CD spectra at various temperatures are unaffected by the addition of 30% sucrose (the maximum concentration used here). There is actually very little direct evidence that sucrose significantly collapses unfolded states and Fig. S2B shows that FRET for a doubly labeled protein actually decreases slightly in 30% sucrose, suggesting the protein is slightly less compact, but this difference is much less than the change in FRET with temperature. Therefore, we assume k_R is independent of sucrose concentration.

Fig. 1.

(A) Determination of the rate of contact formation between the probe, tryptophan (W), and the quencher, cysteine (C), within an unfolded protein. Pulsed optical excitation leads to population of the lowest excited triplet state of tryptophan. Tryptophan contacts cysteine in a diffusion-limited process with rate k_D+, and then either diffuses away or is quenched by the cysteine. (B) Sequence diagram of α-synuclein with positions of measured loops indicated. (C) Transient absorption of the tryptophan triplet state in the 112W-140C loop at pH 7.4, T = 0° C. (D) Observed lifetimes of the triplet state of 39W-69C loop at various temperatures and viscosities. The lines are independent fits of the data at each temperature.

Monomeric α-synuclein is a 140 residue intrinsically disordered protein lacking either Trp or Cys. To probe intramolecular diffusion in α-synuclein, the sequence was mutated to place a single tryptophan and cysteine 25–30 residues apart in sequence. The positions were determined by the Tango algorithm to minimize changes to the intrinsic aggregation propensity from the wild-type protein (Fig. S3A) (30). Fig. 1B shows the positions of the four loops. The gray bar in the middle of the sequence shows the nonamyloid component (NAC) region (residues 65–95), thought to be the nucleation site for aggregation. One mutant, 69C-94W, almost spans this region. Fig. S1 and Fig. S3B show the aggregation kinetics and secondary structure content, respectively, of each mutant and the wild type are virtually identical. We have also introduced the mutation A30P to the 39W-69C loop. This mutation is associated with early onset Parkinson’s disease, yet has a significantly slower aggregation rate as shown in Fig. S3B.

Fig. 1C shows the typical kinetics observed for these mutants. A rapid decay on the microsecond timescale shows that the tryptophan triplet is being rapidly quenched by contact with cysteine. A second decay on the 100 μs to 1 ms timescale is due to other photophysical processes (27). Each trace fits to a single exponential on the microsecond timescale, indicating that there is only one population of conformations that rapidly reconfigures. Long-lived structured states or soluble oligomers would yield two or more exponential phases. All measurements on each sample occur within 20 min after preparation, well within the lag time, so aggregation is minimal.

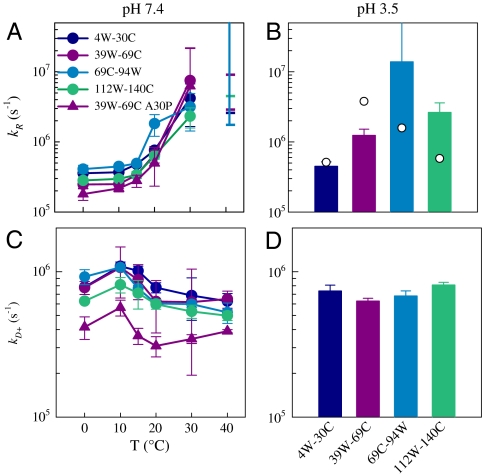
Fig. 1D shows a typical plot of exponential decay times versus viscosity for various temperatures at pH 7.4 (see Fig. S4 for all mutants). Decay times at a single temperature can be fit to lines. As discussed in SI Materials and Methods (and shown in Figs. S5–S8 and Tables S1 and S2), the temperature dependence of both the slopes and intercepts of these lines are quite unusual compared to other proteins and indicates the chain is undergoing a glass transition as temperature is raised or pH is lowered. Fig. 2 plots the reaction-limited and diffusion-limited rates (at η equal to the viscosity of water at each temperature) for all four loops at pH 7.4 (Fig. 2 A and C) and pH 3.5 (Fig. 2 B and D). At pH 7.4, T = 40° C, the intercept of the line is consistent with 1/k_R = 0 so k_R cannot be determined, but the lower limit of this rate can be estimated from the error in the intercept. There is remarkable similarity for all loops at pH 7.4, whereas k_R varies significantly at pH 3.5. The familial mutation A30P added to the 39W-69C mutant is plotted as well on Fig. 2 A and C. The reaction-limited rates for the mutation are similar but the diffusion-limited rates are approximately two times smaller. These results suggest that mutating A30 to proline slows diffusion.

Fig. 2.

Reaction-limited (A) and diffusion-limited (C) rates for various loops. (A and C) The rates versus temperature at pH 7.4. At T = 40° C, the dashes represent the lower limit of k_R as determined by inverse error of the intercept. The diffusion-limited rates are calculated for the viscosity of water at each temperature. (B and D) The rates for all temperatures at pH 3.5. Because 1/k_obs at pH 3.5 is temperature independent, plots of k_R and k_D+ versus T would be flat lines. The diffusion-limited rates are calculated for η = 1 cP (20° C in water). The points in B are reaction-limited rates calculated from the probability distributions shown in Fig. S9.

To quantitatively analyze these results we turn to a theory by Szabo, Schulten, and Schulten (SSS) which models intrachain dynamics as diffusion on a one-dimensional potential determined by the probability of intrachain distances [P(r)] (31). The measured reaction-limited and diffusion-limited rates are given by (19)

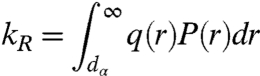[3]

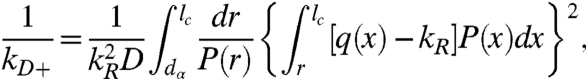[4]

where r is the distance between the tryptophan and cysteine, D is the effective intramolecular diffusion constant, and q(r) is the distance-dependent quenching rate. The distance-dependent quenching rate for the Trp-Cys system drops off very rapidly beyond 4.0 Å, so the reaction-limited rate is mostly determined by the probability of the shortest distances. Very generally, k_R and k_D+ are both inversely proportional to the average volume of the chain and k_D+ is directly proportional to D. Therefore the increase in k_R with temperature at pH 7.4 reflects a collapse of the chain, much larger than has been seen with other unstructured peptides but similar to the collapse observed for unfolded proteins as denaturant is reduced. The reaction-limited rates at pH 7.4 are remarkably similar for all loops at T = 0–30° C, suggesting the chain is collapsing uniformly as temperature is increased. At pH 3.5, the NAC region is significantly higher than the other loops and the N-terminal loop is the lowest.

Using SSS theory, we can directly compare measured to calculated k_R using Eq. 3 and an equilibrium probability distribution of Trp-Cys distances, P(r). Although there are many methods to generate an ensemble of protein conformations, we use two methods that are somewhat realistic and also are relatively efficient at sampling so that accurate probabilities at short distances (r < 10 Å) can be obtained. Below we discuss two methods to determine P(r), all-atom molecular dynamics and a Monte Carlo method to generate realistic polymer chains (backbone only). Once an accurate P(r) for each solvent condition has been determined, we can use it and the measured k_D+ to determine the diffusion coefficient, D using Eq. 4.

Using molecular dynamics with implicit solvent we can simulate all possible physically realistic conformations, given an accurate force field and enough sampling time. Previous work on protein L showed that fully sampling all conformations depends on the intramolecular diffusion coefficient and can take cumulative simulation times much longer than 1 μs (25). Therefore we completed 400 simulations of approximately 200 ns each and combined all Trp-Cys distances (measured every 200 ps) without bias to produce the distributions shown in Fig. S9. These distributions were used to calculate reaction-limited rates using Eq. 3 and shown as circles in Fig. 2B. Although the simulation temperature was set to 273 K, the predicted k_R are in better agreement with rates measured at higher temperatures or low pH. Fig. S9 also shows nonuniform compaction across the chain, with the interior loops more compact than the terminal loops. Also, only the 112W-140C distribution is approximately a Gaussian; the other loops are highly skewed to shorter distances. Nevertheless, the trend of the reaction-limited rates is similar to that measured at pH 3.5 as shown in Fig. 2B.

Because the distributions in Fig. S9 required about 2 mo of computation time (using 40 GPU processors in parallel, where GPU is the graphical processing unit), it was not practical to vary the temperature or solvent conditions. Therefore we also used a much less computationally expensive model, the energy reweighted worm-like chain (WLC) (21). Ten million WLCs with excluded volume were generated and each conformation is scored based on the number of favorable intrachain interactions of similar hydrophobicity using the real sequence of α-synuclein (SI Materials and Methods). Those with the most favorable close-range interactions were given more weight within the distribution than those with the least, thereby shifting the distribution toward shorter distances (see Fig. S10). This model has one adjustable parameter (σ), which can be tuned to produce a distribution that best matches the measured k_R using Eq. 3. Because k_R could not be significantly determined for any measurement at pH 7.4 T = 40° C and 69C-94W at pH 3.5, σ was set to an arbitrary high value which produced k_R larger than the estimates of the lower limits (see Table S3 for values of σ for each loop and condition).

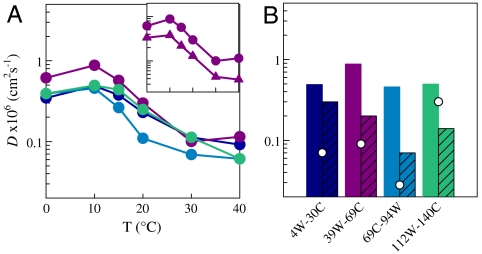
The correct P(r) [or Z(r) in Eq. S7] for each solvent condition, the measured k_D+ and Eq. 4 are used to determine the effective intramolecular diffusion coefficient, D. Fig. 3 shows the diffusion coefficients determined for each loop and each temperature and pH value. D was also calculated for the P(r) from MD simulation using the measured k_D+ at T = 30° C, pH 7.4. D is fairly similar for all loops and drops with temperature. Because k_R at T = 40° C cannot be determined outside error, the calculated k_R should be considered lower limits and D upper limits. Compared to T = 10° C, intramolecular diffusion drops by at least an order of magnitude at T = 40° C, conditions that begin to favor aggregation. At pH 3.5, the diffusion coefficients vary across the chain with the NAC region being the slowest, a reversal of the trend at neutral pH. Finally, the A30P mutation decreases D in the 39–69 loop by about twofold.

Fig. 3.

Diffusion coefficients calculated from measured k_D+ and probability distributions of Trp-Cys distances calculated from the energy reweighted WLC model for (A) pH 7.4 at various temperatures and (B) pH 3.5 at all temperatures (hatched bars). D at pH 7.4 and T = 10° C are shown for comparison in B. The colors correspond to the different loops as designated in Fig. 2. The points are D calculated from probability distributions shown in Fig. S9 and the measured k_D+ at pH 3.5 (Fig. 2D). (Inset) Comparison of diffusion coefficients between 39W-69C (circles) and 39W-69C A30P (triangles).

Discussion

In this work we have attempted to understand the basis of aggregation by investigating the intramolecular dynamics of an intrinsically disordered protein, α-synuclein. Compared to other unfolded proteins, α-synuclein is unusual. With most denatured proteins or intrinsically disordered sequences, the reaction-limited rate increases less than twofold over T = 0–40° C (20, 21, 23), but at pH 7.4 α-synculein increases at least 10-fold and the temperature dependence is highly nonlinear. This increase suggests significant collapse of the unfolded ensemble. Uversky et al. observed an increase in helical structure with increasing temperature at neutral pH (14). The collapse observed here suggests that the helical structure is neither rigid nor contiguous (which would increase intrachain distances compared to a random coil) but rather many small, transient helices that accompany nonlocal intrachain contacts. However, even with the large increase in k_R with temperature, the actual change in the size of the chain is fairly modest. Fig. S2 shows the measured FRET of the protein labeled with fluorophores at residues 9 and 70 increases approximately 10% from T = 0–40° C. Using the reweighted WLC model for the 39W-69C loop, the average Trp-Cys distance decreases from 33.4 to 27.6 Å over T = 0–40° C. This decrease is similar to the decrease in R_G measured by FRET in acid denatured BBL, which was attributed to the hydrophobic effect (32).

Whereas the reaction-limited rates were virtually identical for each loop at pH 7.4, they vary by over an order of magnitude at pH 3.5 and have minimal temperature dependence. These characteristics can also be attributed to some sort of change in nonlocal structure, particularly due to the change in charge distribution from neutral to low pH. The N terminus maintains its slight positive charge over this range, but the negatively charged C terminus at pH 7.4 becomes more neutral at pH 3.5, allowing more collapse over the second half of the chain. Interestingly, the loss of charge in the C-terminal region has the biggest effect on the NAC, which suggests that the hydrophobicity within the NAC would normally force significant compaction, but at neutral pH, interactions with the C-terminal charges keep the NAC from collapsing on itself.

The most unusual aspect of α-synuclein dynamics is the dramatic drop in diffusion coefficient with temperature, which suggests the chain undergoes a glass transition. At pH 3.5 all temperature dependence disappears, suggesting the chain is already in the glassy state. Compared to pH 7.4, T = 10° C, the diffusion coefficient in the NAC region at pH 3.5 is approximately 10 times smaller. Whereas there is a general trend between compaction and slow diffusion, compaction and diffusivity are not perfectly correlated. For example, the transition temperature found from fits to a glass model (see Table S2) of k_R are about 100–200 K lower than for k_D+, implying the chain collapses at a much lower temperature than diffusion slows. Also, the N-terminal loop has about the same compaction at pH 3.5 as at low temperature, pH 7.4, but the diffusion coefficient is about two times lower at pH 3.5. Finally, A30P reduces only the diffusion coefficient. These observations imply that structural probes of compaction, such as FRET and paramagnetic resonance enhancement, and intramolecular diffusion are complementary probes of the unfolded ensemble.

Many NMR measurements have demonstrated significant compaction in α-synuclein compared to an ideal random coil. Dedmon et al. showed strong interactions between the highly charged C terminus and the NAC region (33). Cho et al. showed that compaction increased between the C terminus and the NAC at low pH and the C terminus became more rigid, a similar conclusion to our finding that diffusion slows (6). Recently Trexler and Rhoades measured various intramolecular distances by single molecule FRET and showed substantial collapse at low pH but the effect was largest for the C terminus (34). These studies are broadly in agreement with our results here in which k_R increases substantially between pH 7.4, 20° C and pH 3.5 for 69C-94W and 112W-140C but not for 4W-30C and 39W-69C. Grupi and Haas have recently measured the temperature dependence of several fragments of the N-terminal and NAC regions of the chain using time-resolved FRET and determined end-to-end probability distributions. For most segments, there was a slight compaction and broadening of the distributions, in qualitative agreement with our measured increase in k_R with temperature (35). This broadening suggests the possibility that the trend in Fig. 2A does not represent significant compaction, but only a change in the probability at the shortest distances, but because the FRET studies were conducted without the full chain, it is hard to compare these results quantitatively.

Previous work on this sequence using intramolecular contact formation has obtained results at neutral pH similar to ours. Lee et al. measured rates of Trp triplet quenching by nitro-tryosine of 1.6–5.3 × 10⁵ s^-1 for various loops, similar to our k_obs (36). This quenching mechanism is likely not diffusion-limited, but reaction-limited rates were not determined. Later work estimated D at approximately 20° C in the NAC approximately 2–3 × 10^-6 cm² s^-1, slightly faster than measured in this work (37). Recently Grupi and Haas directly measured diffusion-limited rates on several peptide fragments and calculated D that are 20% to 10 times higher than our values (17). These results suggest that dynamics of the full chain, particularly at the N terminus, are significantly slowed by interactions with residues distant in sequence.

Can the large changes in the reconfiguration time of unstructured α-synuclein explain the significant increase in aggregation rates with solvent conditions or mutation? We can estimate a time for the disordered chain to completely reconfigure as diffusion of individual residues across the diameter of the chain, τ = (2R_G)²/4D, where R_G is the radius of gyration given by the appropriate energy reweighted WLC model. Table 1 gives these values for different loops, conditions and for bimolecular association. Thus at pH 7.4, T = 10° C, when aggregation is slow, reconfiguration is 30 times faster than bimolecular association, and at pH 3.5, when aggregation is fast, the rates of reconfiguration and bimolecular association are within a factor of 10. To relate intramolecular diffusion and aggregation, we can construct a model in which the reconfiguration time allows sampling of aggregation-prone disordered conformations (i.e., hydrophobes are solvent-exposed), which can combine to form a bimolecular encounter complex. If one member of the complex can reconfigure to a non-aggregation-prone conformation, the complex comes apart. Otherwise, the complex converts irreversibly to an oligomer. Chen et al. used this model to show that the rate of oligomer formation depends strongly on the relative speed of reconfiguration compared to bimolecular association; aggregation is fastest when τ and 1/k_bi are the same order of magnitude and slower when τ is much faster or slower than 1/k_bi (22). This model shows that oligomerization is kinetically controlled by intramolecular diffusion. However, most studies measure the formation of fibrils by thioflavine T (ThT) fluorescence or other methods. Therefore, this model can be expanded to include subsequent steps in aggregation to yield a lag phase 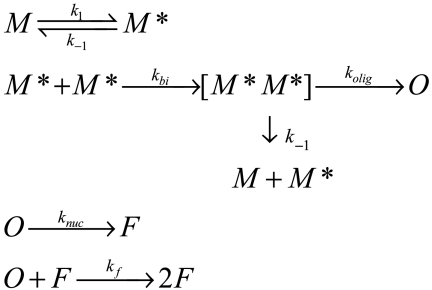where M and M^∗ are the nonaggregation and aggregation-prone monomer conformations, respectively, [M^∗M^∗] is the encounter complex, O is the oligomer state, and F is the fibrillar state.

Table 1.

Rates of reconfiguration and bimolecular association

Sequence	Conditions	RG (Å)	D (cm2 s-1)	τ (μs)	k1 (s-1)
39W-69C	pH 7.4, T = 10° C	33.1	8.8 × 10-7	0.12	8.0 × 106
39W-69C	pH 7.4, T = 40° C	30.9	1.1 × 10-7	0.87	1.2 × 106
69C-94W	pH 3.5, all T	30.4	7.0 × 10-8	1.3	7.7 × 105
39W-69C A30P	pH 7.4, T = 40° C	30.3	3.0 × 10-8	3.1	3.2 × 105
Bimolecular		250 (100 μM)	1.0 × 10-6	6.2	kbi = 1.6 × 105

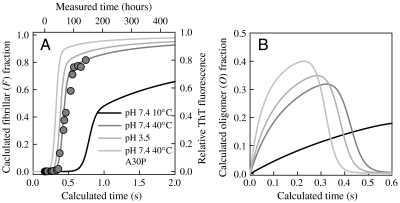
Using the values for k₁ = k_-1 and k_bi in Table 1, k_olig = 100 s^-1, k_nuc = 1 × 10^-3 s^-1, and k_f = 100 s^-1, the model can be solved over several seconds (a larger separation of timescales between k₁ and k_f makes the model computationally intractable). Fig. 4A shows the formation of the fibril state, F, is much slower for the faster reconfiguration rate at low temperature and neutral pH than for high temperature, low pH, or with the mutation A30P. Aggregation has been experimentally shown to increase with temperature or with lower pH, but Fig. S3B shows that aggregation of A30P is actually significantly slower than the wild type. However, the model shows that the fibrillar fraction, which is what is detected by ThT fluorescence, depends on more rates than just k₁. A30P may have slower k_nuc and k_f than the wild type. Yonetani et al. has shown that fibrillization of A30P and wild type appear to be different processes (38), and Conway et al. showed that an earlier stage of oligomerization is actually faster for A30P than wild type (39). Fig. 4B shows that the calculated formation of the O state for A30P is indeed faster than the wild type. The fact that bimolecular association appears to be fast whereas fibrillization is slower for A30P, a mutation associated with early onset Parkinson’s disease, than wild type lends support for the idea that this disease is caused by the earliest stages of aggregation and that these stages are controlled by intramolecular diffusion.

Fig. 4.

(A) Fibrillar fraction calculated from the model given in the text (state F) for 39W-69C at pH 7.4, T = 10° C (black line), pH 7.4, T = 40° C (dark gray line), 69C-94W at pH 3.5 (medium gray line), and 39W-69C A30P at pH 7.4, T = 40° C (light gray line) using the rates given in Table 1. The circles are experimental measurements of aggregation of mutant 69C-94W detected by ThT fluorescence (right and top axes) scaled to match the calculated rates (left and bottom axes). (B) Oligomer fraction (state O) calculated from the model using the same rates as A.

Conclusion

We have demonstrated a correlation between aggregation propensity of α-synuclein and intramolecular diffusion, indicating that aggregation, a days-long process, is under kinetic control by monomer reconfiguration, a microsecond process. This result does not rule out the potential effect of structure on later stages of aggregation, particularly nucleation of fibril formation. But given the difficulty in determining the conformation of aggregation precursors, the findings in this work suggest a unique path to understanding aggregation.

Materials and Methods

The plasmid for α-synuclein was a gift from Gary Pielak, University of North Carolina, Chapel Hill, NC. The protein was mutated, expressed, and purified as described in the SI Materials and Methods. The purified protein was dissolved to a concentration of 20 μM in either 25 mM sodium phosphate buffer (pH 7.4) or 25 mM sodium acetate buffer (pH 3.5), 1 mM TCEP and various sucrose concentrations that had been bubbled with N₂O to eliminate oxygen and scavenge solvated electrons created in the UV laser pulse.

Triplet lifetime decay kinetics were measured with an instrument similar to one described previously (23). Briefly, the tryptophan triplet is populated simultaneously with the singlet state within a 10 ns pulse of laser at 289 nm created from the fourth harmonic of an Nd:YAG laser and a 1 m Raman cell filled with 450 psi of D₂ gas. The triplet population is probed at 441 nm by a HeCd laser (Kimmon). The probe and a reference beam are measured by silicon detectors and combined in a differential amplifier (LeCroy, DA 1853A) with an additional stage of a 350 MHz preamplifier (Stanford Research Systems, SR445A). The total gain is 50×. The temperature and viscosity were controlled as described previously. Measurement of each sample at six temperatures takes approximately 20 min, so aggregation during this time is minimal. The viscosity of each solvent at each temperature was measured independently using a cone-cup viscometer (Brookfield Engineering).

CD, ThT fluorescence, FRET, and modeling methods are described in SI Materials and Methods.