Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2012 Jan 11;28(5):664–671. doi: 10.1093/bioinformatics/bts005

Predicting folding free energy changes upon single point mutations

Zhe Zhang 1, Lin Wang 1, Yang Gao 1, Jie Zhang 1,2, Maxim Zhenirovskyy 1, Emil Alexov 1,*
PMCID: PMC3289912  PMID: 22238268

Abstract

Motivation: The folding free energy is an important characteristic of proteins stability and is directly related to protein's wild-type function. The changes of protein's stability due to naturally occurring mutations, missense mutations, are typically causing diseases. Single point mutations made in vitro are frequently used to assess the contribution of given amino acid to the stability of the protein. In both cases, it is desirable to predict the change of the folding free energy upon single point mutations in order to either provide insights of the molecular mechanism of the change or to design new experimental studies.

Results: We report an approach that predicts the free energy change upon single point mutation by utilizing the 3D structure of the wild-type protein. It is based on variation of the molecular mechanics Generalized Born (MMGB) method, scaled with optimized parameters (sMMGB) and utilizing specific model of unfolded state. The corresponding mutations are built in silico and the predictions are tested against large dataset of 1109 mutations with experimentally measured changes of the folding free energy. Benchmarking resulted in root mean square deviation = 1.78 kcal/mol and slope of the linear regression fit between the experimental data and the calculations was 1.04. The sMMGB is compared with other leading methods of predicting folding free energy changes upon single mutations and results discussed with respect to various parameters.

Availability: All the pdb files we used in this article can be downloaded from http://compbio.clemson.edu/downloadDir/mentaldisorders/sMMGB_pdb.rar

Contact: ealexov@clemson.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Protein folding free energy is an important characteristic directly related to protein stability. Some proteins are very stable, while others unfold under very small perturbation of the native conditions. In both cases, not all amino acids contribute equally to the protein stability and interactions, some of them being crucial and frequently termed ‘hot spots’ (Acuner Ozbabacan et al., 2010; Dixit et al., 2009) while others contributing very little to the folding free energy. However, the contribution of a given amino acid to protein stability cannot be easily predicted, even if the 3D structure of the corresponding protein is available. Therefore, developing methods to improve predictions of hot spots and even more to assess the contribution of a given amino acid to the folding or binding free energy is of great importance (Gromiha, 2007; Moreira et al., 2007). Accurate predictions [see Khan and Vihinen (2010) for comparison of different methods] will be beneficial for understanding the role of individual amino acids on protein stability and to rationalize the effects of non-synonymous single nucleoside polymorphism (Shastry, 2009; Teng et al., 2008) and missense mutations on the protein fold (Witham et al., 2011; Zhang et al., 2010, 2011).

Of particular interest is predicting the effects caused by disease-causing missense mutations since the function of protein can be affected in a variety of ways (Teng et al., 2008; Yue and Moult, 2006; Yue et al., 2006). Among them, the most common effect is changing protein stability, i.e. destabilizing or stabilizing the wild-type protein fold (Capriotti et al., 2005a; Karchin et al., 2005; Ramensky et al., 2002; Wang and Moult, 2001, 2003; Ye et al., 2006; Zhang et al., 2011; Zhou et al., 2004), in addition to altering the macromolecular interactions (Teng et al., 2009), hydrogen bond network (Chen et al., 2001; Hunt et al., 2008; Zhang et al., 2010) and many other effects (Eriksson et al., 1992; Xu et al., 1998). However, the predictions about the changes of the folding energy should not only indicate if they favor the stability or not, but also the predicted absolute magnitude should be accurate as well to allow to distinguish between disease-causing and harmless mutations. Because of this significance, efforts were devoted to develop methods and approaches to evaluate the stability changes upon amino acid substitutions, but despite of the efforts, accurate calculations of folding free energy are still a challenge (Beveridge and DiCapua, 1989).

Currently, there are several distinctive approaches that were developed to predict the protein stability changes due to mutations. They can be classified into four categories: (i) first principle methods, which calculate the folding free energy changes based on detailed atomic models (Bash et al., 1987; Duan and Kollman, 1998; Khare et al., 2006; Kuhlman and Baker, 2000; Lee, 1995; Lee and Levitt, 1991; Miyazawa and Jernigan, 1994; Pitera and Kollman, 2000; Prevost et al., 1991; Tidor and Karplus, 1991; Vorobjev and Hermans, 1999) and may be quite computationally expensive and may not be applicable in cases of large set of mutations (Kollman et al., 2000). (ii) Methods using statistical potentials (BenNaim, 1997; Thomas and Dill, 1996), which were successfully used to estimate the change of protein stability upon the mutations (Gilis and Rooman, 1996, 1997, 1999, 2000; Hoppe and Schomburg, 2005; Ota et al., 2001; Topham et al., 1997; Zhou and Zhou, 2002). (iii) Methods utilizing empirical potential combining both physical force fields and free parameters fitted with the experimental data (Bordner and Abagyan, 2004; Domingues et al., 2000; Munoz and Serrano, 1997; Takano et al., 1999; Villegas et al., 1996; Xiong, 1986). (iv) Machine learning methods, generating predictions based on learned relations delivered from the training set (Carpriotti et al., 2004; Casadio et al., 1995; Frenz, 2005; Joachims, 2002; Masso and Vaisman, 2008).

The approaches, utilizing physics-based energies to calculate the folding free energy or its change upon mutation(s), have to address the issue of how to model the unfolded state as well. This is non-trivial task, since the unfolded state, perhaps, has different characteristics for each particular protein and may differ depending on the experimental conditions (for example, thermal unfolding versus urea unfolding). Over the years, various approaches were reported in the literature, some of them starting from the original X-ray structure and modeling unfolding by either increasing van der Waals radii of the atom (Elcock and McCammon, 1998) or the temperature above the normal (Ma and Nussinov, 2003; Yan et al., 2010). Others, starting from extended amino acid chain and modeling unfolded as a Gaussian chain (Zhou, 2002, 2003; Zhou et al., 2004) or quasi-random distribution of amino acids (Kundrotas et al., 2002a, 2002b). In terms of assessing the difference between unfolded state energy of wild type (WT) and mutant protein, alternative approaches assumed either no interactions in unfolded state (Zhang et al., 2010, 2011) or interactions limited within a short segment of residues centered at the site of mutation (Alexov, 2004; Ofiteru et al., 2007). All the above-mentioned methods have advantages and disadvantages with respect to the computational time and the applicability to full-scale energy calculations.

Typically, a modeling utilizing all-atoms energy calculations is accomplished using a particular force field and plausible concern could be to what extent it can be applied in conjunction with the another force field. In the past, we were attempting to address such a question in terms of electrostatic component protein–protein binding energy (Talley et al., 2008) and effect of single point mutations on protein stability and interactions (Zhang et al., 2010, 2011). In our hands, the trend of the results was generally similar among different force fields, but individual cases were frequently strongly force field dependent. Such an observation motivated us to suggest averaging over the results obtained with different force fields (Zhang et al., 2010, 2011), an approach that we apply in this study as well.

In the past years, several prominent methods and web servers for predicting free folding energy changes upon mutations have immerged. One of them is Eris (Ding and Dokholyan, 2006; Yin et al., 2007a, 2007b), developed by Dokholyan and coworkers, which utilizes Medusa force field (Ding and Dokholyan, 2006). It was tested against 595 mutants with experimentally available data and the resulting root mean square deviation (RMSD) was reported as 2.4 kcal/mol. Recently, Zhou and Zhou constructed a residues specific all-atom potential of mean force from 1011 protein structures and used it to calculate the folding free energy change for 895 mutants (Zhou and Zhou, 2002). The benchmarking resulted in RMSD of 1.52 kcal/mol. The FoldX is perhaps the most popular web server (Schymkowitz et al., 2005) for predicting folding free energy changes. It was developed by Serrano and coworkers. FoldX is based on empirical potential function and was tested against 667 mutants (Guerois et al., 2002). From machine learning algorithms, the most prominent is I-Mutant (version 2.0), developed by Casadio and coworkers. It was benchmarked against 2087 data points (Capriotti et al., 2005b).

In this work, we apply molecular mechanics Generalized Born (MMGB) approach to estimate the folding free energy of the WT and the mutants in conjunction with a specific model of the unfolded state. Since it is established in the literature (Benedix et al., 2009) that MMGB/PB approaches tend to overestimate the free energy changes, we scale down the originally predicted changes by a linear function and optimize the weights against experimental data points of 662 mutants. To reduce the sensitivity of the results with respect to the particular choice of force field, the calculations are done with three force field parameters (Charmm, Amber and OPLS) and then results averaged. Then the optimized weights were used to carry a blind test against 447 experimentally determined folding free energy changes resulting in RMSD of 1.78 kcal/mol. The slope of the corresponding fitting line was 1.0382 with the correlation coefficient of 0.3 and the SD was 0.54 kcal/mol.

2 MATERIALS AND METHODS

2.1 Experimental dataset

The experimental dataset was derived from the ProTherm website (Thermodynamic Database for Proteins and Mutants: http://gibk26.bio.kyutech.ac.jp/jouhou/Protherm/protherm_search.html) (Bava et al., 2004; Chen et al., 2002; Gromiha and Sarai, 2010). The ProTherm database provides information of various experimental conditions including pH of the experiment. For the purpose of this study, we choose the experimental pH to be between 6 and 8, assuming that at such pH the ionizable residues will have default charged states. No pKa calculations were performed to either explore experiments done at low/high pH or to adjust charges of amino acids with pKa shifted away from the standard values. This was done to avoid the effect of plausible errors in assigning charges of titratable groups. In addition, only cases of single mutations were collected resulting in 2395 experimentally determined changes of the folding free energy (ΔΔG).

During the initial screening of the data, it was noticed that for some mutations the change of the folding free energy was reported by either different sources or different experimental methods [for example, the change of the folding free energy for the mutant C112S in azurin from Pseudomonas aeruginosa (the pdb ID: 5AZU) (Nar et al., 1991) has reported 15 times and the ΔΔG values range from −4.4 kcal/mol to −0.24 kcal/mol at pH of 7.5]. In all such cases, including cases with available data for different pH (6 < pH < 8) and temperature, we took the average value, since there is no indication which data point is the most reliable.

The ProTherm database provides the Protein Data Base (PDB) identifiers for the corresponding 3D structures of the proteins for which experimental ΔΔG were collected in the database. These structures are the core of our approach. However, frequently the 3D structures in PDB have missing atoms, residues or entire structural segment. In order to carry our analysis, we need polypeptide chain not to have missing atoms, residues and gaps. To fix such structural defects, we used Profix software, developed by Barry Honig lab (see next section for details). During this procedure, some structures with unusual numbering or long missing segments failed to be fixed properly. They were deleted from the initial dataset. In addition, our protocol requires the wild-type structure and the structure of the corresponding in silico built mutant to be energy minimized with TINKER (Ponder, 1999) (see next section for details). It was noticed that several proteins failed to be minimized because TINKER generated identical hydrogen coordinates [for example, maltodextrin/maltose-binding protein, pdb ID: 3MBP (Quiocho et al., 1997) and barnase, pdb ID: 1BNI (Buckle et al., 1993)]. The proteins corresponding to either of the above cases were filtered out from our dataset resulting in a final dataset containing 1109 mutants from 60 wild-type proteins.

2.2 Fixing structural defects and in silico mutant generation

The PDB files were downloaded from the Protein Data Bank (Berman et al., 2000; Kouranov et al., 2006). However, it was found that frequently the corresponding structures had either missing atoms or residues. Thus, the first task was to generate in silico these missing atoms back to the protein according to the protein sequence record located at the top of each pdb file. It was done by ‘Profix’, a program in Jackal package (http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software:Jackal), which can be downloaded from Barry Honig's Lab, Columbia University. The parameters that were used in our approach are Amber force field in conjunction with the option of fixing the structural defect using heavy atoms representation (no hydrogens). The hydrogen will be added later with ‘pdbxyz’ module in the TINKER package (Ponder, 1999).

All the mutants were made by the program SCAP (Xiang and Honig, 2001) in Jackal package as well. SCAP-generated mutations were done with both Amber and Charmm force field using the option ‘heavy atom modeling’. No significant differences were found for the predictions made with Amber and Charmm force fields, but this dual option was used in cases where SCAP failed to generate mutant side chain with Amber/Charmm force field and vice versa.

2.3 Folding free energy calculation

The folding free energy changes upon single point mutations were calculated as described in our previous works (Witham et al., 2011; Zhang et al., 2011; Zhang et al., 2010). Here for consistency we briefly outline this approach (Fig. 1). The folded state is considered to be represented by the energy minimized structure, either the WT or in silico-generated mutant. The unfolded state is considered to be represented by two structural elements: (i) a structural segment of length ‘x’ (x=3, 5, 7, 9, 13,…) centered at the mutation site and (ii) rest of the protein. Assuming that the residue at the site of mutation does not interact with the rest of protein, this approach will result in identical energies of unfolded state ‘b’ of WT and mutant protein, i.e. the unfolded state that excludes the structural segment of length ‘x’.

Fig. 1.

Fig. 1.

Open in a new tab

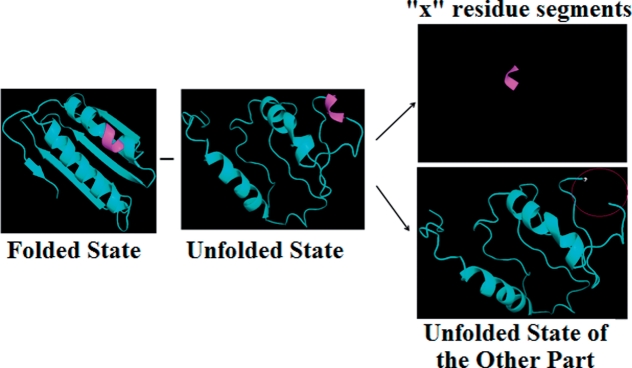
Ribbon presentation of the approach of modeling folded and unfolded states representative structures. The magenta part represents the ‘x’ residue segments, and the cyan part represents the ‘the rest of protein’. The unfolded state is split into two parts which are ‘x residue segments’ and ‘unfolded state of the rest of protein’.

Technically, it was done by energy minimizing all WT and mutants proteins using the program ‘minimize’ in TINKER package (Ponder, 1999) using the Limited Memory BFGS Quasi-Newton Optimization algorithm and we set the final RMS gradient (G-RMS) 0.01 per atom. The solvent was modeled using the Still Generalized Born model and the protein internal dielectric constant was set as 1.0. In this work, all the protein structures were minimized with three force field parameters, such as Amber98 (Case et al., 2005), Charmm27 (Brooks et al., 2009) and OPLS (Jorgensen and Tiradorives, 1988). After a successful minimization, a length of ‘x’ residues segments (x = odd numbers like 3, 5, 7, 9, 13,…, for example x=3 means three residue segments) at the center of the mutation site is extracted from the minimized structures (both WT protein and the mutants). After this step, all minimized structures (the entire protein and ‘x’ residue segment) were subjected to ‘analyze’ module in TINKER package for calculating the potential energy, and then the results were averaged among the three force field parameters to test the sensitivity of the results.

The folding free energy of both the WT protein and the mutants is calculated as:

graphic file with name bts005m1.jpg (1)

where G(folded) is the total potential energy of the folded state and the G(unfolded) is the total potential energy of the unfolded state. The free energy, G(unfolded), of unfolded state, is split into two terms, G0(unfolded) and Gx(unfolded), as discussed above and in our previous works (Witham et al., 2011; Zhang et al., 2010, 2011). Gx(unfolded) is the free energy of the unfolded state of ‘x’ residue segments at the center of mutation site, whereas G0(unfolded) is the free energy of the unfolded state of the rest of protein (Fig. 1). Under our assumption, the G0(unfolded) is identical for WT and mutants and cancels out in Equation (2) and therefore does not need to be calculated.

The folding free energy change due to a mutation is calculated with the following equation:

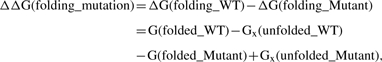graphic file with name bts005m2.jpg (2)

where ΔΔG(folding_mutation) represents the folding free energy change due to a mutation; ΔG(folding_WT) and ΔG(folding_Mutant) are folding free energy of the WT protein and the mutant, respectively.

The ΔΔG(folding_mutation) are calculated with the three force field parameters mentioned above and then results averaged:

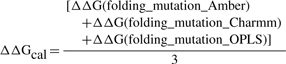graphic file with name bts005m3.jpg (3)

where ΔΔG(folding_mutation_Amber), ΔΔG(folding_mutation_ Charmm) and ΔΔG(folding_mutation_OPLS) are the folding free energy change due to a single mutation calculated with the force field parameters Amber98, Charmm27 and OPLS, respectively.

Here four assumptions were made: (i) we assume that missense mutation affects only a small region surrounding the mutation sites, which is described by ‘x’ residue segments part, and cause negligible effect to the rest of the protein, hence G0(unfolded) will be the same for WT protein and the mutants and will cancel in Equation (2); (ii) the entropy in the WT and mutant proteins are considered to be very similar, therefore it will cancel out in Equation (2) as well. The applicability of this assumption will be discussed later in this article; (iii) the non-polar term of the solvation energy is not taken into account due to its relatively small contribution to the energy and the fact that the accessible surface area of the WT and the mutant protein are very similar (single point mutation); (iv) the approach is based on single-point calculations where the folded and unfolded states are represented by a structure instead of ensemble of structures. This assumes that the potential wells do not change upon the mutation.

2.4 Obtaining the fitting weights

The above-described approach is essentially a simplified version of the MMGB method (Hou et al., 2011; Kollman et al., 2000; Still et al., 1990) with a specific model of unfolded state (Witham et al., 2011; Zhang et al., 2010, 2011). It is recognized that MMGB method tends to overestimate the magnitude of the predicted free energy changes (compared with the experimental data) and because of that the predicted ΔΔG may have to be scaled to match the experimentally determined changes of the folding free energy. Here we carry the following optimization procedure to minimize the RMSD between the scaled calculated results and the experimental data. The calculated ΔΔGcal are scaled by a linear function with two adjustable parameters ‘a’ and ‘b’ and the resulting scaled ΔΔG (sΔΔG) is:

graphic file with name bts005m4.jpg (4a)

The RMSD is calculated by Equation (4b) below using the scaled ΔΔG (sΔΔG):

graphic file with name bts005m5.jpg (4b)

where ‘n’ is the number of data points; ΔΔGcal and ΔΔGexp are calculated and experimental ΔΔG, respectively. The optimal values of the adjustable parameters ‘a’ and ‘b’ are obtained by the regular conditions of finding optimum:

graphic file with name bts005m6.jpg (5)
graphic file with name bts005m7.jpg (6)

Solving Equations (5) and (6) with respect to the adjustable parameters ‘a’ and ‘b’ results in the following expressions:

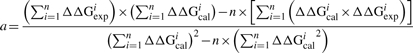graphic file with name bts005m8.jpg (7)
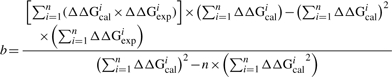graphic file with name bts005m9.jpg (8)

For the purpose of this work, the database of experimentally determined ΔΔG is split into two parts: training (60%) and test (40%) sets. The training set was used to find the optimal values of the parameters ‘a’ and ‘b’, whereas the test set was used for benchmarking. The selection of the sets was done by ranking the wild-type protein PDB ID based on alphabet and chose the first 37 wild-type protein with 405 mutants as the part of the training database. The next protein in the dataset with respect to the alphabetical order is the staphylococcal nuclease (PDB ID: 1STN) (Hynes and Fox, 1991) which has 537 mutants, almost half of the whole database. In our analysis, we refer to the mutations as mutation involving charged residue (for example, A → E), mutations do not involving charged residue (for example, A → L), mutations preserving the charge (for example, E → D) and mutations reversing the charge (for example, E → K). Since mutations in the 1STN represent such a significant fraction of the entire dataset, the cases for the training set were selected to have proportional presentation for the above-mentioned classes. Thus, there are 171 1STN mutations involving charged residue (for example, 1STN_E57G) and half of them, 85, were selected for the training set. There are 342 1STN mutations not involving charged group and half of them, 172, were included in the training dataset. The total number of mutations from 1STN protein that was included in the training set is 172+85=257, resulting in 662 cases in the final training set. Note that rare mutations in the 1STN protein, as two charges shift like 1STN_K28E and zero charge shifts like 1STN_E43D were not included in the training set, but included in the benchmarking set. In addition, the training and benchmarking sets were shuffled to test the sensitivity of the method (Supplementary Table S1).

3 RESULTS

3.1 Obtaining the optimal values of the parameters ‘a’ and ‘b’ using the training set

The changes of the folding free energy, ΔΔG, were calculated as described in Section 2 [Equation (2)] for the mutants in the training set. The length of the segment ‘x’ was fixed to be equal to three (x=3). The effect of different lengths is discussed latter in this article.

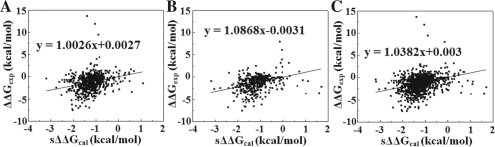
Using Equations (7) and (8) with 662 training data points to minimize the RMSD, one obtains the following values for the adjustable parameters: ‘a’ = 0.093 and ‘b’ =−1.088. Using these values, sΔΔG is calculated with Equation (4a) (Supplementary Table S2) and plotted against the experimental data of the training set (Fig. 2A). The slope of the fitting line is 1.0026, and the correlation coefficient R=0.28. The corresponding SD is 0.51 kcal/mol and RMSD between ΔΔGexp and sΔΔGcal is 1.79 kcal/mol. While the correlation coefficient is not impressive, mostly due to several outliers at the top of the figure, the corresponding RMSD is very good. Another indication of the success of the approach is that the slope of the fitting line is practically one and the free coefficient is practically zero and this was achieved without enforcing such conditions in the optimization procedure.

Fig. 2.

Fig. 2.

Open in a new tab

Comparison between experimental ΔΔG (ΔΔGexp) and scaled calculated ΔΔG (sΔΔGcal). The parameters of the fitting line are provided in the graph. (A) For the training database and the correlation coefficient R is 0.28; (B) for the blind test and the corresponding correlation coefficient R is 0.34; (C) for the entire dataset and the correlation coefficient R is 0.3.

3.2 Blind test using the obtained optimal values for ‘a’ and ‘b’ parameters

The blind test was done on the rest 40% of the data points (447 mutants) using the optimal parameters obtained above. Detailed results are provided in Supplementary Table S3. Figure 2B shows the correlation of experimental ΔΔG (ΔΔGexp) and scaled calculated ΔΔG (sΔΔGcal) for the blind test. The slope of the fitting line is 1.0868 and the free coefficient is practically zero. The corresponding correlation coefficient R is 0.34, the resulting SD is 0.58 kcal/mol and the RMSD between ΔΔGexp and sΔΔGcal is 1.76 kcal/mol. These results are very similar to the results obtained with the training set indicating the training was successful. The low correlation coefficient is due to the outliers on the right-hand side of the graph, wrongly predicted due to structural defects or deficiencies of our protocol.

3.3 Testing the method against the entire dataset

To further test the protocol and to demonstrate that the results are independent of the specific choice of the training and testing datasets, we benchmark the scaled ΔΔG, sΔΔG, against all experimental values collected for our work (Fig. 2C). The results are fitted with a straight line with slope practically one and zero free coefficient, again demonstrating the validity of the proposed method. The corresponding SD is 0.54 kcal/mol and the RMSD between ΔΔGexp and sΔΔGcal for the entire 1109 mutants is 1.78 kcal/mol.

To address the sensitivity of the results with respect to the choice of the training and benchmarking sets, the entire dataset was reshuffled and randomly split into two equal parts and then the above procedure was repeated. The results (Supplementary Table S1 a,b) show that the protocol is not sensitive to the selection of the training set.

3.4 Finding the optimal length of the segment ‘x’

The results above were obtained using a fixed length of three for the segment ‘x’. However, different lengths may generate better results. To test the effect of the segment ‘x’ length on the performance of our method, the calculations, including finding the optimal parameters ‘a’ and ‘b’ were repeated with x=3, 5, 7, 9, 11 and 13. The results are shown in Supplementary Figure S1.

The results shown in Supplementary Figure S1 and Table 1 indicate that sΔΔG calculated with different length of segment ‘x’ are practically the same. The calculations were repeated against the test dataset and entire dataset and the corresponding parameters are provided in Table 1 as well. One can see that the slopes of the fitting lines, the RMSDs and R values are practically unchanged as ‘x’ takes different lengths. More details are provided in the Supplementary Table S4: Supplementary Table S4 (a) for the Training Database, Supplementary Table S4 (b) for the Blind Test and Supplementary Table S4 (c) for the Entire Dataset.

Table 1.

Comparison of linear regression of ΔΔGexp versus sΔΔGcal with the sΔΔGcal performed with different length of residue segments for Training Database/Blind Test/Entire Dataset

Segments Slope R value RMSD
3 seg. 1.003/1.087/1.038 0.28/0.34/0.3 1.79/1.76/1.78
5 seg. 1.017/1.128/1.066 0.25/0.32/0.28 1.80/1.77/1.79
7 seg. 0.999/1.168/1.073 0.23/0.3/0.26 1.82/1.78/1.8
9 seg. 0.995/1.114/1.043 0.23/0.28/0.25 1.82/1.79/1.8
11 seg. 0.999/1.084/1.033 0.22/0.26/0.24 1.82/1.8/1.81
13 seg. 1.001/0.965/0.980 0.23/0.25/0.24 1.82/1.8/1.81
Open in a new tab

The parameters shown in Table 1 indicate the similarity of sΔΔGcal calculated with different length of segment ‘x’. However, a slight tendency is observed such that with the increase of the segment length, the RMSD tend to increase and the correlation coefficient to decrease. The optimal value is x=3.

3.5 Comparison with other existing methods

To the best of our knowledge, currently three methods dominate the field of predicting folding free energy change upon single point mutations: Eris (Ding and Dokholyan, 2006; Yin et al., 2007a, 2007b), FoldX (Guerois et al., 2002) and I-Mutant 2.0 (Capriotti et al., 2005b). It is desirable to compare our method against these leading solutions in order to assess the performance. Below we outline the results obtained with each of the above-mentioned solutions on our dataset.

Before presenting the results, it should be pointed out that the predictions with Eris were done with fixed backbone without pre-relaxation. Eris failed to generate results involving Cys, and therefore these cases were omitted from our analysis. With respect to FoldX and I-Mutant 2.0 generated predictions, we used the default parameters for the temperature and pH, namely T = 298K and pH = 7.0. The details of calculated results with Eris, FoldX and I-Mutant 2.0 are shown in Supplementary Table S5: Supplementary Table S5 (a) for the Training Database, Supplementary Table S5 (b) for the Blind Test and Supplementary Table S5 (c) for the Entire Dataset. The linear regressions of ΔΔGexp versus ΔΔGcal were performed and the comparison of these three methods is shown in Table 2 alone with our method. The receiver-operating characteristic curve was also calculated following the methodology described by Khan and Vihinen (2010) and results are shown in Supplementary Figure S2 and Table S6. Comparing with results reported in Khan and Vihinen (2010), one can see that sMMGB slightly underperforms at very low false positives (FPR < 0.1), but outperforms servers listed in the same reference at FPR >0.1.

Table 2.

Comparison of linear regression of ΔΔGexp versus ΔΔGcal with the ΔΔGcal performed with different methods

Slope R value RMSD Mean of ΔΔGcal SD
sMMGB T 1.003 0.28 1.79 −1.2 0.51
B 1.087 0.34 1.76 −1.17 0.58
E 1.038 0.3 1.78 −1.19 0.54
Eris T 0.554 0.29 3.92 −1.26 1.87
B 1.082 0.48 3.83 −1.38 1.93
E 0.754 0.36 3.89 −1.3 1.89
FoldX T 0.458 0.17 5.29 −1.2 1.87
B 0.683 0.34 3.57 −1.6 3.73
E 0.544 0.22 4.67 −1.23 1.86
I-Mutant T 0.518 0.32 1.86 −1.24 1.17
B 0.783 0.52 1.65 −1.00 1.24
E 0.624 0.4 1.78 −1.14 1.2
Open in a new tab

T: for the Training Database (662 mutants); B: for the Blind Test (447 mutants); E: for the Entire Dataset (1109 mutants).

Table 2 provides interesting trends of the performance of the methods. With respect to the mean value, all methods predict mean ΔΔG of similar magnitude. The mean value is negative indicating that all methods, including ours, tend to overpredict the destabilizing effect of mutations. In terms of the correlation coefficient, the best performer is the I-Mutant; however, all four methods result in poor correlation coefficient. The RMSD is an important characteristic of the predictions and our method together with I-Mutant outperforms the others. Similarly, the SD of our protocol is much smaller than other methods, including I-Mutant, indicating that our predictions are less scattered. Lastly, the slope of the fitting line is the best for our method, almost equal to one, whereas all other methods give much worst coefficients. Similar observations were made by excluding the data points used to train I-Mutant (Supplementary Table S7).

4 DISCUSSION

4.1 Analysis of scaled calculated sΔΔGcal

Summarizing the results of sMMGB predictions benchmarked against various datasets (Table 3), one can see that there is not much difference of the corresponding RMSDs, mean and SD of the corresponding distributions. The correlation coefficient in all cases is not impressive, but has a slight tendency to get better in the blind test, compared with the training dataset. However, the effect is small. The low correlation coefficient is due to relatively small fraction of outliers, which we choose not to remove from our analysis. In summary, the results indicate that the choice of the optimal value for the adjustable parameters ‘a’ and ‘b’ is not dataset specific and results in performance almost identical across different datasets. In addition, the optimal value for the ‘b’ parameter is small, about a unity, indicating that there is no significant constant shift in our predictions. The fact that the optimal adjustable parameter ‘a’ is close to 1/10 reflects the trend that standard MMGB approach overpredicts the energy changes by factor of 10.

Table 3.

The results of linear regression for training database, blind test and the entire dataset

Database Slope R value RMSD Mean of ΔΔGcal SD
Training database 1.0026 0.28 1.79 −1.2 0.51
Blind test 1.0868 0.34 1.76 −1.17 0.58
Entire dataset 1.0382 0.3 1.78 −1.19 0.54
Open in a new tab

4.2 Analysis of the performance of the sMMGB approach with respect to assumptions taken

The model of unfolded state in our approach assumes that the ‘x’ residue segments have the same conformation in folded and in unfolded states. Obviously, this is a simplification that does not necessary should hold for all cases. In addition, the probability of having different conformations in folded and in unfolded states should increase with the length of the segment ‘x’. In another words, large ‘x’ should make this assumption less valid. Indeed, Table 1 shows that the results correspond to such an expectation. With increase of the residue segment ‘x’ length, the correlation coefficient decreases from 0.34 (x=3) to 0.25 (x=13). Therefore, the optimal length is recommended to be x=3.

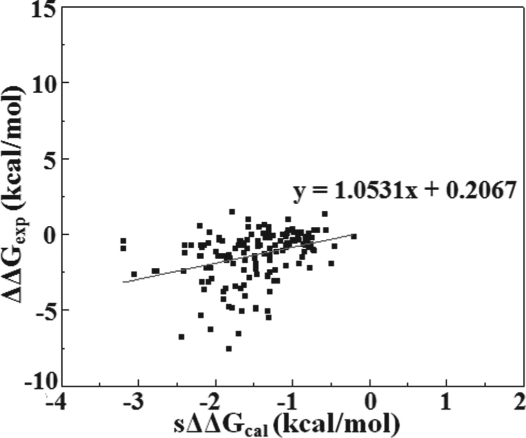
Another hypothesis which the sMMGB implies is to assume the entropy of the WT protein is very similar to that of the mutant. Thus, the entropy terms would cancel out in Equation (2). While it is beyond the scope of the present work to investigate the role of conformational ensembles of folded and unfolded states on the output of the predicted sΔΔGcal on such large set of mutations, here will present an analysis based on the side chain entropy estimation using side chain length as measure of the side chain entropy. Ala and Gly are two amino acids having much shorter/smaller side chains comparing to rest of the amino acids. Assuming that the entropy of an amino acid can be estimated from the degree of freedom of its side chain, the Ala and Gly residues should have much less entropy than the other types amino acids and substitution to another type of residues should involve change of the entropy. To probe the effect, we select mutations involving Ala/Gly from the entire dataset (termed ‘Entropy test data set’), and then use Equation (2) and the empirical parameters ‘a = 0.093’ and ‘b =−1.088’ to obtain sΔΔGcal. The data are shown in Figure 3 together with the parameters of the linear fit. Additional parameters are shown in Supplementary Table S8. The slope is 1.0531 and the correlation R is 0.35. The SD is 0.56 kcal/mol and RMSD is obtained as 1.6 kcal/mol. Comparing these values with previously obtained (Fig. 2), we see that they are very similar, i.e. the slope is quite close to unity, and RMSD is quite small. The absence of significant difference between cases involving short and long side chains indicates that side chain entropy is not a dominant factor for the sMMGB analysis.

Fig. 3.

Fig. 3.

Open in a new tab

Linear regression of ΔΔGexp versus sΔΔGcal—for the entropy test dataset.

4.3 Effect of different force field parameters

The sMMGB predictions were made with three force field parameters: Amber98 (Case et al., 2005), Charmm27 (Brooks et al., 2009) and Oplsaa (Jorgensen and Tiradorives, 1988), to minimize the 3D structures of both WT proteins and the mutants and to obtain the corresponding molecular mechanics and solvation energies. The resulting energy changes per mutation were found to differ among the force fields, which confirm our previous observation made for protein–protein interactions (Talley et al., 2008) and protein stability (Zhang et al., 2010, 2011). In some exceptional cases, the predicted sΔΔGcal was found to vary >30 kcal/mol across different force fields. For global comparison, Supplementary Figure S3 shows sΔΔGcal calculated with different force field parameters and the trend of prediction is quite similar, but there are some outliers which are not associated with the same mutation for each force field parameters. The fact that the calculations with different force field parameters started with identical 3D structures (of the WT and the mutant), but generated different predictions indicate how sensitive the results are with respect to the choice of the force field [detailed results are provided in Supplementary Table S9: Supplementary Table S9 (a) for the Training Database, Supplementary Table S9 (b) for the Blind Test and Supplementary Table S9 (c) for the Entire Dataset]. Overall, the best results in terms of RMSD (between ΔΔGexp versus calculated ΔΔGcal) were obtained with AMBER force field parameters (RMSD = 7.97 kcal/mol), while the worst performance was obtained with OPLS force field parameters resulting in RMSD = 8.18 kcal/mol. Such a sensitivity of the results with the respect to the force field parameters was our motivation for averaging the results across different force fields. Indeed, the averaged ΔΔGcal perform much better, resulting in RMSD = 5.53 kcal/mol. These RMSDs are taken without scaling of ΔΔG, i.e. prior to performing the optimization. After scaling, the corresponding RMSD were RMSDAMBER=1.80 kcal/mol, RMSDOPLS=1.81 kcal/mol and RMSDAVE=1.78 kcal/mol.

During the time the article was under review, new experimental data was added to ProTherm database and we used these new entries to perform an additional test the results of which are presented in Supplementary Tables S10 and S11.

Additional test was done using an optimized linear combination of the results obtained with each force field parameters, but the performance was found to be worse (Supplementary Table S12 a, b).

Funding: This work was supported by funds from National Institutes of Health, grant number (1R01GM093937).

Conflict of Interest: none declared.

Supplementary Material

Supplementary Data
supp_28_5_664__index.html (2.4KB, html)

REFERENCES

  1. Acuner Ozbabacan S.E., et al. Conformational ensembles, signal transduction and residue hot spots: application to drug discovery. Curr. Opin. Drug Discov. Dev. 2010;13:527–537. [PubMed] [Google Scholar]
  2. Alexov E. Numerical calculations of the pH of maximal protein stability. The effect of the sequence composition and three-dimensional structure. Eur. J. Biochem. 2004;271:173–185. doi: 10.1046/j.1432-1033.2003.03917.x. [DOI] [PubMed] [Google Scholar]
  3. Bash P.A., et al. Free energy calculations by computer simulation. Science. 1987;236:564–568. doi: 10.1126/science.3576184. [DOI] [PubMed] [Google Scholar]
  4. Bava K.A., et al. ProTherm, version 4.0: thermodynamic database for proteins and mutants. Nucleic Acids Res. 2004;32:D120–D121. doi: 10.1093/nar/gkh082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Benedix A., et al. Predicting free energy changes using structural ensembles. Nat. Methods. 2009;6:3–4. doi: 10.1038/nmeth0109-3. [DOI] [PubMed] [Google Scholar]
  6. BenNaim A. Statistical potentials extracted from protein structures: Are these meaningful potentials? J. Chem. Phys. 1997;107:3698–3706. [Google Scholar]
  7. Berman H.M., et al. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Beveridge D.L., DiCapua F.M. Free energy via molecular simulation: applications to chemical and biomolecular systems. Annu. Rev. Biophys. Biophys. Chem. 1989;18:431–492. doi: 10.1146/annurev.bb.18.060189.002243. [DOI] [PubMed] [Google Scholar]
  9. Bordner A.J., Abagyan R.A. Large-scale prediction of protein geometry and stability changes for arbitrary single point mutations. Proteins. 2004;57:400–413. doi: 10.1002/prot.20185. [DOI] [PubMed] [Google Scholar]
  10. Brooks B.R., et al. CHARMM: the biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Buckle A.M., et al. Crystal structural analysis of mutations in the hydrophobic cores of barnase. J. Mol. Biol. 1993;234:847–860. doi: 10.1006/jmbi.1993.1630. [DOI] [PubMed] [Google Scholar]
  12. Carpriotti E., et al. Proceedings of the 2004 Conference on Intelligent Systems for Molecular Biology (ISMB04). Oxford University Press; 2004. A neural network-based method for predicting protein stability changes upon single point mutations. [DOI] [PubMed] [Google Scholar]
  13. Capriotti E., et al. A neural-network-based method for predicting protein stability changes upon single point mutations. Bioinformatics. 2004;20(Suppl. 1):i63–i68. doi: 10.1093/bioinformatics/bth928. [DOI] [PubMed] [Google Scholar]
  14. Capriotti E., et al. I-Mutant2.0: predicting stability changes upon mutation from the protein sequence or structure. Nucleic Acids Res. 2005b;33:W306–W310. doi: 10.1093/nar/gki375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Casadio R., et al. Predicting free energy contributions to the conformational stability of folded proteins from the residue sequence with radial basis function networks. Proc. Int. Conf. Intell. Syst. Mol. Biol. 1995;3:81–88. [PubMed] [Google Scholar]
  16. Case D.A., et al. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Chen H., et al. Missense polymorphism in the human carboxypeptidase E gene alters enzymatic activity. Hum. Mutat. 2001;18:120–131. doi: 10.1002/humu.1161. [DOI] [PubMed] [Google Scholar]
  18. Chen Z.Y., et al. Gut-enriched Kruppel-like factor represses ornithine decarboxylase gene expression and functions as checkpoint regulator in colonic cancer cells. J. Biol. Chem. 2002;277:46831–46839. doi: 10.1074/jbc.M204816200. [DOI] [PubMed] [Google Scholar]
  19. Ding F., Dokholyan N.V. Emergence of protein fold families through rational design. Plos Comput. Biol. 2006;2:725–733. doi: 10.1371/journal.pcbi.0020085. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Dixit A., et al. Computational modeling of structurally conserved cancer mutations in the RET and MET kinases: the impact on protein structure, dynamics, and stability. Biophys. J. 2009;96:858–874. doi: 10.1016/j.bpj.2008.10.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Domingues H., et al. Improving the refolding yield of interleukin-4 through the optimization of local interactions. J. Biotechnol. 2000;84:217–230. doi: 10.1016/s0168-1656(00)00327-8. [DOI] [PubMed] [Google Scholar]
  22. Duan Y., Kollman P.A. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science. 1998;282:740–744. doi: 10.1126/science.282.5389.740. [DOI] [PubMed] [Google Scholar]
  23. Elcock A.H., McCammon J.A. Electrostatic contributions to the stability of halophilic proteins. J. Mol. Biol. 1998;280:731–748. doi: 10.1006/jmbi.1998.1904. [DOI] [PubMed] [Google Scholar]
  24. Eriksson A.E., et al. Response of a protein structure to cavity-creating mutations and its relation to the hydrophobic effect. Science. 1992;255:178–183. doi: 10.1126/science.1553543. [DOI] [PubMed] [Google Scholar]
  25. Frenz C.M. Neural network-based prediction of mutation-induced protein stability changes in Staphylococcal nuclease at 20 residue positions. Proteins. 2005;59:147–151. doi: 10.1002/prot.20400. [DOI] [PubMed] [Google Scholar]
  26. Gilis D., Rooman M. Stability changes upon mutation of solvent-accessible residues in proteins evaluated by database-derived potentials. J. Mol. Biol. 1996;257:1112–1126. doi: 10.1006/jmbi.1996.0226. [DOI] [PubMed] [Google Scholar]
  27. Gilis D., Rooman M. Predicting protein stability changes upon mutation using database-derived potentials: solvent accessibility determines the importance of local versus non-local interactions along the sequence. J. Mol. Biol. 1997;272:276–290. doi: 10.1006/jmbi.1997.1237. [DOI] [PubMed] [Google Scholar]
  28. Gilis D., Rooman M. Prediction of stability changes upon single-site mutations using database-derived potentials. Theor. Chem. Acc. 1999;101:46–50. [Google Scholar]
  29. Gilis D., Rooman M. PoPMuSiC, an algorithm for predicting protein mutant stability changes: application to prion proteins. Protein Eng. 2000;13:849–856. doi: 10.1093/protein/13.12.849. [DOI] [PubMed] [Google Scholar]
  30. Gromiha M.M. Prediction of protein stability upon point mutations. Biochem. Soc. Trans. 2007;35:1569–1573. doi: 10.1042/BST0351569. [DOI] [PubMed] [Google Scholar]
  31. Gromiha M.M., Sarai A. Thermodynamic database for proteins: features and applications. Methods Mol. Biol. 2010;609:97–112. doi: 10.1007/978-1-60327-241-4_6. [DOI] [PubMed] [Google Scholar]
  32. Guerois R., et al. Predicting changes in the stability of proteins and protein complexes: a study of more than 1000 mutations. J. Mol. Biol. 2002;320:369–387. doi: 10.1016/S0022-2836(02)00442-4. [DOI] [PubMed] [Google Scholar]
  33. Hoppe C., Schomburg D. Prediction of protein thermostability with a direction- and distance-dependent knowledge-based potential. Protein Sci. 2005;14:2682–2692. doi: 10.1110/ps.04940705. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hou T., et al. Assessing the performance of the molecular mechanics/Poisson Boltzmann surface area and molecular mechanics/generalized Born surface area methods. II. The accuracy of ranking poses generated from docking. J. Comput. Chem. 2011;32:866–877. doi: 10.1002/jcc.21666. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Hunt D.M., et al. Single nucleotide polymorphisms that cause structural changes in the cyclic AMP receptor protein transcriptional regulator of the tuberculosis vaccine strain Mycobacterium bovis BCG alter global gene expression without attenuating growth. Infect. Immun. 2008;76:2227–2234. doi: 10.1128/IAI.01410-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Hynes T.R., Fox R.O. The crystal structure of staphylococcal nuclease refined at 1.7 A resolution. Proteins. 1991;10:92–105. doi: 10.1002/prot.340100203. [DOI] [PubMed] [Google Scholar]
  37. Joachims T. Dissertation. London: Springer/Kluwer; 2002. Learning to classify text using support vector machines. [Google Scholar]
  38. Jorgensen W.L., Tiradorives J. The Opls potential functions for proteins - energy minimizations for crystals of cyclic-peptides and crambin. J. Am. Chem. Soc. 1988;110:1657–1666. doi: 10.1021/ja00214a001. [DOI] [PubMed] [Google Scholar]
  39. Karchin R., et al. LS-SNP: large-scale annotation of coding non-synonymous SNPs based on multiple information sources. Bioinformatics. 2005;21:2814–2820. doi: 10.1093/bioinformatics/bti442. [DOI] [PubMed] [Google Scholar]
  40. Khan S., Vihinen M. Performance of protein stability predictors. Hum. Mutat. 2010;31:675–684. doi: 10.1002/humu.21242. [DOI] [PubMed] [Google Scholar]
  41. Khare S.D., et al. FALS mutations in Cu, Zn superoxide dismutase destabilize the dimer and increase dimer dissociation propensity: a large-scale thermodynamic analysis. Amyloid. 2006;13:226–235. doi: 10.1080/13506120600960486. [DOI] [PubMed] [Google Scholar]
  42. Kollman P.A., et al. Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc. Chem. Res. 2000;33:889–897. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
  43. Kouranov A., et al. The RCSB PDB information portal for structural genomics. Nucleic Acids Res. 2006;34:D302–D305. doi: 10.1093/nar/gkj120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Kuhlman B., Baker D. Native protein sequences are close to optimal for their structures. Proc. Natl Acad. Sci. USA. 2000;97:10383–10388. doi: 10.1073/pnas.97.19.10383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Kundrotas P.J., Karshikoff A. Model for calculation of electrostatic interactions in unfolded proteins. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002a;65:011901. doi: 10.1103/PhysRevE.65.011901. [DOI] [PubMed] [Google Scholar]
  46. Kundrotas P.J., Karshikoff A. Modeling of denatured state for calculation of the electrostatic contribution to protein stability. Protein Sci. 2002b;11:1681–1686. doi: 10.1110/ps.4690102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Lee C. Testing homology modeling on mutant proteins: predicting structural and thermodynamic effects in the Ala98–>Val mutants of T4 lysozyme. Fold Des. 1995;1:1–12. [PubMed] [Google Scholar]
  48. Lee C., Levitt M. Accurate prediction of the stability and activity effects of site-directed mutagenesis on a protein core. Nature. 1991;352:448–451. doi: 10.1038/352448a0. [DOI] [PubMed] [Google Scholar]
  49. Ma B., Nussinov R. Molecular dynamics simulations of the unfolding of beta(2)-microglobulin and its variants. Protein Eng. 2003;16:561–575. doi: 10.1093/protein/gzg079. [DOI] [PubMed] [Google Scholar]
  50. Masso M., Vaisman , II Accurate prediction of stability changes in protein mutants by combining machine learning with structure based computational mutagenesis. Bioinformatics. 2008;24:2002–2009. doi: 10.1093/bioinformatics/btn353. [DOI] [PubMed] [Google Scholar]
  51. Miyazawa S., Jernigan R.L. Protein stability for single substitution mutants and the extent of local compactness in the denatured state. Protein Eng. 1994;7:1209–1220. doi: 10.1093/protein/7.10.1209. [DOI] [PubMed] [Google Scholar]
  52. Moreira I.S., et al. Hot spots–a review of the protein-protein interface determinant amino-acid residues. Proteins. 2007;68:803–812. doi: 10.1002/prot.21396. [DOI] [PubMed] [Google Scholar]
  53. Munoz V., Serrano L. Development of the multiple sequence approximation within the AGADIR model of alpha-helix formation: comparison with Zimm-Bragg and Lifson-Roig formalisms. Biopolymers. 1997;41:495–509. doi: 10.1002/(SICI)1097-0282(19970415)41:5<495::AID-BIP2>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
  54. Nar H., et al. Crystal structure analysis of oxidized Pseudomonas aeruginosa azurin at pH 5.5 and pH 9.0. A pH-induced conformational transition involves a peptide bond flip. J. Mol. Biol. 1991;221:765–772. doi: 10.1016/0022-2836(91)80173-r. [DOI] [PubMed] [Google Scholar]
  55. Ofiteru A., et al. Structural and functional consequences of single amino acid substitutions in the pyrimidine base binding pocket of Escherichia coli CMP kinase. FEBS J. 2007;274:3363–3373. doi: 10.1111/j.1742-4658.2007.05870.x. [DOI] [PubMed] [Google Scholar]
  56. Ota M., et al. Knowledge-based potential defined for a rotamer library to design protein sequences. Protein Eng. 2001;14:557–564. doi: 10.1093/protein/14.8.557. [DOI] [PubMed] [Google Scholar]
  57. Pitera J.W., Kollman P.A. Exhaustive mutagenesis in silico: multicoordinate free energy calculations on proteins and peptides. Proteins. 2000;41:385–397. [PubMed] [Google Scholar]
  58. Ponder J.W. TINKER-Software Tools for Molecular Design, 3.7. Washington University, St Luis.; 1999. [Google Scholar]
  59. Prevost M., et al. Contribution of the hydrophobic effect to protein stability: analysis based on simulations of the Ile-96—Ala mutation in barnase. Proc. Natl Acad. Sci. USA. 1991;88:10880–10884. doi: 10.1073/pnas.88.23.10880. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Quiocho F.A., et al. Extensive features of tight oligosaccharide binding revealed in high-resolution structures of the maltodextrin transport/chemosensory receptor. Structure. 1997;5:997–1015. doi: 10.1016/s0969-2126(97)00253-0. [DOI] [PubMed] [Google Scholar]
  61. Ramensky V., et al. Human non-synonymous SNPs: server and survey. Nucleic Acids Res. 2002;30:3894–3900. doi: 10.1093/nar/gkf493. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Schymkowitz J., et al. The FoldX web server: an online force field. Nucleic Acids Res. 2005;33:W382–W388. doi: 10.1093/nar/gki387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Shastry B.S. SNPs: impact on gene function and phenotype. Methods Mol. Biol. 2009;578:3–22. doi: 10.1007/978-1-60327-411-1_1. [DOI] [PubMed] [Google Scholar]
  64. Still W.C., et al. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am.. Chem.. Soc. 1990;112:6127–6129. [Google Scholar]
  65. Takano K., et al. Experimental verification of the ‘stability profile of mutant protein’ (SPMP) data using mutant human lysozymes. Protein Eng. 1999;12:663–672. doi: 10.1093/protein/12.8.663. [DOI] [PubMed] [Google Scholar]
  66. Talley K., et al. On the electrostatic component of protein-protein binding free energy. PMC Biophys. 2008;1:2. doi: 10.1186/1757-5036-1-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Teng S., et al. Modeling effects of human single nucleotide polymorphisms on protein-protein interactions. Biophys. J. 2009;96:2178–2188. doi: 10.1016/j.bpj.2008.12.3904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Teng S., et al. Approaches and resources for prediction of the effects of non-synonymous single nucleotide polymorphism on protein function and interactions. Curr. Pharm. Biotechnol. 2008;9:123–133. doi: 10.2174/138920108783955164. [DOI] [PubMed] [Google Scholar]
  69. Thomas P.D., Dill K.A. Statistical potentials extracted from protein structures: how accurate are they? J. Mol. Biol. 1996;257:457–469. doi: 10.1006/jmbi.1996.0175. [DOI] [PubMed] [Google Scholar]
  70. Tidor B., Karplus M. Simulation analysis of the stability mutant R96H of T4 lysozyme. Biochemistry. 1991;30:3217–3228. doi: 10.1021/bi00227a009. [DOI] [PubMed] [Google Scholar]
  71. Topham C.M., et al. Prediction of the stability of protein mutants based on structural environment-dependent amino acid substitution and propensity tables. Protein Eng. 1997;10:7–21. doi: 10.1093/protein/10.1.7. [DOI] [PubMed] [Google Scholar]
  72. Villegas V., et al. Stabilization of proteins by rational design of alpha-helix stability using helix/coil transition theory. Fold. Des. 1996;1:29–34. [PubMed] [Google Scholar]
  73. Vorobjev Y.N., Hermans J. ES/IS: estimation of conformational free energy by combining dynamics simulations with explicit solvent with an implicit solvent continuum model. Biophys. Chem. 1999;78:195–205. doi: 10.1016/s0301-4622(98)00230-0. [DOI] [PubMed] [Google Scholar]
  74. Wang Z., Moult J. SNPs, protein structure, and disease. Hum. Mutat. 2001;17:263–270. doi: 10.1002/humu.22. [DOI] [PubMed] [Google Scholar]
  75. Wang Z., Moult J. Three-dimensional structural location and molecular functional effects of missense SNPs in the T cell receptor Vbeta domain. Proteins. 2003;53:748–757. doi: 10.1002/prot.10522. [DOI] [PubMed] [Google Scholar]
  76. Witham S., et al. A missense mutation in CLIC2 associated with intellectual disability is predicted by in silico modeling to affect protein stability and dynamics. Proteins. 2011;79:2444–2454. doi: 10.1002/prot.23065. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Xiang Z., Honig B. Extending the accuracy limits of prediction for side-chain conformations. J. Mol. Biol. 2001;311:421–430. doi: 10.1006/jmbi.2001.4865. [DOI] [PubMed] [Google Scholar]
  78. Xiong X.M. Study of isochronal annealing behavior of neutron-irradiated hydrogen Fz silicon by positron-annihilation. Chinese Phys. 1986;6:763–768. [Google Scholar]
  79. Xu J., et al. The response of T4 lysozyme to large-to-small substitutions within the core and its relation to the hydrophobic effect. Protein Sci. 1998;7:158–177. doi: 10.1002/pro.5560070117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  80. Yan C., et al. Temperature-induced unfolding of epidermal growth factor (EGF): insight from molecular dynamics simulation. J. Mol. Graph. Model. 2010;29:2–12. doi: 10.1016/j.jmgm.2010.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Ye Y., et al. Modeling and analyzing three-dimensional structures of human disease proteins. Pac. Symp. Biocomput. 2006:439–450. [PubMed] [Google Scholar]
  82. Yin S., et al. Eris: an automated estimator of protein stability. Nat. Methods. 2007a;4:466–467. doi: 10.1038/nmeth0607-466. [DOI] [PubMed] [Google Scholar]
  83. Yin S., et al. Modeling backbone flexibility improves protein stability estimation. Structure. 2007b;15:1567–1576. doi: 10.1016/j.str.2007.09.024. [DOI] [PubMed] [Google Scholar]
  84. Yue P., Moult J. Identification and analysis of deleterious human SNPs. J. Mol. Biol. 2006;356:1263–1274. doi: 10.1016/j.jmb.2005.12.025. [DOI] [PubMed] [Google Scholar]
  85. Yue P., et al. SNPs3D: candidate gene and SNP selection for association studies. BMC Bioinformatics. 2006;7:166. doi: 10.1186/1471-2105-7-166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  86. Zhang Z., et al. Computational analysis of missense mutations causing Snyder-Robinson syndrome. Hum. Mutat. 2010;31:1043–1049. doi: 10.1002/humu.21310. [DOI] [PMC free article] [PubMed] [Google Scholar]
  87. Zhang Z., et al. In silico and in vitro investigations of the mutability of disease-causing missense mutation sites in spermine synthase. PLoS One. 2011;6:e20373. doi: 10.1371/journal.pone.0020373. [DOI] [PMC free article] [PubMed] [Google Scholar]
  88. Zhou H.X. A Gaussian-chain model for treating residual charge-charge interactions in the unfolded state of proteins. Proc. Natl Acad. Sci. USA. 2002;99:3569–3574. doi: 10.1073/pnas.052030599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  89. Zhou H.X. Direct test of the Gaussian-chain model for treating residual charge-charge interactions in the unfolded state of proteins. J. Am. Chem. Soc. 2003;125:2060–2061. doi: 10.1021/ja0298491. [DOI] [PubMed] [Google Scholar]
  90. Zhou H., Zhou Y. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 2002;11:2714–2726. doi: 10.1110/ps.0217002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  91. Zhou M.I., et al. Tumor suppressor von Hippel-Lindau (VHL) stabilization of Jade-1 protein occurs through plant homeodomains and is VHL mutation dependent. Cancer Res. 2004;64:1278–1286. doi: 10.1158/0008-5472.can-03-0884. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_28_5_664__index.html (2.4KB, html)
supp_bts005_Figure_supplementary.doc (151.5KB, doc)
supp_bts005_Table_1S.doc (34.5KB, doc)
supp_bts005_Table_2S.xls (84.5KB, xls)
supp_bts005_Table_3S.xls (64KB, xls)
supp_bts005_Table_4S_a.xls (302KB, xls)
supp_bts005_Table_4Sb.xls (211.5KB, xls)
supp_bts005_Table_4Sc.xls (489KB, xls)
supp_bts005_Table_5Sa.xls (187.5KB, xls)
supp_bts005_Table_5Sb.xls (131.5KB, xls)
supp_bts005_Table_5Sc.xls (296KB, xls)
supp_bts005_Table_6S.doc (28KB, doc)
supp_bts005_Table_7S.doc (31.5KB, doc)
supp_bts005_Table_8S.xls (36KB, xls)
supp_bts005_Table_9Sa.xls (192.5KB, xls)
supp_bts005_Table_9Sb.xls (138KB, xls)
supp_bts005_Table_9Sc.xls (306.5KB, xls)
supp_bts005_Table_10S.xls (224.5KB, xls)
supp_bts005_Table_11S.doc (32.5KB, doc)
supp_bts005_Table_12S.doc (50.5KB, doc)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES