Determinants of Reactivity and Selectivity in Soluble Epoxide Hydrolase from Quantum Mechanics/Molecular Mechanics Modeling

Abstract

Soluble epoxide hydrolase (sEH) is an enzyme involved in drug metabolism that catalyzes the hydrolysis of epoxides to form their corresponding diols. sEH has a broad substrate range and shows high regio- and enantioselectivity for nucleophilic ring opening by Asp333. Epoxide hydrolases therefore have potential synthetic applications. We have used combined quantum mechanics/molecular mechanics (QM/MM) umbrella sampling molecular dynamics (MD) simulations (at the AM1/CHARMM22 level) and high-level ab initio (SCS-MP2) QM/MM calculations to analyze the reactions, and determinants of selectivity, for two substrates: trans-stilbene oxide (t-SO) and trans-diphenylpropene oxide (t-DPPO). The calculated free energy barriers from the QM/MM (AM1/CHARMM22) umbrella sampling MD simulations show a lower barrier for phenyl attack in t-DPPO, compared with that for benzylic attack, in agreement with experiment. Activation barriers in agreement with experimental rate constants are obtained only with the highest level of QM theory (SCS-MP2) used. Our results show that the selectivity of the ring-opening reaction is influenced by several factors, including proximity to the nucleophile, electronic stabilization of the transition state, and hydrogen bonding to two active site tyrosine residues. The protonation state of His523 during nucleophilic attack has also been investigated, and our results show that the protonated form is most consistent with experimental findings. The work presented here illustrates how determinants of selectivity can be identified from QM/MM simulations. These insights may also provide useful information for the design of novel catalysts for use in the synthesis of enantiopure compounds.

Epoxide hydrolases (EHs) make up an important family of enzymes that catalyze the hydrolysis of epoxides to their corresponding diols.¹ Epoxides can be generated via endogenous biochemical pathways or, e.g., via oxidation of xenobiotics, for example, by cytochrome P450.²⁻⁴ This reaction is important in drug metabolism, as epoxides formed during the oxidation of drug molecules can react with proteins and DNA, causing damage to cells. There are five known mammalian epoxide hydrolases: microsomal and soluble epoxide hydrolases (mEH and sEH, respectively), leukotriene A4 hydrolase, cholesterol epoxide hydrolase, and hepoxilin epoxide hydrolase.⁵ Although found throughout the body, sEH is highly concentrated in the kidneys and, in addition to detoxification, is involved in the metabolism of epoxyeicosatrienoic acids (EETs).^2,3,6 Inhibition of sEH is a potential treatment for many diseases, including kidney failure, high blood pressure, and atherosclerosis.^3,7−11 sEH has a broad substrate range, and because of its role in detoxification and biochemical modification of drugs, or their metabolites, the regioselectivity of the epoxide ring-opening reaction has important medical relevance, because of possible differences in activity between products. EHs are also used in the preparation and refinement of enantiopure diols and epoxides, which are important synthons in organic synthesis.¹² Engineered EHs with designed specificities would expand their range of application considerably.¹³

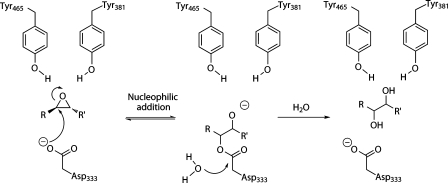
sEH is a member of the α/β-hydrolase family. This hydrolase family shares a common catalytic triad (nucleophile-histidine-acid) and two-step mechanism, which involves the formation of a covalent ester intermediate (Scheme 1).^14,15 The hydrolase activity of the enzyme is performed in the C-terminal domain, while the N-terminal domain has phosphatase activity.¹⁶⁻¹⁹ Previously proposed mechanisms for sEH suggested direct attack on the epoxide by an activated water molecule,²⁰ but the mechanism involving the ester intermediate is now widely accepted.²¹⁻²⁴ sEH can distinguish between two chemically similar epoxide carbon atoms,²² but the determinants of this regioselectivity are not known. Murine sEH preferentially attacks the intrinsically more reactive phenyl carbon of a range of aromatic substituted epoxides, including trans-diphenylpropene oxide (t-DPPO)^22,25[i.e., C(1) in Figure 1], whereas murine mEH attacks preferentially at the less hindered benzylic epoxide carbon.²⁶ In Solanum tuberosum epoxide hydrolase 1 (StEH1), attack at the benzylic carbon occurs exclusively for (S,S)-trans-methylstyrene oxide (t-MSO), but for (R,R)-t-MSO, the epoxide is attacked at either position, with a slight preference for the benzylic carbon.²⁷ A temperature and pH dependence has been observed for the regioselectivity of nucleophilic attack of (R,R)-t-MSO in StEH1, revealing interconversion between two different Michaelis complexes for this particular EH.²⁸ Engineered mutations in StEH1 have also been used to alter the regioselectivity for nucleophilic attack by this enzyme.^29,30 Understanding the causes of regioselectivity in sEH is potentially important in drug development as well as for the application of EH enzymes in biocatalysis.

Scheme 1. Proposed Mechanism^31,33 for Hydrolysis of Epoxide RCHOCHR′ by sEH.

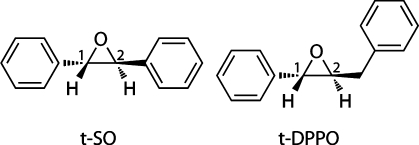
Figure 1.

Chemical structures of (S,S)-trans-stilbene oxide (t-SO) and (S,S)-trans-diphenylpropene oxide (t-DPPO), the substrates modeled here. The numerals 1 and 2 represent the two epoxide carbon atoms on each substrate at which nucleophilic ring opening by Asp333 can be initiated.

Two tyrosine residues (Tyr381 and Tyr465 in murine sEH) are found in the active site of all known EH enyzmes and are believed to be important in catalysis.³³⁻³⁶ One of these tyrosine residues has been proposed to act as a general acid catalyst in the ring-opening reaction, while the other forms a hydrogen bond to the epoxide oxygen atom in the substrate.³³⁻³⁶ Mutation of both of these tyrosine residues to phenylalanine leads to a 90% loss of reactivity.³⁶ Mutation studies of EH from Agrobacterium radiobacter AD1³⁴ suggest that the residue equivalent to Tyr465 is important for the regioselectivity of the ring-opening reaction. MD simulations of sEH suggested that a so-called “near-attack conformation” (NAC, involving the nucleophilic Asp333 carboylate oxygen atom and the benzylic carbon atom of t-MSO) is populated 4 times more frequently when the epoxide oxygen atom forms a hydrogen bond to the Tyr465 side chain.³⁷ While superficially attractive, the NAC idea suffers from problems such as the lack of a unique definition;³⁸ also, studying reactant complexes alone can lead to misleading conclusions about enzyme reactivity.³⁹ In general, it is important to study reactions to draw reliable conclusions. An experimental study of the hydrolysis of trans-stilbene oxide by S. tuberosum epoxide hydrolase 1 (StEH1) suggested that Tyr381 and Tyr465 act as electrophilic catalysts and do not provide a proton to the epoxide oxyanion.³² A similar role has been observed for Tyr115 in the epoxide ring-opening step in glutathione S-transferase M1-1.⁴⁰ Regardless of whether they act as proton donors, it is widely accepted that Tyr381 and Tyr465 play an important role in the stabilization of the transition state and ring-opened intermediate.

In general, reliable conclusions about determinants of selectivity will require the calculation of activation energy barriers for enzyme-catalyzed reactions, including thorough consideration of conformational sampling and reliable quantum chemical (or empirical valence bond⁴¹) methods.^4,42 Possible causes of regioselectivity in an enzyme include intrinsic reactivity, binding mode, and specific stabilization of key species in the enzyme. QM/MM modeling is well-suited to the analysis of factors involved in regio- and stereoselectivity in enzymes, as demonstrated in a recent study of a cytochrome P450 enzyme;⁴ in that work, conformational sampling was found to be important in making accurate predictions of selectivity. QM/MM methods have also been used to identify a single amino acid as the likely key determinant of selectivity observed in the epoxide ring opening of phenanthrene 9,10-oxide by a glutathione S-transferase (GST).⁴⁰ As with EH, the ring-opening reaction catalyzed by GST involves initial nucleophilic attack at one of the epoxide carbon atoms. In contrast to EH, in which an aspartate carboxylate oxygen atom performs this attack, in GST enzymes the nucleophilic attack is conducted by the negatively charged sulfur atom of the glutathione anion.⁴⁰ In the case of transition metal-containing enzymes, such as the cytochrome P450 enzymes, consideration of conformational sampling is limited to calculating a few adiabatic mapping pathways, starting from different snapshots taken from molecular dynamics simulations.⁴ This is due to the poor treatment of transition metals by most semiempirical methods. For enzymes such as sEH, with no active site transition metal, semiempirical QM methods can be used to model the active site chemistry, allowing the use of sampling methods, such as MD, for generation of free energy barriers.

An important question relating to the mechanism of sEH, which has yet to be answered conclusively, is whether the Nε atom of His523 (corresponding to the residue numbering in murine sEH) is protonated or unprotonated in the resting state of the enzyme, under normal conditions. This residue forms part of the catalytic triad that is mentioned above, and mutagenesis studies of both murine sEH⁴³ and potato StEH1⁴⁴ have revealed that mutation of this residue results in a drastic loss of catalytic activity. The pK_a of a typical imidazole side chain of a histidine residue is 6.0, whereas the estimated pK_a of this residue in the murine sEH crystal structure [Protein Data Bank (PDB) entry 1CQZ] is 8.4 (calculated with PROPKA⁴⁵). Microscopic and semimacroscopic methods are available for the calculation of pK_a values of titratable amino acid residues in proteins;⁴⁶ however (to the best of our knowledge), these have not been applied to sEH. The optimal pH range from 6.5 to 7.4 for sEH has been measured experimentally.⁴⁷ It is therefore possible that His523 may be either neutral (unprotonated) or ionized (protonated) in the active site of murine sEH. The protonation state of His523 has mechanistic implications because this residue is thought to be involved in the activation (deprotonation) of a water molecule prior to the hydrolysis step, which would require the Nε atom to be deprotonated. It has been suggested that His523 is deprotonated after the ring-opening reaction via a “proton shuttle”, in which the Nε proton is transferred to the deprotonated oxygen atom of Tyr465,³⁷ but this mechanism has not yet been confirmed. As mentioned above, it has also been suggested that the hydroxyl groups of Tyr381 and Tyr465 do not lose their protons during the catalytic cycle,³² in which case the Nε proton could be transferred instead to the oxyanion formed upon ring opening.

In the crystal structures that have been obtained for various forms of EH,^31,48,49 the proximity of the Nε atom of His523 to the Asp333 side chain suggests that the Nε atom is protonated prior to the ring-opening reaction and donates a hydrogen bond to one of the Asp333 side chain oxygen atoms. In a MD study by Schiott et al.,³⁷ it was found that NACs corresponding to nucleophilic attack of t-MSO by murine sEH were observed more frequently in a model with His523 protonated than in a neutral His model. The authors observed that protonation of His523 prevents Asp333 from forming H-bonds to other H-bond donors that otherwise would prevent nucleophilic attack of the epoxide. Hopmann et al. modeled the ring opening of t-MSO in a small model of sEH using density functional theory (DFT), with the His523 Nε atom being treated as neutral.⁵⁰ This static model does not allow for the formation of hydrogen bonds between Asp333 and surrounding amino acid residues, as found in the MD study by Schiott et al.³⁷ Hopmann et al. observed the transfer of a proton from the Tyr465 side chain to the epoxide oxygen, following the ring-opening step. A lower barrier (by 3.2 kcal/mol) was observed for nucleophilic attack at the epoxide carbon with the less-hindered methyl substituent, compared to that with a phenyl substituent. Hopmann et al. also modeled the hydrolysis of the ester intermediate and observed a barrier higher than that calculated for the ring-opening reaction, consistent with hydrolysis being the rate-limiting step in experimental studies.⁵¹ Despite the agreement between experimental observations and the calculations of Hopmann et al., their study does not conclusively identify the correct protonation state of His523.

The effects of the protein environment are a key factor in the reactivity of sEH, and hence, a modeling method that takes these into account, such as QM/MM, is well-suited to this type of problem. In this study, the ring-opening reaction of two epoxide substrates in murine sEH is modeled. The substrates are trans-stilbene oxide (t-SO) and trans-diphenylpropene oxide (t-DPPO) (Figure 1). The regioselectivity of nucleophilic attack in t-DPPO has been determined experimentally, using ¹⁸O-labeled substrate, and found to occur preferentially (97%) at the phenyl carbon atom [i.e., C(1) in Figure 1].²² The two epoxide carbon atoms in t-SO are chemically equivalent, and hence, modeling the reaction with this substrate allows for determinants other than the relative reactivity of the two epoxide carbon atoms to be probed. The substrates chosen here allow us to test the ability of these QM/MM methods to predict regioselectivity and also investigate possible factors that control the regioselectivity of the ring-opening process.

Here we model the nucleophilic attack by Asp333 at each of the two epoxide carbon atoms in t-SO and t-DPPO in multiple QM/MM (AM1/CHARMM22) umbrella sampling MD simulations. Extensive sampling, such as that used here, is very important when modeling selectivity in enzymes, as has been shown in recent studies.^4,52 Relative barrier heights to nucleophilic attack at the two epoxide carbon atoms in t-DPPO are compared and found to be consistent with the experimentally observed regioselectivity.²² A large difference in the free energy barriers to nucleophilic attack for the two epoxide carbons atoms in t-SO is observed, despite the chemical equivalence of the two atoms. High-level ab initio QM calculations are used to correct the AM1 energies, yielding barriers that are in quantitative agreement with barriers derived from experimentally determined rate constants for similar reactions. The results are analyzed to identify the causes of this selectivity in the active site. Our QM/MM calculations reveal important interactions that influence the selectivity of ring opening, including the proximity of the epoxide carbon atoms to the nucleophile, the chemical environment of the epoxide carbon, and the hydrogen bonding interactions between the epoxide oxygen atom and the Tyr381 and Tyr465 side chains. These calculations provide insight into the factors that control stereoselectivity in epoxide hydrolase and may be of use in the design of novel catalysts.⁵³

Computational Methods

Model Setup

The crystal structure of murine sEH without substrate (PDB entry 1CQZ)³¹ was obtained from the Protein Data Bank.^54,55 In murine sEH, the epoxide hydrolase activity is conducted in the C-terminal catalytic domain (Val235–Ala544); hence, only this region is modeled. The coordinates of an inhibitor, N-cyclohexyl-N′-(3-phenyl)propylurea, from another sEH structure (PDB entry 1EK1)³³ were docked into the active site of the catalytic domain of strand A. The inhibitor was modified to the required substrate, t-SO or t-DPPO (Figure 1). The S,S enantiomer of each substrate was modeled, as these have been shown experimentally in murine sEH to be turned over (slightly) faster than the corresponding R,Renantiomer.²⁵ There are two possible orientations for t-DPPO in the active site, because of asymmetry about the epoxide ring, so simulations were performed for both of these orientations (Figure 2). Hence, three enzyme–substrate complexes,termed t-SO, t-DPPO(1), and t-DPPO(2), are modeled. Similar approaches have been applied successfully in modeling other enzymes.^4,39,56−58 Further details of the setup of each model system, including addition of hydrogen atoms, solvation, minimization, and stochastic boundary conditions, are provided in the Supporting Information.

Figure 2.

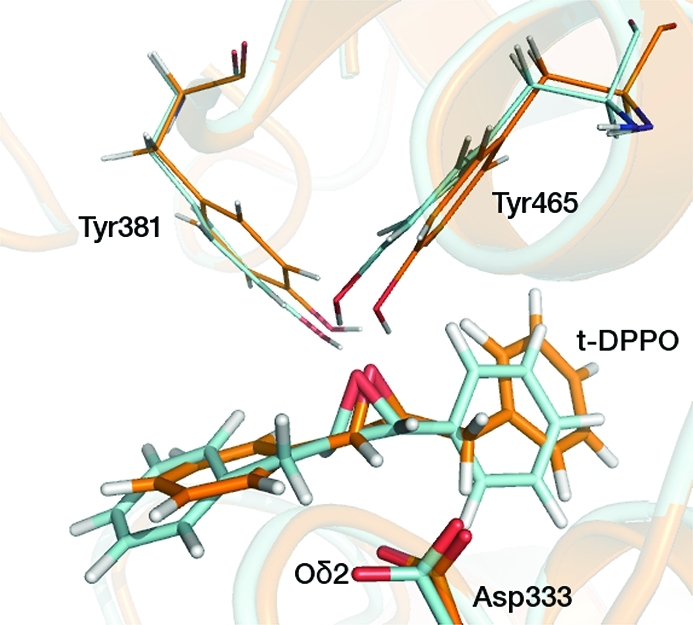
Two different binding orientations of t-DPPO modeled in this study. The t-DPPO(1) and t-DPPO(2) orientations are colored blue and orange, respectively. The structures were obtained from unrestrained QM/MM MD simulations.

Initial QM/MM MD Simulations

Starting structures for the QM/MM umbrella sampling MD simulations were generated by performing ten 14 ps stochastic boundary QM(AM1)/MM(CHARMM22) MD simulations on the same starting structure, for each enzyme–substrate complex. Each simulation was given a different set of initial velocities by supplying a different seed value to the random number generator, to generate different starting conformations for the umbrella sampling MD simulations. For each enzyme–substrate complex, the substrate and nucleophilic Asp333 side chain were treated quantum mechanically at the AM1 level of theory.⁵⁹ The rest of the enzyme and solvent were treated with the CHARMM22 MM force field.⁶⁰ A hydrogen link atom⁶¹ was used to partition the covalent bond between the QM and MM regions, placed between the Cβ and Cα atoms of the Asp333 residue.

QM/MM Umbrella Sampling MD Simulations

Ten simulations of the nucleophilic attack at C(1) or C(2) of the epoxide ring were conducted for each substrate (defined in Figure 1) using QM(AM1)/MM(CHARMM22) umbrella sampling MD. The coordinates of the final structures from the unrestrained simulations described above were used as the initial structures. Multiple starting geometries were used to enhance the amount of conformational sampling, which has been found to be important in other enzyme studies.⁴ On the basis of each starting geometry, the reaction was modeled using umbrella sampling with conditions and protocols similar to those developed and tested for QM/MM simulations of other enzymes.^40,56,57,62 The reaction coordinate (denoted herein as r) was defined as the difference between two interatomic differences: the epoxide O–C(1) or −C(2) distance minus the Oδ2 (Asp333)–C(1) or −C(2) distance, corresponding to the bonds being broken or formed, respectively. Similar reaction coordinates have been used in previous studies of other enzymes.^40,56,57 The Oδ1 atom of Asp333 is not in a position to favor nucleophilic attack at either epoxide carbon atom; hence, only nucleophilic attack by Oδ2 is considered. Series of simulations were performed with the reaction coordinate harmonically restrained at values between −2.0 and 0.5 Å in 0.05 Å steps, using a force constant of 100 kcal mol^–1 Å^–2. All other aspects of the umbrella sampling MD simulations were identical to those used for the unrestrained MD simulations, described above. Each simulation consisted of 5 ps of equilibration dynamics and 25 ps of sampling dynamics, initiated by using the end point of the first 5 ps from the previous simulation.^58,63 The weighted histogram analysis method (WHAM)⁶⁴was used to combine the reaction coordinate statistics of the simulations along the reaction coordinate. Multiple umbrella sampling MD runs were performed, to test the validity and reproducibility of the results. The free energy barriers were calculated by combining the statistics from all of the simulations performed for each reaction in the WHAM unbiasing calculation. Such approaches have been applied successfully in previous work for other enzymes.^40,56,57

Preliminary umbrella sampling simulations were performed with the His523 Nε atom either protonated or unprotonated, to identify the most likely protonation state of this residue. In these simulations, five different simulations were run using the same setup and QM/MM methodology described above, but with the following exceptions: r was varied in steps of 0.1 Å, and the simulations consisted of 1 ps of equilibration dynamics and 9 ps of sampling dynamics.

Higher-Level QM/MM Calculations and Energy Corrections

AM1, like other semiempirical QM methods, often overestimates activation barriers for chemical reactions (by ≥10 kcal/mol).^53,65 Higher-level QM methods provide more accurate calculations of activation barriers, but their computational cost prohibits MD sampling. Instead, the AM1-based free energy barriers were corrected afterward using the following (previously used) protocol.⁶⁵ The end point of the umbrella sampling simulation with the value of r corresponding to the highest point on each free energy surface (i.e., corresponding to the transition state) was used as the initial geometry for AM1/CHARMM22 potential energy calculations. Potential energy surfaces (PESs) were calculated in CHARMM: a series of geometry optimizations was performed, with the reaction coordinate (r) fixed successively to a range of values. These PESs were initiated at an r of −0.2 Å (transition state) and followed downhill in energy to r values of −2.0 and 0.5 Å, corresponding to the reactant complex and covalent ester intermediate, respectively (details in the Supporting Information). As with all other energy barriers calculated in this work, energy barriers were calculated as the difference in energy between the transition state and reactant complex. An activation entropy⁶⁵ was calculated by computing the difference between the free energy barrier mentioned above and the Boltzmann-weighted average of the AM1/CHARMM22 potential energy barriers (ΔE_ave^⧧) for the same process, using the expression in eq 1.⁴

1

The activation entropy was added to the B3LYP/CHARMM22 and SCS-MP2//B3LYP/CHARMM22 barriers (detailed below) to yield approximate free energy barriers. This approach gives only an approximate estimate of the activation entropy but has been shown to be reasonable for other enzymes. Composite calculations of this sort have previously given activation free energies in “quantitative” agreement with experiment for other enzymes, such as chorismate mutase and p-hydroxybenzoate hydroxylase.^65,66 The activation entropy is small for sEH and is not expected to differ significantly between different substrates; hence, the same average entropy correction is applied in all models. Entropic contributions to activation free energy barriers have been calculated for the enzyme subtilisin in a more rigorous manner by Warshel et al.⁶⁷ and were shown to be small (∼2.5 kcal/mol at 300 K).

PESs were calculated with (DFT)QM/MM methods using QoMMMa,⁶⁸ which uses Tinker⁶⁹ with the CHARMM22⁶⁰ force field for the MM part of the calculation and Jaguar⁷⁰ for the QM part. PESs for all systems were calculated at the B3LYP/6-31G(d)/CHARMM22 level using the transition state structures from the corresponding AM1/CHARMM22 PESs as initial geometries. The reaction coordinate used in the AM1/CHARMM22calculations was also used for the DFT/MM calculations. Structures were fully optimized at the DFT level, subject to reaction coordinate constraints. All atoms located more than 20 Å from the center of the system (Oδ2 of Asp333) were held fixed. Two PESs for t-SO were also optimized at the BP86/6-31G(d)/CHARMM22 and BHandHLYP/6-31G(d)/CHARMM22 levelsof theory, to test the dependence of the barriers on the density functional. The basis set dependence of the B3LYP/CHARMM22 energies was investigated by performing single-point energy calculations at the B3LYP/6-311+G(d,p) level on the B3LYP/6-31G(d)/CHARMM22 geometries. Ab initio QM/MM potential energy profiles were calculated using MOLPRO,⁷¹ by performing single-point energy calculations on the QM region taken from the B3LYP/CHARMM22 geometries and including the point charges from the MM region in the QM Hamiltonian. B3LYP/CHARMM22 geometries have been used previously for higher-level single-point energies and were found to perform well at predicting geometries in other systems. Ab initio QM energies were obtained using spin-component-scaled second-order Møller–Plesset perturbation theory (SCS-MP2),⁷² with the correlation-consistent polarized valence triple-ζ basis set (cc-pVTZ) developed by Dunning and co-workers.⁷³⁻⁷⁵ Additional diffuse functions were included on the epoxide oxygen atom (aug-cc-pVTZ). When a small basis set is employed, SCS-MP2 calculationscan be less accurate than B3LYP calculations with the same basisset. However, SCS-MP2 is usually more accurate than B3LYP when a larger basis set is used, such as the one used in this work.^58,76 SCS-MP2 is a correlated ab initio method and hence the most accurate QM method of those used here and has been shown to calculate values of energy barriers within 0.5 kcal/mol of those calculated with the LCCSD(T) coupled cluster method (with the same basis set).⁵⁸ LCCSD(T) QM/MM calculations have been shown to give energy barriers that approach chemical accuracy (1 kcal/mol). Only one SCS-MP2//B3LYP/CHARMM22 barrier was computed for C(1) and C(2) attack in each substrate model, because of the computational cost.

Results and Discussion

Unrestrained QM/MM MD Simulations

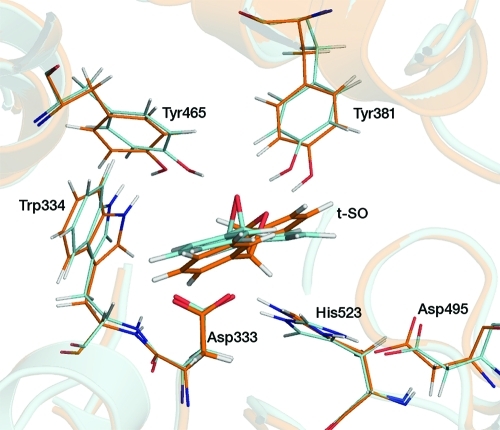
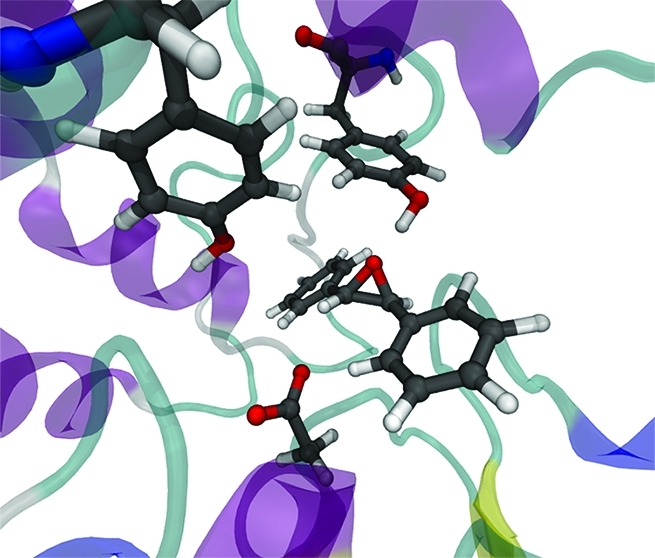
The active site structures from the 15 ps unrestrained QM/MM MD simulations performed prior to umbrella sampling simulations were very similar (in terms of interatomic distances, hydrogen bonding, etc.) for each enzyme–substrate model system. A representative structure from the t-DPPO(1) simulation is shown in Figure 3. The Nε atom of His523 is protonated in this structure (also see below). There are several important interactions common to all three enzyme–substrate model systems. These include hydrogen bonds between the epoxide oxygen atom of each substrate and the hydroxyl groups of Tyr381 and Tyr465 and a hydrogen bond between the Nε hydrogen of His523 and the Oδ2 atom of Asp333. The latter interaction is absent in the enzyme–substrate models in which the His523 Nε atom is not protonated. The values of the interatomic distances involved in the definition of the reaction coordinate, averaged over the 10 starting structures for each model system, are listed in Table 1. The substrate orientation in the active site appears to favor nucleophilic attack by the Oδ2 atom of Asp333 at C(1) for both the t-SO and t-DPPO(2) models, as the Oδ2–C(1) distances are significantly shorter than the Oδ2–C(2) distances (by >0.6 Å). The C(1) atom in t-DPPO corresponds to the phenyl epoxide carbon (as shown in Figure 1). The distinction is less clear for the t-DPPO(1) model; the orientation of the substrate does not suggest a preference in the regioselectivity of nucleophilic attack, as the difference between the Oδ2–C(1) and Oδ2–C(2) distances is small (∼0.1 Å).

Figure 3.

Representative structure from an AM1/CHARMM22 umbrella sampling MD simulation (at r = −2.0 Å) of the t-DPPO(1) system, showing important residues. The His523 residue is protonated at the Nε atom in the model shown here and forms a hydrogen bond with the Oδ2 atom of Asp333.

Table 1. Average Oδ2–C(x) Distances (in angstroms) Calculated from the Structures from the End of Each of Ten 15 ps Unrestrained QM/MM MD Simulations Performed for the t-SO, t-DPPO(1), and t-DPPO(2) Systems.

model system	Oδ2–C(1)	Oδ2–C(2)
t-SO	2.91 ± 0.27	3.77 ± 0.44
t-DPPO(1)	3.21 ± 0.38	3.32 ± 0.24
t-DPPO(2)	2.76 ± 0.17	3.40 ± 0.25

Protonation State of His523

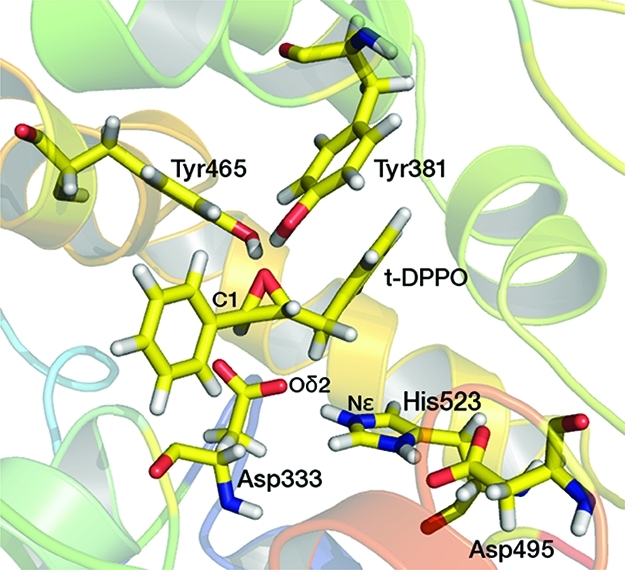
As mentioned in the introductory section, the protonation state of His523 responsible for activity remains a subject of debate.^37,50 Free energy profiles were obtained from preliminary AM1/CHARMM22 umbrella sampling MD simulations, in which 10 ps of MD was performed at each value of the reaction coordinate (r). The free energy barriers for the reaction, calculated by combining the trajectories from the five simulations for each system, are listed in Table 2. The barriers to nucleophilic attack at C(1) in all three sEH models studied [t-SO, t-DPPO(1), and t-DPPO(2)] are significantly higher when His523 is neutral (N) than when it is protonated (P). The barriers for attack at C(2) are largely unaffected by the protonation state of His523. Consequently, the regioselectivity of the ring-opening reaction is significantly affected by the protonation state of His523; the relative barriers suggest a preference for attack at C(1) in the protonated models and at C(2) in the neutral models, albeit to a lesser extent for the latter. The higher barriers for attack at C(1) in the neutral His523 models could be due to the lack of a hydrogen bonding interaction between the Tyr465 side chain and epoxide oxygen atom, which has been suggested to be important in stabilizing the TS.⁷⁷ In the unprotonated models, the Tyr465 side chain donates a hydrogen bond to the Asp333 Oδ2 carboxylate atom in the substrate complex. In contrast, the Tyr465 side chain donates a hydrogen bond with the epoxide oxygen atom in the protonated models (Figure 4). As the nucleophilic attack progresses [at either C(1) or C(2)] and the TS is formed, this hydrogen bond to the Asp333 Oδ2 atom is lost, but the Tyr465 hydroxyl group remains unable to donate a hydrogen bond to the epoxide oxygen atom. The presence of a hydrogen bond from Tyr465 to the epoxide oxygen not only stabilizes the covalent ring-opened intermediate but also lowers the barrier to its formation, because of stabilization of the transition state, as is discussed below. The protonated Nδ atom of His523 donates a hydrogen bond to the Oδ2 atom of Asp495, another member of the catalytic triad, for all simulations of all models (according to the hydrogen bond definitions detailed below). Asp495 has been postulated to be involved in a “charge-relay” mechanism during the hydrolysis step.⁵⁰ Given the proximity of the His523 Nε and Asp333 Oδ2 atoms in the crystal structure (2.41 ų¹) and the fact that the experimentally observed regioselectivity for the ring-opening reaction in t-DPPO is only correctly predicted in the simulations in which the Nε atom is protonated, it seems most likely that the His523 side chain is protonated at both the Nδ and Nε positions during the initial stages of the sEH-catalyzed reaction. For this reason, only the simulations in which the His523 Nε atom is protonated (i.e., positively charged) are discussed further.

Table 2. Activation Free Energies, ΔG^⧧ (in kilocalories per mole) for the Nucleophilic Ring-Opening Reaction at the C(1) and C(2) Atoms of the Epoxide Substrate in the Enzyme–Substrate Models t-SO, t-DPPO(1), and t-DPPO(2)^a.

	ΔG⧧(P)		ΔG⧧(N)
model system	C(1)	C(2)	C(1)	C(2)
t-SO	21.8	33.2	32.1	31.8
t-DPPO(1)	23.5	24.5	29.3	26.5
t-DPPO(2)	18.4	27.6	28.9	27.0

^aAll energies were calculated by combining the trajectories of five preliminary AM1/CHARMM22 umbrella sampling MD simulations, with 10 ps of dynamics simulated at each value of r. P denotes the enzyme model in which the His523 Nε atom is protonated (and His523 is positively charged). N denotes the enzyme model in which the His523 Nε atom is not protonated (and His523 is neutral).

Figure 4.

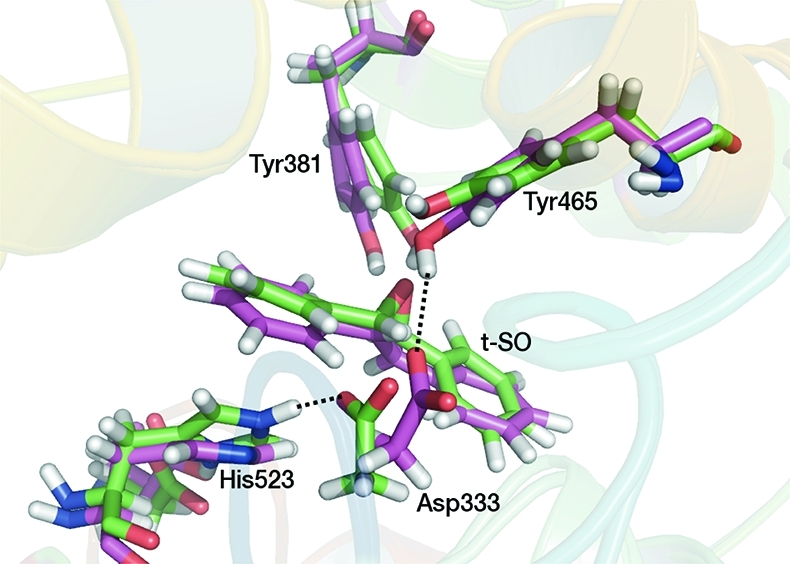
Active site structures from AM1/CHARMM22 umbrella sampling MD simulations of sEH complexed with t-SO for two systems differing in the protonation state of His523: one in which His523 is protonated at the Nε atom and positively charged (green) and one in which His523 is not protonated at the Nε atom and is neutral (purple). The structures correspond to the reactant complexes, in which r = −2.0 Å. In the former, a hydrogen bond is observed between the His523 Nε proton and Oδ2 atom of Asp333. In the latter, a hydrogen bond is observed between the Oδ2 atom of Asp333 and the phenol hydrogen of Tyr465. Important hydrogen bonds are shown by dotted lines.

Free Energy Barriers

To increase the amount of conformational sampling for the free energy profiles, additional AM1/CHARMM22 umbrella sampling calculations were performed on the t-SO, t-DPPO(1), and t-DPPO(2) model systems. The barriers obtained from these simulations (given in Table 3) indicate the same predicted regioselectivity as the free energy barriers from the shorter simulations shown in Table 2, but the barriers differ by up to 5 kcal/mol. Combining the two sets of simulations (preliminary and additional) in the WHAM calculation of the free energy barriers gave barriers identical to those obtained for the additional simulations alone, suggesting that adequate sampling has been performed in the latter simulations. Individual barriers for each simulation were also calculated, and these are provided in the Supporting Information.The individual barriers correspond to different starting geometries, taken from the unrestrained QM/MM MD simulations. The barriers calculated from different simulations differ significantly in some cases: the highest and lowest barriers for the same process differ by as much as 10 kcal/mol and correspond to different conformational minima on the free energy surface of the protein. These findings highlight the need for adequate conformational sampling in simulations of this type, as shown previously.⁴

Table 3. QM/MM Free Energy Barriers (in kilocalories per mole) for the Nucleophilic Attack at Each of the Epoxide Carbons, C(1) and C(2), from the Extended Umbrella Sampling MD Simulations of the t-SO, t-DPPO(1), and t-DPPO(2) Model Systems.

	ΔG⧧(P)
	t-SO		t-DPPO(1)		t-DPPO(2)
QM method	C(1)	C(2)	C(1)	C(2)	C(1)	C(2)
AM1a	22.7	30.1	19.0	25.0	23.4	30.7
B3LYP/6-31G(d)	7.3	16.6	9.7	11.0	6.8	13.9
SCS-MP2/(aug)-cc-pVTZ	12.3	19.9	12.8	15.8	13.2	21.8

^aEnergy barriers calculated from extended umbrella sampling simulations with His523 protonated at the Nε position.

QM/MM calculations with higher levels of QM theory gave barriers that were considerably lower than those calculated at the AM1/CHARMM22 level. For example, the B3LYP/CHARMM22 potential energy barriers were generally 10–15 kcal/mol lower than the corresponding AM1/CHARMM22 potential energy barriers (given in the Supporting Information). However, the same reactivity trends are predicted with all levels of QM theory tested here.

The free energy barriers are discussed below in two parts. First, the relative free energy barriers and experimental regioselectivity observations are compared, and second, the free energy barriers are compared with experimentally determined reaction rates for a range of EH substrates.

Comparison with Experiment

Regioselectivity

The free energy barriers to nucleophilic attack on t-DPPO in the protonated model, from the preliminary and extended umbrella sampling simulations (Tables 2 and 3), show a preference for attack at C(1) over C(2). This is in qualitative agreement with the experimentally determined regioselectivity for murine sEH reported by Borhan et al., who measured a 97:3 ratio of attack at C(1) to the less-hindered C(2).²² This ratio corresponds to a difference in the barrier of ∼2 kcal/mol. This selectivity is in contrast to that observed for microsomal EH, where attack at the less hindered C(2) is preferred.²⁶ It is encouraging to note that the regioselectivity predictions are broadly the same, regardless of the QM method used, as lower barriers for C(1) attack are observed for all of the QM methods used (see below). The preference for attack at C(1) over C(2) is observed for both orientations of t-DPPO (1 and 2); i.e., there is a lower barrier to attack, regardless of which carbon atom is closer to the nucleophilic Asp333 oxygen atom in the reactant complex. The barrier to nucleophilic attack is lower for C(1) attack than for C(2) attack, because the transition state to attack at both C(1) and C(2) requires partial sp² hybridization of the carbon atom undergoing attack. When nucleophilic attack occurs at C(1), the proximal phenyl ring stabilizes this sp² hybrid carbon to a larger extent than in the case of C(2) attack. This is an intrinsic electronic effect present in the substrate and is not due to the enzyme.

The binding mode of t-DPPO in the t-DPPO(1) model is likely to be more catalytically relevant in the enzyme than the binding mode in the t-DPPO(2) model, because lower free energy barriers are observed for the former than for the latter. Additionally, similar distances are observed between the Asp333 Oδ2 atom and C(1) and C(2) in the unrestrained MD simulations of t-DPPO(1), whereas C(1) is significantly closer to the Asp333 Oδ2 atom in the t-DPPO(2) simulations (Table 1). For t-SO, the calculated free energy barriers suggest a large preference for nucleophilic attack at C(1) over C(2). Such a large effect is surprising, given that the two carbon atoms are chemically equivalent. However, C(1) is much closer to the Oδ2 atom of Asp333 than C(2) in the unrestrained MD simulations and hence is in a more favorable position for nucleophilic attack at C(1) than at C(2) (see Table 1).

The quantitative agreement between the experimental and theoretical values for the relative barriers to C(1) and C(2) nucleophilic attack in t-DPPO (ΔΔG^⧧) is summarized in Table 4. It is clear that although AM1 shows the correct selectivity preference, this is significantly overestimated. A difference in the barrier of 6 kcal/mol would result in exclusive attack at C(1), whereas the experimental observation is a 97:3 preference.²² A much better agreement is found in the B3LYP and SCS-MP2 values (1.7 and 3.0 kcal/mol, respectively). As discussed below, this is because the agreement between theory and experiment for the absolute values of the barriers calculated with B3LYP and SCS-MP2 is greatly superior to that in AM1.

Table 4. Summary of the Agreement between Experiment and QM/MM Calculations for the t-DPPO(1) Model^a.

	experiment	AM1	B3LYP	SCS-MP2//B3LYP
ΔG⧧[C(1)]	13–16b	19.0	9.7	12.8
ΔΔG⧧[C(2)–C(1)]	2.1c	6.0	1.3	3.0
selectivity [C(1):C(2)]	32:1c	23755:1	9:1	154:1

^aΔG^⧧[C(1)] and ΔΔG^⧧[C(2)–C(1)] are the activation free energy for nucleophilic attack at C(1) and the difference between the C(1) and C(2) barriers (in kilocalories per mole), respectively. Selectivity [C(1):C(2)] refers to the ratio of products, predicted by the ratio of the calculated rate constants from ΔΔG^⧧[C(2)–C(1)].

^bEstimated from rate constants obtained for similar epoxide hydrolases and substrates.^27,44,51,79

^cFrom the 97:3 ratio observed by Borhan et al. for the reaction of t-DPPO in murine sEH.²²

Reaction Rate

The potential energy barriers calculated at the AM1/CHARMM22, B3LYP/CHARMM22, and SCS-MP2//B3LYP/CHARMM22 levels of theory are given in theSupporting Information. The average activation entropy correction (at 300 K)⁶⁵ is 1.8 kcal/mol. This value is small and is comparable to the calculated⁶⁵ and experimental⁷⁸ values of entropic contribution (TΔS^⧧) for the conversion of chorismate to prephenate in chorismate mutase at 300 K (2.5 and 2.7 kcal/mol, respectively).

As mentioned above, the B3LYP/CHARMM22 potential energy barriers are significantly lower than the corresponding AM1/CHARMM22 potential energy barriers, but the optimized geometries and hydrogen bonding environments are very similar (bond lengths and bond angles are provided in the Supporting Information). As found for the AM1/CHARMM22 free energy and potential energy barriers, the B3LYP potential energy barriers span a wide range of values [e.g., 4.7–11.2 kcal/mol for attack at C(1) of t-SO (see the Supporting Information)] over the 10 profiles obtained for each of the three model systems. This variation is due to differences in the conformation of the enzyme, and the orientation of the substrate, in the initial structures. The effect of basis set size was explored by calculating B3LYP/6-311+G(d,p) single-point energies for the B3LYP/6-31G(d) geometries and yielded energy barriers within 0.1 kcal mol^–1 of the B3LYP/6-31G(d) energy barriers. The average B3LYP/CHARMM22 potential energy barrier for nucleophilic attack at C(1) of t-SO (7.9 kcal/mol) is in good agreement with the barrier of 7.8 kcal/mol reported for the nucleophilic ring opening of t-MSO by human sEH in a DFT study on an active site model by Hopmann et al.⁵⁰

We are not aware of any published experimental rate constant values for the nucleophilic ring opening in murine sEH with the substrates used in this study. However, for S. tuberosum epoxide hydrolase 1 (StEH1) reacting with t-SO, rate constants corresponding to formation of the covalent ester intermediate of 18 and 100 s^–1 have been measured.^27,44 The formation of an ester intermediate between EH isolated from A. radiobacter and (R)-styrene oxide was found to have a rate constant of 1100 s^–1.⁷⁹ Additionally, a rate constant of 330 s^–1 has been measured for microsomal EH with the substrate glycidyl-4-nitrobenzoate.⁵¹ These rate constants correspond to a range of activation free energies of 13–16 kcal/mol. Hence, the B3LYP/CHARMM22 calculated free energy barrier of 7.3 kcal/mol for nucleophilic attack at C(1) of t-SO is rather low compared to the value calculated from experiment. Likewise, the free energy barrier of 6.8 kcal/mol for attack at C(1) in the t-DPPO(2) model is lower than expected.

It is a common tendency for B3LYP to under- or overestimate reaction barriers for some systems.⁸⁰ The neglect of dispersion in B3LYP is one cause of inaccuracies in the calculation of barriers. For example, a significant improvement in the relative barriers calculated for epoxidation and hydroxylation reactions catalyzed by cytochrome P450 is observed when an empirical dispersion correction is applied to the B3LYP functional.⁸¹ The missing dispersion interaction in B3LYP is unlikely to be important here, as including an empirical dispersion correction would be expected to lower the barriers even further. Testing different density functionals is generally a good idea, as different potential energy barriers are often observed when calculated for the same reaction with different functionals.⁵⁸ As mentioned in Computational Methods, several adiabatic mapping energy profiles were calculated using the BP86 and BHandHLYP functionals. The potential energy barriers obtained with these functionals are detailed in the Supporting Information. It should be noted that both of these functionals share the same lack of dispersion as B3LYP. The BP86 barriers were found to be typically 2–3 kcal/mol lower than the same barriers calculated with B3LYP. In contrast, the BHandHLYP barriers were found to be 5–7 kcal/mol higher than the corresponding B3LYP barriers. The optimized geometries calculated with all three density functionals were almost indistinguishable. As mentioned above, the functional dependence of calculated energy barriers is not uncommon and has been observed previously.⁵⁸ The exchange correlation functional, which varies between different density functionals, is not systematically improvable. It is therefore important to compare the values of energy barriers calculated with DFT to those obtained with high-level correlated ab initio methods, such as coupled cluster and SCS-MP2.⁶⁵

The small number of QM atoms required to model the reaction in the active site of sEH allows the use of correlated ab initio quantum chemical methods, such as SCS-MP2, in QM/MM calculations, which are of a higher level of accuracy and able to include the effects of dispersion in a nonempirical manner. The SCS-MP2 potential energy barriers are higher (by ∼4 kcal/mol) than the corresponding B3LYP barriers. The barriers calculated with the BHandHLYP functional are closest in energy to those calculated with SCS-MP2. This has been found previously in similar calculations on citrate synthase.⁵⁸ B3LYP has been found to perform reasonably well in the calculation of activation energy barriers for chorismate mutase and p-hydroxybenzoate hydroxylase.⁶⁵ For chorismate mutase, the authors reported barriers calculated with B3LYP that were lower than those calculated with local coupled cluster theory, LCCSD(T0) (of very high accuracy), by ∼5 kcal/mol.

The SCS-MP2//B3LYP/CHARMM22 potential energy barriers (given in the Supporting Information) were used to calculate the corresponding free energy barriers that are listed in Table 3. The SCS-MP2//B3LYP/CHARMM22 free energy barrier for attack at C(1) in t-SO is 5.0 kcal/mol higher than the value calculated with B3LYP/CHARMM22. The SCS-MP2//B3LYP/CHARMM22 barrier of 12.3 kcal/mol for t-SO is in good agreement with the 13–15 kcal/mol range, derived from experiment. The SCS//B3LYP/CHARMM22 barrier calculated for C(1) attack in t-DPPO(1) (12.8 kcal/mol) is also in good agreement with the experimentally derived range of values. In fact, all of the SCS-MP2//B3LYP/CHARMM22 free energy barriers for attack at the preferred carbon atom are within 1 kcal/mol of the estimated experimental barriers. However, it should be emphasized that the quoted range of experimental values is for different substrates in different EH enzymes, and hence, perfect agreement should not be expected. A summary ofthe agreement between experiment and theory for the t-DPPO(1) model is shown in Table 4. It should be emphasized also that the excellent agreement between calculations and experiment is only observed in this work where the highest level of QM theory (SCS-MP2) is used. Despite this, B3LYP (and AM1) do predict the correct regioselectivity and are hence suitable for qualitative predictions of reactivity. This has also been found to be true for other enzymes.⁶⁵ While B3LYP underestimates barrier heights in this example, in calculations for citrate synthase, it was found to overestimate barriers.⁵⁸

Hydrogen Bonding Analysis

As mentioned above, there are several important hydrogen bonding interactions present in the active site of sEH. Hydrogen bonding analysis was performed on all umbrella sampling MD simulations (using CHARMM), to gain insight into the lifetimes of these interactions and how they vary during the nucleophilic attack and to assess their effect on the calculated reaction barriers. A hydrogen bond was defined as being present when the distance between the donor (D) and acceptor (A) heavy atoms was less than 2.8 Å and the A–H–D angle was greater than 90°. This definition has been used in previous work.⁸² Detailed data are given in the Supporting Information, and the most interesting features are described below.

In all of the MD simulations in which the His523 residue is protonated at the Nε position, the Nε proton is involved in a hydrogen bond with the Asp333 Oδ2 atom, which is conserved throughout the simulations. The Asp333 Oδ1 atom (the carboxylate oxygen atom that does not act as the nucleophile) accepts hydrogen bonds from the backbone NH groups of Phe265 and Trp334. These hydrogen bonds have been identified as being important in stabilizing the negative charge that accumulates on the Asp333 Oδ1 atom upon formation of the ester intermediate.^33,50 A hydrogen bond is formed between the epoxide oxygen atom and the hydroxyl group of Tyr381 for the entire duration of all umbrella sampling MD simulations, in the ring-opened and closed forms of the substrate. This hydrogen bond becomes stronger as the reaction progresses, as signified by a decrease in the distance between the epoxide oxygen atom and hydroxyl proton of Tyr381 of ∼0.2 Å. The hydrogen bond between the epoxide oxygen and the Tyr465 hydroxyl group shows more variance, as is discussed below.

Tyr381 and Tyr465 have both been identified as being involved in the catalytic mechanism of sEH, by stabilization of the oxyanion hole formed after nucleophilic attack.³³⁻³⁶ It has not been conclusively established whether these residues are directly involved in any bond-breaking or -forming processes. As Tyr381 and Tyr465 were not included in the QM region in this work, it was not possible to observe protonation of the ring-opened epoxide by either of these residues. However, the excellent agreement between our high-level (SCS-MP2) free energy barriers and those derived from experimental rate constants supports a mechanism in which neither of the active site tyrosine residues is deprotonated. Instead, it is believed that the tyrosine residues act as hydrogen bond donors, as found with glutathione S-transferase M1-1.⁸²

In the t-SO umbrella sampling MD simulations of nucleophilic attack at C(2), a hydrogen bond is not observed between the Tyr465 hydroxyl group and the epoxide oxygen in the TS for the majority of the simulations (Figure 5). This hydrogen bond is present in the simulations of C(1) attack that gave the lowest barriers, but it is not present in those with higher energy barriers (details in the Supporting Information). When not donating a hydrogen bond to the epoxide oxygen atom, the hydroxyl group of Tyr465 in the protonated His523 model points toward the phenyl group of Phe265 and is not involved in any hydrogen bonding. The Tyr465–epoxide oxygen hydrogen bond does not form in any of the simulations with the neutral His523 model, because the hydroxyl group of Tyr465 instead donates a hydrogen bond to the Asp333 Oδ2 atom, as shown in Figure 3. The ability of Tyr465 to form a hydrogen bond to the Asp333 Oδ2 atom (when His523 is neutral) may be significant for the proton shuttle step during hydrolysis. In the simulations of nucleophilic attack at C(2) of t-SO, the hydrogen bond between the backbone NH group of Phe265 and Oδ1 of Asp333 is only present for 50% of the simulation time, after r = −0.2 Å (corresponding to the TS).

Figure 5.

Active site structures taken from AM1/CHARMM22 umbrella sampling MD simulations, corresponding to the transition states for the reaction of t-SO. The blue and orange structures correspond to nucleophilic attack at C(1) and C(2), respectively.

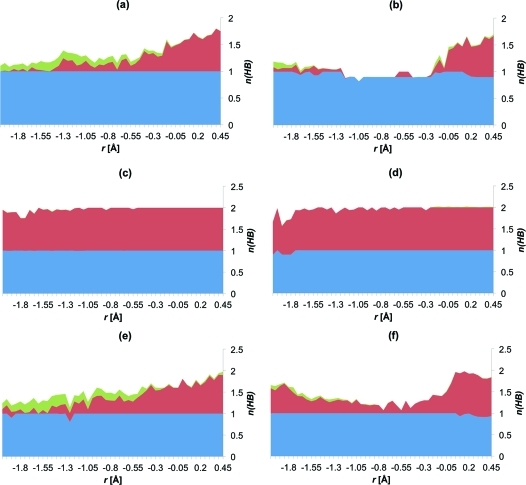
In all of the t-DPPO(1) simulations in which His523 is protonated, a hydrogen bond is present between the hydroxyl group of Tyr465 and the epoxide oxygen for most of the time, throughout the reaction, for nucleophilic attack at C(1) and C(2). This explains the lower barriers that are observed for the t-DPPO(1) simulations, compared to those of t-SO (Table 3), where this interaction is only present for a fraction of the simulation time. In gas phase single-point B3LYP/6-31G(d) energy calculations (details below), the “intrinsic” barriers to C(1) attack in t-SO and t-DPPO were found to be similar. The hydrogen bond between Tyr465 and the epoxide oxygen is not always present in the t-DPPO(2) simulations, for attack at C(1) or C(2), as shown in Figure 6. The transition state (free energy maximum) is located at r = −0.2 Å in both cases.

Figure 6.

Hydrogen bonding to the epoxide oxygen atom during nucleophilic attack at (a) C(1) of t-SO, (b) C(2) of t-SO, (c) C(1) of t-DPPO(1), (d) C(2) of t-DPPO(1), (e) C(1) of t-DPPO(2), and (f) C(2) of t-DPPO(2). The height of the graph corresponds to the total number of hydrogen bonds to the epoxide oxygen, n(HB), at each value of r, during the extended AM1/CHARMM22 umbrella sampling MD simulations, averaged over all profiles. The contributions from Tyr381, Tyr465, and Trp334 are colored blue, red, and green, respectively. The reactant complex is at r = −2.0 Å; the alkyl–enzyme intermediate is at r = 0.5 Å, and the transition state is around r = −0.2 Å (see the text for the definition of r).

The hydrogen bond analysis, together with the free energy barriers in Table 3, indicates that the hydrogen bond between the hydroxyl group of Tyr465 and the epoxide oxygen atom plays a significant role in lowering the barrier to nucleophilic attack in t-SO: higher barriers for nucleophilic attack at C(1) were observed when this interaction was not present in the TS (see the Supporting Information for details). This interaction was not observed during attack at C(2) for t-SO, which is likely to explain the difference between the barrier for attack at C(1) and C(2). The binding mode of t-SO in murine sEH may be an additional factor contributing to the lower barrier for attack at C(1). The O–C(1) distance is 0.86 Å shorter than the O–C(2) distance, on average, at the end of unrestrained simulations of t-SO (Table 1). Considering that the two carbon atoms are chemically equivalent, this is likely to be responsible for the preference for attack at C(1).

To analyze the effect of the enzyme environment on the barriers, we calculated B3LYP/6-31G(d) single-point energies for the QM atoms in the absence of the MM region. This was performed on structures corresponding to the highest and lowest points on the B3LYP/CHARMM22 PESs for C(1) and C(2) nucleophilic attack for the t-SO, t-DPPO(1), and t-DPPO(2) models (with His523 protonated). The gas phase barriers were higher than those calculated in the enzyme by 3–10 kcal/mol (Table 5). This represents a rate acceleration of 10²–10⁵-fold in the enzyme, compared with that in the gas phase.

Table 5. Activation Barriers (in kilocalories per mole) Calculated for Nucleophilic Attack at C(1) and C(2) in t-SO, t-DPPO(1), and t-DPPO(2) for the Protonated His523 Model with B3LYP/6-31G(d)/CHARMM22 (ΔE_QM/MM^⧧) and from Single-Point [B3LYP/6-31G(d)] Energy Calculations on the QM Atoms of the B3LYP/6-31G(d)/CHARMM22 Structures in the Gas Phase (ΔE_gas) and with Continuum Solvation (ΔE_gas+solv^⧧).

		ΔEQM/MM⧧	ΔEgas⧧	ΔEgas+solv⧧
t-SO	C(1)	6.9	14.7	15.6
	C(2)	14.8	17.8	20.5
t-DPPO(1)	C(1)	6.7	14.9	13.0
	C(2)	10.5	20.2	19.2
t-DPPO(2)	C(1)	9.2	14.3	14.0
	C(2)	11.3	17.8	20.2

To make the most meaningful analysis of the rate acceleration achieved by an enzyme, the activation barrier of the reaction in the enzyme should be compared to that of the same reaction in solution.⁴¹ B3LYP/6-31G(d) single-point energies were also calculated for the QM atoms in the absence of the MM region for the structures detailed above, including the Poisson–Boltzmann solvation model in Jaguar (with a dielectric constant of 80.37 and a probe radius of 1.40 Å).⁷⁰ All of the barriers calculated with solvation are higher than their corresponding QM/MM barriers, by 4.8–9 kcal/mol (Table 5). For t-SO, the solvent-corrected barriers are ∼2 kcal/mol higher than the corresponding gas phase barriers, indicating a rate acceleration by the enzyme even greater than that predicted by the gas phase calculations. For t-DPPO(1) and -(2), the barriers calculated with solvation are lower than their gas phase counterparts by approximately the same amount. This might suggest that the nucleophilic attack of t-SO is more favored kinetically in a hydrophobic environment and that the reverse is true for t-DPPO. However, it is possible that the solvation effect is not significant, given the small difference in energy, which is within the expected error margins of B3LYP and continuum solvent models. There are no water molecules present in the active site in the enzyme–substrate complexes in any of the QM/MM calculations, as there is insufficient space. As a water molecule is required for the hydrolysis step, it is possible that the enzyme undergoes a structural rearrangement, with the corresponding entrance of water, prior to the hydrolysis step.

There are several discrepancies between the work presented here and the DFT study by Hopmann et al.⁵⁰ First, our calculations indicate that the most likely protonation state of His523 is the positively charged species, whereas Hopmann et al. modeled the neutral species and do not appear to have considered the protonated model in their study. Also, their work is based on a small static structure of the enzyme taken from a crystal structure, whereas our modeling consists of a larger enzyme model and molecular dynamics simulations, where the mobility of amino acid residues is included. Second, Hopmann et al. suggest that the oxyanion formed after the nucleophilic attack is protonated by Tyr465. While we do not model the protonation by Tyr465 in this study, it seems unlikely to us that this step is necessary. Tyrosine is not a very strong acid, and it is likely that the proton would more readily come from the protonated His523, mediated by a water molecule. This would then leave His523 in a neutral state and allow it to activate the water molecule responsible for the hydrolysis step. This would be an interesting route for further investigation.

Conclusions

Epoxide hydrolases have the potential to act as highly selective biocatalysts in the large-scale production of enantiopure compounds. Understanding the nature of the chemical transformations taking place in the enzyme, together with the factors that dictate the stereochemistry of the products, will lead to a better realization of their power for synthetic purposes.

The nucleophilic epoxide ring opening by Asp333 has been studied here for two different epoxides: t-SO and t-DPPO. These similar epoxides differ in that the two epoxide carbon atoms are equivalent in t-SO but are not in t-DPPO. A combination of QM(AM1)/MM(CHARMM) umbrella sampling MD simulations, B3LYP/CHARMM22, and SCS-MP2 potential energy calculations has been used to obtain free energy barriers to nucleophilic attack at both epoxide carbon atoms in the two substrates.

For t-DPPO, the nucleophilic attack was modeled for two binding orientations, placing one of the two epoxide carbon atoms closer to the nucleophile. In both cases, the nucleophilic attack at the phenyl epoxide carbon atom was found to be preferred over attack at the benzylic carbon atom. This observation is in agreement with experimental studies.²² Our AM1/CHARMM22 umbrella sampling MD simulations give relative free energy barriers that are in good agreement with experimental regioselectivity data for t-DPPO. While the difference between barriers is in good agreement, the absolute values of the free energy barriers calculated at this level of theory are too high, because of the limitations of the AM1 method. Corrections from potential energy barriers calculated with higher levels of QM theory give free energy barriers that are closer to experiment. While the barriers calculated at the B3LYP/CHARMM22 QM/MM level are somewhat too low, correction with SCS-MP2 results in free energy barriers that quantitatively agree with the range of values derived from experimental rate constants.

Our work suggests that the regioselectivity of nucleophilic attack for t-DPPO in sEH is mostly due to the relative electrophilicity of the two epoxide carbon atoms. In the t-SO calculations, despite the chemical equivalence of the two epoxide carbon atoms, a preference for attack at the carbon atom closer to the nucleophile in the enzyme–substrate complex was observed. In the case of t-DPPO, the proximity of the nucleophile appears to have a weaker effect on the predicted regioselectivity, compared with electronic factors. This observation may be important in the design of epoxide hydrolase enzymes for the catalysis of specific transformations. The results indicate that simple models based purely on geometric factors³⁷ are unlikely to be generally successful in predicting regioselectivity.

Analysis of the hydrogen bonding to the epoxide oxygen atom during the ring-opening reaction revealed that lower barriers were observed when a hydrogen bond was present between the epoxide oxygen atom and the hydroxyl group of Tyr465 in the transition state. The hydrogen bond between the Tyr381 hydroxyl group and the epoxide oxygen was found to always be present during all simulations. The results also support the roles of the active site tyrosine residues as being electrophilic catalysts, rather than performing general acid catalysis, in agreement with experimental proposals.³²

The calculations presented here support the protonated form of His523 to be present during the nucleophilic ring-opening step. Evidence of this involvement includes correct prediction of regioselectivity, lower activation free energies, and increased hydrogen bond stabilization of transition states. These features are exclusive to this protonation state (i.e., are not found when it is modeled as neutral).

This work provides a further example of a case in which QM/MM modeling can provide useful insight into the mechanism of an enzyme-catalyzed reaction, highlighting important interactions involved in the stabilization of key reacting species. Consideration of possible protonation states of active site residues, and where necessary, alternative binding poses, may be necessary. We demonstrate that, as long as adequate conformational sampling is performed, reliable predictions of selectivity can be made with relatively low levels of QM theory. However, to obtain absolute values of free energy barriers to near-chemical accuracy, corrections with higher-level correlated ab initio methods are required.

Supporting Information Available

Details of the system setup, free energy barriers, potential energy barriers, atomic charges, absolute energies, some bond lengths, coordinates of selected species, and hydrogen bonding information. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.