A two-compartment mathematical model of neuroglial metabolism using [1-¹¹C] acetate

Abstract

The purpose of this study was to develop a two-compartment metabolic model of brain metabolism to assess oxidative metabolism from [1-¹¹C] acetate radiotracer experiments, using an approach previously applied in ¹³C magnetic resonance spectroscopy (MRS), and compared with an one-tissue compartment model previously used in brain [1-¹¹C] acetate studies. Compared with ¹³C MRS studies, ¹¹C radiotracer measurements provide a single uptake curve representing the sum of all labeled metabolites, without chemical differentiation, but with higher temporal resolution. The reliability of the adjusted metabolic fluxes was analyzed with Monte-Carlo simulations using synthetic ¹¹C uptake curves, based on a typical arterial input function and previously published values of the neuroglial fluxes V_tca^g, V_x, V_nt, and V_tcaⁿ measured in dynamic ¹³C MRS experiments. Assuming V_x^g=10 × V_tca^g and V_xⁿ=V_tcaⁿ, it was possible to assess the composite glial tricarboxylic acid (TCA) cycle flux V_gt^g (V_gt^g=V_x^g × V_tca^g/(V_x^g+V_tca^g)) and the neurotransmission flux V_nt from ¹¹C tissue-activity curves obtained within 30 minutes in the rat cortex with a beta-probe after a bolus infusion of [1-¹¹C] acetate (n=9), resulting in V_gt^g=0.136±0.042 and V_nt=0.170±0.103 μmol/g per minute (mean±s.d. of the group), in good agreement with ¹³C MRS measurements.

Introduction

The brain meets its energetic demands at rest and during activation largely, if not exclusively by oxidative combustion of fuels. The tricarboxylic acid (TCA) cycle is central to oxidative cerebral metabolism and its metabolic rate is thus particularly important to measure when studying brain energetic needs under different physiological conditions. In addition to the generation of energy for brain cells ultimately in the form of high-energy phosphates such as ATP, the TCA cycle is involved in the metabolism of amino acids, such as the major excitatory neurotransmitter glutamate.

The major substrate for brain metabolism is glucose. However, a limitation in the use of labeled glucose or analogs to study brain metabolism is that these tracers must pass through the glycolysis before reaching the TCA cycle and do not reflect directly TCA cycle activity. Deoxyglucose derivates, such as the most frequently used fluorodeoxyglucose (FDG) do not even enter the glycolysis. They are trapped after phosphorylation by hexokinase to (fluorodeoxy)-glucose-6-phosphate and thus cannot reflect oxidative metabolism. A solution is to use a direct TCA cycle precursor, entering the metabolic pathway after the glycolytic branch point. Acetate, which is metabolized to acetyl-CoA and enters the TCA cycle through citrate synthetase, similarly to pyruvate, is an example of such a precursor.

Moreover, the compartmentation of glutamate metabolism in brain opens the way to in vivo studies of neuroglial interaction, using glial- or neuronal-specific substrates, or tracers metabolized simultaneously by both cells. In contrast to glucose, acetate is uniquely metabolized in the glial compartment (Waniewski and Martin, 1998) and turns out to be an ideal substrate to probe glial oxidative metabolism and to increase the sensitivity of the measurement of the glutamate-glutamine cycle (de Graaf et al, 2003b; Henry et al, 2006). Labeled with the positron emitting carbon-11, [1-¹¹C] acetate is thus a suitable substrate to assess glial oxidative metabolism and local neurotransmission using positron emission tomography (PET) or beta-probes (Wyss et al, 2009, 2011). However, to date, no metabolic model has been presented to analyze brain [1-¹¹C] acetate studies, based on the biochemical reactions involved in acetate utilization (e.g., TCA cycles, glutamate-glutamine cycle). The aim of this study was to develop a kinetic model for brain [1-¹¹C] acetate infusion experiments, based on the modeling methods used for Nuclear Magnetic Resonance spectroscopy, compatible with the analysis of data acquired with PET or beta-probe (Weber et al, 2003). The model was evaluated on experimental data acquired with a beta-probe in vivo in rat brains, after an intravenous bolus injection of [1-¹¹C] acetate.

Materials and methods

Beta-Probe Measurements

The metabolic model presented in this study was developed and tested with in vivo experimental data from [1-¹¹C] acetate infusion studies, obtained from the PET center in Zurich and published elsewhere (Wyss et al, 2009). Data were acquired in urethane anesthetized Sprague-Dawley rats. All animal experiments were approved by the veterinary authorities of the Canton of Zurich and were performed in accordance with their guidelines. The experiments were performed by licensed investigators. Briefly, a dedicated β-scintillator (Swisstrace, Zurich, Switzerland) was carefully inserted into the cortex at a depth of ∼1.4 mm below the dura avoiding large blood vessels. With the ¹¹C nuclide, the probe measures the local radioactivity density of the tissue over time in a detection sphere of ∼2 mm of radius yielding tissue-activity curves (Pain et al, 2002).

To measure the arterial input function (AIF) after bolus injection of 230 to 260 MBq of [1-¹¹C] acetate, an arteriovenous shunt from the right femoral artery to the right femoral vein was used in conjunction with a γ coincidence counter to measure whole blood radioactivity. Data were acquired during a minimum of 20 minutes, both for the AIF and the brain tissue activity. The input function had a time resolution of 2 seconds, while each beta-probe measurement was averaged over 50 seconds.

Standard One-Tissue Compartment Model

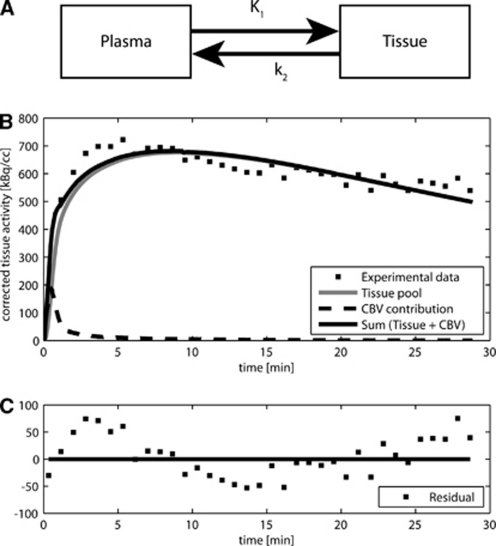
A previous model for brain studies is the one-tissue compartment model originally developed for ¹¹C-acetate cardiac studies (Buck et al, 1991). This model, composed of two pools, is provided for completeness in Figure 1A. The first pool represents acetate radioactivity concentration in the plasma, known as AIF. The second pool represents the total brain tissue activity. This pool is the sum of the activity concentrations of all labeled metabolites. The rate of label transfer between the two pools is typically calculated from the first-order rate constants K₁ and k₂, representing the uptake of ¹¹C-acetate and the clearance of ¹¹C through the molecules resulting from brain metabolism of acetate (predominantly ¹¹CO₂), respectively (Wyss et al, 2009).

Figure 1.

(A) One-tissue model of acetate metabolism originally developed for ¹¹C-acetate cardiac studies (Buck et al, 1991). (B) Typical result obtained using this model on brain beta-probe data. (C) The residuals show an unsatisfactory modeling of the experimental data, suggesting a more complex dynamics. CBV, cerebral blood volume.

The measured total activity curve includes the tissue compartment and the vascular compartment. The vascular volume fraction or cerebral blood volume (CBV) in the rat cerebral cortex is on the order of 2% to 3% (Todd et al, 1993a; Weeks et al, 1990). The experimental curve is, therefore, fitted to a linear combination of the two pools:

where α corresponds to the relative CBV. Using the measured AIF, the model was fitted to the tissue-activity curve by varying the three parameters K₁, k₂, and α. The plot in Figure 1C shows a systematic deviation of residuals from zero, which was consistently observed with most experimental data.

Neuroglial Model

In this study, metabolic modeling was developed using a compartmentalized neurotransmitter approach previously applied in ¹³C Nuclear Magnetic Resonance studies (Gruetter et al, 2001). Brain tissue is mainly composed of glial and neuronal cells. It is now well accepted that glial cells are actively involved in excitatory neurotransmission, e.g., through the uptake of the neurotransmitter glutamate from the synaptic cleft (Arriza et al, 1994). The model, therefore, consists of two main metabolic compartments corresponding to the two cell types. Each compartment consists of the respective TCA cycle as well as of the glutamate-glutamine cycle, linking the metabolism of both compartments.

Acetate is almost exclusively metabolized in astrocytes (glial compartment) (Lebon et al, 2002; Waniewski and Martin, 1998). As a consequence, the inflow of new label from the substrate is occurring only through the glial TCA cycle. Nevertheless, the neuronal TCA cycle rate was accounted for, since it provides unlabeled carbons originating from neuronal pyruvate metabolism to the glutamate-glutamine cycle, which affects overall tissue activity.

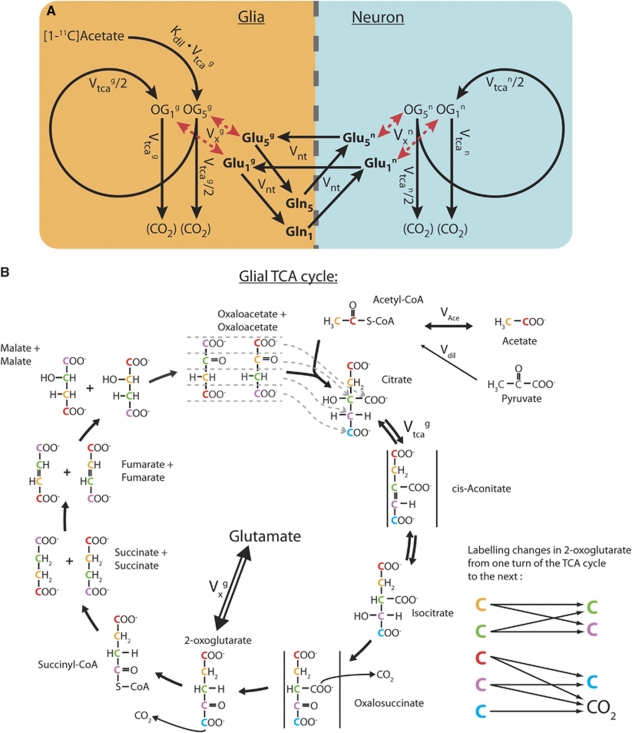
The resulting model is presented in Figure 2A. To illustrate how label is transferred within a molecule in the TCA cycle, we added the detailed scheme in Figure 2B. ¹¹C from [1-¹¹C] acetate enters the glial TCA cycle at the position 5 of citrate. Pyruvate metabolism in the glial compartment dilutes the acetyl-CoA pool. In the first turn of the TCA cycle, ¹¹C reaches the position 5 of 2-oxoglutarate with a total net flux K_dil × V_tca^g (Supplementary Appendix A), where K_dil represents the affinity of glial metabolism to acetate. K_dil was fixed to 0.76, as found in ¹³C magnetic resonance spectroscopy (MRS) rat studies, in similar physiological conditions (Duarte et al, 2011). 2-Oxoglutarate exchanges label with cytosolic glutamate. This transmitochondrial label exchange, denoted by V_x^g, transfers label from the carbon position 5 of 2-oxoglutarate to the position 5 of glutamate. Due to the symmetry of the succinate molecule, the second turn of the TCA cycle brings half of the labeled carbons of the position 5 of 2-oxoglutarate to the position 1 of 2-oxoglutarate and half of it is eliminated as CO₂. Through the transmitochondrial flux V^g_x, [1-¹¹C] glutamate is formed from [1-¹¹C] 2-oxoglutarate. In glia, metabolic pathways involving aspartate were assumed to be negligible (Wurdig and Kugler, 1991).

Figure 2.

(A) Schematic view of the compartmental metabolic model used for brain [1-¹¹C] acetate metabolism. The diagram shows the ¹¹C labeling flows from acetate to the positions 5 and 1 of glutamate, glutamine and to CO₂, through the glial and neuronal tricarboxylic acid (TCA) cycles. (B) Detailed view of the carbon labeling flow through the glial TCA cycle. The neuronal TCA cycle is similar, except that no carbon coming from acetate enters the neuronal TCA cycle. The colors enable the follow-up of the carbons from one molecule to the next. The arrows on the right show how carbons are moving in the carbon chain of 2-oxoglutarate from one TCA cycle turn to the next. The carbons 4 and 5 of citrate are always coming from acetyl-CoA. The carbon positions of glutamate (and glutamine) are identical to those of 2-oxoglutarate. Two carbons are lost in CO₂ at the level of oxalosuccinate and 2-oxoglutarate in each TCA cycle turn.

On the neuronal side, label entering the TCA cycle in the first turn from acetate is neglected, consistent with the glial-specific uptake of acetate. Nevertheless, once neuronal glutamate is sufficiently labeled by the action of the glutamate-glutamine cycle (V_nt), the exchange between glutamate and 2-oxoglutarate through Vⁿ_x allows in principle a labeling of the glutamate at position 1 from the glutamate at position 5 in the second turn of the TCA cycle. The fractional enrichments (concentration of labeled molecules divided by the total concentration of this molecule in the pool) of the neuronal glutamate pools are expected to be low, because acetate is entering only on the glial side and because the infusion experiments are short (20 minutes in Wyss et al, 2009) on the time scale of neuronal glutamate turnover times. Therefore, the labeling of aspartate through the malate–aspartate shuttle on the neuronal side was assumed to be negligible.

Carbon Dioxide Labeling

In radiotracer experiments, the measured radioactivity curve represents all labeled compounds. Therefore, the contribution to the total tissue activity of labeled CO₂, present in high concentrations of ∼13.8 to 15.1 μmol/g in the brain (Thompson and Brown, 1960; Thompson et al, 1980), needs to be additionally taken into account. For the modeling of CO₂ labeling, we assumed a typical value of 15 μmol/g of total brain CO₂, which includes bicarbonate, in rapid exchange with CO₂ due to the action of carbonic anhydrase.

The input of label into the CO₂ pool originates from both glial and neuronal TCA cycles. In fact, two CO₂ molecules are released per turn in the TCA cycle (Figure 2B). An additional CO₂ molecule is produced in the glycolysis for both compartments. Using the metabolic steady-state assumption for CO₂, the efflux of the CO₂ pool V_out is:

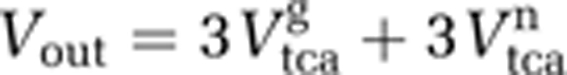When infusing C1-labeled acetate, the first release of label to CO₂ occurs in decarboxylation of oxalosuccinate in the second TCA cycle turn. Since 2-oxoglutarate can exchange its carbon chain with glutamate, this label loss originates either from acetate or from glutamate C5. The second loss of labeled carbon to CO₂ occurs in decarboxylation of 2-oxoglutarate, also in the second TCA cycle turn. This labeled carbon can originate directly from an exchange with glutamate C1, from glutamate C5 or acetate. Thus, CO₂ can also be labeled from the neuronal TCA cycle, but only from neuronal glutamate C5 and C1, which both are likely to be only weakly labeled, since acetate does not directly enter neurons. The third CO₂ molecule produced in the glycolysis is unlabeled in both compartments. The relative contribution of each of these pools to CO₂ labeling is elaborated in Supplementary Appendix B.

CO₂ diffuses almost freely across the blood–brain barrier. It was estimated (Supplementary Appendix B) that the total amount of CO₂ in blood, considering all the transport modes (dissolved, buffered with water as bicarbonate, bound to proteins, particularly hemoglobin), is similar to brain CO₂ concentration (Pocock and Richards, 2004). Assuming a fast exchange between these modes compared with brain metabolism (Geers and Gros, 2000) and a cerebral blood flow in the range of 1.3 mL/g per minute (Todd et al, 1993a, 1993b), an influx of 20 μmol/g per minute of unlabeled CO₂ is estimated. This flux is large compared with the TCA cycle fluxes and reduces the ¹¹CO₂ activity and, therefore, its contribution to the total tissue-activity curve. Including the ¹¹CO₂ pool introduces an additional differential equation to the existing differential system, but no extra parameter (flux) to adjust.

Units of the Data and Derived Fluxes

Positron emission data are measured in kBq/mL and not directly as a concentration (in μmol/g). They are corrected for radioactive decay and delay between the plasma measurement and brain measurement due to blood circulation. The Nuclear Magnetic Resonance metabolic modeling approach expresses the total concentration of metabolites (labeled or not) in μmol/g and the labeling of each chemical pool in terms of fractional or isotopic enrichment (Uffmann and Gruetter, 2007). For this study, standard total concentrations of 3.5 μmol/g for glutamine, 1 μmol/g for glial glutamate, and 8 μmol/g for neuronal glutamate were assumed (Kunz et al, 2010; Xin et al, 2010).

However, a conversion of the data from kBq/mL to μmol/g was not necessary, since we are dealing with linear differential equations (see Supplementary Appendix A) in which both beta-probe data and AIF are given in kBq/mL.

Using absolute concentrations in μmol/g for the chemical pool sizes allows determining metabolic fluxes between the pools in μmol/g per minute from the adjusted rate constants. To solve the differential system, the fractional enrichment of plasma acetate (AIF) was calculated assuming a typical blood acetate concentration of 1 μmol/g in the rat (Cetin et al, 2003).

Model Analysis

First, the standard one-tissue compartment model (Figure 1A) was applied to different tissue-activity time courses acquired in vivo.

To assess the validity of the suggested new modeling approach, the two-compartmental (neuroglial) model was then implemented and studied under four different sets of assumptions, further described below.

A system of linear differential equations was derived for the neuroglial model, assuming metabolic steady-state (i.e., no net metabolite concentration changes are occurring). As previously shown (Uffmann and Gruetter, 2007), the temporal change of the labeling of the TCA intermediates, present in low concentrations, can be eliminated from the mathematical model without modifying the dynamics of the labeling of glutamate, resulting in a 7-pools model (Glu₅^g, Glu₁^g, Gln₅, Gln₁, Glu₅ⁿ, Glu₁ⁿ, and CO₂) characterized by five fluxes (V_tca^g, V_x^g, V_nt, V_tcaⁿ, and V_xⁿ). The detailed derivation of the labeling equations is provided in Supplementary Appendix A.

The models were developed using Matlab (MathWorks, Natick, MA, USA). To assess the precision and accuracy of the different parameters, Monte-Carlo simulations of the neuroglial model were undertaken, based on the simulated time courses created with the complete model and generated with the following flux values (V_tca^g=0.06, V_tcaⁿ=0.56, V_x^g=V_xⁿ=0.57, and V_nt=0.17 μmol/g per minute), consistent with human and anesthetized rat brain (Gruetter et al, 2001). Gaussian noise (of similar variance σ² than the one found in experimental beta-probe data) was added to the simulated activity curve, which was then fitted using the different hypotheses described in the scenarios 1 to 4 (see below). Monte-Carlo simulations (500 fits) were undertaken to estimate the uncertainty and mean value of each flux in the different cases. The initial values of the fluxes were taken randomly between 0 and 1 μmol/g per minute and the values were constrained to be nonnegative.

The following four scenarios were investigated:

Case 1:

V_tca^g, V_x^g, V_nt, V_tcaⁿ, V_xⁿ unconstrained.

Case 2:

V_x^g=10 × V_tca^g and V_xⁿ=V_tcaⁿ.

Case 3:

as Case 2 but with 5% CBV and ¹¹CO₂ contribution added to the simulated experimental curve. A zero weight was given to the data points from the first 2 minutes.

Case 4:

as Case 3, but the pool of CO₂ was added to the fitted model.

In Case 3, ¹¹CO₂ production and CBV contribution were added to the simulated tissue-activity curves but not to the model used to fit the data. In this way, the impact of these two additional labeling pools on the estimated fluxes could be investigated.

In Case 4, a sensitivity analysis was also performed to visualize the effect on the tissue curve of varying V_nt and the composite fluxes V_gt^g and V_gtⁿ by steps of 10%. V_gt^g and V_gtⁿ are defined as follows:

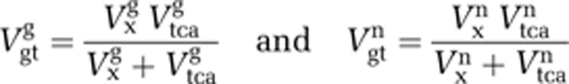The neuroglial model with the assumptions used in Case 4 was finally fitted to nine sets of AIFs and tissue measurements obtained on different rats in resting conditions, under urethane anesthesia (Wyss et al, 2009). Mean value and uncertainty of V_nt and the composite TCA fluxes V_gt^g and V_gtⁿ were estimated with Monte-Carlo simulation.

Results

Standard One-Tissue Compartment Model

First, the standard one-tissue compartment model (Figure 1A) was fitted to the measured in vivo tissue-activity time courses. A typical result and fit residual are shown in Figure 1. The contribution of blood activity to the total measured curve was largely limited to the first 2 minutes. After this initial period, the radioactivity originating from blood was close to the experimental noise. For this illustrating example, the signal contribution from blood was estimated by the fit to be α=3.3%, and varied between 2.5% and 5% for all animals. The plot in Figure 1C clearly shows a systematic deviation of residuals from zero, which was consistently observed in most studies, suggesting that the complex dynamics of brain acetate metabolism cannot be fully described by the one-tissue compartment model of Figure 1.

Neuroglial Model

In each case, the mean value of the different fluxes (V_tca^g, V_x^g, V_nt, V_tcaⁿ, V_xⁿ, V_gt^g, and V_gtⁿ) is reported (Table 1), as well as their s.d. (calculated from the Monte-Carlo simulations). To check the quality of the fit in the different treated approximations, the fit residual and its s.d. in each case are also indicated.

Table 1. Flux values and uncertainties determined by Monte-Carlo simulation.

μmol/g per minute	Vtcag	ΔVtcag	Vxg	ΔVxg	Vgtg	ΔVgtg	Vnt	ΔVnt	Vtcan	ΔVtcan	Vxn	ΔVxn	Vgtn	ΔVgtn	RSS (AU)	ΔRSS (AU)
Case 1	0.314	0.354	0.424	0.370	0.048	0.007	0.455	0.332	0.507	0.274	0.476	0.275	0.189	0.072	11,902	3,139
Case 2	0.059	0.003	0.590	0.025	0.054	0.002	0.438	0.339	0.429	0.193	0.429	0.193	0.214	0.097	12,315	3,446
Case 3	0.063	0.003	0.633	0.031	0.058	0.003	0.464	0.382	0.475	0.213	0.475	0.213	0.238	0.106	13,159	3,669
Case 4	0.061	0.003	0.615	0.033	0.056	0.003	0.488	0.387	0.490	0.211	0.490	0.211	0.245	0.106	13,452	3,740
True value	0.060	—	0.570	—	0.054	—	0.170	—	0.560	—	0.570	—	0.282	—	—	—

Table summarizing the values and uncertainties found in the fit of the simulated data with V_tca^g=0.06, V_tcaⁿ=0.56, V_x^g=V_xⁿ=0.57 and V_nt=0.17 μmol/g per minute, under the different constraints (Cases 1 to 4) presented in Materials and methods. To enable a direct comparison between the Cases 1 to 2 and Cases 3 to 4, the residual sum of squares (RSS) was calculated starting from the second minute. The uncertainties were evaluated with Monte-Carlo simulations (500 artificial data).

Table 2 shows the average correlations found for the estimated fluxes in the Monte-Carlo procedure for each case of the four.

Table 2. Correlation between the adjusted metabolic fluxes.

Correlation	Vtcag	Vxg	Vnt	Vtcan	Vxn
(A)
Vtcag	1.00	−0.77	−0.11	0.01	−0.01
Vxg	−0.77	1.00	−0.10	0.08	0.04
Vnt	−0.11	−0.10	1.00	−0.16	−0.09
Vtcan	0.01	0.08	−0.16	1.00	−0.43
Vxn	−0.01	0.04	−0.09	−0.43	1.00

Correlation	Vtcag	Vnt	Vtcan
(B)
Vtcag	1.00	−0.43	0.37
Vnt	−0.43	1.00	−0.19
Vtcan	0.37	−0.19	1.00
(C)
Vtcag	1.00	−0.32	0.24
Vnt	−0.32	1.00	−0.22
Vtcan	0.24	−0.22	1.00
(D)
Vtcag	1.00	−0.47	0.41
Vnt	−0.47	1.00	−0.26
Vtcan	0.41	−0.26	1.00

Correlation of the fitted fluxes in the different simulated scenarios: (A) Case 1, all fluxes unconstrained, (B) Case 2 (V_x^g=10 × V_tca^g and V_xⁿ=V_tcaⁿ), (C) Case 3 (with cerebral blood volume (CBV) and ¹¹CO₂ contamination in the measured tissue curve), and (D) Case 4, (like Case 3, CO₂ labeling added to the model).

In the following section, we describe the results summarized in Tables 1 and 2 for each different set of assumptions (Cases 1 to 4).

Analysis of the Monte-Carlo Simulation for the Four Different Cases

Case 1 (All Five Parameters Unconstrained)

The model with five free parameters presented a significant correlation between V_tca^g and V_x^g (−0.77), as well as, to a smaller extent, between V_tcaⁿ and V_xⁿ (−0.43; Table 2A), while their respective uncertainties were relatively large (50% to 100% Table 1). However, the variance of the corresponding composite fluxes V_gt^g and V_gtⁿ was significantly decreased (15% and 38%, respectively). V_nt was uncorrelated and presented an uncertainty of 73%.

Case 2 (V_x^g=10 × V_tca^g and V_xⁿ=V_tcaⁿ)

Constraining V_x^g and V_xⁿ to reduce the uncertainty of neuronal and glial V_tca and V_gt fluxes was without effect on the quality of the fit compared with Case 1, as judged from the fit residual variation, which was within 3%. In addition, the correlation between the fitted fluxes was reduced to <0.43 in absolute value (Table 2B).

In Case 2, the fitted fluxes were close to the ‘true' values (on which the Monte-Carlo simulation is based), except for V_nt, which presented also a high uncertainty (77%). The true V_nt value was within the 95% confidence interval of the estimated V_nt.

Case 3 (with Cerebral Blood Volume and ¹¹CO₂ Contamination in the Measured Tissue Curve)

In Case 3, where CBV and CO₂ contributions were added, the three fitted fluxes showed low correlations <0.32 in absolute value (Table 2C). The uncertainty of V_gt^g was particularly low (5%). V_gtⁿ presented a higher uncertainty of ∼45%, while V_nt was overestimated and presented a high uncertainty of ∼80%. The omission of the two first minutes in the fitting procedure allowed keeping a good fit quality (a fit residual 7% worse compared with Case 2) and similar fitted values, despite the fact that blood activity and ¹¹CO₂ contributions were not taken into account. V_gt^g, V_nt, and V_gtⁿ differed from their ‘true' value by 7%, 173%, and 16%, respectively.

Case 4 (like Case 4, CO₂ Labeling Added to the Model)

In Case 4, the activity of the CO₂ pool was added to the fitted curve. A very similar fit residual (residual 9% worse compared with Case 2), flux values and uncertainties were found in Case 4 compared with Case 3. V_gt^g, V_nt, and V_gtⁿ showed a s.d. of 5%, 79%, and 43%, respectively, diverging from the ‘true' value by 4%, 187%, and 13%, respectively. These three fluxes were also well uncorrelated (Table 2D), with the strongest correlation of −0.47 between V_tca^g and V_nt.

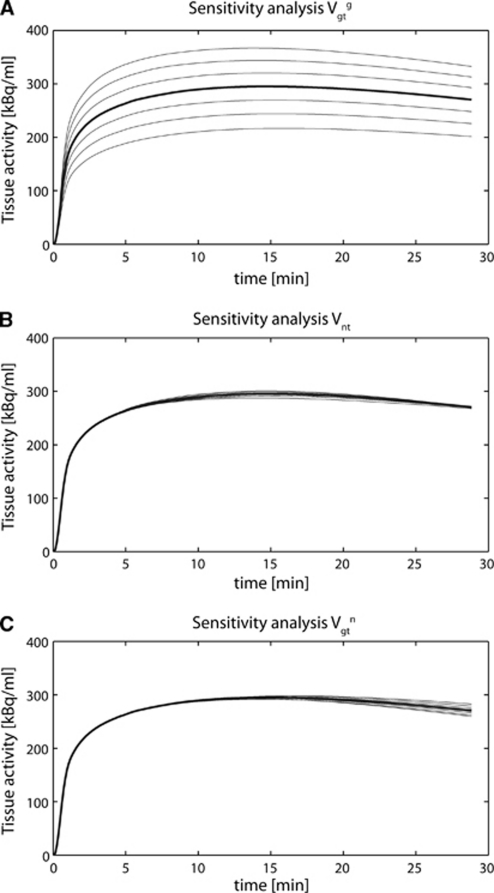
Sensitivity Analysis

Figure 3 shows the sensitivity analysis of the neuroglial model to the fitted fluxes, using the assumptions of Case 4. A typical [1-¹¹C] acetate bolus injection curve was considered as AIF. The analysis was made starting from the typical flux values already used before (V_tca^g=0.06, V_tcaⁿ=0.56, V_x^g=V_xⁿ=0.57, and V_nt=0.17 μmol/g per minute). The thick line is the simulated curve with these parameters, while each thinner line represents a step variation of 10% for the considered flux (V_gt^g in Figure 3A, V_nt in Figure 3B, and V_gtⁿ in Figure 3C). The result showed that the tissue-activity curve was very sensitive to the glial composite flux V_gt^g. V_nt and V_gtⁿ had a much smaller influence on the total brain tissue-activity curve. The low sensitivity of the fitted tissue curve to V_gtⁿ and V_nt was reflected by the relatively large uncertainties found for these fluxes in the Monte-Carlo study.

Figure 3.

Sensitivity analysis of the model relatively to the parameters V_gt^g (A), V_nt (B), and V_gtⁿ (C). The thick line represents the simulated data for (V_tca^g=0.06, V_tcaⁿ=0.56, V_x^g=V_xⁿ=0.57, and V_nt=0.17 μmol/g per minute), using a typical arterial input function. The thinner lines represent each time a step of 10% increase or decrease in the corresponding parameter value. The sensitivity analysis shows that the curve is predominantly driven by the composite flux V_gt^g, characterizing the label input in the glial glutamate C5 position.

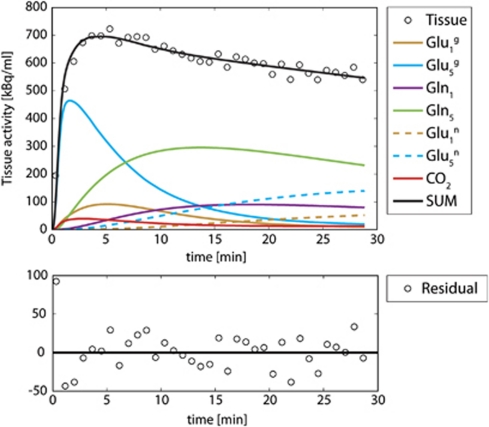
Experimental Data

Figure 4 shows a typical fit of an experimental tissue-activity curve obtained with the beta-probe. The assumptions used were those of Case 4, i.e., V_x^g=10 × V_tca^g, V_xⁿ=V_tcaⁿ and the two first minutes of experiment were neglected in the fit to minimize CBV contributions to the signal. The goodness of fit is showed by the random distribution of the residual around zero. The experimental data correspond to that presented in Figure 1, where the one-tissue compartment model was fitted.

Figure 4.

Fit of the same experimental data as in Figure 3, but using the neuroglial model with the assumption exposed in Case 4. The fit residuals are uniformly distributed around zero. The higher experimental values at the beginning compared with the fit are due to the contamination of the blood activity in brain tissue. However, thanks to the bolus injection of [1-¹¹C] acetate, this problem can be solved by fitting the curve starting only from minute 2.

The neuroglial model was able to characterize the time course, as no discrepancy between experimental data and model was visible. This observation was consistently made for all nine fitted experimental curves.

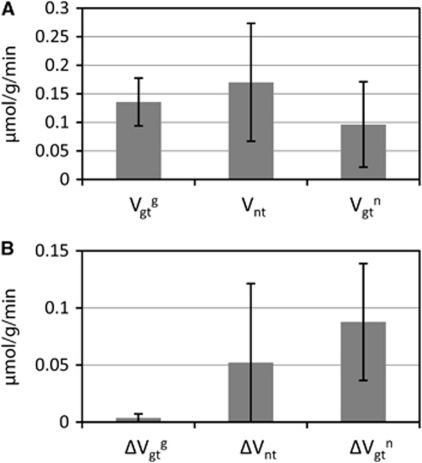
Figure 5 summarizes the group average and s.d. of fluxes obtained on nine rats in resting conditions. The mean values for V_gt^g, V_nt and V_gtⁿ were, respectively, 0.136±0.042, 0.170±0.103, and 0.096±0.075 μmol/g per minute (mean±s.d. of the group). The group average of the flux uncertainties for V_gt^g, V_nt, and V_gtⁿ was, respectively, 0.004±0.004, 0.052±0.069, and 0.088±0.051 μmol/g per minute (mean±s.d. of the group). V_gt^g had a reproducible value among the different animals and its uncertainty was low in each individual case, making it a very accurate parameter measured in [1-¹¹C] acetate experiments. V_nt was measured with a typical uncertainty of ∼30%.

Figure 5.

(A) Group average and s.d. of fluxes obtained on nine rats in resting conditions. (B) Group average of the flux uncertainties obtained on the same nine rats. V_gt^g has a reproducible value among the different animals and its uncertainty is low in each individual case, making it a very accurate parameter measured in [1-¹¹C] acetate experiments. V_nt is measured with a typical uncertainty of ∼30%.

Discussion

In this study, we built a brain metabolic model for [1-¹¹C] acetate infusion experiments based on the radiotracer techniques to measure tissue-activity curves. The modeling approach was based on a two-compartment model typically used in brain ¹³C-labeling studies. The sensitivity of the model to the involved biochemical fluxes was assessed by fitting an artificial tissue-activity curve, based on a typical AIF and standard metabolic fluxes. This Monte-Carlo approach based on the simulated data, in which the ‘true' flux values are known, allowed a direct assessment of the accuracy and precision of the model under different assumptions. Finally, using the more suitable working assumptions, the model was successfully fitted to nine experimental data sets acquired in vivo from adult rat brain using a beta-probe (Wyss et al, 2009).

Measurable Fluxes: Unreliability of the Separate V_x^g and V_tca^g Estimation

The dynamics of glial glutamate C5 labeling is affected by the composite flux V_gt^g and by the neurotransmission flux V_nt. Hence, V_x^g cannot be determined separately from V_tca^g when using the glutamate C5 curve only. The labeling dynamics of all the metabolites labeled at C5 is symmetric to the exchange of V_x^g and V_tca^g and all pairs of these two fluxes resulting in a same V_gt^g will fit identically the C5 metabolites labeling curves (Henry et al, 2006). This underdetermination can be partially removed by additional information coming from the C1-labeled metabolites enrichment data. The differential equation related to the labeling of glial glutamate C1 (Supplementary Appendix A, eq. 10) shows that V_x^g and V_tca^g act differently on the two precursors of glial glutamate C1 through the glial TCA cycle, namely [1-¹¹C] acetate and glial glutamate C5. With a perfect tissue-activity curve, a single pair of V_x^g and V_tca^g would fit properly the data.

However, in radiotracer experiments, the information on C1-labeled metabolites cannot be acquired separately. It is added to the activity from all other labeled metabolites in the tissue. The contribution of the C1 positions to the total tissue activity is low (Figure 4), typically <10%. The separate measurement of V_x^g and V_tca^g is thus unreliable, as illustrated by the Monte-Carlo simulation for Case 1 (all fluxes unconstrained). The uncertainties of V_x^g and V_tca^g were high and their values remained strongly correlated.

As a consequence, it was more appropriate to fit the experimental data by adjusting V_tca^g and constraining V_x^g to 10 times the value of V_tca^g, following the results of several Nuclear Magnetic Resonance studies (Choi et al, 2002; Gruetter et al, 1992, 2001; Henry et al, 2002), while V_gt^g was reported. A similar approach was used for V_tcaⁿ and V_xⁿ, where V_xⁿ was fixed to the value of V_tcaⁿ. These constraints were used for the remaining cases, i.e., 2 to 4, which affected the quality of the fit marginally, yet improved the precision on the remaining fluxes (V_gt^g, V_nt, and V_gtⁿ).

The affinity of glial metabolism to acetate, represented by K_dil, could be theoretically extracted from the steady-state enrichment of the glutamine labeling positions. However, due to bolus injection of [1-¹¹C] acetate, a labeling steady-state was never achieved. As a consequence, including K_dil as free parameter was leading to a high uncertainty on its value. We chose, therefore, to fix K_dil to the value found in ¹³C MRS rat studies, in similar physiological conditions (Duarte et al, 2011).

Glial Fluxes

With the aforementioned assumptions for V_x and V_tca (V_x^g=10 × V_tca^g and V_xⁿ=V_tcaⁿ), the composite glial TCA cycle flux V_gt^g was determined with high precision in all Cases 2 to 4, with a s.d. of <6% for Case 4. The sensitivity of the measured tissue-activity curve toward V_gt^g is significant (Figure 3A).

The accuracy of V_gt^g was hardly dependent on the working assumptions studied in Cases 2 to 4, varying from 0.054 to 0.058 μmol/g per minute for a ‘true' value of 0.054 μmol/g per minute. Therefore, V_gt^g is a highly reliable flux when measured with [1-¹¹C] acetate.

Neuronal Fluxes

Using the assumptions that V_x^g=10 × V_tca^g and V_xⁿ=V_tcaⁿ (Cases 2 to 4), V_tca^g, V_nt, and V_tcaⁿ were adjusted. Despite the goodness of fit, V_nt and V_gtⁿ presented relatively high uncertainties (77% and 45%, respectively) (Table 1, Case 2) due to their low impact on the measured curve, as seen with the sensitivity analysis in Figures 3B and 3C. In acetate infusion experiments, the role played by the neuronal fluxes is limited to dilute the neuronal glutamate C5 pool and by partially labeling neuronal glutamate C1 from glutamate C5. Both of these pools have a low activity throughout the experiment and contribute weakly to the total measured tissue-activity curve (Figure 4). Variations in labeling of these pools are thus imprecisely measured.

In the experimental cases, the value of V_nt impacted the precision of V_gtⁿ (data not shown): with higher V_nt, the fractional enrichment of the neuronal glutamate positions increased faster and the impact of V_gtⁿ on the tissue-activity curve was thus stronger, resulting in a higher precision of the fitting procedure on V_gtⁿ. The precision of this flux was thus case dependent.

To analyze the impact of neglecting completely the neuronal dilution in the fit, the simulated data were fitted with neuronal fluxes fixed to 0 μmol/g per minute (data not shown). The fit residual was clearly increasing (by 110% compared with Case 2, where V_tcaⁿ is adjusted); V_nt diverged from its real value, while the glial fluxes were less affected by this hypothesis. As a consequence, although poorly determined, the neuronal fluxes V_xⁿ and V_tcaⁿ should be adjusted during the fit.

Neurotransmission Flux

V_nt converts glial glutamate-labeling positions to glutamine and eventually to neuronal glutamate. Since the sum of all the activity of these pools is measured, an increase in V_nt generates a faster transit of ¹¹C through the glutamate-glutamine cycle, without affecting significantly the shape of the total tissue-activity curve (sum of the glutamate and glutamine positions), as can be seen on the sensitivity analysis in Figure 3B.

As a consequence, the fitted value of V_nt had a relatively high uncertainty compared with V_gt^g (Table 1, Cases 1 to 4). In Case 4, V_nt was not strongly correlated with the neuronal and glial TCA cycle fluxes and has therefore low impact on the value found for V_gt^g and V_gtⁿ (Table 2D).

Blood Partial Volume

As shown in the decomposition of the total tissue-activity curve in Figure 4, the tissue pool dominating the total labeling in the first minutes is glutamate C5. From its labeling equation (Supplementary Appendix A, eq. 9), it can be seen that the slope of glutamate C5 labeling at early time points is equal to V_gt^g × K_dil. As already mentioned in the case of the one-tissue compartment model, the activity contribution due to blood partial volume effect in the measured voxel is mainly limited to the first 2 minutes: fitting the complete tissue-activity curve with a variable blood partial volume would lead to a strong correlation between V_gt^g and the blood partial volume, since both are closely related to the first points of the tissue-activity curve (data not shown). These points have also the lowest signal-to-noise ratio of the experiment. As a consequence, CBV values can only be unreliably extracted from the fitting procedure. Likewise, assuming a standard brain blood partial volume value may depend on the position of the probe in the brain and might vary between animals leading to biased V_gt^g values.

Therefore, it was preferred to neglect the first 2 minutes of data following the ¹¹C bolus injection and to neglect the blood partial volume contribution. As a matter of fact, in the simulations of Cases 3 and 4, a 5% blood partial volume contribution was added to the simulated total tissue curve, while the model was fitted starting after the second minute without taking into account the blood contamination. Table 1 Case 3 (with CBV contamination) compared with Case 2 (without CBV contamination) shows that blood contamination of the signal resulted in a slight increase in the fit residual, while this working assumption minimally affected the value and precision of the adjusted fluxes (<8% for V_tca^g, V_x^g, and V_nt and 11% for V_tcaⁿ and V_xⁿ). In Case 3, CBV and ¹¹CO₂ contributions were added simultaneously, to avoid the generation of too many scenarios in the fitting assumptions. Adding only the CBV contribution to the simulated data resulted in similar fluxes values, uncertainties and correlations (not shown).

Inclusion of the CO₂ Labeling in the Model

In Case 3, the labeling of CO₂ was also added to the simulated tissue-activity curve but not to the model used. As discussed above regarding the CBV contribution, the fitted flux values were minimally affected by this additional contribution. Adding the CO₂ pool without the CBV contribution to the simulated tissue-activity curve led to the same observation (not shown). This is consistent with the low activity of ¹¹CO₂ compared with the total tissue activity observed in the fits of the experimental data (Figure 4). As a consequence, the contribution of CO₂ to total tissue activity can be considered negligible.

Adding the CO₂ pool to the fitted model (Case 4) had a positive impact especially on V_gt^g, whose value was getting closer to the ‘true' value used for the simulation. Adding the pool of CO₂ in the model is, therefore, desirable to obtain unbiased quantification of the glial TCA cycle activity, which is the most precisely determined flux of this neuroglial model when using ¹¹C-acetate beta-probe data. For these reasons, the assumptions used in Case 4 were further used to fit the experimental data and are proposed in general to fit the model presented here to [1-¹¹C] acetate brain studies.

Fluxes Derived from the Experimental In Vivo Data

The model was fitted to nine tissue-activity curves with corresponding AIFs (Figure 4). The consistently uniform distribution of the residuals around zero reflects the good quality of the fit of the model. The precision on V_gt^g, V_nt, and V_gtⁿ obtained with the fit of the experimental data with the neuroglial model were of the same order as the results of the Monte-Carlo simulations.

In the experimental results, the group average V_gtⁿ is as large as the corresponding group s.d. (V_gtⁿ=0.10 μmol/g per minute, ΔV_gtⁿ=0.09 μmol/g per minute). Therefore, we conclude that V_gtⁿ cannot be reliably extracted from the fit. For V_nt, the average uncertainty is ∼30% of the flux value, which makes it a less sensitive flux in [1-¹¹C] acetate infusion studies, compared with V_gt^g. The average V_nt is in good agreement with the values found in ¹³C MRS studies (de Graaf et al, 2003a; Sibson et al, 1997, 2001; Duarte et al, 2011).

V_gt^g, characterizing glial oxidative metabolism, can be reliably and reproducibly determined with this protocol of [1-¹¹C] acetate infusion. The average V_gt^g is comparable to the literature values found in ¹³C MRS studies (de Graaf et al, 2003a; Sibson et al, 2001; Duarte et al, 2011). In some studies, V_x (assumed identical in the neuronal and glial compartments) was found to be significantly bigger than V_tca^g. In this case, the composite flux V_gt^g is almost equal to V_tca^g. The average V_gt^g found in the present study was, therefore, compared with the values of V_tca^g of these studies.

The experimental precision on V_gt^g found in this study is comparable or even higher than those found with ¹³C MRS in the literature. The comparison with ¹³C glucose infusion experiments should be performed with care, since the value found in these cases for V_tca^g might be subject to high uncertainties (Shestov et al, 2007). Glucose being metabolized both on the neuronal and glial sides and V_tcaⁿ being typically five times bigger than V_tca^g, the labeling of glutamate is mainly reflecting neuronal activity and the data obtained in glucose ¹³C MRS studies are much less sensitive to glial metabolism.

In the glial compartment, pyruvate carboxylation affects the position C1 of glial glutamate, as an additional dilution flux, in the second turn of the TCA cycle. However, the C1-labeling positions have a low contribution to the total tissue-activity curve (Figure 4); and therefore, pyruvate carboxylation affects marginally the ¹¹C tissue uptake curves. Fitting a tissue-activity curve generated with the inclusion of pyruvate carboxylation, but fitted with the presented model had negligible impact on the derived metabolic fluxes V_gt^g, V_nt, and V_gtⁿ (data not shown). The pyruvate carboxylation pathway was, therefore, neglected in this model.

The flux V_gt^g determined with the neuroglial model has a similar role as the uptake parameter K₁ of the previously applied one-tissue compartment model. However, the dynamics of ¹¹C release from brain tissue is more complex and requires the modeling of the neuroglial interaction. The glutamate-glutamine cycle is buffering ¹¹C, storing the label temporarily before its release as ¹¹CO₂ from the glial or neuronal TCA cycle. This delayed ¹¹C release was already noticed with the one-tissue compartment model. k₂ was decreasing significantly when fitting only the first 5 minutes of the uptake curve compared with the fit of the complete curve (Wyss et al, 2009).

Compared with ¹³C MRS, the determination of glial oxidative metabolism with [1-¹¹C] acetate infusion and positron emission measurements has several advantages. First, the high sensitivity of radiotracer detection enables measuring glial metabolism under physiological conditions due to trace amounts of [1-¹¹C] acetate infusion (∼0.5 nmol). Second, the experiment can be realized in only 20 to 30 minutes, while ¹³C MRS studies, with a typical time resolution of 10 minutes, need at least 2 to 3 hours of acquisition. The spatial resolution of this technique (∼8 μL with beta-probe) is higher than what can be achieved with ¹³C MRS, thanks to the high sensitivity of positron emitter detection.

Using a PET scanner instead of the beta-probe would allow whole brain coverage in a single experiment with less impact on brain tissue, while obtaining similar or better spatial resolution. A cerebral mapping of V_gt^g is therefore conceivable, provided a nearby cyclotron is available.

However, the absence of chemical information on the molecule emitting the positron reduces the number of determined metabolic fluxes compared with ¹³C MRS. The precise measurement of the AIF and its correction is an important step of the measurement to obtain accurate results and is probably the most limiting factor.

Like in ¹³C MRS studies, a measurement of the total plasma acetate is also necessary to further extract the fractional enrichment of acetate, the precursor of all the modeled pools. However, in [1-¹¹C] acetate studies, one single measurement should be enough since the injection of the tracer is negligible compared with the natural plasma acetate concentration, which should therefore not vary significantly during the experiment. The requirement is thus similar to an ¹⁸FDG study, in which the plasma glucose concentration is needed for quantification.

Conclusion

We conclude that the presented new model for in vivo brain metabolic studies using [1-¹¹C] acetate infusion is able to describe the kinetics in ¹¹C-acetate radiotracer as well as ¹³C-acetate MRS experiments, allowing to estimate V_gt^g and V_nt for the rat in <30 minutes.

We further conclude that radiotracer experiments using [1-¹¹C] acetate infusion can be used for the study of local glial oxidative metabolism. Minimal invasiveness and short acquisition periods make it an interesting method for human—possibly clinical—PET applications.

The authors declare no conflict of interest.