A dynamic approach for reconstructing missing longitudinal data using the linear increments model

Abstract

Missing observations are commonplace in longitudinal data. We discuss how to model and analyze such data in a dynamic framework, that is, taking into consideration the time structure of the process and the influence of the past on the present and future responses. An autoregressive model is used as a special case of the linear increments model defined by Farewell (2006. Linear models for censored data, [PhD Thesis]. Lancaster University) and Diggle and others (2007. Analysis of longitudinal data with drop-out: objectives, assumptions and a proposal. Journal of the Royal Statistical Society, Series C (Applied Statistics, 56, 499–550). We wish to reconstruct responses for missing data and discuss the required assumptions needed for both monotone and nonmonotone missingness. The computational procedures suggested are very simple and easily applicable. They can also be used to estimate causal effects in the presence of time-dependent confounding. There are also connections to methods from survival analysis: The Aalen–Johansen estimator for the transition matrix of a Markov chain turns out to be a special case. Analysis of quality of life data from a cancer clinical trial is analyzed and presented. Some simulations are given in the supplementary material available at Biostatistics online.

1. INTRODUCTION

Longitudinal data often have missing observations. We shall analyze such data from a dynamic point of view, meaning that we consider explicitly the direction of time and how the past may influence the present and the future. We consider informative, or dependent, missingness; that is, whether an observation is missing or not may depend on time-dependent covariates and previous developments of the process. This may include information that would otherwise not be a part of the statistical analysis. When, for instance, comparing 2 treatments, one would be wary of using time-dependent covariates in the analysis because this might give a false representation of the treatment effect (Fosen and others, 2006; Aalen and others, 2008). But such time-dependent covariates may still be used in the adjustment for missingness.

Farewell (2006) and Diggle and others (2007) introduced the linear increments model as a tool for analyzing longitudinal data with dropouts. While the common likelihood approaches for longitudinal data analysis is based on mixing models and other methods that do not take account of the time ordering, the work of Farewell (2006) and Diggle and others (2007) exploits efficiently the dynamic structure in the data. The method bears some analogy to the additive hazards regression model for survival data (see Martinussen and Scheike, 2006; Aalen and others, 2008). We shall introduce a multivariate version of the linear increments model and apply it to missing data, where we include both monotone and nonmonotone missingness. Previous work for this model focused on monotone missingness, meaning that if a response is missing, then all later responses are also missing. Nonmonotone missingness means that observation may be resumed later after one or more missing responses. This creates its own complications which we shall discuss.

We shall actually study a special case of the linear increments model with an autoregressive structure. It belongs to the general class of panel data models, but our dynamic treatment of missing data appears to be new.

The model may be used to reconstruct the missing longitudinal measurements thereby creating a complete hypothetical data set. This may be done in 2 ways, either the reconstructed data set consists of predicted values using the concept of compensators or we estimate the hypothetical data by an imputation technique designed for this particular model. The mean structure of this data set will be correct, under certain assumptions, since everything is based on linear models, but the variation of the reconstructed values may not necessarily reflect real measurement error. Therefore, uncertainty estimation can be based on bootstrap analysis, where each bootstrap iteration goes through the construction of a new hypothetical data set. Due to simple least square calculations, this is easy to implement (see also Gunnes, Farewell, and others, 2009).

The linear increments model is an alternative to the inverse probability weighting methods often used for missing data. For references to the latter method, see, for example, Hernan and others (2006), Horvitz and Thompson (1952), and Robins and others (1995). Inverse probability weighting is more general, while the present procedures rest on linear model assumptions. On the other hand, our procedure would be simpler to implement in many cases and does not rely on a model for the missingness mechanism. The reconstructed data set can be used for further statistical analysis.

The aim of this paper is to give a general formulation of linear increments modeling with an autoregressive structure. We start by explaining how the unobserved responses due to dropout may be reconstructed. One interesting aspect is that the approach can also be used for causal analysis in connection with time-dependent treatment confounding. Furthermore, the approach can be shown to include a time-discrete version of the empirical transition matrix (Aalen–Johansen estimator) from survival analysis.

One of the approaches discussed here (the compensator approach) was used as well in Gunnes, Farewell, and others (2009) and Gunnes, Seierstad, and others (2009). Here, we give a theoretical justification for the procedure within an autoregressive model, as well as presenting alternative techniques.

There is a considerable literature on longitudinal data analysis with missing data. Two simple approaches are the last-observation-carried-forward method (see e.g. Shao and Zhong, 2003) and the last-residual-carried-forward method (Diggle and others, 2007). There is also the much used method of multiple imputation (Rubin, 1987). This may be implemented with Markov chain Monte Carlo methods (see e.g. Schafer, 1999). Furthermore, the expectation–maximization algorithm of Dempster and others (1977) is frequently used for likelihood estimation from incomplete data. The fitting of a mixed(-effects) model (Diggle and others, 2002, e.g.) is a further example of a likelihood-based method that is commonly applied. Also methods based on inverse probability weighting are commonly employed (see e.g. Carpenter and others, 2006).

2. STATISTICAL MODEL AND MISSING DATA ASSUMPTIONS

As explained by Hogan and others (2004), see also Borgan and others (2007), missingness can be viewed both in a dynamic sense, respecting the structure of time, and in a nondynamic sense. The classical concepts of “missing completely at random” (MCAR) or “missing at random” (MAR) belong to the latter category where time is not considered, while the concept of “sequentially missing at random” (S-MAR) implies conditioning with respect to the past and so is a dynamic concept. We shall not define these well-established concepts here, but refer to Hogan and others (2004) for a good introduction focusing on longitudinal data. We note that the S-MAR assumption is related to the “independent censoring” of survival analysis (see e.g. Aalen and others, 2008), in particular to discrete-time independent censoring (DTIC) on which we shall focus below, see (2.4).

The type of missingness assumptions made has implications for the analytic method used. The MAR assumption is typically used in connection with likelihood methods, while the S-MAR and DTIC assumptions are related to dynamic semiparametric or nonparametric linear models. This is expressed particularly well by Hogan and others (2004): “. the likelihood-based methods tend to treat longitudinal data as clustered data that happen to be temporally aligned . regardless of where drop-out occurs, whereas with semi-parametric inference from weighted estimating equations, the S-MAR assumption conditions only on elements . realized prior to a fixed time.” The latter part of the statement also holds for the present linear models, where the focus on time dynamics is essential. We also quote Diggle and others (2007): “In our view, the analysis of longitudinal data, particularly when subject to missingness, should always take into account the time ordering of the underlying longitudinal processes.”

2.1. The linear increments model

We assume the (hypothetical) existence of a true complete data set, which is then only partially observed due to missing data. There is no requirement that the missingness shall be monotone, nonmonotone missingness where individuals may be unobserved at some times and then observed again at later times is also included. Following Diggle and others (2007), we start with a description of the complete data set: Let $\tilde{Y}\left(t\right)$ be an $n\times m$ matrix of multivariate individual responses defined for a set of times $t\in \{0,\dots ,k\}$, with $\tilde{Y}\left(0\right)=y_0$, where the matrix $y_0$ contains the fixed starting values for the processes. The number of columns of $\tilde{Y}\left(t\right)$ corresponds to the number m of variables measured for an individual, while the number of rows corresponds to the number n of individuals.

A key aspect of the approach of Farewell (2006) and Diggle and others (2007) is the focus on increments of the observed processes. The reason why this is important is that the increments represent the changes taking place over time and hence are representative of the dynamics in the process. We define the increment $\Delta \tilde{Y}\left(t\right)=\tilde{Y}\left(t\right)-\tilde{Y}(t-1)$ and assume for each t that $\Delta \tilde{Y}\left(t\right)$ satisfies the model

(2.1)

where $\beta \left(t\right)$ is an $m\times m$ parameter matrix, while $\tilde{\epsilon }\left(t\right)$ is an $n\times m$ error matrix. The errors are defined as zero mean martingale increments derived from a Doob decomposition (see Diggle and others, 2007), such that $E(\tilde{\epsilon }\left(t\right)|{ℱ}_{t-1})=0$, where ${ℱ}_t$ is the history up to and including time t. It follows that

(2.2)

Although for simplicity we denote all measurements as “responses,” one should note that some of the components in $\tilde{Y}\left(t\right)$ may be responses of major interest, while others may be covariates. Baseline covariates fixed at the starting time are also included in this setup; they will correspond to zero β parameters and zero errors.

We use here an autoregressive version of the model that is less general than the one considered by Farewell (2006) and Diggle and others (2007). The reason for this is to carry through the theoretical arguments concerning expectations below. It is also clear that in the autoregressive case as formulated in model (2.1), it makes no difference whether there is an increment or a response value on the left-hand side because of linearity. But when considering missing data assumptions below, we have to make a clear distinction between response and increment.

It should further be noted that model (2.1) is a special case of a well-known general model structure for longitudinal data, including autoregressive models and so-called panel data as special cases (for a general introduction, see Gardiner and others, 2009). The special aspect here is in our dynamic handling of missing data.

Diggle and others (2007) refer to martingale theory (see also Aalen and others, 2008). One important martingale concept is that of a compensator which is related to the Doob decomposition of a process. The compensator $\tilde{\Lambda }\left(t\right)$ of $\tilde{Y}\left(t\right)$ is given as

The compensator is the unique process such that $\tilde{Y}\left(t\right)-\tilde{\Lambda }\left(t\right)$ is a martingale, which is defined as follows in terms of the errors:

For the linear statistical model presented in (2.1), we get

(2.3)

2.2. Missing data assumptions

Let $Y\left(t\right)$ denote the actually observed data, with components zero when data are not observed, and define the increments $\Delta Y\left(t\right)=Y\left(t\right)-Y(t-1)$. The relation between the true and observed responses and increments are

where $R_0\left(t\right)$ and $R\left(t\right)$ are $n\times n$ diagonal matrices with response indicators on the diagonal defined as follows: For individual i the ith diagonal element of $R_0\left(t\right)$ equals 1 when the complete response ${\tilde{Y}}_i\left(t\right)$ is observed and 0 otherwise. Similarly, we define the ith diagonal element of $R\left(t\right)$ equal to 1 when the increment $\Delta {\tilde{Y}}_i\left(t\right)$ is observed and 0 otherwise. (Notice that if just a subset of responses or increments is observed at a given time, then the indicator equals 0.) We assume here that the observation of an increment $\Delta \tilde{Y}\left(t\right)$ is taken to imply that both values $\tilde{Y}(t-1)$ and $\tilde{Y}\left(t\right)$ are observed, hence a one in the relevant place of $R\left(t\right)$ would imply a corresponding one in $R_0\left(t\right)$ but not the other way round. In case of monotone missingness, the 2 indicators would be identical, but for nonmonotone missingness, it is quite possible that there might be a one in $R_0\left(t\right)$ but a zero in the corresponding diagonal element of $R\left(t\right)$. This will happen when a response is measured, while the one prior to it was not observed. Hence, we do not know the last increment but may still want to use the last response.

We shall assume here a discrete time point of view. Often one would consider that there is an underlying continuous process which just happens to be observed discretely. Following Gunnes, Farewell, and others (2009), we shall assume in this case that $R_0\left(t\right)$ and $R\left(t\right)$ may only depend on $\tilde{Y}\left(t\right)$ until time $t-1$ and not on what happens on the interval $(t-1,t)$. This is clearly a simplifying and somewhat disputable assumption; the effect of deviation from this assumption is discussed in Gunnes, Farewell, and others (2009). The impact is relatively small unless the difference in time between observations is great. Let ${ℛ}_0\left(t\right)$ and $ℛ\left(t\right)$ denote the strict past history of the processes $R_0\left(t\right)$ and $R\left(t\right)$, respectively, that is, up to and including time $t-1$.

We shall make the assumption of DTIC discussed in Gunnes, Farewell, and others (2009). This assumption places constraints on the expected values of the increments $\Delta \tilde{Y}\left(t\right)=\tilde{Y}\left(t\right)-\tilde{Y}(t-1)$ of the hypothetical response:

(2.4)

It is important to note that the DTIC assumption is really an assumption about missingness of responses and not about censoring of the individual. The reason for the term censoring being used here is the analogy to the independent censoring of survival analysis (see Gunnes, Farewell, and others, 2009).

We can then do the following computations:

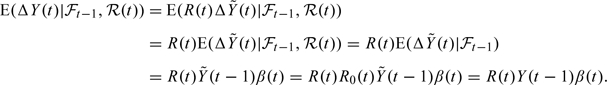(2.5)

Hence, the DTIC assumption guarantees that the observed data will satisfy the model defined in (2.1) so that we can write

(2.6)

where $\epsilon \left(t\right)=R\left(t\right)\tilde{\epsilon }\left(t\right)$ (Diggle and others, 2007; Gunnes, Farewell, and others, 2009). These residuals are martingale increments with respect to the history $\{{ℱ}_{t-1}\vee ℛ\left(t\right)\}$.

One may also formulate a DTIC assumption for full responses in analogy with the one above:

(2.7)

It can be proven that this implies the DTIC assumption for increments in (2.4). It also follows that

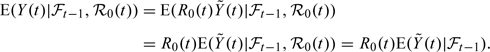2.3. Monotone missing data

The simplest case would be the one with monotone missing data (which is similar to right-censoring in survival analysis). The DTIC assumption for full responses and for increments will now be the same. In this case, the DTIC assumption (2.4) amounts to assuming that the probability of being missing at some time t is only dependent on the observed past values $\left\{Y\right(s),s<t\}$.

However, the methods discussed in this paper may be valid also in cases with nonmonotone missingness, which will be discussed next.

2.4. Nonmonotone missing data

In many cases, it would be a waste of information to ignore possible later information if data are missing at a given time. However, using data from later times may be a tricky issue. It is rather obvious that if an observation is missing at, say, a single occasion, due to causes unrelated to the underlying development, then the later values for this individual should not be ignored. Such accidentally missing data are probably quite common. If, on the other hand, data for an individual are missing for a longer time, and the individual is then returning to participation in the study, one might think that this individual is not representative of the population of missing ones. The question is therefore whether data from this individual should be used. This issue goes beyond the DTIC assumption.

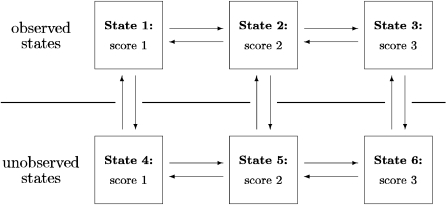
In fact, it is important to realize the nature of the independent censoring assumption for nonmonotone missing data. In this paper, we use a discrete-time version (DTIC), but for the present argument, we shall argue in terms of the continuous independent censoring assumption (CTIC) used especially in survival analysis. Consider as an example Figure 1, which is a 6-state Markov model that consists of both “observed” states (1–3) and “unobserved” states (4–6). Subjects in the unobserved states constitute the missing ones. Possible transitions between various states in the model are indicated by arrows. In this model independent censoring means that the rates for the “horizontal” transitions are the same at the observed (top) level as at the unobserved (bottom) level. That is, whether a process is observed or not should not influence or be related to the development of the process.

Fig. 1.

A Markov model for generating longitudinal data. This consists of both observed states (1–3) and unobserved states (4–6). Subjects in the unobserved states constitute the missing ones. Possible transitions between various states in the model are indicated by arrows.

One should note that this does not say anything about the rates of “vertical” movements in the figure, from observed to unobserved or vice versa. The individuals returning to observation may therefore not be representative of those not under observation at that time. As an example, there might be a preponderance of individuals with score 3 returning to observation. In a medical setting, it is possible that the likelihood of returning to observation (e.g. taking a medical examination) may be greater if the person detects symptoms. But once an individual has returned to observation the further movements are, under the DTIC or CTIC assumptions, independent of the fact that he was recently unobserved.

In general, we have to distinguish between the causes why an individual gets missing and why he returns to observation. Clearly, there might be several periods when the individual is missing from observation, and the below considerations may hold for each of them. We shall consider 4 different types of “return scenarios” and look at the first occasion of a missing observation for an individual and the subsequent possible return to observation. In all cases, we presume the DTIC assumption for increments, that is, the changes or increments in the process are unrelated to missing status.

1. The probability that the individual gets missing “is unrelated to” the progress of the individual (in terms of the response $\tilde{Y}\left(t\right)$). The probability of returning to observation “does not depend” on the progress while missing.

2. The probability that the individual gets missing “is related to” the progress of the individual prior to the missing time. The probability of returning to observation “does not depend” on the progress while missing.

3. The probability that the individual gets missing “is unrelated to” the progress of the individual. The probability of returning to observation “does depend” on the progress while missing.

4. The probability that the individual gets missing “is related to” the progress of the individual. The probability of returning to observation “does depend” on the progress while missing.

Case 1 above also satisfies an MCAR assumption, while case 2 satisfies an MAR assumption. In these 2 cases, progress after returning to observation should be used in the analysis, unless one accepts a loss of power by just using monotone missing data.

In case 3, the use of monotone missing data would be safe. However, it is not obvious that information from individuals returning to observation should be ignored. So the observation taken after return should not be considered representative of missing individuals; however, it is quite possible that the further progress given this first value after return could be representative and should be used. These considerations would also be relevant in case 4.

2.5. Distinguishing between types of missingness: how to handle death

Longitudinal measurements will frequently be carried out in situations where the death of an individual is unlikely; in that case the remarks made here are not relevant. However, there are also cases where several individuals may die during the study; an example could be a cancer clinical trial where one measures quality of life or some other indicator of the status of patients. The question of how to study the development of a response over time in a setting where many individuals may die can be very challenging. Then data may be missing for several different reasons: the patient may still be in the study but simply not having filled out the forms or given the appropriate information; or the patient may be censored from the study; or the patient may have died. Several authors have stressed the importance of distinguishing between these types of missingness, see, for example, Dufouil and others (2004) and the discussion in Diggle and others (2007). One might want to adjust for ordinary missingness (including censoring) but not for death since individuals dying should be removed from further analysis. In the literature (e.g. Dufouil and others, 2004), one distinguishes between “mortal” cohorts where this distinction is made and “immortal” cohorts where all types of missingness are handled together and adjusted for, whether it is death or ordinary missingness.

The argument for the mortal cohort view is that in the case of death the missing data simply do not exist. Therefore, we may want to adjust only for the real missing ones. This requires that missing response data do not preclude knowledge about times of death, only about the longitudinal observations, whether they be measurements of clinical variables, quality of life variables, or something else. If the times of death are known, we may simply follow the imputation approach described below and successively exclude individuals dying from the analysis after time of death. This procedure would not complicate our analysis.

Superficially, one might think that the concept of mortal cohorts constitutes the only sensible view since using immortal cohorts would in effect project estimates of, for example, quality of life beyond death. However, things are more complicated than this. First, when individuals are censored in a survival study, then information about the time of a later death is not available, so one cannot simply remove all individuals dying from further analysis. Second, the study of a longitudinal measurement (often called time-dependent covariate or marker process in the survival literature) often cannot be separated from the study of risk of death. When comparing 2 treatments, it may be that one treatment improves survival in such a way that patients with low quality of life survive longer. Assume, for instance, that one treatment, A, results in a higher number of deaths than another treatment, B. Then treatment A might show a better quality of life for surviving patients than B simply because the fewer patients surviving with A are in a better shape, and B might be more efficient to keep weak patients alive. So the superior treatment may come out with a negative quality of life effect simply due to a prolongation of life. Using the concept of an immortal cohort, adjusting for all missingness, including death, might give a more fair comparison of treatments. The actual estimates may then be somewhat idealized concepts. For further discussion and an example, see Gunnes, Seierstad, and others (2009).

One should note the similarity between this issue and that of competing risks. Consider, for instance, the estimation of divorce rates. A competing risk for dissolution of marriage by divorce would be the dissolution by death of one of the spouses. Usually this will be considered as part of the censoring, implying that the survival estimate, say a Kaplan–Meier curve, would refer to a cohort where none of the spouses dies, that is, an “immortal” cohort. Still it may be the sensible procedure, in particular when applied to young and middle-aged cohorts where relatively few people die.

3. RECONSTRUCTION OF THE DATA

The linear structure defined above allows easy reconstruction of missing data. We shall present 2 different approaches, one that yields estimates of compensators and one that amounts to imputation of missing data. Both methods may have their advantages: The imputation approach tries to reconstruct the actual data, but the limitation may be that imputed missing values do not have the random error variation that they should have. When estimating compensators, we do not focus on individual data but on conditional expected increments.

The linear structure in the model allows simple and intuitive procedures to be used for reconstruction. We can use all relevant information, also time-dependent covariates and markers, to adjust for informative missingness. After the data have been reconstructed, they can be used for appropriate statistical analysis.

An important aspect of this reconstruction is that it can also handle the “artificial” censoring discussed in, for example, Hernan and others (2006) which is used for analyzing the effect of treatment under time-dependent confounding.

We only study the expectation of the proposed procedures, establishing conditions for unbiasedness. The variances can also be studied, but in practice we will use bootstrap methods for analysis, so that theoretical results for variances or for testing are not needed.

3.1. Estimating the parameters from increments

We assume a nonparametric model over time, so that there is no assumed connection between $\beta (t_1)$ and $\beta (t_2)$ for 2 different times $t_1$ and $t_2$. It then follows from the linear model (2.6) that the parameter matrices $\beta \left(t\right)$ can be estimated unbiasedly by the least squares approach from observed increments; we denote these estimates as $\widehat{\beta }\left(t\right)$. Define $U=R\left(t\right)Y(t-1)$. The least square estimate of $\beta \left(t\right)$ is given by

(3.1)

A requirement is that there must be a sufficient number of observed increments at any given time to perform a reasonable estimation (what this actually means in practice may vary from case to case). If there is insufficient data at some time, estimation is not done; in practice, this often occurs toward the end of the study where it is reasonable to stop estimation anyway.

Due to the assumption (2.4), we will have $E(\widehat{\beta }\left(t\right)|{ℱ}_{t-1},ℛ\left(t\right))=\beta \left(t\right)$. In order to show this, we use (2.5) which was derived by this assumption, and make the following argument:

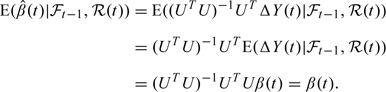(3.2)

The estimates are also unbiased in the following sense:

(3.3)

since $E(\widehat{\beta }\left(t\right)|{ℱ}_{t-1})=E(E(\widehat{\beta }\left(t\right)|{ℱ}_{t-1},ℛ\left(t\right)\left)\right|{ℱ}_{t-1})=\beta (t)$.

Similarly, we can use (2.7) to derive that $E(\widehat{\beta }\left(t\right)|{ℱ}_{t-1},{ℛ}_0\left(t\right))=\beta \left(t\right)$:

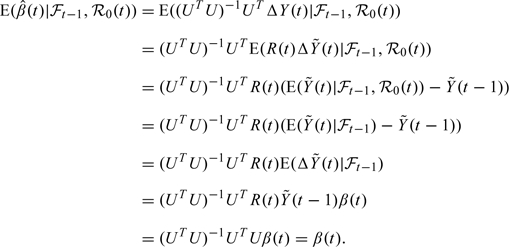(3.4)

3.2. Estimating the compensator

We shall first consider the issue of estimating the expectation of the process as a function of time, following the approach outlined by Gunnes, Farewell, and others (2009, Section 2.3). It is actually convenient to view this more generally as a problem of estimating the compensator. When comparing treatments starting at random times in causal analysis one would like to consider the expectation before and after this time, which is more naturally formulated in terms of compensators. However, this issue is not dealt with in the present paper; here we only consider the special case of estimating an expectation given different starting values.

The compensator, or in this case the expectation, can be estimated iteratively as follows:

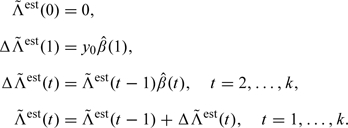(3.5)

We shall show that the estimate has the right expectation under the DTIC assumption (2.4). There is no requirement of monotone missingness. First, we have

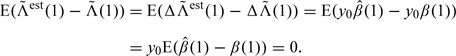Furthermore, using formula (3.3) we derive:

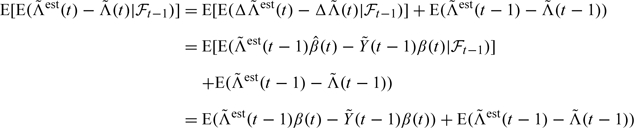(3.6)

using formula (2.3). Using, furthermore, the martingale property of $\tilde{Y}\left(t\right)-\tilde{\Lambda }\left(t\right)$ it follows that $E(\tilde{Y}(t-1)-\tilde{\Lambda }(t-1))=0$, and hence expression (3.6) can be written as

We now make the induction hypothesis that $E({\tilde{\Lambda }}^{est}(t-1)-\tilde{\Lambda }(t-1))$ is 0. We have then proved that the following also holds: $E({\tilde{\Lambda }}^{est}\left(t\right)-\tilde{\Lambda }\left(t\right))=0$. Since the statement has already been proven for $t=1$, we have a complete induction argument and the estimator is therefore unbiased.

3.3. Estimating hypothetical responses: imputation

We now introduce our imputation technique. The idea is to use the actual observations as long as they are nonmissing and then to substitute the increments by iteratively updated estimates once the observations get missing. For nonmonotone missing data, an individual may return to observation, and we then use the actual measurements for the individual once they become available. In principle, this process of getting missing and then returning may repeat itself several times. We now use the indicator $R_0\left(t\right)$ that is equal to 1 when the value $\tilde{Y}\left(t\right)$ is observed. The hypothetical complete predicted data values can be estimated iteratively as follows:

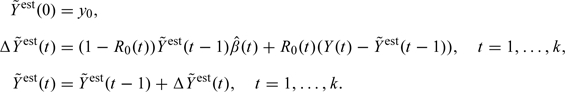Note that when observation takes place, the estimated value ${\tilde{Y}}^{est}\left(t\right)$ simply equals $Y\left(t\right)$. When there is no observation, the increments are updated according to the model, just like in the compensator iteration (3.5).

We shall prove that this expression is unbiased under the following assumption, which is a formulation of the requirement that whether observation takes place or not, shall not depend on previous “unobserved” values.

(3.7)

The meaning of this assumption is as follows. There are 2 possibilities for each row in the matrix inside the expectation: Let us consider row i. Then $R_0\left(t\right)$ may be 0 at the ith diagonal element in which case the expression inside the expectation is necessarily 0. Alternatively, $R_0\left(t\right)$ may be 1 at this element, in which case there are 2 new possibilities. Either $R_0(t-1)$ is also 1 at the ith diagonal element, this would occur when $R\left(t\right)$ is 1 at this element and in particular for monotone missingness. In such a case, one sees from the definition of the imputation procedure above that ${\tilde{Y}}^{est}(t-1)=\tilde{Y}(t-1)$ and hence what is inside the expectation is still 0. The other possibility is that $R_0(t-1)$ is 0 at the ith diagonal element, implying that the response at $t-1$ is unobserved for individual i. This means that at time t, there is a return to observation for individual i. If this return was dependent on values at the previous unobserved time, then it would mean that those returning were a select group and one might expect a bias in the estimation. Hence, the assumption is basically a statement about individuals returning to observation, saying that the decision to return shall not depend (in a linear, correlation type fashion) on previous unobserved values. The independent censoring assumption (DTIC) discussed above does not concern itself with this issue, see also the remarks in Section 2.4, and that is why we require an additional assumption. Note that this is related to the 4 return scenarios in Section 2.4, meaning that we should have scenario 1 or 2 and not 3 or 4.

Using the DTIC assumption for full responses (2.7), together with the results in (2.2) and (3.4), we may compute the following expectations:

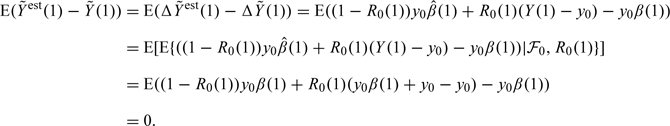Furthermore,

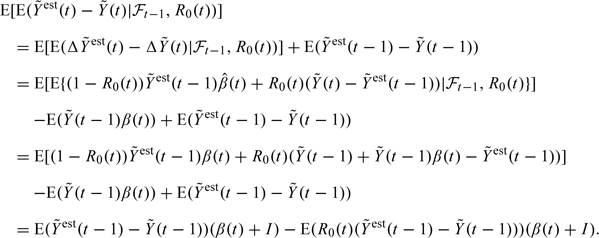By the assumption (3.7), the second expression in the last line equals 0. We now make the induction hypothesis that $E({\tilde{Y}}^{est}(t-1)-\tilde{Y}(t-1))$ is 0. It then follows by induction that generally $E({\tilde{Y}}^{est}\left(t\right)-\tilde{Y}\left(t\right))=0$, which yields unbiasedness.

3.4. Analyzing reconstructed responses

The predicted values may be used for statistical analysis. We shall here only focus on one issue, namely how to estimate the mean of the hypothetical response $\tilde{Y}\left(t\right)$. In the imputation case, let ${\tilde{Y}}_i^{est}\left(t\right)$ be the estimated hypothetical response for individual i. A sensible estimate is the mean of the predicted values:

(3.8)

For the compensator case, we take a similar average. In the case of monotone missingness data, the average in expression (3.8) would be identical to the corresponding compensator estimate but in general they will be different. When the assumptions discussed above for correct expectations are fulfilled, the means will also be unbiased.

3.5. Delayed entry (left truncation)

Just like in survival analysis (Aalen and others, 2008), individuals entering late can easily be accommodated in the analysis by simply including the new individual from the time of entry. This is particularly relevant when analyzing time-dependent confounding, see below.

3.6. Simulations

In the supplementary material available at Biostatistics online, we present simulations to illustrate how these reconstruction methods work in practice.

The first study is based on a simulation of a time-continuous process with a discrete state space. The multistate model corresponding to the process has the Markov property. Observation takes place only at discrete times. The estimated values of the mean of the process using the 2 different approaches of the linear increments method give a considerable correction of the bias that results if one merely calculates the average of the observed data at each point in time. The compensator and imputation approaches give the same results for monotone missing data, whereas for nonmonotone missing data the 2 differ with respect to bias and variability.

The second study is of a simulated time-discrete continuous response. That is, the process is discrete in time but the response takes continuous values. Two different rules of missingness are applied; the first rule states that a response is missing if the previous response exceeded a specific value, and the second rule states that a response is missing if the previous response exceeded a specific value and, in addition, was observed. The latter makes sure that missingness can never occur 2 times in a row. Once again, the 2 approaches of the linear increments method give the same results in the case of monotone missing data and differing results in the case of nonmonotone missing data. It is seen from the figures that the bias of the observed measurements can be very considerable, and that the estimation perform very good corrections.

4. TIME-DEPENDENT CONFOUNDING: CAUSAL ANALYSIS

There is a close relationship between the issue of missing data and the problem of estimating causal effects. We shall explain how the present methods can also be used in causal analysis.

A difficult issue in both longitudinal data and survival analysis is the estimation of treatment effects when treatment is confounded with the disease status of the patient. An example is HIV infection where one usually would not start treatment before the CD4 level of the patient declines below a certain level. Hence, the patients who are treated are those who are more seriously affected, and a naive comparison of treated and untreated individuals might give the impression that the treated individuals fare worse (Hernan and others, 2000). When considering survival data, a correct statistical analysis of this issue may be achieved by the marginal structural model (Hernan and others, 2000) or by a type of sequential Cox analyses (Gran and others, 2010).

For longitudinal data, however, another and simpler procedure may also be used. Assume that we want to compare 2 treatments, A and B, but that this is not a randomized study, rather the choice of treatment is dependent on the state of the patient. We follow the idea of Hernan and others (2006), see also Gran and others (2010), that changing treatment group at some time t may be viewed as artificial censoring. If an individual has been in treatment group A up to time t and then changes to treatment group B, he may be considered as being censored (or missing) from group A, and entering group B as “delayed entry”(left truncation). This idea is important because it shows that when we shall assess the causal effect of a treatment that is started according to the progress of the patient, then this can be viewed as a missing data problem.

After time t, we reconstruct the hypothetical further development had the patient stayed in group A using the method described previously. This can then be compared to the actual development which is observed for the patient in group B. By using sufficient covariates as columns of the $\tilde{Y}$-matrix one may adjust for covariates determining whether treatment is started by using all relevant, possibly time-dependent information. The reconstruction of the data is done first, and the statistical analysis is performed on the reconstructed data. This would be an alternative to the inverse probability weighting procedures.

So, for each individual starting on treatment, we attempt to reconstruct the counterfactual development that had been seen had the individual not started treatment. There are 2 reasons why this works, first the linear model that makes the reconstruction of data quite simple as explained above and second the nonparametric nature of the statistical model.

5. THE EMPIRICAL TRANSITION MATRIX

Quite interestingly, the present framework also includes a standard tool for the analysis of Markov chains in survival analysis. Consider a time-continuous Markov chain with m states, and define the m-dimensional response vector ${\tilde{Y}}_i\left(t\right)$ for individual i as consisting of zeros apart from a one at the component indicating the state that is presently occupied by individual i. Define $P(t-1,t)$ as the matrix of transition probabilities from time $t-1$ to time t. The expectation of ${\tilde{Y}}_i\left(t\right)$ is the probability distribution on the state space at time t, and hence

Introducing the observables we may write

that is,

For the observed values at time t, we have under the DTIC assumption:

Hence, we still have a linear structure.

In order to estimate the transition matrix, we apply least squares estimation to the following representation:

In analogy with formula (3.1), the least square estimate is given by

where $U=Y(t-1)$.From the definition of the response vectors in this case, one sees that ${(UTU)}^{-1}$ is a diagonal matrix where the rth diagonal element is ${({\sum }_{i=1}^{n}1\{Y_i(t-1)=r\left\}\right)}^{-1}$. It is further seen that the $(r,s)$ matrix element of $\widehat{P}(t-1,t)$ equals

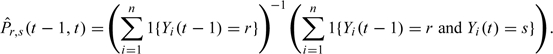Multiplying together the matrices, which is justified by the Markov assumption, we get the following transition matrix for the time interval (0, t):

This is a time-discrete version of the empirical transition matrix (Aalen and others, 2008), often denoted the Aalen–Johansen estimator. By choosing a very fine partition of the time axis so that at most one transition in the state space occurs in each interval, one can derive the standard Aalen–Johansen estimator as the limit.

If we want to estimate the marginal distribution on the state space at a time t that would have been observed in the absence of censoring, we just use the method described in (3.5) and (3.8). This is the basis for the Markov method for estimating the hypothetical mean as described in Gunnes, Farewell, and others (2009). Hence, we see that the Markov method can be perceived as a special case of the linear increments model.

6. QUALITY OF LIFE

In this section, we consider substantive longitudinal measurements of self-reported quality of life. The data are obtained from a randomized phase III study of radiation therapy with concurrent chemotherapy versus radiation therapy alone in non–small-cell lung (NSCLC), stage III A/B. The study medication administration was divided into a study arm (arm A) and a standard arm (arm B). The former involved 6 weeks of radiation therapy, given 5 days a week, combined with weekly infusion of the generic agent “docetaxel,” while the latter involved 6 weeks of radiation therapy alone. The decision on whether 2 courses of induction chemotherapy would be given before start of treatment was made by each involved centre prior to inclusion of its first patient. The original sample consisted of 261 patients diagnosed with NSCLC, stage III A (inoperable) or stage III B, who were included in the study between April 2000 and June 2006. Due to the following exclusion of 12 included patients, the final study sample consisted of 249 patients (157 men and 92 women). Upon inclusion, the patients were independently randomized to one of the 2 treatment arms. Within the study sample, 119 (48%) of the patients were randomized to arm A and, 130 (52%) of the patients were randomized to arm B. More details regarding the clinical trial can be found in Gunnes, Seierstad, and others (2009).

6.1. The data

Translated versions of the EORTC QLQ-C30 (EORTC, 1995), supplemented by a lung cancer module, were administered to the patients immediately before start of treatment (control week 0), at the end of treatment (control week 6), 6 weeks after end of treatment (control week 12), and then every 12 weeks until dropout, death or closure of the study. These are validated self-report, multi-item questionnaires developed by the European Organisation for Research and Treatment of Cancer (EORTC) to assess the quality of life of cancer patients participating in clinical trials. Each item is assigned an integer score value corresponding to one of the precoded response options. Since the timing of the questionnaires for 9 patients in arm A and 10 patients in arm B differed from protocol, their scores have all been discarded.

Our main response of interest is item 30 in the EORTC QLQ-C30, given in the form of the following question: “How would you rate your overall quality of life during the past week?”. This can be regarded as a summary measure of quality of life. The item is assigned an integer score value in the range from, and including, 1 (“very poor”) to, and including, 7 (“excellent”). Our 2 secondary responses of interest are item 9 (“Have you had pain?”) and item 27 (“Has your physical condition or medical treatment interfered with your social activities?”) in the EORTC QLQ-C30. These items are both assigned integer score values in the range 1–4, where 1 corresponds to “not at all” 2 corresponds to “a little,” 3 corresponds to “quite a bit,” and 4 corresponds to “very much,”

The expected increments of the above-mentioned response processes are assumed to be influenced by whether induction chemotherapy was received, and by sex and treatment arm. Therefore, to correct for potential sample heterogeneity with respect to missingness, we consider 3 baseline covariates: (1) an indicator for having received induction chemotherapy, (2) an indicator for being woman, and (3) an indicator for being randomized to arm A. Obviously, the covariates are all fixed in time.

We wish to estimate the mean score of item 30 in a hypothetical drop-out-free population. We then let $\tilde{Y}\left(t\right)$ be an $n\times 6$-dimensional matrix of which the first, second, and third column correspond to items 9, 27, and 30 at time t. The fourth, fifth, and sixth column of the matrix correspond to the 3 baseline covariates.

6.2. Results from the data analysis

In conformity with the theory presented in previous sections, we make no requirements as to whether the missingness in the data is of a monotone or nonmonotone kind. However, for a response being regarded as observed at a certain point in time, we demand that all the responses under consideration must be observed at that particular time. The same applies for the response increments. That is, for an arbitrary subject, $R_0\left(t\right)$ equals 1 when the respective answers to items 9, 27, and 30 are all given at time t and 0 otherwise. Correspondingly, $R\left(t\right)$ equals 1 when the answers are all given at both time t and time $t-1$. Otherwise, $R\left(t\right)$ equals 0. Table 1 presents the numbers of observed sets of responses and response increments, respectively, at different filling-in times of the EORTC QLQ-C30.

Table 1.

Number of observed sets of responses, ${\sum }_i$R_0i, and number of observed sets of response increments, ${\sum }_i$ R_i, at different control weeks since treatment onset

Control week	Arm A		Arm B
	${\sum }_i$R0i	${\sum }_i$Ri	${\sum }_i$R0i	${\sum }_i$Ri
0	97	—	96	—
6	78	70	89	76
12	91	69	100	79
24	74	73	89	87
36	65	59	78	77
48	59	55	63	57
60	40	40	50	45
72	35	33	48	43
84	30	29	34	34
96	27	26	27	25
108	18	18	24	22

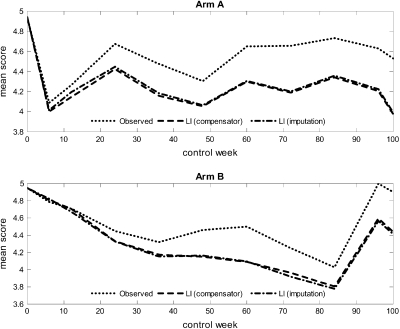
Figure 2 displays the observed and estimated mean scores of item 30, as functions of weeks since treatment onset. Notice that there is little difference between the compensator and the imputation-based estimates. In the plot corresponding to arm A, we notice an initial sudden drop in the curves in the period during which treatment is given. At control week 6, the curves start to rise again. In the plot corresponding to arm B, we see that the curves decline more gradually. The curve of the observed mean score lies above the curves of the estimated mean scores in both plots. This implies a possible overestimation of the true mean score by simply using the average of the observed scores at a certain time.

Fig. 2.

Observed and estimated mean scores of item 30 (quality of life), as functions of weeks since treatment onset in the 2 treatment arms. The estimates are computed by the compensator and the imputation approach.

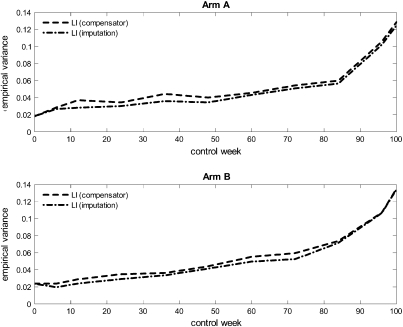
Figure 3 displays the empirical variance of the mean score estimates of item 30, based on 1000 bootstrap samples, as functions of weeks since treatment onset. There is not much difference in variability between the estimated mean score achieved by using the compensator technique and the estimated mean score achieved by using the imputation technique, neither in arm A nor in arm B.

Fig. 3.

The empirical variance of the mean score estimates of item 30 (quality of life), based on 1000 bootstrap samples, as functions of weeks since treatment onset.

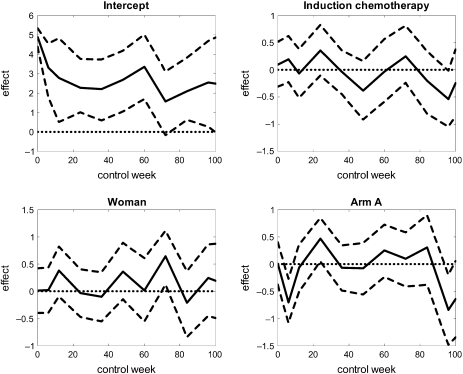
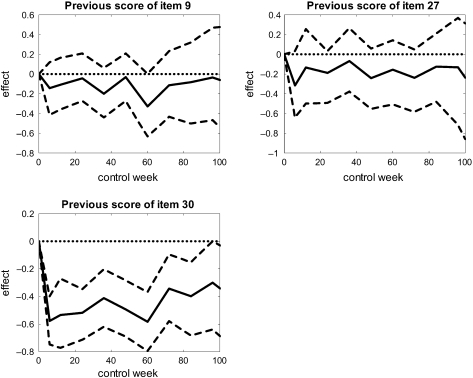
Figures 4 and 5 display the least squares estimates of the effects of the baseline covariates and the previous responses, respectively, on the current increment of the score of item 30, as functions of weeks since treatment onset. Also presented are 95% confidence intervals based on percentile limits from the bootstrap replications. Based on these there seems to be a significant negative effect of being randomized to arm A compared to arm B at 6 weeks after treatment onset. The respective effects of being woman and having received induction therapy, however, seem not to be significant. Hence, one might conclude that sex and induction therapy have no influence on the expected increment of the score of item 30.

Fig. 4.

Least squares estimates of the effects of baseline covariates on the increment score of item 30 (quality of life). The 95% confidence intervals are computed by bootstrap.

Fig. 5.

Least squares estimates of the effects of previous responses on the increment score of item 30 (quality of life). The 95% confidence intervals are computed by bootstrap.

7. DISCUSSION

We have shown the feasibility of a simple approach to correct longitudinal data for missing observations. The dynamic approach clarifies the assumptions needed for both monotone and nonmonotone data in order to get unbiased estimates. Our methods show the usefulness of the linear increments model of Farewell (2006) and Diggle and others (2007).

In this paper, we have not focused on diagnostic and robustness issues. As regards the first aspect, this has been treated in the paper by Diggle and others (2007), and particularly in the follow-up paper by Elgmati and others (2010). This includes both graphical procedures for checking residuals and formal tests. It is partly based on the notion of martingale residuals as presented in Aalen and others (2008). These methods can be easily adapted to the present case. Elgmati and others (2010) also give a robust diagnostic procedure. Another follow up paper of Diggle and others (2007) is the one by Farewell (2010) which also contain considerations on the issue of robustness.

As further regards the robustness of our approach, we expect that similar considerations would hold as in ordinary linear regression. Since a least squares approach is used the estimation might be vulnerable to very skewed distributions. A common way to handling this is to transform the data, for example, taking a logarithmic transformation. This was not judged to be necessary in the analysis of the quality of life data here, due to the limited scale used. It would also be interesting to develop influence measures, like those known from linear regression, to judge whether some individuals or measurements have an undue influence on the results.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

Norwegian Cancer Society (70120/001) to N.G.