Abstract
Missing data arise in genetic association studies when genotypes are unknown or when haplotypes are of direct interest. We provide a general likelihood-based framework for making inference on genetic effects and gene–environment interactions with such missing data. We allow genetic and environmental variables to be correlated while leaving the distribution of environmental variables completely unspecified. We consider 3 major study designs—cross-sectional, case–control, and cohort designs—and construct appropriate likelihood functions for all common phenotypes (e.g. case–control status, quantitative traits, and potentially censored ages at onset of disease). The likelihood functions involve both finite- and infinite-dimensional parameters. The maximum likelihood estimators are shown to be consistent, asymptotically normal, and asymptotically efficient. Expectation–Maximization (EM) algorithms are developed to implement the corresponding inference procedures. Extensive simulation studies demonstrate that the proposed inferential and numerical methods perform well in practical settings. Illustration with a genome-wide association study of lung cancer is provided.
Keywords: Association studies, EM algorithm, Genotype, Haplotype, Hardy–Weinberg equilibrium, Maximum likelihood, Semiparametric efficiency, Single nucleotide polymorphisms, Untyped SNPs
1. INTRODUCTION
Many diseases of utmost public health significance, including cancer, hypertension, diabetes, and schizophrenia, are influenced by both genetic and environmental factors, as well as gene–environment interactions. Identifying genetic contributions to such complex diseases requires association studies, which explore population relationships between disease phenotypes and genetic variants, particularly single nucleotide polymorphisms (SNPs). In fact, there is now a proliferation of SNP-based association studies worldwide thanks to the availabilities of dense SNP maps across the human genome (e.g. The International Human Genome Sequencing Consortium, 2001; The International HapMap Consortium, 2005) and precipitous drops in genotyping costs. An increasing number of these studies survey the entire genome with high-density genotyping chips containing 0.5–1 million SNPs; such studies are referred to as genome-wide association studies. The case–control design is popular; cross-sectional and cohort designs are also commonly used.
Missing data present a major challenge in genetic association studies. An important form of missing data arises in the analysis of haplotype–disease association. A haplotype is a specific sequence of nucleotides on the same chromosome of a subject. Because haplotypes incorporate the linkage disequilibrium information (i.e. correlation structure) of multiple SNPs, the use of haplotypes can yield more efficient analysis of disease association than the use of individual SNPs, especially when the causal SNPs are not directly measured or when multiple mutations occur on the same chromosome. Unfortunately, current genotyping technologies do not separate a subject's 2 homologous chromosomes, so that we can only observe the combination of the 2 haplotypes, which is referred to as the (unphased) genotype.
Missing data are also encountered in the analysis of the effects of individual SNPs. Even with high-quality genotyping, some study subjects will have missing genotypes at certain SNP sites because of assay failures. Genotype data may also be missing by design to reduce genotyping costs. An extreme form of missing data arises when investigators are interested in untyped SNPs, that is, the SNPs that are not even on the genotyping chip used in the study and are thus missing on all study subjects. Conducting association analysis at untyped SNPs can facilitate the selection of SNPs to be genotyped in follow-up studies and enable investigators to compare or combine results from multiple studies with different genotyping chips.
A number of methods have been proposed to assess haplotype–disease association based on unphased genotype data (e.g. Schaid and others, 2002; Zhao and others, 2003; Epstein and Satten, 2003; Stram and others, 2003; Lake and others, 2003; Lin and others, 2005; Spinka and others, 2005; Lin and Zeng, 2006). In addition, several methods have been developed to analyze untyped SNPs in case–control studies (Nicolae, 2006; Marchini and others, 2007; Lin and others, 2008). In the presence of missing data, it is not possible to make inference without imposing restrictions on the distribution of genetic variables. All the aforementioned work assumes Hardy–Weinberg equilibrium (HWE) (or certain 1-parameter extensions thereof) and independence of genetic and environmental factors (or absence of environmental factors). The assumption of gene–environment independence fails in some applications. For example, certain genes may influence both environmental exposure and disease occurrence. Violation of the independence assumption can cause serious bias in the analysis (e.g. Spinka and others, 2005).
Recently, Chen and others (2008) relaxed the assumption of gene–environment independence by postulating a polytomous logistic regression model for the distribution of the haplotypes conditional on the environmental factors and constructed appropriate estimating equations. They were able to detect an interaction between smoking and a NAT2 haplotype in the development of colorectal adenoma that was undetected under the assumption of gene–environment independence. Their work is confined to case–control studies and does not deal with analysis of untyped SNPs.
In this paper, we provide a unified framework for assessing the roles of individual SNPs (including untyped SNPs) or their haplotypes in the development of disease. The effects of genetic and environmental factors on disease phenotypes are formulated through flexible regression models that incorporate appropriate genetic mechanisms and gene–environment interactions. The dependence between genetic and environmental factors is characterized by a class of odds ratio functions. The marginal distribution of environmental factors is completely unspecified, while genetic variables may be in HWE or disequilibrium. We construct appropriate likelihoods for all commonly used study designs (including cross-sectional, case–control, and cohort designs) and a variety of disease phenotypes/traits. Unlike the case of gene–environment independence, the likelihoods involve the (potentially infinite dimensional) distribution of environmental variables even under cross-sectional and cohort designs and are thus difficult to handle both theoretically and numerically. We establish the theoretical properties of the maximum likelihood estimators by appealing to modern asymptotic techniques and develop efficient and stable numerical algorithms to implement the corresponding inference procedures. We evaluate the proposed methods through extensive simulation studies and apply them to a major genome-wide association study of lung cancer (Amos and others, 2008).
2. METHODS
2.1. Notation and assumptions
We consider a set of SNPs that are in linkage disequilibrium (i.e. correlated). We may have a direct interest in the haplotypes of these SNPs or wish to use the haplotype distribution to infer the unknown value of 1 SNP from the observed values of the other SNPs. Let H and G denote the diplotype (i.e. the pair of haplotypes on the 2 homologous chromosomes) and genotype, respectively. We write if the diplotype consists of h and , in which case . We allow the values in G to be missing at random. Note that H cannot be determined with certainty on the basis of G if the 2 constituent haplotypes differ at more than one position or if any SNP genotype is missing.
Let Y and X denote, respectively, the phenotype of interest and the environmental factors or covariates. We allow X to include both covariates that are potentially correlated with H and those known to be independent of H. For cross-sectional and case–control studies, the effects of X and H on Y are characterized by the conditional density of given and , denoted by , where α, β, and ξ pertain to intercepts, regression parameters, and nuisance parameters (e.g. variance and overdispersion parameters), respectively. The regression effects are specified through the design vector , which is a vector function of X and H. For example, if we are interested in the additive genetic effect of a risk haplotype and its interactions with X, then we may specify
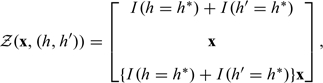 |
(2.1) |
where is the indicator function. For dominant and recessive models, we replace by and , respectively; the codominant model contains both additive and recessive effects. If we are interested in the additive effect of a particular SNP, then we replace by the value of at that SNP position; dominant, recessive, and codominant effects are defined similarly.
Let K be the total number of haplotypes that exist in the population. For , we denote the kth haplotype by . Define and , . Under HWE,
| (2.2) |
We also consider 2 forms of Hardy–Weinberg disequilibrium (HWD),
| (2.3) |
and
| (2.4) |
where 0 < πk ≤ 1, , , and (Lin and Zeng, 2006). Both (2.3) and (2.4) reduce to (2.2) if . Excess homozygosity (i.e. πkk > πk2, k = 1,…,K) and excess heterozygosity (i.e. πkk < πk2,k = 1,…,K) arise when ρ > 0 and ρ < 0, respectively, although the range of heterozygosity is restrictive. Denote the probability function of H by , where γ consists of under (2.2) and π and ρ under (2.3) or (2.4).
We formulate the dependence of X on H through the conditional density function . Because of missing genetic data, cannot be completely nonparametric. Mimicking Chen's (2004) idea, we define the general odds ratio function
where and are fixed points in the sample spaces of H and X, respectively. Then,
so the conditional density function is represented by the odds ratio function η and the conditional density at a fixed point . We abbreviate as and denote the corresponding distribution function by .
Without loss of generality, set . If X consists of S covariates that are either continuous or dichotomous, then we may specify that
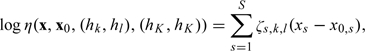 |
where , , and are log-odds ratios with . Any categorical covariate of m levels can be represented by dichotomous variables. Specific mode of inheritance is imposed on to ensure identifiability. Under the additive model, with . If a certain component of X, indexed by , is known to be independent of H, then we set the corresponding to 0. In general, , where ζ is a set of log-odds ratio parameters and is a set of distance measures. This formulation encompasses all generalized linear models for X with canonical links to H.
REMARK 2.1
Chen and others (2008) assumed HWE and decomposed the joint density function as . Because generally does not follow HWE when is in HWE, Chen and others (2008) defined the intercepts in their polytomous logistic model for as implicit functions of all other parameters so as to impose HWE on . Those constraints complicate the estimation process. By contrast, we decompose as , so that the population genetics assumption on can be incorporated directly and there are no constraints on other parameters. The odds ratios associated with and are the same and can be interpreted as the effects of H on X or the effects of X on H.
In the sequel, denotes the set of diplotypes that are compatible with genotype G, denotes a haplotype that differs from h at only one SNP site, and . For any parameter θ, we use to denote its true value when the distinction is necessary. We assume that the true value of any Euclidean parameter θ belongs to the interior of a known compact set within the domain of θ and that is twice continuously differentiable with positive derivatives in its support.
2.2. Cross-sectional studies
In a cross-sectional study, we measure the phenotype Y, genotype G, and covariates X on a random sample of n subjects, so the data consist of . The phenotype or trait Y can be any type (e.g. binary or continuous) and possibly multivariate. As mentioned in Section 2.1, the conditional density of Y given X and H is given by , which can be formulated by generalized linear models for univariate traits and by generalized linear mixed models for multivariate traits.
Write θ = α, β, γ, ζ). The likelihood for θ and F is
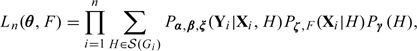 |
(2.5) |
where
We use the nonparametric maximum likelihood estimation (NPMLE) approach. In this approach, the distribution function is treated as a right-continuous function with jumps at the observed X. The objective function to be maximized is obtained from (2.5) by replacing with the jump size of F at X. The maximization can be carried out by the expectation–maximization (EM) algorithm described in Section 2.1 of the supplementary material available at Biostatistics online.
2.3. Case–control studies
In a case–control study, we measure X and G on cases () and controls (). It is natural to formulate the effects of X and G on Y through the logistic regression model
| (2.6) |
where α is an intercept and β is a set of log-odds ratios.
Write . To reflect case–control sampling, we employ the retrospective likelihood:
| (2.7) |
There is very little information about α in case–control data, so the problem is virtually nonidentifiable. We focus on 2 tractable situations: when the disease is rare and when the disease rate is known. Under such conditions, the haplotype distribution of the general population can be estimated reliably from case–control data.
Rare disease
When the disease is rare, model (2.6) simplifies to Then the likelihood given in (2.7) becomes
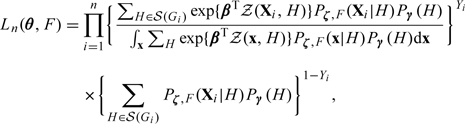 |
(2.8) |
in which θ consists of β, γ, and ζ only. We again adopt the NPMLE approach, which is implemented via the EM algorithm described in Section 2.2 of the supplementary material available at Biostatistics online.
Known disease rate
Let be the known disease rate. We maximize the likelihood given in (2.7) or equivalently
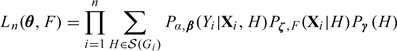 |
subject to the constraint that We show in Section 2.3 of the supplementary material available at Biostatistics online that the NPMLEs of θ and F can be obtained via an EM algorithm.
REMARK 2.2
Chen and others (2008) also focused on the situations of rare disease and known disease rate. Because their estimating equations are not likelihood score equations and involve constraints for the intercepts of their polytomous logistic model, the convergence properties of their EM-like algorithm are unclear, and their estimators are not asymptotically efficient. By contrast, our objective functions are likelihood functions, which are guaranteed to increase at each step of the EM algorithms, and the resulting estimators are asymptotically efficient.
2.4. Cohort studies
In a cohort study, we follow a random sample of n at-risk subjects to
observe their ages at onset of disease. The subjects who are disease-free during the
follow-up contribute censored observations. Let Y and C
denote the time to disease occurrence and the censoring time, respectively. It is assumed
that C is independent of Y and H
conditional on X and G. The data consist of
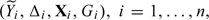 where
where
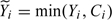 and .
and .
We formulate the effects of X and H on Y through a class of semiparametric transformation models
where is the cumulative hazard function of Y given X and H, is an unspecified increasing function, and is a 3-time differentiable function with and Q′(x) > 0 and satisfying condition (e) of Zeng and Lin (2007). Here and in the sequel, and . The choices of and yield the proportional hazards model (Cox, 1972) and the proportional odds model (Bennett, 1983), respectively.
Write . The likelihood concerning θ, Λ, and F takes the form
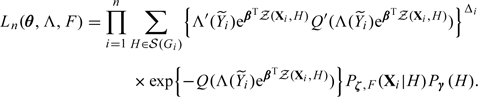 |
(2.9) |
Adopting the NPMLE approach, we regard Λ and F as
right-continuous functions and replace 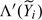 and in (2.9)
with the jump size of Λ at
and in (2.9)
with the jump size of Λ at 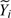 and the jump size of F at
x. The estimation can be carried out through EM
algorithms; see Section 2.4 of the supplementary material available at Biostatistics
online.
and the jump size of F at
x. The estimation can be carried out through EM
algorithms; see Section 2.4 of the supplementary material available at Biostatistics
online.
2.5. Asymptotic properties
The NPMLEs in Sections 2.2–2.4, denoted by 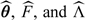 , are consistent, asymptotically normal, and asymptotically
efficient; rigorous statements and proofs are provided in Section 1 of the supplementary material available at Biostatistics online.
The limiting covariance matrix of
, are consistent, asymptotically normal, and asymptotically
efficient; rigorous statements and proofs are provided in Section 1 of the supplementary material available at Biostatistics online.
The limiting covariance matrix of 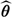 can be consistently estimated by inverting the information matrix
for all parameters (including the jump sizes of nuisance functions) or by using the
profile likelihood function (Murphy and van der Vaart,
2000).
can be consistently estimated by inverting the information matrix
for all parameters (including the jump sizes of nuisance functions) or by using the
profile likelihood function (Murphy and van der Vaart,
2000).
2.6. Untyped SNPs
When one of the SNPs in G is untyped, that is, missing on all study subjects, the haplotype distribution π cannot be estimated from the study data alone. Fortunately, external databases, such as the HapMap, can be used to estimate π provided that the external sample and the study sample are generated from the same underlying population.
Let denote the likelihood for π based on the
external sample. If the external sample consists of 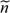 unrelated subjects, then
unrelated subjects, then 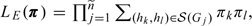 where is the genotype of the jth subject. The
HapMap database provides genotype information for trios. For an external sample of
where is the genotype of the jth subject. The
HapMap database provides genotype information for trios. For an external sample of
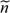 trios, the genotype data for the
jth trio consist of
trios, the genotype data for the
jth trio consist of 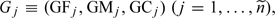 where , , and denote the genotypes for the father, mother, and child,
respectively. Then,
where , , and denote the genotypes for the father, mother, and child,
respectively. Then,
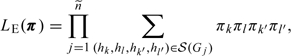 |
where means that is compatible with , is compatible with , and , , or is compatible with .
Denote the likelihood for the study data by , in which θ consists of π, as well as all other finite- and infinite-dimensional parameters in the likelihood. The likelihood for θ that combines the study data and the external data is We maximize in the same manner as in the maximization of ; the score function and information matrix for are provided in Appendix B of Lin and others (2008). The resulting estimators of θ are consistent, asymptotically normal, and asymptotically efficient.
3. SIMULATION STUDIES
We conducted extensive simulation studies to assess the operating characteristics of the proposed methods in realistic scenarios. We considered 5 SNPs (rs10519198, rs13180, rs3743079, rs8034191, and rs3885951) in a gene on chromosome 15 that is known to affect both smoking behavior and lung cancer (Amos and others, 2008). Table 1 displays the haplotype frequencies of the 5 SNPs. We simulated genotype data from those haplotype frequencies under HWE.
Table 1.
Observed haplotype frequencies from a lung cancer study
| Index | Haplotype | Frequency |
| h1 | 00000 | 0.0278 |
| h2 | 00010 | 0.2101 |
| h3 | 00011 | 0.0923 |
| h4 | 01000 | 0.2080 |
| h5 | 01001 | 0.0005 |
| h6 | 01010 | 0.0026 |
| h7 | 10010 | 0.0078 |
| h8 | 10011 | 0.0083 |
| h9 | 11100 | 0.1465 |
| h10 | 11110 | 0.0158 |
| h11 | 10000 | 0.2803 |
Our first set of studies was concerned with the inference on haplotype effects and haplotype– environment interactions in case–control studies. We simulated disease status from the logistic regression model with an additive effect of :
where X is Bernoulli with . We let , where , , , and .
For making inference on , we set and and varied from to ; for making inference on , we set and varied from to . We chose and to yield disease rates between 5% and 15%. We let and adopted the rare disease assumption in the analysis. We also included the method of Lin and Zeng (2006), which assumes haplotype–environment independence. The results are summarized in Table 2.
Table 2.
Simulation results for estimating and testing haplotype effects and haplotype–environment interactions in case–control studies
| Proposed |
Lin–Zeng |
||||||||||
| α | β1 | Bias | SE | SEE | CP | Power | Bias | SE | SEE | CP | Power |
| − 2.1 | − 0.5 | 0.001 | 0.138 | 0.137 | 0.989 | 0.861 | − 0.051 | 0.131 | 0.131 | 0.985 | 0.955 |
| − 0.25 | 0.000 | 0.132 | 0.132 | 0.989 | 0.250 | − 0.049 | 0.125 | 0.125 | 0.987 | 0.433 | |
| 0 | 0.003 | 0.129 | 0.127 | 0.990 | 0.010 | − 0.047 | 0.121 | 0.120 | 0.985 | 0.015 | |
| 0.25 | 0.002 | 0.123 | 0.125 | 0.993 | 0.287 | − 0.047 | 0.114 | 0.117 | 0.988 | 0.198 | |
| 0.5 | 0.002 | 0.122 | 0.123 | 0.992 | 0.940 | − 0.046 | 0.114 | 0.114 | 0.982 | 0.918 | |
| − 3 | − 0.5 | − 0.001 | 0.138 | 0.139 | 0.992 | 0.863 | − 0.052 | 0.131 | 0.132 | 0.988 | 0.951 |
| − 0.25 | 0.002 | 0.133 | 0.133 | 0.988 | 0.239 | − 0.048 | 0.126 | 0.126 | 0.985 | 0.416 | |
| 0 | 0.003 | 0.127 | 0.128 | 0.993 | 0.007 | − 0.048 | 0.119 | 0.120 | 0.985 | 0.015 | |
| 0.25 | 0.003 | 0.123 | 0.124 | 0.991 | 0.290 | − 0.047 | 0.116 | 0.116 | 0.982 | 0.203 | |
| 0.5 | 0.000 | 0.124 | 0.122 | 0.991 | 0.941 | − 0.050 | 0.114 | 0.113 | 0.984 | 0.916 | |
|
α |
β3 |
||||||||||
| − 2.1 | − 0.5 | − 0.003 | 0.270 | 0.270 | 0.992 | 0.243 | 0.284 | 0.190 | 0.193 | 0.842 | 0.052 |
| − 0.25 | − 0.010 | 0.261 | 0.260 | 0.989 | 0.052 | 0.255 | 0.178 | 0.178 | 0.857 | 0.011 | |
| 0 | − 0.004 | 0.259 | 0.254 | 0.990 | 0.010 | 0.217 | 0.167 | 0.167 | 0.891 | 0.109 | |
| 0.25 | − 0.004 | 0.253 | 0.251 | 0.991 | 0.051 | 0.161 | 0.158 | 0.158 | 0.937 | 0.519 | |
| 0.5 | − 0.017 | 0.257 | 0.252 | 0.989 | 0.250 | 0.082 | 0.149 | 0.151 | 0.981 | 0.899 | |
| − 3 | − 0.5 | − 0.001 | 0.273 | 0.270 | 0.989 | 0.227 | 0.248 | 0.194 | 0.193 | 0.883 | 0.079 |
| − 0.25 | − 0.002 | 0.256 | 0.259 | 0.988 | 0.051 | 0.238 | 0.176 | 0.178 | 0.880 | 0.009 | |
| 0 | − 0.002 | 0.255 | 0.251 | 0.988 | 0.012 | 0.221 | 0.164 | 0.165 | 0.882 | 0.118 | |
| 0.25 | − 0.003 | 0.245 | 0.246 | 0.991 | 0.052 | 0.195 | 0.155 | 0.155 | 0.901 | 0.612 | |
| 0.5 | − 0.010 | 0.249 | 0.243 | 0.989 | 0.282 | 0.154 | 0.148 | 0.148 | 0.936 | 0.967 | |
NOTE: Bias and SE are the bias and standard error of the parameter estimator. SEE is the mean of the standard error estimator. CP is the coverage probability of the 99% confidence interval. Power pertains to the 0.01-level test of zero parameter value and corresponds to the type I error under the null hypothesis. Each entry is based on 5,000 replicates.
The proposed estimator for is virtually unbiased. The proposed estimator for seems to be slightly biased downward when the disease rate is close to 15%. The proposed variance estimators accurately reflect the true variabilities, the Wald tests have proper type I error, and the confidence intervals have reasonable coverage probabilities. The rare-disease assumption is a good approximation even when the disease rate is as high as 15%. Under the Lin–Zeng method, the estimators are biased, the type I error is inflated, and the confidence intervals have poor coverage probabilities, especially for interactions.
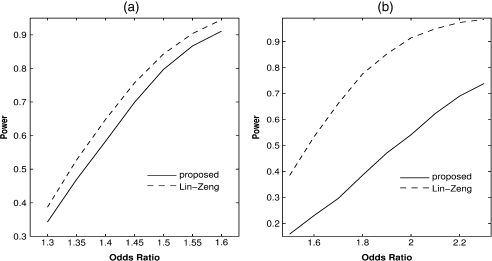
To assess the efficiency loss of modeling gene–environment dependence when the independence assumption actually holds, we modified the above simulation set-up by letting . For making inference on , we set , , and and varied from to 1.6; for making inference on , we set and varied from 1.5 to 2.3. As shown in Figure 1, the power loss is more substantial in testing interactions than in testing main effects. In practice, one should incorporate the independence assumption into the analysis if it is known to be true. Indeed, our formulation allows one to impose independence on any subset of X and yields the Lin–Zeng method if independence is imposed on the entire X.
Fig. 1.
Power of testing (a) main effects and (b) interactions at the 1% nominal significance level for the proposed and Lin–Zeng methods when the independence assumption holds.
The aforementioned studies pertain to a binary covariate and to risk haplotype , which has a relatively high frequency. Additional simulation studies revealed that the above conclusions continue to hold for other haplotype frequencies and other covariate distributions. For example, the left panel of Table 3 shows the results under the logistic regression model
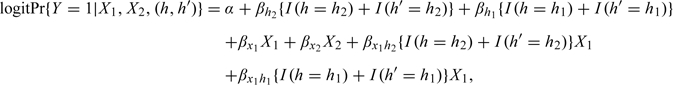 |
Table 3.
Simulation results for estimating and testing haplotype effects and haplotype–environment interactions in case–control studies with 2 risk haplotypes and 2 covariates
| Para. | True value | Correctly specified
P(X|H) |
Misspecified
P(X|H) |
||||||||
| Bias | SE | SEE | CP | Power | Bias | SE | SEE | CP | Power | ||
| 0.25 | 0.000 | 0.116 | 0.114 | 0.992 | 0.361 | 0.010 | 0.113 | 0.114 | 0.989 | 0.378 | |
| 0.25 | 0.003 | 0.288 | 0.283 | 0.990 | 0.041 | 0.013 | 0.298 | 0.287 | 0.989 | 0.045 | |
| 0.3 | 0.003 | 0.084 | 0.083 | 0.991 | 0.859 | 0.014 | 0.060 | 0.059 | 0.988 | 0.997 | |
| 0.3 | − 0.005 | 0.129 | 0.130 | 0.991 | 0.377 | 0.001 | 0.131 | 0.132 | 0.989 | 0.385 | |
| .0 | − 0.002 | 0.109 | 0.105 | 0.987 | 0.013 | − 0.017 | 0.070 | 0.071 | 0.989 | 0.011 | |
| .0 | 0.005 | 0.267 | 0.269 | 0.991 | 0.009 | − 0.008 | 0.181 | 0.182 | 0.990 | 0.010 | |
NOTE: See the note to Table 2.
coupled with the odds ratio function where and are independent conditional on H, the conditional distribution of given is standard normal, is Bernoulli with 0.4 success probability, , , , , , , and .
To assess the robustness of the proposed method, we modified the above setting to simulate a conditional distribution of X given H that does not fit into the odds ratio formulation. Specifically, we let the conditional density of given be , where t follows a 3 d.f. t-distribution truncated at . The results are provided in the right panel of Table 3. The proposed method is robust to misspecification of the dependence structure.
We also compared the proposed method to that of Chen and others (2008). We simulated data from the logistic regression model
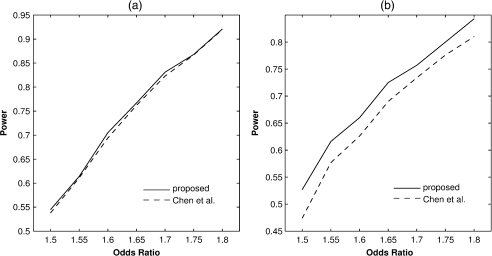
and the odds ratio function , where the conditional distribution of X given is standard normal, , , , and . We set and . For making inference on , we set and and varied from 1.5 to 1.8; for making inference on , we set and varied from 1.5 to 1.8. For each combination of simulation parameters, we generated 1,000 data sets. Our algorithm always converged, whereas the algorithm of Chen and others (2008), as implemented in their SAS program, failed to converge in about 3% of the data sets. Figure 2 presents the power curves of the 2 methods based on the data sets in which the algorithm of Chen and others converged. The proposed method is uniformly more powerful than the method of Chen and others, especially in detecting interactions.
Fig. 2.
Power of testing (a) main effects and (b) interactions at the 1% nominal significance level for the proposed method and the method of Chen and others.
Our final set of studies dealt with analysis of untyped SNPs in cohort studies. We simulated ages at onset of disease from the proportional hazards model where is the number of allele “1” at the 4th locus of H and X is the same as in the first set of case–control studies. We generated censoring times from the uniform distribution, where τ was chosen to yield approximately 250, 500, or 1,000 cases under 5,000. We set and varied from to . We set the 4th SNP to be missing in the observed data and generated an external data set of 30 trios from the haplotype distribution of Table 1. As shown in Table 4, the proposed method performs very well.
Table 4.
Simulation results for the analysis of an untyped SNP in cohort studies
| β3 | Cases | Bias | SE | SEE | CP | Power |
| 0 | 250 | − 0.003 | 0.236 | 0.233 | 0.990 | 0.010 |
| 500 | 0.004 | 0.164 | 0.163 | 0.992 | 0.008 | |
| 1,000 | 0.001 | 0.120 | 0.120 | 0.990 | 0.010 | |
| − 0.25 | 250 | − 0.003 | 0.262 | 0.256 | 0.991 | 0.049 |
| 500 | 0.003 | 0.180 | 0.178 | 0.988 | 0.112 | |
| 1,000 | 0.001 | 0.130 | 0.129 | 0.990 | 0.254 | |
| − 0.5 | 250 | − 0.009 | 0.295 | 0.285 | 0.990 | 0.194 |
| 500 | − 0.000 | 0.203 | 0.197 | 0.991 | 0.491 | |
| 1,000 | 0.001 | 0.144 | 0.142 | 0.989 | 0.842 | |
| 0.25 | 250 | 0.001 | 0.217 | 0.215 | 0.991 | 0.077 |
| 500 | 0.003 | 0.154 | 0.153 | 0.991 | 0.177 | |
| 1,000 | 0.000 | 0.114 | 0.115 | 0.992 | 0.345 | |
| 0.5 | 250 | 0.000 | 0.203 | 0.202 | 0.991 | 0.457 |
| 500 | 0.002 | 0.147 | 0.146 | 0.991 | 0.813 | |
| 1,000 | − 0.003 | 0.113 | 0.112 | 0.991 | 0.973 |
NOTE: See the note to Table 2.
4. LUNG CANCER STUDY
Lung cancer is the most common type of cancer in terms of both incidence and mortality, with the highest rates in Europe and North America. Although this malignancy is attributable to environmental exposures, primarily cigarette smoking, genetic factors influencing lung cancer susceptibility have been reported in numerous studies. Recently, a genome-wide case–control association study of histologically confirmed non–small-cell lung cancer was conducted to identify common low-penetrance alleles influencing lung cancer risk Amos and others (2008). Controls were matched to cases according to smoking behavior, age (in 5-year groups), and sex, and former smokers were further matched by years of cessation. The study population was restricted to individuals of self-reported European descent to minimize confounding by ethnic variation.
In the discovery phase of the study, 1,154 ever-smoking cases and 1,137 ever-smoking controls were genotyped for 317 498 tagging SNPs on Illumina HumanHap300 v1.1 BeadChips. Two SNPs, rs1051730 and rs8034191, mapping to a region of strong linkage disequilibrium within 15q25.1 containing PSMA4 and the nicotinic acetylcholine receptor subunit genes CHRNA3 and CHRNA5, were found to be significantly associated with lung cancer risk. The investigators kindly provided us data on a cluster of 37 SNPs surrounding those 2 SNPs.
We first investigate haplotype effects and haplotype–smoking interactions with sliding windows of 5 SNPs. For each window, we fit a logistic regression model that compares all haplotypes (with observed frequencies greater than 0.2% in the control group) to the most frequent haplotype under the additive mode of inheritance and includes cigarettes per day as a continuous covariate. Because the SNPs in the region are known to be associated with smoking behavior, we allow all haplotypes (with observed frequencies greater than 0.4% in the control group) to be potentially correlated with the smoking variable in the proposed general odds ratio function. We assume HWE and adopt the rare-disease approximation. For comparisons, we also fit the haplotype–environment independence model of Lin and Zeng (2006).
Table 5 presents the results for a window containing SNP rs1051730. Haplotype 11110 is significantly related to smoking. Haplotype 00000 also has a large effect on smoking, although not significant at the 0.05 level. For those 2 haplotypes, the Lin–Zeng method would declare statistical significance at the 0.05 level for haplotype–smoking interactions, whereas the proposed method would not. These differences are consistent with the simulation results shown in Table 2 that the Lin–Zeng method tends to produce false-positive results for haplotype–environment interactions when the independence assumption fails.
Table 5.
Estimates of haplotype effects and haplotype–smoking interactions for a set of 5 SNPs in the lung cancer study
| Parameters | Proposed | Lin–Zeng |
| Logistic disease-risk model (β) | ||
| 11110 | 0.249(0.069)** | 0.252(0.069)** |
| 11011 | − 0.097(0.084) | − 0.099(0.084) |
| 00000 | 0.198(0.139) | 0.201(0.139) |
| 11010 | − 0.255(.237) | − 0.252(0.237) |
| 00011 | 0.519(0.737) | 0.536(0.748) |
| Smoking | 0.093(0.090) | 0.021(0.071) |
| 11110 × smoking | − 0.013(0.069) | 0.094(0.047)* |
| 11011 × smoking | − 0.032(0.087) | − 0.061(0.062) |
| 00000 × smoking | 0.108(0.132) | 0.190(0.086)* |
| 11010 × smoking | − 0.044(0.236) | − 0.006(0.181) |
| 00011 × smoking | 0.289(0.349) | 0.290(0.348) |
| General odds ratio function (ζ) | ||
| 11110 | 0.108(0.050)* | — |
| 11011 | – 0.030(.061) | — |
| 00000 | 0.083(0.100) | — |
| 11010 | 0.038(0.151) | — |
NOTE: Standard error estimates are shown in parentheses. *P < 0.05. **P < 0.001.
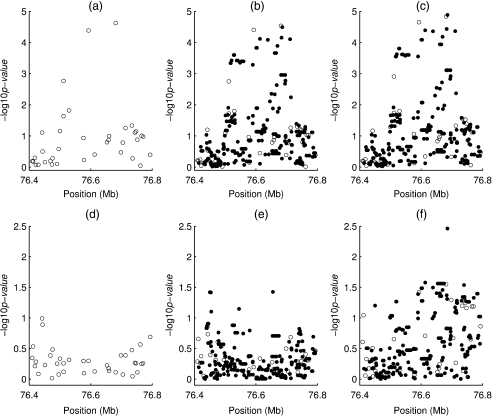
Next, we investigate the effects of individual SNPs and their interactions with smoking in the development of lung cancer for the 37 typed SNPs and 259 untyped HapMap SNPs in the region. In accordance with the study sample, we choose the HapMap sample of Utah residents with ancestry from northern and western Europe as the reference panel in the analysis of untyped SNPs. For each untyped SNP, we identify a set of 4 typed SNPs within 100 000 base pairs that provides the best prediction (Lin and others, 2008). We apply the proposed method and the method of Lin and others (2008). The former allows gene–environment dependence, whereas the latter assumes independence. For typed SNPs, we also perform standard logistic regression analysis, which allows any form of gene–environment dependence and thus serves as a benchmark. The dependence between smoking and SNPs in the region of interest turns out to be very strong; the results are not shown here. Figure 3 displays the results for testing SNP effects (adjusted for smoking) and for testing SNP-smoking interactions. For typed SNPs, the results based on the proposed method and standard logistic regression are highly similar, suggesting that our odds ratio formulation is reasonable; the results of the Lin and others method are different, especially for interactions. For untyped SNPs, the method of Lin and others yields more significant results, especially for interactions, than the proposed method. Because of the strong gene–environment dependence, the results of the Lin and others method are unreliable.
Fig. 3.
Results of association tests for additive effects of individual SNPs in the lung cancer study: the (p-values) for the genotyped and untyped SNPs are shown in circles and dots, respectively; (a), (b), and (c) pertain to testing SNP effects (adjusted for smoking) under the standard logistic regression, the proposed method and the method of Lin and others, respectively; (d), (e), and (f) pertain to testing SNP-smoking interactions under the standard logistic regression, the proposed method and the method of Lin and others, respectively.
5. DISCUSSION
This paper extends the work of Lin and Zeng (2006) to allow gene–environment dependence and to handle untyped SNPs. As demonstrated in the simulation studies and real example, the results of association analysis depend critically on the assumption about gene–environment relationship. If the genetic and environmental factors are known to be independent, then one should impose this structure in the analysis to improve efficiency. If the independence does not hold, then one should avoid this assumption to enhance the validity of inference. If the independence is not known to hold or not, then the empirical Bayes-type shrinkage estimation (e.g. Chen and others, 2009) provides a nice trade-off between efficiency and robustness; see Section 3 of the supplementary material available at Biostatistics online.
Unlike Lin and Zeng (2006), our likelihood functions involve the (potentially infinite dimensional) distribution of covariates even for cross-sectional and cohort studies. Also, Lin and Zeng (2006) did not consider case–control studies with known disease rates. Even for case–control studies with rare disease, our likelihood function is more complicated than that of Lin and Zeng (2006) because the distribution of covariates cannot be profiled out due to the modeling of gene–environment dependence. Thus, our numerical algorithms are fundamentally different from those of Lin and Zeng (2006) for all study designs. Although the basic structures of our theoretical proofs are similar to those of Lin and Zeng (2006), the actual techniques employed are novel. Due to the presence of multiple nonparametric conditional distribution functions of X given H, the proofs of identifiability of parameters and nonsingularity of information matrices are very delicate.
Lin and Zeng (2006) considered the setting in which X is independent of H conditional on G. It is difficult to construct realistic scenarios in which X is independent of H conditional on G but not independent of H unconditionally. Indeed, G is equivalent to H if there is only a single SNP or H consists of or . It is more natural to allow direct association between H and X, as is done in this paper.
Our approach is scalable to genome-wide association scan. With categorical X, the computation is almost as fast as in the case of gene–environment independence. One may discretize continuous covariates to speed up computation. Our software is posted at http://www.bios.unc.edu/∼lin/software.
We have assumed that X is completely observed. In practice, the values of certain environmental variables (e.g. smoking history and dietary information) may be unknown on some study subjects. A major advantage of the odds ratio formulation is that it can readily handle missing covariates (Chen, 2004). Specifically, we express as and represent each conditional density function in terms of a general odds ratio function and an arbitrary 1D distribution function. In this way, we can accommodate arbitrary missing patterns in X and easily extend the theory and numerical algorithms of this paper.
In the genetic and epidemiologic literature, it has become a common practice to infer the haplotypes or the values of untyped SNPs for each subject based on the genotype data alone and then include those imputed values in downstream association analysis. This single imputation approach can yield biased estimates of genetic effects, inflated type I error and reduced statistical power (e.g. Lin and Huang, 2007; Lin and others, 2008).
We infer the unknown value of an untyped SNP nonparametrically from a small set of typed SNPs which is chosen to provide the best prediction among all flanking SNPs. An alternative approach is to use all typed SNPs on the chromosome under a population genetics model. To incorporate the latter approach into our framework, we let G denote all the SNPs on the chromosome and decompose G into the observed component and the missing component . The joint density of the observed data can be written as
We calculate through a hidden Markov model (e.g. Marchini and others, 2007). It is difficult to correctly specify the regression model . For estimating the marginal effect of an untyped SNP, we include only that SNP in the regression model. Even when we are interested in the marginal effect of a single SNP, we need to include all the SNPs on the chromosome that are correlated with X in . Inclusion of a large number of SNPs is computationally infeasible and statistically inefficient, whereas omission of important SNPs can bias the association analysis. We prefer the flanking SNPs approach because it is computationally simpler and yield more robust and possibly more efficient inference.
SUPPLEMENTARY MATERIAL
Supplementary material is available at http://www.biostatistics.oxfordjournals.org.
FUNDING
National Institutes of Health (NIH); Gillings Innovation Laboratory (GIL) award at the UNC Gillings School of Global Public Health.
Supplementary Material
Acknowledgments
The authors are grateful to Dr. Chris Amos for providing the data from the lung cancer study, which was supported by the NIH grants R01CA133996 and R01CA55769. Conflict of Interest: None declared.
References
- Amos CI, Wu XF, Broderick P, Gorlov IP, Gu J, Eisen T, Dong Q, Zhang Q, Gu XJ, Vijayakrishnan J and others. Genome-wide association scan of tag SNPs identifies a susceptibility locus for lung cancer at 15q25.1. Nature Genetics. 2008;40:616–622. doi: 10.1038/ng.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett S. Analysis of survival data by the proportional odds model. Statistics in Medicine. 1983;2:273–277. doi: 10.1002/sim.4780020223. [DOI] [PubMed] [Google Scholar]
- Chen HY. Nonparametric and semiparametric models for missing covariates in parametric regression. Journal of the American Statistical Association. 2004;99:1176–1189. [Google Scholar]
- Chen YH, Chatterjee N, Carroll RJ. Retrospective analysis of haplotype-based case-control studies under a flexible model for gene-environment association. Biostatistics. 2008;9:81–99. doi: 10.1093/biostatistics/kxm011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen YH, Chatterjee N, Carroll RJ. Shrinkage estimators for robust and efficient inference in haplotype-based case-control studies. Journal of the American Statistical Association. 2009;104:220–233. doi: 10.1198/jasa.2009.0104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox DR. Regression models and life-tables (with discussion) Journal of the Royal Statistical Society, Series B. 1972;34:187–220. [Google Scholar]
- Epstein MP, Satten GA. Inference on haplotype effects in case-control studies using unphased genotype data. American Journal of Human Genetics. 2003;73:1316–1329. doi: 10.1086/380204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lake SL, Lyon H, Tantisira K, Silverman EK, Weiss ST, Laird NM, Schaid DJ. Estimation and tests of haplotype-environment interaction when linkage phase is ambiguous. Human Heredity. 2003;55:56–65. doi: 10.1159/000071811. [DOI] [PubMed] [Google Scholar]
- Lin DY, Hu Y, Huang BE. Simple and efficient analysis of disease association with missing genotype data. American Journal of Human Genetics. 2008;82:444–452. doi: 10.1016/j.ajhg.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin DY, Huang BE. The use of inferred haplotypes in downstream analyses. American Journal of Human Genetics. 2007;80:577–579. doi: 10.1086/512201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin DY, Zeng D. Likelihood-based inference on haplotype effects in genetic association studies (with discussion) Journal of the American Statistical Association. 2006;101:89–118. [Google Scholar]
- Lin DY, Zeng D, Millikan R. Maximum likelihood estimation of haplotype effects and haplotype-environment interactions in association studies. Genetic Epidemiology. 2005;29:299–312. doi: 10.1002/gepi.20098. [DOI] [PubMed] [Google Scholar]
- Marchini J, Howie B, Myers S, McVean G, Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nature Genetics. 2007;39:906–913. doi: 10.1038/ng2088. [DOI] [PubMed] [Google Scholar]
- Murphy SA, van der Vaart AW. On profile likelihood. Journal of the American Statistical Association. 2000;95:449–465. [Google Scholar]
- Nicolae DL. Testing untyped alleles (TUNA)—applications to genome-wide association studies. Genetic Epidemiology. 2006;30:718–727. doi: 10.1002/gepi.20182. [DOI] [PubMed] [Google Scholar]
- Schaid DJ, Rowland CM, Tines DE, Jacobson RM, Poland GA. Score tests for association between traits and haplotypes when linkage phase is ambiguous. American Journal of Human Genetics. 2002;70:425–434. doi: 10.1086/338688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spinka C, Carroll RJ, Chatterjee N. Analysis of case-control studies of genetic and environmental factors with missing genetic information and haplotype-phase ambiguity. Genetic Epidemiology. 2005;29:108–127. doi: 10.1002/gepi.20085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stram DO, Pearce CL, Bretsky P, Freedman M, Hirschhorn JN, Altshuler D, Kolonel LN, Henderson BE, Thomas DC. Modeling and E-M estimation of haplotype-specific relative risks from genotype data for a case-control study of unrelated individuals. Human Heredity. 2003;55:179–190. doi: 10.1159/000073202. [DOI] [PubMed] [Google Scholar]
- The International HapMap Consortium. A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The International Human Genome Sequencing Consortium. Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
- Zeng D, Lin DY. Maximum likelihood estimation in semiparametric regression models with censored data (with discussion) Journal of the Royal Statistical Society, Series B. 2007;69:507–564. [Google Scholar]
- Zhao LP, Li SS, Khalid N. A method for the assessment of disease associations with single-nucleotide polymorphism haplotypes and environmental variables in case-control studies. American Journal of Human Genetics. 2003;72:1231–1250. doi: 10.1086/375140. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.