Mixture models with multiple levels, with application to the analysis of multifactor gene expression data

Abstract

Model-based clustering is a popular tool for summarizing high-dimensional data. With the number of high-throughput large-scale gene expression studies still on the rise, the need for effective data- summarizing tools has never been greater. By grouping genes according to a common experimental expression profile, we may gain new insight into the biological pathways that steer biological processes of interest. Clustering of gene profiles can also assist in assigning functions to genes that have not yet been functionally annotated. In this paper, we propose 2 model selection procedures for model-based clustering. Model selection in model-based clustering has to date focused on the identification of data dimensions that are relevant for clustering. However, in more complex data structures, with multiple experimental factors, such an approach does not provide easily interpreted clustering outcomes. We propose a mixture model with multiple levels, 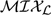, that provides sparse representations both “within” and “between” cluster profiles. We explore various flexible “within-cluster” parameterizations and discuss how efficient parameterizations can greatly enhance the objective interpretability of the generated clusters. Moreover, we allow for a sparse “between-cluster” representation with a different number of clusters at different levels of an experimental factor of interest. This enhances interpretability of clusters generated in multiple-factor contexts. Interpretable cluster profiles can assist in detecting biologically relevant groups of genes that may be missed with less efficient parameterizations. We use our multilevel mixture model to mine a proliferating cell line expression data set for annotational context and regulatory motifs. We also investigate the performance of the multilevel clustering approach on several simulated data sets.

1. INTRODUCTION

Model-based clustering is frequently used to summarize complex high-dimensional gene expression data. The base model is usually Gaussian, though some robust alternatives have recently been proposed (Banfield and Raftery, 1993). The multivariate Gaussian mixture allows for clusters of varying shape and volume (Fraley and Raftery, 2002), (, Fraley04), (, Raftery06). Many nonparametric clustering algorithms have also been proposed for the analyses of genomic data. Nonparametric approaches may seem more flexible than parametric mixture modeling. However, many of the most commonly used nonparametric schemes are in fact very restrictive, in that cluster shapes are implicitly defined by the cost function of the clustering algorithm (Jornsten, 2004). We consider k-means as an example (or any center-based clustering like partition around medoids or the k-median [Kaufman and Rousseeuw, 1990, , Jornsten1]). By making cluster assignment solely dependent on the cluster center, cluster shape is ignored. Thus, k-means tends to produce spherical and equal-size clusters and is thus more restrictive than a model-based clustering approach where the cluster covariances are parameterized.

In this paper, we discuss how to generate interpretable and efficient data representations using multivariate Gaussian mixture models. We address the following limitations of model-based clustering: (1) Model-based clustering usually treats all experimental conditions interchangeably, even in the case of multifactor experiments, and (2) subset model selection for model-based clustering has mainly focused on identifying the “dimensions” that are informative with respect to cluster separation (Law and others, 2004), (, Raftery06), (, Vannucci), (, Hoff06), as opposed to the sparsest representation of each cluster mean. The limitations listed in items (1) and (2) above can result in both an overfit and an underfit of the data. Overfitting might be caused by assigning an unnecessary degree of complexity to some clusters, whereas underfitting concerns the number of clusters.

We propose a multilevel mixture modeling approach that generates interpretable clusters in multiple-factor experiments. Throughout the paper, we will focus on an example data set involving proliferating stem cell lines. Our task is to identify sets of genes that are differentially regulated during neurogenesis and gliogenesis, as indicated by different expression levels in 2 divergent neural stem cell clones. Upon the withdrawal of a growth factor (FGF) from the medium, one clone (L2.3) becomes predominately glial like (expressing glial markers GFAP, GalC). The other (L2.2) differentiates primarily into cells expressing neuronal markers (TuJ1) (Goff and others, 2007). Initially, the cell lines are virtually indistinguishable and are believed to exist in a state of “preconditioning” or “preprogramming”. Thus, sets of neuron-specific and glia-specific genes are active and will determine the cell fate of the clones. The 2 stem cell lines are observed over the course of 3 days. Among the scientific questions of interest raised by the biologists (Goff and others, 2007) are: (a) How do the time-course profiles of the glial-like (L2.3) and neuron-like (L2.2) cell lines differ?, (b) Are there sets of genes for which the expression converges (diverges) between the glial-like and neuron-like cell populations?, and (c) How dominant is the “preprogramming” effect?

For this 2-factor experiment (cell line and time), a 2-level mixture model is appropriate. (We will focus on the 2-level model in detail in the paper and briefly discuss the generalization to multiple levels in the conclusion.) We introduce the model notation in the context of the above experiment. We denote expression of gene g in the glial-like population (L2.3) by x_g and in the neuron-like (L2.2) population by y_g. The feature vectors, x_g and y_g, represent the time-course expression profiles of gene g in the glia and neuron cell lines, respectively. Preliminary analysis indicates that groups of genes exhibit a similar time-course expression profile in the glia cell line but differ in the neuron cell line. Furthermore, the glia cell line is also associated with larger differential expression over time. Thus, if the feature vectors (x_g,y_g) are clustered together, as a single 2×T-dimensional feature, the large expression changes in the glia cell line may dominate the clustering and we might miss the more subtle expression patterns in the neuron cell line. To resolve this issue, and help identify groups of genes whose activity is neuron specific, we use a 2-level mixture model. Thus, we allow for a total of K clusters at the first level, representing the clustering of the glia cell line data. Within each of the k = 1, …, K clusters, we allow for L_k second-level (sub)clusters, representing distinct expression profiles in the neuron cell line. Let R_g and Z_g be 2 gene-specific indicators, denoting the cluster labels at the first and second levels. Our model assumes that

(2.1)

where 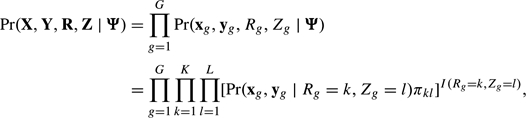and Σ_kl represent the mean and variance–covariance matrix of the lth second-level cluster within the kth first-level cluster. E(x_g|R_g = k,Z_g = l) = μ_k is the expression profile for the glia cell line in cluster k, common to all subclusters l(k) = 1,…,L_k. E(y_g|R_g = k,Z_g = l) = μ_l(k) is the expression profile for the neuron cell line in the lth second-level cluster, within the first-level cluster k. To further enhance interpretability of the clusters, we parameterize the cluster means as μ_kl = Wβ_kl = W(α_k,γ_kl)^′, where α_k denotes the first-level cluster–specific parameters and γ_kl denotes the second-level–specific parameters. W is a design matrix for the multifactor experiment and reflects a scientific question of interest. We perform subset selection on the “parameters”, not the dimensions, and thus obtain cluster means that are directly interpretable in terms of the between-experimental factors and within-experimental factor expression. We discuss specific choices of parameterizations in Section 2.

While we focus on a 2-factor experiment in this paper, the multilevel cluster model is generally applicable to, for example, experiments involving multiple species or varying treatment dosages and regimens. In this example, as in our study, it is of interest to focus particularly on differential effects across levels of an experimental factor of interest (e.g. species, dose).

A few other schemes with a multilevel flavor have been proposed. Li (2005) introduced a layered mixture model to allow for flexible within-cluster structures. Akin to mixture discriminant analysis (Hastie and Tibshirani, 1996) for classification, each cluster (class) is assumed to come from a mixture of normals and can thus incorporate more complex cluster (class) shapes. The number of clusters is assumed known, and clusters do not share any mixture components with other clusters. Our multilevel mixture model differs from Li's approach in that an unknown number of clusters may share components and model parameters and that the levels of the mixture relate to the experimental factors. Yuan and Kendziorski (2006) recently proposed a multilevel approach to gene clustering. Each cluster is assumed to be generated from a mixture of differential expression patterns (overexpressed, underexpressed, and no differential expression). An empirical Bayes strategy is adopted to fit the model. The motivation is that the clustering induces a regularization of the gene effect estimates, and thus power of detection of differential expression is increased. Our multilevel approach allows for a more flexible parameterization of the cluster means across multiple experimental conditions. We identify differential expression patterns both within and between the experimental factors through subset model selection.

The paper is structured as follows. In Section 2, we introduce the multilevel mixture model, 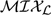, and propose a method for subset selection and validation of the number of clusters. In Section 3, we apply 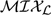to a multifactor gene expression data set. In Section 4, we illustrate the strengths of our approach on several simulated data sets. We conclude this paper with a discussion.

2. THE 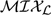MODEL

2.1. A multilevel parameterization for model-based clustering

We present the 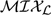model in the case of 2 populations (e.g. cell lines) of interest, and samples from both these populations are collected across T time points as in the experiment described in Section 1. (We briefly discuss generalizations in Section 5.) Let x_g denote the observations across T = 3 time points for gene g (g∈{1,…,G}) in cell line 1 (glia like), and similarly y_g in cell line 2 (neuron like). We denote the total number of clusters at the first level (glia) by K and the number of second-level clusters (neuron) within each first-level cluster k by L_k. Let R_g and Z_g be 2 gene-specific cluster indicators denoting the cluster labels at the first and second level. Our model assumes that

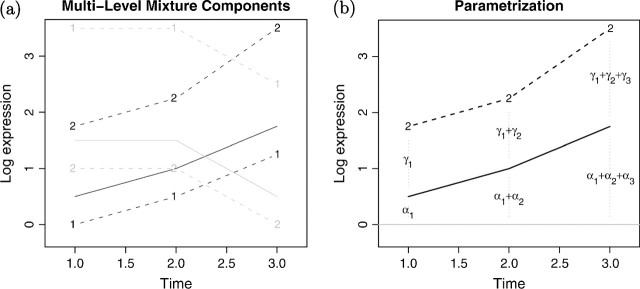
where 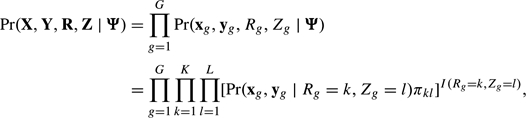and Σ_kl represent the mean and variance–covariance matrix of the lth second-level cluster within the kth first-level cluster. The first T components of the μ_kl vector, μk, correspond to the mean levels of x_g. The last T components, μ_l(k), correspond to the mean levels of y_g (Figure 1(a)). Note, if we let L_k = 1 for all k, the model formulation in (1) coincides with a standard mixture model.

Fig. 1.

(a) An illustration of a mixture model with 2 levels; 2 first-level clusters for cell line 1 (solid lines). The 2 sets of dashed lines represent the corresponding subclusters (level 2) for cell line 2. Thus, here K = 2, and L₁ = 2, L₂ = 2. (b) The “dynamic differential expression (DE) parameterization”. The α parameters model the time-course expression profile for cell line 1, whereas the γ parameters model the time course of “cell line differential” expression.

The multilevel framework allows for various interpretable parameterizations at each level. We parameterize the cluster mean as μ_kl = Wβ_kl = W(α_k,γ_kl)′. The α-parameter vector represents first-level–specific parameters, and the γ vector represents the second-level model parameters. Next, we will consider the following 3 parameterizations in detail:

PARAMETERIZATION I.

Mean differential expression

The vector (α_k1, α_k2, α_k3) represents cell line 1 expression at time points (t₁, t₂, t₃) in cluster k. The vector (γ_kl1, γ_kl2, γ_kl3) represents the cell line differences at each time point in subcluster l(k). Here, the main scientific question addressed is thus the differential expression between the cell lines, at any given time point.

PARAMETERIZATION II.

Dynamical differential expression

In the second parameterization (see Figure 1(b)), the time-course profile of the glial-like population is modeled directly and, for example, flat time profiles are efficiently represented (α_k2 = α_k3 = 0). The γ-vector represents the differential expression “time-course” of the 2 cell lines (e.g. parallel [γ_kl2 = γ_kl3 = 0] or divergent [γ_kl1 = 0, γ_kl3 ≠ 0]).

PARAMETERIZATION III.

Preprogramming differential expression

The third parameterization efficiently models each time-course profile and a main differential cell line effect for time point t₁. Thus, flat glia time profiles are efficiently represented (α_k2 = α_k3 = 0), and similarly flat time-course profiles for the neuron cell line are obtained if γ_kl2 = γ_kl3 = 0. The only direct comparison between the cell lines is at time point t₁.

Other data sets and experimental structures may require a different set of parameterizations. Ultimately, the choice of parameterization should depend on the biological context and the scientific questions of interest.

In all parameterizations, the variance–covariance matrix Σ_kl also includes parameters specific to the levels of the model:

The variance–covariance structure allows for dependencies between gene expression measurements at all time points and all levels. We further assume that, conditional on the multilevel cluster assignments, the genes are independent of each other. Therefore, we have the following complete-data likelihood:

where Ψ = {μ_kl, Σ_kl, k = 1, …, K, l(k) = 1, …, L_k} represents the overall parameter set of the model and π_kl are the mixing proportions. Due to the multilevel parameterization and the general variance–covariance structure, the complete-data likelihood does not factorize into terms over which maximization for each parameter can be carried out separately. Therefore, the standard maximization step for the expectation–maximization (EM) algorithm of the mixture models does not lead to closed-form updates. To resolve this issue, we derive a profile expectation–maximization (PEM) algorithm that relies on the factorization of the likelihood into the likelihood of the first level of the hierarchy and the conditional likelihood of the second level of the hierarchy given the first level. Additionally, each component of the factorized likelihood is maximized by profiling of the corresponding expected complete-data log-likelihood. Although purely motivated by the factorization of the expected full-data likelihood, the proposed PEM algorithm can be classified as an expected conditional maximization algorithm proposed by Meng and Rubin (1993)

2.2. PEM algorithm for fitting the multilevel mixture model

We now describe the PEM algorithm for fixed K and L_?,∀k. Here, r refers to rth EM iteration, and we suppress the dependence on r to ease the notation.

Initial values.

The algorithm requires initial values of π_kl, μ_kl, and Σ_kl. These are obtained via a k-means clustering of the data with M = ∑_kL_k clusters. We then collapse a subset of the M clusters for the first-level data (x_g, glia cell line data) to form K first-level clusters. Within each first- and second-level clusters, we estimate the parameters. Details of the initialization are discussed in the supplementary materials, available at Biostatistics online.

E-step.

This step is a regular E-step in fitting mixtures of multivariate normals. We have posterior class probabilities given by

M-step.

In the M-step, we are dealing with the following maximization problem:

(2.2)

where W is the design matrix, β_kl = (α_k, γ_kl), and u_g = (x_g, y_g). (We provide explicit forms of the design matrices of the 3 parameterizations in the supplementary materials, available at Biostatistics online.) As discussed in Section 2.1, the main reason for a nonstandard mixture model M-step is due to the cross talk between the 2 levels. The first part of the parameter vector β_kl, denoted by α_k, is the same for all l, and similarly the left upper diagonal block Σ_k^X of Σ_kl. Hence, the corresponding estimates need to pool information across all second-level clusters of the kth first-level cluster. We use a regularized profiling method for maximizing the expected complete-data log-likelihood given in (2.2). Our general iterative scheme is to factorize the joint likelihood of x_g and y_g as the product of marginal likelihood of x_g and the conditional likelihood of y_g given x_g. We first maximize the marginal likelihood of x_g by profiling to obtain estimates of α_k and Σ_k^X. Given these estimates, we maximize the conditional likelihood of y_g given x_g, again by profiling over the mean and the variance–covariance matrix. We thus obtain estimates γ_kl and the second-level components of Σ_kl. The estimates of α_k and γ_kl are obtained via 2 weighted generalized least squares procedures. We provide details of these derivations, as well as computational considerations, in Section 2 of the supplementary materials, available at Biostatistics online.

PEM algorithm

1. E-step. Compute $\widehat{n}$_gkl, g = 1, …, G, k = 1, …, K and l = 1, …, L_k.

2. M-step.

• (a) Update $\widehat{\pi }$_kl, k = 1, …, K and l = 1, …, L_k.

• (b) M-step-Profile-1. (marginal x_g)

  • i. Update Σ_k^X.
  • ii. Update μ_k by reestimating $\widehat{a}$_k via weighted generalized least squares.
  • iii. Iterate (i) and (ii) till convergence. (c)
• (c). M-step-Profile-2. (conditional y_g|x_g)

  • i. Update conditional covariances and the mean Σ_kl^YX, Σ_kl^Y|X, Σ_kl^Y and μ_kl^Y|X.
  • ii. Update μ_kl by reestimating γ_kl via weighted generalized least squares and set $\widehat{\beta }$_kl = ($\widehat{\alpha }$_k, $\widehat{\gamma }$_kl)′.
  • iii. Iterate (i) and (ii) till convergence.

All the update states in the PEM algorithm are in closed form, which makes the implementation of the multilevel mixture free of black-box optimization. Although, the profiling steps could in principle benefit from internal iterations (iii above), it is in general more advantageous to spend the computing time on the outer EM iterations (1 and 2).

2.3. Model selection

Model selection in multilevel model-based clustering involves (1) selection of the appropriate parameterization for each cluster and (2) selection of the number of first-level clusters K and the number of (sub)clusters {L_k, k = 1, …, K}, ∀k.

Cluster parameterizations and subset selection.

Let us first consider the case with fixed K and {L_k, k = 1, …, K}, ∀k. We want to select a sparse representation for each cluster to enhance the objective interpretability of the clustering outcome. For example, is a particular cluster model representing (i) a static cell line difference or (ii) a dynamic one, and if so for which time points do the cell lines really differ?

Recently, several papers have appeared on the topic of variable selection for model-based clustering. These papers focus on the selection of a subset of variables or dimensions of the feature vector that can discriminate between cluster components (e.g. Friedman and Meulman, 2002; Law and others, 2004; Raftery and Dean, 2006; Hoff, 2006; Tadesse and others, 2005).

In our parameterization of the cluster means, we allow for cluster-specific descriptions of contrasts between variables “within” a cluster, as well as “between” clusters. For each cluster, we allow for a subset of “parameters” to be nonzero. The subset of coefficients that are set to 0 does not necessarily correspond to dimensions that are irrelevant for clustering. Take as an example parameterization I; if for cluster k, a subset of α_k are set to 0, then these dimensions are unrelated to the clustering; if, however, parameters γ_kl are set to 0, this implies that the cluster consists of a set of genes for which there is no cell line effect.

To perform cluster subset selection, we threshold the posterior probabilities η_gkl to obtain cluster-specific data sets of size n_kl for each subcluster {k, l} (or n_k for a first-level cluster k). For a first-level cluster, k, x_g = W_Kαk + ε, ε ∼ N(0, Σ_K^X) for the n_k genes g in the cluster. W_K and Σ_k^X refer to the first-level–specific partition of the design matrix and covariance matrix, respectively. After hard thresholding of the posterior probabilities, model selection for each cluster has thus been reduced to a model selection task in regression. We hold Σ_K fixed during the model selection. We select the subset of nonzero α_k parameters that minimize the BIC and thus obtain a cluster-specific model. Model selection for a second-level cluster proceeds in a similar fashion. Given the first-level parameters α_k and the first-level data x_g, we perform model selection in the regression setting for y_g|x_g. We identify a subset of nonzero second-level parameters, γ_kl, that minimize the BIC. A detailed discussion of the model selection can be found in Section 2.2.1 of the supplementary materials, available at Biostatistics online.

Selecting the number of clusters.

The selection of the number of clusters is usually based on criteria such as BIC, Cluster Information Criterion, or minimum description length (e.g. Fraley and Raftery, 2002; Raftery and Dean, 2006). Here, we will use BIC. Let us consider a multilevel parameterization, where the dimensionality of the data vectors at the first level is Dim(1) and at the second level is Dim(2). We denote the model coefficients at the first level by α_k, k = {1, …, K}, and the model coefficients at the second level by γ_kl, l_(k) = {1, …, L_k} for all k = {1, …, K}. The subcluster structure of the model is summarized by the vector L_K = {L_k, k = 1, …, K}.

In Section 2.3.1, we considered subset model selection for each cluster {k,l}. Thus, the number of nonzero coefficients α_k≠0 may be less than Dim(1), and similarly for γ_kl. We denote the number of nonzero coefficients at each cluster {k,l} by (dim(α_k), dim(γ_kl)). We gather all parameters into a set Θ(K,L_K) = {π_kl,α_k,γ_kl,Σ_kl,k = {1,…,K},l(k) = {1,…,L_k}}. Then, the total model complexity is given by

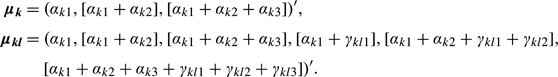where term (1) is the number of mean parameters estimated at the first and second levels, term (2) is the first-level covariance estimates, term (4) is the second-level covariance estimates and cross-covariance estimates between the first and second levels, and term (3) is the number of estimated cluster proportions. For each given K and L_K, we can compute the log-likelihood

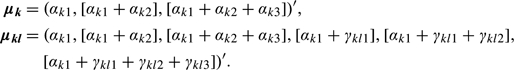We then compute the BIC value as

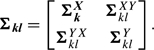The model space {K,L_K} is very large, and a complete search across all numbers of clusters and subcluster constellations is prohibitively expensive. We explored several different search strategies for identifying the optimal multilevel model. The best performance was obtained using a backward search. We thus searched over a total number of clusters M = ∑_kL_k, where for each M we considered a multilevel model with K = M,…,1 first-level clusters. We provide a complete outline of the model search in a flowchart in Section 2.2.2 of the supplementary materials, available at Biostatistics online.

For both subset selection and the selection of the number of clusters, we adopt greedy searches. While it is true that such schemes can converge to local optima, a fully exhaustive search is computationally prohibitive. To remedy the problem, we run the full algorithm several times while initiating from different starting values.

3. APPLICATION TO DATA

3.1. The proliferating cell line data

We apply the 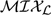model with subset selection to the data set of proliferating stem cell lines (Goff and others, 2007) introduced in Section 1. mRNA was extracted for array analysis at t = 0,1, and 3 days after the withdrawal of a growth factor from the medium (to speed up differentiation). The ABI system rat-chips, with 28 000 probes, were used for the array experiments. Of these probes, we studied a subset of 15 111 probes with complete annotation. We refer the reader to Section 3 of the supplementary materials, available at Biostatistics online, for a description of the preprocessing of these data. Preliminary significance analysis of the expression data identified 780 genes of the 15 111 as being differentially expressed between the cell lines and/or time points at false discover rate 1% (using the Welch F-test and the Benjamini–Hochberg p-value corrections). Similar results were obtained using the limma software of Smyth (2004). For each of the 780 selected genes, we computed the mean gene profile across replicates and standardized the mean profiles to have standard deviation 1, with a baseline of expression 0 for t = 0 in the glial-like population. The final data set to be analyzed is thus of dimension 780 by 5. We denote gene expression in the glial-like population (L2.3) by x, where Dim(x) is 2 (for t = 1 and t = 3). We denote the gene expression in the neuron-like population by y, where Dim(y) is 3 (t = 0,1, and 3).

3.2. Subset selection of cluster model profiles

We first investigate the impact of subset selection on clustering by fitting single-level models with the 3 parameterizations, W_I, W_II, and W_III, described in Section 2.

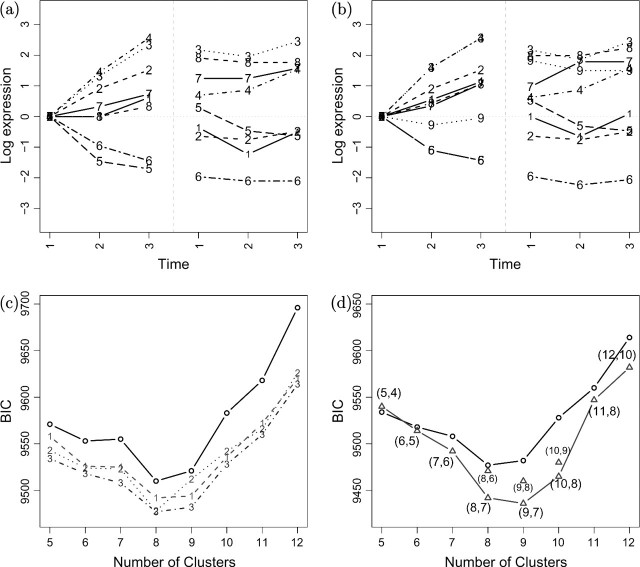
Figure 2(c) depicts the BIC curves obtained for various numbers of clusters K in a single-level fit (SF). The solid line is the BIC curve obtained without subset selection (i.e. a standard Gaussian mixture model). The dashed and dotted lines are annotated with “1”, “2”, and “3”, referring to the 3 parameterizations W_I,W_II, and W_III, respectively. Across all numbers of clusters, the W_III (cell fate preprogramming) parameterization provides the best fit, as indicated by the lower BIC values. The sparsity of each model is summarized in Table 1. With an efficient parameterization, K = 8 and K = 9 are equally competitive. The W_III parameterization identifies cluster profiles that are static between t = 0 and t = 1, indicating a later developmental activity in one or both cell lines (e.g. clusters 1, 8) (see Figure 2(a)). We focus on the most efficient parameterization (W_III) in Section 3.3.

Fig. 2.

(a) Cluster mean profiles of the best SF (K = 8). The glial-like population is depicted in the left panel, the neuron-like in the right panel (parameterization W_III). (b) Cluster mean profiles of the best MF K = 7, M = 9, with 2 sets of subclusters (parameterization W_III). (c) The BIC curves obtained using the SF. Solid line: no subset selection. Dashed and dotted curves annotated with the respective parameterization (W_I,W_II,W_III). The W_III–BIC curve is the lowest, indicating that the W_III parameterization is the most efficient for this data set. (d) The BIC curves obtained from the SF and MF, using the W_III parameterization. The MF always gives a lower BIC for the same total number of clusters (M). The numbers in the figures (M,K) refers to the total number of clusters and the number of first-level clusters, respectively. The best BIC values are obtained with M = 9 clusters in total and K = 7 first-level clusters.

Table 1.

Number of coefficients set to 0 by subset selection for the SF with the 3 parameterizations

K	WI: ∑k1 {βk = 0}	WII: ∑k1 {βk = 0}	WIII: ∑k1 {βk = 0}
5	2	5	7
6	6	4	7
7	4	4	7
8	2	5	5
9	3	6	6
10	5	7	9
11	5	7	7
12	6	8	10

3.3. Multilevel model-based clustering of the cell line study

In Figure 2(a), we depict the clustering outcome of an SF using parameterization W_III. As can be seen from the figure, the glial-like population exhibits larger time differential effects than the neuron-like population. Furthermore, for some clusters (e.g. clusters 3 and 4 at the top of the left panel of the figure), the glial-like cluster expression profiles almost coincide, whereas the neuron cluster profiles differ substantially. To identify neuron-specific variations, we will thus treat the glial-like population data as the first level in the 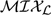model.

Figure 2(d) illustrates the additional efficiency of multilevel parameterizations. With the exception of the case with 5 total clusters, the multi-level fit (MF) always produces a lower BIC value. We select M = 9 clusters in total (cf. 8 clusters with the SF) and K = 7 first-level clusters. That is, we gain one more cluster. One can view this as a reallocation of model complexity. In model selection, we aim to balance the fit and model complexity (number of parameters). By setting some cluster parameters to 0 (within-cluster subset selection) and letting some clusters share parameters at the first level (between-cluster parameter constraints), we save on complexity and can “afford” to form another cluster. In Table 2, we summarize the results listing for each cluster the number of parameters set to 0 via subset selection, as well as the number of parameter constraints from the MF. For this data set, the larger gains are made when the number of clusters increases. For example, 11 out of 49 parameters were set to 0 (or constrained) in the (M = 11,K = 8) MF.

Table 2.

Number of coefficients set to 0 by subset selection for the SF and MF using parameterization W_III

Single level		Multilevel
K	∑k1 {βk = 0}	(M, K)	∑kl1 {βkl = 0}	Multilevel constraints
5	7	(5, 4)	5	2
6	7	(6, 5)	11	2
7	7	(7, 6)	2	2
8	5	(8, 7)	4	2
9	6	(9, 7)	4	4
10	9	(10, 8)	4	4
11	7	(11, 8)	11	6
12	10	(12, 10)	6	4

The cluster profile that is the most unique in the MF is cluster 9 (Figure 2(b) compared with (a)), which as we shall see in Section 5 provides some interesting insight into neuron-specific activity. In addition, we have identified 2 groups of gene clusters (3 and 4, 5 and 6) for which the glial-like population exhibits identical expression patterns and a subdivision of genes exhibit radically different expression patterns in neurons. Expression profiles of the 9 clusters generated by the 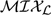fit are depicted in Supplementary Figure 1, available at Biostatistics online. Clusters 1–6 have an almost complete correspondence between the SF (Figure 2(a)) and the MF (Figure 2(b)). However, the multilevel model allows us to objectively state that clusters 3 and 4, as well as 5 and 6, constitute clusters for which there is a neuron-specific difference of expression only. Clusters 7–9 do not have clear counterparts among the single-level clusters.

3.4. Interpreting the clustering outcome

The 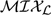model description allows for one extra cluster compared with the SF. In addition, 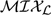provides a sparse representation for each cluster. Clusters 3 and 4, as well as clusters 5 and 6, form subclusters for which the expression pattern coincides in the glial-like population but differs in the neuron-like population. We used GOstat (Beissbarth and Speed, 2004) to identify the significant gene ontology (GO) categories for each of the 9 clusters. Tables 1–4 in the supplementary materials, available at Biostatistics online, report top 10 significant GO categories for the 9 clusters. Among all clusters (780 genes), developmental terms and neurogenesis are overrepresented compared with all annotated probes (15 111) on the array.

Cluster 9 was detected as a result of the efficient 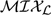parameterization and contains genes that are upregulated in neurons compared with glia at all times. Many of the top GO categories associated with this cluster are linked to phosphorus binding. Phosphor is an activator of brain-derived neurotrophic factor binding, a primary regulator of dendrite branching during neuron development.

Clusters 3 and 4 form one set of subclusters. The expression of the glia cell line is steadily increasing for both clusters. In the neuron cell line, cluster 3 represents genes with a steady high level of expression, whereas cluster 4 represents a profile of expression which increases over time. Genes in cluster 3 are associated with neuron development and axon formation. Genes in cluster 4 are linked with dendrite formation and growth. These subclusters thus appear to be related to different neuron-specific developmental processes.

Clusters 5 and 6 are another subcluster formation. The expression profile of the glia cell line is decreasing in both clusters. Genes in cluster 6 are persistently underexpressed in the neuron cell line, whereas genes in cluster 5 are overexpressed, compared with glia. Genes in cluster 6 (underexpressed in neurons) are primarily associated with acid synthesis. Glial cells are believed to synthesize some acids that assist in neuron development and migration. Cluster 5 (overexpressed in neurons) is associated with acid metabolism, which is one process by which neurons generate neurotransmitters.

The annotations of the 9 clusters are summarized in the supplementary materials, available at Biostatistics online. There, we also discuss several transcription factors detected by mining the genomic sequences of genes in the neuron-specific subclusters for regulatory motifs.

4. SIMULATION STUDIES

We use the estimated best SF and MF (see Section 3) to generate mixtures of multivariate normal data from realistic scenarios. We use the simulated data sets to validate (a) selection of the number of (sub)clusters and (b) subset model selection for each cluster. The best single-level model is referred to as Mod(1) and the best multilevel model as Mod(2).

Mod(1) is a single-level model with K = 8 clusters. The cluster means for this model are depicted in Figure 2(a). The cluster means are parameterized with 5 × 8 coefficients, and 5 parameters were set to 0 by subset selection. Mod(2) is the multilevel model with M = 9 clusters and K = 7 first-level clusters. Four parameters were set to 0 by the subset selection, and 4 parameters constrained by the multilevel structure of the model (see Table 2). We generate 50 simulated data sets (of the same dimensions as the original data) each from Mod(1) and Mod(2). We then fit single- and multi-level models and perform cluster subset model selection. For each simulated data set, we record the selected number of (sub)clusters. We also compare the selected subset model (for the true number of clusters) to the true model and record the total number of selection errors (the number of coefficients erroneously set to 0 or nonzero).

In Table 3, we summarize the results (see also Supplementary Figure 3 available at Biostatistics online). Cluster subset selection always produces a better model in terms of the BIC validation index (Supplementary Figure 3(a) available at Biostatistics online). In addition, an MF always reduces the BIC compared with an SF when a multilevel structure is truly present (Mod(2)) and produces comparable results with an SF when a single-level structure is true (Mod(1)) (see Supplementary Figure 3(c) and (d) available at Biostatistics online). The subset selection performance is highly satisfactory (Supplementary Figure 3(b) available at Biostatistics online), that is, the generative subset model is often correctly identified. The multilevel approach produces subset selection results closer to the correct subset model, compared with the single-level approach. This is because selection is undertaken separately for the first- and second-level clusters (see supplementary materials available at Biostatistics online).

Table 3.

Top panel: the percent of times a number (M, K) of clusters are selected with the SF and MF for the Mod(1) data. The correct K = 8. Both fitting strategies perform well, and the MF correctly identifies an SF (bold face in table) in almost all cases. Lower panel: the percent of times a number (M, K) of clusters are selected with the SF and MF for the Mod(2) data. The correct M = 9, with 7 first-level clusters (K = 7). In almost all cases, the MF correctly identifies a subcluster structure (bold face in table), rather than single-level model

	SF(Mod 1)	MF(Mod 1)
	K = M	K = 7	K = 8	K = 9
M = 8	88	2	86
M = 9	12	0	4	8

	SF(Mod 2)	MF(Mod 2)
	K = M	K = 6	K = 7	K = 8	K = 9	K = 10
M = 7	2	2	0
M = 8	14	4	6	2
M = 9	30	0	14	16	4
M = 10	54	0	4	14	22	12

In Table 3, we present the selected number of clusters for the Mod(1) and Mod(2) data sets, using the SF and MF. In the case of Mod(1) data, the MF in almost all cases identifies the SF as the correct model structure. In the case of Mod(2) data, the MF in almost all cases identifies an MF (with subclusters) as the correct model structure. In the case of Mod(2), both fitting strategies have trouble identifying the correct total number of clusters. The reason for this is that cluster 7 in Mod(2) is sparsely populated. In some simulations, cluster 7 is split into 2 clusters, producing a total of M = 10 clusters. Sometimes “genes” in cluster 7 are simply allocated to nearby clusters, producing a total of M = 8 clusters.

In summary, the MF can correctly identify a single-level model as well as a multilevel model. In addition, the BIC is much reduced if the multilevel structure of the data is accounted for. Subset selection also reduces the BIC, in both single-level and multilevel models. Our simulations thus illustrate the benefits of sparse multilevel representations of cluster profiles in model-based clustering.

5. DISCUSSION

We propose a mixture model with multiple levels to more efficiently model multiple-factor experimental data. In addition, we introduce a subset selection method to generate sparse representations of cluster profiles, under various parameterizations. We illustrate on real and simulated data that sparse multilevel mixture models can substantially improve the fit, significantly reducing the BIC, compared with standard mixture models. We show that our multilevel mixture modeling approach with subset selection can correctly identify both single-level and multilevel data structures. Furthermore, in our simulation setting, we show that the subset selection procedure is highly accurate.

Our multilevel approach identifies interesting and biologically relevant groups of genes in the proliferating cell line data. A more thorough study of our findings is now underway in collaboration with biologists at Rutgers University. We stress that the findings we presented in this paper are preliminary. A small perturbation study, where we randomly altered 5% of the selected gene list, did provide clustering results that substantially overlapped with the original outcome (IQR 84–98% concordance). However, as additional data become available we expect that other cluster structures may be detected.

Efficient cluster model representations (multiple levels and subset selection) will have a larger impact in high-dimensional settings, for example, time-course data with more time points. It is in these cases that a multilevel approach with subset selection has the largest potential to substantially reduce the number of parameters in the model. In addition, while we did not consider efficient representations of the cluster covariances, this is another area in which modeling efficiency may be explored. Fraley and Raftery (2002) compared mixture models with parameterized cluster covariances. Incorporating covariance parameterization and subset selection into our multilevel approach is an interesting future research topic.

While we demonstrated our multilevel approach on a proliferating cell line data, with a 2-level factor of interest, the method can in theory be extended to more factors and factors with more levels. Let us consider the case where we have a 3-level factor of interest (e.g. 3 cell lines) and denote the specific data sets by x_g,y_g, and v_g, respectively. The most simple extension is to use one of the cell lines as reference, for example, x_g. At the second level of the modeling hierarchy, we thus model contrasts with respect to the reference: y_g, v_g|x_g. This approach is quite reasonable in experiments involving multiple species or strains, where a “wild-type” or reference strain constitutes a natural basis for comparison. In other experiments, a modeling hierarchy is induced by ordering the factor levels. Thus, the first modeling hierarchy models x_g, the second level models y_g|x_g, and the third level involves v_g|x_g, y_g. The modeling structure at the third level is of the same mathematical form as the second level, so falls under the 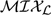framework we presented in the paper. The generalization of the 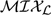model requires the selection of the optimal assignment of the factor levels to the levels of the modeling hierarchy. This constitutes an interesting research problem we plan to explore in the future.

The R implementation of the 2-level 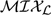model is available from the corresponding author upon request.

FUNDING

National Science Foundation (DMS0306360) and USEPA-funded Environmental Bioinformatics and Computational Toxicology Center (GAD R 832721-010) to R.J.; Wisconsin Alumni Research Foundation (University of Wisconsin, Madison) and National Institutes of Health (1-R01-H603747-01) to S.K.