Abstract
We conducted a prospective study of 18 adult volunteers (male-to-female ratio of 1) whose body mass index fell into categories of <25, 25 to 40, or >40 kg/m2, who received a single oral dose of 1,600 mg ethambutol. Only individuals with normal renal function were recruited. The minimum body mass (M) was 45.6 kg, the median was 90.8 kg, and the maximum weight was 160.4 kg. Ethambutol pharmacokinetics were best described by a two-compartment model. Inclusion of weight as a covariate dramatically improved the model, with a relative likelihood approaching infinity. The typical clearance was 42.6 liters/h. Ethambutol systemic clearance was proportional to (M/45.6)3/4 and thus obeyed fractal geometry-based laws. This means that the area under the concentration-time curve (AUC) actually decreased for obese patients compared to that for leaner patients, reducing chances of concentration-dependent toxicity. On the other hand, such reduced AUCs could lead to therapy failure. Thus, new and individualized ethambutol dosing regimens need to be designed for obese and extremely obese patients.
INTRODUCTION
Mycobacterial diseases remain a significant cause of morbidity and mortality worldwide. Tuberculosis (TB) is responsible for approximately two million deaths per year. TB has historically been regarded as a thin man's disease. Yet in our studies in Texas, a considerable proportion of the patients have been overweight and obese (33, 34). In addition, other studies have demonstrated that patients with diabetes mellitus, who are often overweight as part of metabolic syndrome, are at an increased risk of developing active pulmonary TB (20, 30). This is a problem given that the “average” American's weight has increased by 10 kg in the last 4 decades, so that 2 in every 3 Americans are now overweight (body mass index [BMI] ≥ 25 kg/m2), 1 in 3 are obese (BMI ≥ 30 kg/m2), and 6% are morbidly obese (BMI ≥ 40 kg/m2) (10, 32). In high-burden TB countries in southern Africa and South America, obesity has also become a major problem, rivaling even that in the United States, with considerable proportions of overweight/obese people and underweight/malnourished people coexisting within the same populations (9, 23). In Egypt, for example, obesity rates among women are >45%, while in the Pacific Islands of Samoa and Tonga they are 60 to 70% (39). Approximately 1.3 billion out of the 6 billion humans are at least overweight, so clearly the entire species is becoming obese (31). This is a major challenge, given that anti-TB dosing regimens were designed decades ago for an underweight population of patients with “consumption.”
Body mass (M) or weight is a physical phenomenon. Physical phenomena occur on a large range of scales. As an example, the mass of living things can vary from about ∼6 × 10−16 kg for a bacterium to ∼6 × 104 kg for a sperm whale, a span of 1020. Scaling biochemical relationships using linear relationships across such a large span is often inaccurate. Second, the shapes of most natural objects, such as human organs, trees, mountains, and galaxies, do not follow smooth Euclidean geometrical shapes, such as parallelograms and cubes. The human heart, for example, is not a sphere, and the brain is not a cube. The roughness and true exact shape of anatomical shapes of living things, such as leaves, tree trunks, blood vessels, and kidneys, are a result of maximization of energy and metabolite transfer by evolution. Third, many of these rough shapes, from snowflakes to human anatomical shapes, demonstrate a recursive pattern, since dimensions change over the large dimension spans discussed above. Examples are branching of the cardiovascular system from the aorta through the capillaries and back or bronchi and bronchioles, essential for delivery of oxygen and metabolites. Fourth, such shapes can have dimensions that are fractions. Fractal geometry explains relationships across such large scales of dimensions, across recursive scaling patterns, and across nonregular (rough) shapes (27, 28). In the late 1930s, it was observed that metabolic rates of different animal species across a large span of M were proportional to M3/4 (21, 22). Recent work has demonstrated that this “3/4 power law” applies to metabolism of all organisms and is due to fractal geometry constraints: in other words, 3/4 is dimension that scales metabolic rate to mass (43, 44). Recent work by us and others has demonstrated that the between-patient systemic clearance (SCL) of echinocandins also obeys this rule within the human species alone, even over a span of weight with only 4-fold variation (16, 17, 19). Here we investigated if this was also true in the case of ethambutol in obese persons.
Ethambutol continues to be a mainstay of first-line treatment in patients with active TB (4). TB is a global problem, affecting 12 million people per year, and will thus be diagnosed in patients with weight that varies over a wide span. Moreover, ethambutol is also a vital part of first-line treatment for patients with Mycobacterium avium complex (MAC). MAC affects approximately 3,000 persons per year in the United States and has a treatment failure rate of 40 to 60% (11–14, 40, 41). In addition, several pathogenic Mycobacterium species are also susceptible to ethambutol, including M. kansasii, M. gordonae, M. marinum, M. scrofulaceum, and M. szulgai (15). Thus, ethambutol is a broad antimycobacterial agent with uses beyond treatment of TB.
We have demonstrated that microbial killing by ethambutol is concentration dependent while resistance suppression best correlates with the percentage of the dosing interval in which the drug concentration is above the MIC (TMIC) (8, 36). Since the 24-h area under the concentration-time curve (AUC0–24) is inversely proportional to SCL, and TMIC decreases with faster SCL, between-patient variability of SCL will alter both microbial kill and resistance suppression. This is a crucial factor, given that we have recently demonstrated that low drug exposures due to pharmacokinetic variability are a more important cause of multidrug-resistant (MDR) TB emergence than directly observed therapy (37). Thus, it is crucial to determine if between-patient ethambutol variability is due to differences in weight and thus provide a pathway for designing optimal ethambutol dosing in obese patients.
(This work was presented in part at the 50th Interscience Conference on Antimicrobial Agents and Chemotherapy [abstract no. A1-058] and the 3rd International Workshop on Clinical Pharmacology of Tuberculosis Drugs.)
MATERIALS AND METHODS
Regulatory compliance.
The study was approved by the Institutional Review Boards (IRB) of the Texas Tech University Health Sciences Center (A09-3545) and University of Texas Southwestern Medical Center at Dallas (082009-009). The study protocol was registered at www.clinicaltrials.gov (NTC01048697) prior to enrollment of the first volunteer.
Study population.
Volunteers were recruited to the Clinical Trials Research Center (CTRC) at UT Southwestern Medical Center between January 2010 and December 2010. Volunteers were eligible for study participation if they were at least 18 years of age and able to provide written informed consent. Exclusion criteria were as follows: creatinine clearance of <70 ml/min as estimated by the Cockcroft-Gault equation (6), pregnant or nursing mothers, women unwilling to use a reliable contraception method during the study, a history of gout, a history of an allergy to ethambutol, any other medical contraindication for ethambutol, and abnormal liver function tests. Abnormal liver function test results were defined as either transaminases at >10 times the upper limit of normal, alkaline phosphatase at >5 times the upper limit of normal, or total bilirubin at >5 times the upper limit of normal.
Experimental design.
The study was designed to recruit a total of 18 volunteers into the following body mass index (BMI) categories: <25 kg/m2 (normal weight; n = 6), 25 to 39.9 kg/m2 (overweight and class I/II obese; n = 6), and ≥40 kg/m2 (class III obese; n = 6). Half of the volunteers recruited into each BMI group were to be male.
Study and sampling procedures.
Volunteers received ethambutol (1,600 mg orally) as a single fasting dose. Blood draws were performed through an intravenous catheter, which was flushed between blood draws. Each volunteer had 10 ml of blood drawn at each of the seven time points: t = 0 h (predose) and 2, 6, 11, 18, and 24 h following ethambutol administration. This sampling scheme was based on the α and β half-lives of ethambutol in previous studies (24, 25, 35, 46). The blood was spun down for serum separation, and the serum was stored at −80°C until transport for measurement of the ethambutol concentration. Volunteers had vitals performed prior to study drug administration, as well as 0.5, 1, 2, and 24 h after ethambutol administration. Blood was also collected at discharge for a complete blood count and comprehensive metabolic panel.
Subject safety and data monitoring.
Any serious adverse events were to be reported to the IRB within 24 h. All three investigators (R.G.H., M.A.S., and T.G.) met with the study coordinators for routine data safety monitoring before submitting the study for continuing review to the IRB.
Statistical analysis.
Continuous variables were not assumed to be normally distributed. Therefore, the Mann-Whitney U test was utilized to assess if body weight or dose (mg/kg of body weight) was significantly different based on gender using the GraphPad Prism software program (version 5.04; GraphPad Software).
Ethambutol analysis.
Drug concentrations were determined at the Texas Tech University Health Sciences Center Pediatric Pharmacology Research and Development Center. Ethambutol concentrations were measured using a Shimadzu high-performance liquid chromatography (HPLC) system interfaced with a tandem, triple-quadrupole mass spectrometer (API 3000; AB Sciex). Equal volumes (100 μl) of serum and internal standard (clarithromycin) were extracted using 3.5 ml ethyl acetate and 4 M NaOH (100 μl). The organic phase was evaporated and reconstituted with 200 μl of 0.3% formic acid in water for injection. Following injection (20 μl), chromatographic separation was performed using an Inertsil 5-μm (50 by 2.1 mm) column with isocratic elution of 0.1% formic acid in water: 0.1% formic acid in methanol (50:50) at 0.2 ml/min (40°C). Ethambutol and internal standard were analyzed using positive electrospray ionization combined with multiple reaction monitoring and the respective precursor → product ion combinations of 205.10 → 116.0 and 748.50 → 590.30 m/z. The standard curve was linear (r = 0.998) and ranged from 0.040 μg/ml to 8 μg/ml. Intra- and interday precision were equivalent and were less than 5% relative square deviation (RSD) throughout the validated range of concentrations.
Pharmacokinetic analysis.
Ethambutol concentrations were modeled using the ADAPT 5 software program of D'Argenio and colleagues (7). The strategy that was used included generating initial pharmacokinetic parameters using the standard two-stage estimation method for a one-, two-, and three-compartment model. The parameters were then used as initial estimates in the POPINIT subroutine of ADAPT. Thereafter, population parameter estimates for a one-, two-, and three-compartment model were identified using the maximum-likelihood solution via the expectation-maximization algorithm (MLEM). The best model was then chosen using both Akaike's information criterion (AIC), the Bayesian (Schwarz) information criterion (BIC), and log likelihoods (1, 26). The relative likelihood (or evidence ratio) that one model, compared to another, best explained the data was calculated as follows: relative likelihood = 1/(e−0.5 × ΔAIC), where ΔAIC is the difference between AIC scores of the two models being compared.
The chosen model constituted the base model. The relationship between each pharmacokinetic parameter and either creatinine clearance, body mass, gender, or age was examined in scatter plots, and an initial estimate of the slope was determined, which together with these covariates was then entered into the COVMOD subroutine of ADAPT. The relationship between pharmacokinetic and covariate parameters was then further examined with MLEM. The model that included body mass, or each of the other covariates, was then compared to the base model using AIC, BIC, and log likelihoods. Our report follows recommendations by the FDA (5).
RESULTS
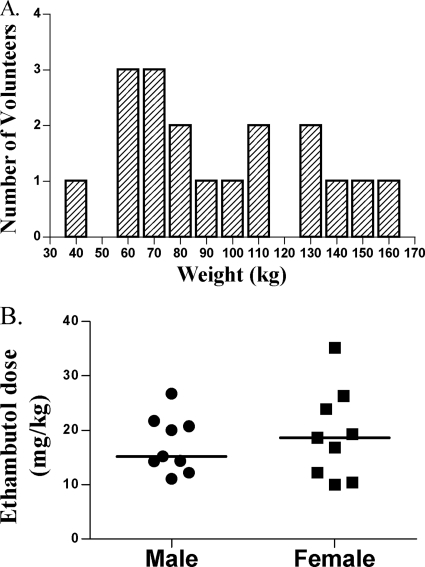
The average age of the 18 people who completed the study was 36.6 ± 11.3 years. Half of the volunteers were male. The study population consisted of 11 Caucasian-Americans, 6 African-Americans, and one Asian-American. Half of the volunteers had chronic comorbid conditions, with 39% taking medications and 17% having one or more components of the metabolic syndrome. The mean and median serum creatinine levels were 0.92 and 0.88 mg/dl, respectively (range, 0.63 to 1.37 mg/dl). The weight distribution in the volunteers is shown in Fig. 1A. The minimum weight was 45.6 kg, the median was 90.8 kg, and the maximum weight was 160.4 kg. The median weight for men was 105 kg, versus 86.2 kg for women (P = 0.93, Mann-Whitney U test). The distribution of ethambutol dose in mg/kg is shown in Fig. 1B. Women received an 18.56-mg/kg dose, versus a 15.22-mg/kg dose in men (P = 0.96, Mann-Whitney U test).
Fig 1.
Weight distribution in people recruited into the ethambutol study. (A) The recruitment was meant to capture all extremes of weight, and thus the weight is not normally distributed. (B) Distribution of ethambutol dosing indexed to weight (mg/kg) by gender.
Overall, the ethambutol dose was well tolerated by the volunteers. One volunteer developed a nosebleed after the ethambutol was administered; this was judged to be unrelated to the ethambutol dose. The nosebleed was not considered serious and resolved without medical intervention. No volunteer complained of symptoms suggestive of a loss of visual acuity, color vision, or visual field problems.
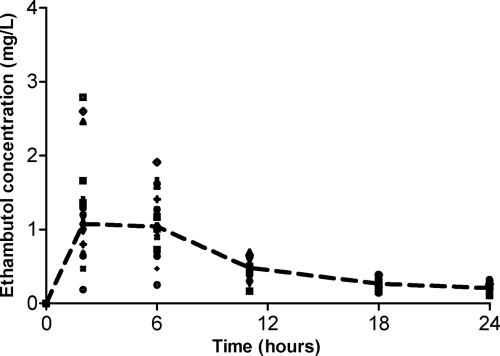
There were 108 serum samples that were analyzed, which revealed concentrations shown in Fig. 2. The ratio of the highest peak concentration to the lowest was 7.26. The ratio of the highest trough concentration to the lowest was 3.38. The population pharmacokinetics of ethambutol were best described by a two-compartment model, best on scores for all three criteria used for model selection, as shown in Table 1. To put this in the context of relative likelihood (RL), the RL that a two-compartment model explained the data better than a three-compartment model was 2 × 1017, while the RL compared to a one-compartment model approached infinity. Figure 3 demonstrates the observed-versus-predicted concentration plots for the two-compartment base model. Table 2 shows the ethambutol pharmacokinetic parameter estimates in the base model. The α-half-life was 2.13 ± 0.92 h, and the β-half-life was 24.4 ± 7.44 h. The results shown in Table 2 are consistent with those of prior studies at steady-state ethambutol concentrations in TB patients (29, 46).
Fig 2.
Concentrations of ethambutol (mg/liter) achieved after administration of a single dose of ethambutol. This line is the median concentration using naive pooling and demonstrates a biphasic decline consistent with a two-compartment model. The circles represent volunteers with a body mass index classified as normal weight.
Table 1.
Model comparison for several ethambutol compartmental modelsa
| Method of assessment | Value for model |
|||
|---|---|---|---|---|
| One-compartment | Two-compartment | Three-compartment | Two-compartment with wt as covariate | |
| AIC | −1,543.41 | −3,831.76 | −3,751.95 | −5,684.56 |
| BIC | −1,522.03 | −3,799.69 | −3,714.53 | −5,652.49 |
| Log likelihood | −1,559.41 | −3,885.76 | −3,779.95 | −5,708.56 |
AIC, Akaike's information criterion; BIC, Bayesian (Schwarz) information criterion; wt, wild type.
Fig 3.
Observed versus predicted concentrations of ethambutol in the base model. Concentrations are in mg/liter.
Table 2.
Ethambutol pharmacokinetic parameter estimates in base model
| Parametera | Estimate | SD | % RSE |
|---|---|---|---|
| CLt (liters · h−1) | 78.2 | 21.2 | 39.9 |
| CLd (liters · h−1) | 82.7 | 15.8 | 35.6 |
| Vc (liters) | 446 | 258 | 83.6 |
| Vp (liters) | 925 | 226 | 87.5 |
| Ka (h−1) | 0.52 | 0.10 | 81.6 |
CLt, total clearance; CLd, clearance from peripheral compartment; Ka, absorption rate constant; Vc, volume of central compartment; Vp, volume of peripheral compartment.
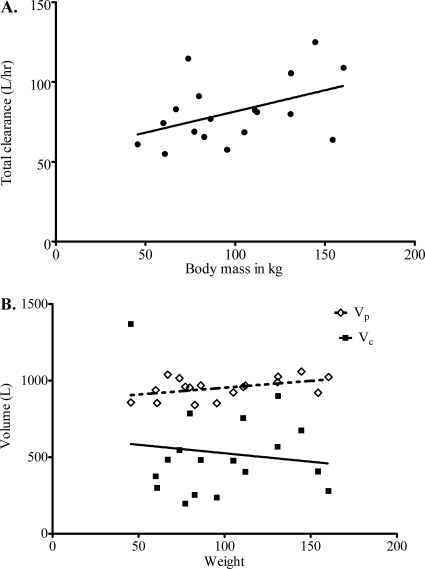
There was no obvious relationship between age, gender, or creatinine clearance and any pharmacokinetic parameter. In addition, when BMI was used, the highest r2 value was only 0.15, which was in relation to the volume of the peripheral compartment (Vp). However, the relationship between body mass (weight) and either SCL or volume is shown in Fig. 4. Inclusion of patient body mass as a covariate in MLEM led to AIC, BIC, and −2 negative log likelihoods shown in Table 1. These data demonstrate a remarkable improvement in all three scores when weight is included as a covariate. The RL for choosing the two-compartment model that includes weight as a covariate compared to the base model approached infinity. The relationship between body mass (M) and SCL was given by the fractal relationship: SCL = 42.6 × (M/45.6)3/4, with a percent relative standard error (RSE) of 36.9%. The final pharmacokinetic parameter estimates in this model are shown in Table 3.
Fig 4.
Effect of mass (kg) on ethambutol pharmacokinetic parameters. (A) Weight versus systemic clearance. (B) Weight versus volume of distribution. Vp is represented by open diamonds; Vc is represented by filled squares.
Table 3.
Pharmacokinetic parameter estimates in final model
| Parametera | Mean | SD | % RSE |
|---|---|---|---|
| Ka (h−1) | 0.573 | 0.100 | 112 |
| Vc (liters) | 491 | 283 | 99.7 |
| CLd (liters · h−1) | 80.8 | 18.6 | 67.1 |
| Vp (liters) | 1070 | 181 | 93.2 |
See footnote a of Table 2.
DISCUSSION
The fact that all regulatory and drug-licensing bodies in the world have yet to prioritize the inclusion of overweight and obese persons in phase I and II studies is surprising given that the human species has now become obese. As a result, few studies are available to provide the insight required for dose individualization for this patient population where many drugs will most commonly be used. Here, we prove that ethambutol SCL in obese and extremely obese people obeys the 3/4 power law, a consequence of fractal geometry (22, 28, 42–44). In this study, this law applied only to weight and not to BMI. This presumably means that height and area do not significantly impact ethambutol pharmacokinetics. The physiological reasons as to why ethambutol SCL increases with weight are as yet unclear. Approximately 80% of ethambutol is renally excreted as unchanged drug, while 20% is converted to metabolites by alcohol dehydrogenase (ADH) (15). We did not observe creatinine clearance to be a significant covariate with any of the pharmacokinetic parameters of ethambutol. An alternative explanation may be that the metabolism of ethambutol by ADH is increased as body weight increases. A recent study documented an increased expression of ADH in patients with obesity-related nonalcoholic steatohepatitis compared to results for controls (3). Therefore, an increase in ADH could conceivably explain increased ethambutol SCL with weight. However, the data on metabolism of ethambutol by ADH and renal excretion are old, so that the disposition of this drug warrants newer studies.
Recently, we demonstrated that increased patient weight has a profound influence on failure of anti-TB therapy (33, 34). We have proposed that between-individual pharmacokinetic variability of anti-TB drugs is the major culprit behind therapy failure and the emergence of MDR TB (37). Since weight is a significant covariate of ethambutol SCL, there will be a decreased likelihood of achieving the AUC0–24/MIC ratio and TMIC ratios associated with optimal microbial killing, and suppression of resistance is a potential reason for an increased risk of anti-TB treatment failure in overweight and obese persons (38). This concern is particularly highlighted given that the CDC and WHO guidelines for all orally administered first-line anti-TB drugs are based on ideal body weight and mandate capping ethambutol doses at 1,600 mg a day regardless of weight (4, 45). Similarly, for disseminated MAC, the peak concentration (Cmax)-to-MIC ratio has been demonstrated to optimize killing, with a serum 90% effective concentration (EC90) of 1.23 (8). Eighty-three percent of volunteers achieved a Cmax of <2 mg/liter. Since 90% of clinical isolates have MICs of ≥1 mg/liter, it means most patients (>90%) will achieve a Cmax/MIC well below the EC90 (8). On the other hand, our findings of increased ethambutol clearance in heavier persons appear to contradict the speculation of a recent case series suggesting that obesity increases the risk of optic neuropathy (2, 18). However, further study is required to validate the clinical significance of this finding.
Our study has several limitations. The study population received a single dose of ethambutol, and concentrations measured were not steady-state concentrations. Second, in many situations the disease being treated may alter the pharmacokinetic parameter estimates. Nevertheless, the pharmacokinetic parameter estimates in our base model did not differ from those based on steady-state concentration identified by others in patients with active TB. Finally, we did not examine disposition routes, and thus the physiological mechanisms behind increased ethambutol clearance in heaver patients remain unknown.
In conclusion, the relationship derived in this study should help optimize ethambutol dosing for obese patients in the future. Microbial killing by ethambutol for M. tuberculosis is linked to AUC/MIC, while suppression of resistance is linked to TMIC. This means that an increased SCL in obese patients has the potential to affect the efficacy of the drug for obese TB patients around the world. Development of a clinically useful dosing regimen that accounts for the increased variability introduced by body weight is the next step needed to provide dose individualization for overweight and obese patients.
ACKNOWLEDGMENTS
R.G.H.'s time was supported by grant KL2RR024983 to UT Southwestern Medical Center from the NCRR/NIH. Recruitment, admission of volunteers for the study, and collection of blood samples were performed by UT Southwestern Medical Center's Clinical and Translational Research Center personnel within the center, which is supported by the NIH CTSA grant UL1 RR024982.
Footnotes
Published ahead of print 12 December 2011
REFERENCES
- 1. Akaike H. 1974. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19:716–723 [Google Scholar]
- 2. Alffenaar JW, van der Werf TS. 2010. Dosing ethambutol in obese patients. Antimicrob. Agents Chemother. 54:4044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Baker SS, Baker RD, Liu W, Nowak NJ, Zhu L. 2010. Role of alcohol metabolism in non-alcoholic steatohepatitis. PLoS One 5:e9570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Blumberg HM, et al. 2003. American Thoracic Society/Centers for Disease Control and Prevention/Infectious Diseases Society of America: treatment of tuberculosis. Am. J. Respir. Crit. Care Med. 167:603–662 [DOI] [PubMed] [Google Scholar]
- 5. Center for Drug Evaluation Research 1999. Guidance for industry. Population pharmacokinetics. CP 1 Food and Drug Administration, Rockville, MD [Google Scholar]
- 6. Cockcroft DW, Gault MH. 1976. Prediction of creatinine clearance from serum creatinine. Nephron 16:31–41 [DOI] [PubMed] [Google Scholar]
- 7. D'Argenio DZ, Schumitzky A, Wang X. 2009. ADAPT 5 user's guide: pharmacokinetic/pharmacodynamic systems analysis software. Biomedical Simulations Resource, Los Angeles, CA [Google Scholar]
- 8. Deshpande D, Srivastava S, Meek C, Leff R, Gumbo T. 2010. Ethambutol optimal clinical dose and susceptibility breakpoint identification by use of a novel pharmacokinetic-pharmacodynamic model of disseminated intracellular Mycobacterium avium. Antimicrob. Agents Chemother. 54:1728–1733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Filozof C, Gonzalez C, Sereday M, Mazza C, Braguinsky J. 2001. Obesity prevalence and trends in Latin-American countries. Obes. Rev. 2:99–106 [DOI] [PubMed] [Google Scholar]
- 10. Flegal KM, Carroll MD, Ogden CL, Curtin LR. 2010. Prevalence and trends in obesity among US adults, 1999–2008. JAMA 303:235–241 [DOI] [PubMed] [Google Scholar]
- 11. Griffith DE. 2007. Therapy of nontuberculous mycobacterial disease. Curr. Opin. Infect. Dis. 20:198–203 [DOI] [PubMed] [Google Scholar]
- 12. Griffith DE, et al. 2007. An official ATS/IDSA statement: diagnosis, treatment, and prevention of nontuberculous mycobacterial diseases. Am. J. Respir. Crit. Care Med. 175:367–416 [DOI] [PubMed] [Google Scholar]
- 13. Griffith DE, Brown BA, Cegielski P, Murphy DT, Wallace RJ., Jr 2000. Early results (at 6 months) with intermittent clarithromycin-including regimens for lung disease due to Mycobacterium avium complex. Clin. Infect. Dis. 30:288–292 [DOI] [PubMed] [Google Scholar]
- 14. Griffith DE, et al. 2005. Ethambutol ocular toxicity in treatment regimens for Mycobacterium avium complex lung disease. Am. J. Respir. Crit. Care Med. 172:250–253 [DOI] [PubMed] [Google Scholar]
- 15. Gumbo T. 2010. Chemotherapy of tuberculosis, Mycobacterium avium complex disease, and leprosy, p 1549–1570 In Brunton LL, Chabner B, Knollmann B. (ed), Goodman & Gilman's The pharmacological basis of therapeutics, 12th ed McGraw Hill Medical, New York, NY [Google Scholar]
- 16. Gumbo T, et al. 2008. Population pharmacokinetics of micafungin in adult patients. Diagn. Microbiol. Infect. Dis. 60:329–331 [DOI] [PubMed] [Google Scholar]
- 17. Hall RG, Swancutt MA, Gumbo T. 2011. Fractal geometry and the pharmacometrics of micafungin in overweight, obese, and extremely obese people. Antimicrob. Agents Chemother. 55:5107–5112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Hasenbosch RE, et al. 2008. Ethambutol-induced optical neuropathy: risk of overdosing in obese subjects. Int. J. Tuberc. Lung Dis. 12:967–971 [PubMed] [Google Scholar]
- 19. Hope WW, et al. 2007. Population pharmacokinetics of micafungin in pediatric patients and implications for antifungal dosing. Antimicrob. Agents Chemother. 51:3714–3719 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Jeon CY, Murray MB. 2008. Diabetes mellitus increases the risk of active tuberculosis: a systematic review of 13 observational studies. PLoS. Med. 5:e152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Kleiber M. 1932. Body size and metabolism. Hilgardia 6:315–353 [Google Scholar]
- 22. Kleiber M. 1947. Body size and metabolic rate. Physiol. Rev. 27:511–541 [DOI] [PubMed] [Google Scholar]
- 23. Kruger HS, Puoane T, Senekal M, van der Merwe MT. 2005. Obesity in South Africa: challenges for government and health professionals. Public Health Nutr. 8:491–500 [DOI] [PubMed] [Google Scholar]
- 24. Lee CS, Brater DC, Gambertoglio JG, Benet LZ. 1980. Disposition kinetics of ethambutol in man. J. Pharmacokinet. Biopharm. 8:335–346 [DOI] [PubMed] [Google Scholar]
- 25. Lee CS, Gambertoglio JG, Brater DC, Benet LZ. 1977. Kinetics of oral ethambutol in the normal subject. Clin. Pharmacol. Ther. 22:615–621 [DOI] [PubMed] [Google Scholar]
- 26. Ludden TM, Beal SL, Sheiner LB. 1994. Comparison of the Akaike information criterion, the Schwarz criterion and the F test as guides to model selection. J. Pharmacokinet. Biopharm. 22:431–445 [DOI] [PubMed] [Google Scholar]
- 27. Mandelbrot B. 1967. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 156:636–638 [DOI] [PubMed] [Google Scholar]
- 28. Mandelbrot BB. 1982. The fractal geometry of nature. W.H. Freeman and Company, San Francisco, CA [Google Scholar]
- 29. McIlleron H, et al. 2006. Determinants of rifampin, isoniazid, pyrazinamide, and ethambutol pharmacokinetics in a cohort of tuberculosis patients. Antimicrob. Agents Chemother. 50:1170–1177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Nijland HM, et al. 2006. Exposure to rifampicin is strongly reduced in patients with tuberculosis and type 2 diabetes. Clin. Infect. Dis. 43:848–854 [DOI] [PubMed] [Google Scholar]
- 31. Obesity Task Force 25 October2005. Global strategy on diet, physical activity and health: obesity and overweight. World Health Organization, Geneva, Switzerland: http://www.who.int/hpr/NPH/docs/gs_obesity.pdf [Google Scholar]
- 32. Ogden CL, Fryar CD, Carroll MD, Flegal KM. 2004. Mean body weight, height, and body mass index, United States 1960–2002. Advance data from vital and health statistics; no. 347. National Center for Health Statistics, Hyattsville, MD: [PubMed] [Google Scholar]
- 33. Pasipanodya JG, Hall R, Weis S, Gumbo T. 2009. Fat, fractals, and failure of antituberculosis pharmacotherapy. Abstr. 49th Intersci. Conf. Antimicrob. Agents Chemother., abstr L1-1660 [Google Scholar]
- 34. Pasipanodya JG, Weis S, Gumbo T. 2010. Weight not diabetes mellitus predicts failure of anti-tuberculosis therapy in treated tuberculosis patients with concurrent diabetes mellitus. Abstr. 50th Intersci. Conf. Antimicrob. Agents Chemother., abstr A1-059 [Google Scholar]
- 35. Peloquin CA, et al. 1999. Pharmacokinetics of ethambutol under fasting conditions, with food, and with antacids. Antimicrob. Agents Chemother. 43:568–572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Srivastava S, et al. 2010. Efflux-pump-derived multiple drug resistance to ethambutol monotherapy in Mycobacterium tuberculosis and the pharmacokinetics and pharmacodynamics of ethambutol. J. Infect. Dis. 201:1225–1231 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Srivastava S, Pasipanodya JG, Meek C, Leff R, Gumbo T. 2011. Multidrug-resistant tuberculosis not due to noncompliance but to between-patient pharmacokinetic variability. J. Infect. Dis. 204:1951–1959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Srivastava S, Sherman C, Meek C, Leff R, Gumbo T. 2011. Pharmacokinetic mismatch does not lead to emergence of isoniazid- or rifampin-resistant Mycobacterium tuberculosis but to better antimicrobial effect: a new paradigm for antituberculosis drug scheduling. Antimicrob. Agents Chemother. 55:5085–5089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Swinburn BA, et al. 2011. The global obesity pandemic: shaped by global drivers and local environments. Lancet 378:804–814 [DOI] [PubMed] [Google Scholar]
- 40. Tanaka, et al. 1999. Effect of clarithromycin regimen for Mycobacterium avium complex pulmonary disease. Am. J. Respir. Crit. Care Med. 160:866–872 [DOI] [PubMed] [Google Scholar]
- 41. Wallace RJ, Jr, et al. 1994. Initial clarithromycin monotherapy for Mycobacterium avium-intracellulare complex lung disease. Am. J. Respir. Crit. Care Med. 149:1335–1341 [DOI] [PubMed] [Google Scholar]
- 42. West GB, Brown JH, Enquist BJ. 1997. A general model for the origin of allometric scaling laws in biology. Science 276:122–126 [DOI] [PubMed] [Google Scholar]
- 43. West GB, Brown JH, Enquist BJ. 1999. The fourth dimension of life: fractal geometry and allometric scaling of organisms. Science 284:1677–1679 [DOI] [PubMed] [Google Scholar]
- 44. West GB, et al. 2003. Physiology: why does metabolic rate scale with body size? Nature 421:713. [DOI] [PubMed] [Google Scholar]
- 45. World Health Organization 2010. Treatment of tuberculosis: guidelines, 4th ed WHO/HTM/TB/2009.420. 2010 World Health Organization, Geneva, Switzerland [Google Scholar]
- 46. Zhu M, et al. 2004. Pharmacokinetics of ethambutol in children and adults with tuberculosis. Int. J. Tuberc. Lung Dis. 8:1360–1367 [PubMed] [Google Scholar]