Residue specific vibrational echoes yield 3-dimensional structures of a transmembrane helix dimer

Abstract

Two dimensional vibrational echo spectroscopy has previously been applied to structural determination of small peptides. Here we extend the technique to a more complex, biologically significant system: the homodimeric transmembrane dimer from the α-chain of the integrin αIIbβ3. We prepared micelle suspensions of the pair of 30-residue chains that span the membrane in the native structure, with varying levels of heavy (¹³C=¹⁸O) isotopes substituted in the backbone of the central 10^th through 20^th positions. The constraints derived from vibrational coupling of the precisely spaced heavy residues led to determination of an optimized structure from a range of model candidates: Glycine residues at the 12^th, 15^th and 16^th positions form a tertiary contact in parallel right handed helix dimers with crossing angles of −58° ± 9° and interhelical distances of 7.7 ± 0.5 Å. The frequency correlation established the dynamical model used in the analysis and it indicated the absence of mobile water associated with labeled residues. Delocalization of vibrational excitations between the helices was also quantitatively established.

Two-dimensional infrared spectroscopy (1) (2D IR) has been used to obtain conformations of small peptides (2–3–4–5–6) from the strength and polarization characteristics of the spectral crosspeaks using principles analogous to those of 2D nuclear magnetic resonance (NMR) (7). Nevertheless it remains challenging to apply 2D IR to obtain structures of larger systems such as proteins where many more constraints are needed. Here we use 2D IR to determine the tertiary structure of a homodimeric transmembrane (TM) dimer from the α-chain of the integrin αIIbβ3 which mediates the binding of fibrinogen to platelets. The isolated TM domain from this integrin, that preserves the native state, forms the αIIb homodimers in micelles and bacterial membranes (8), facilitating its preparation and study in isolation from the rest of the protein.

The high degeneracy of the amide transitions in helical proteins complicates efforts aimed at extracting structural constraints using vibrational spectroscopy. This difficulty is overcome by carbon and oxygen isotope replacements in the carbonyl groups of amide units which shift the vibrational frequencies beyond the natural bandwidths in the infrared, enabling resolution of individual and pairs of residues. Therefore, a residue level set of constraints is achievable even for a large system. In addition 2D IR reveals the dynamics of the frequency distributions of the vibrations of each residue, which are sensitive to the presence of water molecules (9,10). Protein conformations that interchange more slowly than ca. 1ps and that are averaged in NMR become accessible as discrete, exchanging, transitions in 2D IR spectroscopy which can become a standard method to determine structures and structural dynamics.

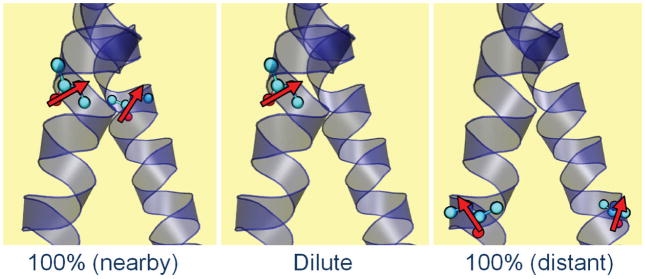
A molecular vibrational excitation creates an oscillating dipole that is sensed by nearby molecules through electrostatic interactions. The oscillatory transfer of the vibrational excitation to a near resonant vibrator depends on the inverse cube of the separation and on the absolute square and orientation of the vibrational transition dipoles. This quantum mechanical effect delocalizes the vibrational excitations of the peptide on (22) or between (23) backbones. The microscopic situation prevailing in the present experiments is illustrated schematically in Figure 1. The relatively large isotope shift (ca. 65 cm⁻¹) from substitution of ¹³C=¹⁸O into the peptide backbone strongly localizes the amide vibration. If there is also a ¹³C=¹⁸O label on the same residue of the neighboring helix of a transmembrane dimer, the vibrational mode may become delocalized over the pair of isotopically isolated vibrational states on the different helices. However if only one helix of the dimer has the isotopic substitution or if the resonance pair separation is too large, the mode will remain localized. Therefore if made from mixtures of isotopically substituted and unsubstituted peptides, the TM dimers will consist of structures having both localized and delocalized pair modes depending on the residue and isotope dilution. The spectral differences between the diluted and undiluted samples provide constraints to determine the three dimensional structure of the dimer. These differences arise only from electrostatic interactions because the amide I modes on different helices have vanishingly small charge overlap.

Fig. 1. Schematic depiction of three possible situations present in the isotope dilution experiment.

The nearby and distant cases depict 100% ¹³C=¹⁸O substituted samples and their localized transition dipoles (red arrows). In the nearby case the dipoles interact significantly through space to cause tertiary delocalization of the vibrational excitation. In the dilute case a ¹³C=¹⁸O residue experiences a localized excitation. In the distant case the excited residues are not close enough to interact so the spectrum does not depend on isotope dilution.

Mackenzie et al. detected inter-helical contacts between nearby amides in the NMR structure of the TM domain of the homodimeric protein, glycophorin (13). This finding suggested that it might be possible to solve structures of membrane proteins by 2D-IR if two methodological and theoretical challenges could be met. First, methods of sample preparation and spectroscopic measurements had to be sufficiently well-optimized to process multiple labels scanned through the interaction site of the TM helices. Second, the coupling between the amide oscillators would be needed for input into calculations of protein structures. Here we provide the spectroscopic and theoretical underpinnings necessary to allow deconvolution of the spectra into static versus dynamic components, and then we derive spectral parameters to guide de novo structure determination of the weakly interacting αIIb homodimer (8) whose components are an essential part of cell signaling apparatus,

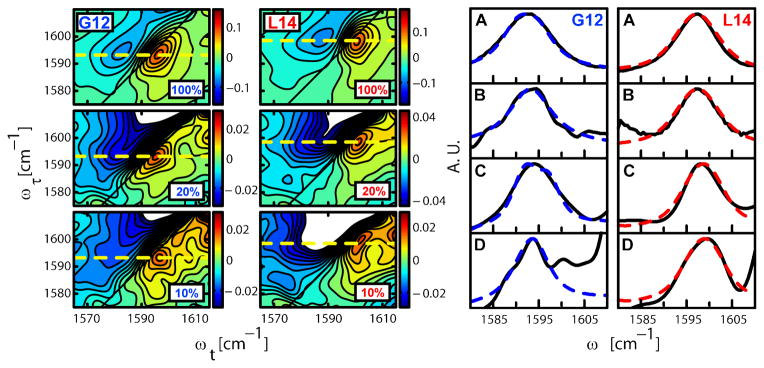
We prepared this peptide with varying degress of ¹³C=¹⁸O incorporation at each of the residues in the central L10 to L20 span. Based on knowledge of the typical sequences of interacting regions of TM dimers (13) and mutagenesis studies of the αIIb homodimer (8) it was anticipated this region would encompass some amides on different helices that would have measurable interactions. We then applied 2D IR spectroscopy to micelle embedded samples of these peptides in solution. The 2D IR spectra displayed in Figure 2 are plots of the coherence frequency ω_τ introduced by the pump laser versus the coherence frequency ω_t probed for various waiting times (T) between the second and third infrared pulses of the three pulse echo experiment. The two overlapping regions with opposite signs corresponding to the v=0→1 transition (red) and to the v=1→2 transition (blue). The elongation along the diagonal of the 2D axes indicates the distribution of vibrational frequencies exhibited by the distribution of dimer structures.

Fig. 2. 2D IR correlation spectra and FTIR spectra with different concentrations of ¹³C=¹⁸O isotopic substitution on residues G12 and L14.

The mixtures of ¹³C=¹⁸O labeled and unlabeled (¹²C=¹⁶O) helices are given as the percentage of the sample that is ¹³C=¹⁸O. The figure on the left shows the 2D IR correlation spectra of peptides substituted to the extent indicated (10 to 100%) with ¹³C=¹⁸O at the G12 (left) and L14 (right) residues. The spectra were taken at T=300fs and a τ range of −2800 fs to 3200 fs. The dashed line indicates the peak assigned to the ¹³C=¹⁸O amide I transition. The corresponding 2D IR diagonal traces for the 100 and 10% samples are shown in (C) and (D) respectively. The subtracted FTIR spectra of (A) 100% and (B) 10% ¹³C=¹⁸O substituted samples at G12 (left) and L14 (right) are shown on the right. The normalized experimental results (black, full) were fitted with the model explained in the text (blue, dotted). For G12 the 100% sample peaks are broader than the 10% sample peaks in the FTIR (A vs. B) and in the 2D IR (C vs. D) spectra, whereas the data for L14 show no significant difference in peak widths for different isotopic dilutions. The peak at ca. 1601 cm⁻¹ in panel D of G12 is a weak transition that becomes evident in the 10% samples where the signal to background ratio is reduced. It is definitely not related to the ¹³C=¹⁸O amide I transition so it was readily subtracted and removed from the analysis (see SOM and Fig. S5).

The data for G12 and L14 in Fig. 2 illustrate the residue dependence of the 2D IR lineshapes at different isotope dilutions. The spectra for the mixtures of the nine remaining residues are presented in Fig. S6. These 2DIR spectra were taken at T=300 fs. The 2D IR spectral shapes as judged by the diagonal and antidiagonal widths and the slopes (25) were found to be identical at T=300 fs and T=1500 fs. The shapes were constant during these T intervals. This result, which cannot be obtained from linear spectroscopy, completely specifies the dynamical picture needed to compute the spectra. The decay of the 2D IR signal of the ¹³C=¹⁸O amide-I band yielded population decay times, T₁, of 800 ± 100 fs. for all residues (see SOM).

The ¹³C =¹⁸O amide I transition of each residue is indicated in Fig. 2 with a dashed horizontal yellow line at ω_τ between 1582 and 1602 cm⁻¹. Two main features are central: the lineshape for the 100% ¹³C =¹⁸O sample is broader than that for the 10% sample in the case of G12, but the corresponding lineshapes are almost the same for L14; and in spectra of the 10% samples G12 shows a circular 2D IR peak whereas L14 shows more diagonally elongated peak. The spectral broadening of G12 in the 100% ¹³C =¹⁸O sample spectrum is a result of the through space coupling between the resonant pair of isotopically replaced residues. The interactions were evaluated from the trace of the 2D IR spectra along the line ω_τ = ω_t + c where c=2.5 cm⁻¹ is the frequency difference between the maxima of the ¹³C=¹⁸O peaks and the diagonal line. The results for G12, where the isotopomer concentration effect is evident, and L14, where it is not, are shown in Fig. 3C and D (see Fig. S6 for the other 9 residues).

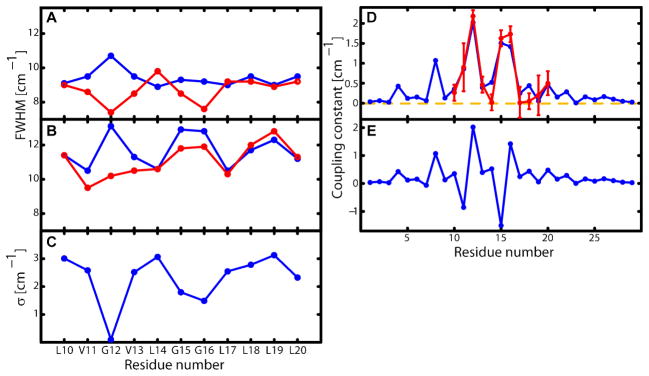
Fig. 3. Residue dependance of the spectral widths.

Full width at half maximum (FWHM) of (A) the diagonal trace of 2D IR spectra and (B) the FTIR spectra for the undiluted 100% (blue) and 10% (red) ¹³C=¹⁸O labeled samples. The FWHM versus residue variation exhibits a ca. 3.6 residue repeat corresponding to the helicity of the monomers. The 2D IR traces of the 10% samples show a change in phase in this oscillation resulting from the higher homogenous component of the residues facing the inside of the dimer (see SOM for discussion of this point). The overall smaller widths of the 2D IR traces compared to the FTIR spectra make the determination of the coupling constant more accurate. (C) The inhomogeneous component σ defining the Gaussian average. It is obtained by varying σ₂, $T_2^{\ast }$ and the zero order frequencies (see SOM) in fits of the FTIR and 2D IR traces to the model explained in the text. This result is consistent with the noticeable elongation of the peaks of the 2D IR spectra and it suggests that the residues involved in the tertiary contact experience a narrower distribution of structures. (D) The absolute value of the coupling constants for the final structure (red) and those obtained from the fit of the experiment (blue). also present a periodicity of ca. 3.6 residues. G12, G15 and G16 form the tertiary contact and present the highest coupling magnitudes. The error bar corresponds to a change in χ² of 0.5(E) The signed coupling constant of the final structure. G15, L19 and V11 have negative coupling constants.

The ¹³C=¹⁸O transitions in the diluted samples, which are so clearly visible in the 2D IR spectra of all the isotopomers, are not processable from the 1D FTIR spectra where optical densities are less than ca. 0.001. The 2D IR spectral signals depend on the fourth power of the transition dipole moment so that for a given absorbance they are proportional to the extinction coefficient of the transition. These factors cause significant suppression of signals with low extinction coefficient like D₂O and the tail of the main band amide I absorption. The FTIR spectra shown in Fig. 3A and B for G12 and L14 were processed using information from the 2D IR spectra as explained in more detail in the text accompanying Figures S1–S3, where FTIR data for the remaining nine residues is given.

An important result is the variation of nonlinear and linear spectral properties with position of the residue along the sequence. For example Fig. 4 shows the alternation with residue number of the spectral widths of the 2D IR diagonal traces and FTIR spectra of the ¹³C=¹⁸O transitions The repeat separation is 3 to 4 residues. The amplitude of the alternation effect is caused mainly by the excitonic coupling between the labeled sites of a dimeric helix. A smaller amplitude alternation is also seen in the 10% samples, which indicates that even when free from coupling the signals are residue sensitive. The dilute (10%) 2D IR spectra in Figure 4, alternate one helix turn out of phase with the other signals (see SOM). Already without quantitative analysis we can posit that the residues V11 to L17 are bracketing the main crossing interactions between the two helices. However to proceed further it is necessary to develop a quantitative description of these spectra in order to obtain the through space coupling constants needed as structure constraints.

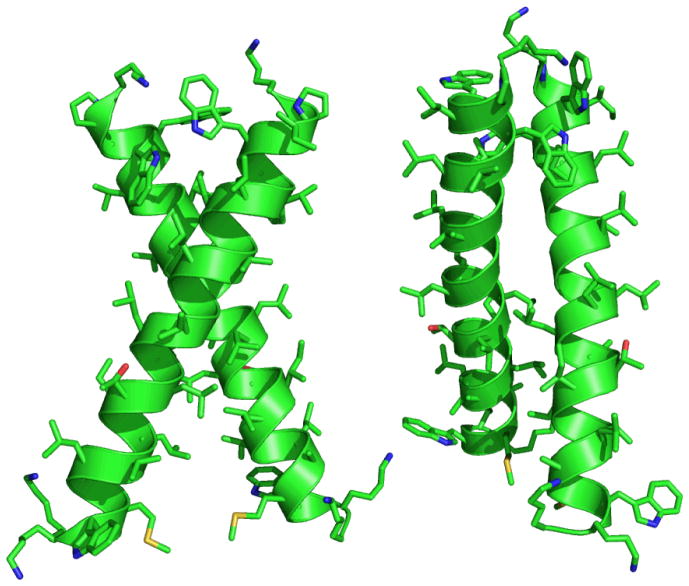
Fig. 4. Front and side views of the lowest energy structure obtained from simulated anneal using the through space coupling constants from the experiment as constraints.

It is a right handed helix dimer with a −55° crossing angle and 7.8 Å interhelical distance. The residues facing the inside of the dimer in the investigated region experience a different environment than those on the outside.

The main results concern the residue positional dependence of the differences between 2D IR spectra at different isotope dilutions. The peptide groups in different helices of a dimer are always separated by more than ca. 4 Å, which is the shortest separation seen in the very stable dimer of GPA (Glycophorin A) (24). Hence the differences between the 100% and 10% shapes must be solely caused by the electrostatic interaction of the transition charge distributions associated with the excitation of the amide I mode. Therefore an exciton model, in which two local sites on each helix couple through space to form new states which are linear combinations of the local ones, was used to describe them. The dynamics of these delocalized states are determined by their population and pure dephasing relaxation. The T-invariance of the 2D IR spectral shapes implies that the distribution of vibrational frequencies constituting the band shapes of the spectra remains constant. This result prompts the use of a dynamical model in which the frequency-frequency correlation function C(T) has two components, one of which decays more quickly and the other much more slowly than the inverse bandwidth of the IR spectrum. The quickly decaying component gives rise to a homogeneous dephasing, $T_2^{\ast }$ of each of the transitions, and the ultraslow decay introduces an inhomogeneous width, σ. Hence the signals are represented by Lorentzian functions averaged over fixed distributions of the frequency. The few ps. decay which occurs when C(T) is influenced by water molecules nearby to the amide groups is absent in the signals, from which we conclude there is no mobile associated water in the sense of (9,10) for any residue.

Each dimer in the ensemble contributes two transitions to the inhomogeneous distribution of frequencies. Deviations of these frequencies from their means are assumed to be uncorrelated on the basis that they are caused by independent, local forces on modes of different helix backbones. The exciton states (called here |+〉 and |−〉) originate from the perturbation of the v=1 states by inter-site, dipole-dipole electrostatic interactions of v=0->1 transitions.

For the computation of the spectra, the linear and nonlinear (26) response functions are calculated in the basis of the eigenstates |±〉 of the Frenkel exciton Hamiltonian. The exciton eigenfrequencies and transition dipole vectors are readily expressed in terms of the pair state variables θ and ϕ, where tan θ = 2|β|/ω₁₂and β = |β|e^iϕ where ω₁₂ is the site frequency gap and β the coupling. Equation 1 is the linear infrared spectrum, S_FTIR (ω), of the amide I transitions of the ¹³C=¹⁸O labeled residues involving components at ω_0± between the ground state and the resonance pair states |±〈, with μ̄_0± being the transition dipoles and γ_0± the homogeneous dephasing rates.

$$S_{\mathit{FTIR}}(\omega )=\frac{1}{3}Re\langle \frac{{\mid {\mu }_{0+}\mid }^2}{i({\omega }_{0+}-\omega )+{\gamma }_{0+}}+\frac{{\mid {\mu }_{0-}\mid }^2}{i({\omega }_{0-}-\omega )+{\gamma }_{0-}}\rangle$$ (1)

The 2D IR spectra (e2 and SOM) are constructed from forty different Liouville pathways (26) which involve all the exciton states from one and two quantum excitations (27) at T=300 fs. Equation 2 shows the spectrum deriving from one typical 2D IR response function in the frequency domain with all the incident fields sharing the same polarization and transitions between the same exciton levels involved in each step of the nonlinear interaction. (The Liouville diagrams and analytical forms for the others are shown in the SOM). In equations 1 and 2 the joint average denoted by angle brackets is taken over the two site frequency distributions assumed to be uncorrelated Gaussians having width σ.

$$R_1({\omega }_{\tau }={\omega }_d,{\omega }_t={\omega }_d+c)=\frac{1}{5}Re\langle \frac{e^{-T/T_1}{\mid {\overrightarrow{\mu }}_{0+}\mid }^4}{\left[i({\omega }_{0+}-{\omega }_d)+{\gamma }_{+0}\right]\left[i({\omega }_{+0}-{\omega }_d-c)+{\gamma }_{+0}\right]}\rangle$$ (2)

The frequency ω_d is the diagonal trace. The Lorentz parameters γ_mn represent the homogeneous widths, for example $2{\gamma }_{mn}=1/2T_1+1/T_2^{\ast }(m,n;\beta ,{\omega }_{12})$, where T₂^*(m,n;β,ω₁₂) is the pure dephasing time of the mn transition which in turn depends on the degree of localization of the excitation determined (28) by β and ω₁₂.

For reference, the dipolar coupling between typical amide I oscillators with μ = 0.35 Debye is 610κ(Ω)/R³cm⁻¹ where κ(Ω) is a geometric parameter −1<κ(Ω)< 2, and R is the point dipole separation in Å units. For two-fold symmetry κ(Ω) = 1 + (cos θ₁₂ − 1) P₂ (cos φ), where the angle between the dipoles is θ₁₂, and φ or φ + π are the azimuths. Therefore at R=5.7 Å we find −3.3 < β < 6.6 cm⁻¹: this is the approximate range of expected couplings. Their magnitudes are comparable with typical linewidths so the exciton transitions are expected to be overlapped. However, such exciton interactions should cause significant broadening of the transitions, which is exactly what is observed and characterized quantitatively in our data.

A structure distribution can be obtained exclusively from the 2D IR traces but we included the FTIR to further constrain the analysis. In contrast, the coupling constants could not be obtained from FTIR data alone because the vibrational frequency dynamics would be undetermined. Furthermore the enhanced signal to background ratio results in the 2D IR diagonal trace having better resolution and diminished background interference, permitting a robust calculation of the coupling constants. The 2D IR width is intrinsically more sensitive to coupling than the linear IR in the range of our parameters (see SOM) but incorporation of both provides a better set of results than does either one.

The FTIR and 2D IR spectra of the 10% and 100% samples were simultaneously fit by least squares minimization to the foregoing model to yield the absolute values of the coupling constants and dynamical parameters that are mutually consistent with four data sets for each of the eleven residues. The peaks in the residue dependence of the coupling in figure 5 show clearly that G12, G15 and G16 have the closest tertiary proximity. The periodicity of this pattern of peaks in the experiment is approximately 3.6 residues, matching the repeat of the α-helix. The fits generate values for the inhomogeneous broadening parameter whose residue positional dependence is shown in figure 4. The alternation of σ (29–30–31) is consistent with the observed trend in the extent of elongation along the diagonal of the 2D IR spectra of the 10% samples. It indicates that those residues in the dimer interface, namely G12, G15 and G16, present significantly narrower static distributions of structures than do the other residues. The results imply there are specific interactions causing local ordering of the residues forming the tertiary contacts, resulting in a narrowing of their frequency distributions such as would occur in a crystal.

A key factor in the structure simulation is the direction of the ¹³C=¹⁸O amide transition dipole in the frame of the peptide link. A perturbation theory estimate using the method described in reference (23) based on the isotope shift being large compared with coupling shows that the coupling of a ¹³C=¹⁸O amide with the remaining ¹²C=¹⁶O residues of a typical helix does not cause its transition dipole to rotate in the peptide frame by more than 3° (see SOM). Therefore the transition dipole for an isolated amide unit (33) was used in the simulation.

To find a family of structures consistent with the experiments we first sampled the whole space of interacting two-fold symmetric ideal helices to identify the pose most consistent with the 2D IR coupling constants. A χ² test revealed 48 structures that were consistent with the experiment within a 75% confidence interval. They were all right handed parallel dimers with an average crossing angle of −63° ± 13° and interhelical distance 8.5 ± 0.3 Å. The structure with an interhelical distance of 8.5 Å and crossing angle of −60° showed the best agreement with the experiments. The model was further refined with the appropriate side chains by a constrained simulated anneal with XPLOR (34–35). A new module was written for XPLOR to account for the deviation from the vibrational dipole-dipole coupling constants obtained from the experiment (SOM). The 48 preselected structures were each taken as starting points for 100 structures. Every structure was first minimized by 500 steps to remove bad contacts, bathed at a high temperature (3000 K) for 1000 steps, followed by cooling to a low temperature (10 K) for another 1000 steps and subjected to Powell minimization for final 2000 steps. More details on the constraints used can be found in the SOM. This simulated annealing using vibrational through space coupling constants as constraints minimizes the energy and accommodates the side chains and the backbone to find a better agreement with the experiment. This procedure yielded 20 parallel right handed helix dimers with crossing angles of −58° ± 9° and interhelical distances of 7.7 ± 0.5 Å. The absolute values of the coupling constants for the structure that presented lowest energy (−55° crossing angle and 7.8 Å interhelical distance) and the experimental results are compared in figure 5. The residues G12, G15 and G16 form the tertiary contact and they present the highest coupling magnitudes. The residues G15, L19 and V11 have negative coupling constants. The view of the final energy minimized structure is shown in figure 6.

The peptide studied here belongs to the overall class of G-XXX-G motifs that drive dimerization in cell membranes and lipid micelles (37). Within this sequence motif, the affinity, specificity, and precise geometric details of the interaction depend critically on the surrounding primary sequence (38). The computed structural model for the αIIb homodimer differs from the original canonical motif seen in glycophorin, which has a somewhat smaller crossing angle, interhelical distance and rotation of each helix about its axis (helical phase). Instead the computed structure fits to a related right-handed motif, cluster #10 of (39), which has an average crossing angle of −60° ± 15° and interhelical distances of 8.6 ± 1.0 Å. A previous site-directed mutagenesis study showed a somewhat surprising phase-shift in the distribution of the residues that contribute to homodimerization in αIIb versus GPA, consistent with a rotation of the helix by 50° (8). The difference was attributed to the fact that αIIb has a GxxGG sequence with a third Gly that contributes to the interface in this homodimer but not in GPA. This interaction is now clearly seen in the spectral widths and couplings at position 15 and 16 in figures 4 and 5. Moreover, the computed structure shows the 50° helical phase shift and the larger crossing angle inferred from site-directed mutagenesis. Thus, these results provide direct structural information that explains the previous mutagenesis study, illustrating the power of 2D-IR as a structural tool. Additional independent constraints could be obtained from further 2D IR experiments on mixed isotopomers.