Actin Network Growth under Load

Abstract

Many processes in eukaryotic cells, including the crawling motion of the whole cell, rely on the growth of branched actin networks from surfaces. In addition to their well-known role in generating propulsive forces, actin networks can also sustain substantial pulling loads thanks to their persistent attachment to the surface from which they grow. The simultaneous network elongation and surface attachment inevitably generate a force that opposes network growth. Here, we study the local dynamics of a growing actin network, accounting for simultaneous network elongation and surface attachment, and show that there exist several dynamical regimes that depend on both network elasticity and the kinetic parameters of actin polymerization. We characterize this in terms of a phase diagram and provide a connection between mesoscopic theories and the microscopic dynamics of an actin network at a surface. Our framework predicts the onset of instabilities that lead to the local detachment of the network and translate to oscillatory behavior and waves, as observed in many cellular phenomena and in vitro systems involving actin network growth, such as the saltatory dynamics of actin-propelled oil drops.

Introduction

Cell crawling, cell blebbing, phagocytosis, endocytosis, and the rocketing motion of endosomes are just a few examples of cellular processes that involve the interaction of growing actin networks with cellular membranes (Fig. 1) (1–4). In addition to its important role in eukaryotic cells, actin network growth is also used by several pathogens, such as the bacterium Listeria monocytogenes, as a means of propulsion inside the host cell (5,6). The widespread use of actin network growth across organisms highlights its versatility and robustness as a cellular mechanism to generate forces and drive cellular movements.

Figure 1.

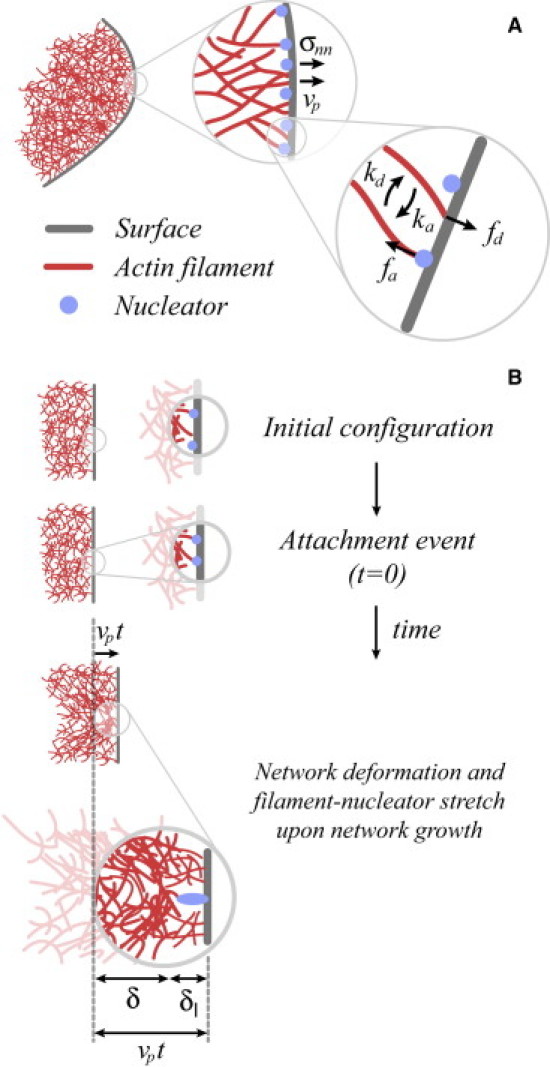
Actin network growth from a surface. (A) Sketch of an actin network (red mesh) growing from a surface (gray) where actin nucleators (blue) are located. The surface is locally subject to an external normal stress σ_nn and the network grows at velocity v_p. The actin filaments interacting with the surface can be either associated to nucleators or dissociated from them. Dissociated filaments, which polymerize toward the surface and generate an average pushing force f_d, associate to nucleators at a rate k_a. Filaments associated to nucleators resist the growth with an average force f_a per filament and dissociate from nucleators at a rate k_d. (B) Nature of the resistive force: After their initial attachment to a nucleator at the surface, attached filaments are continuously loaded by network growth during their lifetime. The initial attachment of a detached filament to a surface nucleator at t = 0 does not impose any instantaneous stretch on either the actin network or the new filament-nucleator link. Once attached to the surface, the new attached filament resists an increasing load over time as a result of network elongation. After a time t, the network has advanced a distance $v_{p}t$, and the combination of this network elongation with the attachment of the filament at the surface generates deformations $\delta \left(t\right)$ and ${\delta }_{\ell }\left(t\right)$ of the actin network and filament-nucleator link, respectively. (In color online.)

In living cells, actin networks grow only from surfaces (e.g., the plasma membrane) where surface-localized proteins (e.g., Arp2/3 and formins) promote actin polymerization (1,7–9). Therefore, understanding actin kinetics at the microscopic scale requires knowledge of the molecular processes that modulate actin filament nucleation, attachment, and branching at surfaces (7–9). The interaction of actin filaments with surfaces (generally membranes) occurs either via their attachment to surface-localized nucleator proteins (nucleators) or via their direct polymerization against the surface (10–12) (Fig. 1 A). Two main molecular routes are employed to nucleate actin filaments: 1), Arp2/3-mediated nucleation and branching; and 2), formin-mediated polymerization (12). Arp2/3 is generally thought to prevent the polymerization of its associated actin filament (8,12), whereas formins are known to allow simultaneous surface attachment and filament elongation (12,13).

Although a persistent attachment of the actin network to the surface is important for its functionality in many cases, an excessively strong attachment can hinder network growth. There even exist specific cellular phenomena, such as cell blebbing (3), in which complete network detachment is important. By modifying the balance between network attachment and elongation, which depend on biochemical cues and local forces, eukaryotic cells can direct the actin networks to perform their multiple tasks. The dynamics of network surface attachment and growth are thus inherently coupled, and it is their interplay that determines the dynamics of the system.

There exist several models of actin network growth at the microscopic level, mainly in the context of Listeria-like motility (14–17). Although some of these models account for the competing forces of attached and detached filaments, they do not identify the origin of the resistive force, which is essential to understand the dynamics of the system. Moreover, most microscopic models extrapolate the local dynamics of actin network growth to the overall motion of an extended object, such as the bacterium Listeria or beads, in which the stress distribution and the actin density are nonuniform. This extrapolation must be made with care, because microscopic theories generally must be combined with mesoscopic descriptions to properly account for the behavior of extended systems.

Here we provide a generic description of the local dynamics of a growing actin network under an externally applied load, accounting for the competing forces of attached and detached filaments. Moreover, we identify the nature of the resistive force of attached filaments: the continuous loading of attachment sites imposed by network growth generates resistive forces that strongly depend on the network growth velocity. As detailed below, the coupling between network elongation and surface attachment constitutes a natural mechanism for regulating the degree of network attachment and filament density as a function of the network growth velocity. Our description attempts to bridge the gap between microscopic models and mesoscopic descriptions of actin-based motility, and thus should be combined with mesoscopic descriptions in studies of extended systems.

Theory

We consider the growth of an actin network with a local surface density of actin filaments ρ_f able to interact with a surface covered by actin nucleators (Fig. 1 A). We assume for simplicity that the surface density of nucleators is much larger than ρ_f, so the nucleator density is not a limiting factor. At any time, there is a density ρ_a of filaments attached to nucleators, and a density ρ_d of filaments dissociated from nucleators. The kinetics of filament association/dissociation to/from nucleators at the surface can be generically written as

$$\begin{array}{l}\frac{d{\rho }_a}{dt}=-k_d{\rho }_a+k_a{\rho }_d,\\ \frac{d{\rho }_d}{dt}=-k_a{\rho }_d+k_d{\rho }_a,\end{array}$$ (1)

where k_a is the rate at which detached filaments associate to nucleators, and k_d is the rate at which attached filaments dissociate from nucleators. The effect of capping proteins, filament branching, etc. (as in autocatalytic growth models (15)) can easily be included in this description. For simplicity, here we neglect these effects, which do not modify our results qualitatively. At steady state, or at timescales > $1/k_a$ and $1/k_d$, Eq. 1 reduces to

$$\frac{{\rho }_a}{{\rho }_f}=\frac{k_a}{k_a+k_d}\text{and}\frac{{\rho }_d}{{\rho }_f}=\frac{k_d}{k_a+k_d}.$$ (2)

When an external normal stress σ_nn is applied to the surface (Fig. 1 A), local normal force balance requires that

$${\sigma }_{nn}=f_a{\rho }_a+f_d{\rho }_d,$$ (3)

where f_a is the average force an individual attached filament generates during the time it stays attached to the surface, and f_d is the average propulsive force an individual detached filament generates by elongating (pushing) against the surface at velocity v_p (Fig. 1 A). Because we are concerned with the local dynamics of the growing network, we can only impose a local force balance (Eq. 3). We assume that the actin network is held far away from the growing region, so that global force balance on the whole system is satisfied.

Combining Eqs. 2 and 3, we obtain

$${\sigma }_{nn}={\rho }_f\frac{k_a}{k_a+k_d\left(v_p\right)}\left[f_a\left(v_p\right)+\frac{k_d\left(v_p\right)}{k_a}{f}_d\left(v_p\right)\right],$$ (4)

which specifies the local velocity v_p of an actin network under an applied local stress σ_nn, given explicit functional forms for the dependence of the association and dissociation rates, k_a and k_d, respectively, and the average forces of attached and detached filaments, f_a and f_d, respectively, on the network velocity v_p. For the sake of simplicity, we assume that the association rate k_a is constant and independent of the local network growth velocity v_p. Below, we derive the explicit forms of the functions $k_d\left(v_p\right)$, $f_a\left(v_p\right)$ and $f_d\left(v_p\right)$ in the different dynamical regimes of the system.

The equations described so far are generic in the sense that they account for many possible molecular dynamics of actin nucleation and polymerization, including the case of polymerization of attached filaments in the presence of formins. The details of the different molecular dynamics will be found in the particular functional forms of the average force of attached and detached filaments, f_a and f_d, respectively, and in the functional form $k_d\left(v_p\right)$.

Detached filaments: average propulsive force $f_d\left(v_p\right)$

Assuming that individual detached filaments behave independently, the local growth velocity of the network is given by the average polymerization velocity of a single filament, which reads (14,18):

$$v_p=v_p^0\exp \left(\frac{f_{d}a}{k_{\text{B}}T}\right),$$ (5)

where $v_p^0$ is the polymerization velocity of the filaments at vanishing force, and a is approximately half the radius of an actin monomer. Inverting Eq. 5, we obtain the average force of detached filaments f_d as a function of the local network velocity v_p: $f_d\left(v_p\right)=k_{\text{B}}T/a\ln \left(v_p/v_p^0\right)$. This relation is only valid for network velocities $v_p\le v_p^0$, because the network cannot grow faster than the maximal polymerization velocity of individual filaments, $v_p^0$.

Attached filaments: dissociation rate $k_d\left(v_p\right)$ and average resistive force $f_a\left(v_p\right)$

Although Eqs. 2 and 3 remain general, here we need to specify the functional forms of the detachment rate of attached filaments as well as the average force they apply on the surface, both of which depend on the details of the molecular dynamics of actin nucleation considered. For the sake of simplicity, in what follows we consider the case in which attached filaments cannot polymerize, a situation that corresponds more closely to Arp2/3-mediated actin growth than to formin-mediated actin polymerization. The dynamics of actin network growth in the presence of formins can be derived in a manner similar to that described below for Arp2/3 nucleation.

In the case of Arp2/3-mediated actin network growth, filaments associated to nucleators do not elongate and attach the network to the surface (11,19–21). In contrast, filaments that are not attached to nucleators can freely polymerize against the surface and exert the necessary forces to drive the forward motion of the surface (9,10). The simultaneous network growth and surface attachment induce a resistive force that opposes network elongation and arises from the continuous loading imposed by network growth on attached filaments (Fig. 1 B).

To understand how network growth affects the dynamics of attached filaments, consider the sequence of events that occur after a filament attaches to a nucleator at the surface (Fig. 1 B). Upon attachment to the surface, the new attached filament resists an increasing load over time as a result of network elongation (Fig. 1 B), until the filament-nucleator link fails and the filament detaches from the surface. Consequently, each filament-nucleator link supports a time-dependent force, $f_{\ell }\left(t\right)$, leading to an instantaneous dissociation rate, $k_{id}\left(t\right)$, that depends on time through its force dependence as (22–24):

$$k_{id}\left(t\right)=k_d^0\exp \left(\frac{f_{\ell }\left(t\right)b}{k_{\text{B}}T}\right),$$ (6)

where $k_d^0$ is the dissociation rate at vanishing load, and b is a length in the nanometer range that characterizes the position of the energy barrier between attached and detached states.

Each attached filament remains connected to the surface an average time τ (which we refer to as the lifetime of the attached filament), during which it individually generates an average resistive force f_a that opposes network growth. The dependence of the lifetime τ on the network velocity v_p can be determined from the probability distribution, $p\left(t\right)$, i.e., the probability that a filament that attaches to a nucleator at time t = 0 will detach from it after a time t. The dissociation probability $p\left(t\right)dt$ in the time interval $\left(t,t+dt\right)$ equals the probability $1-{\int }_0^{t}d{t}^{\prime }p\left(t^{\prime }\right)$ that the filament will still be attached at t, times the probability $k_{id}\left(t\right)dt$ that the filament will dissociate in the time interval dt. For an arbitrary instantaneous dissociation rate $k_{id}\left(t\right)$, the probability distribution $p\left(t\right)$ reads

$$p\left(t\right)=k_{id}\left(t\right)\exp \left(-\underset{0}{\overset{t}{\int }}d{t}^{\prime }{k}_{id}\left(t^{\prime }\right)\right).$$ (7)

Similarly, the average resistive force f_a that an attached filament supports during its lifetime can be evaluated from the probability distribution, $p\left({\delta }_{\ell }\right)$, that a filament-nucleator link is stretched by a length δ_ℓ (Fig. 1 B). Using similar arguments as presented above to calculate $p\left(t\right)$, the probability distribution $p\left({\delta }_{\ell }\right)$ reads

$$p\left({\delta }_{\ell }\right)=\frac{\exp \left(-\underset{0}{\overset{t\left({\delta }_{\ell }\right)}{\int }}d{t}^{\prime }{k}_{id}\left(t^{\prime }\right)\right)}{\underset{0}{\overset{\mathrm{\infty }}{\int }}d{\delta }_{\ell }\exp \left(-\underset{0}{\overset{t\left({\delta }_{\ell }\right)}{\int }}d{t}^{\prime }{k}_{id}\left(t^{\prime }\right)\right)},$$ (8)

where $t\left({\delta }_{\ell }\right)$ corresponds to the inverse function of ${\delta }_{\ell }\left(t\right)$, which we calculate below.

The dissociation rate of attached filaments, k_d, corresponds to the inverse of the average lifetime τ, i.e., $k_d=1/\tau$. In terms of the probability distributions $p\left(t\right)$ and $p\left({\delta }_{\ell }\right)$, the detachment rate k_d and average resistive force f_a are given by

$$k_d^{-1}=\tau =\underset{0}{\overset{\mathrm{\infty }}{\int }}dttp\left(t\right)\text{and}{f}_a=\underset{0}{\overset{\mathrm{\infty }}{\int }}d{\delta }_{\ell }{f}_{\ell }\left({\delta }_{\ell }\right)p\left({\delta }_{\ell }\right),$$ (9)

where $f_{\ell }\left({\delta }_{\ell }\right)$ is the relation between the force $f_{\ell }$ sustained by a filament-nucleator link and the deformation δ_ℓ of the link.

To obtain explicit functional forms for the dependence of both the dissociation rate k_d and the average resistive force f_a on the network velocity v_p, it is necessary to know the time-dependent force $f_{\ell }\left(t\right)$ sustained by a filament-nucleator link during its lifetime.

Loading of attached filaments by network growth: the instantaneous resistive force $f_{\ell }\left(t\right)$

As mentioned above, attached filaments sustain an increasing force over time due to the continuous elongation of the actin network at velocity v_p. The resistive force that each attached filament supports depends on how much the neighboring attached filaments influence each other through the deformation of the actin network created by their attachment to the surface (Fig. 1 B). Depending on the network elasticity and the kinetic parameters of filament dynamics, attached filaments may behave independently from each other or act cooperatively, leading to different behaviors of the resistive force and, consequently, to different dynamical behaviors of the system. Below, we derive the functional form of the instantaneous force $f_{\ell }\left(t\right)$ and determine the different dynamical regimes and the parameters that govern the dynamics in each regime, as detailed in Fig. 2 and Table 1, respectively.

Figure 2.

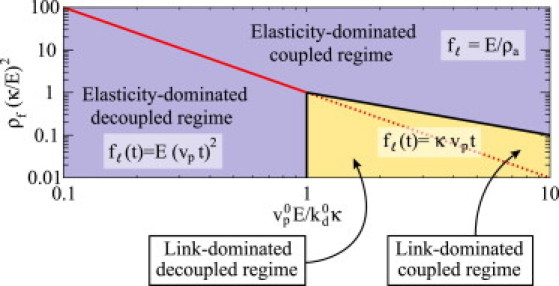
Dynamical regimes and associated filament-link force ${\mathbf{f}}_{\ell }\left(\mathbf{t}\right)$. The dynamical regimes of the system are shown in their most restrictive form (see text for details). Coupled ($v_p^0\sqrt{{\rho }_f}/k_d^0\gg 1$) and decoupled ($v_p^0\sqrt{{\rho }_f}/k_d^0\ll 1$) regimes are separated by the red line (continuous and dotted), which corresponds to $v_p^0/k_d^0=1/\sqrt{{\rho }_f}$. In the decoupled regime, the link force is dominated by either the filament-link deformation ($v_p^0/k_d^0\gg \kappa /E$; the link-dominated decoupled regime) or the network elasticity ($v_p^0/k_d^0\ll \kappa /E$; the elasticity-dominated decoupled regime), in which case $f_{\ell }\left(t\right)=\kappa v_{p}t$ and $f_{\ell }\left(t\right)={\left(E{v}_{p}t\right)}^2$, respectively. Similarly, in the coupled regime, the link force is dominated by the filament-link deformation (${\rho }_f{v}_p^0\kappa /k_d^{0}E\ll 1$; the link-dominated coupled regime) or the network elasticity (${\rho }_f{v}_p^0\kappa /k_d^{0}E\gg 1$; the elasticity-dominated coupled regime), in which case $f_{\ell }\left(t\right)=\kappa v_{p}t$ and $f_{\ell }=E/{\rho }_a$, respectively. The yellow and blue regions correspond to the parameter space where the resistive force is dominated by the link and network deformations, respectively. (In color online.)

Table 1.

Relevant dimensionless parameters in each regime

Regime	Relevant dimensionless parameters
Elasticity-dominated uncoupled regime	$\frac{k_a}{k_d^0}$	$\frac{k_{\ell }^0}{k_d^0}\text{with}{k}_{\ell }^0=\sqrt{\frac{Eb}{k_{\text{B}}T}}{v}_p^0$	$\frac{b}{a}$	$\frac{{\sigma }_{nn}b}{{\rho }_f{k}_{\text{B}}T}$
Link-dominated uncoupled regime	$\frac{k_a}{k_d^0}$	$\frac{k_{\ell }^0}{k_d^0}\text{with}{k}_{\ell }^0=\frac{\kappa v_p^{0}b}{k_{\text{B}}T}$	$\frac{b}{a}$	$\frac{{\sigma }_{nn}b}{{\rho }_f{k}_{\text{B}}T}$
Elasticity-dominated coupled regime	$\frac{k_a}{k_d^0}$	–	$\frac{b}{a}$	$\frac{Eb}{{\rho }_f{k}_{\text{B}}T}$

As the actin network grows, the attachment of a filament to a nucleator at the surface induces deformations δ and δ_ℓ of the network and the filament-nucleator link, respectively (Fig. 1 B). For network velocities $v_p<v_p^0$, these deformations are related by

$$\delta \left(t\right)+{\delta }_{\ell }\left(t\right)=v_{p}t,$$ (10)

at time t after the attachment of a filament to a nucleator. The explicit dependencies of δ and δ_ℓ on time are obtained by balancing the force, $f_{\ell }\left(t\right)$, that is generated at the level of the filament-nucleator link, with the force, $f_{el}\left(t\right)$, that arises from the elastic deformation that the attachment of the filament at the surface induces in the actin network (Fig. 1 B). Assuming that the filament-nucleator link behaves as a linear spring of stiffness κ, the resistive force of each link reads $f_{\ell }\left(t\right)=\kappa {\delta }_{\ell }\left(t\right)$. The elastic force f_el resulting from the deformation of an actin network over a length δ is determined by equating the work $f_{el}\delta$ to the elastic deformation energy U_el.

To obtain the energy U_el associated with the elastic deformation of the actin network induced by the attachment of a filament at the surface, we assume that the actin network behaves as an elastic gel with elastic modulus E on the typical timescales of filament dissociation, i.e., the average lifetime τ. The attachment of a filament at the surface of the actin gel can be described as a point-like force applied at the growing surface of the network (Fig. 1 B). Because there is no characteristic length scale in the bulk of the elastic actin gel (25), the typical length scale of network deformation is set by the characteristic length scale of the localized perturbation applied to the growing actin network edge. A filament that attaches to the surface at time t = 0 generates an increasing network deformation of typical length $v_{p}t$, because this is the length by which the network advances after the initial attachment of the filament at the surface, and is the only characteristic length of the surface-localized perturbation (Fig. 1 B). Therefore, the typical length scale over which the network deformation propagates as a consequence of the attachment of a filament at the surface is $v_{p}t$. At the scaling level, the strain in the network due to an attached filament is $\delta \left(t\right)/v_{p}t$, the volume over which the network is deformed is ${\left(v_{p}t\right)}^3$, and the elastic energy then reads $U_{el}=E{\left(\delta /v_{p}t\right)}^2{\left(v_{p}t\right)}^3$. The elastic force f_el is then given by $f_{el}\delta =U_{el}$.

When the average distance between attached filaments, $1/\sqrt{{\rho }_a}$, is smaller than the characteristic length scale $v_{p}t$ over which the elastic network deformation propagates, several filament-nucleator links contribute to balance the elastic network deformation. The average number of filament-nucleator links that balance the local elastic deformation is, in a first approximation, $1+{\rho }_a{\left(v_{p}t\right)}^2$. Balancing the elastic force with the contributing link forces leads to $f_{el}=\left(1+{\rho }_a{\left(v_{p}t\right)}^2\right)\kappa {\delta }_{\ell }$ and, using Eq. 10, we obtain

$$\begin{array}{l}{f}_{\ell }\left(t\right)=\frac{E{\left(v_{p}t\right)}^2}{1+{\rho }_a{\left(v_{p}t\right)}^2+\frac{E}{\kappa }{v}_{p}t},\\ \delta \left(t\right)=\frac{v_{p}t\left(1+{\rho }_a{\left(v_{p}t\right)}^2\right)}{1+{\rho }_a{\left(v_{p}t\right)}^2+\frac{E}{\kappa }{v}_{p}t},\frac{{\delta }_{\ell }\left(t\right)}{\delta \left(t\right)}=\frac{E}{\kappa }\frac{v_{p}t}{1+{\rho }_a{\left(v_{p}t\right)}^2}.\end{array}$$ (11)

Several limiting regimes can be distinguished in the above expressions:

Decoupled regime

If the average distance between attached filaments, $1/\sqrt{{\rho }_a}$, is such that the network deformation created by one attached filament, $v_{p}t$, does not reach its neighboring filaments during its lifetime τ, then attached filaments behave independently (Fig. 2). This decoupled regime in which the deformation of the network does not couple the dynamics of neighboring attached filaments occurs when

$$v_p\tau \ll \frac{1}{\sqrt{{\rho }_a}}.$$ (12)

The most restrictive form of the last condition is $v_p^0/k_d^0\ll 1/\sqrt{{\rho }_f}$, as $v_p\tau <v_p^0/k_d^0$ and ${\rho }_a<{\rho }_f$. Because the filament-nucleator link and the network sustain forces in series, the resistive force can be governed by either the network elasticity or the filament-nucleator link rigidity. If the effective network spring constant during the lifetime of the link, $E{v}_p\tau$, is smaller than the filament-nucleator rigidity κ, the network elastic deformation will govern the response of attached filaments. This behavior occurs when

$$E{v}_p\tau \ll \kappa .$$ (13)

The most restrictive form of the last condition reads $E{v}_p^0/k_d^0\ll \kappa$, given that $v_p\tau <v_p^0/k_d^0$. In this elasticity-dominated decoupled regime, the resistive force is given by $f_{\ell }\left(t\right)=E{\left(v_{p}t\right)}^2$.

If the filament-nucleator link is softer than the network ($E{v}_p\tau \gg \kappa$- link-dominated decoupled regime), the filament-nucleator link will sustain nearly all of the deformation, and the resistive force is given by $f_{\ell }\left(t\right)=\kappa v_{p}t$.

Coupled regime

There is also a coupled regime in which several filament-nucleator links act in parallel. This occurs when the average distance between attached filaments, $1/\sqrt{{\rho }_a}$, is smaller than the average length $v_p\tau$ over which the elastic deformation generated by the attachment of a filament to the surface propagates (Fig. 2). In similarity to the uncoupled regime, the resistive force in the coupled regime can be governed by either the network elasticity or the rigidity of the filament-nucleator link: when $v_p\tau \ll E/{\rho }_a\kappa$, the filament-nucleator link sustains all the deformation and $f_{\ell }\left(t\right)=\kappa v_{p}t$ (link-dominated coupled regime), whereas if $v_p\tau \gg E/{\rho }_a\kappa$, the network sustains the deformation and the resistive force becomes time-independent and given by $f_{\ell }=E/{\rho }_a$ (elasticity-dominated coupled regime).

Fig. 2 shows a diagram of the different regimes discussed above and their corresponding regions in the parameter space, together with the corresponding limiting expressions for $f_{\ell }\left(t\right)$. Each regime has various dimensionless parameters (defined in Table 1 and derived explicitly in the Supporting Material) that control the possible behaviors of the system. The dimensionless parameters $k_a/k_d^0$, $b/a$, and $k_{\ell }^0/k_d^0$ (with $k_{\ell }^0$ being the natural loading rate, i.e., the rate at which network growth loads attached filaments when growing at its maximal velocity $v_p^0$; see Table 1 for the definition of $k_{\ell }^0$ in each regime), depend only on the structural and/or biochemical properties of actin and its associated proteins (Table 1). Typical values of a and b are such that $a\simeq b$, so we assume for the sake of simplicity that $b/a=1$.

Results

The local dynamics of a growing actin network can be solved in all of the regimes discussed above. For the sake of simplicity, we focus on the link-dominated uncoupled regime and the elasticity-dominated coupled regime because these two regimes are qualitatively different (Fig. 2). Indeed, the link-dominated uncoupled regime and the link-dominated coupled regime share the same functional form of the resistive force $f_{\ell }\left(t\right)$ (Fig. 2), meaning that these regimes also share the same dynamics, because all relevant magnitudes for the dynamics derive from the functional form $f_{\ell }\left(t\right)$. On the other hand, the network dynamics in the elasticity-dominated uncoupled regime is qualitatively similar to that of the link-dominated uncoupled regime. In the Supporting Material we explicitly derive the dissociation rate k_d and average resistive force f_a from the limiting expressions of $f_{\ell }\left(t\right)$ in all regimes.

Network growth under no external load

In the absence of external load (${\sigma }_{nn}=0$), the pushing forces of growing dissociated filaments compete only with the resistive forces of attached filaments.

Link-dominated uncoupled regime

By solving Eq. 4 at vanishing external force (${\sigma }_{nn}=0$) using the functional forms for $k_d\left(v_p\right)$ and $f_a\left(v_p\right)$ derived from the expression of $f_{\ell }\left(t\right)$ in the link-dominated uncoupled regime ($f_{\ell }\left(t\right)=\kappa v_{p}t$; see Fig. 2 and Supporting Material), we obtain the network growth velocity as a function of the relevant parameters in this regime (Table 1). When most of the filaments are detached from the surface, the network velocity reaches almost its maximal value $v_p^0$, because in this case there is almost no resistive force ($k_a/k_d^0\ll 1$; Fig. 3 B). Increasing the fraction of attached filaments ($k_a/k_d^0\gg 1$; Fig. 3 B) leads to a significant decrease in the network velocity. Even in the absence of externally applied stress, v_p can be arbitrarily smaller than the maximal polymerization velocity of individual filaments, $v_p^0$, due to the resistive force of attached filaments (Fig. 3, A and B). For a given value of the ratio $k_a/k_d^0$, the network growth velocity shows a nonmonotonous dependence on the natural loading rate $k_{\ell }^0$, which in this regime is given by $k_{\ell }^0=\kappa v_p^{0}b/k_{B}T$ and measures how fast attached filaments are loaded by network growth. At small loading rates ($k_{\ell }^0/k_d^0\ll 1$; Fig. 3 A), attached filaments are hardly stretched by network growth during their lifetime. As a consequence, there is almost no resistive force and the network advances at its maximal velocity $v_p^0$. In the limit of high loading rates ($k_{\ell }^0/k_d^0\gg 1$; Fig. 3 A), network growth rips off attached filaments from nucleators, leading to a small fraction of attached filaments and a small resistive force that allows the network to advance at its maximal velocity $v_p^0$. In between these two limiting regimes, the network velocity shows a minimum as a function of the natural loading rate, with a minimal value that depends on the ratio $k_a/k_d^0$.

Figure 3.

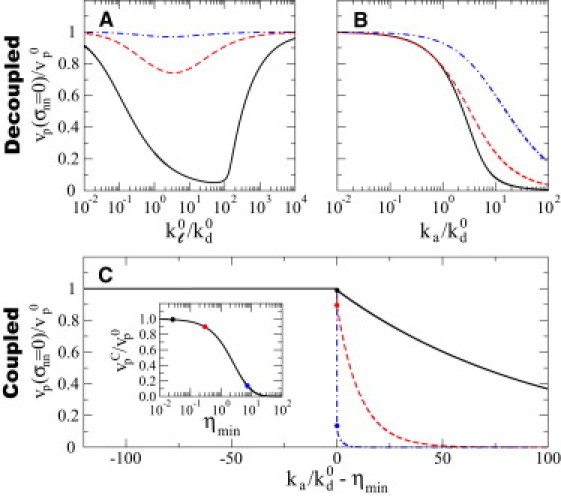
Network velocity at vanishing external load. (A–C) The growth velocity of the network, v_p, relative to the polymerization velocity of individual filaments at vanishing load, $v_p^0$, for both the link-dominated uncoupled regime (A and B) and the elasticity-dominated coupled regime (C), as a function of the relevant dimensionless parameters of each regime (Table 1). (A) Dependence of the network velocity v_p on $k_{\ell }^0/k_d^0$ for different values of $k_a/k_d^0$ ($k_a/k_d^0=10,1,0.1$, continuous black line, dashed red line, and dashed-dotted blue line, respectively). (B) Growth velocity v_p as a function of $k_a/k_d^0$ for $k_{\ell }^0/k_d^0=10,1,0.1$ (continuous black line, dashed red line, and dashed-dotted blue line, respectively). (C) Dependence of v_p on $k_a/k_d^0$ in the elasticity-dominated coupled regime. Below η_min the network is detached from the surface and the detached filaments grow at their maximal velocity $v_p^0$. Above η_min the network velocity decreases for increasing values of $k_a/k_d^0$ because there are more filaments attached that resist the network growth. The different curves correspond to $Eb/{\rho }_f{k}_{\text{B}}T=0.01,0.1,1$ (continuous black line, dashed red line, and dashed-dotted blue line, respectively). The network velocity, $v_p^c$, at the critical point $k_a/k_d^0={\eta }_{min}$ depends on the value of η_min (inset), with the dots highlighting the values of the critical velocity $v_p^c$ at the values of the parameter $Eb/{\rho }_f{k}_{\text{B}}T$ shown in C (same color code). The relation between η_min and $Eb/{\rho }_f{k}_{\text{B}}T$ is shown in Fig. 4. (In color online.)

Elasticity-dominated coupled regime

In this regime, the dynamics in the absence of externally applied stress (${\sigma }_{nn}=0$) depends on $k_a/k_d^0$ and $Eb/{\rho }_f{k}_{B}T$ (Table 1). For each value of the parameter $Eb/{\rho }_f{k}_{B}T$, there is a minimal value η_min of the ratio $k_a/k_d^0$ below which the network loses its contact with the surface (${\rho }_a=0$) (the nature of this threshold is discussed in detail below). The network velocity decreases exponentially with increasing values of $k_a/k_d^0$ away from the threshold ($k_a/k_d^0>{\eta }_{min}$; Fig. 3 C). At the threshold value $k_a/k_d^0={\eta }_{min}$, the network velocity $v_p^C\equiv v_p\left({\eta }_{min}\right)$ can be substantially smaller than $v_p^0$ depending on the value η_min (Fig. 3 C, inset).

In this description, when network detachment occurs for $k_a/k_d^0<{\eta }_{min}$, the network velocity reaches its maximal velocity $v_p^0$ because the resistive force vanishes necessarily in the absence of attached filaments. However, this is unlikely to occur in a real system, because the presence of capping proteins would halt elongation of the network if it was not in contact with the surface.

Network growth under applied load

In the presence of an external load (${\sigma }_{nn}\ne 0$), network growth cannot be sustained for all values of the applied stress. Although all compressive stresses (${\sigma }_{nn}<0$) simply slow down growth, not all pulling stresses (${\sigma }_{nn}>0$) can be resisted, and above a critical stress ${\sigma }_{nn}^c$, the actin network is ripped off the surface. Indeed, for stresses exceeding the critical stress ${\sigma }_{nn}^c$, filament attachment events cannot compensate for filament dissociation from the surface, leading to the loss of contact between the actin network and the surface.

Although the existence of a critical stress is largely independent of the biochemical details of actin polymerization at the surface, the dependence of the growth velocity on the applied stresses (stress-velocity relation) may depend on such details. In particular, capping and/or branching effects (as introduced in the autocatalytic growth model (15)) would change the stress-velocity profiles but not the existence of a critical pulling stress. Our description can be readily extended to account for most of the biochemical details associated with actin network dynamics at a surface.

Below, we derive the critical stresses and stress-velocity relations in both the link-dominated uncoupled regime and the elasticity-dominated coupled regime. However, for the sake of clarity, we first analyze in detail the existence of a critical pulling stress in a simpler case, i.e., a nongrowing actin network.

Nongrowing actin network under load (static limit: $v_p^0=0$)

If filaments associate to and dissociate from nucleators at the surface but are unable to polymerize, there will be no propulsive force, because dissociated filaments do not elongate. In this case, the force balance (Eq. 3) at the interface between the network and the surface to which it is attached reduces to

$${\sigma }_{nn}=f_a{\rho }_a,$$ (14)

This means that each attached filament supports a time-independent force $f_{\ell }=f_a={\sigma }_{nn}/{\rho }_a$ during its lifetime. In these conditions, the dissociation rate takes the simple form: $k_d=k_d^0\exp \left({\sigma }_{nn}b/k_{B}T{\rho }_a\right)$.

In this static limit, the resistive force does not arise from the continuous loading of attached filaments simply because the network does not elongate ($v_p^0=0$). The applied stress σ_nn is resisted by a static deformation δ_s of the links and the network.

Eqs. 2 and 14 fully determine the state of the system. The fraction of attached filaments, ${\rho }_a/{\rho }_f\equiv {\tilde{\rho }}_a$, is given by

$${\tilde{\rho }}_a\left[1+\frac{k_d^0}{k_a}\exp \left(\frac{{\tilde{\sigma }}_{nn}}{{\tilde{\rho }}_a}\right)\right]=1,$$ (15)

and depends on two dimensionless parameters: the normalized stress ${\tilde{\sigma }}_{nn}\equiv {\sigma }_{nn}/{\sigma }_0$ (with ${\sigma }_0\equiv {\rho }_f{k}_{B}T/b$) and the ratio $k_a/k_d^0$. Equation 15 does not have solutions for all values of the parameters. For a given value of the ratio $k_a/k_d^0$, there exists a critical pulling stress ${\sigma }_{nn,s}^c$ above which attached filaments cannot sustain the applied load and the surface loses the contact with the network (the subscript s in ${\sigma }_{nn,s}^c$ stands for static, or nongrowing, network). This instability corresponds to a saddle-node bifurcation, and the dimensionless critical stress ${\tilde{\sigma }}_{nn,s}^c$ is given implicitly by

$$\frac{k_a}{k_d^0}={\tilde{\sigma }}_{nn,s}^c\exp \left(1+{\tilde{\sigma }}_{nn,s}^c\right).$$ (16)

The saddle-node bifurcation implies that for ${\sigma }_{nn}>{\sigma }_{nn,s}^c$ there are no steady-state solutions in which the network can keep contact with the surface v_p. This is because the rate at which attached filaments dissociate from nucleators cannot be balanced by filaments attaching to nucleators, which eventually leads to a complete loss of attached filaments and, therefore, the total loss of contact between the network and the surface from which it is attached.

The critical stress ${\tilde{\sigma }}_{nn,s}^c$ depends on a single dimensionless parameter, namely, the ratio $k_a/k_d^0$ (Fig. 4 D). Using typical values for the different parameters (${\rho }_f=1/{\xi }^2$, where ξ corresponds to the actin network mesh size, and $\xi \simeq 50\text{nm}$; $b\simeq 1\text{nm}$; $k_{B}T\simeq 4\text{pNnm}$; $k_a/k_d^0\sim {10}^{-1}-{10}^2$ (26)), the critical stress lies within the range ${\sigma }_{nn,s}^c\sim \left(0.4-4\right){10}^{3}Pa$, which is smaller than or approximately the elastic modulus of actin networks ($E\sim {10}^3-{10}^{4}Pa$ (6)).

Figure 4.

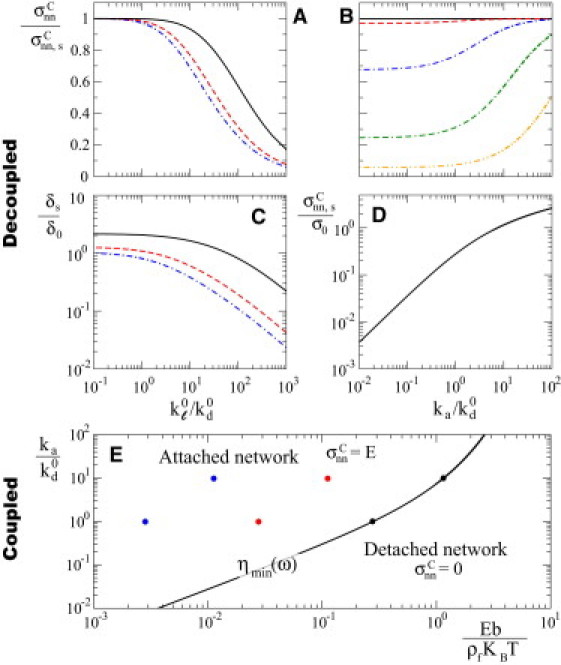
Critical stresses. Maximal pulling stresses above which the network is detached from the surface in both the link-dominated uncoupled regime (A–D) and the elasticity-dominated coupled regime (E). (A and B) Dependence of the critical stress ${\sigma }_{nn}^c$, normalized to the critical stress ${\sigma }_{nn,s}^c$ for a static network, on $k_{\ell }^0/k_d^0$ (A) and $k_a/k_d^0$ (B). The different curves in A correspond to $k_a/k_d^0=10,1,0.1$ (continuous black line, dashed red line and dashed-dotted blue line, respectively), and in B they correspond to $k_{\ell }^0/k_d^0=0.1,1,10,{10}^2,{10}^3$ (continuous black line, dashed red line, dashed-dotted blue line, double dashed-dotted green line, dashed-doubled dotted orange line, respectively). (C) Static stretch δ_s as a function of $k_{\ell }^0/k_d^0$ for $k_a/k_d^0=10,1,0.1$ (same code as in A). (D) Dependence of the critical stress ${\sigma }_{nn,s}^c$ for a static network on $k_a/k_d^0$. (E) Dynamical regimes in the elasticity-dominated coupled regime, which depend only on the parameters $k_a/k_d^0$ and $Eb/{\rho }_f{k}_{\text{B}}T$. The line η_min separates the parameter space in which the network is detached from the surface and that in which the network maintains contact to the surface. In the latter case, the critical stress is ${\sigma }_{nn}^c=E$. (In color online.)

The instability described here has been studied in other systems (23,27,29) and corresponds to the collective breakage of bonds when they sustain a force in a configuration where they act in parallel.

Growing network under applied load: the link-dominated uncoupled regime

Critical stress

Network growth can only be sustained for values of pulling stresses that lead to a network growth velocity $v_p\le v_p^0$; indeed, the network cannot grow faster than the maximal elongation velocity of its constituent filaments. If the pulling stress is such that the network velocity reaches the maximal polymerization velocity of individual filaments, $v_p=v_p^0$, the filament-nucleator links and the network can then accommodate an additional static stretch δ_s, in similarity to the static limit described above. In this case ($v_p=v_p^0$), the sum of the network and filament-nucleator link deformations reads $\delta \left(t\right)+{\delta }_{\ell }\left(t\right)=v_p^{0}t+{\delta }_s$, which replaces Eq. 10. Consequently, the instantaneous link force $f_{\ell }\left(t\right)$ in the link-dominated uncoupled regime for a network growing at velocity $v_p^0$ reads $f_{\ell }\left(t\right)=\kappa \left(v_p^{0}t+{\delta }_s\right)$. Using the latter expression to evaluate the instantaneous detachment rate $k_{id}\left(t\right)$ (Eq. 6), we can calculate the dependence of k_d and f_a on δ_s. For pulling stresses that lead to a growth velocity $v_p^0$, Eq. 4 becomes an equation for the amount of static stretch assumed by the system, which does not have solutions above a critical stress ${\sigma }_{nn}^c$.

The value of the critical stress ${\sigma }_{nn}^c$ for a growing network corresponds to the maximal value of σ_nn that allows finite stable solutions of Eq. 4 for δ_s, with $v_p=v_p^0$. Fig. 4, A and B, show the dependence of the critical stress on the relevant parameters in the link-dominated uncoupled regime, $k_{\ell }^0/k_d^0$ and $k_a/k_d^0$ (Table 1). For small loading rates ($k_{\ell }^0\ll k_d^0$), attached filaments are hardly loaded by network growth during their lifetime, and their static stretch assumes almost all of the deformation (Fig. 4 C). The dynamics of the system is therefore similar to that of a static network and, accordingly, the critical stress in this limit converges to the critical stress of a static network (Fig. 4 A). Increasing loading rates ($k_{\ell }^0\gg k_d^0$) reduce the pulling stress that the network can sustain, leading to smaller values of critical stress compared with those of a static network (${\sigma }_{nn}^c<{\sigma }_{nn,s}^c$). Network growth makes the attachment of the network to the surface more fragile because it adds a contribution to the load that each attached filament must resist. This effect is more pronounced for smaller values of $k_a/k_d^0$ because there are fewer attached filaments that are able to sustain the external pulling stress (Fig. 4 B). At large loading rates, the filaments are almost exclusively dynamically loaded, and the static component of their stretch vanishes asymptotically (Fig. 4 C).

Stress-velocity relation

The stress-velocity relation depends on $k_a/k_d^0$ and $k_{\ell }^0/k_d^0$ in this regime (Fig. 5, A and B). The network growth velocity decreases with stresses opposing network elongation, and larger values of the ratio $k_a/k_d^0$ lead to more a pronounced decrease. At small loading rates the growth velocity shows a stress-independent region for pulling stresses (Fig. 5 A), in which $v_p=v_p^0$, whereas at large loading rates this stress-independent regime is hardly noticeable (Fig. 5 B).

Figure 5.

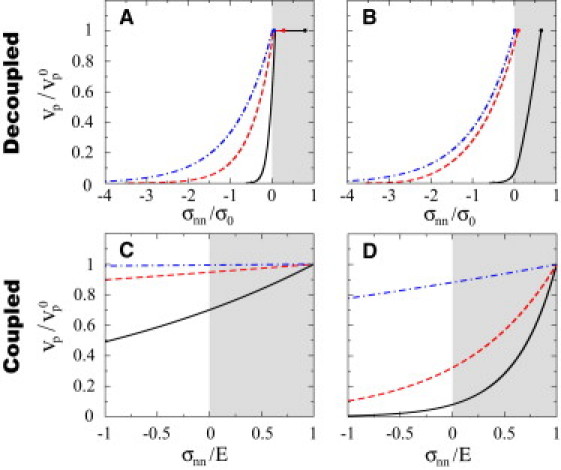
Stress-velocity relations. Network growth velocity v_p as a function of the applied stress σ_nn in both the link-dominated uncoupled regime (A and B) and the elasticity-dominated coupled regime (C and D). Shadowed areas indicate pulling stresses. (A and B) The link-dominated uncoupled regime, showing the dependence of the stress-velocity relation on the ratio $k_a/k_d^0$ ($k_a/k_d^0=10,1,0.1$; continuous black line, dashed red line, and dashed-dotted blue line, respectively) for small and large loading rates, (A) $k_{\ell }^0/k_d^0=0.1$ and (B) $k_{\ell }^0/k_d^0={10}^2$, respectively. The dots correspond to the critical pulling stress of each curve. (C and D) The elasticity-dominated coupled regime, showing the dependence of the stress-velocity relation on the parameter $Eb/{\rho }_f{k}_{\text{B}}T$ for (C) $k_a/k_d^0=1$($Eb/{\rho }_f{k}_{B}T=0.28,0.028,0.0028$; continuous black line, dashed red line, and dashed-dotted blue line, respectively) and (D) $k_a/k_d^0=10$($Eb/{\rho }_f{k}_{\text{B}}T=1.15,0.115,0.0115$; continuous black line, dashed red line, and dashed-dotted blue line, respectively). The values of the parameters for the stress-velocity relations shown are marked as dots in Fig. 4E. (In color online.)

Growing network under applied load: the elasticity-dominated coupled regime

Critical stress

The dynamics in this regime is controlled by two dimensionless parameters: $Eb/{\rho }_f{k}_{\text{B}}T$ and $k_a/k_d^0$ (Table 1). For each value of the parameter $Eb/{\rho }_f{k}_{\text{B}}T$, there exists a minimal value η_min of the ratio $k_a/k_d^0$ below which there is no attachment of the network to the surface (Fig. 4 E). The nature of this threshold is analogous to that found in the static limit (see above), because in this limit the average resistive force per attached filament is constant and given by $f_{\ell }=f_a=E/{\rho }_a$. For values of $k_a/k_d^0$ above threshold ($k_a/k_d^0>{\eta }_{min}$), the critical stress is ${\sigma }_{nn}^c=E$. Below η_min, the critical stress vanishes necessarily.

Stress-velocity relation

The stress-velocity relation depends on $k_a/k_d^0$ and $Eb/{\rho }_f{k}_{\text{B}}T$ in this regime (Fig. 5, C and D). For small values of both parameters, network growth is nearly stress-independent. Stresses larger than E imply very large strains that actin networks would not be able to sustain. For increasing values of $k_a/k_d^0$, network growth is considerably slowed down and shows a much stronger dependence on applied stress (Fig. 5 D).

Discussion and Conclusions

We addressed the local growth of actin networks at surfaces by deriving a local mesoscopic theory that averages over the detailed microscopic kinetics of actin filaments. The physical quantities in our description (e.g., the external stress σ_nn) should be understood as the local values of extended fields when describing mesoscopic systems. Our framework accounts for the competition between detached filaments that elongate and push the surface forward and attached filaments that resist growth. It also highlights the nature of the resistive force, as generated by the continuous loading of attached filaments due to network growth. This generic system-level description can be applied to describe many phenomena involving the growth of actin networks, such as actin-based motility, cell blebbing, and cell crawling (1).

Our framework predicts the existence of a critical stress above which the growing actin network loses contact from the surface from which it is growing, thereby halting network growth. Although the particular value of the critical stress depends on the parameters of each dynamical regime (Figs. 2 and 4), the existence of a critical stress for network attachment is generic. Moreover, network growth lowers the value of the critical stress, meaning that higher network growth velocities lead to a weaker contact between the network and the surface from which it grows. The coupling presented above between the resistive force and the network velocity, which arises naturally from the continuous loading of attached filaments by network growth, provides a natural mechanism to control the degree of network attachment. This control mechanism arises from the dynamics of the system itself and allows the network to grow and maintain contact with the propelled object for a wide range of parameters. Although the description above is more suitable for Arp2/3-mediated actin network growth, the main equations (Eqs. 2 and 3) and the coarse-graining method to calculate the average force of attached filaments as well as their average lifetime are general and can be used to derive the dynamics of actin networks in many other conditions, such as formin-mediated actin polymerization and autocatalytic growth.

The dimensionless parameters ${\rho }_f{\left(\kappa /E\right)}^2$ and $v_p^{0}E/k_d^0\kappa$ that control the different dynamical regimes (Fig. 2) depend on kinetic parameters of actin dynamics at the microscopic scale, and thus can be varied by actin-binding proteins and/or other molecular cues. Specifically, one can vary the actin filament surface density ρ_f, which corresponds to ${\rho }_f=1/{\xi }^2$, with ξ being the network mesh size, by changing the nucleator concentration at the surface and the actin monomer concentration in solution. The Young's modulus E of the actin network can be increased by the addition of cross-linking proteins such as filamin, and the maximal polymerization velocity of actin filaments $v_p^0$ can be modified by changes in profilin and/or actin monomers in solution. Finally, the detachment rate of attached filaments can be modified by the addition of VASP (26,31). These are just some examples of possible molecular perturbations that would affect the dimensionless parameters that control the dynamical regimes. Many more molecular perturbations could be done (8,12), allowing a quantitative exploration of the parameter space and the different dynamical regimes in Fig. 2.

Although it is challenging to perform controlled experiments in vivo, many examples of actin-based motility provide convenient experimental setups to test our results. The in vitro propulsion of disk-like particles (32) coated on one side with actin nucleators would allow one to directly test the predictions on network growth under vanishing external load, because the nucleator density and the concentrations of key proteins (e.g., profilin, VASP, and capping proteins) can be carefully controlled. Other examples of actin-based motility, such as the motion of oil droplets with actin comet tails, are better suited for quantitative measurements of critical stress. Recent experiments showed that changing the lifetime of attached filaments (i.e., $k_d^0$) by the addition of VASP induces the catastrophic detachment of the actin network at the back of oil drops propelled by actin comet tails, leading to their saltatory motion (31). This instability is not observed above a critical drop radius and can be well explained by the existence of a critical pulling stress, as we show in the Supporting Material. Finally, the stress-velocity relation (or, equivalently, force-velocity relation) for a growing actin network can also be accessed experimentally (33). The observed force-velocity relations for the in vitro growth of actin networks (33) can only be explained in our framework if filament branching and capping are explicitly taken into account. (An extension of this work that includes filament branching and capping will be published elsewhere, because they are beyond the scope of this article.) This suggests that changes in actin filament density in the network are critical to explain the force-velocity curves observed experimentally (33).

Our description identifies the relevant physical and biochemical parameters that govern the local dynamics of actin network growth, and thus highlights the molecular and cellular processes that may control and regulate actin-based motility.