Abstract
We quantify the potential landscape to determine the global stability and coherence of biological oscillations. We explore a gene network motif in our experimental synthetic biology studies of two genes that mutually repress and activate each other with self-activation and self-repression. We find that in addition to intrinsic molecular number fluctuations, there is another type of fluctuation crucial for biological function: the fluctuation due to the slow binding/unbinding of protein regulators to gene promoters. We find that coherent limit cycle oscillations emerge in two regimes: an adiabatic regime with fast binding/unbinding and a nonadiabatic regime with slow binding/unbinding relative to protein synthesis/degradation. This leads to two mechanisms of producing the stable oscillations: the effective interactions from averaging the gene states in the adiabatic regime; and the time delays due to slow binding/unbinding to promoters in the nonadiabatic regime, which can be tested by forthcoming experiments. In both regimes, the landscape has a topological shape of the Mexican hat in protein concentrations that quantitatively determines the global stability of limit cycle dynamics. The oscillation coherence is shown to be correlated with the shape of the Mexican hat characterized by the height from the oscillation ring to the central top. The oscillation period can be tuned in a wide range by changing the binding/unbinding rate without changing the amplitude much, which is important for the functionality of a biological clock. A negative feedback loop with time delays due to slow binding/unbinding can also generate oscillations. Although positive feedback is not necessary for generating oscillations, it can make the oscillations more robust.
Introduction
The goal of biology is to understand both function and behavior. In a living cell, biological functions and behaviors are often regulated by the underlying complex and diverse genetic networks. The oscillatory behavior, known as a biological clock, is one of the most interesting and enigmatic phenomena. Such rhythms exist at many levels in living organisms, from the cell proliferation cycle to the circadian sleep-wake cycle of higher organisms (1–11). Recently, many timing mechanisms accompanied with periodic behaviors were studied, including three-gene repressilators (3,12,13), self-repressors with explicit time delays (14,15), cell cycles (1,9,16–18), circadian clock networks (2,6,7,19,20), and engineered two-component motifs from synthetic biology with the interplay of positive feedback and negative feedback (activated repression) (14,17,21,22). These studies shed light on the underlying mechanisms. However, the understanding of global stability and robustness for these biological rhythms remains a challenge.
In the cell, intrinsic fluctuations not present in bulk are unavoidable due to the limited number of proteins. There have been increasing numbers of studies on how the gene regulatory networks can be stable and functional under such highly fluctuating environments (3,13,23). Furthermore, another type of fluctuation, arising from the biochemical reactions of the regulatory proteins binding/unbinding to the genes, can be significant for oscillatory dynamics. Conventionally, it was often assumed that the binding/unbinding is significantly faster than the synthesis and degradation (adiabatic limit) (24). It leads to the expected single stable state for a self-repressor, which can be measured in experiments (25). Although this assumption may hold in some prokaryotic cells in certain conditions, in general there is no guarantee it is true. In fact, one expects in eukaryotic cells and some prokaryotic cells, binding/unbinding can be comparable or even slower than the corresponding synthesis and degradation (nonadiabatic limit). The phrases “adiabatic” and “nonadiabatic” were borrowed from condensed matter physics to refer to fast binding/unbinding and slow binding/unbinding in gene regulatory networks. This can lead to nontrivial stable states appearing as a result of new timescales introduced due to the nonadiabaticity (26–31), which is confirmed by recent single-molecule, single-gene experiments (32,33). Therefore, the challenge for us is to understand how the biological oscillations can be robust and coherent under both intrinsic fluctuations and nonadiabatic fluctuations.
The global stability and robustness of a complex network can be quantitatively studied if the underlying Hamiltonian is known a priori, or in other words, the potential landscape is known. However, most of the dynamical systems are not integrable and not in equilibrium. The potential landscape is not known a priori for these systems, and the global stability will be a challenge. Therefore, with the presence of intrinsic stochasticities, the more appropriate way to describe the dynamics of such nonequilibrium systems is the evolution of probabilistic distributions rather than deterministic trajectories.
In this study, by exploring the underlying master equations describing intrinsic fluctuations, we will quantify the nonequilibrium landscape to explore the global stability and robustness of oscillation networks. The steady-state probability introduces a probabilistic landscape. The underlying potential landscape for a dynamical nonequilibrium system is logarithmically related to the steady-state probability distribution, which can be used to quantitatively address the global stability or robustness of oscillations (11,17–20,22). In particular, we explore a gene network motif in the experimental synthetic biology studies of two genes that mutually repress and activate each other with self-activation and self-repression: i.e., activated repression. This network has been engineered in the experiment of synthetic biology and generated robust oscillations in Escherichia coli (14). In this design, as shown in Fig. 1 a, the hybrid promoter (Plac/ara−1) is composed of an activation operator site from the araBAD promoter and a repression operator site from the lacZYA promoter. The activation operator site is placed in its normal location relative to the transcription starter site, and the repression operator site is placed both upstream of the activation operator site and immediately downstream of the transcription starter site. Plac/ara−1 is activated by the binding of araC protein (A) and repressed by the binding of lacI protein (R). The araC, lacI genes are under the control of Plac/ara−1 to form coregulated transcription modules. It was found that if two identical promoters Plac/ara−1 control the transcription of araC and lacI proteins, the network can generate robust oscillations when the binding/unbinding is fast (14). However, we found that with the same circuit wiring, if the two hybrid promoters controlling AraC and LacI proteins are not identical, robust oscillations can be generated even when the binding/unbinding is slow, which can be tested by single molecule single gene expression experiments in the future.
Figure 1.
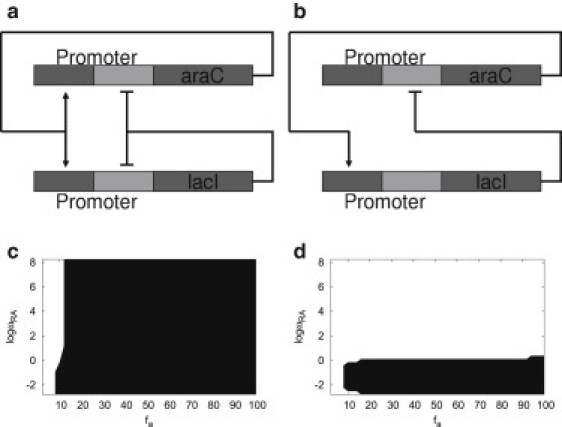
(a) Network diagram of the dual-feedback network: two genes mutually repress and activate each other with self-activation and self-repression. (b) Network diagram of the single loop negative feedback with one intermediate step. (c) Phase diagram of dual-feedback network. (d) Phase diagram of the single loop negative feedback network. (Key: ωRA, binding/unbinding parameter; fa, activation factor of protein synthesis; solid representation, oscillation region; open representation, monostable region.)
When the binding/unbinding speed is slow (nonadiabatic limit), gene regulation processes involve at least two kinds of biochemical reactions: binding/unbinding reactions of regulatory proteins to the promoters, and synthesis/degradation reactions of proteins. It provides another level of complexity for the dynamical process. Therefore, the gene state of the promoter switching on (activated) or off (repressed) is important for the transcription process and the production of functional proteins. We found that stochastic fluctuations generated by protein binding/unbinding processes can be a possible mechanism for robust oscillations. Similar behaviors were shown in competence cycles (5). Furthermore, we also found that even without positive feedback, the coherent oscillation can persist with networks as in Fig. 1 b. Phase diagrams in Fig. 1, c and d, show that positive feedback is not necessary for coherent oscillations in the nonadiabatic regime (slow binding/unbinding). However, positive feedback can make the oscillation more robust with respect to changing parameters, which agrees with previous observations (14).
Methods and Materials
In Fig. 1 a, the hybrid promoter α can be bound by the regulatory protein β with the binding rate hαβ and dissociation rate fαβ (both hαβ and fαβ can depend on protein concentration nβ). The synthesis of protein α is controlled by the gene state of promoter α. There are two types of genes, araC (A) and lacI (R), to be translated into activators araC (A) and repressors lacI (R), respectively. The activator A can bind to the promoter of the gene A (R) to activate the synthesis rate of A (R); the repressor R can bind to the gene A (R) to repress the synthesis rate of A (R). Here, activators A bind on the gene A and R as a dimer with the binding rate
and
respectively; repressors R bind on the gene A and R as a tetramer with the binding rate
and
respectively. Therefore, each gene has four states and the whole system has 16 gene states in total. For simplicity, we neglect the roles of mRNAs by assuming translation processes are very fast. The model can be expressed by the following chemical reactions,
| (1) |
| (2) |
| (3) |
with α = A (R) for the hybrid promoter Plac/ara−1 of gene A (R). For the gene state index ij of gene Oα, the first index i = 1(0) stands for the activator protein A unbound(bound) on the promoter α; the second index j = 1(0) stands for the repressor protein R unbound(bound) on the promoter α. The term gijA(gijR) is the synthesis rate of the protein A (R) when the gene A (R) is in state ij. The probability distribution of the microstate is indicated as Pijkl(nA,nR), where nA and nR are the concentration of the activator A and the repressor R, respectively. The index i (j) represents the gene A occupation state by the protein A (R), and the index k (l) represents the gene R occupation state by the protein A (R).
There are 16 master equations for the probability evolution, as listed in the Supporting Material. The steady-state probability distribution satisfies
for all i, j, k, l (34). The total probability distribution is
A direct way to find the steady state Pss is through kinetic simulations (35). The generalized potential function U of the nonequilibrium network can be quantified as U(nA,nB) = − ln P(ss). It maps to the potential landscape, which gives a quantitative measure of the global stability and function of the underlying network (17).
It is also helpful to study the deterministic moment equations for understanding the qualitative behavior in an approximate way (13,15,36). The mth moment is defined as
where γ indicates the general gene state: 1111, 1100, etc. To get mth-order moment equations, multiply nm and then sum over n on both sides of master equations. In principle, moment equations are equivalent to original master equations if we can include all moment equations to the infinite order. Because an infinite number of moment equations are difficult to deal with, we introduce the Hartree-type approximation and the Poisson assumption to find a smaller, more manageable set of moment equations up to the first-order moments. The Hartree-type approximation, an approximation for electron wave functions in multielectron atoms, considers the probability distribution for each type of protein separated from that of the others and only has a mean-field type of effect on the others, which means
In addition, the Poisson assumption of concentration distributions
and
can truncate moment equations up to the first-order. Therefore, we reached a closed form of 16 deterministic moment equations, which only involve zero-order moments cijA(R) and first-order moments (see the Supporting Material).
Oscillations in Adiabatic/Nonadiabatic Regime
Following experimental reports (14), we performed several sets of parameters with which deterministic limit cycles persist from slow (nonadiabatic) to fast (adiabatic) binding/unbinding. The parameters are set as follows: the protein degradation rate kA = 0.2/min, kR = 0.005/min. Both genes have maximum protein synthesis rate when they are occupied by the activator A and unoccupied by the repressor R: gA01 = κA = 4gR01= 4κR = 8000/min. Also, we set the activation factor fa = 100 and repression factor fr = 100,000: and . The binding/unbinding processes are asymmetric between the gene A and the gene R: hRA ≠ hAA = hA, hAR = hRR = hR, fRA ≠ fAA = fA, and fAR = fRR = fR. We fix ωA = FA/kA = ωR = fR/kR = 1000, which indicates the binding/unbinding of the activator A to the gene A and the repressor R to both genes are fast. The value ωRA = fRA/kA measures the binding/unbinding speed of the activator A to the gene R. Equilibrium constants, which indicate the ratio between unbinding and binding speed, are set as XAeq = fRA/hRA = fAA/hAA = 450 and XReq = fAR/hAR = fRR/hRR = 33,750. All parameters are listed in Table 1.
Table 1.
Reaction parameters in the dual-feedback network
| kA | kR | κA = 4κR | fa | fr | ωA = ωR | XAeq | XReq |
|---|---|---|---|---|---|---|---|
| 0.2/min | 0.005/min | 8000/min | 100 | 100,000 | 1000 | 450 | 33,750 |
In the adiabatic limit, the binding/unbinding processes are much faster than the synthesis/degradation. Therefore, the binding/unbinding processes reach equilibrium faster than the other processes and the probability of the gene state is determined as the function of the concentrations. Then, the system can be simplified into a two-dimensional birth/death process with effective synthesis rates (24,26,27):
| (4) |
| (5) |
The solutions of deterministic moment equations (see the Supporting Material) for different values of ωRA, as in Fig. 2, show that the system can have oscillations and limit cycles in a large range of parameters, as shown in phase diagram of Fig. 1 c, which were also demonstrated by previous experiments (14). However, it is noted that the oscillation mechanism changes from the adiabatic regime (high binding/unbinding rate ωRA) to the nonadiabatic regime (low binding/unbinding rate ωRA). In the adiabatic regime (fast binding/unbinding), oscillations come from the nonlinear cooperative interactions of negative feedback in gene circuits. The trajectories of the activator A are relatively smooth, as shown in Fig. 2, e and f. While in the nonadiabatic regime (slow binding/unbinding), the activator A shows spikes in periodic time series, as shown in Fig. 2, a and b. Such abrupt oscillations are due to the slow binding/unbinding processes, whose kinetic mechanism is very different with oscillations in the adiabatic regime (fast binding/unbinding).
Figure 2.
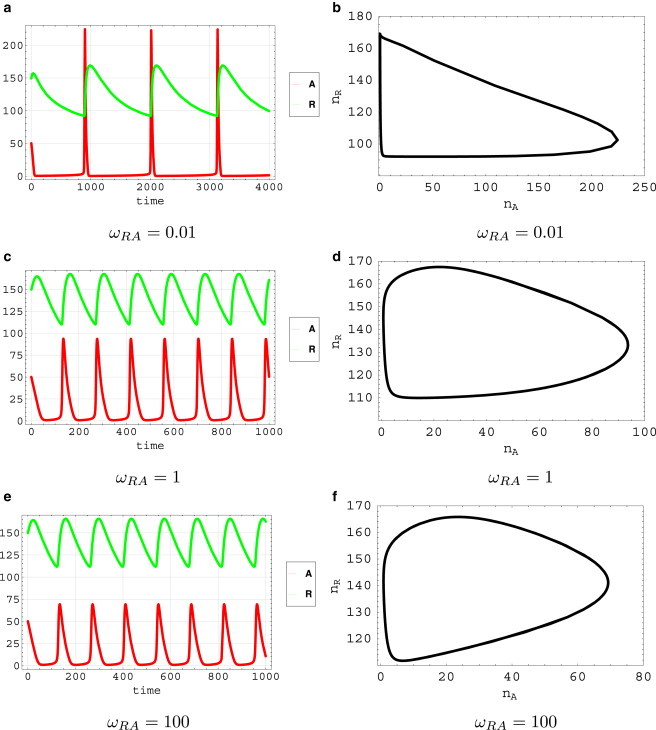
(a, c, and e) Deterministic trajectories of the dual-feedback network for protein concentrations nA and nR versus time t. (b, d, and f) Deterministic trajectories of the dual-feedback network (limit cycles in the counterclockwise direction) in the plane of nA versus nR.
In this circuit, there is a two-step negative feedback loop: R → A → R. Both regulatory steps are realized by the protein binding/unbinding on the promoters. In nonadiabatic regime, the slow binding/unbinding rate of the activator A on the gene R gives significant time delays of this negative feedback. Once the promoter on the gene R is bound by the activator A, the expression of the repressor R will rise to a high level, which will strongly repress the expression of the activator A to a lower level. If the binding/unbinding speed is fast, the lower concentration of the activator A will immediately reduce the activation effect on the repressor R. However, for the nonadiabatic case, where the binding/unbinding rate is low, the activator A will keep binding on the gene R for a long time even when the concentration of the activator A is very low. Thus, the negative feedback is delayed until the activator A dissociates from the gene R. When the activator A dissociates from the gene R, the expression level of the repressor R will decrease. The low nR has less repression on the activator A and a spike of nA occurs until the gene R is bound by the activator A again, which starts another round of limit cycle. Therefore, nonadiabatic limit cycles are realized by the time-delayed negative feedback due to the slow switching of the gene state R. Because the time delay is the major oscillation mechanism, the oscillation period is more controlled by the binding/unbinding rate ωRA of the activator A on the gene R. In Fig. 3, we demonstrated the changing of oscillation periods and amplitudes with respect to the changing of ωRA. We noted that the oscillation period decreases monotonically with the increasing of ωRA. So it can be tuned in a large range by adjusting the binding/unbinding rate ωRA without changing the oscillation amplitude very much, which was observed in the experiments (14). Such gene expression design is important for biological rhythms like heartbeats and cell cycles, which require a near-constant output (amplitude) over a range of frequencies (8). However, in the adiabatic regime (fast binding/unbinding), because of the different oscillation mechanism (nonlinear cooperative interactions for effective average of gene states) in which gene states can be omitted, the oscillation period will not change any more with the change of the binding/unbinding rate.
Figure 3.
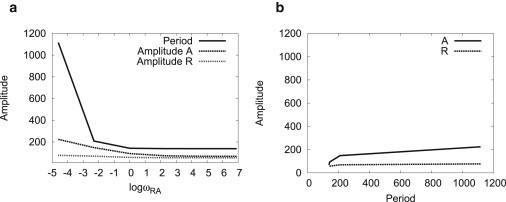
(a and b) Oscillation periods and amplitudes from deterministic trajectories.
Deterministic moment equations give approximation solutions for limit-cycle trajectories without providing further information such as the oscillation coherence. Therefore, probability distributions for the master equations and stochastic trajectories from Gillespie simulations, which do not need any approximations, are necessary to study the coherence of stochastic oscillations. As one can notice, in the intermediate regime of ωRA = 1, although the deterministic equations give oscillation solutions as in Fig. 2, c and d, the probabilistic landscape and phase coherence of stochastic trajectories show that the oscillations are as not as coherent as in the adiabatic regime (fast binding/unbinding) and the nonadiabatic regime (slow binding/unbinding).
Oscillation Landscapes in Adiabatic and Nonadiabatic Regimes
The robustness of oscillations can be shown by probability distributions or potential landscapes. For a stable and coherent oscillation, the landscape in the nA−nR plane should have a clear Mexican-hat shape, because the stochastic trajectories fluctuates around the limit cycle, which leads to a higher probability on the ring than the center and the outside (17,18).
We observed sharp Mexican-hat topography in potential landscapes for both the adiabatic regime (large ωRA) and the nonadiabatic regime (small ωRA), but blurred topography in the intermediate regime between them, as shown in Fig. 4. In the adiabatic regime, the binding/unbinding is very frequent. The resulting landscape is an effective average of different gene states. The oscillation mechanism is then due to this effective potential with the nonlinear cooperative interactions of the negative feedback. Therefore, the ring of the limit cycle in the potential landscape is relatively smooth. In addition, because of fast switching between on- and off-gene states, the coupling between these two gene states is very strong and the resulting potential landscapes of on- and off- gene states are very similar, as in shown Fig. 4 d. In the nonadiabatic regime (small ωRA), the oscillation mechanism is the time delay of the negative feedback due to the infrequent binding/unbinding. The ring of the limit cycle is very bumpy, as shown in Fig. 4 a. There are seemingly disconnected gaps on the right side and the left side of the ring, which are due to the occasional gene state jumping or switching. The landscapes of on- and off- gene states are very different because the coupling between these two gene states is very weak and the synthesis rates are very different between on- and off-states. In the intermediate ωRA regime, the gene state switches between on- and off-states, but not so frequently. As shown in Fig. 4, b and c, the resulting landscapes of on- and off-gene states are qualitatively more similar to each other than in the nonadiabatic regime but not as similar as in the adiabatic regime. The potential landscapes for more parameters are given in the Supporting Material.
Figure 4.
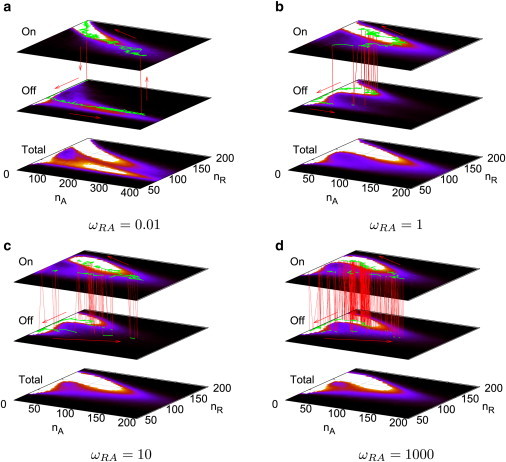
(a–d) For the dual-feedback network, probability distribution landscapes in nA−nR plane of different gene states and stochastic trajectories for different binding/unbinding rate ωRA. Most robust oscillations in (a) the nonadiabatic and (d) the adiabatic regime accompanied with sharpest Mexican hats. (Vertical axis) The terms on(0) and off (1) indicate the sum of states with the gene R bound or unbound by the activator A, respectively. The term Total indicates the sum of probability landscapes of the on-state and the off-state.
Stochastic trajectories associated with the underlying potential landscapes are given in Fig. 4 for different ωRA. The nonadiabatic stochastic limit cycle with small ωRA is shown in Fig. 4 a. Here, because the binding rate of the activator A on the gene R is small, the system will wait for a long time in the on-state with small nA until the activator A is dissociated from the gene R and the gene state switches to the off-state. The oscillation is initiated by this dissociation and the concentration of R will decrease without the activation from A. The low concentration of R will have less repression on A and a spike will occurs, which makes nA jump to a large value. With a large nA, the hybrid promoter on the gene R will have a higher chance to be bound by the activator A because the binding rate is ∼hRA/2 n2A. Once the gene R is occupied by the activator A, nR will increase and repress nA to a smaller value for a long time (because unbinding rate fRA is small in nonadiabatic limit) until the next dissociation of the activator A from the gene R, which starts the next spike and another round of oscillation (limit cycle). In this process, fluctuations arising from the biochemical reactions of protein binding/unbinding to the promoters are significant for oscillatory dynamics. The adiabatic stochastic limit cycle is shown in Fig. 4 d. With large ωRA, the state of gene R switches frequently and the effective protein synthesis rates are given as in Eqs. 4 and 5, which are determined by the average weight of each gene state. Therefore, specific gene states can be effectively omitted in the dynamics and the nonlinear cooperative interactions of between the activator A and the repressor R drive robust limit cycles.
Landscape Topography and Coherence of Adiabatic and Nonadiabatic Oscillations
Barrier height can be used to quantify the landscape topography. In particular, it is a good quantity to measure how sharp the Mexican-hat landscape is for oscillations. It is defined as the potential (U = −lnPSS) difference between the peak inside the limit cycle (top of the hat) and the peak on the limit cycle loop (top of the oscillation ring). When the central barrier of the limit cycle is high, stochastic trajectories can hardly go across it and are forced to run around the barrier, which makes stable limit cycles (oscillations). Therefore, the barrier height measures how stable the limit cycle (oscillation) is. Barrier heights for different ωRA are shown later in Fig. 6 a. As the ωRA increases, the barrier height first decreases then increases. Such turn-over behavior confirmed our observation that there are robust oscillations (sharp Mexican hat) in both the adiabatic regime (large ωRA) and the nonadiabatic regime (small ωRA) but only weak oscillation (blurred Mexican hat) in between.
Figure 6.
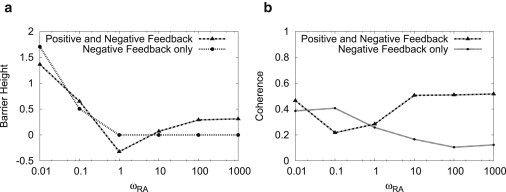
(a) Barrier height and (b) phase coherence of the dual-feedback loops and the single loop negative feedback for different ωRA.
In addition, we calculated the degree of coherence in the oscillation measured by phase coherence to be defined as (12)
| (6) |
where θ is a step function,
| (7) |
| (8) |
and phase angle ϕ(t) is the angle between two consecutive positions N(t) at time t and N(t+τ) at time t+τ on the stochastic trajectories with respect to the potential central peak O of the limit cycle loop, as shown in Fig. 5. When the trajectories move randomly without any coherence, which means N(t) has a half-chance of moving clockwise and a half-chance of moving counterclockwise, we will have
The value |ξ| increases when the regularity of the oscillation increases, which indicates that, statistically, the consecutive trajectories move in one direction more than the other direction. When the oscillation is completely coherent, i.e., the trajectories move in one direction only, we will have
for the counterclockwise direction or
for the clockwise direction. The value τ, the time interval between two consecutive positions, should be much smaller than the oscillation period but should be larger than the fast noisy fluctuations (12). When ϕ(t) is a large angle closing to 180°, it will be hard to tell whether ϕ(t) is positive or negative. To avoid such conditions, we chose τ much smaller than the oscillation period, so that N(t + τ) will not move too far away, respective to N(t). The value of ξ depends on τ. When τ is shorter, the result of ξ will be smaller because more small forward and backward motions in the trajectory will be captured. The phase coherence for different ωRA with τ = 0.01/kR is shown in Fig. 6 b. We noted that strong coherent oscillations in both adiabatic (fast binding/unbinding) and nonadiabatic regimes (slow binding/unbinding). It correlates with the shape of Mexican hat characterized by the barrier heights.
Figure 5.
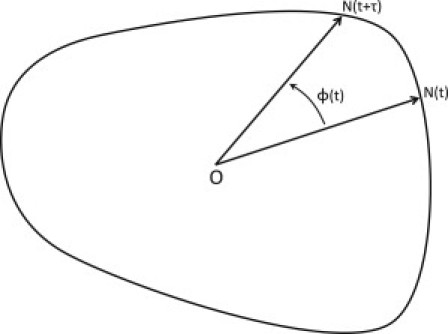
Sketch map for the definition of phase coherence ξ.
Both the barrier heights and phase coherence indicate two mechanisms of oscillations. In the adiabatic regime, the Mexican hat-shape topography of the landscape is mostly determined by the averaged (over the fast binding/unbinding) nature of protein synthesis and degradation. The oscillations emerge from nonlinear cooperative interactions and are more stable because the binding/unbinding is faster. In the nonadiabatic regime, Mexican hat-shape topography of the landscape is mostly determined by the binding/unbinding of regulatory proteins to the genes (averaged over the fast synthesis and degradation of proteins). The oscillations emerge from time delays due to the slow binding/unbinding to the genes and are more stable because the binding/unbinding is slower.
Oscillations with a Single Negative Feedback Loops
In addition, we uncovered another regime in the parameter space, which would support oscillatory behavior controlled by a time delayed negative feedback loop. The network circuit is shown in Fig. 1 b and chemical reactions are
| (9) |
| (10) |
The setup is almost the same as the network in Fig. 1 a, except there is no direct self-repressions in the gene R and no direct self-activations in the gene A in Fig. 1 b. The time-delay effect is from the intermediate step that R can bind on the gene A and repress the synthesis of A, and A can bind on the gene R and enhance the synthesis of R, which forms a two-step negative feedback loop. Thus, the time-delay effect strongly depends on the binding/unbinding rate. With the suitable parameters of kA = 0.2/min, kR = 0.05/min, g1A = 4g0R = k = 80/min, fA = g1A/g0A = 100, fR = g0R/g1R = 100,000, ωA = 0.1, ωR = 1000, and all other parameters (same as listed in Oscillations in Adiabatic/Nonadiabatic Regime), robust oscillations can be generated from this single-loop negative feedback, as shown in Fig. 7. All parameters are listed in Table 2.
Figure 7.
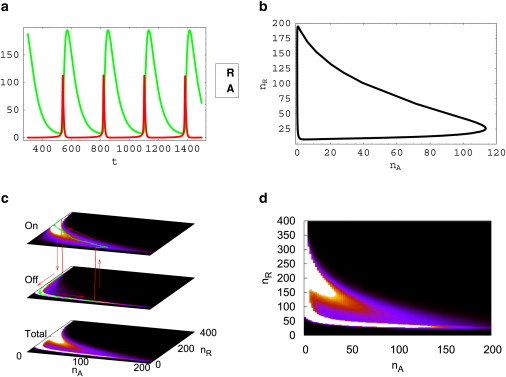
Oscillations from the single loop negative feedback with time delays, ωA = 0.1. (a) Deterministic oscillatory trajectories for protein concentrations nA and nR versus time t. (b) Deterministic limit cycles in the nA−nR plane. (c) Stochastic trajectories between states on(0) and off (1) of the gene R. (d) The Mexican hat-shape probability distribution landscape in the nA−nR plane.
Table 2.
Reaction parameters in the single loop negative feedback
| kA | kR | κA = 4κR | fa | fr | ωA = ωR | XAeq | XReq |
|---|---|---|---|---|---|---|---|
| 0.2/min | 0.05/min | 80/min | 100 | 100,000 | 1000 | 450 | 33,750 |
Because of the relatively slow binding/unbinding speed ωA of the activator A, the dynamics are quite similar to the nonadiabatic (slow binding/unbinding) oscillation case in the dual-feedback loop. According to the deterministic trajectories in Fig. 7, a and b, and stochastic trajectories in Fig. 7 c, the activator A still oscillates with sharp spikes, just as in the case of the dual loop with positive feedback. The oscillation is initiated by the dissociation of the activator A from the promoter site of the gene R. Then, the concentration nR decreases to a level so that it cannot give enough repression on A and a spike of nA is triggered. With the high concentration nA, the activator A rebinds to the gene R. It promotes the concentration nR and a limit cycle finishes. Such stochastic process of the limit cycle is almost the same as the network in Fig. 1 a with dual-feedback loops. It also gives a sharp Mexican-hat shape landscape as shown in Fig. 7, c and d. In Fig. 7, c and d, the ring of the limit cycle is bumpy, which is similar to the nonadiabatic landscape in Fig. 4 a for the network with dual-feedback loops. Also, the landscapes of on- and off- gene states are very different because the coupling between these two gene states is weak. The potential landscapes for more parameters are given in the Supporting Material.
It was shown that with multiple intermediate steps such as transcription, translation, monomers to dimers, dimers to tetramers, and tetramers binding on promoters, oscillations can be generated (14,15). Here we found that with the slow binding/unbinding, robust oscillations can be generated by a two-step, single-loop negative feedback. So the positive feedback is not necessary for a stable oscillation. However, in this regime, the positive feedback can make the oscillation more robust as shown in phase diagrams Fig. 1, c and d. With positive feedback, oscillations robustly exist from small ωRA to large ωRA, while without positive feedback, oscillations are not robust in the adiabatic regime (fast binding/unbinding) and exist only stably in the range of small ωRA or the nonadiabatic regime. The positive feedback is not necessary for a coherent oscillation only in this regime. Outside of this regime, when the binding/unbinding rate is fast, the coherent oscillation and limit cycle will disappear without positive feedback. So, in the fast binding/unbinding regime, the positive feedback is necessary for a coherent oscillation. In nonadiabatic regime (slow binding/unbinding), the positive feedback is not necessary for a coherent oscillation. The barrier heights for different ωRA values are given in Fig. 6 a. It shows that, in the robust oscillation regime, there are sharp Mexican-hat landscapes and the central barrier height of the limit cycle is high. It means that the trajectories are kept on the path on the ring and have little chance of crossing the central barrier. The phase coherence results (for τ = 0.01/kR) as in Fig. 6 b also agree with the landscape topography analysis. The landscape topography is quantified by the barrier heights that characterize the shape of Mexican hat. We see the higher central barrier height, the more robust and coherent oscillations.
Discussion and Conclusion
In this study, we explored the global stability of a biological oscillation. We found that coherent limit cycle oscillations emerge in adiabatic (fast binding/unbinding) and nonadiabatic regimes (slow binding/unbinding). In both regimes, the underlying landscape has the topography of a Mexican hat. The shape of the Mexican hat provides the quantitative description of the capability of the system to communicate with each other. The global stability and robustness are quantitatively determined by the topography of the landscape characterized by the barrier height. The coherence of the oscillations is shown to be correlated with the shape of Mexican hat. In the adiabatic regime, the binding/unbinding of regulatory proteins to the promoters are fast compared with the synthesis/degradation of proteins. The Mexican hat-shape topography of the landscape is mostly determined by the effective protein synthesis and decay. The oscillations are more stable because the binding/unbinding is faster. In the nonadiabatic regime, the binding/unbinding of regulatory proteins to the promoters are slow compared with the synthesis/decay of proteins. The Mexican hat-shape topography of the landscape is mostly determined by the binding/unbinding of regulatory proteins to the genes. The oscillations are more stable because the binding/unbinding is slower.
The two regimes give the two mechanisms of producing robust oscillations: from the adiabatic regime with effective nonlinear cooperative interactions by averaging the gene states, and from the nonadiabatic regime with time delays due to the slow binding/unbinding to the gene. Such oscillations are robust in a large range of parameters. By changing the binding/unbinding rate, the oscillation period can be easily tuned without changing the amplitude much. Such design is suitable for biological rhythms like cell cycles and heartbeats that require a near constant output over an adjustable wide range of frequencies (8). The adiabatic oscillation due to effective cooperative interactions agrees with previous observations (14). The nonadiabatic oscillation patterns due to the slow binding/unbinding can be examined by single-molecule single-gene expression experiments (33). We also generated robust oscillations in both deterministic and stochastic sense with a single-loop, two-step negative feedback with suitable time delays due to the slow binding/unbinding process. It means positive feedback is not necessary for oscillations but can make oscillations more robust.
Our landscape framework and the corresponding analysis on the adiabatic and nonadiabatic fluctuations are general and can be applied to other dynamical systems and networks to explore the global stability and function.
Acknowledgments
We thank the National Science Foundation for support.
Supporting Material
References
- 1.Chen K.C., Calzone L., Tyson J.J. Integrative analysis of cell cycle control in budding yeast. Mol. Biol. Cell. 2004;15:3841–3862. doi: 10.1091/mbc.E03-11-0794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yu W., Hardin P.E. Circadian oscillators of Drosophila and mammals. J. Cell Sci. 2006;119:4793–4795. doi: 10.1242/jcs.03174. [DOI] [PubMed] [Google Scholar]
- 3.Elowitz M.B., Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- 4.Süel G.M., Garcia-Ojalvo J., Elowitz M.B. An excitable gene regulatory circuit induces transient cellular differentiation. Nature. 2006;440:545–550. doi: 10.1038/nature04588. [DOI] [PubMed] [Google Scholar]
- 5.Schultz D., Ben Jacob E., Wolynes P.G. Molecular level stochastic model for competence cycles in Bacillus subtilis. Proc. Natl. Acad. Sci. USA. 2007;104:17582–17587. doi: 10.1073/pnas.0707965104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nakajima M., Imai K., Kondo T. Reconstitution of circadian oscillation of cyanobacterial KaiC phosphorylation in vitro. Science. 2005;308:414–415. doi: 10.1126/science.1108451. [DOI] [PubMed] [Google Scholar]
- 7.Rust M.J., Markson J.S., O'Shea E.K. Ordered phosphorylation governs oscillation of a three-protein circadian clock. Science. 2007;318:809–812. doi: 10.1126/science.1148596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tsai T.Y.C., Choi Y.S., Ferrell J.E., Jr. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science. 2008;321:126–129. doi: 10.1126/science.1156951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nasmyth K. At the heart of the budding yeast cell cycle. Trends Genet. 1996;12:405–412. doi: 10.1016/0168-9525(96)10041-x. [DOI] [PubMed] [Google Scholar]
- 10.Goldbeter A. Cambridge University Press; Cambridge, UK: 1997. Biochemical Oscillations and Cellular Rhythms: The Molecular Bases of Periodic and Chaotic Behavior. [Google Scholar]
- 11.Li C., Wang E.K., Wang J. Landscape and flux decomposition for exploring global natures of non-equilibrium dynamical systems under intrinsic statistical fluctuations. Chem. Phys. Lett. 2011;505:75–80. [Google Scholar]
- 12.Yoda M., Ushikubo T., Sasai M. Roles of noise in single and coupled multiple genetic oscillators. J. Chem. Phys. 2007;126:115101. doi: 10.1063/1.2539037. [DOI] [PubMed] [Google Scholar]
- 13.Kim K.Y., Lepzelter D., Wang J. Single molecule dynamics and statistical fluctuations of gene regulatory networks: a repressilator. J. Chem. Phys. 2007;126:034702. doi: 10.1063/1.2424933. [DOI] [PubMed] [Google Scholar]
- 14.Stricker J., Cookson S., Hasty J. A fast, robust and tunable synthetic gene oscillator. Nature. 2008;456:516–519. doi: 10.1038/nature07389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lepzeltera D., Feng H., Wang J. Oscillation, cooperativity, and intermediates in the self-repressing gene. Chem. Phys. Lett. 2010;490:216–220. doi: 10.1016/j.cplett.2010.03.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Laub M.T., McAdams H.H., Shapiro L. Global analysis of the genetic network controlling a bacterial cell cycle. Science. 2000;290:2144–2148. doi: 10.1126/science.290.5499.2144. [DOI] [PubMed] [Google Scholar]
- 17.Wang J., Xu L., Wang E.K. Potential landscape and flux framework of nonequilibrium networks: robustness, dissipation, and coherence of biochemical oscillations. Proc. Natl. Acad. Sci. USA. 2008;105:12271–12276. doi: 10.1073/pnas.0800579105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang J., Li C., Wang E.K. Potential and flux landscapes quantify the stability and robustness of budding yeast cell cycle network. Proc. Natl. Acad. Sci. USA. 2010;107:8195–8200. doi: 10.1073/pnas.0910331107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang J., Xu L., Wang E.K. Robustness and coherence of a three-protein circadian oscillator: landscape and flux perspectives. Biophys. J. 2009;97:3038–3046. doi: 10.1016/j.bpj.2009.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li C., Wang E.K., Wang J. Landscape, flux, correlation, resonance, coherence, stability, and key network wirings of stochastic circadian oscillation. Biophys. J. 2011;101:1335–1344. doi: 10.1016/j.bpj.2011.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Atkinson M.R., Savageau M.A., Ninfa A.J. Development of genetic circuitry exhibiting toggle switch or oscillatory behavior in Escherichia coli. Cell. 2003;113:597–607. doi: 10.1016/s0092-8674(03)00346-5. [DOI] [PubMed] [Google Scholar]
- 22.Li C., Wang E.K., Wang J. Potential landscape and probabilistic flux of a predator prey network. PLoS ONE. 2011;6:e17888. doi: 10.1371/journal.pone.0017888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Arkin A., Ross J., McAdams H.H. Stochastic kinetic analysis of developmental pathway bifurcation in phage λ-infected Escherichia coli cells. Genetics. 1998;149:1633–1648. doi: 10.1093/genetics/149.4.1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ackers G.K., Johnson A.D., Shea M.A. Quantitative model for gene regulation by λ phage repressor. Proc. Natl. Acad. Sci. USA. 1982;79:1129–1133. doi: 10.1073/pnas.79.4.1129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Austin D.W., Allen M.S., Simpson M.L. Gene network shaping of inherent noise spectra. Nature. 2006;439:608–611. doi: 10.1038/nature04194. [DOI] [PubMed] [Google Scholar]
- 26.Hornos J.E.M., Schultz D., Wolynes P.G. Self-regulating gene: an exact solution. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:051907. doi: 10.1103/PhysRevE.72.051907. [DOI] [PubMed] [Google Scholar]
- 27.Walczak A.M., Onuchic J.N., Wolynes P.G. Absolute rate theories of epigenetic stability. Proc. Natl. Acad. Sci. USA. 2005;102:18926–18931. doi: 10.1073/pnas.0509547102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schultz D., Onuchic J.N., Wolynes P.G. Understanding stochastic simulations of the smallest genetic networks. J. Chem. Phys. 2007;126:245102. doi: 10.1063/1.2741544. [DOI] [PubMed] [Google Scholar]
- 29.Kepler T.B., Elston T.C. Stochasticity in transcriptional regulation: origins, consequences, and mathematical representations. Biophys. J. 2001;81:3116–3136. doi: 10.1016/S0006-3495(01)75949-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Artyomov M.N., Das J., Chakraborty A.K. Purely stochastic binary decisions in cell signaling models without underlying deterministic instabilities. Proc. Natl. Acad. Sci. USA. 2007;104:18598–18963. doi: 10.1073/pnas.0706110104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Feng H., Han B., Wang J. Dominant kinetic paths of complex systems: gene networks. J. Phys. Chem. Lett. 2010;1:1836–1840. [Google Scholar]
- 32.Singh A., Weinberger L.S. Stochastic gene expression as a molecular switch for viral latency. Curr. Opin. Microbiol. 2009;12:460–466. doi: 10.1016/j.mib.2009.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Choi P.J., Cai L., Xie X.S. A stochastic single-molecule event triggers phenotype switching of a bacterial cell. Science. 2008;322:442–446. doi: 10.1126/science.1161427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gardiner C. Springer-Verlag; Berlin, Germany: 2004. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences. [Google Scholar]
- 35.Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- 36.Walczak A.M., Sasai M., Wolynes P.G. Self-consistent proteomic field theory of stochastic gene switches. Biophys. J. 2005;88:828–850. doi: 10.1529/biophysj.104.050666. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


