Abstract
We develop a coalescent-based simulation tool to generate patterns of single nucleotide polymorphisms (SNPs) in a wide region encompassing both the original and duplicated genes. Selection on the new duplicated copy and interlocus gene conversion between the two copies are incorporated. This simulation enables us to explore how selection on duplicated copies affects the pattern of SNPs. The fixation of an advantageous duplicated copy causes a strong reduction in polymorphism not only in the duplicated copy but also in its flanking regions, which is a typical signature of a selective sweep by positive selection. After fixation, polymorphism gradually increases by accumulating neutral mutations and eventually reaches the equilibrium value if there is no gene conversion. When gene conversion is active, the number of SNPs in the duplicated copy quickly increases by transferring SNPs from the original copy; therefore, the time when we can recognize the signature of selection is decreased. Because this effect of gene conversion is restricted only to the duplicated region, more power to detect selection is expected if a flanking region to the duplicated copy is used.
IT has been revealed that gene duplication is abundant in a wide range of eukaryotes (Lynch and Conery 2000; Bailey et al. 2002; Blanc and Wolfe 2004), which is in agreement with the idea that gene duplication plays an important role in genome evolution (Ohno 1970). As well as other mutational mechanisms, gene duplication provides a new mutant (i.e., duplicated copy), whose fate is largely influenced by the selective advantage or disadvantage it confers. In most cases, a duplicated extra copy is deleterious or nearly neutral, so that it is most likely eliminated from the population, but it occasionally happens that a duplicated copy fixes in the population because of its selective advantage, thereby contributing adaptive genome evolution (reviewed in Walsh 2003; Innan and Kondrashov 2010). In either case, a new duplicate has to go through the phase in which it is polymorphic in the population; that is, there is variation in the copy number of the gene (i.e., CNV or copy number variation).
CNVs draw much recent attention in at least two research fields: medical and evolutionary genetics. In humans, there are substantial amounts of effort on identifying CNVs (Iafrate et al. 2004; Sebat et al. 2004; Sharp et al. 2005, 2006; Conrad et al. 2006; Locke et al. 2006; Redon et al. 2006) because of their potential association with genetic diseases (Lupski 1998; Ji et al. 2000; Stankiewicz and Lupski 2002; Lupski and Stankiewicz 2005). In evolutionary genetics, the major interest would be in CNVs that play adaptive roles. Examples include CNVs at CCL3L1 (Gonzalez et al. 2005) and AMY1 (Perry et al. 2007) genes in humans, ASIP gens in sheep (Norris and Whan 2008), and SOX5 gens in chickens (Wright et al. 2009).
One of the major goals of population genetics is to understand the evolutionary mechanism behind genetic variation within a population, and there is growing attention to CNVs in the last decade. To uncover the evolutionary forces behind genetic variation, the common approach in molecular population genetics is to look at the pattern of single nucleotide polymorphisms (SNPs) in the surrounding region of the focal variation, and the coalescent theory plays the central role in such SNP analyses because it provides powerful and flexible simulation tools that makes it possible to perform statistical analysis (Kreitman 2000; Nielsen 2005; Biswas and Akey 2006). For example, coalescent simulations under neutrality can be used to statistically address the question whether the SNP data can be explained by a null neutral model. If not, then coalescent simulations with selection will provide great insight into the mode and intensity of selection that operated on the focal genetic variation. A number of coalescent simulators have been developed, including the commonly used ms software (Hudson 2002) for neutral simulations, and others incorporating selection (Spencer and Coop 2004; Teshima and Innan 2009; Ewing and Hermisson 2010).
This kind of coalescent simulation-based analysis of SNPs can be applied to CNVs, but the currently available coalescent simulators cannot be directly used because there is a duplicate-specific mutational mechanism, that is, interlocus gene conversion. Gene conversion is a recombination process, which is usually described as a copy-and-paste process. This process makes the coalescent process more complicated than the standard single-locus coalescent. The coalescent for a pair of duplicated genes (original and derived copies) with gene conversion under neutrality was first described by Innan (2003), in which it is assumed that the duplicated copy is fixed in the population. This theory allows simulating patterns of polymorphism in both original and duplicated copies simultaneously. Thornton (2007) extended this model such that it can handle a CNV with the assumption that no selection works on the CNV. Another limitation in these works is that SNPs only within the duplicated region are considered.
We here introduce a further extended simulation algorithm that allows simulating patterns of SNPs in a large region encompassing both of the original and duplicated copies. We also incorporate selection on the focal CNV. These two new features make it possible to fully explore the role of natural selection on CNVs.
Model and Simulation
The model is based on the previous works (Innan 2003; Thornton 2007), except for the two major modifications as mentioned above. The evolutionary process is considered under the Wright–Fisher model. The diploid population size is denoted by N, which is assumed constant over time. As mutational mechanisms, we incorporate point mutation, recombination (crossing over) and interlocus gene conversion. The model considers two types of chromosomes: the ancestral one with only the original copy (Figure 1, top) and the derived one with both the original and duplicated copies (Figure 1, bottom). These two types are referred to as classes S and D, respectively. We assume that all duplicated copies in the population originate from a single duplication event (this assumption will be relaxed later). Recombination occurs at any site in the region, while interlocus gene conversion occurs specifically between the original and duplicated regions.
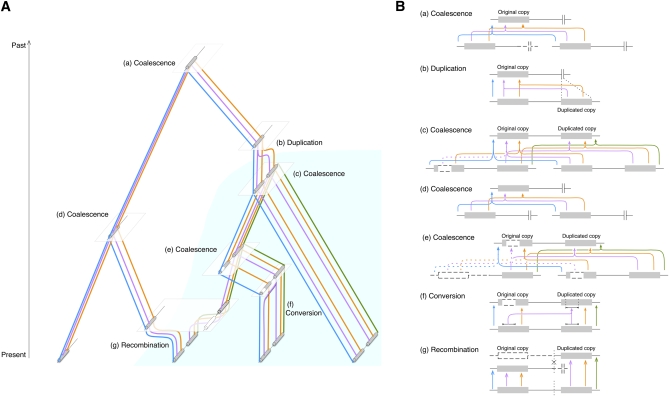
Figure 1 .
Illustration of the simulated region in this study. The shaded areas represent the duplicated pairs of copies, that is, the original and duplicated copies. A single-copy (class S) chromosome has only one copy whereas a duplicated (class D) chromosome has two copies.
To simulate a pattern of SNPs in this entire region illustrated in Figure 1, the coalescent process is considered backward in time. In brief, it first requires construction of an ancestral recombination graph with gene conversion between them (Innan 2003; Thornton 2007). This process handles coalescence, recombination, and gene conversion. Then, point mutations are distributed on the graph, which results in a realization of the SNP pattern.
In the construction of ancestral recombination graph, the coalescent process is considered as follows. The process is basically identical to the biallelic coalescent, where coalescent events occur only between chromosomes in the same class. Suppose that there are single-copy (class S) and duplicated (class D) chromosomes at a certain time point, t. Then, the rate of coalescence within class S is given by
and that within class D is
where f(t) is the frequency of the class D chromosomes at time t. Time is measured in units of 2N generations. Two ancestral lineages are merged by a coalescent event. Thus, coalescence decreases the number of ancestral lineages by one. This process continues backward in time from the present to the origin of the duplicated copy at time T, conditional on the trajectory of the population frequency of the duplicated chromosome, f(t). The trajectory can be obtained by a simple simulation as described later. When t > T, there are only class S chromosomes, the standard coalescent can be applied.
Recombination (crossing over) simultaneously occurs along the coalescent process. It is assumed that the per-site recombination rate (r) is constant across the entire simulated region. The population recombination rate is defined as R = 4Nr. In the coalescent, recombination breaks a chromosome into two parts, and considering backward in time, they will have different coalescent histories before the recombination event. Thus, a recombination event increases the number of ancestral lineages by one. When recombination occurs between a pair of chromosomes within the same class, the process is simple; recombination can occur at any site in the region, and the two parts broken by the recombination stay in the same class. The process is slightly complicated when a recombination occurs between classes S and D, for example, event (g) in Figure 2. Recombination cannot occur in the duplicated region, because this region is absent in the class S chromosome. If recombination between the two copies occurs as illustrated in Figure 2B, then the ancestral lineage of the 5′ part moves to class S and the 3′ part stays as it is (class D).
Figure 2 .
(A) Illustration of ancestral recombination graph of a pair of duplicate copies with gene conversion between them. The process is considered backward in time, from present to past. The area of light blue represents the frequency change of the duplicated copy. (B) Detailed illustrations for the coalescent, recombination, gene conversion, and duplication events in A. (a) Coalescent event to reach the MRCA of the entire region, (b) duplication event, (c–e) coalescent events between a pair of class D chromosomes, (f) gene conversion event between the original and duplicated copies, and (g) recombination between class S and D chromosomes. The recombination breakpoint is shown by X. The open boxes and dashed lines are ancestral lineages that do not originate from the sampled chromosomes.
Interlocus gene conversion transfers a certain length of DNA tract from one copy to the corresponding region in the other copy. We assume that gene conversion can be initiated at any site in the duplicated region at rate g. Then, the elongation of converted tract is randomly terminated at rate 1/ℓ, so that the tract length follows a geometric distribution with mean ℓ. See Teshima and Innan (2004) for a detailed procedure for determining a transferred region. See also Mansai et al. (2011) for an alternative gene conversion model, in which gene conversion is initiated at a double-strand break and elongation follows in both directions. The per-site interlocus gene conversion rate, c, is defined as the rate at which a particular site is converted to the other copy per generation. c is given by g × ℓ, and the population gene conversion rate is defined as C = 4Nc. Interlocus gene conversion occurs not only between paralogous copies on the same chromosome, but also between those on homologous chromosomes. These events are referred to as intra- and interchromosomal gene conversion, respectively, and let w be the proportion of the former. Through this study, we assume w = 1 for convenience, but as was demonstrated by Thornton (2007), the effect of incorporating interchromosomal gene conversion on the pattern of SNPs is small when recombination occurs between the two copies. Gene conversion also occurs between an orthologous pair (i.e., allelic gene conversion), which is ignored in our model. Gene conversion between the paralogous pairs can be considered as a coalescent event between the two copies. Therefore, when gene conversion is active, it is possible to trace the ancestral lineages to the most recent common ancestor (MRCA) of all copies in the sample, including both the original and derived copies (Innan 2003).
The entire coalescent process with recombination and gene conversion proceeds backward in time from present to past. Therefore, if we suppose that there are ns single-copy (class S) and nd duplicated (class D) chromosomes in the sample with size n = ns + nd at present (t = 0), the process starts with the initial condition , where and are the numbers of ancestral lineages for classes S and D, respectively. and decrease with coalescent and increase with recombination. The process is conditional on the trajectory of the frequency f(t) for 0 < t < T, which has to be prepared prior to the coalescent simulation.
Selection is incorporated through the trajectory of the frequency of the duplicated chromosomes, rather than by setting selection parameters directly in the coalescent algorithm (Teshima and Innan 2009). The trajectory reflects a random process with genetic drift and selection, and the coalescent algorithm can be applied conditionally on any trajectory. See Teshima and Innan (2009) for details about trajectory. A trajectory of f(t) can be generated in any method.
To simulate a pattern of SNPs, it is required to continue the coalescent process to the MRCA of all copies in the sample, which is usually much deeper than the MRCA of all orthologs in the sample (Innan 2003). Once an ancestral recombination graph to the MRCA is constructed, point mutations can be placed randomly on it, which results in a SNP pattern. We implemented this coalescent process by modifying a widely used coalescent simulator, ms (Hudson 1991). The software is available upon request.
Thus far, we assumed that all class D chromosomes originated from a single duplication event, and the following recurrent duplication events are not allowed. This assumption is easily relaxed. Let u be the backward duplication rate. Then, an ancestral lineage in class S moves to class D by rate u per generation.
Results
By using coalescent simulations, the behavior of the pattern of SNPs through the fixation of a new duplicated copy was investigated with and without selection. Through this article, it was assumed that the original and duplicated copies are 1 kb long, which are separated by a 9 kb of intervening sequence. In addition, the simulated region includes 1 kb of the upstream region of the original copy and 1 kb of the downstream region of the duplicated copy, so that the entire region is 12 kb (see Figure 1). We fixed the per-site population mutation rate θ = 0.01 and the population recombination rate R = 0.01, which are within typical ranges of eukaryotes (e.g., Hartl and Clark 2006). In the simulation with active gene conversion, the population gene conversion rate was assumed to be C = 1 per site. We also assumed that the average length of converted tracts ℓ = 100, such that the initiation rate of gene conversion (g = C/ℓ) is identical to the recombination rate.
The time of the duplication event is given by t = 0, at which the frequency of the duplicated chromosomes is 1/2N. We considered only trajectories conditional on its fixation. Given a trajectory, 10,000 replications of the coalescent simulation were performed. All duplicated (class D) chromosomes were assumed to be originated from a single duplication event and eventually fix in the population (i.e., u = 0), unless otherwise mentioned. The sample size was fixed to be n = 100 through this article. ns and nd were determined such that they were proportional to their population frequencies, 1 – f and f, respectively. π was computed for each replication and their averages and density distributions were investigated. The average pairwise nucleotide difference (π) was computed by using all sampled chromosomes (n), but for the duplicated copy, because this region is absent in the class S chromosomes, π was computed for all class D chromosomes (nd).
Simulations under neutrality
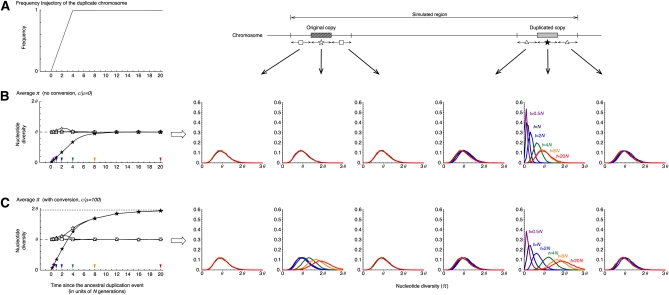
The results under neutrality are summarized in Figure 3. Theoretically, the fixation of a neutral allele takes on average 4N generations. It is known that such a neutral allele that is destined to fix increases in frequency almost linearly (Tajima 1990). Although the fixation time of a neutral allele is variable, to demonstrate the point here, we fixed the trajectory to be a linear function with a fixation time of 4N generations as illustrated in Figure 3A (This assumption will be relaxed later.) Figure 3 shows the averages and density distribution of π obtained from 10,000 replications of the coalescent simulation. We focused on six regions, the original and duplicated regions and their 5′- and 3′-flanking regions. For these six regions, the distributions of π at five different time points are shown on the right (t = 0.5N, N, 2N, 4N, 8N, and 20N presented by purple, navy blue, blue, green, orange, and red, respectively), and on the left their averages are plotted along time. We obtained almost identical results for the two flanking regions of the original (and duplicated) regions, and their average is shown in the left plot. Figure 3B shows the behavior of π with no gene conversion. At time t = 0, a new duplicate arises, so that there is no variation (π = 0) within the duplicated copy, while π has a unimodal distribution with mean in other regions as theoretically expected. As the fixation process proceeds, the level of polymorphism within the duplicated copy increases and becomes almost as much as the other regions when t > 8N. In the franking region to the duplicated copy, is slightly larger than θ when the duplicated copy is in the fixation phase (e.g., t = N and 2N), which is in agreement with the theoretical prediction (Innan and Tajima 1997). Around the original copy, is almost identical to θ through the process because there is a relatively long distance between the two copies so that the original copy is less affected by the fixation.
Figure 3 .
The behavior of the nucleotide diversity, π, along the fixation of a new duplicated (class D) chromosome under neutrality. (A) The assumed trajectory of the frequency of the duplicated chromosomes and the subregions where we measured π. We focused on six 1-kb subregions, the 5′-flanking region of the original copy, the original copy, 3′-flanking region of the original copy, 5′-flanking region of the duplicated copy, the duplicated copy, and 1-kb 3′-flanking region of the duplicated copy. (B) Left shows the changes of the average π for each subregion since the duplication event. The dashed line at (π = θ) is the expectation at equilibrium. Right shows the distributions of π for t = 0.5N (purple), N (navy blue), 2N (blue), 4N (green), 8N (orange), and 20N (red) in the six subregions. The results for the 5′- and 3′-flanking regions of the original (duplicated) copy is almost identical; on the left, their average is shown by open squares (triangles). No conversion is assumed. The arrowheads on the left indicate the time points, at which the level of polymorphism was investigated (the result is shown on the right with the same color). (C) Active gene conversion is assumed (C = 1 or c/μ = 100 with the average tract length ℓ = 100). The broken lines at π = 1.95θ and π = θ on the left are the expectations at equilibrium with and without gene conversion, respectively (Innan 2003). n = 100 and θ = R = 0.01 are assumed in the entire simulations. See text for details about the parameters.
Figure 3C shows the results of selection with gene conversion. The major effect of gene conversion in this process is to equalize the level of polymorphism in the two copies (Innan 2002). As expected, in Figure 3C increases more quickly than in Figure 3B. This is because preexisting SNPs in the original copy are transferred to the duplicated copy, so that the duplicated copy does not have to wait for new mutations to accumulate SNPs. Another effect of gene conversion is to increase the level of polymorphism in both copies; the expectation of π can be almost doubled with active gene conversion unless the two copies are tightly linked (see Innan 2002, 2003 for theoretical expectations). In our setting, the expectation at equilibrium is E(π) ≈ 2θ at both copies, which is in agreement with the simulation results. As time increases, for the two copies approaches 2θ, which is also seen in the density distribution of π. Gene conversion has no effect on other regions.
Simulations with selection
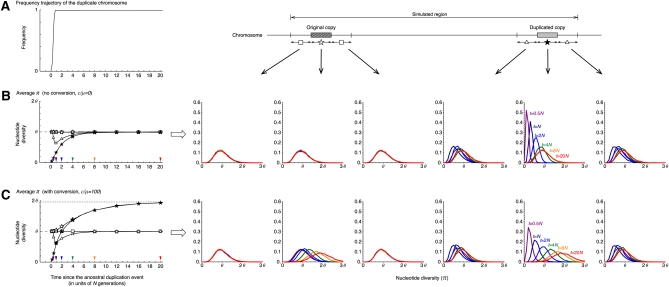
To explore the effect of selection, we considered two levels of selection intensity Ns = 10 and 100, where we assumed a simple directional selection for the duplicated copy with no dominance (s is the selective coefficient for the duplicated chromosome). When Ns = 10 (Figure 4), the fixation time of the duplicated copy is roughly 0.8N generations, which is much shorter than the neutral case in Figure 3. In our simulation, because the relative contribution of genetic drift is negligible with strong selection, we determined the trajectory in a deterministic form (Ewens 2004). With no gene conversion (Figure 4B), the effect of selection is seen in the duplicated copy and its flanking regions. Within the duplicated copy, we observe a slightly faster recovery of π toward θ than that of the neutral case (Figure 3B), because the duplicated copy increases in frequency dramatically and has more chance to accumulate new SNPs within it. In the flanking region, due to this quick fixation, a dramatic reduction of π is observed by the hitchhiking effect. This intensity of selection is not strong enough to affect the original copy and its flanking regions that locate relatively far from the target of selection (i.e., the duplicated copy). When gene conversion is active (Figure 4C), we can confirm the two major effects of gene conversion; that is, increases to 2θ in both copies and this recovery process is faster.
Figure 4 .
The behavior of the nucleotide diversity, π along the fixation of a new duplicated chromosome. Selection is assumed to work for the duplicated chromosomes with intensity Ns = 10. All other parameters are the same as those in Figure 3.
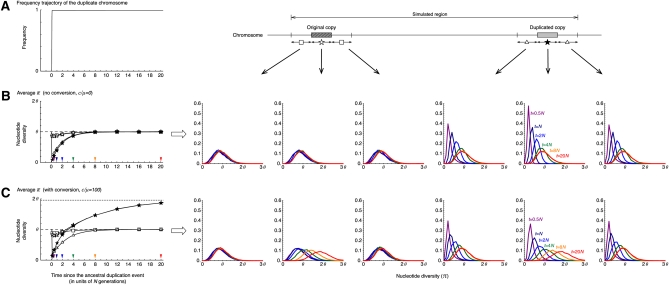
When Ns = 100 (Figure 5), the duplicated copy fixes much faster than the case of Ns = 10, resulting in a drastic reduction in π in the duplicated copy and its flanking regions. A slight reduction is also observed in the original copy and its flanking regions. Then, increases to θ in both copies with no gene conversion (Figure 5B) and to 2θ with gene conversion (Figure 5C).
Figure 5 .
The behavior of the nucleotide diversity, π, along the fixation of a new duplicated chromosome. Selection is assumed to work for the duplicated chromosomes with intensity Ns = 100. All other parameters are the same as those in Figure 3.
Thus, when selection works for a new duplicated copy, it is expected that the level of polymorphism is significantly reduced within and around the duplicated copy, regardless of whether gene conversion is active or not. The reduced polymorphism will be recovered and eventually reaches its expectation at equilibrium, which is θ in nonduplicated regions and >θ in the duplicated region with gene conversion. Therefore, it is suggested that directional selection can be detected by focusing on the reduction of the level of SNPs around the target of selection (i.e., the duplicated copy), a common approach in molecular population genetics (Kim and Stephan 2002; Harr et al. 2002), but a slight caution is needed to interpret the pattern of SNPs within the duplicated copy when gene conversion is active.
Testing for selection
To explore how this idea for detecting selection works, we performed additional simulations. In practice, we focused on the reduction in π in and around the duplicated copy. A statistical test should examine if the observed level of variation within the duplicated chromosomes can be explained under neutrality. This requires a null distribution of π conditional on the current frequency of the duplicated chromosomes in the sample.
We ran 10,000 replications of the coalescent simulation conditional on the current frequency, p. We considered four different frequencies, p = 0.25, 0.5, 0.75, and 0.9. In each replication, we simulated a neutral trajectory given p to incorporate the effect of random genetic drift, and the coalescent simulation was performed conditional on this trajectory. This treatment is different from the previous simulation to demonstrate the average pattern of π under neutrality in Figure 3, where a neutral trajectory was deterministically given. To produce a null distribution of π, we include the effect of random genetic drift by simulating an independent trajectory for each replication of the simulation.
This simulation produced a distribution of π given p under neutrality, which can be used a null distribution to test for selection. Note that this assumes that the population mutation rate θ is known, which is not very unreasonable because we may be able to have a reliable estimate of θ from other unlinked loci. Then, simulations with selection were performed with the same p, and Table 1 summarizes the proportion of the replications where the neutrality is rejected at the 5% level (one-tailed test). In Figures 4 and 5, we have shown that the level of polymorphism is largely affected by selection around the duplicated copy; therefore, we here focused on the region within the duplicated copy and its surrounding region. In this test, we used a 1 kb region within the duplicated copy, and also the same length of the region that is directly 5′ upstream of the duplicated copy (the result was essentially identical when the 3′ downstream region was used). For the duplicated region, we computed π for only the class D chromosomes because there is no duplicated sequence in the class S chromosomes. For the 5′ flanking region, we computed π for the class D chromosomes only and also for all chromosomes (the results for latter are shown in parentheses foll owing those for the former in Table 1).
Table 1 . Proportion of replications (%) that rejected neutrality.
| Duplicated region |
Flaking region |
||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before fixation p |
After fixation t1 |
Before fixation1
p |
After fixation t1 |
||||||||||||||||||
| c/μ | Ns | 0.25 | 0.5 | 0.75 | 0.9 | 0 | N | 2N | 4N | 0.25 | 0.5 | 0.75 | 0.9 | 0 | N | 2N | 4N | ||||
| 0 | 1 | 5.2 | 5.0 | 5.2 | 5.1 | 4.6 | 5.0 | 5.3 | 4.6 | 5.3 | (5.3) | 5.1 | (5.3) | 5.6 | (6.3) | 5.2 | (5.3) | 4.9 | 4.5 | 4.7 | 4.8 |
| 0 | 10 | 12.5 | 23.0 | 30.2 | 28.4 | 23.5 | 10.0 | 7.5 | 5.1 | 12.9 | (7.3) | 17.7 | (10.8) | 19.7 | (16.5) | 17.9 | (17.9) | 15.9 | 8.4 | 6.0 | 5.0 |
| 0 | 100 | 67.3 | 97.5 | 99.9 | 100.0 | 100.0 | 45.3 | 19.0 | 9.8 | 61.3 | (10.1) | 79.9 | (23.3) | 86.8 | (55.8) | 87.2 | (80.4) | 85.8 | 50.5 | 22.9 | 7.7 |
| 100 | 1 | 0.9 | 0.4 | 0.2 | 0.2 | 0.1 | 0.0 | 0.0 | 0.0 | 5.0 | (5.2) | 4.7 | (5.2) | 5.4 | (5.6) | 5.1 | (5.4) | 5.2 | 4.7 | 4.8 | 4.9 |
| 100 | 10 | 3.5 | 3.8 | 3.9 | 2.7 | 1.4 | 0.1 | 0.1 | 0.1 | 13.2 | (7.3) | 18.0 | (11.0) | 18.8 | (15.8) | 17.0 | (17.2) | 15.7 | 7.9 | 6.2 | 4.9 |
| 100 | 100 | 49.9 | 83.5 | 94.5 | 96.4 | 92.3 | 7.2 | 2.2 | 0.5 | 61.7 | (10.6) | 80.5 | (23.5) | 86.3 | (55.8) | 86.7 | (80.2) | 85.4 | 50.4 | 22.3 | 7.8 |
n = 100 and θ = R = 0.01 were assumed in the entire simulations. For the simulations with active gene conversion, we assumed C = 1 or c/μ = 100 with the average tract length ℓ = 100.
1The results when all chromosomes are presented in parentheses. See text for details.
First, we assumed no gene conversion, so that the expectation of π is 0.01 at equilibrium in all regions. Therefore, the sign of selection would be significantly reduced π from 0.01. The observed pattern is what we know from previous works on the reduction of polymorphism by a selective sweep (Kaplan et al. 1988, 1989; Braverman et al. 1995; Fay and Wu 2000; Andolfatto 2001; Kim and Stephan 2002; Przeworski 2002; Wright et al. 2005). The overall power increases with increasing the selection coefficient. When selection is weak (i.e., Ns = 1) the power is very weak (∼5%), but it dramatically increases as Ns increases. In the fixation process (i.e., p < 1), the power increases with increasing p, and the highest power is expected when the duplicate is fixed (i.e., p = 1 and t1 = 0, where t1 is the time since the fixation of the duplicate). Then, it decreases with increasing t1 as neutral mutations accumulate. This overall pattern holds for both the duplicated region and flanking region. The power is lower when π for the flanking region is computed for all chromosomes.
Gene conversion decreases the power of this test because the recovery of neutral polymorphism becomes quick as shown in Figures 3, 4, and 5. Another major effect of gene conversion is to increase the level of polymorphism at equilibrium. The null distribution of the amount of polymorphism is given by a function of the gene conversion rate, which is difficult to estimate from other genomic regions. Therefore, it is safe to perform the test using the null distribution by assuming no gene conversion as a proxy, which makes the test conservative. Table 1 shows that the power is overall decreased for the duplicated region, as expected. However, in the flanking region, where there is no conversion, the power is almost identical to that in the case of no gene conversion, indicating that more power is expected to detect selection for duplicates when using flanking regions.
Another potential factor in decreasing the power of the test is recurrent duplications. All power simulations so far assumed a single origin of the class D chromosomes, and much lower power is expected if the class D chromosomes are originated from multiple duplication events. Table 2 shows the results of power simulations using three different levels of the duplication rate, u = {1, 10, 100} × μ. As u increases, the power dramatically decreases; this applies whether gene conversion is active or not.
Table 2 . Proportion of replications (%) that rejected neutrality when recurrent duplication is allowed.
| Duplicated region |
Flaking region |
|||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before fixation p |
After fixation t1 |
Before fixation p |
After fixation t1 |
|||||||||||||||||||
| u/μ | c/μ | Ns | 0.25 | 0.5 | 0.75 | 0.9 | 0 | N | 2N | 4N | 0.25 | 0.5 | 0.75 | 0.9 | 0 | N | 2N | 4N | ||||
| 1 | 0 | 1 | 5.3 | 5.1 | 5.6 | 5.0 | 4.8 | 4.8 | 4.9 | 5.2 | 5.1 | (5.2) | 4.8 | (4.3) | 5.1 | (5.6) | 4.7 | (4.5) | 5.1 | 5.0 | 4.7 | 5.3 |
| 1 | 0 | 10 | 12.9 | 25.3 | 33.3 | 28.5 | 23.7 | 9.2 | 6.6 | 5.4 | 12.7 | (7.4) | 17.8 | (10.4) | 19.6 | (17.3) | 16.7 | (16.1) | 16.5 | 8.6 | 6.1 | 5.0 |
| 1 | 0 | 100 | 67.5 | 97.9 | 99.9 | 99.9 | 100.0 | 43.5 | 18.2 | 10.2 | 61.5 | (10.3) | 80.4 | (22.9) | 86.1 | (55.5) | 87.2 | (79.0) | 86.0 | 51.2 | 21.7 | 8.4 |
| 1 | 100 | 1 | 1.1 | 0.4 | 0.2 | 0.1 | 0.1 | 0.0 | 0.1 | 0.0 | 5.3 | (5.1) | 5.4 | (5.0) | 5.0 | (5.3) | 5.2 | (5.0) | 5.1 | 5.0 | 4.5 | 4.8 |
| 1 | 100 | 10 | 3.5 | 4.7 | 4.5 | 2.9 | 1.6 | 0.1 | 0.1 | 0.0 | 13.6 | (8.0) | 17.4 | (10.7) | 19.6 | (17.3) | 17.3 | (17.4) | 15.6 | 8.4 | 5.7 | 5.4 |
| 1 | 100 | 100 | 48.6 | 84.7 | 95.3 | 96.5 | 92.0 | 6.7 | 1.9 | 0.5 | 61.9 | (10.4) | 80.4 | (22.1) | 86.4 | (55.2) | 87.1 | (79.1) | 85.3 | 51.1 | 22.7 | 8.5 |
| 10 | 0 | 1 | 5.0 | 4.7 | 5.2 | 4.0 | 4.1 | 4.2 | 4.4 | 5.0 | 4.7 | (5.2) | 4.7 | (4.8) | 4.8 | (5.2) | 4.6 | (4.5) | 4.6 | 4.3 | 4.5 | 4.8 |
| 10 | 0 | 10 | 12.4 | 22.9 | 30. | 25.3 | 20.8 | 9.0 | 6.0 | 5.2 | 12.4 | (7.1) | 16.7 | (10.4) | 17.6 | (15.8) | 15.1 | (15.2) | 15.1 | 8.2 | 5.7 | 5.4 |
| 10 | 0 | 100 | 65.7 | 96.3 | 99.1 | 99.3 | 99.0 | 44.2 | 18.6 | 10.2 | 61.0 | (10.8) | 80.3 | (21.7) | 85.8 | (56.5) | 86.0 | (78.3) | 85.1 | 50.5 | 23.3 | 8.3 |
| 10 | 100 | 1 | 1.1 | 0.5 | 0.3 | 0.2 | 0.1 | 0.0 | 0.0 | 0.0 | 4.9 | (5.1) | 4.8 | (4.6) | 5.0 | (6.1) | 4.4 | (4.3) | 4.9 | 5.1 | 4.5 | 5.0 |
| 10 | 100 | 10 | 3.6 | 4.1 | 4.1 | 2.5 | 1.4 | 0.2 | 0.1 | 0.0 | 12.2 | (7.5) | 17.7 | (10.6) | 18.1 | (15.9) | 16.1 | (15.9) | 14.9 | 8.3 | 5.9 | 5.4 |
| 10 | 100 | 100 | 47.6 | 83.1 | 94.4 | 95.6 | 90.4 | 6.4 | 2.1 | 0.4 | 60.5 | (10.8) | 79.3 | (21.4) | 85.5 | (54.7) | 86.2 | (78.7) | 84.6 | 51.3 | 21.4 | 8.8 |
| 100 | 0 | 1 | 3.2 | 2.0 | 1.1 | 0.7 | 0.6 | 2.2 | 3.1 | 4.5 | 3.6 | (5.5) | 2.5 | (5.5) | 2.6 | (5.1) | 1.9 | (2.8) | 2.0 | 3.6 | 4.0 | 4.8 |
| 100 | 0 | 10 | 8.5 | 10.5 | 11.5 | 6.9 | 4.7 | 5.0 | 4.7 | 5.0 | 9.8 | (7.6) | 11.2 | (9.6) | 11.6 | (13.6) | 8.4 | (10.3) | 7.6 | 5.7 | 5.5 | 5.4 |
| 100 | 0 | 100 | 57.4 | 82.5 | 90.4 | 91.2 | 87.8 | 38.1 | 15.8 | 9.2 | 55.7 | (10.4) | 74.4 | (21.8) | 80.2 | (51.3) | 81.0 | (72.8) | 78.4 | 45.5 | 19.7 | 7.5 |
| 100 | 100 | 1 | 0.8 | 0.3 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.8 | (6.1) | 2.9 | (5.5) | 2.2 | (5.0) | 2.0 | (2.9) | 1.9 | 3.4 | 3.9 | 5.1 |
| 100 | 100 | 10 | 2.4 | 2.6 | 1.9 | 1.0 | 0.5 | 0.1 | 0.1 | 0.0 | 9.6 | (7.2) | 11.3 | (9.2) | 11.0 | (13.0) | 8.4 | (10.1) | 7.3 | 5.4 | 5.1 | 5.4 |
| 100 | 100 | 100 | 41.1 | 69.7 | 82.9 | 84.7 | 74.9 | 5.7 | 2.1 | 0.3 | 55.7 | (9.8) | 74.1 | (21.4) | 80.2 | (51.3) | 81.2 | (72.7) | 77.5 | 45.1 | 20.0 | 7.5 |
Null distributions were generated assuming no recurrent duplication (see text for details). All parameters are the same as those in Table 1 except for allowing recurrent duplications.
Discussion
To understand the selective forces behind the evolution of a gene family, it is crucial to understand the pattern of polymorphism in the copy members (e.g., Innan and Kondrashov 2010). We here developed a coalescent tool with which to simulate patterns of SNPs in a wide region encompassing both original and duplicated regions, which enabled us to explore how selection on the duplicated copy affects the pattern of SNPs. The model basically follows the standard coalescent with recombination (Hudson 1983). A bialletic treatment is used to handle selection (Hudson and Kaplan 1988; Kaplan et al. 1988; Kaplan et al. 1989; Braverman et al. 1995; Barton 1998; Fay and Wu 2000; Kim and Stephan 2002; Przeworski 2002, 2003; Innan and Kim 2004), where the coalescent process is structured into two allelic classes, and selection determines the trajectory of the allelic frequency. The model also incorporates interlocus gene conversion between the original and duplicated regions, which creates a complicated pattern of SNPs (Innan 2003; Thornton 2007).
Using this model, we investigated the change of the level of SNP’s measure by π through the fixation of a newly arisen advantageous duplicated copy. As theoretically expected, if the duplication rate is very low and there is no gene conversion, the simulation results were consistent with what was predicted by the standard selective sweep model (Fay and Wu 2000; Kim and Stephan 2002; Przeworski 2002). That is, the fixation of a duplicate causes a strong reduction in π not only in the duplicated copy but also in its flanking regions. This effect is stronger when the selective coefficient is larger. After fixation, π gradually increases by accumulating neutral mutations and eventually reaches the expected value, θ. Therefore, as demonstrated in Table 1, it is possible to detect the signature of selection from the reduction of π, for a relatively short time after the fixation.
This simple predication does not hold when gene conversion is active. The major role of gene conversion is to shuffle SNPs between the paralogous regions, thereby averaging the levels of SNPs in the two regions. This leveling-off effect is particularly notable when one (original copy) has a sufficient amount of SNPs and the other (duplicated copy) does not. The number of SNPs in the duplicated copy quickly increases by transferring SNPs from the original copy; therefore, the time when we can recognize the signature of selection is decreased (Figures 3, 4, and 5). However, as gene conversion works only within the regions with paralogous sequences, use of the flanking region to the duplicated copy is suggested to avoid the effect of gene conversion.
It should be noted that when there is no gene conversion, the power of other commonly used test statistics (e.g., Tajima 1989; Fu and Li 1993; Fay and Wu 2000) is as previously reported, although the results are not shown here. The effect of gene conversion on these statistics were also investigated (Innan 2003; Thornton 2007), which demonstrated that the effect is not as much as that on the level of polymorphism. Therefore, in this article, we particularly focused on the behavior of π.
Another factor in reducing the power to detect selection is recurrent duplications, which directly increases SNPs within the duplicated copy. In our model, we assumed that recurrent duplications occur such that duplicated copies are inserted at the exact same location. Under this setting, unlike gene conversion, the level of SNPs is also increased in the flanking regions to the duplicate copy, so that it is difficult to avoid this effect. We understand that this is an oversimplified setting, but at least for some cases, this assumption can be justified. Well-known examples are Charcot–Marie–Tooth type 1 disease (CMT1A) and hereditary neuropathy with liability to pressure palsies (HNPP). Both CMT1A and HNPP are common inherited disorders of the peripheral nervous system. It is known that the majority of the CMT1A patients have tandem duplications at chromosome 17p11.2, while most HNPP patients have a deletion of the same region. The duplication and the deletion are reciprocally produced by an unequal crossing over between flanking repeat sequence called CMT1A-REP (Lupski et al. 1996; Timmerman et al. 1997). If duplicated copies are inserted into different genomic locations, they should have different flanking regions. In such a situation, looking at the patterns of SNP in those flanking regions should be most informative to understanding the role of selection.
Our model can be flexible to extending to more complicated ones, which would be future potential projects. For example, if recurrent duplications to different genomic locations are allowed, it is necessary to trace the ancestral recombination graph at all potential sites where duplicates can be inserted. This modification also enables the handling of CNVs with more than two copies. Deletion would be another important factor to be considered in CNVs with multiple copies. Such models make us able to obtain more specific insights into the evolutionary mechanisms behind CNVs. The C-code used in this study is available through the lab web: http://www.sendou.soken.ac.jp/esb/innan/InnanLab/
Acknowledgments
This work is supported from Japan Society for the Promotion of Science (JSPS), Japan Science and Technology Agency (JST), National Science Foundation, National Institutes of Health, and an internal grant of the Graduate University for Advanced Studies to H.I. K.M.T. is also supported by a grant from JSPS.
Footnotes
Communicating editor: Y. S. Song
Literature Cited
- Andolfatto P., 2001. Adaptive hitchhiking effects on genome variability. Curr. Opin. Genet. Dev. 11: 635–641 [DOI] [PubMed] [Google Scholar]
- Bailey J. A., Gu Z., Clark R. A., Reinert K., Samonte R. V., et al. , 2002. Recent segmental duplications in the human genome. Science 297: 1003–1007 [DOI] [PubMed] [Google Scholar]
- Barton N. H., 1998. The effect of hitch-hiking on neutral genealogies. Genet. Res. 72: 123–133 [Google Scholar]
- Biswas S., Akey J. M., 2006. Genomic insights into positive selection. Trends Genet. 22: 437–446 [DOI] [PubMed] [Google Scholar]
- Blanc G., Wolfe K. H., 2004. Widespread paleopolyploidy in model plant species inferred from age distributions of duplicate genes. Plant Cell 16: 1667–1678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braverman J. M., Hudson R. R., Kaplan N. L., Langley C. H., Stephan W., 1995. The hitchhiking effect on the site frequency spectrum of DNA polymorphisms. Genetics 140: 783–796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conrad D. F., Andrews T. D., Carter N. P., Hurles M. E., Pritchard J. K., 2006. A high-resolution survey of deletion polymorphism in the human genome. Nat. Genet. 38: 75–81 [DOI] [PubMed] [Google Scholar]
- Ewens W. J., 2004. Mathematical Population Genetics. Springer, New York [Google Scholar]
- Ewing G., Hermisson J., 2010. MSMS: a coalescent simulation program including recombination, demographic structure and selection at a single locus. Bioinformatics 26: 2064–2065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fay J. C., Wu C.-I., 2000. Hitchhiking under positive darwinian selection. Genetics 155: 1405–1413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Y.-X., Li W.-H., 1993. Statistical tests of neutrality of mutation. Genetics 133: 693–709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez E., Kulkarni H., Bolivar H., Mangano A., Sanchez R., et al. , 2005. The influence of CCL3L1 gene-containing segmental duplications on HIV-1/AIDS susceptibility. Science 307: 1434–1440 [DOI] [PubMed] [Google Scholar]
- Harr B., Kauer M., Schlotterer C., 2002. Hitchhiking mapping: a population-based fine-mapping strategy for adaptive mutations in Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 99: 12949–12954 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartl D. L., Clark A. G., 2006. Principles of Population Genetics. Sinauer, Sunderland, MA [Google Scholar]
- Hudson R. R., 1983. Properties of a neutral allele model with intragenic recombination. Theor. Popul. Biol. 23: 183–201 [DOI] [PubMed] [Google Scholar]
- Hudson R. R., 1991. Gene genealogies and the coalescent process, pp. 1–44 in Oxford Surveys in Evolutionary Biology, Vol. 7, edited by Futuyma D., Antonovics J. Oxford University Press, Oxford [Google Scholar]
- Hudson R. R., 2002. Generating samples under a Wright–Fisher neutral model of genetic variation. Bioinformatics 18: 337–338 [DOI] [PubMed] [Google Scholar]
- Hudson R. R., Kaplan N. L., 1988. The coalescent process in models with selection and recombination. Genetics 120: 831–840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iafrate A. J., Feuk L., Rivera M. N., Listewnik M. L., Donahoe P. K., et al. , 2004. Detection of large-scale variation in the human genome. Nat. Genet. 36: 949–951 [DOI] [PubMed] [Google Scholar]
- Innan H., 2002. A method for estimating the mutation, gene conversion and recombination parameters in small multigene families. Genetics 161: 865–872 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Innan H., 2003. The coalescent and infinite-site model of a small multigene family. Genetics 163: 803–810 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Innan H., Kim Y., 2004. Pattern of polymorphism after strong artificial selection in a domestication event. Proc. Natl. Acad. Sci. USA 101: 10667–10672 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Innan H., Kondrashov F., 2010. The evolution of gene duplications: classifying and distinguishing between models. Nat. Rev. Genet. 11: 97–108 [DOI] [PubMed] [Google Scholar]
- Innan H., Tajima F., 1997. The amounts of nucleotide variation within and between allelic classes and the reconstruction of the common ancestral sequence in a population. Genetics 147: 1431–1444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji Y., Eichler E. E., Schwartz S., Nicholls R. D., 2000. Structure of chromosomal duplicons and their role in mediating human genomic disorders. Genome Res. 10: 597–610 [DOI] [PubMed] [Google Scholar]
- Kaplan N. L., Darden T., Hudson R. R., 1988. The coalescent process in models with selection. Genetics 120: 819–829 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaplan N. L., Hudson R. R., Langley C. H., 1989. The “hitchhiking effect” revisited. Genetics 123: 887–899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y., Stephan W., 2002. Detecting a local signature of genetic hitchhiking along a recombining chromosome. Genetics 160: 765–777 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreitman M., 2000. Methods to detect selection in populations with applications to the human. Annu. Rev. Genomics Hum. Genet. 1: 539–559 [DOI] [PubMed] [Google Scholar]
- Locke D. P., Sharp A., McCarroll S., McGrath S., Newman T., et al. , 2006. Linkage disequilibrium and heritability of copy-number polymorphisms within duplicated regions of the human genome. Am. J. Hum. Genet. 79: 275–290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lupski J. R., 1998. Genomic disorders: structural features of the genome can lead to DNA rearrangements and human disease traits. Trends Genet. 14: 417–422 [DOI] [PubMed] [Google Scholar]
- Lupski J. R., Stankiewicz P., 2005. Genomic disorders: molecular mechanisms for rearrangements and conveyed phenotypes. PLoS Genet. 1: e49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lupski J. R., Roth J. R., Weinstock G. M., 1996. Chromosomal duplications in bacteria, fruit flies, and humans. Am. J. Hum. Genet. 58: 21–27 [PMC free article] [PubMed] [Google Scholar]
- Lynch M., Conery J. S., 2000. The evolutionary fate and consequences of duplicate genes. Science 290: 1151–1155 [DOI] [PubMed] [Google Scholar]
- Mansai S. P., Kado T., Innan H., 2011. The rate and tract length of gene conversion between duplicated genes. Genes 2: 313–331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R., 2005. Molecular signatures of natural selection. Annu. Rev. Genet. 39: 197–218 [DOI] [PubMed] [Google Scholar]
- Norris B. J., Whan V. A., 2008. A gene duplication affecting expression of the ovine ASIP gene is responsible for white and black sheep. Genome Res. 18: 1282–1293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohno S., 1970. Evolution by Gene Duplication. Springer-Verlag, Amsterdam [Google Scholar]
- Perry G. H., Dominy N. J., Claw K. G., Lee A. S., Fiegler H., et al. , 2007. Diet and the evolution of human amylase gene copy number variation. Nat. Genet. 39: 1256–1260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Przeworski M., 2002. The signature of positive selection at randomly chosen loci. Genetics 160: 1179–1189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Przeworski M., 2003. Estimating the time since the fixation of a beneficial allele. Genetics 164: 1667–1676 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redon R., Ishikawa S., Fitch K. R., Feuk L., Perry G. H., et al. , 2006. Global variation in copy number in the human genome. Nature 444: 444–454 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sebat J., Lakshmi B., Troge J., Alexander J., Young J., et al. , 2004. Large-scale copy number polymorphism in the human genome. Science 305: 525–528 [DOI] [PubMed] [Google Scholar]
- Sharp A. J., Locke D., McGrath S., Cheng Z., Bailey J., et al. , 2005. Segmental duplications and copy-number variation in the human genome. Am. J. Hum. Genet. 77: 78–88 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp A. J., Hansen S., Selzer R. R., Cheng Z., Regan R., et al. , 2006. Discovery of previously unidentified genomic disorders from the duplication architecture of the human genome. Nat. Genet. 38: 1038–1042 [DOI] [PubMed] [Google Scholar]
- Spencer C. C., Coop G., 2004. SelSim: a program to simulate population genetic data with natural selection and recombination. Bioinformatics 20: 3673–3675 [DOI] [PubMed] [Google Scholar]
- Stankiewicz P., Lupski J. R., 2002. Genome architecture, rearrangements and genomic disorders. Trends Genet. 18: 74–82 [DOI] [PubMed] [Google Scholar]
- Tajima F., 1989. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123: 585–595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima F., 1990. Relationship between DNA polymorphism and fixation time. Genetics 125: 447–454 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teshima K. M., Innan H., 2004. The effect of gene conversion on the divergence between duplicated genes. Genetics 166: 1553–1560 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teshima K. M., Innan H., 2009. mbs: modifying Hudson’s ms software to generate samples of DNA sequences with a biallelic site under selection. BMC Bioinformatics 10: 166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton K. R., 2007. The neutral coalescent process for recent gene duplications and copy-number variants. Genetics 177: 987–1000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timmerman V., Rautenstrauss B., Reiter L. T., Koeuth T., Lofgren A., et al. , 1997. Detection of the CMT1A/HNPP recombination hotspot in unrelated patients of European descent. J. Med. Genet. 34: 43–49 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh B., 2003. Population-genetic models of the fates of duplicate genes. Genetica 118: 279–294 [PubMed] [Google Scholar]
- Wright D., Boije H., Meadows J. R., Bed’hom B., Gourichon D., et al. , 2009. Copy number variation in intron 1 of SOX5 causes the Pea-comb phenotype in chickens. PLoS Genet. 5: e1000512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. I., Bi I. V., Schroeder S. G., Yamasaki M., Doebley J. F., et al. , 2005. The effects of artificial selection on the maize genome. Science 308: 1310–1314 [DOI] [PubMed] [Google Scholar]