A two-stage strategy to accommodate general patterns of confounding in the design of observational studies

Abstract

Accommodating general patterns of confounding in sample size/power calculations for observational studies is extremely challenging, both technically and scientifically. While employing previously implemented sample size/power tools is appealing, they typically ignore important aspects of the design/data structure. In this paper, we show that sample size/power calculations that ignore confounding can be much more unreliable than is conventionally thought; using real data from the US state of North Carolina, naive calculations yield sample size estimates that are half those obtained when confounding is appropriately acknowledged. Unfortunately, eliciting realistic design parameters for confounding mechanisms is difficult. To overcome this, we propose a novel two-stage strategy for observational study design that can accommodate arbitrary patterns of confounding. At the first stage, researchers establish bounds for power that facilitate the decision of whether or not to initiate the study. At the second stage, internal pilot data are used to estimate key scientific inputs that can be used to obtain realistic sample size/power. Our results indicate that the strategy is effective at replicating gold standard calculations based on knowing the true confounding mechanism. Finally, we show that consideration of the nature of confounding is a crucial aspect of the elicitation process; depending on whether the confounder is positively or negatively associated with the exposure of interest and outcome, naive power calculations can either under or overestimate the required sample size. Throughout, simulation is advocated as the only general means to obtain realistic estimates of statistical power; we describe, and provide in an R package, a simple algorithm for estimating power for a case–control study.

1. INTRODUCTION

The design of observational studies is complex, typically requiring close collaboration between the biostatistician and other scientists to develop strategies to account for numerous potential challenges, including accommodating missing and/or censored data, measurement error, and adjusting for correlation in repeated measures studies. One of the most important scientific challenges is the identification and control of confounding. As such, when planning an observational study, researchers often spend a great deal of time considering potential confounders, deciding which should be measured and planning analyses to ensure appropriate adjustment. Together with substantive knowledge about the underlying mechanisms, causal diagrams are a useful tool at this stage of the design process (Greenland and others, 1999a), (Pearl, 2000).

While there is a vast literature on the consequences of ignoring confounding when analyzing data from observational studies, little research has been devoted to understanding the consequences of ignoring, or not fully accommodating, confounding at the design stage. In this paper, we highlight and examine a number of important considerations for the design of an observational study. First, we show that differences between estimates of power obtained by erroneously assuming some simplified model that ignores confounding and those obtained assuming an appropriately adjusted model, referred to as “structural misspecification,” can be substantially greater than is conventionally thought. These differences can have important implications for the potential success of the study and we argue that the use of formula- based sample size/power calculations for observational studies may be unwise. Second, to overcome the difficulty of eliciting realistic design parameters for the confounding mechanism, we propose a novel two-stage strategy for observational study design that can accommodate arbitrary patterns of confounding. The key feature of the strategy is that internal pilot data are used to estimate design parameters for the confounding mechanism that are then used to obtain realistic estimates of sample size/power. Third, we show that consideration of the nature of confounding is a crucial aspect of the elicitation process. Specifically, depending on whether the confounder is positively or negatively associated with the exposure and outcome, naive power calculations can either severely under- or overestimate the required sample size.

2. INFANT MORTALITY STUDY

The methods and ideas of this paper pertain to study design. To ground this work in a real-life example, we use data compiled by the North Carolina State Center for Health Statistics (http://www.irss.unc.edu/) and consider planning a hypothetical study of the impact of the race on infant mortality, adjusting for a range of established potential confounders (e.g. Michielutte and others, 1994, Iyasu, 2002, Schempf and others, 2007). For simplicity, we restrict attention to comparing births where the race of the baby was indicated as either Caucasian or African-American.

2.1. Designing a case–control study

In the United States, infant mortality (defined as death within the first year of life) is rare, and we therefore consider the case–control design for our hypothetical study (Prentice and Pyke, 1979, Breslow and Day, 1980). Let X be an indicator of race (0/1 = Caucasian/African-American) and Z = {Z₁,…,Z_p} a collection of p potential confounders. Given data collected via the case–control design, valid and efficient estimation of odds ratio parameters is achieved by fitting a logistic regression model of the form:

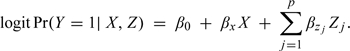(2.1)

We refer to (2.1) as the “fully adjusted” model and emphasize that it is the model that is of scientific interest. That is, it is assumed that all relevant confounders have been identified a priori and model (2.1) has been specified as the primary model of interest in the proposed study analysis plan.

2.2. Sample size/power calculations

Once all relevant confounders have been identified and the analysis plan developed, the key statistical task is to estimate sample size/power with respect to the parameter of interest: β_x = log(θ_x), the log odds ratio for the exposure. Ideally, this calculation explicitly accommodates all features of the proposed design/analysis, although this can be extremely challenging for an observational study. From a technical perspective, methods for sample size/power that simultaneously accommodate the various elements of the analysis plan are typically unavailable and difficult to develop or implement. From a scientific perspective, such methods require greater input from subject matter experts. For example, power calculations based on model (2.1) require information on the joint exposure/confounder distribution, Pr(X,Z₁,…,Z_p), as well as the confounder effects, {β_z1,…,β_zp}; Table SM-1 in the supplementary material (available at Biostatistics online) document provides summary information on these design parameters for p = 6 confounders based on all 225 152 births and 1752 infant deaths in North Carolina in 2003–2004.

When designing an observational study, detailed prior information on Pr(X,Z₁,…,Z_p) and {β_z1,…,β_zp} will typically not be readily available. Furthermore, elicitation of realistic values from collaborators can be very difficult and employing some existing sample size/power tool is a convenient alternative. For our hypothetical case–control study, one could base calculations on the following two-sample formula:

(2.2)

where n₀ and n₁ are the number of controls and cases, respectively, π₀ = Pr(X = 1|Y = 0) is the exposure prevalence in the noncase population, π₁ = Pr(X = 1|Y = 1) = π₀θ_x/{1 + π₀[θ_x − 1]} is the exposure prevalence in the case population and $\stackrel{-}{\pi }=({\pi }_0+{\pi }_1)/2$.

Use of expression (2.2) is appealing in that it is simple to implement and only requires specification of two scientific quantities: π₀ and θ_x. However, the analysis that underlies (2.2) ignores potential confounding and, in particular, corresponds to following “unadjusted” logistic regression model:

(2.3)

To calculate sample size corresponding to the adjusted analysis, one could apply a so-called variance inflation factor. Hsieh and others (1998) showed that for linear and (prospective) logistic regression, one can simply adjust the sample size by a function of the partial correlation coefficient for X given Z. As a general technique, however, the approach is limited in that the specific form of the variance inflation factor was derived under the assumption of multivariate normality for the joint distribution of [X, Z]. Furthermore, the factor does not accommodate the nature of the association between the confounders and the outcome (i.e. the direction and magnitude of §{β_z1,…,β_zp}) which, as we elaborate upon below, is crucial for appropriate power calculation.

More generally, sample size/power formulae have been developed for a range of case–control settings including matched designs, when there are 2 or 3 (categorical or normally distributed continuous) confounders and when effect modification is of interest (e.g. Foppa and Spiegelman, 1997, Edwardes, 2001, Gauderman, 2002, Tosteson and others, 2003, Vaeth and Skovlund, 2004, Sinha and Mukerjee, 2006, Demidenko, 2006, 2007, Novikov and others, 2009). However, to our knowledge, no formula-based sample size/power technique permits the complexity that is inherent in the fully adjusted analysis characterized by (2.1). This is particularly the case since Z is a mixture of discrete and continuous covariates, with no prespecified distributional assumptions. As such, the adoption of any formula-based approach will result in a discrepancy analogous to that between models (2.1) and (2.3). A key statistical concern when performing sample size/power calculations, therefore, is the extent to which the discrepancy between the simplified (unadjusted) and proposed (fully adjusted) analyses impacts the sample size/power calculations and, consequently, the potential success of the study. In the next section, we examine this discrepancy using the infant mortality data.

3. DISCREPANT POWER ESTIMATION

3.1. Structural misspecification

From the perspective of confounder adjustment, basing sample size/power calculations on (2.3) can be viewed in terms of misspecification of the relationships that govern the extent, magnitude, and direction of the impact of confounding. We refer to this phenomenon as structural misspecification.

Clearly, model (2.3) is the strongest form of structural misspecification for our case–control study; all p = 6 confounders are completely ignored. To examine the impact of varying degrees of structural misspecification, we also considered the following “partially adjusted” models:

(3.4)

(3.5)

Model (3.4) solely adjusts for the binary low birth weight covariate (LBW, defined as less than 2500 g) and model (3.5) solely adjusts for the continuous gestational duration covariate.

3.2. Scientific inputs

In the supplementary material (available at Biostatistics online) document, we provide a simulation-based algorithm for estimating power for a case–control study. As with all algorithms, a series of inputs are required. Given a model specification (i.e. any of models (2.1), (2.3), (3.4), and (3.5)), these inputs include (i) the overall outcome prevalence, ${\stackrel{\sim }{\pi }}_y$ (ii) for any potential confounders included in the model, the relationships governing confounding Pr(X,Z₁,…,Z_p) and {β_z1,…,β_zp}, and (iii) the anticipated (clinically relevant) effect size, β_x.

To retain focus on structural misspecification, with the exception of β_x, these inputs were set at the “true” values observed in the complete data (see Table SM-1, supplementary material available at Biostatistics online). For example, across all model/simulation settings, we tailor the value of the intercept to a fixed outcome prevalence of ${\stackrel{\sim }{\pi }}_y$ = 1752/225 152 ≈ 0.0078. For the unadjusted model, we set the exposure prevalence to be Pr(X = 1) = 0.236; for the two partially adjusted models, (3.4) and (3.5), we generated simulated data sets based on the observed Pr(X,Z₅) and Pr(X,Z₆), respectively, and using ${\widehat{\beta }}_{z_5}$ and ${\widehat{\beta }}_{z_6}$ based on a fit of the full data. Power calculations based on the fully adjusted model also used the observed structures in the complete data; hence, these power estimates are based on the “gold standard” situation where everything is known about the joint distribution Pr(Y,X,Z₁,…,Z₆) except for β_x.

Across all four models, we fixed the value of θ_x = exp(β_x) = 1.3. While the interpretation and numerical values of β_x in each of the four models will generally differ, we emphasize that the goal of this section is the investigation of the impact of structural misspecification of confounding on estimates of power. That is we seek to understand how, beyond numerical differences in the parameters, misspecification of the statistical model underlying the calculations can severely bias the sample size/power estimates. This reflects the setting where researchers may plug in reasonable values for the target parameter (i.e. β_x in model (2.1)) into an overly simplistic model. We return to the issue of interpretational and numerical differences in the β_x parameters and their implications for discrepant power estimates, in Section 5.

3.3. Discrepant estimates

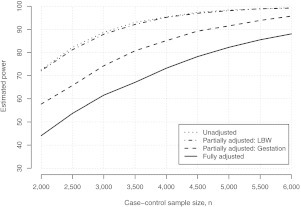
Figure 1 presents estimated power curves for detecting an odds ratio of θ_x = 1.3 under a balanced case–control study, as a function of the case–control sample size n. There is a clear substantial discrepancy in estimated power to detect θ_x = 1.3 between calculations based on the unadjusted and fully adjusted models. We find that to have at least 80% power to detect θ_x = 1.3, power calculations based on the naive unadjusted model would conclude that the study needs to enroll approximately n = 2500 individuals. However, enrolling n = 2500 individuals would only provide an estimated 55% power, based on the appropriate fully adjusted model. Furthermore, to ensure at least 80% power to detect θ_x = 1.3, the study would need to enroll approximately n = 4750 individuals; almost twice the sample size indicated by the calculations based on the unadjusted model. We note that, for these data, the variance inflation factor is 1.05; hence, applying the approach of Hsieh and others (1998), one erroneously concludes that n = 2650 would be sufficient to ensure 80% power. The discrepancy is, in part, explained by the VIF being a poor approximation, for these data at least, of the ratio of the variances of the MLEs for the adjusted analysis and unadjusted analyses. Finally, the conclusions one would draw based on model (3.4) are similar to those based on the unadjusted model, whereas those based on (3.5) are intermediary.

Fig. 1.

Estimated power curves for detecting θ_x = 1.3 under a balanced case–control study, as a function of the case–control sample size n = n₀ + n₁. Each curve corresponds to a model that forms the basis for the power calculation (Sections 2.2 and 3.1). Estimates were obtained using the algorithm in the supplementary material (available at Biostatistics online) with R = 10000.

4. TWO-STAGE SAMPLE SIZE/POWER CALCULATIONS

Section 3 showed that structural misspecification can have a substantial impact on sample size/power calculations. In this particular setting, the substantial overestimation of power would have important implications for the potential success of the study. Furthermore, the estimates based on the partially adjusted models, models (3.4) and (3.5), indicate that the discrepancy in power is not simply a function of having to estimate additional parameters. The nature of the confounder and its relationships with both the exposure of interest and the outcome play an important role. While results are specific to the infant mortality example, it is reasonably representative of a typical observation study; 6 potential confounders are not unusual (and may be low) and the confounders themselves are a mix of continuous and categorical, with varying strengths of association between both the exposure and the outcome.

Based on these results, and our experience in other settings, we believe that the reliance on formula-based approaches for sample size/power calculations in observational studies may be unwise and advocate the use of simulation. For the case–control design, the algorithm outlined in the supplementary material (available at Biostatistics online) is simple and easily implemented. However, the elicitation of required scientific inputs, from subject matter collaborators or the scientific literature, presents a challenging problem. While the specification of β_x is required for all sample size/power calculations, the additional need for realistic elicitation of the joint exposure/confounder distribution, Pr(X,Z₁,…,Z_p), and the direction/magnitudes of the confounder coefficients, {β_z1,…,β_zp}, renders the task all the more difficult. This will be particularly so when p is greater than 3 or 4, as might be expected in a typical observational study.

In some circumstances, researchers may have access to pilot data that can inform these inputs. Ideally, the pilot data would consist of information on all important exposures/confounders and be specific to the population under investigation. This will not always be the case though. Indeed, the present study may be motivated by previous investigations not having been comprehensive in their adjustment of confounding or having been conducted in different populations. Towards taking advantage of pilot data while resolving this difficulty, we propose the following two-stage framework for simulation-based sample size/power calculations in observational studies:

• (I) During the design and proposal development phase, establish bounds for sample size/power across a range of scenarios concerning confounding. These bounds are used to inform the potential success of the study and, consequently, the decision of whether or not the study should funded.

• (II) Assuming the study is initiated, as data collection proceeds, use accrued information as internal pilot data to inform realistic estimates of Pr(X,Z₁,…,Z₆) and {β_z1,…,β_zp}. Use these estimates to refine the power calculations.

4.1. Stage I: establish bounds for sample size/power

During the design and proposal development phase, sample size/power calculations are used to provide evidence of the potential success of the study. Practically, this is often done by estimating power across a range of potential sample sizes as well as varying scenarios for the effect size(s). As is clear from Section 3, obtaining realistic estimates of power for an observational study must account for the eventual need to control for confounding. In the absence of comprehensive, realistic information on Pr(X,Z₁,…,Z₆) and {β_z1,…,β_zp}, the only reasonable strategy is to examine a range of scenarios for potential confounding. In essence, perform a sensitivity analysis to investigate the number of potential confounders as well as the nature of the confounding (i.e. strength and/or direction).

Table 1 provides a illustrative sensitivity analysis for the infant mortality example. Specifically, it presents estimated power to detect θ_x = 1.3 based on a case–control study with n₀ = n₁ = 1750. Throughout we take the exposure prevalence to be E[X] = 0.2, approximately that observed for race in the North Carolina data. Each row represents a scenario regarding the underlying structures that govern confounding and adjustment for {Z₁,…,Z_p}, for p = 1,…,6. For each scenario, we examine the cumulative impact of sequentially incorporating up to p = 6 potential confounders; Z₁, Z₃, and Z₅ are continuous and distributed according to a Normal (0, 1); Z₂, Z₄, and Z₆ are binary with E[Z_j] = 0.2. In the supplementary material (available at Biostatistics online), we provide a simple approach to generating {X,Z₁,…,Z₆} with these features, based on an latent multivariate normal distribution. Finally, the results of Table 1 assume independence across the Z_j.

Table 1.

Initial estimated bounds for power to detect an odds ratio (OR) of θ_x = 1.3, based on a case–control design with n₀ = n₁ = 1750. The exposure of interest, X, is binary with E[X] = 0.2. Up to 6 confounders are considered; zero confounders corresponds to an unadjusted analysis. Estimates were obtained using the algorithm in the supplementary material (available at Biostatistics online) with R = 10 000

	OR between	OR between	Number of confounders, p
Scenario	Zj and X, ϕxzj	Zj and Y, θzj	0	1	2	3	4	5	6
Constant strength
1. Weak	1.5	1.5	89	89	88	87	87	86	86
2. Moderate	2.0	2.0	89	86	86	82	81	77	76
3. Strong	2.5	2.5	89	84	83	76	73	63	59
Diminishing strength
4. Moderate	3.0 → 1.5	3.0 → 1.5	89	82	80	75	74	71	71
5. Strong	4.0 → 1.5	4.0 → 1.5	90	78	74	65	62	59	59

Scenarios 1–3 consider “constant” confounding in that each confounder has the same odds ratio relationship with both the exposure, denoted ϕ_xzj, and the same relationship with the outcome, denoted θ_zj. Note, for continuous confounders, ϕ_xzj is based on a unit change in Z_j. The results indicate lower estimates of power as one sequentially incorporates the 6 potential confounders, with the impact increasing as the strength of confounding increases. For example, assuming moderate constant confounding (ϕ_xzj = θ_zj = 2.0), basing calculations on a model that incorporates all 6 confounders, one would conclude that the design only has approximately 76% power to detect θ_x = 1.3. This is in contrast to the estimated 89% power that one would conclude the study to have had the calculations been based on the naive unadjusted model (see the first column of Table 1 with p = 0).

While scenarios 1–3 may provide useful bounds, to assume that all 6 potential confounders have equally strong relationships with both the exposure and outcome is realistic. It may therefore be of interest to permit the strength of confounding to vary across the Z_j. Scenarios 4 and 5 assume the associations between {Z₁,…,Z₆} and both the exposure and outcome to diminish. For each row, the 6 confounders are incorporated from the strongest to the weakest. Table 1 indicates that, under two reasonable scenarios, by incorporating all 6 confounders into the power analysis, we would conclude that a case–control design with n₀ = n₁ = 1750 would have between 60% and 70% power to detect θ_x = 1.3.

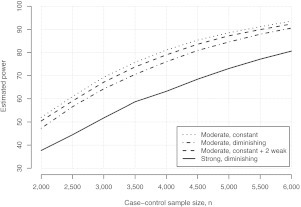
In addition to examining sensitivity to the number of potential confounders, and their strength/direction, it will typically be of interest to examine sensitivity to sample size, n. Figure 2 presents estimated power curves under four confounder scenarios. These include scenarios 2, 4, and 5 from Table 1 and an additional scenario that consists of 8 confounders; the first 6 have moderate constant strength of ϕ_xzj = θ_zj = 2.0, while the last two have weaker strength of ϕ_xzj = θ_zj = 1.5. Based on these four scenarios, the study would need to collect between 4000 and 6000 case–control samples to have at least 80% power to detect θ_x = 1.3.

Fig. 2.

Estimated bounds for power to detect θ_x = 1.3, based on a case–control design, as a function of case–control sample size n for various scenarios for confounding. Estimates were obtained using the algorithm in the supplementary material (available at Biostatistics online) with R = 10000.

We emphasize that the results of Table 1 and Figure 2 are illustrative in that they present a limited range of potential confounding scenarios; in practice, researchers will likely need to run a broader range. For example, one could also investigate the consequences of modifying the marginal characteristics of the confounders (i.e. the prevalence for binary confounders and/or the variance for the continuous confounders) or the consequences of introducing dependence between the confounders. We examined the latter by repeating the simulation of Table 1 assuming moderate (common) correlation in the latent multivariate normal distribution: corr(Z_j,Z_k) = 0.25. Although details are not presented, we found that, for the scenarios we consider, there is generally a reduction in estimated power, although it typically did not exceed more than 5%.

4.2. Stage II: internal pilot data

Within the proposed strategy, the purpose of Stage I is to inform the decision of whether or not to initiate the study by establishing realistic bounds for sample size/power across a range of scenarios for potential confounding. Assuming the study goes forward, data are collected as participants are enrolled and the study progresses. Prior to the final analysis (where estimation and inference with respect to the exposure of interest is performed), the accrued data can be viewed as “internal pilot data” that can then be used to refine the calculations. Specifically, updated estimates of sample size/power can be obtained by using the internal pilot data to inform steps (a) and (b) of the algorithm in the supplementary material (available at Biostatistics online).

Suppose the internal pilot data consist of a case–control sample of size m. Step (a) of the algorithm requires constructing a (hypothetical) population of size N, with joint exposure/confounder distribution Pr(X,Z₁,…,Z₆). However, under the traditional case–control design, one observes random samples from the outcome-specific joint exposure/confounder distributions. We denote these as ${\widehat{Pr}}_0(X,Z_1,\dots ,Z_6)$ and ${\widehat{Pr}}_1(X,Z_1,\dots ,Z_6)$ for the controls and cases, respectively. To generate a population of size N in step (a) with Pr(X,Z₁,…,Z₆), we sample $(1-{\stackrel{\sim }{\pi }}_y)N$ individuals with replacement from ${\widehat{Pr}}_0(X,Z_1,\dots ,Z_6)$ and ${\stackrel{\sim }{\pi }}_{y}N$ individuals with replacement from ${\widehat{Pr}}_1(X,Z_1,\dots ,Z_6)$, where ${\stackrel{\sim }{\pi }}_y=Pr(Y=1)$ is the overall outcome prevalence. For step (b) of the algorithm, estimates of the confounder effects, $\{{\widehat{\beta }}_{z_1},\dots ,{\widehat{\beta }}_{z_6}\}$, are obtained via a fit of the fully adjusted model (2.1) to the pilot case–control data. Recall, this model is the one that would be specified in the study analysis plan and, hence, is the ideal model for power calculations.

We examined this strategy in the context of estimating power to detect θ_x = 1.3 in the infant mortality example, under on a balanced case–control design. Figure 3 presents estimated power curves, as a function of n, for 4 independent realizations of the approach using m = 250, m = 500, and m = 1000. That is, each subfigure presents simulation-based estimates of power that one would have seen had the study been initiated, data collection begun and estimates of Pr(X,Z₁,…,Z₆) and {β_z1,…,β_z6} obtained at each of the three internal pilot sample sizes. As m increases, we mimicked reality by adding to the previous samples. So the pilot data with m = 500 consists of the original m = 250 subsamples together with an additional 250 subsamples. Throughout, we took controls and cases to be accrued in parallel (i.e. m₁ = m₀ = m/2) and estimates of power were based on the fully adjusted model. For comparison, each subfigure also shows the unadjusted and “fully adjusted” power curves from Figure 1. The latter represents the gold standard in that it is the power curve that uses estimates of Pr(X,Z₁,…,Z₆) and {β_z1,…,β_zp} based on the complete data (i.e. all 223 400 births) and on the appropriate model (i.e. model (2.1)).

Fig. 3.

Results from four independent realizations of stage II, with pilot data sample sizes of m = 250, m = 500, and m = 1000. In each subfigure, power curves based on complete data (CD) for the unadjusted and fully adjusted models. Estimates were obtained using the algorithm in the supplementary material (available at Biostatistics online) with R = 10000.

We find that for three of four realizations, power estimates based on internal pilot data with as little as m = 250 are already close to those based on the complete data. In all cases, estimates based on the pilot data are much closer to the gold standard than to the naive power curves that ignore confounding. Finally, as m increases, the estimated power curves get closer to the gold standard. To further examine the operating characteristics of the process, we ran a total of 1000 implementations of stage II for the infant mortality data. For a balanced case–control design with n = 5000, the mean estimated power is approximately 77%, 79%, and 81% based on m = 250, m = 500, and m = 1000, respectively (see Figure SM-1 of the supplementary material, available at Biostatistics online). Even with relatively small m (5% or 10% of n = 5000), calculations based on internal pilot data provide a much more realistic assessment of power than naive calculations based on the unadjusted model. From Figure 1, basing power calculations on the unadjusted model would indicate approximately 98% power for n = 5000. Basing power on the fully adjusted model and knowing the actual Pr(X,Z₁,…,Z₆) and {β_z1,…,β_z6} would indicate 82% power. As one would expect, as m increases, the additional precision in characterizing the underlying Pr(X,Z₁,…,Z₆) translates into increased precision for the estimation of power. Across the 1000 repetitions, the standard deviation of the estimated power is 8.1%, 6.0%, and 4.1% for m = 250, m = 500, and m = 1000, respectively.

4.3. Caveat regarding the specification of β_x

The key advantage of using the internal pilot data is that it provides direct comprehensive information on key scientific quantities for the population of interest that can then be used in refined power calculations. However, without modifications to the basic design, one cannot use the accrued stage II internal pilot data to obtain an estimate of β_x for use in the refined calculations. By only conditioning on $\widehat{Pr}(X,Z_1,\dots ,Z_6)$ and $\{{\widehat{\beta }}_{z_1},\dots ,{\widehat{\beta }}_{z_6}\}$, the nominal type I error rate is maintained since no interim information regarding β_x is used for study progression. This is analogous to group sequential testing in which only estimates of variability are used for maintaining study power but the probability of study discontinuation is zero at all interim analyses (Lan and DeMets, 1983; Burington and Emerson, 2003). In contrast, by conditioning on ${\widehat{\beta }}_x$ in stage II, the nominal type I error rate is not maintained and repeated inferential assessments with respect to β_x may lead to a situation where one samples to a foregone conclusion: one of statistical significance (Berry, 1987). Group sequential methods provide a framework within which information from ${\widehat{\beta }}_x$ may be used.

5. DISCREPANT TARGETS OF ESTIMATION/INFERENCE

Section 4 outlines a strategy to overcome the challenging problem of specifying design parameters for confounding when performing sample size/power calculations for an observational study. In addition to Pr(X,Z₁,…,Z_p) and {β_z1,…,β_zp}, sample size/power calculations also require specification of the effect size β_x. However, as noted in Section 3.2, the interpretation and numerical of β_x differs across models. Such differences may have important implications for the elicitation process where researchers often appeal to the pilot studies or the published literature to inform scientifically relevant effect sizes and yet ignore discrepancies between the analyses that underlie such studies and those proposed in their grant. To emphasize differences in parameter interpretation, we introduce more specific notation for the unadjusted and fully adjusted models as follows:

(5.6)

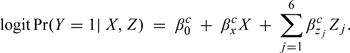(5.7)

The superscript “m” in model (5.6) highlights that the interpretation of β_x^m is marginal with respect to adjustment for Z. In model (5.7), the superscript “c” highlights that the interpretation of β_x^c is “conditional” on Z. Note this parameter corresponds to β_x in model (2.1) and is therefore the parameter of primary scientific interest for the hypothetical case–control study. Finally, for notational convenience, we let θ_x^m = exp{β_x^m} and θ_x^c = exp{β_x^c} denote the marginal and conditional odds ratio parameters, respectively.

Assuming a (marginal) exposure prevalence of Pr(X = 1) = 0.2, basing calculations on the marginal model (5.6), one would conclude that n₀ = n₁ = 2500 provides approximately 78% power to detect θ_x^m = 1.3. We refer to this as the “apparent” power of the study in that it ignores the eventual need to adjust for confounding. Beyond the consequences of structural misspecification, this naive power calculation also ignores fundamental differences between θ_x^m and θ_x^c. Specifically, while interpretational differences are not relevant for study design (since scientific interest solely lies in the model eventually fit as part of the final study analyses), numerical differences between θ_x^m and θ_x^c will be relevant. In the next two sections, we explore the relationship between the two parameters and the implications for sample size/power.

5.1. Relationship between marginal and conditional parameters

The notation of models (5.6) and (5.7) highlight that θ_x^m and θ_x^c are fundamentally different parameters with differing interpretations. The extent to which the parameters differ numerically depends on the Z–Y and Z–X relationships. When Z is independent of the outcome (i.e. β_z^c = 0), model (5.7) reduces to model (5.6) and θ_x^m≡θ_x^c numerically; in this case, Z is not a confounder in the usual sense (e.g. Greenland and others, 2008). In the presence of confounding, however, θ_x^m and θ_x^c will differ. To see this, suppose X in models (5.6) and (5.7) is binary. The marginal odds ratio θ_x^m is defined as

(5.8)

Each of the probabilities in (5.8) can be written as

(5.9)

Inspection of expression (5.9) reveals that the values of θ_x^m and θ_x^c are directly related via the Pr(Y = y|X = x,Z = z) terms. Unfortunately, the exact nature of the relationship between θ_x^m and θ_x^c is complex. For simplicity, we consider a single binary Z and calculate the value of θ_x^c for a given θ_x^m using expressions (5.8) and (5.9). The calculation requires specification of Pr(Y = y|X = x,Z = z) and Pr(Z = z|X = x). The former is given by model (5.7); we parameterize the latter via two quantities: (i) the probability of the confounder among the unexposed, Pr(Z = 1|X = 0), which we fix at 0.2, and (ii) the odds ratio association between X and Z, denoted by ϕ_xz, which is permitted to vary between 0.33 and 3.00. We also varied θ_z^c between 0.33 and 3.00 and, for any given confounding scenario, set the value of β₀^c such that the (marginal) outcome prevalence was Pr(Y = 1) = 0.05 (see Section B of the supplementary material, available at Biostatistics online).

The top half of Table 2 provides the values of θ_x^c that corresponds to θ_x^m = 1.3, under a range of scenarios for potential confounding. As expected, if θ_z^c = 1.0, then θ_x^c = θ_x^m = 1.3. For the settings considered in Table 2, the same occurs when ϕ_xz = 1.0, although this is not generally the case. Specifically, due to the nonlinearity of the logistic function, if θ_z^c≠1.0, then θ_x^m≠θ_x^c even if ϕ_xz = 1.0 (and Z is, therefore, not a confounder), a phenomenon referred to as “non-collapsibility” (Greenland and others, 1999b; Janes and others, 2010). For a rare outcome, however, the strength of the Z–Y relationship needs to be quite strong for meaningful differences between θ_x^m and θ_x^c, as evidenced by Table 2. For common outcomes, the strength of the Z–Y relationship does not have to be as strong for differences to manifest (Schoenfeld and Borenstein, 2005).

Table 2.

Value of the conditional odds ratio, θ^c_x, (top half) and corresponding estimates of actual power (bottom half), based on a case–control study with n₀ = n₁ = 1250, for an assumed marginal effect size of θ^m_x = 1.3, under various scenarios for the strength of confounding. The (marginal) outcome and exposure prevalences are Pr(Y = 1) = 0.05 and Pr(X = 1) = 0.2, respectively, and the (conditional) confounder prevalence among the unexposed is fixed at Pr(Z = 1|X = 0) = 0.2

	Confounder/exposure odds ratio, ϕxz
Confounder effect, θcz	0.33	0.50	0.67	1.00	1.50	2.00	3.00
Conditional odds ratio, θcx
0.33	1.19	1.22	1.25	1.30	1.38	1.44	1.57
0.50	1.22	1.24	1.26	1.30	1.35	1.40	1.49
0.67	1.25	1.26	1.27	1.30	1.33	1.36	1.42
1.00	1.30	1.30	1.30	1.30	1.30	1.30	1.30
1.50	1.38	1.36	1.34	1.30	1.26	1.23	1.18
2.00	1.45	1.41	1.37	1.30	1.23	1.17	1.10
3.00	1.59	1.49	1.42	1.30	1.18	1.09	0.98
Estimated actual power
0.33	41	52	62	77	90	96	100
0.50	51	59	66	77	88	94	98
0.67	61	66	71	78	84	89	93
1.00	76	77	77	78	78	77	76
1.50	90	88	84	78	66	55	38
2.00	96	94	89	76	55	36	15
3.00	100	98	94	76	38	15	5

Arguably, the impact of confounding is of most concern when the magnitude of the adjusted parameter is smaller than that of the unadjusted parameter: θ_x^c < θ_x^m. From Table 2, we see this occurs when the directions of the Z–Y and Z–X associations are the same; Z is either positively or negatively associated with both Y and X. For example, if θ_z^c = ϕ_xz = 2.0, then θ_x^c = 1.17 or if θ_z^c = 0.33 and ϕ_xz = 0.50, then θ_x^c = 1.22, both of which are less than θ_x^m = 1.3. However, if the directions differ, then the numerical value of the adjusted parameter is greater than that of the unadjusted parameter: θ_x^c > θ_x^m. For example, if θ_z^c = 2.00 (i.e. the confounder is positively associated with “risk” of outcome) and ϕ_xz = 0.33 (i.e. confounder is negatively associated with the “risk” of exposure), then θ_x^c = 1.45 > θ_x^m = 1.3.

5.2. Implications for sample size/power calculations

While the results of Section 3 show that structural misspecification of the model that underlies power calculations can lead to erroneous estimates of power, numerical differences between θ_x^m and θ_x^c can also have important ramifications for estimation of sample size/power. To see this, within the simple setting of Section 5.1, suppose that θ_z^c = ϕ_xz = 2.0. As noted in Table 2, for θ_x^m = 1.3, the true value of θ_x^c is 1.17. At the design stage, the ideal calculations would acknowledge the impact of confounding on the numerical value of the target parameter. Based on (5.7), the lower half of Table 2 indicates that a case–control study with n₀ = n₁ = 1250 would only provide approximately 36% power to detect θ_x^c = 1.17. We refer to this as the “actual” power of the study and contrast it with the estimated 78% apparent power to detect θ_x^m = 1.3. If the confounding is somewhat weaker with θ_z^c = ϕ_xz = 1.5, then an appropriate power calculation would indicate that n₀ = n₁ = 1250 provides an estimated 66% actual power to detect θ_x^c = 1.26.

As we have noted, for the simple setting of a single binary confounder, if the directions of the Z–Y and Z–X relationships differ then, θ_x^c > θ_x^m. For example, suppose θ_z^c = 2.00 and ϕ_xz = 0.33. From the upper half of Table 2, the true value of θ_x^c is 1.45. From the lower half, we find that the estimated actual power to detect θ_x^c = 1.45 is 96%. This can also be contrasted with the estimated apparent power of 78% to detect θ_x^m = 1.3. We therefore find that the actual power to detect θ_x^c maybe larger or smaller than the apparent power to detect θ_x^m.

5.3. Implications for elicitation

While the proposed two-stage strategy provides researchers with a framework for specifying realistic design parameters for the confounding mechanism, biostatisticians will still be required to specify numerical values for the hypothesized effect size. Eliciting scientifically relevant effect sizes from collaborators can be difficult and one must often appeal to the published literature or to external pilot data. In doing so, it is important to understand the structure and setting of the studies that yielded this information and, in particular, how they differ from the study currently being designed. For example, suppose the current study is motivated by the desire to build on previous work in which the control of confounding was found to be inadequate. Or, suppose the current study was preceded by a small pilot study that, due to financial constraints, did not collect comprehensive confounder information. In either of these settings, the available information may suggest a value for the hypothesized effect size that more closely corresponds θ_x^m than θ_x^c. As we have shown, differences between θ_x^m and θ_x^c can have important implications for sample size/power calculations, particularly since the conditional (adjusted) parameter may be smaller or larger than the marginal (unadjusted) parameter, depending on the nature of the confounding.

6. DISCUSSION

Using a realistic hypothetical case–control study, we have shown that ignoring confounding when designing an observational study can lead to substantial differences in estimates of sample size/power, which may influence the decision to initiate the study and its potential success. At best, this may result in an inefficient use of resources if the study is ultimately overpowered; at worst, the study is underpowered and is unable to discriminate between relevant scientific hypotheses. We have proposed a two-stage framework that permits the use of internal pilot data to better inform realistic design parameters and, therefore, yield realistic estimates of power and assessments of sample size. The structure of the two-stage framework permits researchers to update estimates of Pr(X,Z₁,…,Z₆) and {β_z1,…,β_z6} as the study progresses. Assuming inference with respect to the parameter of interest, β_x, is not conducted, there is no penalty paid for the repeated reassessment of Pr(X,Z₁,…,Z₆) and {β_z1,…,β_z6}. We are currently extending the strategy to exploit group sequential methods for randomized clinical trials to permit interim analyses with respect to β_x.

Based on the results in this paper and our observations in other settings, we believe that, except in trivial settings, the use of formula-based techniques for sample size/power calculations in observational study design is unwise and we advocate simulation-based estimation of power. The use of simulation, however, is subject to numerous challenges. Practically, there are technical challenges in that software will typically have to be developed and tailored to specific settings and, depending on the desired level of precision for the estimates, the calculations may require longer computing times. For the setting of a case–control study, we have provided a simple algorithm for calculating power (as well as other operating characteristics). The algorithm is implemented in the osDesign package for R (Haneuse and others, 2011).

Finally, we emphasize that a key strength of both simulation and the data-oriented two-stage strategy is its flexibility beyond logistic regression analyses of case–control studies. Indeed, the methods presented here could easily be applied to other common designs and analyses. The osDesign package, for example, has an algorithm for the two-phase study design (Breslow and Chatterjee, 1999). Furthermore, the methods can easily be expanded to accommodate common statistical challenges, such as missingness and correlation, that often have a large impact on study power.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

National Institutes of Health (R01 CA125081 and R03 CA135671).